- 1Department of Physics, Zhejiang Normal University, Jinhua, ZJ, China
- 2Center for Phononics and Thermal Energy Science, China-EU Joint Laboratory on Nanophononics, Shanghai Key Laboratory of Special Artificial Microstructure Materials and Technology, School of Physics Science and Engineering, Tongji University, Shanghai, China
Nonequilibrium thermal transport in circuit quantum electrodynamics emerges as one interdisciplinary field, due to the tremendous advance of quantum technology. Here, we study steady-state heat flow in a two-mode qubit-resonator model under the influence of both the qubit-resonator and resonator-resonator interactions. The heat current is suppressed and enhanced by tuning up resonator-resonator interaction strength with given weak and strong qubit-resonator couplings respectively, which is cooperative contributed by the eigen-mode of coupled resonators and qubit-photon scattering. Negative differential thermal conductance and significant thermal rectification are exhibited at weak qubit-resonator coupling, which are dominated by cycle transition processes. Moreover, the heat flow through the resonator decoupled from the qubit can be dramatically enhanced via the resonator-resonator interaction, which is attributed by the generation of eigen-mode channels of resonators.
Introduction
The microscopic interaction between bosonic fields (e.g., light and vibration) and quantum matter plays a cornerstone role in the study of quantum optics [1–4], quantum phononics [5, 6], and quantum technology [7–9]. The significant advance of superconducting and quantum-dot circuit quantum electrodynamics (cQED) fertilizes nonequilibrium heat transport in light-matter interacting systems, by integrating cQED components (e.g., resonator and qubit) with thermal and electric reservoirs [10–16]. Bounded by the second law of thermodynamics, the heat flow can be modulated via the nonequilibrium temperature bias [10], geometric heat pump [17, 18], and quantum correlations [19].
The seminal quantum Rabi model (QRM) is one generic system to describe quantum light-matter interaction, i.e., a single-mode photon field transversely coupled with a two-level qubit. QRM nowdays has been extensively realized in various quantum systems, ranging from quantum electrodynamics [2, 20], trapped ions [21, 22], and semiconductors with spin-orbital coupling [23]. Theoretically, though the eigensolution is rather difficult to obtain, D. Braak [24] and Chen et al. [25] separately proposed mapping ways a decade ago, trying to achieve the exact solution of QRM. While considering the interface between the subsystems in cQED and mesoscopic thermal reservoirs, the powerful platform to detect steady-state heat transport has been established [10, 12] to deepen the understanding of quantum thermodynamics, condensed-matter physics, and functional thermal devices. The analogous setup nowadays can also be found in optomechanics [26]. As a consequence, theoretical studies of quantum thermal transport in two-bath QRM have been preliminarily carried out [27–29].
Meanwhile, the longitudinal qubit-resonator model, as an alternative representative system, was also experimentally realized based on cQED devices [30–32], which is able to reach quite strong qubit-resonator coupling. Such longitudinal interaction leads to tremendous intriguing applications, e.g., generation of nonclassical photon states [33, 34], scalable quantum computation [35], and efficient quantum readout [36, 37]. Moreover, as a basic member in the multi-mode qubit-resonator family [30, 38, 39], the two-mode qubit-resonator model has been designed in cQED with longitudinal coupling [40–42], which is able to exhibit quantum switch effect [43]. While for nonequilibrium thermal transport in the longitudinal qubit-resonator system, an inspiring cooling by heating effect was reported, which causes the photon antibunchinig [44]. Besides, several typical nonlinear thermal effects were also proposed [45–47]. Hence, it should be intriguing to explore the transport pictures and microscopic mechanisms in the dissipative two-mode qubit-resonator model.
In this work, we apply the quantum dressed master equation (DME) combined with coherent photon states to study the steady-state heat current of the dissipative two-mode qubit-resonator model. The main points of this study are listed as follows: 1) The steady-state heat flow is suppressed under the influence of the resonator-resonator interaction with given weak qubit-resonator coupling, whereas it is enhanced by increasing the resonator-resonator interaction strength at strong qubit-resonator coupling, which is unavailable for the single-mode qubit-resonator model [29, 45]. The underlying mechanisms are illustrated based on the eigen-modes of resonators (4) and coherent state overlap coefficient (15). 2) The nonlinear thermal effects, e.g., negative differential thermal conductance and thermal rectification are unraveled in weak qubit-resonator coupling regime. They are attributed by two kinds of cycle transition processes (20a-20 b), which fertilizes microscopic transport pictures in the single-mode qubit-resonator model. 3) The resonator-resonator interaction induced indirect heat transport is also investigated. It is interesting to find that at the condition of identical resonators, even weak resonator-resonator interaction can significantly enhance heat current via the resonator isolated from the qubit, due to the eigen-modes of resonators.
The paper is organized as follows: In Section 2 we introduce the two-mode qubit-resonator model, obtain the corresponding eigenvalues and coherent photon eigenstates, and derive the DME. In Section 3 we study steady-state heat current under the influence of both qubit-resonator interaction and resonator-resonator coupling. Typical nonlinear thermal effects and resonator-resonator induced indirect heat transport is discussed. Finally, we give a summary in Section 4.
Model and method
Two-mode qubit-resonator model
The Hamiltonian of the longitudinal two-mode qubit-resonator system, composed of one two-level qubit longitudinally coupled with two optical resonators in Figure 1A, reads
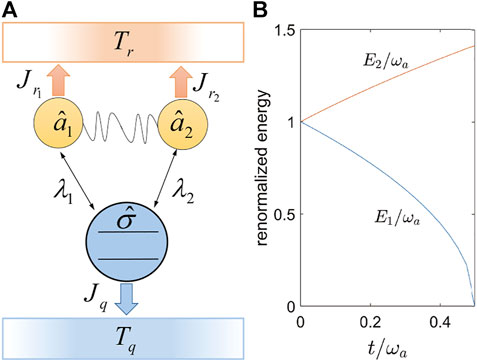
FIGURE 1. (Color online) (A) Schematic illustration of the nonequilibrium two-mode qubit-resonator model. The yellow circle marked with
Where
Next, we try to obtain the eigenvalues and eigenstates of the Hamiltonian (Section 1). Specifically, if we include the coordinate and momentum operators of the resonators as
Hence, the Hamiltonian (Section 1) is reexpressed as
where
under the bound
With θ1 = θ, θ2 = θ + π. The constant coefficient in Eq. 3 is ignored for safety for dissipative dynamics and steady state. Hence, the eigenstates are expressed as
with σ = {↑, ↓},
with ɛ↑ = ɛ, ɛ↓ = −ɛ, and n = [n1, n2] (ni = 0, 1, 2, ⋯ ). In absence of t, the eigen-energy Ei (4) is reduced to ωi, and the modified coupling strengths become
Quantum dressed master equation
In practice, the quantum system inevitably interacts with surrounding environments. Hence, the qubit and optical resonators may individually interact with bosonic thermal baths. Accordingly, the total Hamiltonian, including the quantum system, thermal reservoirs, and their interactions, is expressed as
Specifically, the r-th thermal reservoir connecting is described as
where
with gk,q being the coupling strength, which is characterized as the spectral functions γq(ω) = 2π|gk,q|2δ(ω − ωk). We select the Ohmic case of the spectral functions in this work, i.e., γu(ω) = αuω exp( − |ω|/ωc), with αu the dissipation strength and ωc the cutoff frequency.
Then, we assume the interactions between the quantum system and thermal reservoirs are weak. Under the Born-Makov approximation, we may properly perturb them to obtain the quantum master equation within the eigenstate basis of
Where
The transition rate contributed by the i-th resonator and r-th reservoir is described as
By considering relations
Where Θ(x) = 1 for x > 0 and Θ(x) = 0 for x ≤ 0, the coherent state overlap coefficient is specified as [54, 55].
and the Bose-Einstein distribution function is given by
The transition rate 13) involved with the r-th thermal reservoir and the i-th resonator is individual contributed by two eigen-mode channels, (i.e.,
Based on DME (11), the steady-state heat current mediated by the subsystem component (resonators and qubit) into the corresponding thermal reservoir is expressed as
Where the dynamical equation of the density matrix element is given by
Results and discussions
Steady-state heat current
We first study the influence of resonator-resonator coupling t on the behavior of steady-state heat current into the q-th thermal reservoir in Figure 2A. Before the analysis, we approximately characterize the weak couplings as t/ωa≲0.01 and λ/ωa≲0.01, which may fulfill the relations t/ωa≪1 and λ/ωa≪1. While for strong couplings, we quantify as t/ωa≳0.2 and λ/ωa≳1, where multi-photon processes may be included. In the weak qubit-resonator coupling regime with a given λ/ωa, Jq is monotonically suppressed by tuning the resonator-resonator interaction strength. On the contrary, at strong qubit-resonator coupling the heat current is dramatically enhanced by increasing t. Furthermore, Jq generally exhibits nonmonotonic behavior with the increase of the qubit-resonator interaction strength. We also give a comprehensive picture of the effects of both qubit-resonator and resonator-resonator couplings on the heat current in Figure 2B. It is shown that at strong λ and large t the optimal regime of Jq is broadened compared to the one with t = 0. Hence, we conclude that the resonator-resonator interaction indeed significantly contributes to the steady-state heat current.
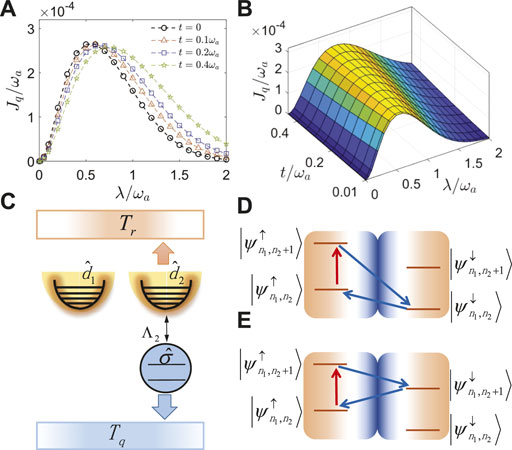
FIGURE 2. (Color online) (A) Steady state heat current Jq/ωa as a function of the qubit-resonator interaction strength λ/ωa, with typical resonator-resonator couplings t/ωa. (B) Heat current Jq/ωa as functions of λ/ωa and t/ωa. (C) Schematic illustration of the Hamiltonian at Eq. 3 with Λ1 = 0. (D) and (E) are cyclic current components in Eq. 20a and Eq. 20b, respectively. Other system parameters are given by ɛ = ωa, λ1 = λ2 = λ, α1 = α2 = 0.001ωa, ωc = 20ωa, Tr = 1.5ωa, and Tq = 0.5ωa.
Next, we try to analyze the heat current from the analytical view. Based on the case of identical resonators we set in Figure 2, the modified qubit-resonator coupling strengths (5a) and (5 b) are specified as Λ1 = 0 and
At weak qubit-resonator coupling (λ/ωa≪1), the coherent state overlap coefficient 15) with Λ2/E2≪1 is simplified as
And the zeroth order of steady state population is obtained as.
With βu = 1/kBTu. Moreover, if we reexpress the populations in the vector form |ρs⟩, the steady-state solution based on Eq. 11 becomes
where.
Which are described in Figure 2D,E. Physically, the loop of I1(E2) is established as
While at strong qubit-resonator coupling, e.g., λ/ωa≳1, qubit-photon scattering effects dominate the transition processes, which are characterized as the coefficient (15). Such analogous effects generally suppress the heat transport, as shown in Figure 2A and previous works, e.g., nonequilibrium spin-boson model [56–59] and quantum Rabi model [29]. In particular, the crucial factor to quantify such scattering is Λ2/E2. Thus, by increasing t it is found that the factor shows monotonic reduction. As a consequence, the scattering processes are weakened accordingly, which finally enhances the heat current. Therefore, we explain the underlying mechanisms of the influence of the resonator-resonator interaction on the heat current in weak and strong qubit-resonator coupling limits.
Negative differential thermal conductance and thermal rectification
Inspired by the cycle transition features of the steady state heat current with weak qubit-resonator interaction, we first study the negative differential thermal conductance (NDTC) in the two-mode qubit-resonator model. NDTC is widely considered as one generic nonlinear feature in nonequilibrium heat transport [60–64], which is characterized as the heat current, e.g., Jq, being reduced with the increase of the reservoir temperature bias ΔT = Tr − Tq. In phononics, NDTC was originally introduced by B. Li and his colleges to analyze heat flow in classical phononic lattices [63]. As a consequence, tremendous open quantum systems have been unraveled to exhibit NDTC. In particular, D. Segal [65] and Cao et al. [66] individually applied the noninteracting blip approximation and canonically transformed Redfield equation to explore the effect of NDTC with strong system-bath interactions. Ren et al. [67] included the spin-boson-fermion systems to propose spin-NDTC based on the Landauer formula expression of the heat current. Moreover, Giazotto et al. [68] designed the superconducting devices to measure NDTC by modulating the superconducting gap with the temperature.
Here, we show NDTC in the two-mode qubit-resonator model with identical resonators in Figure 3A. In absence of the resonator-resonator interaction, the heat current is reduced to
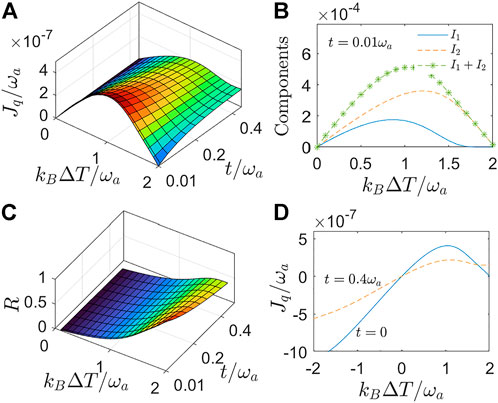
FIGURE 3. (Color online) (A) Steady-state heat current into the q-th reservoir Jq/ωa; (B) current components I1 (20a), I2 (20b), and I1 + I2 as functions of kBΔT/ωa at t = 0.01ωa; (C) thermal rectification factor R as a function of the temperature bias and resonator-resonator coupling strength; (D) the asymmetric behavior of heat current Jq/ωa by tuning kBΔT/ωa. Other system parameters are given by ω1 = ω2 = ωa, ɛ = ωa, λ1 = λ2 = 0.01ωa, α1 = α2 = 0.001ωa, ωc = 20ωa, Tr = ωa/kB + ΔT/2, and Tq = ωa/kB − ΔT/2.
We also study the thermal rectification effect by modulating the temperature bias, which is another representative nonlinear character in nonequilibrium thermal transport. The concept of thermal rectification is introduced as that the heat flow in one direction is larger than the counterpart in the opposite direction [63, 69]. We characterize the rectification by the factor
where Jq(ΔT) denotes the current under the setting of temperatures Tr = ωa/kB + ΔT/2 and Tq = ωa/kB − ΔT/2. Such effect becomes perfect as |Jq(ΔT)|≫|Jq( − ΔT)| (i.e., R = 1) and vanishing as Jq(ΔT) ≈ − Jq( − ΔT) (i.e., R = 0). Figure 3C clearly exhibits the giant heat amplification factor at large temperature bias, mainly due to the asymmetric behavior of heat current Jq by tuning ΔT from negative to positive regimes, as shown in Figure 3D. Specifically, the disappearance of the current at ΔT = 2ωa and t = 0 results in the perfect thermal rectifier, whereas the existence of resultant current at finite t comparatively reduces thermal rectification factor. Therefore, we conclude that microscopic cycle transition processes are crucial to exhibit NDTC and significant thermal rectification in two-mode qubit-resonator model.
Resonator-resonator coupling enhances heat transport
To show the ability of the resonator-resonator interaction to modulate the heat transport, we tune off the interaction between the 1-st resonator and the qubit, as shown in Figure 4A. Straightforwardly, the heat current
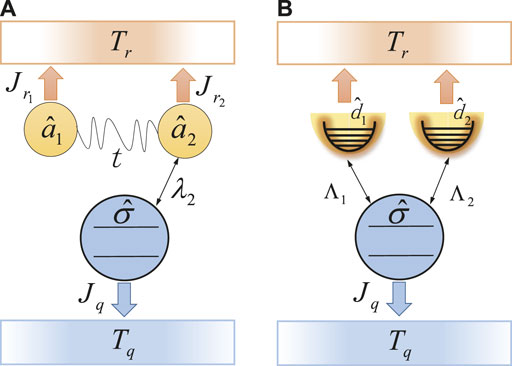
FIGURE 4. (Color online) (A) Schematic illustration of the two-mode qubit-resonator model with λ1 = 0 and (B) the corresponding eigen-mode model.
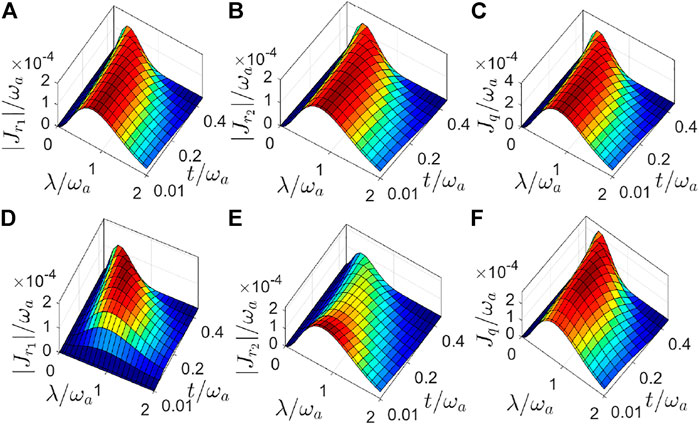
FIGURE 5. (Color online) Steady-state heat currents as functions of qubit-resonator (λ/ωa) and resonator-resonator (t/ωa) coupling strengths. We obtain (A–C) at ω1 = ω2 = ωa and (D–F) at ω1 = 0.9ωa and ω2 = 1.1ωa. Other system parameters are given by ɛ = ωa, λ1 = 0, λ2 = λ, α1 = α2 = 0.001ωa, ωc = 20ωa, Tr = 1.5ωa, and Tq = 0.5ωa.
Moreover, we analyze the effect of the resonator-resonator interaction on
Conclusion
To summarize, we study nonequilibrium thermal transport in the dissipative two-mode qubit-resonator model by applying quantum DME combined with extended coherent photon states, where optical resonators and the qubit are individually coupled with thermal reservoirs. By properly treating the resonator-resonator interaction, we obtain the eigensolution of the two-mode qubit-resonator model. Then, we analyze the influence of the qubit-resonator coupling and resonator-resonator interaction on steady-state behaviors of heat currents. The currents are suppressed with the increase of resonator-resonator interaction strength at weak qubit-resonator coupling. It mainly results from the eigen-mode energies of coupled resonators (4), based on the analytical expression of cycle heat current components (19). In contrast, the currents are monotonically enhanced in strong qubit-resonator coupling regime, which is mainly attributed to the reduction of the effective qubit-resonator coupling in Eq. 15 by tuning up resonator-resonator interaction strength. Hence, the resonator hybridization and the directional cycle transition processes cooperatively contribute to the nontrivial behaviors of steady-state heat currents.
Inspired by cycle transition components of heat current at weak qubit-resonator coupling, we also investigate two representative nonlinear thermal effects, i.e., NDTC and thermal rectification. NDTC is unraveled at large temperature bias and keeps robust even with strong resonator-resonator interaction strength. The microscopic cycle transition processes (20a) and (20b) determine the appearance of NDTC. Meanwhile, the significant thermal rectification effect is observed in a wide regime of qubit-resonator and resonator-resonator couplings, which becomes perfect in absence of the resonator-resonator interaction.
Moreover, we show the effect of the resonator-resonator interaction on indirectly heat transport, by tuning off the interaction between the 1-st resonator and the qubit. It is interesting to find that for identical resonators the heat current
We hope that the analysis of quantum heat transport and thermal management in the two-mode qubit-phonon system may provide physical insight for smart energy control in photon-based hybrid quantum systems. In the future, it should be intriguing to explore the steady-state heat flows in multi-mode qubit-resonator systems, e.g., three-mode qubit-resonator model [70].
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Author contributions
F-YW: analytical and numerical work, manuscript writing J-CL: numerical work ZW: analytical work CW: guiding project, analysis, manuscript writing JR: guiding project, analysis, manuscript writing.
Funding
F-YW, L-WD, and CW are supported by the National Natural Science Foundation of China under Grant No. 11704093 and the Opening Project of Shanghai Key Laboratory of Special Artificial Microstructure Materials and Technology. J-CL, ZW, and JR acknowledges the support by the National Natural Science Foundation of China (No. 11935010 and No. 11775159), Natural Science Foundation of Shanghai (No. 18ZR1442800 and No. 18JC1410900), and the China Postdoctoral Science Foundation (Grant No. 2020M681376).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
2. Forn-Diaz P, Lamata L, Rico E, Kono J, Solano E. Ultrastrong coupling regimes of light-matter interaction. Rev Mod Phys (2019) 91:025005. doi:10.1103/RevModPhys.91.025005
3. Kockum AF, Miranowicz A, De Liberato S, Savasta S, Nori F. Ultrastrong coupling between light and matter. Nat Rev Phys (2019) 1:19. doi:10.1038/s42254-018-0006-2
4. Blais A, Girvin SM, Oliver WD. Quantum information processing and quantum optics with circuit quantum electrodynamics. Nat Phys (2020) 16:247–56. doi:10.1038/s41567-020-0806-z
6. Gustafsson MV, Santos PV, Johansson G, Delsing P. Local probing of propagating acoustic waves in a gigahertz echo chamber. Nat Phys (2012) 8:338–43. doi:10.1038/nphys2217
7. Wallquist M, Hammerer K, Rabl P, Lukin M, Zoller P. Hybrid quantum devices and quantum engineering. Phys Scr (2009) T137:014001. doi:10.1088/0031-8949/2009/t137/014001
8. Kurizki G, Bertet P, Kubo Y, Molmer K, Petrosyan D, Rabl P, et al. Quantum technologies with hybrid systems. Proc Natl Acad Sci U S A (2015) 112:3866–73. doi:10.1073/pnas.1419326112
9. Clerk AA, Lehnert KW, Bertet P, Petta JR, Nakamura Y. Hybrid quantum systems with circuit quantum electrodynamics. Nat Phys (2020) 16:257–67. doi:10.1038/s41567-020-0797-9
10. Ronzani A, Karimi B, Senior J, Chang YC, Peltonen JT, Chen CD, et al. Tunable photonic heat transport in a quantum heat valve. Nat Phys (2018) 14:991–5. doi:10.1038/s41567-018-0199-4
11. Senior J, Gubaydullin A, Karimi B, Peltonen JT, Ankerhold J, Pekola JP, et al. Heat rectification via a superconducting artificial atom. Commun Phys (2020) 3:40. doi:10.1038/s42005-020-0307-5
12. Pekola JP, Karimi B. Colloquium: quantum heat transport in condensed matter systems. Rev Mod Phys (2021) 93:041001. doi:10.1103/revmodphys.93.041001
13. Gubaydullin A, Thomas G, Golubev DS, Lvov D, Peltonen JT, Pekola JP, et al. Photonic heat transport in three terminal superconducting circuit. Nat Commun (2022) 13:1552. doi:10.1038/s41467-022-29078-x
14. Delbecq MR, Schmitt V, Parmentier FD, Roch N, Viennot JJ, Fve G, et al. Coupling a quantum dot, fermionic leads, and a microwave cavity on a chip. Phys Rev Lett (2011) 107:256804. doi:10.1103/physrevlett.107.256804
15. Mi X, Cady JV, Zajac DM, Deelman PW, Petta JR. Strong coupling of a single electron in silicon to a microwave photon. Science (2016) 355:156–8. doi:10.1126/science.aal2469
16. Lu JC, Wang RQ, Ren J, Kulkarni M, Jiang JH. Quantum-dot circuit-QED thermoelectric diodes and transistors. Phys Rev B (2019) 99:035129. doi:10.1103/physrevb.99.035129
17. Ren J, Hanggi P, Li B. Berry-phase-induced heat pumping and its impact on the fluctuation theorem. Phys Rev Lett (2010) 104:170601. doi:10.1103/physrevlett.104.170601
18. Wang Z, Wang LQ, Chen JZ, Wang C, Ren J. Geometric heat pump: controlling thermal transport with time-dependent modulations. Front Phys (Beijing) (2022) 17:13201. doi:10.1007/s11467-021-1095-4
19. Micadei K, Peterson JPS, Souza AM, Sarthour RS, Oliveira IS, Landi GT, et al. Reversing the direction of heat flow using quantum correlations. Nat Commun (2019) 10:2456. doi:10.1038/s41467-019-10333-7
20. Haroche S, Brune M, Raimond JM. From cavity to circuit quantum electrodynamics. Nat Phys (2020) 16:243–6. doi:10.1038/s41567-020-0812-1
21. Pedernales JS, Lizuain I, Felicetti S, Romero G, Lamata L, Solano E, et al. Quantum Rabi model with trapped ions. Sci Rep (2015) 5:15472. doi:10.1038/srep15472
22. Cai ML, Liu ZD, Zhao WD, Wu YK, Mei QX, Jiang Y, et al. Observation of a quantum phase transition in the quantum rabi model with a single trapped ion. Nat Commun (2021) 12:1126. doi:10.1038/s41467-021-21425-8
23. Xie QT, Cui S, Cao JP, Amico L, Fan H. Anisotropic rabi model. Phys Rev X (2014) 4:021046. doi:10.1103/physrevx.4.021046
24. Braak D. Integrability of the rabi model. Phys Rev Lett (2011) 107:100401. doi:10.1103/physrevlett.107.100401
25. Chen QH, Wang C, He S, Liu T, Wang KL. Exact solvability of the quantum rabi model using bogoliubov operators. Phys Rev A (Coll Park) (2012) 86:023822. doi:10.1103/physreva.86.023822
26. Yang C, Wei XR, Sheng JT, Wu HB. Phonon heat transport in cavity-mediated optomechanical nanoresonators. Nat Commun (2020) 11:4656. doi:10.1038/s41467-020-18426-4
27. Yamamoto T, Kato T. Heat transport through a two-level system embedded between two harmonic resonators. J Phys : Condens Matter (2021) 33:395303. doi:10.1088/1361-648x/ac1281
28. Xu M, Stockburger JT, Ankerhold J. Heat transport through a superconducting artificial atom. Phys Rev B (2021) 103:104304. doi:10.1103/physrevb.103.104304
29. Chen ZH, Che HX, Chen ZK, Wang C, Ren J. Tuning nonequilibrium heat current and two-photon statistics via composite qubit-resonator interaction. Phys Rev Res (2022) 4:013152. doi:10.1103/physrevresearch.4.013152
30. Niemczyk T, Deppe F, Huebl H, Menzel EP, Hocke F, Schwarz MJ, et al. Circuit quantum electrodynamics in the ultrastrong-coupling regime. Nat Phys (2010) 6:772. doi:10.1038/nphys1730
31. Forn-Diaz P, Lisenfeld J, Marcos D, Garcia-Ripoll JJ, Solano E, Harmans CJPM, et al. Phys Rev Lett (2010) 105:237001.
32. Yoshihara F, Fuse T, Ashhab S, Kakuyanagi K, Saito S, Semba K, et al. Superconducting qubit–oscillator circuit beyond the ultrastrong-coupling regime. Nat Phys (2017) 13:44–7. doi:10.1038/nphys3906
33. Zhao YJ, Liu YL, Liu YX, Nori F. Generating nonclassical photon states via longitudinal couplings between superconducting qubits and microwave fields. Phys Rev A (Coll Park) (2015) 91:053820. doi:10.1103/physreva.91.053820
34. Wang X, Miranowicz A, Li HR, Nori F. Multiple-output microwave single-photon source using superconducting circuits with longitudinal and transverse couplings. Phys Rev A (Coll Park) (2016) 94:053858. doi:10.1103/physreva.94.053858
35. Richer S, DiVincenzo D. Circuit design implementing longitudinal coupling: a scalable scheme for superconducting qubits. Phys Rev B (2016) 93:134501. doi:10.1103/physrevb.93.134501
36. Didier N, Bourassa J, Blais A. Fast quantum nondemolition readout by parametric modulation of longitudinal qubit-oscillator interaction. Phys Rev Lett (2015) 115:203601. doi:10.1103/physrevlett.115.203601
37. Grimsmo AL, Smith TB. Majorana qubit readout using longitudinal qubit-resonator interaction. Phys Rev B (2019) 99:235420. doi:10.1103/physrevb.99.235420
38. Egger DJ, Wilhelm FK. Multimode circuit quantum electrodynamics with hybrid metamaterial transmission lines. Phys Rev Lett (2013) 111:163601. doi:10.1103/physrevlett.111.163601
39. Bosman SJ, Gely MF, Singh V, Bruno A, Bothner D, Steele GA, et al. Multi-mode ultra-strong coupling in circuit quantum electrodynamics. Npj Quan Inf (2017) 3:46. doi:10.1038/s41534-017-0046-y
40. Reuther GM, Zueco D, Deppe F, Hoffmann E, Menzel EP, Weißl T, et al. Two-resonator circuit quantum electrodynamics: dissipative theory. Phys Rev B (2010) 81:144510. doi:10.1103/physrevb.81.144510
41. Baust A, Hoffmann E, Haeberlein M, Schwarz MJ, Eder P, Goetz J, et al. Tunable and switchable coupling between two superconducting resonators. Phys Rev B (2015) 91:014515. doi:10.1103/physrevb.91.014515
42. Baust A, Hoffmann E, Haeberlein M, Schwarz MJ, Eder P, Goetz J, et al. Ultrastrong coupling in two-resonator circuit QED. Phys Rev B (2016) 93:214501. doi:10.1103/physrevb.93.214501
43. Mariantoni M, Deppe F, Marx A, Gross R, Wilhelm FK, Solano E, et al. Two-resonator circuit quantum electrodynamics: a superconducting quantum switch. Phys Rev B (2008) 78:104508. doi:10.1103/physrevb.78.104508
44. Naseem MT, Mustecaplioglu OE. Antibunching via cooling by heating. Phys Rev A (Coll Park) (2022) 105:012201. doi:10.1103/physreva.105.012201
45. Wang C, Wang LQ, Ren J. Managing quantum heat transfer in a nonequilibrium qubit-phonon hybrid system with coherent phonon states. Chin Phys Lett (2021) 38:010501. doi:10.1088/0256-307x/38/1/010501
46. Wang C, Wang LQ, Ren J. Impact of counter-rotating-wave term on quantum heat transfer and phonon statistics in nonequilibrium qubit–phonon hybrid system*. Chin Phys B (2021) 30:030506. doi:10.1088/1674-1056/abcfa8
47. Wang C, Chen H, Liao JQ. Nonequilibrium thermal transport and photon squeezing in a quadratic qubit-resonator system. Phys Rev A (Coll Park) (2021) 104:033701. doi:10.1103/physreva.104.033701
48. Emary C, Brandes T. Chaos and the quantum phase transition in the dicke model. Phys Rev E (2003) 67:066203. doi:10.1103/physreve.67.066203
49. Mezzacapo A, Las Heras U, Pedernales JS, DiCarlo L, Solano E, Lamata L, et al. Digital quantum rabi and dicke models in superconducting circuits. Sci Rep (2014) 4:7482. doi:10.1038/srep07482
50. Li SW, Cai CY, Sun CP. Steady quantum coherence in non-equilibrium environment. Ann Phys (N Y) (2015) 360:19–32. doi:10.1016/j.aop.2015.05.004
51. Beaudoin F, Gambetta JM, Blais A. Dissipation and ultrastrong coupling in circuit QED. Phys Rev A (Coll Park) (2011) 84:043832. doi:10.1103/physreva.84.043832
52. Settineri A, Macri V, Ridolfo A, Omar Di Stefano , Kockum AF, Nori F, et al. Dissipation and thermal noise in hybrid quantum systems in the ultrastrong-coupling regime. Phys Rev A (Coll Park) (2018) 98:053834. doi:10.1103/physreva.98.053834
53. Le Boite A. Theoretical methods for ultrastrong light–matter interactions. Adv Quan Tech (2020) 3:1900140. doi:10.1002/qute.201900140
54. Chen QH, Zhang YY, Liu T, Wang KL. Numerically exact solution to the finite-size Dicke model. Phys Rev A (Coll Park) (2008) 78:051801. doi:10.1103/physreva.78.051801
55. Ren J, Zhu JX, Gubernatis JE, Wang C, Li B. Thermoelectric transport with electron-phonon coupling and electron-electron interaction in molecular junctions. Phys Rev B (2012) 85:155443. doi:10.1103/physrevb.85.155443
56. Nicolin L, Segal D. Quantum fluctuation theorem for heat exchange in the strong coupling regime. Phys Rev B (2011) 84:161414. doi:10.1103/physrevb.84.161414
57. Wang C, Ren J, Cao JS. Nonequilibrium energy transfer at nanoscale: a unified theory from weak to strong coupling. Sci Rep (2015) 5:11787. doi:10.1038/srep11787
58. Xu DZ, Cao JS. Non-canonical distribution and non-equilibrium transport beyond weak system-bath coupling regime: a polaron transformation approach. Front Phys (Beijing) (2016) 11:110308. doi:10.1007/s11467-016-0540-2
59. Wang C, Ren J, Cao JS. Unifying quantum heat transfer in a nonequilibrium spin-boson model with full counting statistics. Phys Rev A (Coll Park) (2017) 95:023610. doi:10.1103/physreva.95.023610
60. Li B, Wang L, Casati G. Negative differential thermal resistance and thermal transistor. Appl Phys Lett (2006) 88:143501. doi:10.1063/1.2191730
61. He DH, Buyukdagli S, Hu B. Origin of negative differential thermal resistance in a chain of two weakly coupled nonlinear lattices. Phys Rev B (2009) 80:104302. doi:10.1103/physrevb.80.104302
63. Li NB, Ren J, Wang L, Zhang G, Hanggi P, Li B, et al. Colloquium: phononics: manipulating heat flow with electronic analogs and beyond. Rev Mod Phys (2012) 84:1045–66. doi:10.1103/revmodphys.84.1045
64. Chan HK, He DH, Hu B. Scaling analysis of negative differential thermal resistance. Phys Rev E (2014) 89:052126. doi:10.1103/physreve.89.052126
65. Segal D, Nitzan A. Molecular heat pump. Phys Rev E (2006) 73:026109. doi:10.1103/physreve.73.026109
66. Cao XF, Wang C, Zheng H, He DH. Quantum thermal transport via a canonically transformed redfield approach. Phys Rev B (2021) 103:075407. doi:10.1103/physrevb.103.075407
67. Ren J. Predicted rectification and negative differential spin seebeck effect at magnetic interfaces. Phys Rev B (2013) 88(R):220406. doi:10.1103/physrevb.88.220406
68. Fornieri A, Timossi G, Bosisio R, Solinas P, Giazotto F. Negative differential thermal conductance and heat amplification in superconducting hybrid devices. Phys Rev B (2016) 93:134508. doi:10.1103/physrevb.93.134508
69. Li B, Wang L, Casati G. Thermal diode: rectification of heat flux. Phys Rev Lett (2004) 93:184301. doi:10.1103/physrevlett.93.184301
70. Zhang YY, Hu ZX, Fu LB, Luo HG, Pu H, Zhang XF, et al. Quantum phases in a quantum rabi triangle. Phys Rev Lett (2021) 127:063602. doi:10.1103/physrevlett.127.063602
Appendix A: Derivation of Eq. 11.
Starting from Eq. 8, we assume that system-bath interactions are weak. Under the Born-Markov approximation, we individually perturb
Where the rate is given by κu(ω) = γu(ω)nu(ω), with the Bose-Einstein distribution function nu(ω) = 1/[ exp(ω/kBTu) − 1], the projecting operators based on the eigenstates are given by
It should be noted that for the finite-time evolution, the off-diagonal elements of the density operator are generally coupled with the diagonal ones in the eigenspace. However, after a long-time evolution, the off-diagonal elements gradually become ignored in the present model. Hence, the populations are naturally decoupled from the off-diagonal elements, which reduces the pair of projecting operators
Where the dissipative is given by
Based on DME (section A2) and specifying |ψk⟩ = |ψn,σ⟩ and Ek = En,σ, the dynamical equation of the density matrix element
Keywords: nonequilibrium thermal transport, circuit quantum electrodynamics, qubit-resonator interaction, quantum master equation, cycle transition process
Citation: Wang F-Y, Lu J-C, Wang Z, Duan L-W, Wang C and Ren J (2022) Nonequilibrium thermal transport in the two-mode qubit-resonator system. Front. Phys. 10:964858. doi: 10.3389/fphy.2022.964858
Received: 09 June 2022; Accepted: 07 July 2022;
Published: 25 August 2022.
Edited by:
Ying Li, Zhejiang University, ChinaReviewed by:
Dazhi Xu, Beijing Institute of Technology, ChinaHai-Rui Wei, University of Science and Technology Beijing, China
Copyright © 2022 Wang, Lu, Wang, Duan, Wang and Ren. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chen Wang, d2FuZ2NoZW5AempudS5jbg==; Jie Ren, WG9uaWNzQHRvbmdqaS5lZHUuY24=
 Fei-Yu Wang1
Fei-Yu Wang1 Jin-Cheng Lu
Jin-Cheng Lu Zi Wang
Zi Wang Chen Wang
Chen Wang Jie Ren
Jie Ren