Photoacoustic waves of a fluidic elliptic cylinder: Analytic solution and finite element method study

In this study, we focused on the photoacoustic wave production of a fluidic elliptic cylinder for modelling blood vessels, where the consideration of the elliptic cross section can be important for some diagnosis of vascular diseases. First, under the condition of optically-thin absorption, the analytic solution based on the photoacoustic Helmholtz equation in elliptic cylinder coordinates by using Mathieu functions was derived. Then, the finite element method (FEM) model was established to verify the analytic solution. In addition to photoacoustic waves and corresponding photoacoustic power spectra, both near- and far-field photoacoustic amplitude angular distributions were compared. The results revealed that the angular dependent photoacoustic power spectra are critical indicators of the ellipse shape variation. This finding can provide a considerable insight into the photoacoustic diagnosis of the blood vessel changes not only in terms of sizes but also shapes.

Introduction

The geometry shape of blood vessels is highly correlated to vascular diseases such as vascular blockage, thrombosis, tumour, and myocardial infarction [1, 2]. Although the circular cross section is generally applied to model the blood vessels, in several situations, such as variations in tension and blood pressure and the compression resulting from the surrounding tissue, the noncircular cross section of the blood vessel should be considered [3–7].

As a slightly complex model, elliptic cross section has been justified in various blood vascular studies. For example, in magnetic resonance imaging, the elliptic cross section of the aorta in healthy volunteers exhibited an ellipticity (ξ) of 0.8 [8]. Because of the thin walls of the tube, the cross section of vein deforms anisotropically on being subjected to forces. Therefore, the elliptic cross section can be an important parameter for modelling blood vessels [9, 10]. When the elliptic microvessels bend considerably, numerous reactants adhere to the inner wall of the microvessels resulted in thrombosis [11].

Because of rapid advances in biomedical imaging, considerable progress has been achieved in photoacoustic imaging through three-dimensional (3D) visualisation of blood vascular systems in disease diagnosis [12, 13]. Currently, photoacoustic imaging can reveal information of blood vascular deep morphology in biological tissues ranging from brain to breast [14, 15]. Furthermore, noninvasive analysis of arterial tortuousness of blood vessels in eyes and hands has been realised [16, 17]. In term of function, photoacoustic imaging can be used to determine whether a vessel is an artery or a vein based on haemoglobin oxygen saturation [18] and to detect changes in the vessel diameter and density related to the cardiovascular and metabolic diseases [17, 19]. However, photoacoustic imaging is yet to be realised for detailing cross-section changes of blood microvessels.

To accurately detail variations in the cross section of the blood vessels in terms of both size and shape, analyzing the photoacoustic power spectra can be an effective approach. Previous studies have revealed that in spherical [20], oblate spherical [21, 22] and various nonspherical axisymmetric particle models [23–26], the photoacoustic power spectra can be used to investigate the differences in the cell structure during early development and disease. The cylindrical model [27] has been developed and applied in blood vessel photoacoustic imaging [28, 29]. However, to the best of our knowledge, the photoacoustic power spectra of elliptic cylinder blood vessels are yet to be examined. By considering the elliptic cross section as an idealisation of the geometry of a compressed blood vessel, we derived an analytical solution for investigating photoacoustic waves generated from a fluidic elliptic cylinder and calculated various results based on this analytical solution.

For comparison and confirmation, we also developed the FEM model to perform simulation. The proposed FEM model is based on previously reported models [30–32]. In FEM simulation, the photoacoustic wave is caused by the expansion of light-absorbing fluidic elliptical cylinders and the displacement of a thin adjacent layer of water treated as expandable solid. We used multiphysics simulation software (COMSOL) to develop our FEM programme to investigate various physics processes.

The rest of the paper is organised as follows: in Section 2, the analytical solution based on the Mathieu function was discussed and the proposed FEM simulation model was described. In Section 3, results of spectral response and radiation distribution are provided. Finally, in Section 4, discussion and conclusion are presented. The proposed FEM simulations are consistent with results of the analytic solution, and the angular dependent photoacoustic power spectra can be used as an indicator of the shape changes of the elliptic blood vessels.

Methods

Analytic solution

An infinite long elliptical cylinder filled with light-absorbing fluid was considered to represent the blood vessel (Figure 1). Therefore, the analytic solution expressed with two-dimensional Mathieu wave functions was derived in elliptical coordinates [33–35].

FIGURE 1

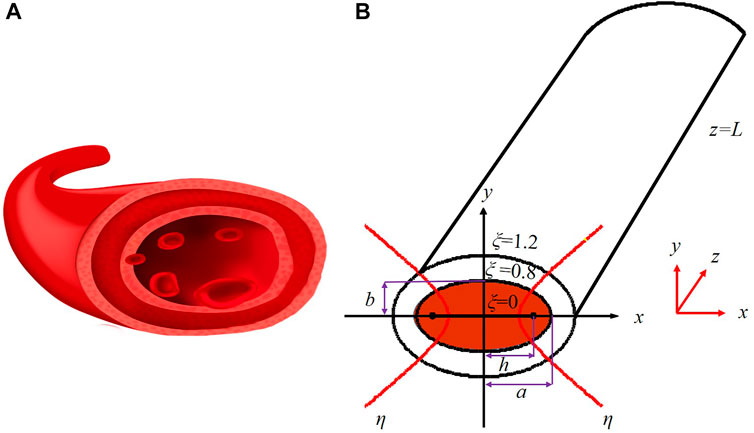
FIGURE 1. Illustration of the model for deriving the analytic solution. (A) Illustration of a blood vessel. (B) The corresponding model of the infinite long fluidic elliptic cylinder in the elliptical coordinates. The semi-major and semi-minor axis of the elliptic cylinder is a and b, respectively. In the z-direction, L is infinite. The half focal distance (the focal radius) is denoted by h.

Assuming the optically thin absorption condition, the photoacoustic pressure wave generation equation with the omission of the heat conduction and the fluidic viscosity [36] can be expressed as follows:

$\left({\nabla }^2-\frac{1}{c^2}\frac{{\partial }^2}{\partial t^2}\right)p=-\frac{\beta }{C_{\mathrm{p}}}\frac{\partial H}{\partial t}(1)$

where β is the thermal expansion coefficient, C_p is the heat capacity of the irradiated fluid, c is the speed of sound, and H is a function that describes the optical heating of the elliptical cylinder per unit time and volume.

For a short laser pulse with the intensity profile of I(t), the following equation can express H:

$H=\alpha I\left(t\right)(2)$

where α represents the optical absorption coefficient of the fluidic elliptic cylinder. However, the spectral decomposition method based on the Fourier transform can be applied to first solve the problem of single frequency intensity modulated laser illumination as follows:

$H=\alpha I_0{e}^{-i\omega t}(3)$

where the frequency originates from the following expression:

$I\left(t\right)=\frac{1}{2\pi }\underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}{\stackrel{\sim }{I}}_0\left(\omega \right)e^{-i\omega t}d\omega (4)$

Next, the final solution can be obtained through Fourier integration.

By incorporating Eq. 3 into Eq. 1 (which is essentially considering that the intensity modulated laser illuminates the fluidic elliptical cylinder uniformly), according to [27], the solution can be separated into two parts. In one part, the solution of inhomogeneous wave equation is expressed as follows (only for the region inside the elliptical cylinder):

$p_1=p_0{e}^{-i\omega t}=\frac{i\alpha \beta I_0{c}_c^2}{\omega C_p}{e}^{-i\omega t}(5)$

in the next part, the solution related to the homogeneous photoacoustic wave Helmholtz equation is expressed as follows:

$\left({\nabla }^2-\frac{1}{c^2}\frac{{\partial }^2}{\partial t^2}\right)p_2=0(6)$

The Helmholtz equation can be solved in the elliptical coordinates and expressed by the radial and angular Mathieu functions. This approach is similar to the acoustic scattering problem of an elliptical cylinder [37, 38]. Because of the constrains of finite values both at the origin point located inside the elliptical cylinder and at the infinite point outside the elliptical cylinder, the solution inside and the solution outside are respectively expressed by Mathieu–Bessel functions $J{e}_m\left(\xi ,s\right)$, and Mathieu–Hankel functions $H{e}_m\left(\xi ,s\right)$. A further constrain exists specifically for photoacoustic wave generation (but not for the acoustic scattering or the light scattering): the mirror symmetry requirement according to the symmetry of an ellipse. Therefore, radial functions $J{e}_m\left(\xi ,s\right)$and $H{e}_m\left(\xi ,s\right)$both can only take even orders. Therefore, by considering contribution described in Eq. 5, the solution inside and outside can be expressed as follows:

$p_c\left(\omega ,\xi ,\eta \right)=p_0\left(1+{\displaystyle \sum }_{m=0}^{\infty }{C}_{2m}^{c}J{e}_{2m}\left(\xi ,s_c\right)c{e}_{2m}\left(\eta ,s_c\right)\right)e^{-i\omega t}(7)$

$p_f\left(\omega ,\xi ,\eta \right)=p_0{\displaystyle \sum }_{m=0}^{\infty }{C}_{2m}^{f}H{e}_{2m}\left(\xi ,s_f\right)c{e}_{2m}\left(\eta ,s_f\right)e^{-i\omega t}(8)$

where subscript or superscript “c” denotes quantities of the fluidic elliptic cylinder, and “$f$” denotes those of the surrounding fluid. Here, $c{e}_{2m}\left(\eta ,s\right)$ represents angular Mathieu functions, which only take the even order and are periodic in nature, $C_{2m}^c$ and $C_{2m}^f$ represent the coefficients to be determined, and the dimensionless variables s_c and s_f are related to the frequency ω and defined as follows:

$s_c=\frac{1}{4}\frac{{\omega }^2}{c_c^2}{h}^2,s_f=\frac{1}{4}\frac{{\omega }^2}{c_f^2}{h}^2(9)$

with 2h the inter-focal distance, and c_c and c_f the velocity of sound in the fluidic elliptic cylinder and the surrounding fluid, respectively.

To solve the coefficients in Eqs 7, 8, we applied the boundary conditions, which require continuity of the pressure and the acceleration (related to the first derivative of the pressure respective to the radial coordinate $\xi$). The elliptic boundary is determined by the single-parameter radial coordinate $\xi ={\xi }_0$, which clearly reflects the convenience of using the elliptical coordinates. In these two boundary condition equations, we can further bring in the expansion formula for the angular Mathieu functions as follows:

$c{e}_{2m}\left(\eta ,s\right)={\displaystyle \sum }_{k=0}^{\infty }{A}_{2k}^{2m}\left(s\right)\cos 2k\eta (10)$

and apply the orthogonal condition of cos2kη. Therefore, we obtain that for every k, we have the following equation:

${\delta }_{k0}+{\displaystyle \sum }_{m=0}^{\infty }{C}_{2m}^{c}J{e}_{2m}\left({\xi }_0,s_c\right)A_{2k}^{2m}\left(s_c\right)={\displaystyle \sum }_{m=0}^{\infty }{C}_{2m}^{f}H{e}_{2m}\left({\xi }_0,s_f\right)A_{2k}^{2m}\left(s_f\right)(11)$

${\displaystyle \sum }_{m=0}^{\infty }{C}_{2m}^{c}J{e}_{2m}^{\prime }\left({\xi }_0,s_c\right)A_{2k}^{2m}\left(s_c\right)=\frac{{\rho }_c}{{\rho }_f}{\displaystyle \sum }_{m=0}^{\infty }{C}_{2m}^{f}H{e}_{2m}^{\prime }\left({\xi }_0,s_f\right)A_{2k}^{2m}\left(s_f\right)(12)$

where ${\rho }_c$ and ${\rho }_f$ denote the density of the fluidic elliptical cylinder and the surrounding fluid respectively, and $J{e}_{2m}^{\prime }$ and $H{e}_{2m}^{\prime }$ both denote the first derivative with respect to ξ.

Eqs 11 and 12 contain a series of such linear equations with the total number determined by the number of k. Therefore, these linear equations can be transformed into a square-matrix form by setting the dimension in k equal to that in m, thereby arriving at the following equations:

$\stackrel{⌢}{M}+{\stackrel{⌢}{P}}^c{\overline{R}}_c{\overline{A}}_c={\stackrel{⌢}{P}}^f{\overline{R}}_f{\overline{A}}_f(13)$

${\stackrel{⌢}{P}}^c{\overline{R}}_c^{\prime }{\overline{A}}_c=\stackrel{\sim }{\rho }{\stackrel{⌢}{P}}^f{\overline{R}}_f^{\prime }{\overline{A}}_f(14)$

where $\stackrel{\sim }{\rho }$ is the ratio of the inside density of elliptic cylinder ${\rho }_c$ to outside density ${\rho }_f$. Here, the row vector ${\stackrel{⌢}{P}}^c$ and ${\stackrel{⌢}{P}}^f$ that are to be solved are constituted by $C_{2m}^c$ and $C_{2m}^f$ as their elements. Another row vector $\stackrel{⌢}{M}$ can be expressed as follows (where ${\delta }_{ij}$ is the Kronecker delta symbol):

$\stackrel{⌢}{M}={\delta }_{1i}(15)$

Furthermore, ${\overline{R}}_c$, ${\overline{R}}_c^{\prime }$, ${\overline{R}}_f$, and ${\overline{R}}_f^{\prime }$ are related to Je_2m, Jeʹ_2m, He_2m and Heʹ_2m, which are diagonal square matrixes. ${\overline{A}}_c$ and ${\overline{A}}_f$ are also square matrixes and related to $A_{2k}^{2m}\left(s_c\right)$ and $A_{2k}^{2m}\left(s_f\right)$, respectively.

With the matrix algebra, the coefficient vectors ${\stackrel{⌢}{P}}^c$ and ${\stackrel{⌢}{P}}^f$ can be solved from Eqs 13 and 14, which result in the following expression:

${\stackrel{⌢}{P}}^c=\stackrel{⌢}{M}{\left[\frac{1}{\stackrel{\sim }{\rho }}{\overline{R}}_c^{\prime }{\overline{A}}_c{\left({\overline{A}}_f\right)}^{-1}{\left({\overline{R}}_f^{\prime }\right)}^{-1}{\overline{R}}_f{\overline{A}}_f-{\overline{R}}_c{\overline{A}}_c\right]}^{-1}(16)$

${\stackrel{⌢}{P}}^f=\stackrel{⌢}{M}{\left[{\overline{R}}_f{\overline{A}}_f-\stackrel{\sim }{\rho }{\overline{R}}_f^{\prime }{\overline{A}}_f{\left({\overline{A}}_c\right)}^{-1}{\left({\overline{R}}_c^{\prime }\right)}^{-1}{\overline{R}}_c{\overline{A}}_c\right]}^{-1}(17)$

Finally, the time-dependent solution according to the laser pulse expressed in Eq. 4 can be achieved as follows:

$p_c\left(t,\xi ,\eta \right)=\frac{1}{2\pi }\underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}\frac{{\stackrel{\sim }{I}}_0\left(\omega \right)}{I_0}{p}_0\left[1+{\displaystyle \sum }_m^{\infty }{C}_{2m}^{c}J{e}_{2m}\left(\xi ,s_c\right)c{e}_{2m}\left(\eta ,s_c\right)\right]e^{-i\omega t}d\omega (18)$

$p_f\left(t,\xi ,\eta \right)=\frac{1}{2\pi }\underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}\frac{{\stackrel{\sim }{I}}_0\left(\omega \right)}{I_0}{p}_0{\displaystyle \sum }_m^{\infty }{C}_{2m}^{f}H{e}_{2m}\left(\xi ,s_f\right)c{e}_{2m}\left(\eta ,s_f\right)e^{-i\omega t}d\omega (19)$

Calculation method based on the analytic solution

To calculate the photoacoustic wave generated by the fluidic elliptical cylinder, the integral of Eq. 19 is premised on the coefficient $C_{2m}^f$ from Eq. 17. Apparently, accurate calculation of various Mathieu functions and coefficients in Eq. 10 is the prerequisite. Here we applied the MATLAB Mathieu function package provided by Zhang and Jin [39, 40].

Another critical feature is the calculation of Eq. 17. The dimension of the matrix should be limited to a small value, otherwise, the converging solution can not be reached. A similar situation has been extensively studied previously [38, 41]. In our calculation, we investigated the trial-and-look approach, and revealed that the truncation dimension should be enlarged with the frequency by using the following optimum setting: if s_f ≤ 0.1, the truncation number N should set to one; if s_f is between 0.3 and 0.5, the truncation number N should set to is four; the truncation number N is set to seven for all of the other s_f values studied here.

FEM modelling

Considering the infinite long cylinder geometry, we established a two-dimensional FEM simulation model in the COMSOL Multiphysics platform as displayed in Figure 2. Spatially, this model is composed by four distinction functional regions. The innermost region is as the red area that represents the fluidic elliptic cylinder. The next adjacent region represents a thin layer of water, which is specifically treated as an elastic solid layer [30–32]. Next, the region is followed by a region representing the surrounding liquid. The outmost region functions as the perfect match layer (PML).

FIGURE 2

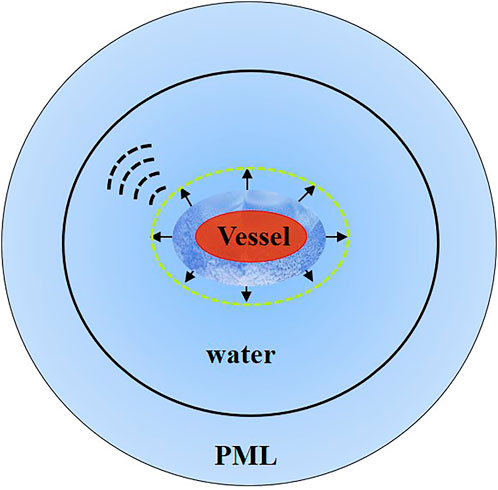
FIGURE 2. Schematic of the two-dimensional cross section model of the fluidic elliptic cylinder for finite element modelling (FEM) simulation of photoacoustic waves. The small arrows denote the thermal expansion due to both fluidic elliptic cylinder and adjacent thin layer of water treated as the elastic solid. The photoacoustic pressure is simulated in the surrounding liquid.

The maximum size of mesh elements is set to 1/6 of the photoacoustic wavelength according to the general guideline for FEM simulation of acoustic wave. Because the water elastic solid layer typically has a thickness of approximately 100nm, its mesh size is the smallest. Based on the general guideline, the PML that was applied to optimum the acoustic wave simulation was divided into eight layers by using the mesh sweeping method.

Based on previous studies [30–32], the simulation is based on multiphysics coupling and proceeds in the following four sequential steps. 1) electromagnetic wave heating: the uniform heating of the fluidic elliptic cylinder because of the linear polarisation plane wave, which is limited to the innermost region. 2) transient heat transfer: the temperature rise resulting from the initial heat source and the subsequential of the heat diffusion. 3) thermal expansion: the displacement due to thermal expansion, which is limited to the region of the fluidic elliptic cylinder, and also the adjacent water layer treated as the elastic solid. 4) acoustic wave propagation: the photoacoustic wave is generated and propagated in the surrounding liquid region, which also includes PML.

Notably, FEM simulation takes the approach of the transition model deployed in the time domain. The frequency response is obtained from the Fourier transformation. This procedure is opposite to the calculation based on the analytical solution. In the FEM model, the direct simulation results can be obtained only in the near region. However, the COMSOL Multiphysics platform can be used to obtain the far-field results based on the boundary integral method to extend the near-field results onto the far field. This type of far-field calculation is performed in the frequency domain.

Table 1 lists all the parameters used in the FEM simulations, where shear modulus and bulk modulus of water represent the parameters for the thin water layer treated as solid.

TABLE 1

TABLE 1. Parameters have been used for PA FEM model.

Results

Spectral response and the corresponding temporal profile

First, we simulated the photoacoustic wave generated using the small fluidic elliptic cylinder with the size setting of $h=5\mu m$ and ${\xi }_0=0.8$, respectively. The mass density and acoustic velocity of the wave are ρ_c = 1060 kg/m³ and c = 1590 m/s, respectively. Figure 3 presents a comparison of the results from the analytical solution as well as the FEM simulation. Here, the calculation is performed at the spatial point of ${\xi }_0=1.2$ and $\eta =0°$, respectively. The laser pulse is set with a Gaussian profile with standard deviation $\sigma =\left(\tau /2\sqrt{\left(2\ln 2\right)}\right)$ and pulse width $\tau =1\mathrm{n}\mathrm{s}$.

FIGURE 3

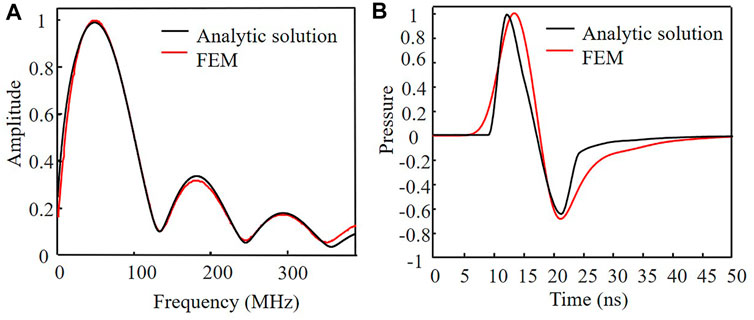
FIGURE 3. Calculation results of the photoacoustic wave based on the analytical solution and compared with the FEM simulation results. (A) Amplitude with respect to the frequency. (B) Corresponding temporal profiles.

Both the spectral response and the temporal profile were consistent, especially the period structure in Figure 3A and pulse location in Figure 3B. The major difference in Figure 3B can be attributed to the following factors: in analytical solutions, stronger approximations were made, that is, the heat conduction and the fluidic viscosity were both omitted; the photoacoustic pulse is calculated from the power spectra, and the effective number of data points for describing the pulse is limited by the maximum frequency. In FEM calculation, the pulse is first calculated and the resulting frequency range is wider than that presented in Figure 3A. The results revealed consistency between MATLAB calculation programme and FEM simulation programme.

Spectral response at various parameter settings

We focused on the calculation based on the analytical solution and considered various parameters setting, as displayed in Figure 4. The varying parameters included various focal radii [Figure 4A], various mass densities and sound velocities [Figure 4B], various acoustic transport distances [Figure 4C] and different acoustic transport angle [Figure 4D]. These parameters are critical in the study of photoacoustic effect of blood vessels.

FIGURE 4

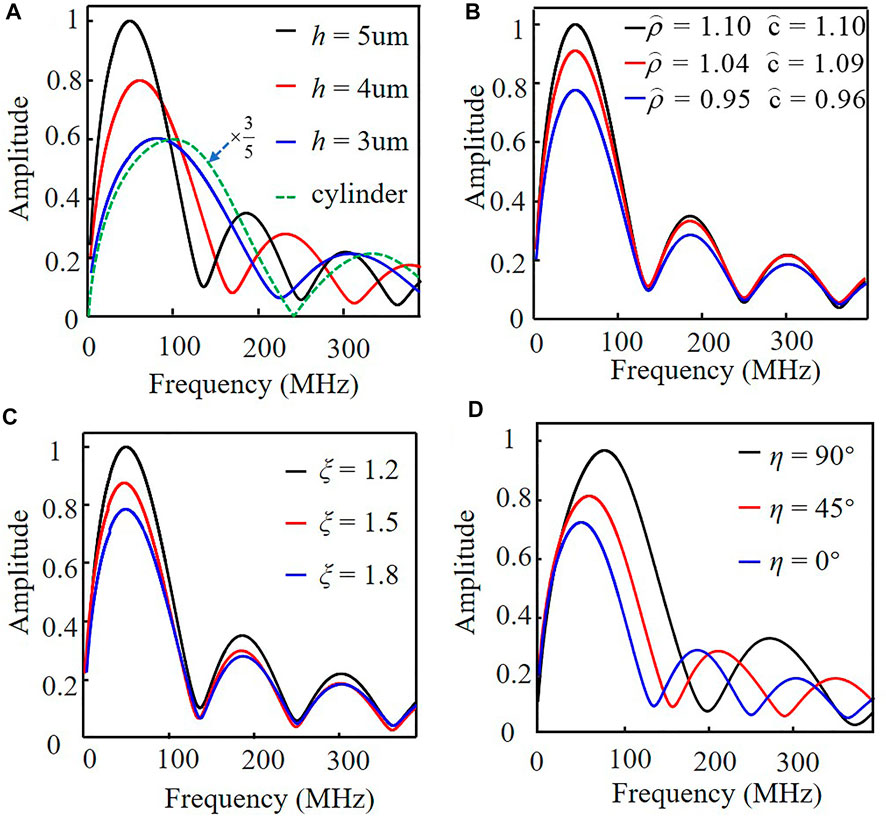
FIGURE 4. Calculated photoacoustic spectral amplitude of the fluidic elliptic cylinder with respect to (A) focal radius h, (B) density ρ_c and acoustic speed c, (C) detecting distance ξ, and (D) polar angles η.

Figure 4A displays the effect of the shape and size of blood vessels. The radial parameter was fixed at ${\xi }_0=0.8$, whereas the focal radius was varied. Thus, the ratio of the major axis length to the minor axis length was fixed but the overall size changed. The other parameters including spatial location, the mass density and the sound speed were the same as those used for calculating Figure 3. When the size increased, the oscillation period in frequency decreased and the frequency of the first maximum and the first minimum shifted to a lower value, which is consistent with the trend of the cylinder [27]. As displayed in Figure 4A, the result for the cylinder (with $=3\mu m$ ) is calculated using the following equation: $p_f\left(\stackrel{⌢}{q}\right)=\frac{i\lambda }{\stackrel{⌢}{q}}(\frac{J_1\left(\stackrel{⌢}{q}\right)H_0^{\left(1\right)}\left(\stackrel{⌢}{c}\stackrel{⌢}{q}\stackrel{⌢}{r}\right)}{J_1\left(\stackrel{⌢}{q}\right)H_0^{\left(1\right)}\left(\stackrel{⌢}{c}\stackrel{⌢}{q}\right)-\rho c{J}_0\left(\stackrel{⌢}{q}\right)H_1^{\left(1\right)}\left(\stackrel{⌢}{c}\stackrel{⌢}{q}\right)})e^{-i\stackrel{⌢}{q}\stackrel{⌢}{t}}$. The comparison revealed that the result of the elliptic cylinder with the smallest h is the result most close to that of the cylinder, which agrees with the expectation.

For calculations in Figures 4B–D, the elliptical cylinder size is fixed to the case of $h=5\mu m$ and ${\xi }_0=0.8$, respectively. The calculation in Figure 4B can reveal the effect of the slight change in the mass density and the sound velocity. The spatial point of ${\xi }_0=1.2$ and $\eta =0°$ is still considered. The apparent change is only the magnitude, not the overall shape of the curves (especially the oscillation structure).

In the calculation in Figure 4C, only the spatial distance of the calculated point changes, and the other parameters remain the same in case of Figure 3. The results also clearly revealed that the distance only changes the magnitude of the spectral response.

Finally, we investigated the effect of changes in the angular coordinates presented in Figure 4D (all the other parameters are the same as those used in Figure 3). At different acoustic transport angles (η), both the position of maximal PA spectral amplitude and the amplitude value of the photoacoustic spectrum changed drastically with the decrease in the angle. These results indicated that the major characteristic in the spectral response should be angular dependence because the elliptical cylinder became anisotropic compared with the cylinder.

We have performed the FEM simulation for the same parameter settings of Figure 4A, Figure 4C and Figure 4D and the corresponding results are almost the same as those shown in Figure 4. The results of Figure 4B can not be directly simulated since the FEM model does not consider the sound wave (thus the sound velocity) inside the elliptical cylinder.

Near- and far-field angular dependence

Figure 4D reveals that at angles η = 0°, 45°, 90°, the spectral response curves differ considerably. The change at all other angles was also noted. We further calculate the polar distribution pattern of the photoacoustic wave amplitude. In this case, we displayed the results for four frequencies f = 40, 100, 200, and 300 MHz (which correspond to s_f = 0.16, 1.01, 4.39, and 9.85) as the representative. Their results calculated for the near field at ξ = 1.2 are displayed from Figures 5A–D.

FIGURE 5

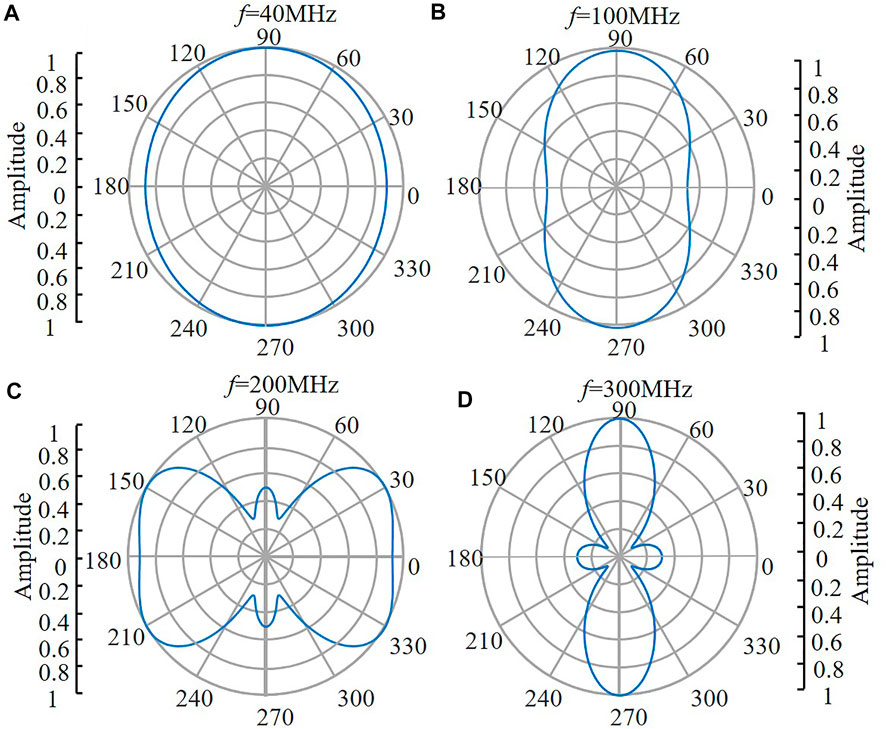
FIGURE 5. Polar distribution patterns of the photoacoustic amplitude at the near-field ξ = 1.2 for various frequencies (A–D) Respectively for the frequency of 40, 100, 200, and 300 MHz. The amplitude distribution of each frequency is normalised to its maximum value, which are 0.08, 0.1, 0.03, and 0.05, respectively.

As displayed in Figure 5, the polar distribution is approximately isotropic at the low frequency of 40 MHz. When the frequency increases, the anisotropy of the distribution pattern becomes pronounced. To understand these results, we analysed the separated orders of modes calculated by Eq. 8 (see Appendix A). The combination coefficient of $C_{2m}^f$and $H{e}_m\left(\xi ,s\right)$decrease rapidly for the higher orders, which reveals that the final results are predominated by the contribution of a few lowest modes. The combination results of Figure 4D and Figure 5 strongly suggest that the polar distribution measurement of the photoacoustic wave can provide a signature signal to differentiate the fluidic elliptical cylinders. However, the aforementioned simulations are performed in the near field, which is only several micrometres away from the elliptical cylinder boundary, whereas the usual photoacoustic measurement is considered at the far-field region. Therefore, calculating the photoacoustic measure in far-field case is critical to evaluate if these announced anisotropic patterns displayed in Figure 5 can still exist.

In Figure 6, the results revealed when the distance moves to ξ = 6 (which corresponds to the distance of 1000um) when keeping other parameters unchanged as applied in Figure 5. Notably, the polar distributions appear similar to those in Figure 5. We trace back to Eq. 8, which reveals that these results indicate radial Mathieu functions $H{e}_m\left(\xi ,s\right)$ did not change the proportional contribution, that is, each order exhibits a similar decreasing trend with the increase in the distance (see Appendix B).

FIGURE 6

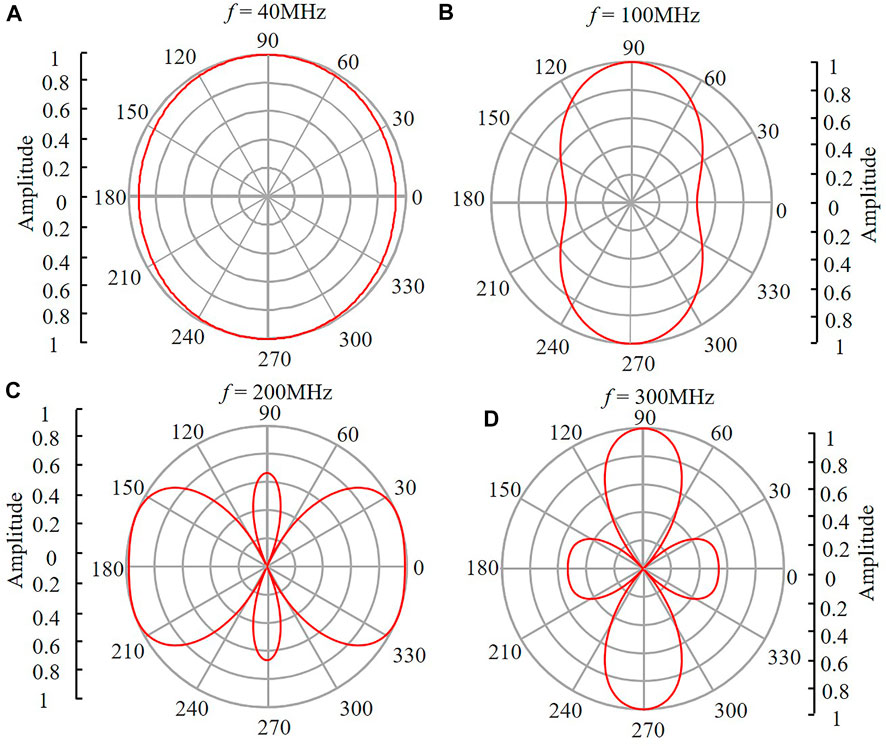
FIGURE 6. Polar distribution patterns of the photoacoustic amplitude at the far-field ξ = 6 for various frequencies. (A–D) Respectively for the frequency of 40, 100, 200 and 300 MHz. The amplitude distribution of each frequency is normalised to its maximum value, which were 0.0073, 0.0085, 0.0024, and 0.0027.

Finally, we performed FEM simulation for the near-field and far-field polar distributions. The results are displayed in Figure 7. These results are consistent with those in Figures 5, 6.

FIGURE 7

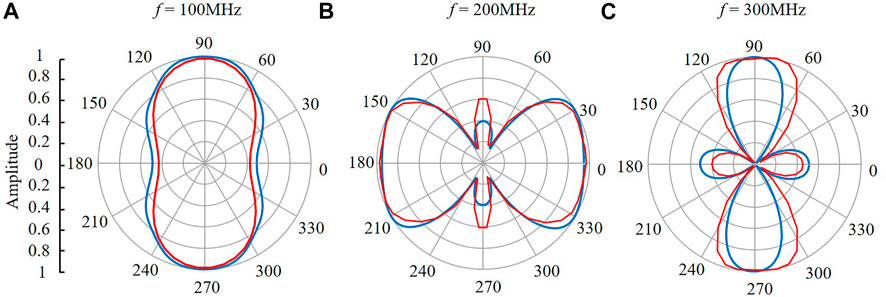
FIGURE 7. FEM simulation of the photoacoustic amplitude polar distribution patterns at the near-field ξ = 1.2 (blue line) and far-field ξ = 6 ((red line) for various frequencies. (A–C) respectively for the frequency of 100, 200 and 300 MHz.

Discussions and conclusion

For the light-absorbing fluidic elliptical cylinder, we performed calculation based on the analytic solution derived and FEM modelling in this study. The comparison results presented in Figure 3 and in Figures 5–7 reveal consistency of these two approaches. In practice, the FEM simulation should provide more accurate results and also are more flexible. For example, the light attenuation inside the fluidic elliptical cylinder due to the light absorption can be easily incorporated into the FEM simulation which is difficult in deriving the analytical solution. However, the calculation based on the analytical solution is considerably faster and can conventionally provide physical insight regarding the impact of different parameters: the results in Figure 4 revealed the size and the shape changes considerably affect the shape of the power spectra, whereas the density and acoustic speed primarily affect the overall magnitude. Moreover, the analytical solution can be potentially very useful for the eigen mode analysis of the elliptical cylinder, as referring to the previous study of the circular cylinder [42].

In the current study, we have omitted the possible acoustic attenuation of the surrounding fluid medium. This should not be a problem for the near field solution but will affect the far field solution, especially the far field photoacoustic amplitude spectra. The impact is worth for further study both in the FEM modeling [43–45] and the analytical solution derivation. However, since the acoustic attenuation should not affect the polar profile at a specified frequency, the major conclusions deduced from Figures 5–7 should still be valid.

In summary, the major finding of our current study is that the polar angular radiation patterns of the photoacoustic wave of a fluidic elliptic cylinder exhibit anisotropic characteristics, which is true even for the far-field case. It strongly suggests that the method of measuring the photoacoustic pulses in various angles and analyzing the angular dependent amplitude spectra can be used to differentiate the small blood vessels with elliptical cross section. We expect that the experimental study regarding this method will be performed in the near future.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

YZ and HF contributed to write and edit the manuscript. HF contributed to the conception of study. YZ, HW and HF have discussed this research.

Funding

This study is supported by the National Natural Science Foundation of China (12074268); Nature Science Foundation of Guangdong Province (2018B030311048); Natural Science Foundation of Shenzhen City (the Stable Support Plan Program) (20200814164819001).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Nagy JA, Chang SH, Shih SC, Dvorak AM, Dvorak HF. Heterogeneity of the tumor vasculature. Semin Thromb Hemost (2010) 36:321–31. doi:10.1055/s-0030-1253454

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Wootton DM, Ku DN. Fluid mechanics of vascular systems, diseases, and thrombosis. Annu Rev Biomed Eng (1999) 1:299–329. doi:10.1146/annurev.bioeng.1.1.299

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Zhang XM, Weng CC, Wu SL, Cai JY, Wu HQ, Li ZF, et al. Photoacoustic identification of blood vessel deformation under pressure. AIP Adv (2019) 9(7):075019. doi:10.1063/1.5108852

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Carmeliet P, Jain RK. Principles and mechanisms of vessel normalization for cancer and other angiogenic diseases. Nat Rev Drug Discov (2011) 10(6):417–27. doi:10.1038/nrd3455

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Robertson MB, Köhler U, Hoskins PR, Marshall I. Flow in elliptical vessels calculated for a physiological waveform. J Vasc Res (2001) 38(1):73–82. doi:10.1159/000051032

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Haslam M, Zamir M. Pulsatile flow in tubes of elliptic cross sections. Ann Biomed Eng (1998) 26:780–7. doi:10.1114/1.106

PubMed Abstract | CrossRef Full Text | Google Scholar

7. O'Flynn PM, O'Sullivan G, Pandit AS. Geometric variability of the abdominal aorta and its major peripheral branches. Ann Biomed Eng (2010) 38(3):824–40. doi:10.1007/s10439-010-9925-5

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Moreno MR, Moore JE, Meuli R. Cross-sectional deformation of the aorta as measured with magnetic resonance imaging. J Biomech Eng (1998) 120(1):18–21. doi:10.1115/1.2834298

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Nichols WW, O’Rourke MF. McDonald’s blood flow in arteries, theoretical, experimental and clinical principles. London: Arnold (1998).

Google Scholar

10. Delfino A, Moore JE, Meister JJ. Lateral deformation and movement effects on flow through distensible tube models of blood vessels. Biorheology (1994) 31(5):533–47. doi:10.3233/bir-1994-31503

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Qin L, Mirc D, Fu BM. Mechanical mechanisms of thrombosis in intact bent microvessels of rat mesentery. J Biomech (2008) 41(12):2726–34. doi:10.1016/j.jbiomech.2008.06.013

CrossRef Full Text | Google Scholar

12. Li L, Wang LV. Recent advances in photoacoustic tomography. BME Front (2021) 9823268:1. doi:10.34133/2021/9823268/

CrossRef Full Text | Google Scholar

13. Tang YQ, Wu HY, Klippel P, Zhang BH, Huang HYS, Jing Y, et al. Deep thrombosis characterization using photoacoustic imaging with intravascular light delivery. Biomed Eng Lett (2022) 12(2):135–45. doi:10.1007/s13534-022-00216-0

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Hu S, Wang LV. Photoacoustic imaging and characterization of the microvasculature. J Biomed Opt (2010) 15(1):011101. doi:10.1117/1.3281673

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Lin L, Hu P, Tong X, Na1 S, Cao R, Yuan XY, et al. High-speed three-dimensional photoacoustic computed tomography for preclinical research and clinical translation. Nat Commun (2021) 12(1):882–10. doi:10.1038/s41467-021-21232-1

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Matsumoto Y, Asao Y, Yoshikawa A, Sekiguchi H, Takada M, Furu M, et al. Label-free photoacoustic imaging of human palmar vessels: A structural morphological analysis. Sci Rep (2018) 8(1):786–8. doi:10.1038/s41598-018-19161-z

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Zhao H, Wang G, Lin R, Gong X, Song L, Li T, et al. Three-dimensional Hessian matrix-based quantitative vascular imaging of rat iris with optical-resolution photoacoustic microscopy in vivo. J Biomed Opt (2018) 23(4):1–11. doi:10.1117/1.JBO.23.4.046006

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Matsumoto Y, Asao Y, Sekiguchi H, Yoshikawa A, Ishii T, Nagae K, et al. Visualising peripheral arterioles and venules through high-resolution and large-area photoacoustic imaging. Sci Rep (2018) 8(1):14930–11. doi:10.1038/s41598-018-33255-8

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Shan T, Zhao Y, Jian S, Jiang H. In-vivo hemodynamic imaging of acute prenatal ethanol exposure in fetal brain by photoacoustic tomography. J Biophotonics (2020) 13(5):e201960161. doi:10.1002/jbio.201960161

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Khan MI, Diebold GJ. The photoacoustic effect generated by an isotropic solid sphere. Ultrasonics (1995) 33(4):265–9. doi:10.1016/0041-624X(95)00034-Z

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Li Y, Fang H, Min CJ, Yuan XC. Simulating photoacoustic waves produced by individual biological particles with spheroidal wave functions. Sci Rep (2015) 5:14801–11. doi:10.1038/srep14801

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Li Y, Fang H, Min CJ, Yuan XC. Analytic theory of photoacoustic wave generation from a spheroidal droplet. Opt Express (2014) 22:19953–69. doi:10.1364/OE.22.019953

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Strohm EM, Hysi E, Kolios MC. Photoacoustic measurements of single red blood cells. IEEE Int Ultrason Symp (Ius) (2012) 2012 1406–9. doi:10.1109/ULTSYM.2012.0351

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Strohm EM, Berndl ESL, Kolios MC. Probing red blood cell morphology using high-frequency photoacoustics. Biophys J (2013) 105(1):59–67. doi:10.1016/j.bpj.2013.05.037

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Saha RK, Karmakar S, Adhikari A, Kolios MC. Photoacoustic field calculation for nonspherical axisymmetric fluid particles. Biomed Phys Eng Exp (2017) 3:015017. doi:10.1088/2057-1976/aa555f

CrossRef Full Text | Google Scholar

26. Saha RK. A simulation study on the quantitative assessment of tissue microstructure with photoacoustics. IEEE T Ultrason Ferr (2015) 62:881–95. doi:10.1109/TUFFC.2015.006993

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Khan MI, Sun T, Diebold GJ. Photoacoustic waves generated by absorption of laser radiation in optically thin cylinders. J Acoust Soc Am (1993) 94(2):931–40. doi:10.1121/1.408195

CrossRef Full Text | Google Scholar

28. Hoelen CGA, De Mul FFM, Pongers R, Dekker A. Three-dimensional photoacoustic imaging of blood vessels in tissue. Opt Lett (1998) 23:648–50. doi:10.1364/OL.23.000648

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Siphanto RI, Kolkman RGM, Huisjes A, Pilatou MC, De Mul FFM, Steenbergen W, et al. Imaging of small vessels using photoacoustics: An in vivo study. Lasers Surg Med (2004) 35:354–62. doi:10.1002/lsm.20100

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Hatef A, Darvish B, Dagallier A, Davletshin YR. Analysis of photoacoustic response from gold-silver alloy nanoparticles irradiated by short pulsed laser in water. J Phys Chem (2015) 119:24075. doi:10.1021/acs.jpcc.5b08359

CrossRef Full Text | Google Scholar

31. Yu HQ, Yao J, Wu XW, Wu DJ, Liu XJ. Tunable photoacoustic properties of gold nanoshells with near-infrared optical responses. J Appl Phys (2017) 122:134901. doi:10.1063/1.4985860

CrossRef Full Text | Google Scholar

32. Kumar D, Ghai DP, Soni RK. Simulation studies of photoacoustic response from gold-silica core-shell nanoparticles. Plasmonics (2018) 13:1833. doi:10.1007/s11468-018-0697-3

CrossRef Full Text | Google Scholar

33. Alhargan FA. Algorithms for the computation of all Mathieu functions of integer orders. ACM Trans Math Softw (2000) 26(3):390–407. doi:10.1145/358407.358420

CrossRef Full Text | Google Scholar

34. Shen J, Wang LL. On spectral approximations in elliptical geometries using Mathieu functions. Math Comput (2009) 78(266):815–44. doi:10.1090/S0025-5718-08-02197-2

CrossRef Full Text | Google Scholar

35. Gutierrez-Vega JC, Rodriguea-Dagnino RM, Meneses-Nave MA. Chavez-cerda S. Mathieu functions, a visual approach. Am J Phys (2003) 71(3):233–42. doi:10.1119/1.1522698

CrossRef Full Text | Google Scholar

36. Diebold GJ. Photoacoustic monopole radiation: Waves from objects with symmetry in one, two, and three dimensions. In: LV Wang, editor. Photoacoustic imaging and spectroscopy. Oxfordshire United Kingdom: Taylor & Francis (2009).

Google Scholar

37. Sohei N, Yuya N, Nguyen T. Acoustic performance of an elliptical cavity on the application for soundproof ventilation units installed in dwelling walls. Appl Acoust (2020) 168:107418–0. doi:10.1016/j.apacoust.2020.107418

CrossRef Full Text | Google Scholar

38. Ancey S, Bazzali E, Gabrielli P, Mercier M. Acoustic scattering by elastic cylinders of elliptical cross-section and splitting up of resonances. J Appl Phys (2014) 15(19):194904. doi:10.1063/1.4876678

CrossRef Full Text | Google Scholar

39. Zhang S, Jin J. Computation of special functions. New York: John Wiley (1996).

Google Scholar

40. Lee WM. Acoustic scattering by multiple elliptical cylinders using collocation multipole method. J Comput Phys (2012) 231(14):4597–612. doi:10.1016/j.jcp.2012.02.032

CrossRef Full Text | Google Scholar

41. Hussein MI, Hamid AK. Electromagnetic scattering by a lossy dielectric elliptic cylinder. J Electromagn Waves Appl (2001) 15:1469–82. doi:10.1163/156939301X00021

CrossRef Full Text | Google Scholar

42. Gao XX, Tao C, Zhu R, Liu XJ. Noninvasive low-cycle fatigue characterization at high depth with photoacoustic eigen-spectrum analysis. Sci Rep (2018) 8(1):7751. doi:10.1038/s41598-018-26140-x

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Cao YN, Diebold GJ. Effects of heat conduction and viscosity on photoacoustic waves from droplets. Opt Eng (1997) 36(2):417–22. doi:10.1117/1.601213

CrossRef Full Text | Google Scholar

44. El-Busaidy S, Baumann B, Wolff M, Duggen L. Modelling of open photoacoustic resonators. Photoacoustics (2020) 18:100161. doi:10.1016/j.pacs.2020.100161

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Shi YJ, Yang F, Wang Q. Photoacoustic viscoelasticity imaging dedicated to mechanical characterization of biological tissues. J Innov Opt Health Sci (2017) 10(4):1730005. doi:10.1142/S1793545817300051

CrossRef Full Text | Google Scholar

Appendix A: Analysis of the mode contribution in the polar radiation pattern

To understand the near-field polar distribution patterns displayed in Figure 5, we refer to Eq. 8 and analyse the contribution from various orders. As indicated in Eq. 8, the polar distribution pattern is primarily determined by the angular Mathieu function $c{e}_{2m}\left(\eta ,s\right)$ and the combination coefficient of $C_{2m}^f$ and $H{e}_m\left(\xi ,s\right)$ determines the weight of each order. As displayed in the left column in Figures 8A–D, the amplitude of the combination coefficient decreased rapidly after a few orders. This phenomenon is true for all of the four frequencies investigated. Therefore, only the lowest few modes contribute to the final polar distribution pattern. This analysis can be visualised by comparing Figure 8 with the final pattern shown in Figure 5: for f = 40 and 100MHz, only the first order m = 0 dominates; for f = 200 MHz, the contribution combing from the second order m = 1 becomes clear; for f = 300 MHz, the third order m = 2 starts a comparable contribution as the first two orders.

FIGURE 8

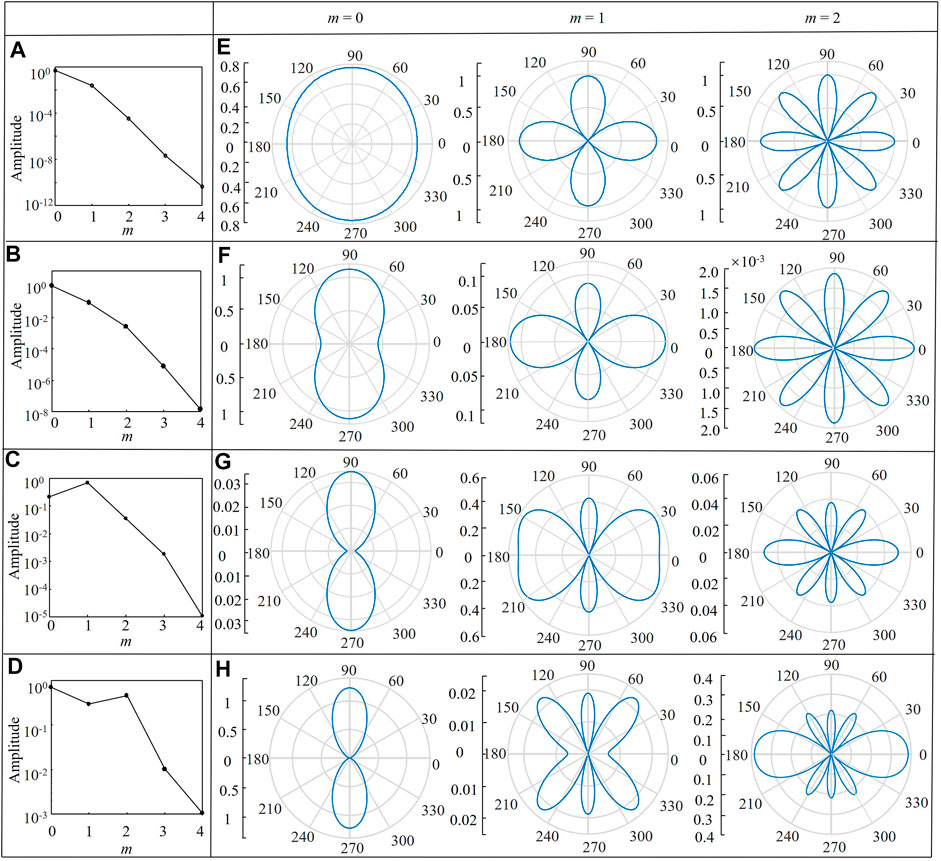
FIGURE 8. Near-field contribution of various modes for photoacoustic wave with various frequencies. (A–D) Mode contribution coefficients for 40, 100, 200, and 300 MHz. (E–H) The mode polar distribution patterns of the three lowest modes for each frequency.

Appendix B: Distance dependent curves of various orders of the radial mathieu function

To investigate the similarity of the far-field polar distribution patterns of Figure 6 comparing to the near-field patterns shown in Figure 5, we traced back to Eq. 8. The combination coefficient of $C_{2m}^f$ and $H{e}_m\left(\xi ,s\right)$ versus the distance ξ were plotted in Figure 9. As displayed, the combination coefficient curves of various orders exhibit almost identical decreasing trend. The angular Mathieu functions $c{e}_{2m}\left(\eta ,s\right)$ do not depend on ξ, the polar distribution pattern should not change considerably from the near field to the far field.

FIGURE 9

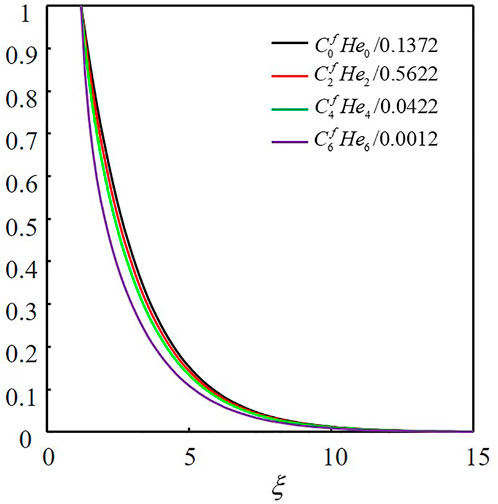
FIGURE 9. Curves of the combination coefficient of various order with the distance. The curves are normalised relative to their maximum value at ξ = 1.2.