Enabling real-time adaptation of machine learning models at x-ray Free Electron Laser facilities with high-speed training optimized computational hardware

The emergence of novel computational hardware is enabling a new paradigm for rapid machine learning model training. For the Department of Energy’s major research facilities, this developing technology will enable a highly adaptive approach to experimental sciences. In this manuscript we present the per-epoch and end-to-end training times for an example of a streaming diagnostic that is planned for the upcoming high-repetition rate x-ray Free Electron Laser, the Linac Coherent Light Source-II. We explore the parameter space of batch size and data parallel training across multiple Graphics Processing Units and Reconfigurable Dataflow Units. We show the landscape of training times with a goal of full model retraining in under 15 min. Although a full from scratch retraining of a model may not be required in all cases, we nevertheless present an example of the application of emerging computational hardware for adapting machine learning models to changing environments in real-time, during streaming data acquisition, at the rates expected for the data fire hoses of accelerator-based user facilities.

1 Introduction

In this manuscript we motivate using machine learning (ML) acceleration engines that enable continuous data acquisition streams to accommodate rapid intermittent self-calibration in order to accommodate both sensor and source variation. Extendable to a wide variety of scientific use cases, there is an explosive trajectory for autonomous and semi-autonomous control systems across the spectrum of accelerator applications [1–3]. Many of these use cases require either real-time model update in a reinforcement learning approach in support of active control systems or they require predictive planning for optimised experimental parameter exploration, e.g. “next shot” planning for DIII-D tokamak.

We concentrate on a particular detector currently under development for the Department of Energy’s premiere ultra-high data-rate x-ray Free Electron Laser (xFEL), the Linac Coherent Light Source II (LCLS-II) [4], an angle resolving array of charged particle Time-of-Flight (ToF) spectrometers [5]. For this demonstration we simulate 128 sensor channels of an angular array. Although the current physical system as described in Ref. [5] is comprised of only 20 total sensor angles, our motivation for the oversampling lies in the potential for generalization across multiple domains that share a common tomographic-like image reconstruction/classification pattern.

There is an impending need to develop advanced computational hardware accelerators to process, analyze, and act upon—in real-time—the ultra-high rate data that will stream from the detectors at next generation particle accelerator facilities [6,7]. We foresee a coming broad adoption of transformer models [8–10], originally engineered for language interpretation, that will accommodate situations where unlabeled data is abundant but task-specific labeled data is rare. An inspiring example comes from the extension of GPT-2 to the very different task of music interpretation [11]. This exemplifies the pattern of using a deep encoding network as a structure preserving “featurizer.” The resulting latent representation can then feed many downstream models that manage experiment-specific tasks with significantly smaller labeled data sets.

The featurizing, or embedding, model poses a unique challenge for real experimental systems. Although we concentrate here on simulation based results, our motivation is the ultimate physical detector system of electron spectrometers [5]. In such spectrometers, there is a series of electron focusing and retarding electrostatic lenses. Physically, these are copper rings and meshes, each having different high voltage static electric potentials that energetic electrons must pass through on their way to the detection sensor. This forms an electrostatic potential hill for the electrons to climb, shedding the majority of their kinetic energy, such that the drift time in a flat field region more favorably scales with energy. This hill is a compound electrostatic lens with a comparable length to the post-hill drift length with up to 0.25 eV resolution on a 500 eV electron (∼2000 resolving power). As such, a simple deterministic equation is quite challenging and would nevertheless exclude the physical particulars of a given detector channel such as high voltage supply variations. The typical for the environmental conditions inside the experimental end-station as well as the changing accelerator operating conditions and user experimental plan changes on the 20–30 min to hourly time-scale. Furthermore, raw data will stream unaltered through the acquisition stream at 0.1% of the full 1 MHz frame rate, at 1 kHz. At this rate, a freshly updated 900k sample-size training set will accumulate every 15 min, thus allowing a fresh update of the embedding model to accommodate the environment, end-station, and accelerator variation. For the sake of such convergence of variation timescales, we target a 15 min model retraining cadence in this manuscript.

In this study, we compare the model training time for a noise eliminating encoder-decoder network, CookieNetAE [12]. We demonstrate the power of parallel training in batches for moving quickly through a large, 900k images, training set. We evaluate a new AI optimized hardware accelerator, the SambaNova Reconfigurable Dataflow Unit^TM (RDU), and compare it to a benchmark DGX node available at the Argonne Leadership Computing Facility (ALCF) with 8 A100 Graphics Processing Units (GPUs). We additionally compare to a more commonly available training engine of up to 8 V100 GPUs also hosted in a single node. We investigate the performance of RDUs versus GPUs for scientific ML training applications and discuss our results in the context of high data rate accelerator-based scientific facilities where diagnostics and detectors provide continuous streams of data to keep 1M sample size training sets continuously refreshed.

The remainder of the paper is organized as follows. In Subsection 2.1, we present an overview of the RDU AI accelerator involved in this study and give a description of the distributed training on RDUs in Subsection 2.2. We do not review the GPU accelerator owing to community familiarity with GPUs for ML tasks. In Subsection 2.3, we discuss briefly the data generation process and we give the structure of the CookieNetAE model [12] in Subsection 2.4. We briefly describe the experimental setup in Subsection 2.5. Obtained accuracy and performance results are provided in Subsections 3.1 and 3.2 for single and multi-accelerator cases, respectively, with comparisons with the two generations of GPU. Finally, concluding remarks and thoughts on future work are given in Section 4.

2 Materials and methods

Foreseeing a future of transformer models for distilling information from streaming scientific sensors, we have targeted an encoder-decoder network as a demonstrating case for training acceleration. To relieve concerns about discovery information being lost, we have chosen the downstream task of reconstructing Y′, the noise free probability distribution function (PDF) used to produce the under-sampled and grainy X, the input. This reconstruction can only perform well if all of the physically relevant information is contained in the latent representation, otherwise the variation in stochastic sampling of the PDF would dominate the mean-squared-error (MSE) loss between Y and the predicted Y′.

The structure of the encoding side of our CookieNetAE network [12] closely matches that of the embedding side of transformer models, and therefore we take this as a first stage in ML-enabled data featurization for streaming acquisition at so-called data fire hose facilities like the next generation of the Linac Coherent Light Source (LCLS-II) [4,6] and the Upgraded Advanced Photon Source (APS-U) [13]. Although downstream models will be experiment specific, changing on the daily or weekly time scale, the upstream embedding (encoder) layers will be closely tied to the shared detectors. Nevertheless, they will need to accommodate a minutes scale “breathing” of experimental and accelerator conditions. Embedding model retraining must therefore be accelerated to handle such frequent—likely continuous—retraining, thus motivating our exploration of uniquely engineered training accelerators like the SambaNova RDU in comparison to the familiar family of GPU accelerators, Nvidia V100 and A100.

2.1 Sambanova reconfigurable dataflow architecture

We investigated the SambaNova solution for its flexible, dataflow-oriented execution model that enables pipeline operations and programmable data access patterns as will be required of our high velocity data pipelines from streaming scientific detectors. For multi-user facilities, reconfigurability is essential; thus our interest in an architecture that can be programmed specifically for any model application but nevertheless results in an application-specific optimized accelerator. The core of the SambaNova Reconfigurable Dataflow Architecture^TM (RDA) [14,15] is a dataflow-optimized processor, the Reconfigurable Dataflow Unit^TM (RDU). It has a tiled architecture that is made up of a network of programmable compute (PCUs), memory (PMUs) and communication units. There are 640 PCUs and 640 PMUs connected to one another and the external world via the communication units. The PCUs yield a peak performance of over 300 TFLOPs per RDU. The PMUs provide over 300 MB of on-chip memory and 150 TB/s of on-chip bandwidth. These units are programmed with the structure of the dataflow graph that instantiates the ML application, allowing the RDU to use its own parallelism to natively leverage the parallel patterns that are inherent to dataflow graphs.

SambaFlow^TM is the framework used to leverage RDUs. As a complete software stack, it takes computational graphs as input from common ML frameworks such as PyTorch [16] and automatically extracts, optimizes, and maps the dataflow graph onto one or more RDUs. SambaFlow achieves performance without the need for low-level kernel tuning.

2.2 Distributed training

The RDA is a scalable solution that not only leverages highly-parallel on-chip computation but also enables parallel computation across multiple RDUs. The SambaFlow framework automatically handles the parallelization used here for data parallel training with the DataScale^® platform, a rack-level, datacenter accelerated computing platform. The platform consists of one or more DataScale SN10-8 nodes with integrated networking and management infrastructure in a standards-compliant data center rack—the DataScale SN10-8R [15]. We used up to 4 SN10-8 nodes for the results presented here, each consisting of a host module and 8 RDUs. The RDUs on a node are interconnected via the RDU-Connect^TM fabric while the multiple SN10-8 nodes communicate via Remote direct memory access over Converged Ethernet (RoCE). Beyond the more traditional model parallelism—large models spread across multiple devices—we use the node interconnects to enable data parallelism across all RDUs in the system.

Data parallelism spreads the training workload across multiple accelerator devices, each with its own copy of the full model to be trained. Each device uses the same model with different training samples. For every iteration, each device runs the forward and backward passes to compute gradients on a batch of its respective data. The gradients from all the devices are then aggregated to compute the averaged gradients which are in turn transmitted back to each device to update the local model weights and proceed with the next iteration.

2.3 Data generation

We concentrate on x-ray pulse time-energy reconstruction for two reasons. First, it is one of the more compute-intensive examples of attosecond angular streaking [17], and it is associated with a detector suite that is fully capable of the highest data acquisition rates in the early stages of the LCLS-II [5]. In angular streaking, x-ray induced photoelectron spectra are modulated by the dressing laser field. This modulation can be crudely simulated in the energy domain simply by adding a sinusoidal excess energy to photo-electrons depending on the angle of emission and phase of the dressing laser field. This simplified simulation [18] begins with an electron emission probability distribution,

$Y_{\text{pdf}}=\sum _{i=0}^N{p}_i\left({\nu }_i,\theta ,{\varphi }_i\right).(1)$

The sum over p_i in Eq. 1 runs for each of N sub-spikes where p_i itself is a function of the photon energy (ν_i), the emission angle (θ), and a random phase (ϕ_i) that represents the sub-spike arrival time relative to the optical carrier field of the dressing laser. From this we draw random samples from Y_pdf, plus a uniform dark-count likelihood, for every measurement angle θ and sub-spike energy ν_i. These draws form a list of energies X_hits for each measurement angle (row in Figure 1A) which are in turn used to update the image X_img. Therefore, the goal of CookieNetAE is an optimal inverse mapping from X_img (Figure 1A) to Y_pdf (Figure 1C). In so doing, we have confidence that the latent representation of CookieNetAE (Figure 1D) holds all information that could be used as an input feature vector for any relevant classification or regression task. We note that noise is included insofar as we have dark counts at such a level in physical measurements, but the more insidious difference between actual measurements of X_img and that simulated here is that the conversion to energy domain, here a pre-supposition from upstream featurizing algorithm, loses calibration, then the rows of X_img would not align, suffering arbitrary relative shifts. Such an artifiact, interestingly, would be effectively trained out by just the sort of adaptation of CookieNetAE by applying the corrective shift to recover smooth sinusoidal curves of Y_pdf; re-training would therefore accommodate the expected effects of power supply drift and resister failure in the electronics of the individual spectrometers.

FIGURE 1

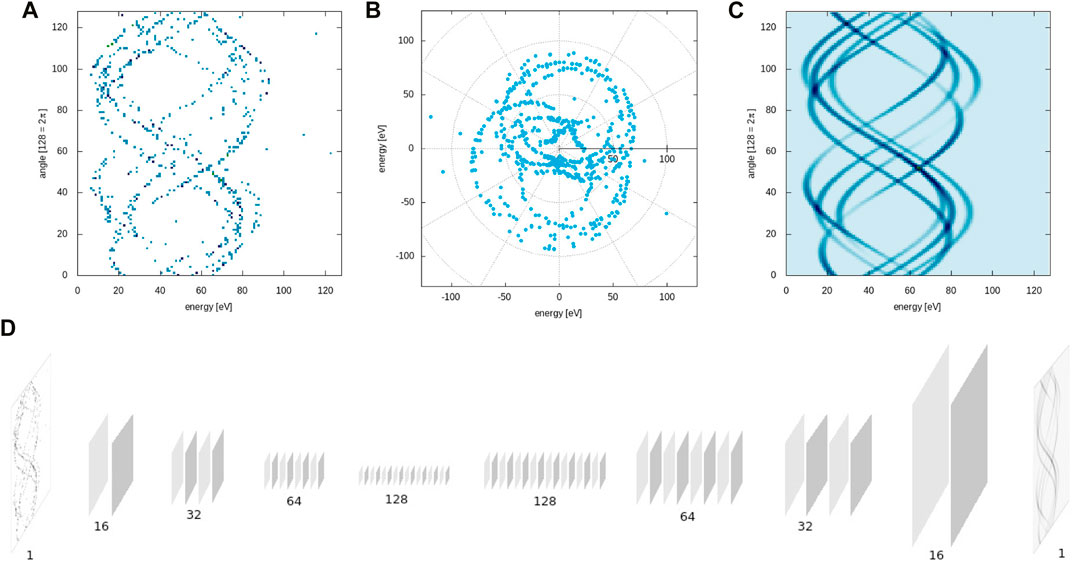
FIGURE 1. (A). Cartesian “image” representation of the in energy-angle space (our input X). (B). Polar representation of an example streaking shot. (C). Cartesian “image” representation of the energy-angle emission probability distribution (our output Y). (D). Schematic of the CookieNetAE as described in Table 1.

Algorithmic xFEL pulse reconstruction requires inverting the angle-resolved photo-electron spectra as per Refs. [17,19] and is much the same as tomographic image reconstruction. A principle challenge here is the high frame rate of the x-ray source. In preparation, we create a simulated dataset of one million example images. The full simulated dataset spans nearly 80 GB and yet represents only one second of acquisition of the LCLS-II. These examples are used with 90% for training and 10% are held out for validation and testing of the CookieNetAE model.

2.4 Encoder-decoder model

CookieNetAE [12] is a convolutional encoder-decoder network designed to infer the angle-energy probability density function of photoionized noble gas electrons. Since we are free in simulation to explore any number of angular samples, we increase the number of evenly distributed angles to 128 around the plane perpendicular to x-ray pulse propagation. In Figure 1A we show an unwrapped (Cartesian) example such that each row in the image corresponds to an energy histogram with 128 energy bins of 1 eV width; panel B shows the polar representation of the electrons emitted. We also show the to-be-recovered Y_pdf in panel C with a schematic of the encoder-decoder in panel D (see Ref. [12]). From the input at left in Figure 1D to the output probability distribution at right, we indicate schematically the halving of spatial dimensions and doubling of channels as the filter-depth of layer denoted; this is detailed in Table 1. The encoder contains three convolution layers with the corresponding max pooling layers followed by a single convolution layer to get the latent space representation of the input image. The decoder contains four transposed convolution layers followed by a single convolution layer to get the output. The model is trained by using a standard MSE loss with the following hyperparameters: a maximum number of epochs of 51, a learning rate of 3 × 10^–4 for the Adam optimizer, and the ReLU activation function at relevant layers.

TABLE 1

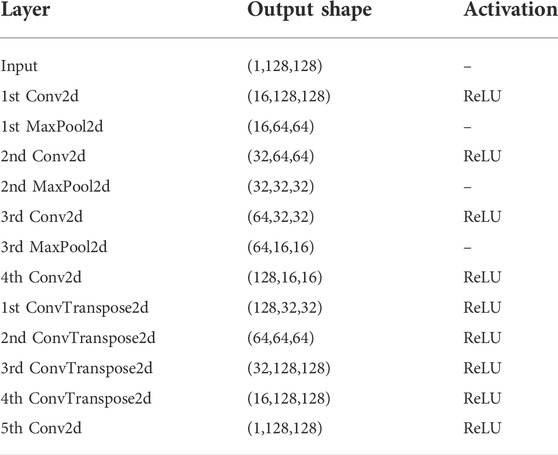
TABLE 1. Network structure of the CookieNetAE [12].

The model architecture was chosen for reconstruction fidelity and to serve as a somewhat generic model form representing auto-encoders like a “U-net” but without skip-connects. Avoiding the skip-connections holds closer to a scheme that is consistent with compression at sensor and decompression at acquisition when the model is used in inference at the recording node and was held fixed since the scope of the manuscript is taken to be a survey of data-parallel training across the different training accelerators rather than model architectures. Of course different model forms are likely to instantiate with better or worse performance for different acceleration hardware architectures, and we do indeed plan to investigate this in future research across multiple scientific domains.

2.5 Experimental setup

We compare accelerators by measuring the training time for the SambaNova DataScale SN10-8R in comparison with an Nvidia DGX node of A100 GPUs and another Nvidia node of V100 GPUs. For both the A100 and V100 GPU tests, the CookieNetAE model is run with the PyTorch API v1.9 in data parallel training with Horovod [20]. For the DataScale SN10-8R, the SambaFlow software stack v1.11.2 compiles the model from the same PyTorch reference. For all hardware, we measure the average training time per epoch.

We perform these measurements by examining the dependence of model training time on variation of batch sizes for single accelerator as well as data-parallel training across multiple accelerators. Because the batch size is an important hyperparameter in deep neural networks, we investigate the hardware performance for a wide variety of local and global batch sizes in order to exercise the available design space defined by the number of accelerators and batch size. The local batch size (LBS) is the batch size per device, while the global batch size (GBS) is the batch size across all devices. This design space clearly impacts hardware utilization and convergence characteristics of the learning algorithm [21]. Results from Ref. [22] show that training with batch sizes of 32 samples or smaller can help improve training stability and model generalization. On the other hand, larger batch sizes expose more computational workload per weight update and therefore often result in better hardware utilization. For these reasons, we span a broad range of relevant batch/parallelization parameters. In particular, given the relative novelty of the SambaNova hardware, a more extensive survey of its performance landscape is conducted compared to the GPU landscape.

3 Results

3.1 Single-processor runs

The CookieNetAE model is validated against a held out set of samples not used by the model for parameter updating. A low MSE value of 2.763 × 10^–4 is observed for this validation dataset for the case with the reference batch size of 128, indicating that the model performs in the desired manner and without overfitting. Example predictions shown in Figure 2 indicate excellent agreement with the ground truth data.

FIGURE 2

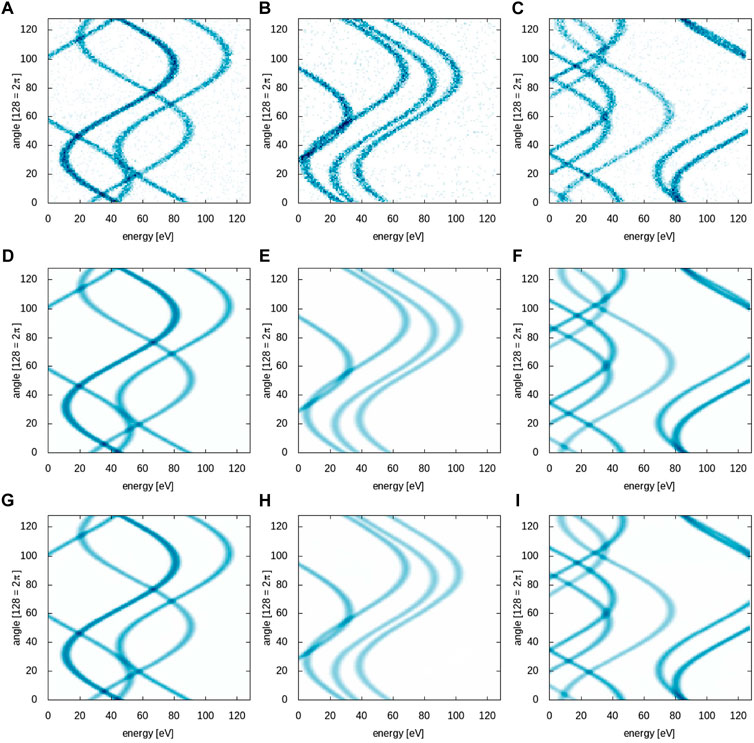
FIGURE 2. Comparison of model input (A–C), ground truth (D–F) and model prediction (G–I) for three example hold-out test samples from the single-RDU run with a batch size of 128. The MSE values are 6.255×10^–4, 3.036×10^–4, and 9.162×10^–4, respectively.

The variation of the training time per epoch versus the batch size is shown in Figure 3A for a single RDU as filled black circles, a single A100 as open black circles, and a single V100 as open black squares (color denotes the number of accelerators used). Numerical values are listed in Tables 3 and 4. For the single RDU case, results are included for batch sizes as few as 8 and as large as 1024, while for the single GPU cases only batch sizes 64–1024 are tested. The training time per epoch is defined as the time taken to run over all the batches in a given epoch. Both the A100 and RDU are roughly twice as fast as V100 in terms of training time, and the RDU is comparable or faster than A100 for all but one batch size, i.e., batch size of 64. The RDU shows a speedup of up to 1.82 times over V100, and up to 1.09 times over A100. Additional results for the RDU with very small batch sizes (i.e., 8, 16 and 32) are also included in Figure 3A and Table 3. We note Ref. [23] demonstrated that FPGA has a performance advantage over GPU on small batch size ResNet-50 inference workloads. Given that RDU and FPGA are both instances of reconfigurable architectures, it remains as an interesting future work to compare very small batch size CookieNetAE training performance between RDU and GPU.

FIGURE 3

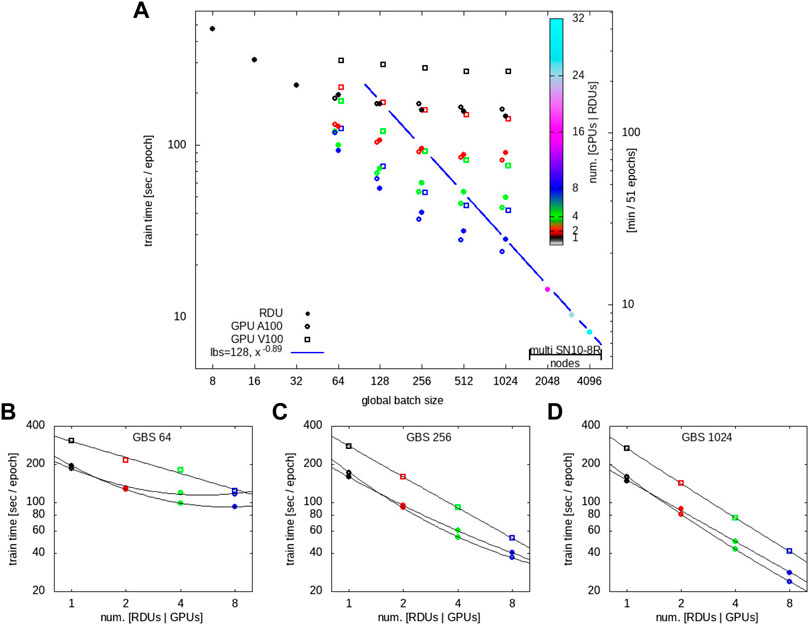
FIGURE 3. (A). Per epoch training time versus the global batch size (GBS). The number of accelerators used for data-parallel training is represented by symbol color as indicated in panel A: 1 = black, 2 = red … 32 = cyan. Note that we have added a slight “jitter” shift around the x-axis value for ease of data point visibility—all GBSs and number of devices are indeed integer powers of 2. The thick blue line indicates that, for a constant LBS of 128, increasing the number of RDUs scales the training time as x^−0.89. That the V100 (open squares) line up with A100 (open circles) with a color offset of one (a doubling) indicates that for this workload the A100 generally performs twice as fast as the equivalent V100 condition. (B–D). Training time versus number of accelerators for GBSs of 64, 256, and 1024 as indicated with symbol color remaining consistent with panel A convention.

3.2 Multi-processor runs

For fixed LBS of 128, Figure 4 shows the variation of the end-to-end training time versus the number of RDUs. This time includes data loading, model initialization, training and validation for 51 epochs along with printing selected output variables to file. As one can see, the end-to-end training time is reduced as the number of RDUs is increased. For example, it is 162 min for the case with one RDU while only 8.3 min for the case with 32 RDUs. This corresponds to a speedup factor of more than 19 times. The parallel efficiency, defined as the ratio of the speedup factor to the number of RDUs, is around 78% of linear scaling for the case of one SN10-8 node with 8 RDUs and only decreases gradually as the number of nodes is increased, reaching 61% for the case of 32 RDUs (4 nodes). From this weak scaling analysis, we observe that two or more SN10-8 nodes (16 or more RDUs) are capable of achieving end-to-end training times in under 15 min. The MSEs for validation data are shown in Table 2, indicating that the accuracy is not significantly affected with the increase in the number of RDUs, and consequently the GBS; the error remains below 5 × 10^–4.

FIGURE 4

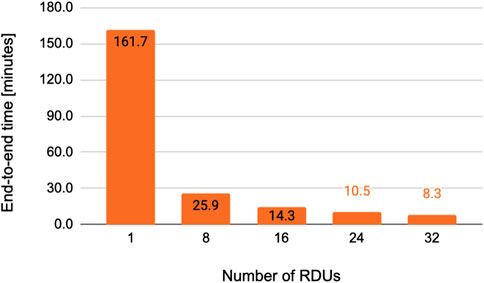
FIGURE 4. Variation of the end-to-end training time with the number of RDUs. This end-to-end time begins with the loading of data from system memory, includes 51 epochs of training into convergence (no early stopping), and return of trained model back to system memory. Results are shown using a fixed LBS of 128 and up to 32 RDUs.

TABLE 2

TABLE 2. MSE values on validation data for multi-RDU runs.

The variation of the training time per epoch versus the GBS for multiple RDUs, A100s and V100s is shown in Tables 3 and 4 and visualized in Figure 3. For GPUs, results are shown using up to 8 devices with GBSs up to 1024, while for RDUs results are shown using up to 32 devices with GBSs up to 4096. Both RDUs and A100s outperform V100s in terms of training time for all tested conditions. For the comparison between RDUs and A100s, a mixed picture is observed, where the result depends on the batch size and number of devices. For given GBS and number of devices, when the resulting LBS is small, RDUs outperform A100s, for example, GBS of 64 with 2, 4 and 8 devices, which correspond to LBS of 32, 16 and 8, respectively. For GBS of 128, results are closely comparable between the two architectures, with RDUs slightly faster by a factor of 1.13 for the case with 8 devices. For GBS of 1024, A100s appear to be slightly faster than RDUs by a factor of up to 1.17 for the cases with 2, 4 and 8 devices. Additional performance data for RDUs with 16, 24 and 32 devices are included in Table 3, which correspond to cases with end-to-end training times below 15 min (cf. Figure 4).

TABLE 3

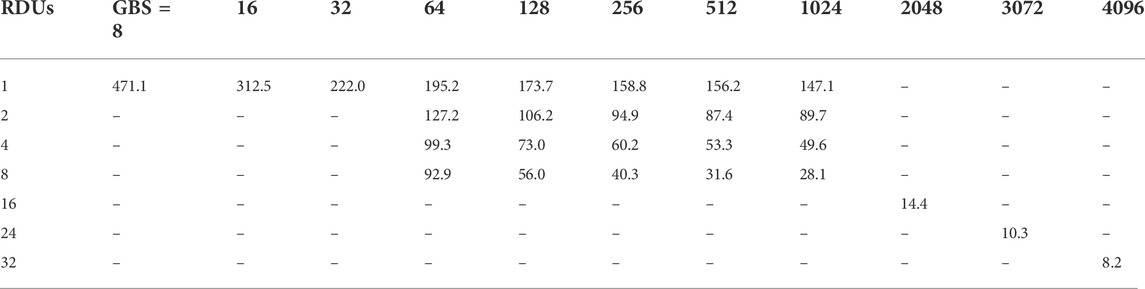
TABLE 3. Strong scaling, training time in seconds for one epoch with different GBSs using RDUs. Cases not carried out are indicated with dashes.

TABLE 4

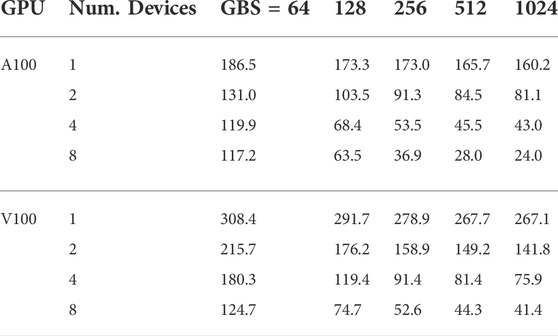
TABLE 4. Strong scaling, training time in seconds for one epoch with different GBSs using GPUs. The A100s were made available as a single DGX node with NVlink while the V100s were available across the PCI bus of a single node multi-GPU server.

The thick blue line in Figure 3A indicates the power law of x^−0.89 scaling for constant LBS of 128 for RDUs, quite close to inverse scaling, even when the training workload is distributed across multiple SN10-8 nodes. The general trends in Figures 3B–D indicate that RDUs tend to give a performance advantage for smaller LBSs, for example at LBS = 8 (GBS = 64, num. devs = 8) the RDU has a 1.26x and 1.34x advantage over the A100 and V100, respectively. Overall, we find that the CookieNetAE model can be efficiently trained at scale on multiple RDUs with relative performance versus A100 between a 1.26 advantage to a 0.85 disadvantage for GBS of 64 and 1024, respectively. The RDUs therefore comparable to the A100 with a slight disadvantage for GBS above 128 and a performance advantage for GBS at or below 128. These results are promising, point to the benefits for alternative architectures in regions of hyperparameter space, and motivate further research using other scientific ML models.

4 Discussion

The rapid adoption of ML for scientific data processing is triggering an explosion in researchers’ appetites for data [24]. An often overlooked challenge for such appetites, mining that voluminous data becomes its own challenge for which researchers quickly lose a taste. There has been a growing effort at accelerator-based user facilities to distill sensor data into physics-informed representations automatically in real-time [7]. When physics information is available as a stream of results, one can consider adaptive experimental campaigns that can rapidly explore parameters for faster scientific discovery. In the context of tokamak plasma fusion, this experimental redirection would occur between shots, e.g. one would incorporate the previous shot into an adaptive “shot plan” for the upcoming shots. This shot interval at the DIII-D reactor is 10 min which sets the timescale for our conservative expectation of 10–15 min training time in order to incorporate the last shot results into the adaptive sensor interpretation model for between-shot adaptation. A similar paradigm is an active pursuit for upcoming United States facilities as the LCLS-II [25] and APS-U [13] and existing foreign facilities like the EuroXFEL, each of which faces data acquisition rates that are pushing the limits of what can be transferred continuously over a network. Addressing this challenge, researchers are exploring reduced representations that retain as much of the relevant information contained in the original raw data while mapping to a more information-dense representation for storage and downstream use. This is a particular challenge for scientific cases whereby representation bias could poison data production pipelines. This negative aspect reduces trust of supervised ML approaches both for the fear that it will implicitly exclude novel discovery results or propagate errors undetected.

The attractiveness of recent developments in transformers [8–10] lies in their tendency to be forgiving in situations where task-specific labeled data is rare but unlabeled data, upon which deep embedding models can be trained, is abundant. Scientific use cases, though they rarely involve natural language processing, can in many situations treat multi-sensor data streams as if they were multi-channel audio streams as in analogy with MuseNET of Ref. [11]. The flexibility of transformer architectures to encode general structures into the feature embedding will allow researchers to leverage volumes of unlabeled results at our user facilities, leaving them with significantly less parameters to train with the highly valuable, but scarce, labeled datasets.

This manuscript was driven by our interest in retraining such embedding models frequently in order to accommodate sensor, light-source, and experimental variation. Our embedding models will continuously evolve with a running experiment, at the human and thermal timescale of minutes to hours, while the downstream task specific layers will be constant throughout an experimental campaign—days to weeks. In this case, the task-specific layers are significantly more static than the deep embedding layers. This is very much opposite to transformer use in language tasks. By analogy, imagine the spellings of the words in your vocabulary vary appreciably every 15 min during an extended conversation. This is exactly the case for the deep embedding model in scientific use cases, as the experimental environment varies, so too does the encoded representation of the incoming data stream. Our aspirations to keep on top of these variations, accommodating the experimental variations, is why we have chosen the encoder-decoder CookieNetAE example [12] for our benchmark.

Our measured results demonstrate rapid retraining of the network that is sufficiently deep to capture all relevant information needed for a broad range of domain specific tasks. We show that the expected 15-min scale of experimental evolution can be accommodated with the use of as few as 16 RDUs (two SN10-8 nodes) in data parallel training. Our work finds that the RDU architecture provides for an attractive system, one that is unique from GPUs, that accelerates ML workloads for scientific applications. The general trends seem to point that the RDU represents an advantage to the A100 GPU for training data that is broadly distributed among devices and shallow in each batch while the A100 favors deeper and less broadly distributed training data.

We add to the potential advantage to a shallow and broadly distributed training data, e.g. smaller LBSs and more number of devices [22]. In particular, for ensembles of models, a gradual increase in the variance of outputs could indicate the onset of concept drift. In such a case, having the ability to quickly add new individuals to a larger ensemble of smaller training batches, potentially enlisting additional RDUs for the growing ensemble, would allow for rapid adaptation to this drift. Since accelerator systems like free-electron lasers are typically in a state of fluctuation—much less calm than their synchrotron brethren—they are just such a case for wide, shallow, and dynamic training data sets.

Given the impending TB/s scale of data ingest at the LCLS-II [6], it is imperative that we leverage the trickle of raw—pre-scaled—data for adapting running inference models. Because this new machine [4] and others of its ilk [13] are quickly ramping the data velocity, we expect that an increasing number of users will explore ways to move as much of the pre-processing into the various operations that can be accelerated by dataflow architectures. These accelerators and the downstream user beamlines are dynamic environments where experimental configurations change on the 15 min timescale. The rapid retraining of the associated models could opportunistically leverage intermittent pauses in acquisition, typically every 20–30 min, but only for model retraining that consumes a small fraction of that cadence, e.g. one to few minutes. This cadence is set by the human driven environment at the xFEL where human interpretation of interactive data visualization consumes of order 15 min of collaborator discussion before deciding how best to drive the next steps in experimental campaign. In the fusion case, as noted above, the 10 min of between-shot time likewise sets a natural few shots and then discuss cadence to experimental campaigns. To date, this cadence represents a loose constraint as the results of such diagnostic interpretation models are not yet incorporated into accelerator feedback control systems dynamically, but such plans to feed dynamic model output into machine controls are actively being pursued by this and other groups at FELs and tokamaks. This study serves as a timely impetus for benchmarking short training time with emerging new computational hardware.

In conclusion, the advent of new architectures and the continual improvement in data parallel training will be a win for advancing our accelerator-based scientific user facilities. It will enable the kind of dynamic autonomous control that is required of these large accelerator facilities as is already being incorporated into fields as far reaching as neutron diffraction [1] and magnetic confinement fusion [2]. As the scientific data velocity accelerates in the coming years, and as control systems move to include low-latency high throughput inference, we will find an ever increasing need to match ML acceleration architectures to the scientific facilities that best take advantage of them.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/supplementary material.

Author contributions

PM and HR performed and collected all RDU results and ZL performed and collected all GPU results. NL and RC designed the initial CookieNetAE model architecture while ZL adapted for use in RDU and ThetaGPU. RC built the data simulation code and performed the analysis and presentation of all results. PM and HR contributed equally to the optimization of the RDU results, and CM described the SambaNova system in the manuscript. PM and RC contributed equally to the analysis and presentation of results and composition of the manuscript. HR, CM, and ZL also provided significant contribution to the preparation of the manuscript.

Funding

This work was funded by the Department of Energy, Office of Science, Office of Basic Energy Sciences under Field Work Proposal 100643 “Actionable Information from Sensor to Data Center.” Simulation of the detector was funded by Field Work Proposal 100498 “Enabling long wavelength Streaking for Attosecond X-ray Science.” The Argonne Leadership Computing Facility is a DOE Office of Science User Facility supported under Contract DE-AC02-06CH11357. The Linac Coherent Light Source (LCLS), SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515.

Acknowledgments

RNC acknowledges support from the Department of Energy, Office of Science, Office of Basic Energy Sciences for funding the development of the detector array itself under Grant Number FWP 100498 “Enabling long wavelength Streaking for Attosecond X-ray Science.” He also acknowledges synergistic support for computational method development by the Office of Fusion Energy Science under Field Work Proposal 100636 “Machine Learning for Real-time Fusion Plasma Behavior Prediction and Manipulation.” This research used resources of the Argonne Leadership Computing Facility, a DOE Office of Science User Facility supported under Contract DE-AC02-06CH11357, for collecting GPU related benchmarks.

Conflict of interest

Authors Petro Junior Milan, Hongqian Rong and Craig Michaud were employed by SambaNova Systems, Inc.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. McDannald A, Frontzek M, Savici AT, Doucet M, Rodriguez EE, Meuse K, et al. On-the-fly autonomous control of neutron diffraction via physics-informed bayesian active learning. Appl Phys Rev (2022) 9:021408. doi:10.1063/5.0082956

CrossRef Full Text | Google Scholar

2. Degrave J, Felici F, Buchli J, Neunert M, Tracey B, Carpanese F, et al. Magnetic control of tokamak plasmas through deep reinforcement learning. Nature (2022) 602:414–9. doi:10.1038/s41586-021-04301-9

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Zhang C, Shao YT, Baraissov Z, Duncan CJ, Hanuka A, Edelen AL, et al. Bayesian optimization for multi-dimensional alignment: Tuning aberration correctors and ptychographic reconstructions. Microsc Microanal (2022) 28:3146–8. doi:10.1017/S1431927622011692

CrossRef Full Text | Google Scholar

4. Schoenlein R. New science opportunities enabled by lcls-ii x-ray lasers. SLAC Report SLAC-R-1053 (2015). p. 1–189.

Google Scholar

5. Walter P, Kamalov A, Gatton A, Driver T, Bhogadi D, Castagna JC, et al. Multi-resolution electron spectrometer array for future free-electron laser experiments. J Synchrotron Radiat (2021) 28:1364–76. doi:10.1107/S1600577521007700

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Thayer JB, Carini G, Kroeger W, O’Grady C, Perazzo A, Shankar M, et al. Building a data system for lcls-ii. Piscataway, NJ, USA: Institute of Electrical and Electronics Engineers Inc. (2018). doi:10.1109/NSSMIC.2017.8533033

CrossRef Full Text | Google Scholar

7. Liu Z, Ali A, Kenesei P, Miceli A, Sharma H, Schwarz N, et al. Bridging data center ai systems with edge computing for actionable information retrieval. In: 2021 3rd Annual Workshop on Extreme-scale Experiment-in-the-Loop Computing (XLOOP). Lemont, IL, USA: IEEE (2021). p. 15–23.

CrossRef Full Text | Google Scholar

8. Devlin J, Chang M, Lee K, Toutanova K. BERT: Pre-training of deep bidirectional transformers for language understanding (2018). CoRR abs/1810.04805.

Google Scholar

9. Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez AN, et al. Attention is all you need (2017). doi:10.48550/ARXIV.1706.03762

CrossRef Full Text | Google Scholar

10. Radford A, Wu J, Child R, Luan D, Amodei D, Sutskever I. Language models are unsupervised multitask learners (2018).

Google Scholar

11. Payne C. Musenet (2019). Available from: openai.com/blog/musenet.

Google Scholar

12.[Dataset] Layad N, Liu Z, Coffee RN. Open source implementation of the cookienetae model (2022). Available from: https://github.com/AISDC/CookieNetAE.

Google Scholar

13. Hansard B. Advanced photon source upgrade will transform the world of scientific research (2020). Available from: https://www.anl.gov/article/advanced-photon-source-upgrade-will-transform-the-world-of-scientific-research.

Google Scholar

14. SambaNova Systems . Accelerated computing with a reconfigurable dataflow architecture (2021). Available from: https://sambanova.ai/wp-content/uploads/2021/06/SambaNova_RDA_Whitepaper_English.pdf.

Google Scholar

15. Emani M, Vishwanath V, Adams C, Papka ME, Stevens R, Florescu L, et al. Accelerating scientific applications with sambanova reconfigurable dataflow architecture. Comput Sci Eng (2021) 23:114–9. doi:10.1109/MCSE.2021.3057203

CrossRef Full Text | Google Scholar

16. Paszke AT. Pytorch: An imperative style, high-performance deep learning library. In: H Wallach, H Larochelle, A Beygelzimer, F d’Alché Buc, E Fox, and R Garnett, editors. Advances in neural information processing systems 32. Red Hook, NY, USA: Curran Associates, Inc. (2019). p. 8024–35.

Google Scholar

17. Hartmann N, Hartmann G, Heider R, Wagner MS, Ilchen M, Buck J, et al. Attosecond time–energy structure of x-ray free-electron laser pulses. Nat Photon (2018) 12:215–20. doi:10.1038/s41566-018-0107-6

CrossRef Full Text | Google Scholar

18.[Dataset] Coffee RN. Cookiesimslim: Slim simulator for lcls-slac cookiebox detector (2022). Available from: https://github.com/ryancoffee/CookieSimSlim.

Google Scholar

19. Li S, Guo Z, Coffee RN, Hegazy K, Huang Z, Natan A, et al. Characterizing isolated attosecond pulses with angular streaking. Opt Express (2018) 26:4531–47. doi:10.1364/OE.26.004531

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Uber I. Horovod (2022). Available from: https://github.com/horovod/horovod.git.

Google Scholar

21. Goodfellow I, Bengio Y, Courville A. Deep learning. Cambridge, MA, USA: MIT Press (2016). Available from: http://www.deeplearningbook.org.

Google Scholar

22. Masters D, Luschi C. Revisiting small batch training for deep neural networks (2018). doi:10.48550/ARXIV.1804.07612

CrossRef Full Text | Google Scholar

23. Duarte J, Harris P, Hauck S, Holzman B, Hsu SC, Jindariani S, et al. Fpga-accelerated machine learning inference as a service for particle physics computing. Comput Softw Big Sci (2019) 3:13–5. doi:10.1007/s41781-019-0027-2

CrossRef Full Text | Google Scholar

24. Sanchez-Gonzalez A, Micaelli P, Olivier C, Barillot TR, Ilchen M, Lutman AA, et al. Accurate prediction of x-ray pulse properties from a free-electron laser using machine learning. Nat Commun (2017) 8:15461. doi:10.1038/ncomms15461

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Corbeil Therrien A, Herbst R, Quijano O, Gatton A, Coffee R. Machine learning at the edge for ultra high rate detectors. In: 2019 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC). Manchester, UK: IEEE (2019). p. 1–4. doi:10.1109/NSS/MIC42101.2019.9059671

CrossRef Full Text | Google Scholar