The manipulation of ultracold atoms of high orbitals in optical lattices

Ultracold atoms in optical lattices are a powerful tool for quantum simulation, precise measurement, and quantum computation. A fundamental problem in applying this quantum system is how to manipulate the higher bands or orbitals in Bloch states effectively. Here we mainly review our methods for manipulating high orbital ultracold atoms in optical lattices with different configurations. Based on these methods, we construct the atom-orbital qubit under nonadiabatic holonomic quantum control and Ramsey interferometry with trapped motional quantum states. Then we review the observation of the novel quantum states and the study of the dynamical evolution of the high orbital atoms in optical lattices. The effective manipulation of the high orbitals provides strong support for applying ultracold atoms in the optical lattice in many fields.

1 Introduction

Ultracold atoms confined in optical lattices are a powerful tool for quantum simulation [1–3, 3–6], precision measurement [7], and quantum computation [8]. An optical lattice is formed by the interference of laser beams, creating a spatially periodic potential for ultracold atoms. The periodic potential generates the Bloch bands and Bloch states corresponding to different orbitals. Different to the study of ground band of optical lattice, by effectively manipulating the orbital degrees of freedom of ultracold atoms in the optical lattice, novel quantum states are found [9–12], and new qubits [8] and interferometers [13] based on the atomic orbitals are realized. In applying these high orbital ultracold atoms in optical lattices, a fundamental problem is how to manipulate the orbitals. Unlike internal states of atoms, the effective manipulation of Bloch states in optical lattices is complex because of the lack of selection rules [14]. Recently, methods to effectively manipulate Bloch states and high orbitals of optical lattices have been proposed, such as stimulated Raman transitions [15], shortcut method [14, 16–21], phase imprint [22], moving lattices [23], and band swapping technique [9, 11, 12, 24].

In this paper, we review our practical methods for manipulating high orbital atoms in optical lattices. These methods contain the shortcut method [14], band swapping technique [9, 11, 12, 24], and the amplitude modulation method to manipulate atoms in optical lattices [25]. The shortcut is a nonadiabatic coherent control composed of lattice pulse sequences [14]. The band swapping technique refers to quickly switching the structure of deep and shallow composite lattice, realizing the inversion of Bloch bands, and pumping atoms to the target band [9]. The manipulation of atoms in an optical lattice by amplitude modulation is another flexible way to control Bloch states coherently. In this method, the modulation with more than one frequency is applied to the lattice, couples the different orbitals, and realizes a large-momentum-transfer beam splitter [25]. We can manipulate any Bloch state of optical lattices with different configurations based on these methods. All the experiments in this paper are based on a Bose-Einstein-Condensate (BEC) of ⁸⁷Rb prepared in a hybrid trap with the harmonic trap frequencies (ω_x, ω_y, ω_z) = 2π × (28, 55, 60) Hz [21]. The experiments are mainly carried out in one dimensional (1D) and two dimensional (2D) triangular optical lattices. For 1D lattice, atoms are confined in more than 50 discrete pancakes with each pancakes containing 2000 atoms on average [10]. For triangular lattice, there are around 800 tubes with each tube containing 60 atoms on average [12].

The structure of this review is organized as follows. In section 2, we introduce the Bloch bands of atoms in optical lattices and review three methods for manipulating high orbital atoms in optical lattices. Then, we review the related applications based on these methods in section 3, including the atom-orbital qubit under nonadiabatic holonomic quantum control, Ramsey interferometry with trapped motional quantum states of the optical lattice. In section 4, we review the observations of exotic quantum states of p-orbital ultracold atoms. In section 5, we analyze the dynamical character of high orbital atoms in optical lattices. Finally, section 6 is the summary of this paper.

2 Manipulation of high orbital atoms in optical lattices

2.1 Bloch bands of atoms in optical lattice

An optical lattice is formed by the interference of a set of laser beams with electric field amplitude ${\vec{E}}_i$, which provides a spatially periodic potential for atoms:

$V\left(\mathit{r}\right)=\alpha \sum _{i,j}{\mathit{E}}_i\cdot {\mathit{E}}_j\cos \left(\left({\mathit{k}}_i-{\mathit{k}}_j\right)\cdot \mathit{r}+\left({\beta }_i-{\beta }_j\right)\right)(1)$

where k_i is the wave number and β_i is the initial phase of laser beams i, and α is the coefficient related to detuning, atomic energy level, etc. For red detuned beams, α is negative. After neglecting the interactions between atoms, the Hamiltonian for single atom in optical lattice is $\widehat{H}=\frac{{\widehat{p}}^2}{2m}+V(\mathit{r})$. According to the Bloch’s theorem, the periodic potential can generate Bloch bands and Bloch states Ψ_n,q, which can be expressed by

${\mathrm{\Psi }}_{n,\mathit{q}}\left(\mathit{r}\right)=u_{n,\mathit{q}}\left(\mathit{r}\right)e^{i\mathit{q}\cdot \mathit{r}},(2)$

where n = 1, 2, 3 … is the index of the Bloch bands, q is the quasi-momentum, and u_n,q is a periodic function. The bloch states Ψ_n,q, or the eigenstates of $\widehat{H}$ can be projected onto a series of momentum eigenstates:

${\mathrm{\Psi }}_{n,\mathit{q}}=\sum _{{\ell }_1,{\ell }_2,{\ell }_3}{c}_{{\ell }_1,{\ell }_2,{\ell }_3}^{n,\mathit{q}}|\hslash \left({\ell }_1{\mathit{b}}_1+{\ell }_2{\mathit{b}}_2+{\ell }_3{\mathit{b}}_3\right)+\mathit{q}\rangle (3)$

where b_i is the reciprocal lattice vector.

Figure 1 shows two different configurations of optical lattices, 1D lattice and triangular lattice. As for the 1D lattice in Figure 1A, the lattice constant is d = λ/2 and the band spectrum is shown in Figure 1B (when lattice depth V = 5E_r, where E_r = ℏ²k²/2m is the recoil energy and k = 2π/λ). From the bottom to the top of the spectrum, the Bloch bands are S-, P-, D-, F-, and G-band, corresponding to n = 1, 2, 3, 4, 5, respectively. In Figure 1C, the triangular lattice with lattice constant 2/3λ, is constructed by three laser beams. The spectrum of this triangular lattice is different from that of the 1D lattice, where Bloch bands split into some different bands, as shown in Figure 1D (when the lattice depth is 3E_r).

FIGURE 1

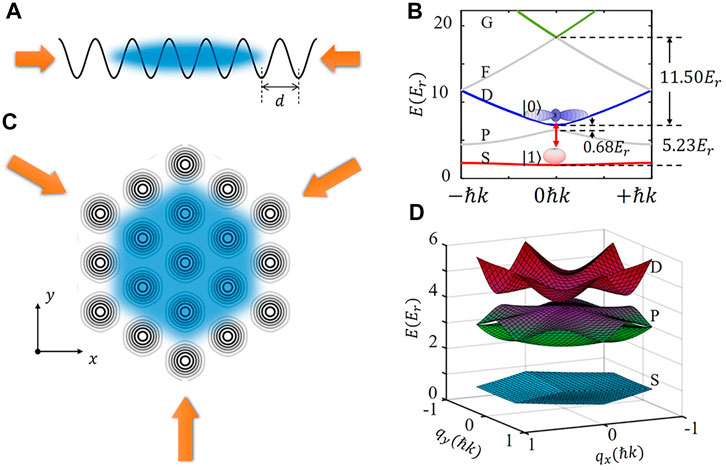
FIGURE 1. Schematic diagram and band structure of optical lattices. (A) is a 1D optical lattice with the lattice constant d. (B) The band-gap structures of 1D optical lattice for lattice depth V = 5E_r with laser wavelength 1,064 nm. (C) is a triangular optical lattice, with the corresponding band structure (D) for lattice depth V = 3E_r.

Before introducing the manipulation of the atoms in Bloch bands, we review the methods used in our experiments to probe the Bloch states. The first method is the band mapping technique [14, 15, 26–28]. In the experiment, if we switch off the lattice adiabatically within around 1 ms, the atoms in different bands can be mapped to different momentum components, measured after the time of flight (TOF). In addition, the value of quasi-momentum can be obtained from the position of atoms in corresponding Brillouin zones after the band mapping process and TOF. Figure 2A shows the band mapping result of atoms in a triangular lattice. Atoms are mainly distributed in the fourth Brillouin zone, corresponding to the D-band.

FIGURE 2

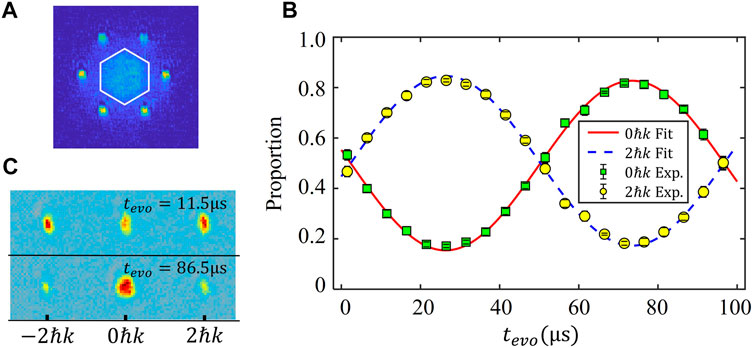
FIGURE 2. (A) Experimental result of atoms in D-band after band mapping process. The white hexagon is the boundary of the first Brillouin zone of the triangular lattice. The atoms are mainly distributed in the fourth Brillouin zone. (B) TOF quantum state tomography process. The initial state is a superposition Bloch state of the 1D optical lattice. After different evolution time t_evo, the atom number proportion at 0ℏk and ± 2ℏk are shown by the green and yellow points. (C) The momentum distribution of atoms at t_evo = 11.5μs and 86.5μs. The lattice depth is V = 5E_r.

The band mapping method is easy to implement in the experiment, and the atomic population of different Bloch bands can be obtained. However, in this mapping process, the phase information of the Bloch state is lost. Then we use a TOF quantum state tomography (TOFQST) method to extract full information about the Bloch states [8]. For example, we use the TOFQST to detect the superposition of Bloch states in a 1D optical lattice with depth V = 5E_r. In the experiment, we let the state evolve in the static lattice for a certain time t_evo. Then we turn off the lattice diabatically and measure the momentum distribution after 31 ms TOF, which is shown in figure 2BC. By fitting the experimental data, we can obtain the full information of the states $\psi =\sqrt{0.493}{\mathrm{\Psi }}_{\mathrm{1,0}}+\sqrt{0.507}{e}^{i\cdot 0.987\pi }{\mathrm{\Psi }}_{\mathrm{3,0}}$.

2.2 Shortcut to manipulating atoms in optical lattice

2.2.1 Introduction of the shortcut method

This section demonstrates a shortcut method for manipulating atoms in different Bloch bands [14, 16–21]. This method is characterized by short time and high fidelity, which can directly transfer ultracold atoms from the ground state in the harmonic trap to any Bloch state, and accurately manipulate atoms of different orbitals in optical lattices. The shortcut is composed of a series of optical lattice pulse sequences, which is shown in 3A. Each pulse pulse-i consists of two parts. First, the lattice is turned on for $t_j^{\text{on}}$, and then the interval is $t_j^{\text{off}}$. The time $\{t_j^{\text{on}},t_j^{\text{off}}\}$ are optimized to achieve the goal of manipulating quantum states.

We consider a general situation for transferring an arbitrary initial state |ψ_i⟩ to a target state |ψ_t⟩, where the states |ψ_i⟩ and |ψ_t⟩ can be the Bloch eigenstates or the superposition states. This shortcut applied to the initial state can be expressed as an evolution operator ${\widehat{U}}_s={\prod }_{j=M}^1{\widehat{U}}_j^{t_j^{\text{on}},t_j^{\text{off}}}$. Here ${\widehat{U}}_j$ represents evolution operator of the jth pulse, ${\widehat{U}}_j=e^{-i({\widehat{H}}_j^{\text{on}}{t}_j^{\text{on}}+{\widehat{H}}_j^{\text{off}}{t}_j^{\text{off}})}$, with ${\widehat{H}}_j^{\text{on}}=\frac{{\widehat{p}}^2}{2m}+V(\mathit{r})$ and ${\widehat{H}}_j^{\text{off}}=\frac{{\widehat{p}}^2}{2m}$. The final state after the shortcut is $|{\psi }_f\rangle ={\widehat{U}}_s|{\psi }_i\rangle$. Then we define the fidelity F of the manipulation

$F=|\langle {\psi }_f|{\psi }_t\rangle |=|\langle {\psi }_f|\prod _{j=M}^1{\widehat{U}}_j^{t_j^{\text{on}},t_j^{\text{off}}}|{\psi }_i\rangle |.(4)$

By optimizing the pulse sequences $\{t_j^{\text{on}},t_j^{\text{off}}\}$ to maximize F, the operation process with high fidelity for manipulating Bloch states or high orbital atoms in an optical lattice is obtained.

To verify the effectiveness of the shortcut, we demonstrate some experimental results in Figures 2, 3. In Figure 3C, we list some pulse sequences for manipulating Bloch states, where the initial states are all the ground states of the harmonic trap, |p = 0⟩ zero momentum state. For 1D optical lattice, we achieve to transfer atoms from zero momentum state to D-band, G-band, and the superposition states of S and D band with zero quasi-momentum, which corresponds to Figure 3B1B2, and Figure 2BC, and this theory fidelity is more than 99% [14]. For the D-band of the triangular optical lattice with depth V = 3E_r, we give the shortcut sequence with 99.95% fidelity in Figure 3C, and the experimental band mapping results is shown in Figure 2A [21].

FIGURE 3

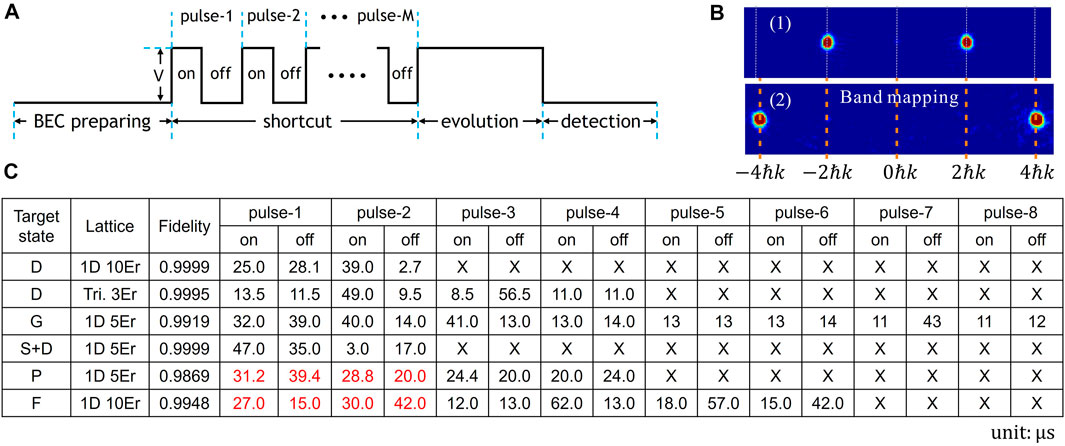
FIGURE 3. (A) The timing diagram of the shortcut. (B) The band mapping result of D-band (top) and G-band (bottom) with zero quasi-momentum for 1D optical lattice. (C) The parameters of shortcut for different target states and optical lattice. The red time parameter is for the sequence of misplacement lattice for the P-band and F-band sequences. The quasi-momentum of all target states in this figure is zero. This symbol X indicates that there is no pulse.

2.2.2 Manipulating bloch states with different symmetries

The symmetry of Bloch states with different energy bands and quasi momentum is different. For example, in the 1D optical lattice, Eq. 3 is rewritten as

${\mathrm{\Psi }}_{n,\mathit{q}}=\sum _{\ell }{c}_{\ell }^{n,q}|\ell \cdot 2\hslash k+q\rangle .(5)$

The parity of Bloch states on S-, D-, and G-bands with zero quasi-momentum is even, which is shown in Figure 4A. On the contrary, the P- and F-bands with zero quasi-momentum are odd parity. Moreover, the symmetries of Bloch states with non-zero quasi-momentum are also different from that of zero quasi-momentum states. On the other hand, the symmetries of the 1D optical lattice and the initial states |p = 0⟩ are even. Hence, we can easily prepare and manipulate even parity Bloch states, such as S-, D-, and G-bands with zero quasi-momentum. However, it is challenging to prepare states with different parity or change the symmetry. In order to expand the application scope of the shortcut, we propose two methods.

FIGURE 4

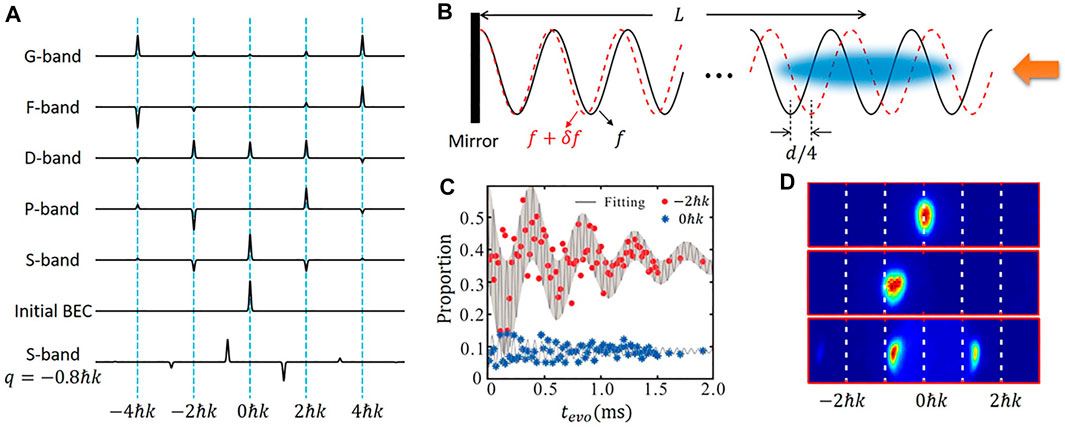
FIGURE 4. (A) From the bottom to the top, the solid lines represent the momentum distributions of different states (S-band with q = −0.8ℏk, initial BEC with p = 0, S-, P-, D-, F-, and G-band with zero quasi-momentum). (B) Two 1D lattices with a d/4 position shift. (C) Population oscillations around momenta − 2ℏk (red points) and 0ℏk (blue stars). The solid lines are the fitting curves. (D) The experimental images: from top to bottom, the images are for the initial BEC with p = 0, the BECs with p₀ = −0.8ℏk after acceleration, and the final states Ψ_1,−0.8ℏk.

The first method is to use two misplacement lattices [10, 14, 18]. In experiments, we realize this configuration through a reflective optical path and two laser beams with frequency difference δf, as shown in Figure 4B. When the distance L between BECs and mirror and laser frequency f are fixed, we can realize the misplacement of d/4 of the two sets of standing wave optical lattices by adjusting the frequency difference δf. Because δf ≪ f, the lattice constants of the two lattices can be regarded as the same. As an example, we transfer atoms from |p = 0⟩ to P-band with zero quasi-momentum Ψ_2,0. We apply two sets of shortcut sequences in turn. The first one is of the lattice with frequency f + δf, and the second is of f. When the first sequence is switched to the second, each momentum state component c_ℓ|ℓ ⋅ 2ℏk⟩ will be attached with a phase and becomes $e^{i\cdot \frac{\pi }{2}\ell }{c}_{\ell }|\ell \cdot 2\hslash k\rangle$. We design the first sequence to make c_ℓ = 0 for ℓ = 2, 4, 6 … and keep only c_ℓ for ℓ = 1, 3, 4 …. So the result is that after the first sequence, the quantum state changes to odd parity, c_ℓ = −c_−ℓ for all ℓ. Finally, we use the second sequence to adjust this odd parity state to Ψ_2,0. In the experiment, we use TOFQST to detect the final state in the 1D lattice with depth V = 5E_r, shown in Figure 4C, and the experimental fidelity is more than 90%. The parameters of these sequences are shown in Figure 3C [18]. Similarly, we can also use this scheme to load atoms into the F-band [14], and the sequence is shown in Figure 3C.

The second method is to change the symmetry of the initial state. For example, we demonstrate how to transfer atoms from initial BEC to non-zero quasi-momentum Bloch state in S-band. As shown in Figure 4D, the atoms with p = 0 is accelerated to obtain a momentum p₀ = −0.8ℏk. Immediately afterward, the designed shortcut sequence is used to transfer atoms into the S-band at − 0.8ℏk quasi-momentum. The bottom figure of 4D is the momentum distribution of the final state in the experiment [14].

Hence, our shortcut method can be applied to manipulate arbitrary Bloch states in any Bloch band within a very short time and with high fidelity. Moreover, This shortcut can be applied to optical lattices with different configurations.

2.2.3 Atomic momentum patterns with narrower intervals

The previous method is mainly for the Bloch state with a certain single quasi-momentum, and the intervals of the momentum peaks are 2ℏk (for 1D optical lattice). The manipulation of the entire Bloch band and the preparation of narrow momentum peak distribution will also appear in many applications, such as the atom interferometer [29–31]. However, the manipulation of this superposition state with different quasimomenta is seldom studied [19]. In this section, we expand the shortcut to manipulating the superposed Bloch states with different quasi-momenta. Figure 5A shows the time sequence for the manipulating process of the superposed states. The first challenge is to prepare the superposition states |ψ(0)⟩ with different quasi-momentum that spread the whole S-band, as shown in Figure 5B. In the experiment, we first prepare a superposed state $\frac{1}{\sqrt{2}}({\mathrm{\Psi }}_{\mathrm{1,0}}+{\mathrm{\Psi }}_{\mathrm{3,0}})$ by shortcut and hold the lattice for a time t_OL. When t_OL = 30 ms, the atoms are almost all in the first Brillouin zone of S-band, which is due to collisions during the holding time, as shown in Figure 5C [19].

FIGURE 5

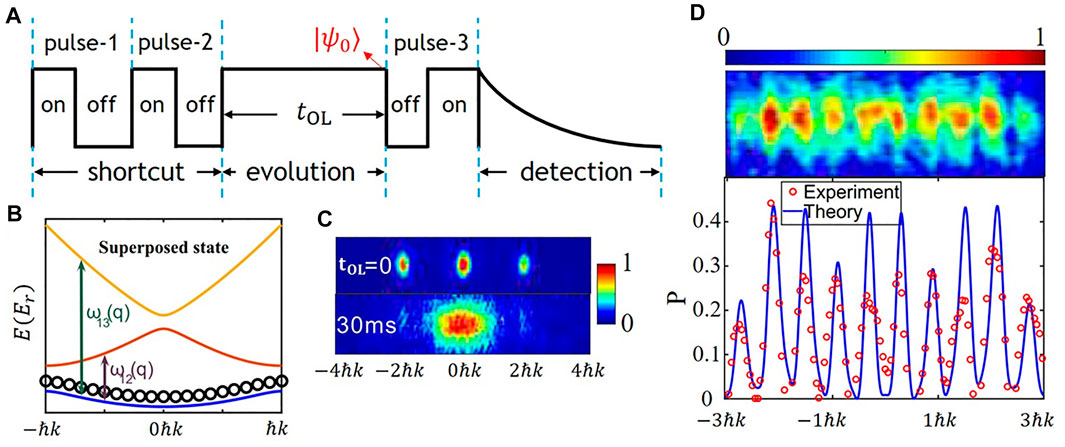
FIGURE 5. (A) Time sequence: after the first two pulses and the 30 ms holding time in the optical lattice, the state becomes the superposition of the Bloch states in S-band with quasi-momentum taking the values throughout the first Brillouin zone, denoted as |ψ(0)⟩. (B) The superposition of Bloch states of S-band spreading the whole S-band. (C) The comparison of the experimental results between t_OL = 0 ms and t_OL = 30 ms. These results are obtained after the sequence in (A) but without pulse-3. (D) Patterns with ten main peaks for the experimental measurements (the red circles) and the theoretical curves (the solid blue line).

The next challenge is how to design the pulse-3 in Figure 5A for atomic momentum patterns with narrower intervals. First, we analyze the action of the pulse on |ψ(0)⟩. The initial state can be expressed as

$|\psi \left(0\right)\rangle =\frac{1}{\sqrt{N}}\sum _{q=-\hslash k}^{\hslash k}{\mathrm{\Psi }}_{1,q}.(6)$

After the pulse-3 (with interal $t_3^{\text{off}}$ and duration $t_3^{\text{on}}$), the momentum distribution P (0, q) is

$P\left(0,q\right)\approx C_1+C_2\cos \left(W_{\mathrm{1,0}}{t}_3^{\text{off}}\right)+C_3\cos \left(W_{-\mathrm{1,0}}{t}_3^{\text{off}}\right)+C_4\cos \left({\omega }_{\mathrm{1,2}}{t}_3^{\text{on}}\right)+C_5\cos \left({\omega }_{\mathrm{1,3}}{t}_3^{\text{on}}\right),(7)$

where C_i is the corrresponding amplitudes from the numerical calculations, W_ℓ,ℓ′ = ℏ² [(2ℓk + q)² − (2ℓ′k + q)²]/2m and ω_n,n′ = E^n,q − Eⁿ′^,q (the band gap between n and n′ band at quasi-momentum q) corresponds to the energy difference between different momentum states and Bloch states, respectively. By designing the $t_3^{\text{off}}$ and $t_3^{\text{on}}$, we can get the momentum patterns P (0, q) with narrower intervals. In Figure 5D, we use the sequence $t_3^{\text{off}}=118\mu s$ and $t_3^{\text{on}}=19\mu s$, and obtain ten main peaks with 0.6ℏk interval for lattice depth 10E_r [19].

2.3 Band swapping tecnique for loading atoms into high bands

The band swapping technique is another method for loading atoms into high Bloch bands, which can be used to study the characteristics of Bloch bands and orbits. This technique is first proposed in [9] to load atoms into the P-band of a checkerboard square lattice and is also applicable to other configurations of optical lattices. The key to realizing this technology is constructing a controllable composite optical lattice, including deep and shallow wells. Compared with the shortcut method, the band swapping technique is more suitable for the study of ground state or metastable state.

Here, we take a hexagonal lattice as an example to show the process of band swapping [12]. We choose triangle lattice because it is more complex than square lattice, and it is impossible to separate variables in two directions directly. Three intersecting far-red-detuned laser beams form the hexagonal lattice in the x − y plane with an enclosing angle of 120^o. Each beam is formed by combining two linearly polarized lights with polarization directions oriented in the x − y plane (denoted as ϵ light) and along the z axis (denoted as ϵ′ light), respectively. The ϵ light form a honeycomb lattice as shown in Figure 6A. The ϵ′ light form a triangular lattice as shown in Figure 6B. The superposition of the two groups of optical lattices is the configuration shown in Figure 6C, which consists of two wells with different depths (denoted as $\mathcal{A}$ and $\mathcal{B}$). The optical potential takes the form

$V\left(\mathit{r}\right)=-V_{{ϵ}^{\prime }}\sum _{i,j}\cos \left[\left({\mathit{k}}_i-{\mathit{k}}_j\right)\cdot \mathit{r}+{\theta }_j-{\theta }_i\right]+\frac{1}{2}{V}_{ϵ}\sum _{i,j}\cos \left[\left({\mathit{k}}_i-{\mathit{k}}_j\right)\cdot \mathit{r}\right],(8)$

where ${\mathit{k}}_1=(\sqrt{3}\pi ,-\pi )/\lambda$, ${\mathit{k}}_2=(-\sqrt{3}\pi ,-\pi )/\lambda$, k₃ = (0, 2π)/λ, and V_ϵ (V_ϵ′) is the depth of the honeycomb (triangular) lattice. The depth difference between the two wells $\mathcal{A}$ and $\mathcal{B}$ can be adjusted by the ϵ-to-ϵ′ light intensity ratio (denoted as tan²α = V_ϵ′/V_ϵ), and the relative phases θ_1,2,3. First, we adiabatically load the BEC into the ground band with zero quasi-momentum of the optical lattice. The phase differences are initially set to be θ_1,2,3 = (2π/3, 4π/3, 0), for which the $\mathcal{B}$ wells are deeper than the $\mathcal{A}$ wells. In real space, atoms mainly reside in the s orbitals of $\mathcal{B}$ wells as shown in Figure 6D. Then we switch the relative phases rapidly to θ_1,2,3 = (4π/3, 2π/3, 0), making $\mathcal{A}$ wells much lower than $\mathcal{B}$. In this way, the atomic sample is directly projected onto the excited band. The key is to select appropriate parameters (ϵ′ and ϵ) to make the distribution of the wave function (Figure 6D) of the ground band before the switch consistent with that (Figure 6E) of the second band after the switch (at zero quasi-momentum). In our experiment, the range of parameter selection is in the black circle of Figure 6F, where the total lattice depth is 30E_r and α = 14°. As shown in Figure 11A, after this band swapping process, the atoms are pumped into the second band [12].

FIGURE 6

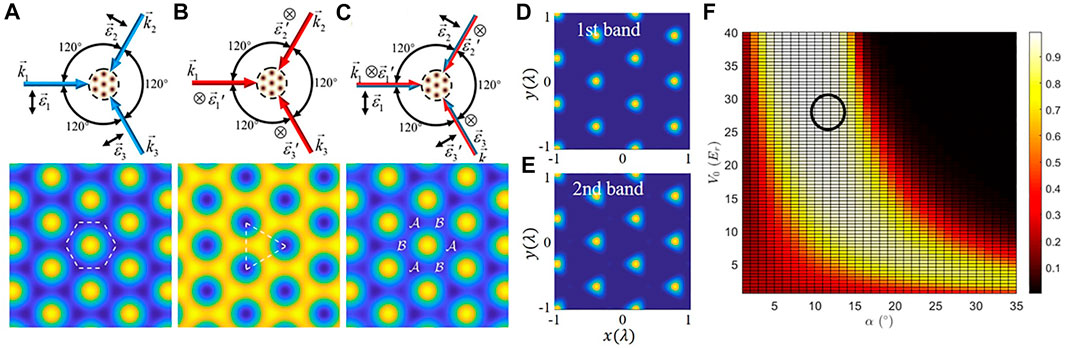
FIGURE 6. The arrangement of the laser beams forms the honeycomb (A) and triangular (B) lattice. The two groups of sublattices form a composite hexagonal lattice (C), which consists $\mathcal{A}$ and $\mathcal{B}$ wells. (D) and (E) represent the wave function distributions in the real space of the ground band and the second band with zero quasi-momentum, respectively. (F) The wavefunction overlap with different lattice depth and light intensity ratios.

2.4 Manipulation of atoms in optical lattice by amplitude modulation

The modulation with more than one frequency component to optical lattices provides a flexible way to control quantum states coherently [25]. In this section, we demonstrate bi-frequency modulations, which can be used to couple the S- and G-band of 1D optical lattice and realize a large-momentum-transfer beam splitter.

For atoms in an amplitude modulated lattice system along the x axis, as schematically shown in Figure 7A, the time-dependent Hamiltonian can be written as

$H\left(t\right)=\frac{p_x^2}{2m}+V_0{\cos }^2\left(kx\right)+\sum _i{V}_i\cos \left({\omega }_{i}t+{\varphi }_i\right){\cos }^2\left(kx\right).(9)$

The second term on the right hand represents optical lattice potential without modulation. The last term is the amplitude modulation with modulation amplitude V_i, the frequency ω_i, and the phase ϕ_i of each frequency component [25].

FIGURE 7

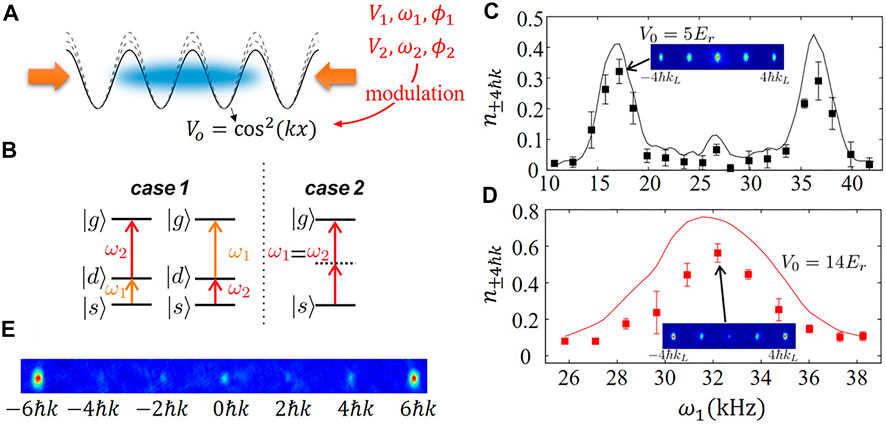
FIGURE 7. (A) Schematic diagram of the polychromatic amplitude modulation lattice. (B) Two special cases in detecting the transfer population spectrum. In case 1, absorption of photons with ω₁ or ω₂ is resonant with D-band. In case 2, two frequencies are equal. Spectrum for the population on ± 4ℏk states with increasing of modulation frequency ω₁ for (C) V₀ = 5E_r with V₁ = 1.4E_r, V₂ = 1.6E_r, modulation time t = 300μs, and for (D) V₀ = 14E_r with V₁ = V₂ = 2.5E_r, and t = 150μs. (E) A large-momentum-transfer beam splitter with a separation of 12ℏk.

According to the Floquet’s theorem, a bi-frequency modulation induced two-photon process between S- and D-band is described by an effective Hamiltonian H_SG as

$H_{SG}=\left(\begin{array}{cccccc}\hfill E_S\hfill & \hfill e^{i{\varphi }_1}{V}_1{\mathrm{\Omega }}_{SD}\hfill & \hfill e^{i{\varphi }_2}{V}_2{\mathrm{\Omega }}_{SD}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill e^{-i{\varphi }_1}{V}_1{\mathrm{\Omega }}_{SD}^{\ast }\hfill & \hfill E_D-\hslash {\omega }_1\hfill & \hfill 0\hfill & \hfill e^{i{\varphi }_2}{V}_2{\mathrm{\Omega }}_{DG}\hfill & \hfill e^{i{\varphi }_1}{V}_1{\mathrm{\Omega }}_{DG}\hfill & \hfill 0\hfill \\ \hfill e^{-i{\varphi }_2}{V}_2{\mathrm{\Omega }}_{SD}^{\ast }\hfill & \hfill 0\hfill & \hfill E_D-\hslash {\omega }_2\hfill & \hfill e^{i{\varphi }_1}{V}_1{\mathrm{\Omega }}_{DG}\hfill & \hfill 0\hfill & \hfill e^{i{\varphi }_2}{V}_2{\mathrm{\Omega }}_{DG}\hfill \\ \hfill 0\hfill & \hfill e^{-i{\varphi }_2}{V}_2{\mathrm{\Omega }}_{DG}^{\ast }\hfill & \hfill e^{-i{\varphi }_1}{V}_1{\mathrm{\Omega }}_{DG}^{\ast }\hfill & \hfill E_G-\hslash \left({\omega }_1+{\omega }_2\right)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill e^{-i{\varphi }_1}{V}_1{\mathrm{\Omega }}_{DG}^{\ast }\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill E_G-2\hslash {\omega }_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill e^{-i{\varphi }_2}{V}_2{\mathrm{\Omega }}_{DG}^{\ast }\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill E_G-2\hslash {\omega }_2\hfill \end{array}\right),(10)$

where Ω_nn′ = ⟨Ψ_n,0| cos² (kx)|Ψ_n′,0⟩ with Ψ_n,0 the Bloch states on n band at zero quasi-momentum. We include six nearly degenerate states considering four main process in the excitation, which are |E_S⟩, |E_D − ℏω₁⟩, |E_D − ℏω₂⟩, |E_G − ℏ(ω₁ + ω₂)⟩, |E_G − 2ℏω₁⟩, and |E_G − 2ℏω₂⟩. Using this basis a general state ${(v_1,V_2,V_3,V_4,v_5,v_6)}^T$ gives complex coefficient of the six dressed states. Population on S-band is |v₁|², while population on G-band is $|v_4{e}^{i({\omega }_1+{\omega }_2)t}+v_5{e}^{2i{\omega }_{1}t}+v_{6}2i{\omega }_{2}t{|}^2$, given by coherent superposition of all G band states dressed with different Floquet photons. This effective model provides us a better understanding of the mutiphoton process. However, in the calculation more states associated with higher order processes could be included to get a more accurate result.

In the experiment, we keep the frequences ω₁ and ω₂ satisfying ω₁ + ω₂ = ω_SG. According to Eq. 10, there are two cases which would benefit the excitation process (shown in Figure 7B).

Case 1: Resonant two-photon process. When ω₁ = ω_SD or ω₂ = ω_SD, atoms are transferred from Ψ_1,0 to Ψ_5,0 with the assistance of D band as an intermediate band.

Case 2: Equal frequency two-photon process. When ω₁ = ω₂ = ω_SG/2, two modulations with the same frequency can be added together, and the coupling strength of the process is doubled.

In the experiments, we sweep the frequency ω₁ for different lattice depth V = 5E_r and 14E_r, and measure the population on momentum states ± 4ℏk that relect the transfer rate to G-band. For V = 5E_r, in Figure 7C, two peaks appear at ω₁ = ω_SD and ω₂ = ω_SD follows Case 1. And the central peak at frequency ω₁ = ω₂ = ω_SG/2 following Case 2 is much lower than Case 1. For V = 14E_r, only one peak is measured in Figure 7D, which means Case 1 and Case 2 are fulfilled simultaneously. Under this condition, the coupling is greatly enhanced. This bi-frequency modulation can also be applied to realize a large-momentum-transfer beam splitter, such as a distribution at ± 6ℏk. We choose the frequency ω₁ = ω_SD = ω_DG and ω₂ = ω_GI (with I the seventh Bloch band). The experimental result is shown in Figure 7E [25].

This polychromatic amplitude modulation can be further improved to achieve more complex manipulation. We can control each period of the modulation waveform separately. Each period can be regarded as a pulse, which is shown in Figure 8A. The modulation amplitude A_i, phase ϕ_i, and frequency ω_i are optimized to achieve more accurate Bloch states manipulation, such as holonomic quantum control [8], which will be discussed in detail next section.

FIGURE 8

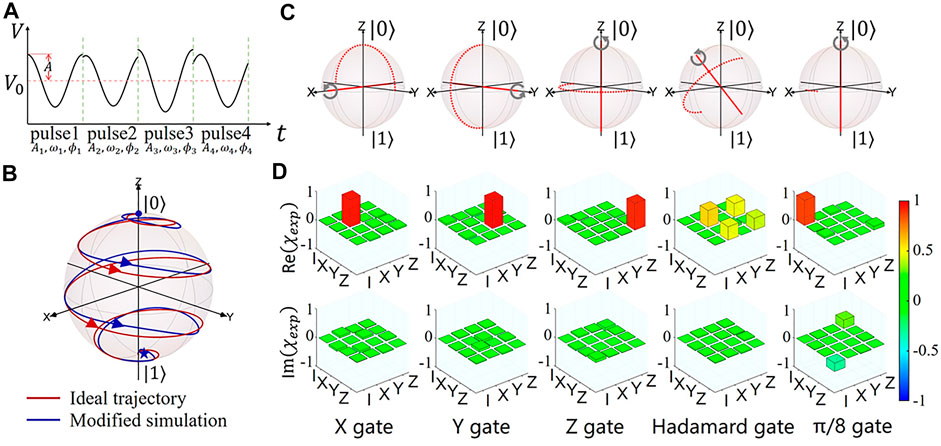
FIGURE 8. (A) The pulse sequence of the holonomic gate. (B) Simulated time evolution of the |0⟩ on the Bloch sphere under the holonomic X gate. (C) The schematic illustration of the quantum process. (D) Process matrices of the implemented holonomic X, Y, Z, Hadamard, and π/8 gates by quantum process tomography measurements.

In this section, we list three methods for manipulating ultracold atoms of high orbitals in optical lattices. The shortcut method is characterized by short time and high fidelity, which can directly transfer ultracold atoms from the ground state in the harmonic trap to any Bloch state, and accurately manipulate atoms of different orbitals in optical lattices. This method can be used to construct atomic orbital interferometers and qubits and to study the dynamic properties of high orbital atoms in optical lattices. The band swapping technique considers the interaction between atoms and the additional potential trap (such as harmonic trap) besides the optical lattice, which is more suitable for studying the ground and metastable states of the system. The amplitude modulation focuses on coupling different Bloch bands and can be used to realize quantum gates and the large-momentum-transfer beam splitter.

3 Application of manipulating high orbital atoms in optical lattices

3.1 Atom-orbital qubit under nonadiabatic holonomic quantum control

In section 2.4, we mentioned that the amplitude modulation pulses could realize the holonomic quantum control. This section demonstrates an atom-orbital qubit by manipulating the s and d orbitals of BECs in the 1D optical lattice. Moreover, we achieve noise-resilient single-qubit gates by performing holonomic quantum control, allowing geometrical protection. The atom-orbital qubit and quantum control are based on the shortcut and amplitude modulation methods [8].

As shown in Figure 1A, the band gap between S and D band (5.23E_r) is much smaller than that between D and G band (11.50E_r) for optical lattice depth V = 5E_r. With leakage to other bands neglected, the system corresponds to a two-level system, defining our atom-orbital qubit, Ψ_3,0 and Ψ_1,0 being orbital states identified as the qubit basis states |0⟩ and |1⟩. The 1D optical lattice potential is V_p(x) = V₀ cos² (kx), which is formed by 1,064 nm laser beams. We use shortcut method to initialize the qubit to an arbitrary state, |ψ⟩ = cos θ|0⟩ + sin θe^iφ|1⟩. By TOFQST, we extract the fidelities of initial states $\{|0\rangle ,|1\rangle ,\frac{1}{\sqrt{2}}(|0\rangle +|1\rangle ),\frac{1}{\sqrt{2}}(|0\rangle -|1\rangle ),\frac{1}{\sqrt{2}}(|0\rangle +i|1\rangle ),\frac{1}{\sqrt{2}}(|0\rangle -i|1\rangle )\}$, and the averaged fidelity is 99.72 (7)%. The relaxation time and dephasing time are 4.5 ± 0.1 ms and 2.1 ± 0.1 ms, respectively [8].

The modulation pulses on potential takes form

$\mathrm{\Delta }V\left(x,t\right)=A\sin \left(\omega t+\varphi \right)V_p\left(x\right),(11)$

where amplitude A, phase ϕ and frequency ω programmable in our experiment. After a rotating wave approximation, we have a qubit control Hamiltonian H(t)

$H\left(t\right)=\frac{1}{2}\mathrm{\Delta }{\sigma }_z+\frac{1}{2}\lambda \left[-\cos \left(\omega t+\varphi \right){\sigma }_y+\sin \left(\omega t+\varphi \right){\sigma }_x\right],(12)$

with Δ the gap between the S and D bands at zero quasi-momentum, and the induced coupling by the lattice modulation

$\lambda =A\int dx{V}_p\left(x\right){\mathrm{\Psi }}_{\mathrm{3,0}}\left(x\right){\mathrm{\Psi }}_{\mathrm{1,0}}\left(x\right),(13)$

We implement nonadiabatic holonomic orbital control base on dynamical invariant of the Hamiltonian in Equation (12). To exploit the geometrical protection, the dynamical phase has to be canceled, which corresponds to

${\lambda }^2+\mathrm{\Delta }\left(\mathrm{\Delta }-\omega \right)=0.(14)$

Then, we calculate a control sequence of lattice modulation frequency, amplitude, and phase, denoted by Θ ≡ (ω_i, A_i, ϕ_i). After orbital leakage elimination, the gate fidelity is improved to above 98% in the multiorbital numerical simulation. The simulated time evolution of the |0⟩ on the Bloch sphere under the holonomic X gate is shown in Figure 8B. Besides, we also design the holonomic X, Y, Z, Hadamard, and π/8 gates. We further perform quantum process tomography to characterize the holonomic quantum gates, which is shown in Figure 8D. The measured quantum process fidelities are 98.47(9)%, 98.35(11)%, 97.81(13)%, 98.53(8)%, 98.63(15)%, and 98.63 (15)%, for the X, Y, Z, Hadamard, and π/8 gates, respectively [8]. There are four main factors limiting fidelities: a) orbital leakage: although we have greatly eliminated the band leakage, there are still a small number of atoms in high bands that affect the current fidelities. b) De-phasing mechanism: the quasi-momentum broadening of BEC and the non-uniformity of light intensity of optical lattice will lead to the de-phasing effect, which causes the decrease of fidelity. c) Atom interaction: As discussed in section 5.1, atoms in the D band will be scattered to the ground band due to collision, which will affect the fidelities. d) Error caused by measurement: It is mainly caused by the vibration of the imaging system during the absorption imaging process. For a) and b), we can overcome them through super lattice or more complex lattice. We can construct a more perfect two-level so that the G-band is far away from the D-band. Further, by constructing flat bands, the dephasing effect brought by momentum broadening and non-uniformity of the light can be suppressed, so as to greatly improve the fidelity. If we want to further improve the fidelity, we need to consider the factors of c) and d). We can use Feshbach resonance technology to reduce the atomic interaction, and reduce the imaging error through the improvement of the mechanical structure of the imaging system.

3.2 Ramsey interferometry with trapped motional quantum states of the optical lattice

Ramsey interferometry (RI) using internal electronic or nuclear states find wide applications in science and engineering [32]. In this section, we review a new RI with the S- and D-bands in an optical lattice [13], similar to Figure 1B (in this section, the laser wavelength of the optical lattice is 852 nm, and the lattice depth is 10E_r). A key challenge for constructing this RI is to realize π-pulse and π/2-pulse analogous to those in conventional RIs. In section 3.1, we have achieved the arbitrary holonomic quantum control, which ensures the noise-resilient but increases the control time. However, we want to study the quantum many-body lattice dynamics by this RI, which requires the time duration of the π-pulse and π/2-pulse to be as short as possible. Hence, we use the shortcut method to design these pulse sequences.

The full time sequence for RI with two shortcut π/2-pulses $\widehat{R}(\pi /2)$ we use in experiments is shown in Figure 9A. First the atoms in the harmonic trap are transferred into the S-band by shortcut, then the first pulse $\widehat{R}(\pi /2)$ is applied to prepare an initial superposition state $\frac{1}{\sqrt{2}}({\mathrm{\Psi }}_{\mathrm{1,0}}+{\mathrm{\Psi }}_{\mathrm{3,0}})$. After evolution in the optical lattice for time t_OL and a second π/2-pulse, the final state can be expressed as Ψ_f = a_SΨ_1,0 + a_DΨ_3,0. Then we apply band mapping to read out the final state, and obtain the population of atoms in S (D) band, denoted as N_S (N_D). We define the signal of this RI as p_D (t_OL) = N_D/(N_S + N_D). For the ideal single-atom system, where the imperfection and decoherence can be neglected, the signal p_D (t_OL) = [1 + cos (ωt_OL + ϕ)]/2, with ω corresponding to the energy difference between Ψ_1,0 and Ψ_3,0. However, when t_OL gets longer, the oscillation amplitude decays, as shown in Figure 9B. The contrast C (t_OL) can be obtained by fitting the amplitude of oscillation p_D (t_OL) with

$p_D\left(t_{OL}\right)=\left[1+C\left(t_{OL}\right)\cos \left(\omega t_{OL}+\varphi \right)\right]/2.(15)$

FIGURE 9

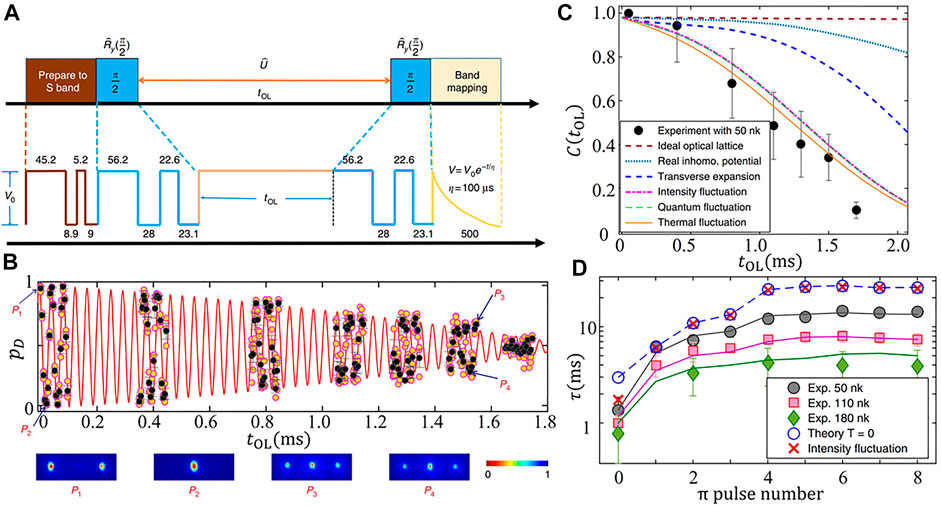
FIGURE 9. (A) Time sequences for the Ramsey interferometry. The atoms are first loaded into the S-band, followed by the RI sequence π/2-pulse, holding time t_OL, and the second π/2-pulse. Finally, band mapping is used to detect the number of atoms in the different bands. The used sequences designed by the shortcut method are shown in the figures (unit: μs). (B) The oscillation of the population of atoms in the D-band p_D. The images below show typical time of flight pictures after band mapping. (C) The experimental contrast (black points) and the theoretical calculation for V₀ = 10E_r. In theory, we begin with an ideal optical lattice and gradually add the effect of lattice inhomogeneity, transverse expansion of atom cloud, intensity fluctuation of laser amplitude, quantum fluctuation, and thermal fluctuation. (D) Coherence time τ vs the number of applied π-pulse n with different temperatures.

In order to improve the performance of the RI, we now investigate the mechanisms that lead to RI signal attenuation. The decay of the contrast, shown by the black points in Figure 9C, mainly comes from de-phasing and de-coherence mechanisms. These mechanisms are caused by the imperfect design of the π/2 pulse, non-uniform potential distribution of the Gaussian beam in the radial direction, atom-atom interaction leading to transverse expansion, intensity fluctuation of the lattice, and thermal fluctuations of the system. The theoretical calculation with different mechanisms is shown in Figure 9C, which is consistent with the experimental results. The expansion leads to a significant reduction in contrast (blue dashed line in Figure 9C). In our experiment, the influence of the quantum fluctuation is not significant.

To further improve the contrast of the RI, we develop a matter-wave band echo technique. A π-pulse is designed, which swaps the atom population in the S- and D-band. The π-pulse is inserted into the center of the evolution process. After implementing one π-pulse, the intensity fluctuation can be well suppressed. After applying six echo pulses, the effects of non-uniform lattice potential and transverse expansion are eliminated. The coherence times τ (defined as the time when the contrast C (t_OL) drops to 1/e) with different echo pulses are shown in Figure 9D. The coherent time is increased from 1.3 to 14.5 ms by the echo pulses [13].

4 Exotic quantum states of p-orbital ultracold atoms in optical lattices

4.1 Observation of a dynamical sliding phase superfluid with P-Band bosons

The Sliding phase [33], which is introduced to characterize intricate phase transitions in a wide range of the many-body system, appears under extreme conditions for thermal equilibrium systems or quantum ground states, causing a grievous challenge in experimental implementation [34–40]. Here, we review the observation of a sliding phase superfluid in a dynamical system of ultracold atoms in the P-band [10]. We load the atoms into P-band with zero quasi-momentum by the shortcut as shown in Figure 4. The quantum system is driven to a far-out-of-equilibrium but a phase-coherent state. We hold the condensate in the P-band for a certain time t_evo. Then the TOF images are taken in two probe directions with probe light along the z-axis (denoted as probe-1) and along the x-axis (denoted as probe-2). The distribution in different probe directions is analyzed via a bimodal fitting, as shown in Figure 10A. We extract the coherent fraction from the bimodal fitting so that the phase coherence of the dynamical many-body state can be inferred [10].

FIGURE 10

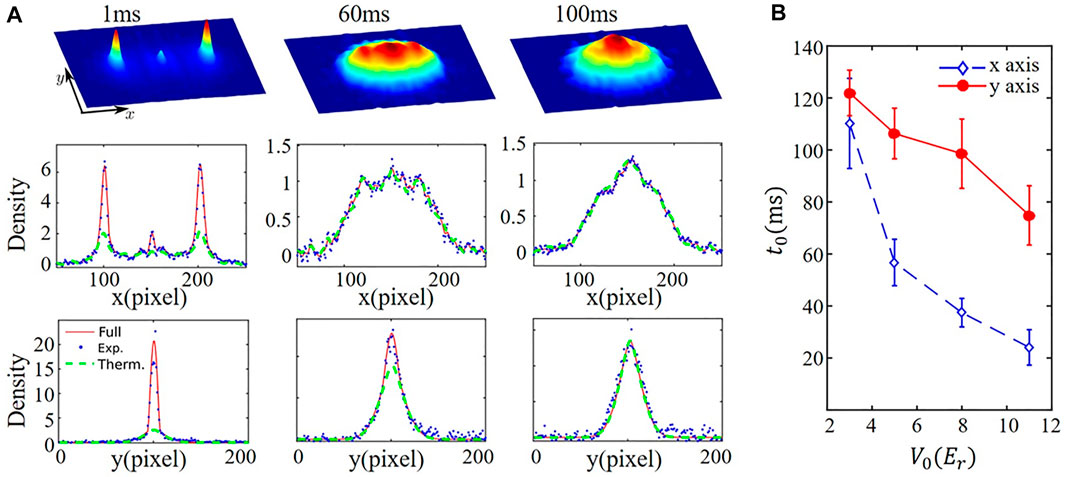
FIGURE 10. (A) Momentum distributions measured at three different holding times t_evo = 1, 60, 100 ms, along different directions (with V₀ = 5E_r). The corresponding distribution along the x-direction is given in the second row with blue dots. The solid red line gives a full fitting line, while the green dashed line gives the distribution of the thermal component. The third row shows the atomic distribution in the y-direction for images measured by probe 2. (B) The time t₀ for the atoms to lose coherence in lattice and pancake directions with different optical-lattice depths. The blue diamonds are for the x-direction (lattice) by probe one and the dotted points are for the y-direction (pancake). The optical lattice is the 1D lattice.

From the time evolution, we identify three distinct dynamical regions. At an early time, the system has superfluid phase in all directions, as shown in Figure 10A at t_evo = 1 ms. In the second state, the phase coherence of the quantum gas survives partially. The bimodal fitting in Figure 10A at t_evo = 60 ms shows that there is a finite condensed component in the pancake directions, but no such component in the lattice direction, which is called the sliding phase. At the last state, the quantum gas has rethermalized with a complete loss of phase coherence. The bimodal fitting shows that all atoms are thermal in the complete absence of any condensed component. We define the lifetime t₀ for the atoms to lose coherence in lattice and pancake directions, which is shown in Figure 10B for different lattice depth. We find that with the total atom number fixed in the experiment, a critical lattice depth appears beyond which the sliding phase superfluid starts to emerge. Moreover, we also verify that P-band is necessary to realize the dynamical sliding phase in our experiment, and the sliding phase is absent for cold atoms in the S-band at equilibrium [10].

4.2 Observation of a potts-nematic superfluidity in a hexagonal sp² optical lattice

In this section, we review the observation of a Potts-nematic quantum state in a system of cold atoms loaded into the second band of a hexagonal optical lattice [12]. We use the band swapping method to load the atoms into the second band, as shown in section 2.3. After the atoms are transferred into the band maximum of the second band, the phase coherence in the state will immediately disappear. After a few milliseconds, the phase coherence reemerges, and the quantum state spontaneously chooses one orientation, giving rise to a three-state Potts nematicity. We divide the experimental TOF images into three classes and take the average within each class [12]. The post-classification averaged results are shown in Figure 11B.

FIGURE 11

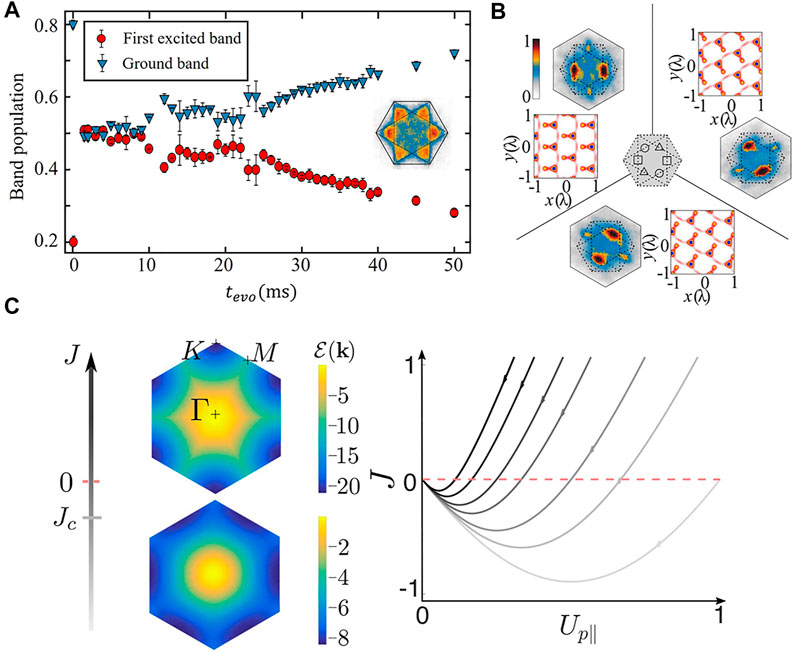
FIGURE 11. (A) The measured time evolution of the atomic population in the ground and the second bands of the hexagonal optical lattice. (B) The averaged momentum distribution for three symmetries. (C) Theoretical quantum phase transitions varying the orbital Josephson coupling. The energy ɛ(k) for a plane-wave condensate at a lattice momentum k. The energy ɛ(k) has minima at K (M) points for J > J_c (J < J_c). The right figure is the sketch of the renormalization of the p-orbital couplings to low energy.

To gain insight into the mechanism supporting the Potts-nematic order in the sp²-orbital hybridized band, we provide a mean-field theory analysis assuming a plane-wave condensate. The interaction can be expressed as

$H_{\mathit{int}}=\frac{1}{2}\sum _{\mathit{r}\in \mathcal{B}}{U}_s{\widehat{s}}_{\mathit{r}}^{†}{\widehat{s}}_{\mathit{r}}^{†}{\widehat{s}}_{\mathit{r}}{\widehat{s}}_{\mathit{r}}+\sum _{\mathit{r}\in \mathcal{A}}\left\{J\left[{\widehat{p}}_{x,\mathit{r}}^{†}{\widehat{p}}_{x,\mathit{r}}^{†}{\widehat{p}}_{y,\mathit{r}}{\widehat{p}}_{y,\mathit{r}}+H.c.\right]\right\}+\frac{1}{2}\sum _{\mathit{r}\in \mathcal{A}}\sum _{\alpha ,\beta \in \left\{x,y\right\}}{U}_{p,\alpha \beta }{\widehat{p}}_{\alpha ,\mathit{r}}^{†}{\widehat{p}}_{\beta ,\mathit{r}}^{†}{\widehat{p}}_{\beta ,\mathit{r}}{\widehat{p}}_{\alpha ,\mathit{r}}(16)$

where $\widehat{s}$ and $\widehat{p}$ represent quantum mechanical annihilation operators for s and p orbitals, and the p-orbital couplings are constrained by $U_{p,xx}=U_{p,yy}\equiv U_{p_{\Vert }}$, $U_{p,xy}=U_{p,yx}\equiv U_{p_{\perp }}$, $J=U_{\left.\right(p_{\Vert }-U_{p_{\perp }}\left.\right)}/2$. Taking a trial condensate wave function with ⟨s_r⟩ = ϕ_se^ik⋅r, ⟨p_x,y,r⟩ = ϕ_x,ye^ik⋅r, with ϕ_s, ϕ_x,y the variational parameters. For each lattice momentum k, we minimize the energy by varying ϕ_s,x,y, and the resultant energy is denoted as ɛ(k) and shown in Figure 11C. With the orbital Josephson coupling J > 0, both the kinetic and interaction energies favor a condensate at K points which breaks the time-reversal symmetry but respects the rotation symmetry. With the Josephson coupling J < 0, minimizing the kinetic and interaction energies meets frustration, as interaction favors p-orbital polarization. Figure 11C shows the possible value range of J considering renormalization effects [12].

5 Dynamical evolution for atoms in high bands of optical lattices

5.1 The scattering channels induced by two-body collision of D-band atoms in optical lattices

The mechanism of atomic collisions in excited bands plays an essential role in the atomic dynamics in high bands of optical lattices and the simulation of condensed matter physics [21]. Atoms distributed in an excited band of an optical lattice can collide and decay to other bands through different scattering channels [17, 21]. The decay rate and scattering channels of optical lattices with different configurations are different. Here, we first compare the lifetime of atoms in the D-band for one-dimensional lattice and triangular lattice. In experiments, we utilize the shortcut method to load BECs to the D (D1) band of the 1D optical lattice (triangular optical lattice). Then the BECs in the optical lattice evolve for a certain time t_evo. Finally, we apply band mapping to measure the proportion p_D (t_OL) of atoms in the D-band, which is shown in Figure 12A for 1D lattice and 12B for triangular lattice. We define the lifetime τ of atoms in the D-band as the proportion p_D reduces to 1/e. The lifetime for the triangular lattice is 5.0 ms, which is much longer than that of the 1D lattice, 2.1 ms. The difference in collisional scattering cross-section leads to the difference of a lifetime. Next, we will carefully analyze the scattering cross-section and the scattering channels [21].

FIGURE 12

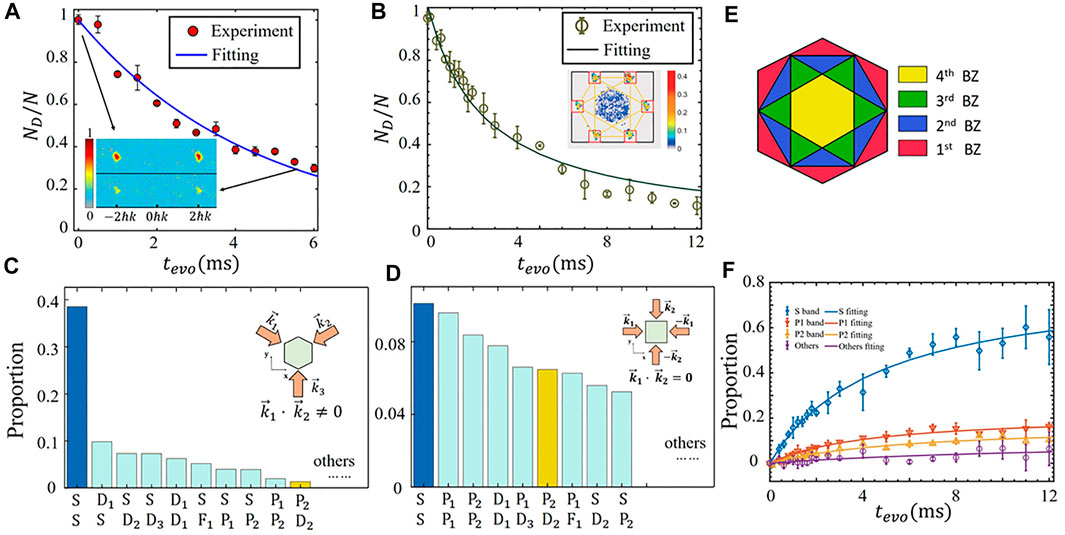
FIGURE 12. (A) The proportion of D-band over the evolution time in 1D lattice. (B) The proportion of the first D-band (D1-band) in the triangular lattice. The proportions of several main scattering channels are shown in (C) (triangular lattice) and (D) (square lattice). The inserts show the diagram of a square optical lattice and triangular optical lattice. (E) Schematic diagram of the first four Brillouin zones of a triangular optical lattice. Yellow, green, blue, and red areas represent 1st, 2nd, 3rd, 4th BZ, respectively. (F) The atomic proportion in S (P1, P2 band, and others), of which the solid lines with the same color fit lines.

We take triangular and square lattices as examples to study the difference in the scattering process. We use the scattering theory to calculate the cross-section of each scattering channel in those two types of lattices. Two-body collisional scattering cross section for two atoms initially at the Γ point ((q_x, q_y)=(0,0)) of D1 band jumping to band n₁ and n₂ can be written as:

$\sigma \left(n_1,n_2\right)=\frac{4\pi m\hslash }{v_a}\int d\mathit{q}\times |-2\pi i\frac{4\pi a_s}{m}{\zeta }_{n_1,n_2}\left(\mathrm{0,0};\mathit{q},-\mathit{q}\right){|}^2,(17)$

where v_a is the atomic velocity and a_s is atomic s-wave scattering length. And the overlapping integral of eigenstates ${\zeta }_{n_1,n_2}(\mathrm{0,0};\vec{q},-\vec{q})$ is given by:

${\zeta }_{n_1,n_2}\left(\mathrm{0,0};\mathit{q},-\mathit{q}\right)=\int d\mathit{r}\times {\mathrm{\Psi }}_{n_1,\mathit{q}}^{\ast }\left(\mathit{r}\right){\mathrm{\Psi }}_{n_2,-\mathit{q}}^{\ast }\left(\mathit{r}\right){\mathrm{\Psi }}_{d,0}\left(\mathit{r}\right){\mathrm{\Psi }}_{d,0}\left(\mathit{r}\right)(18)$

where Ψ_n,q(r) is Bloch function of the eigenstate at quasi-momentum q in the n band. In the calculation, we assume the periodic boundary conditions, and consider that $|{\zeta }_{n_1,n_2}(\mathrm{0,0};\mathit{q},-\mathit{q}){|}^2=\int d\mathit{r}\times |{\mathrm{\Psi }}_{n_1,\mathit{q}}^{*}(\mathit{r}){\mathrm{\Psi }}_{n_2,-\mathit{q}}^{*}(\mathit{r}){\mathrm{\Psi }}_{d,0}(\mathit{r}){\mathrm{\Psi }}_{d,0}(\mathit{r}){|}^2$. After neglecting the scattering channels of higher bands, we calculate the scattering channels, as shown in Figure 12CD. In the square lattice, the cross-section of the strongest channel SS, P₁P₁ and P₂P₂ are all around 10% of the total cross-section respectively. Besides, there are many smaller channels included in ‘Others.’ There is no significant difference in scattering cross-section values among the first six channels, which means no dominant scattering channel in a square lattice. By contrast, in the triangular lattice, the proportion of scattering cross-section of the SS channel is 38.5%, while that of the second strong channel D₁S is only 9.8%. Besides, the proportion of other channels is much lower than that of channel SS. Consequently, the channel SS is dominant in the two-body scattering process of the triangular optical lattice. The experimental results are consistent with the theoretical results, as shown in Figure 12F. For example, at time t_evo = 12 ms, the experimental proportion of the S-band is 55.8%, which is roughly equal to the theoretical prediction of 57.3% [21].

5.2 Quantum dynamical oscillations of ultracold atoms in the F and D bands

Here we review the observation of quantum dynamical oscillations of ultracold atoms in the F and D bands of the 1D optical lattice [20]. We can control the Bragg reflections at the Brillouin-zone edge up to the third order and observe three different types of quantum oscillations [20].

The BECs is initially loaded in the G band, where the atoms mostly populate at momenta 4ℏk, as shown in Figure 3B(2). Then the atoms fall into the F-band due to the small gap between G- and F-bands. The following trace of the atoms is shown in the extended band structures as shown in Figure 13D. Once the BECs are in the F-band, it loses momentum while gaining potential energy from the harmonic confinement (A₁ → A₂). Once arriving A₂, the atoms face different dynamics depending on the lattice depth. When the depth is small $(\sim 5E_r)$, and the Bragg reflections at A₂ are weak, the BECs will continue into the D-band by a Landau-Zener transition and reach A₃. Then the atoms will be Bragg reflected to A₄ and reverse its dynamics (A₄ → A₅ → A₆). This oscillation is shown in Figure 13A. When the lattice is strong $(\sim 15E_r)$, and the gap at A₂ is large, the Bragg reflection can dominate the dynamics, forbidding the atoms from tunneling from the F band to the D band. Instead, the atoms at A₂ will transfer to A₅ and oscillate only within the F-band, which is shown in Figure 13C. For intermediate depth $(\sim 7.5E_r)$, these two oscillation modes exist simultaneously, as shown in Figure 13B [20].

FIGURE 13

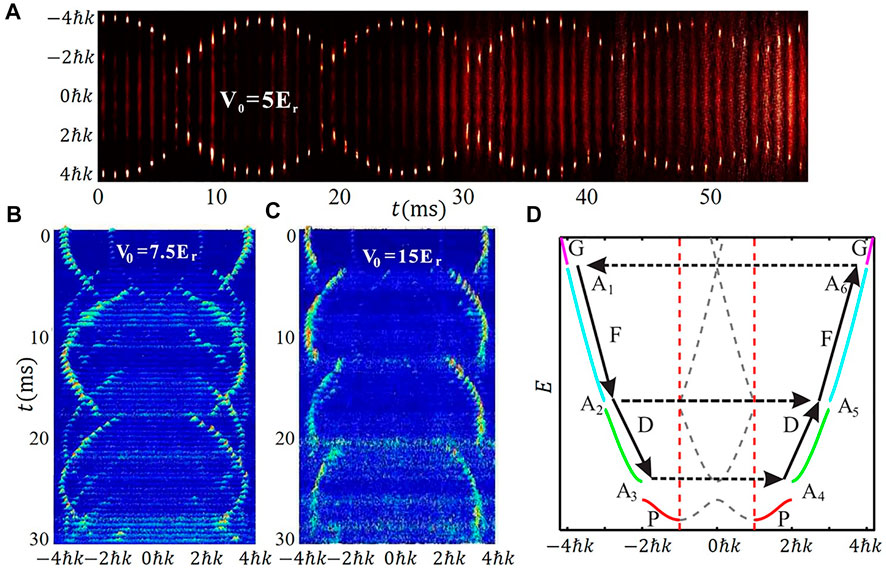
FIGURE 13. Quantum oscillations of the BECs in higher bands of the 1D optical lattice. Experimental results in momentum space with lattice depth (A) 5E_r, (B) 7.5E_r, and (C) 15E_r. (D) Schematic of extended Bloch bands of the 1D optical lattice.

5.3 Nonlinear dynamical evolution for P-band ultracold atoms in 1D optical lattice

The dynamical evolution for atoms in P-band is different from that of F- and D-bands [18]. After loading the BECs into the P-band with zero quasi-momentum for the lattice depth 5E_r, we hold the BECs for time t_evo and then measure the momentum distribution. The momentum distributions at different holding time t_evo are shown in Figure 14A. We use the normalized populations W_ℓ(t_evo) of momentum states |ℓ ⋅ 2ℏk + q⟩ to better quantify the dynamical evolution of atoms. At the beginning of the evolution process t_evo < 1.5 ms, we find W_ℓ(t_evo) oscillating rapidly, as shown in Figure 4C and Figure 14A(1) [2]. Then, after a short transition time, a different type of oscillation begins to emerge around t_evo = 2 ms. The period of this oscillation is 14.9 ms, which is shown in Figures 14A,B [3-5].

FIGURE 14

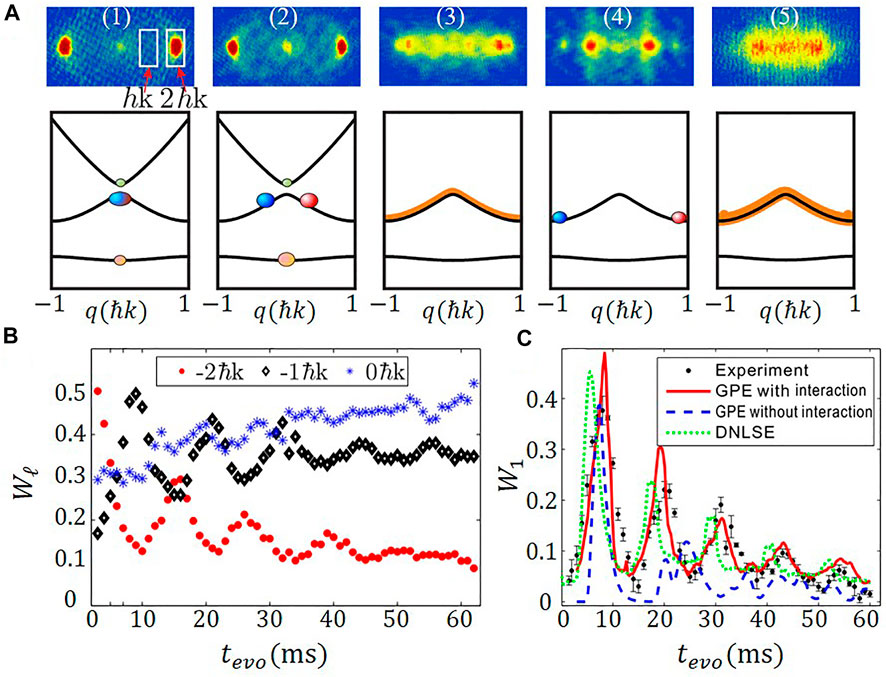
FIGURE 14. (A) First row: the measured momentum distributions of the BEC in the P-band of the 1D lattice at different holding times (0 ms, 2 ms, 5 ms, 7 ms, and 30 ms), and the white rectangles are the region for us to calculate the proportion of different momentum states; the second row: schematic illustration of the corresponding population distributions in the Bloch band. (B) Population oscillations around momenta 0ℏk (blue stars), − ℏk (black diamonds), and − 2ℏk (red dots) with t > 2 ms. The oscillation period is about 14.9 ms with V = 5E_r. (C) Population for ℏk vs. time t_evo. The experimental results and theoretical simulations with and without the interaction correspond to the black dots with an error bar, red solid curves, and blue dashed curves, respectively.

The short-period oscillations shown in Figure 4C are beating signals due to the coherent superposition of different bands. From the numerical analysis, the superposed state is close to $|\psi (t_{\mathit{evo}}=0)=\sqrt{0.9}{\mathrm{\Psi }}_{\mathrm{2,0}}+\sqrt{0.05}{\mathrm{\Psi }}_{\mathrm{1,0}}+\sqrt{0.05}{\mathrm{\Psi }}_{\mathrm{3,0}}$. The rapid oscillations disappear at about 1.5 ms. Then a long-period oscillation begins to emerge at around 2 ms. There are five cycles of the long-period oscillation in Figure 14C. The long-period oscillation reflects the random phase between neighboring lattice sites, which can be well captured by the simulation with the Gross-Pitaevskii equation (shown by the red line in Figure 14C). This experiment paves the way to study the long-time dynamical evolution of the high orbital physics for other novel quantum states, such as the sliding phase [18].

6 Discussion and conclusion

In this review, we concentrate on the methods to prepare and control the BEC in optical lattices linked to one-body physics. The many-body interactions also play an important role in the system of ultracold atoms in the optical lattices. For the control methods mentioned in this review, such as the shortcut method, amplitude modulation, and nonadiabatic holonomic control, the operation time ($<1$ ms) is much shorter than the time when the interaction has a significant effect. Therefore, the control schemes designed ignoring the influence of many-body interaction is still very successful. The effects of the interaction mainly occur in the long-term evolution process in the optical lattice after we manipulate or prepare the Bloch states, such as the de-coherence in the Ramsey interferometry with motional states, the two-body collision of D-band atoms, and the emergency of the exotic quantum states of p-orbitals. On the other hand, we can also utilize the interactions to expand the methods of atomic manipulation in optical lattices. For example, a two-qubit gate can be achieved by adapting the interaction scheme based on the method shown in section 3.1. Considering two nearby sites, denoted as a and b, the orbital states are |s_as_b⟩, |d_ad_b⟩, |d_as_b⟩, |s_ad_b⟩. The relevant interactions between neighboring sites contain this term $U_0(s_a^{†}{d}_b^{†}{d}_b{s}_a+d_a^{†}{s}_b^{†}{s}_b{d}_a)$. A $\sqrt{\mathrm{s}\mathrm{w}\mathrm{a}\mathrm{p}}$ gate control can be reached by letting atoms interact for a time duration πℏ/(4U₀). In a word, we can use these control methods to observe the special dynamic mechanism and novel quantum states produced by the interaction of different orbitals of optical lattices, and we can also use the interactions to achieve more manipulation.

In summary, we review our practical methods for manipulating the high orbitals of ultracold atoms in optical lattices. The shortcut method is characterized by short time and high fidelity, which can directly transfer ultracold atoms from the ground state in the harmonic trap to any Bloch state, and accurately manipulate atoms of different orbitals in optical lattices. This method can be used to construct atomic orbital interferometers and qubits and to study the dynamic properties of high orbital atoms in optical lattices. The band swapping technique considers the interaction between atoms and the additional potential trap (such as harmonic trap) besides the optical lattice, which is more suitable for studying the ground and metastable states of the system. The amplitude modulation focuses on coupling different Bloch bands and can be used to realize quantum gates and the large-momentum-transfer beam splitter. Based on these methods, the atom-orbital qubit under nonadiabatic holonomic quantum control and Ramsey interferometry with trapped motional quantum states of the optical lattice can be constructed. Many exotic quantum states of the high orbital atoms have been observed. Then we study the quantum dynamical evolution of atoms in high bands. The effective manipulation of the high orbitals provides strong support for applying the ultracold atoms in the optical lattice in quantum simulation, quantum computing, and quantum precision measurement.

Author contributions

SJ: Drafting the manuscript XC: Revising the manuscript XZ: Revising the manuscript.

Funding

This work is supported by the National Natural Science Foundation of China (Grants No. 12104020, No. 61727819, and No. 11334001), the National Basic Research Program of China (Grants No. 2021YFA0718300 and No. 2021YFA1400901), the Project funded by China Postdoctoral Science Foundation (Grant No. 2020TQ0017), the Science and Technology Major Project of Shanxi (No. 202101030201022), and the Space Application System of China Manned Space Program.

Acknowledgments

Thank Yiqiu Wang for establishing this experimental group of ultra-cold atoms in China. In completing the above work, thank Xiaopeng Li, Jörg Schmiedmayer, Biao Wu, Hongwei Xiong, Guangjiong Dong, Peng Zhang, and Lan Yin.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Greiner M, Mandel O, Esslinger T, Hänsch TW, Bloch I. Quantum phase transition from a superfluid to a mott insulator in a gas of ultracold atoms. Nature (2002) 415:39–44. doi:10.1038/415039a

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Bloch I, Dalibard J, Nascimbène S. Quantum simulations with ultracold quantum gases. Nat Phys (2012) 8:267–76. doi:10.1038/nphys2259

CrossRef Full Text | Google Scholar

3. Bloch I, Dalibard J, Zwerger W. Many-body physics with ultracold gases. Rev Mod Phys (2008) 80:885–964. doi:10.1103/RevModPhys.80.885

CrossRef Full Text | Google Scholar

4. Goldman N, Budich JC, Zoller P. Topological quantum matter with ultracold gases in optical lattices. Nat Phys (2016) 12:639–45. doi:10.1038/nphys3803

CrossRef Full Text | Google Scholar

5. Georgescu IM, Ashhab S, Nori F. Quantum simulation. Rev Mod Phys (2014) 86:153–85. doi:10.1103/RevModPhys.86.153

CrossRef Full Text | Google Scholar

6. Gross C, Bloch I. Quantum simulations with ultracold atoms in optical lattices. Science (2017) 357:995–1001. doi:10.1126/science.aal3837

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Moan ER, Horne RA, Arpornthip T, Luo Z, Fallon AJ, Berl SJ, et al. Quantum rotation sensing with dual sagnac interferometers in an atom-optical waveguide. Phys Rev Lett (2020) 124:120403. doi:10.1103/PhysRevLett.124.120403

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Shui H, Jin S, Li Z, Wei F, Chen X, Li X, et al. Atom-orbital qubit under nonadiabatic holonomic quantum control. Phys Rev A (Coll Park) (2021) 104:L060601. doi:10.1103/PhysRevA.104.L060601

CrossRef Full Text | Google Scholar

9. Wirth G, Ölschläger M, Hemmerich A. Evidence for orbital superfluidity in the p-band of a bipartite optical square lattice. Nat Phys (2011) 7:147–53. doi:10.1038/nphys1857

CrossRef Full Text | Google Scholar

10. Niu L, Jin S, Chen X, Li X, Zhou X. Observation of a dynamical sliding phase superfluid with p-band bosons. Phys Rev Lett (2018) 121:265301. doi:10.1103/PhysRevLett.121.265301

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Wang XQ, Luo GQ, Liu JY, Liu WV, Hemmerich A, Xu ZF. Evidence for an atomic chiral superfluid with topological excitations. Nature (2021) 596:227–31. doi:10.1038/s41586-021-03702-0

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Jin S, Zhang W, Guo X, Chen X, Zhou X, Li X. Evidence of potts-nematic superfluidity in a hexagonal sp² optical lattice. Phys Rev Lett (2021) 126:035301. doi:10.1103/PhysRevLett.126.035301

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Hu D, Niu L, Jin S, Chen X, Dong G, Schmiedmayer J, et al. Ramsey interferometry with trapped motional quantum states. Commun Phys (2018) 1:29. doi:10.1038/s42005-018-0030-7

CrossRef Full Text | Google Scholar

14. Zhou X, Jin S, Schmiedmayer J. Shortcut loading a Bose-Einstein condensate into an optical lattice. New J Phys (2018) 20:055005. doi:10.1088/1367-2630/aac11b

CrossRef Full Text | Google Scholar

15. Müller T, Fölling S, Widera A, Bloch I. State preparation and dynamics of ultracold atoms in higher lattice orbitals. Phys Rev Lett (2007) 99:200405. doi:10.1103/PhysRevLett.99.200405

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Liu X, Zhou X, Xiong W, Vogt T, Chen X. Rapid nonadiabatic loading in an optical lattice. Phys Rev A (Coll Park) (2011) 83:063402. doi:10.1103/PhysRevA.83.063402

CrossRef Full Text | Google Scholar

17. Zhai Y, Yue X, Wu Y, Chen X, Zhang P, Zhou X. Effective preparation and collisional decay of atomic condensates in excited bands of an optical lattice. Phys Rev A (Coll Park) (2013) 87:063638. doi:10.1103/PhysRevA.87.063638

CrossRef Full Text | Google Scholar

18. Hu D, Niu L, Yang B, Chen X, Wu B, Xiong H, et al. Long-time nonlinear dynamical evolution for p-band ultracold atoms in an optical lattice. Phys Rev A (Coll Park) (2015) 92:043614. doi:10.1103/PhysRevA.92.043614

CrossRef Full Text | Google Scholar

19. Yang B, Jin S, Dong X, Liu Z, Yin L, Zhou X. Atomic momentum patterns with narrower intervals. Phys Rev A (Coll Park) (2016) 94:043607. doi:10.1103/PhysRevA.94.043607

CrossRef Full Text | Google Scholar

20. Wang Z, Yang B, Hu D, Chen X, Xiong H, Wu B, et al. Observation of quantum dynamical oscillations of ultracold atoms in the f and d bands of an optical lattice. Phys Rev A (Coll Park) (2016) 94:033624. doi:10.1103/PhysRevA.94.033624

CrossRef Full Text | Google Scholar

21. Guo X, Yu Z, Peng P, Yin G, Jin S, Chen X, et al. Dominant scattering channel induced by two-body collision of d-band atoms in a triangular optical lattice. Phys Rev A (Coll Park) (2021) 104:033326. doi:10.1103/PhysRevA.104.033326

CrossRef Full Text | Google Scholar

22. Taie S, Ozawa H, Ichinose T, Nishio T, Nakajima S, Takahashi Y. Coherent driving and freezing of bosonic matter wave in an optical lieb lattice. Sci Adv (2015) 1:e1500854. doi:10.1126/sciadv.1500854

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Browaeys A, Häffner H, McKenzie C, Rolston SL, Helmerson K, Phillips WD. Transport of atoms in a quantum conveyor belt. Phys Rev A (Coll Park) (2005) 72:053605. doi:10.1103/PhysRevA.72.053605

CrossRef Full Text | Google Scholar

24. Ölschläger M, Wirth G, Hemmerich A. Unconventional superfluid order in the f band of a bipartite optical square lattice. Phys Rev Lett (2011) 106:015302. doi:10.1103/PhysRevLett.106.015302

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Niu L, Hu D, Jin S, Dong X, Chen X, Zhou X. Excitation of atoms in an optical lattice driven by polychromatic amplitude modulation. Opt Express (2015) 23:10064–74. doi:10.1364/OE.23.010064

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Köhl M, Moritz H, Stöferle T, Günter K, Esslinger T. Fermionic atoms in a three dimensional optical lattice: Observing fermi surfaces, dynamics, and interactions. Phys Rev Lett (2005) 94:080403. doi:10.1103/PhysRevLett.94.080403

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Kastberg A, Phillips WD, Rolston SL, Spreeuw RJC, Jessen PS. Adiabatic cooling of cesium to 700 nk in an optical lattice. Phys Rev Lett (1995) 74:1542–5. doi:10.1103/PhysRevLett.74.1542

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Greiner M, Bloch I, Mandel O, Hänsch TW, Esslinger T. Exploring phase coherence in a 2d lattice of bose-einstein condensates. Phys Rev Lett (2001) 87:160405. doi:10.1103/PhysRevLett.87.160405

PubMed Abstract | CrossRef Full Text | Google Scholar

29. de Saint-Vincent MR, Brantut JP, Bordé CJ, Aspect A, Bourdel T, Bouyer P. A quantum trampoline for ultra-cold atoms. Europhys Lett (2010) 89:10002. doi:10.1209/0295-5075/89/10002

CrossRef Full Text | Google Scholar

30. Impens F, Santos FPD, Bordé CJ. The theory of quantum levitators. New J Phys (2011) 13:065024. doi:10.1088/1367-2630/13/6/065024

CrossRef Full Text | Google Scholar

31. Cronin AD, Schmiedmayer J, Pritchard DE. Optics and interferometry with atoms and molecules. Rev Mod Phys (2009) 81:1051–129. doi:10.1103/RevModPhys.81.1051

CrossRef Full Text | Google Scholar

32. Riehle F, Kisters T, Witte A, Helmcke J, Bordé CJ. Optical ramsey spectroscopy in a rotating frame: Sagnac effect in a matter-wave interferometer. Phys Rev Lett (1991) 67:177–80. doi:10.1103/PhysRevLett.67.177

PubMed Abstract | CrossRef Full Text | Google Scholar

33. O’Hern CS, Lubensky TC, Toner J. Sliding phases in XY models, crystals, and cationic lipid-dna complexes. Phys Rev Lett (1999) 83:2745–8. doi:10.1103/PhysRevLett.83.2745

CrossRef Full Text | Google Scholar

34. Granato E, Kosterlitz JM. Critical behavior of coupled xy models. Phys Rev B (1986) 33:4767–76. doi:10.1103/PhysRevB.33.4767

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Choi MY, Doniach S. Phase transitions in uniformly frustrated xy models. Phys Rev B (1985) 31:4516–26. doi:10.1103/PhysRevB.31.4516

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Feigel’man M, Geshkenbein V, Larkin A. Pinning and creep in layered superconductors. Physica C: Supercond (1990) 167:177–87. doi:10.1016/0921-4534(90)90502-6

CrossRef Full Text | Google Scholar

37. Klemm RA, Luther A, Beasley MR. Theory of the upper critical field in layered superconductors. Phys Rev B (1975) 12:877–91. doi:10.1103/PhysRevB.12.877

CrossRef Full Text | Google Scholar

38. Stoebe T, Mach P, Huang CC. Unusual layer-thinning transition observed near the smectic-a-isotropic transition in free-standing liquid-crystal films. Phys Rev Lett (1994) 73:1384–7. doi:10.1103/PhysRevLett.73.1384

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Cheng M, Ho JT, Hui SW, Pindak R. Electron-diffraction study of free-standing liquid-crystal films. Phys Rev Lett (1987) 59:1112–5. doi:10.1103/PhysRevLett.59.1112

PubMed Abstract | CrossRef Full Text | Google Scholar

40. O’Hern CS, Lubensky TC. Sliding columnar phase of dna-lipid complexes. Phys Rev Lett (1998) 80:4345–8. doi:10.1103/PhysRevLett.80.4345

CrossRef Full Text | Google Scholar