DREENA-A framework as a QGP tomography tool

QGP tomography aims to constrain the QGP parameters by exploiting both low and high-p_⊥ theory and data. With this goal in mind, we present a fully optimised framework DREENA-A based on a state-of-the-art energy loss model. The framework can include any, in principle arbitrary, temperature profile within the dynamical energy loss formalism. Thus, “DREENA” stands for Dynamical Radiative and Elastic ENergy loss Approach, while “A” stands for Adaptive. DREENA-A does not adjust parameters within the energy loss model, allowing it to exploit differences in temperature profiles which are the only input in the framework. The framework applies to light and heavy flavor observables, different collision energies, and large and smaller systems. This, together with the ability to systematically compare data and predictions within the same formalism and parameter set, makes DREENA-A a unique multipurpose QGP tomography tool. The provided code allows researchers to use their own QGP evolution models to straightforwardly generate high-p_⊥ predictions.

1 Introduction

QCD predicted that a new form of matter [1, 2]— consisting of quarks, antiquarks, and gluons that are no longer confined—is created at extremely high energy densities. According to the current cosmology, this new state of matter, called Quark-Gluon Plasma (QGP) [3–7], existed immediately after the Big Bang [8]. Today, QGP is created in ‘Little Bangs’, when heavy ions collide at ultra-relativistic energies [5, 6]. Such collisions lead to an expanding fireball of quarks and gluons, which thermalises to form QGP; the QGP then cools down, and when the temperature reaches a critical point, quarks and gluons hadronise.

Successful production of this exotic state of matter at the Relativistic Heavy Ion Collider (RHIC) and the Large Hadron Collider (LHC) allowed systematical testing of different models of QGP evolution against experimental data. Up to now, it has been established that QGP is formed at the LHC and RHIC experiments through two main lines [5, 6, 9] of evidence: 1) by comparison of low momentum (p_⊥) measurements with relativistic hydrodynamic predictions, which implied that created QGP is consistent with the description of a nearly perfect fluid [10–12], 2) by comparison of high-p_⊥ data [13–17] with pQCD predictions, which showed that high-p_⊥ partons (jets) significantly interact with an opaque medium. Beyond this discovery phase, the current challenge is to investigate the properties of this extreme form of matter.

While high-p_⊥ physics had a decisive role in the QGP discovery [5], it was rarely used for understanding the bulk medium properties. On the other hand, low-p_⊥ observables do not provide stringent constraints to all parameters of the models used to describe the evolution of QGP [18–21]. Thus, it is desirable to explore QGP properties through independent theory and data set. We argue that this is provided by jet energy loss and high-p_⊥ data, complementing the low-p_⊥ constraints to QGP.

To use high-p_⊥ theory and data as a QGP tomography tool, it is necessary to have a realistic high-p_⊥ parton energy loss model. We use our dynamical energy loss formalism, which has the following properties: 1) It is based on finite size, finite temperature field theory [22, 23], and takes into account that QGP constituents are dynamical (moving) particles. Consequently, all divergences are naturally regulated in the model. 2) Both collisional [24] and radiative [25, 26] energy losses are calculated in the same theoretical framework. In radiative energy loss, finite size effects induce a non-linear path length dependence of the energy loss, recovering both the incoherent Gunion Bertsch and destructive Landau-Pomeanchuk-Migdal limit [25, 26]. For collisional energy loss, we show that finite size effects can be neglected [24], i.e., path-length dependence is close to linear. 3) It is applicable to both light and heavy flavors, so it can provide predictions for an extensive set of probes. 4) Temperature is a natural variable in the framework [27], so that the T profiles resulting from bulk medium simulations are a direct input in the model. 5) The non-perturbative effects related to screening of the chromo-magnetic and chromo-electric fields are included [28] through the generalized hard-thermal-loop (HTL) approach. For radiative energy loss, the effective cross-section is handled through sum-rules [29], which allows consistent inclusion of non-perturbative medium-related interactions captured by lattice QCD (see [28] for more details). For collisional energy loss, the nonperturbative effects were included at the leading order through modification of the running coupling, following the procedure from [30] (see [31] for more details). 6) No parameters are adjusted when comparing the dynamical energy loss predictions with high-p_⊥ data [32, 33], i.e., we use fixed parameter values consistent with other studies (specified in Subsection 2.1). The formalism explained a wide range of high-p_⊥ data [31, 34–37], including puzzling data [37] and generating predictions for future experiments [35]. This suggests that the model realistically describes high-p_⊥ parton-medium interactions. While other available energy loss models (see e.g. [38–48]) have some of the above properties, none have all (or even most of them), making the dynamical energy loss an advanced framework for QGP tomography¹. As the temperature is the only input in the energy loss model, this allows further exploiting different temperature profiles that agree with low-p_⊥ data by testing their agreement with high-p_⊥ data. Consequently, a systematic comparison of data and predictions obtained by the same formalism and parameter set allows constraining the QGP parameters from both low and high-p_⊥ theory and data.

Including full medium evolution in the dynamical energy loss is, however, a highly non-trivial task, as all the model properties have to be preserved [49], without additional simplifications in the numerical procedure. Furthermore, to be effectively used as a precision QGP tomography tool, the framework needs to efficiently (timewise) generate a comprehensive set of light and heavy flavor suppression predictions through the same numerical framework and the same parameter set. Such predictions can then be compared with the available experimental data, sometimes even repeatedly (i.e., iteratively)—for different combinations of QGP medium parameters–to extract medium properties that are consistent with both low and high-p_⊥ data.

To introduce the medium evolution in the dynamical energy loss, we took a step-by-step approach, allowing us to check the consistency of each consecutive step by comparing its results with the previous (simpler) framework versions. Consequently, we first developed the DREENA-C framework [50] (‘C’ stands for constant temperature), continuing to DREENA-B [51] (‘B’ stands for Bjorken expansion). In this manuscript, we present a fully optimised DREENA-A framework, where ‘A’ stands for ‘adaptive’ (i.e., arbitrary) temperature evolution. The convergence speed of the developed numerical procedure is analysed, as well as consistency with other (earlier) versions of the framework, as necessary for the reliable and efficient QGP tomography tool. Finally, as a utility check of the DREENA-A framework, the sensitivity of high-p_⊥ observables to different temperature profiles is presented.

The link to the software code implementing the DREENA-A framework (with usage instructions and example data) is provided at https://github.com/DusanZigic/DREENA-A. Using this software, researchers can generate high-p_⊥ predictions for their own (different) models of medium evolution and compare the results with experimental data.

2 Methods

2.1 Theoretical outline

The calculation of the final hadron spectrum includes initial high-p_⊥ parton (quark and gluon) distributions from perturbative QCD, energy loss (if the QCD medium is formed), and fragmentation into hadrons. The cross section for quenched spectra is schematically written as [52, 53]:

$\frac{E_f{d}^3{\sigma }_q\left(H_Q\right)}{d{p}_f^3}=\frac{E_i{d}^3\sigma \left(Q\right)}{d{p}_i^3}\otimes P\left(E_i\to E_f\right)\otimes D\left(Q\to H_Q\right),(1)$

where ⊗ is a generic convolution, and the change in the initial spectra due to energy loss in QGP is denoted P (E_i → E_f). If the medium is not created, then Eq. 1 reduces to cross section for unquenched spectra

$\frac{E_f{d}^3{\sigma }_u\left(H_Q\right)}{d{p}_f^3}=\frac{E_i{d}^3\sigma \left(Q\right)}{d{p}_i^3}\otimes D\left(Q\to H_Q\right).(2)$

More specifically, $\frac{E_f{d}^3{\sigma }_q(H_Q)}{d{p}_f^3}$ is the final hadron spectrum in the presence of QGP, while $\frac{E_f{d}^3{\sigma }_u(H_Q)}{d{p}_f^3}$ is the spectrum in the absence of QGP. ‘i’ and ‘f’ correspond to ‘initial’ and ‘final’, respectively. Q denotes quarks and gluons, while H_Q denotes hadrons. Initial parton spectrum is denoted by $E_i{d}^3\sigma (Q)/d{p}_i^3$, and computed at next to leading order [54–56] for light and heavy partons. P (E_i → E_f) is the probability for energy transfer, which includes medium induced radiative [25, 26] and collisional [24] contributions in a finite size dynamical QCD medium with running coupling [31]. Both contributions include multi-gluon fluctuations, introduced according to Refs. [31, 57] for radiative and [52, 58] for collisional energy loss (for more details, see below). Q to hadron H_Q fragmentation is denoted by D (Q → H_Q). For charged hadrons we use DSS [59], for D mesons BCFY [60, 61] and for B mesons KLP [62] fragmentation functions, respectively.

In DREENA-A, the medium temperature needed to calculate P (E_i → E_f) depends on the position of the parton according to a temperature profile given as an input. Therefore, the temperature that the parton experiences along its path, becomes a function of the coordinates of its origin (x₀, y₀), the angle of its trajectory ϕ, and the proper time τ:

$T\left({\mathrm{x}}_0,{\mathrm{y}}_0,\varphi ,\tau \right)=T_{\mathit{profile}}\left({\mathrm{x}}_0+\tau \cos \varphi ,{\mathrm{y}}_0+\tau \sin \varphi ,\tau \right),(3)$

where T_profile is, in principle, arbitrary. This temperature then appears in the expressions below.

The collisional energy loss is given by the following analytical expression [51]:

$\begin{array}{ll}\hfill \frac{d{E}_{\mathit{col}}}{d\tau }& =\frac{2C_R}{\pi v^2}{\alpha }_S\left(ET\right){\alpha }_S\left({\mu }_E^2\left(T\right)\right)\hfill \\ \hfill & \times {\int }_0^{\infty }{n}_{eq}\left(|\vec{\mathbf{k}}|,T\right)d|\vec{\mathbf{k}}|\left({\int }_0^{|\vec{\mathbf{k}}|/\left(1+v\right)}d|\vec{\mathbf{q}}|{\int }_{-v|\vec{\mathbf{q}}|}^{v|\vec{\mathbf{q}}|}\omega d\omega +{\int }_{|\vec{\mathbf{k}}|/\left(1+v\right)}^{|\vec{\mathbf{q}}{|}_{\mathit{max}}}d|\vec{\mathbf{q}}|{\int }_{|\vec{\mathbf{q}}|-2|\vec{\mathbf{k}}|}^{v|\vec{\mathbf{q}}|}\omega d\omega \right)\hfill \\ \hfill & \times \left(|{\mathrm{\Delta }}_L\left(q,T\right){|}^2\frac{{\left(2|\vec{\mathbf{k}}|+\omega \right)}^2-|\vec{\mathbf{q}}{|}^2}{2}+|{\mathrm{\Delta }}_T\left(q,T\right){|}^2\frac{\left(|\vec{\mathbf{q}}{|}^2-{\omega }^2\right)\left({\left(2|\vec{\mathbf{k}}|+\omega \right)}^2+|\vec{\mathbf{q}}{|}^2\right)}{4|\vec{\mathbf{q}}{|}^4}\left(v^2|\vec{\mathbf{q}}{|}^2-{\omega }^2\right)\right).\hfill \end{array}(4)$

Here we used the following notation: k is the 4-momentum of the incoming medium parton; T is the current temperature along the path, given by Eq. 3; $n_{eq}(|\vec{\mathbf{k}}|,T)=\frac{N}{e^{|\vec{\mathbf{k}}|/T}-1}+\frac{N_f}{e^{|\vec{\mathbf{k}}|/T}+1}$ is the equilibrium momentum distribution [63] at temperature T including quarks and gluons. N = 3 and N_f represent, respectively, the number of colors and flavors, where we assume N_f = 3 for the LHC and N_f = 2.5 for RHIC; $q=(\omega ,\vec{\mathbf{q}})$ is the 4-momentum of the exchanged gluon; E² = p² + M² denotes the initial jet energy, p is the jet momentum, while M is the mass (specified below) of the quark or gluon jet; $v=p/\sqrt{p^2+M^2}$ denotes velocity of the incoming jet; $C_R=\frac{4}{3}$ for quark jet and three for gluon jet; Δ_L(T) and Δ_T(T) are effective longitudinal and transverse gluon propagators [64, 65], while the electric screening (the Debye mass) μ_E(T) is obtained by self-consistently solving the expression from [66] (Λ_QCD is perturbative QCD scale):

$\frac{{\mu }_E{\left(T\right)}^2}{{\mathrm{\Lambda }}_{\mathit{QCD}}^2}\ln \left(\frac{{\mu }_E{\left(T\right)}^2}{{\mathrm{\Lambda }}_{\mathit{QCD}}^2}\right)=\frac{1+N_f/6}{11-2/3N_f}{\left(\frac{4\pi T}{{\mathrm{\Lambda }}_{\mathit{QCD}}}\right)}^2.(5)$

Note that such solution leads to the Debye mass consistent with lattice QCD results [66, 67].

Running coupling α_S (Q²) is defined as [68].

${\alpha }_S\left(Q^2\right)=\frac{4\pi }{\left(11-2/3N_f\right)\ln \left(Q^2/{\mathrm{\Lambda }}_{\mathit{QCD}}^2\right)},(6)$

where, in the collisional energy loss case, the coupling appears through the term ${\alpha }_S^2$ [24], which can be factorised to ${\alpha }_S({\mu }_E^2){\alpha }_S(ET)$ [30] (see also [31]).

The radiation spectrum [51] is:

$\begin{array}{ll}\hfill \frac{d^2{N}_{\mathrm{r}\mathrm{a}\mathrm{d}}}{dxd\tau }& =\int \frac{d^{2}k}{\pi }\frac{d^{2}q}{\pi }\frac{2C_R{C}_2\left(G\right)T}{x}\frac{{\mu }_E{\left(T\right)}^2-{\mu }_M{\left(T\right)}^2}{\left({\mathit{q}}^2+{\mu }_M{\left(T\right)}^2\right)\left({\mathit{q}}^2+{\mu }_E{\left(T\right)}^2\right)}\frac{{\alpha }_S\left(ET\right){\alpha }_S\left(\frac{{\mathit{k}}^2+\chi \left(T\right)}{x}\right)}{\pi }\hfill \\ \hfill & \times \frac{\left(\mathit{k}+\mathit{q}\right)}{{\left(\mathit{k}+\mathit{q}\right)}^2+\chi \left(T\right)}\left(1-\cos \left(\frac{{\left(\mathit{k}+\mathit{q}\right)}^2+\chi \left(T\right)}{x\left(E+p_z\right)}\tau \right)\right)\left(\frac{\left(\mathit{k}+\mathit{q}\right)}{{\left(\mathit{k}+\mathit{q}\right)}^2+\chi \left(T\right)}-\frac{\mathit{k}}{{\mathit{k}}^2+\chi \left(T\right)}\right).\hfill \end{array}(7)$

Here C₂(G) = 3; χ(T) ≡ M²x² + m_g(T)², where x is the longitudinal momentum fraction of the jet carried away by the emitted gluon, p_z is longitudinal component of initial jet momentum, and $m_g(T)={\mu }_E(T)/\sqrt{2}$ is the effective gluon mass in finite temperature QCD medium [69], where μ_E(T) is Debye mass defined above; M = 1.3 GeV for charm, 4.5 GeV for bottom [54–56, 70, 71] and ${\mu }_E(T)/\sqrt{6}$ for light quarks (where thermal mass originates from gluon propagators); μ_M(T) is magnetic screening, where different non-perturbative approaches suggest 0.4 < μ_M(T)/μ_E(T) < 0.6 [67, 72]; q and k are transverse momenta of exchanged (virtual) and radiated gluon, respectively. $Q_k^2=\frac{{\mathit{k}}^2+\chi (T)}{x}$ in ${\alpha }_S(\frac{{\mathit{k}}^2+\chi (T)}{x})$ corresponds to the off-shellness of the jet prior to the gluon radiation [25]. Note that, all α_S terms in Eqs 4, 7 are infrared safe (and moreover of a moderate value) [31]. Thus, contrary to majority of other approaches, we do not need to introduce a cut-off in α_S (Q²).

We further assume that radiative and collisional energy losses can be separately treated in P (E_i → E_f), i.e., jet quenching is performed via two independent branching processes [31, 52]. We first calculate the modification of the quark and gluon spectrum due to radiative energy loss, then collisional energy loss (we checked that change of order is unimportant within our model). This is a reasonable approximation when the radiative and collisional energy losses can be considered small (which is in the essence of the soft-gluon, soft-rescattering approximation widely used in energy loss calculations) and when radiative and collisional energy loss processes are decoupled, as is the case in the generalized HTL approach [73] used in our energy loss calculations.

To obtain the radiative energy loss contribution to the suppression [57], we start with Eq. 7 and, for a given trajectory, we first compute the mean number of gluons emitted due to induced radiation (further denoted as ${\bar{N}}_{tr}(E)$), as well as the mean number of gluons emitted per fractional energy loss x (i.e., $\frac{d{\bar{N}}_{tr}(E)}{dx}$, for compactness further denoted as ${\bar{N}}_{tr}^{\prime }(E,x)$):

${\bar{N}}_{tr}\left(E\right)=\underset{tr}{\int }\left(\int \frac{d^2{N}_{\mathrm{r}\mathrm{a}\mathrm{d}}}{dxd\tau }dx\right)d\tau ,{\bar{N}}_{tr}^{\prime }\left(E,x\right)=\underset{tr}{\int }\frac{d^2{N}_{\mathrm{r}\mathrm{a}\mathrm{d}}}{dxd\tau }d\tau ,(8)$

where the subscript tr indicates that the value depends on the trajectory. Radiative energy loss suppression takes multi-gluon fluctuations into account, where we assume that the fluctuations of gluon number are uncorrelated. Such assumption is reasonable, as Ref. [74] studied full splitting cascade and found that independent branchings reasonably well approximate a full branching. The radiative energy loss probability can then be expressed via Poisson expansion [31, 57]:

$\begin{array}{ll}\hfill P_{\mathit{rad}}^{tr}\left(E_i\to E_f\right)& =\frac{\delta \left(E_i-E_f\right)}{e^{{\bar{N}}_{tr}\left(E_i\right)}}+\frac{{\bar{N}}_{tr}^{\prime }\left(E_i,1-\frac{E_f}{E_i}\right)}{E_i{e}^{{\bar{N}}_{tr}\left(E_i\right)}}+\hfill \\ \hfill & +\sum _{n=2}^{\infty }\frac{e^{-{\bar{N}}_{tr}\left(E_i\right)}}{n!E_i}\int d{x}_1\cdots d{x}_n{\bar{N}}_{tr}^{\prime }\left(E_i,x_1\right)\cdots {\bar{N}}_{tr}^{\prime }\left(E_i,x_{n-1}\right){\bar{N}}_{tr}^{\prime }\left(E_i,1-\frac{E_f}{E_i}-x_1-\cdots -x_{n-1}\right).\hfill \end{array}(9)$

E_i and E_f are initial and final jet energy (before and after) radiative process.

To calculate the parton spectrum after radiative energy loss, we apply

$\frac{E_{f,R}{d}^3\sigma }{d{p}_{f,R}^3}=\frac{E_i{d}^3\sigma \left(Q\right)}{d{p}_i^3}\otimes P_{\mathit{rad}}^{tr}\left(E_i\to E_{f,R}\right),(10)$

where the final spectra is obtained after integrating over p_i > p_f,R.

To find collisional energy loss contribution, Eq. 4 is first integrated over the given trajectory:

${\bar{E}}_{\mathrm{c}\mathrm{o}\mathrm{l}}^{tr}\left(E\right)=\underset{tr}{\int }\frac{d{E}_{\mathit{col}}}{d\tau }d\tau .(11)$

For collisional energy loss, the full fluctuation spectrum is approximated by a Gaussian centered at the average energy loss ${\bar{E}}_{\mathrm{c}\mathrm{o}\mathrm{l}}^{tr}(E)$ [52, 58].

$P_{\mathrm{c}\mathrm{o}\mathrm{l}}^{tr}\left(E_i,E_f\right)=\frac{1}{\sqrt{2\pi }{\sigma }_{\mathrm{c}\mathrm{o}\mathrm{l}}^{tr}\left(E_i\right)}\exp \left(-\frac{{\left(E_i-E_f-{\bar{E}}_{\mathrm{c}\mathrm{o}\mathrm{l}}^{tr}\left(E_i\right)\right)}^2}{2{\sigma }_{\mathrm{c}\mathrm{o}\mathrm{l}}^{tr}{\left(E_i\right)}^2}\right),(12)$

with a variance

${\sigma }_{\mathrm{c}\mathrm{o}\mathrm{l}}^{tr}\left(E\right)=\sqrt{2\overline{T^{tr}}{\bar{E}}_{\mathrm{c}\mathrm{o}\mathrm{l}}^{tr}\left(E\right)},(13)$

where $\overline{T^{tr}}$ is the average temperature along the trajectory, E_i and E_f are initial and final energy (before and after collisional processes).

To calculate the quenched hadron spectrum after collisional energy loss, we apply

$\frac{E_f{d}^3{\sigma }_q\left(H_Q\right)}{d{p}_f^3}=\frac{E_{i,C}{d}^3\sigma \left(Q\right)}{d{p}_{i,C}^3}\otimes P_{\mathit{col}}^{tr}\left(E_{i,C}\to E_f\right)\otimes D\left(Q\to H_Q\right),(14)$

where we assume E_i,C = E_f,R, i.e. the final jet energy after radiative quenching corresponds to the initial jet energy for collisional quenching. Since both collisional energy loss and gain contribute to the final spectra [24, 52], both E_i,C > E_f and E_i,C < E_f have to be taken into account in Eq. 14. Finally, the hadron suppression $R_{AA}^{tr}(p_f,H_Q)$ for the single trajectory, after radiative and collisional energy loss, is equal to the ratio of quenched and unquenched momentum spectra

$R_{AA}^{tr}\left(p_f,H_Q\right)=\frac{E_f{d}^3{\sigma }_q\left(H_Q\right)}{d{p}_f^3}/\frac{E_f{d}^3{\sigma }_u\left(H_Q\right)}{d{p}_f^3},(15)$

where $\frac{E_f{d}^3{\sigma }_u(H_Q)}{d{p}_f^3}$ is given by Eq. 2. $R_{AA}^{tr}(p_f,H_Q)$ then needs to be averaged over trajectories with the same direction angle ϕ to obtain the suppression as a function of angle, R_AA (p_f, ϕ, H_Q). This is an important intermediary step since, depending on the details of QGP temperature evolution and the spatial variations in the temperature profile, energy loss may significantly depend on the parton’s direction of motion². Once we have calculated R_AA (p_f, ϕ, H_Q), we can easily evaluate R_AA and v₂ observables as [75] (we here omit H_Q in the expressions, and denote p_f = p_⊥)³:

$R_{AA}\left(p_{\perp }\right)=\frac{1}{2\pi }{\int }_0^{2\pi }{R}_{AA}\left(p_{\perp },\varphi \right)d\varphi ,(16)$

$v_2\left(p_{\perp }\right)=\frac{\frac{1}{2\pi }{\int }_0^{2\pi }\cos \left(2\varphi \right)R_{AA}\left(p_{\perp },\varphi \right)d\varphi }{R_{AA}\left(p_{\perp }\right)}.(17)$

While the general expressions of the dynamical energy loss formalism are the same as in the DREENA-B framework [51], the fact that, in DREENA-A, the temperature entering the Eqs 4–7 explicitly depends on the current parton position, notably complicates the implementation of these formulas, as we discuss in the following section.

2.2 Framework outline

Our previous DREENA-C and DREENA-B frameworks were based on computationally useful, but rough, approximations of the medium evolution: while in DREENA-C, there was no evolution, and the temperature remained constant both in time and along spatial dimensions, in DREENA-B, the medium was assumed to evolve according to 1D Bjorken approximation [76]. Due to these approximations, parton energy loss depended on its path length independently of its direction or production point. This allowed to analytically integrate energy-loss formulas to a significant extent, which notably reduced the number of required numerical integrations. Furthermore R_AA only needed to be averaged out over precalculated path-length distributions. Thus, these approximations of the medium evolution straightforwardly led to efficient computational algorithms for DREENA-C and DREENA-B.

DREENA-A framework, on the other hand, addresses fully general medium dynamics, with arbitrary spatio-temporal temperature distribution. The main input to the algorithm is the temperature profile T_profile given as a three-dimensional matrix of temperature values at points with coordinates (x, y, τ) (in the input file, the values should be arranged in an array of quartets of the form (τ, x, y, T_profile), and the lowest value of τ appearing in the data is taken to be τ₀). In addition to the temperature profile, the DREENA-A algorithm also takes, as inputs, the initial parton p_⊥ distributions $\frac{d^2\sigma }{d{p}_{\perp }^2}$ (each as an array of $(p_{\perp },\frac{d^2\sigma }{d{p}_{\perp }^2})$ pairs) and the jet production probability distribution (as a matrix of probability density values in the transversal plane, formatted analogously as the profile temperature values). This level of generality requires a different approach than in previous frameworks. Since the DREENA-A algorithm takes arbitrary medium temperature evolution as the input, the energy loss has to be individually calculated for each parton trajectory.

This means that for each trajectory–given by the coordinates x₀ and y₀ of the parton origin (in the transversal plane) and the direction angle ϕ–we must first numerically evaluate integrals (8) and (11). Since the current parton position–for a given trajectory–becomes a function of the proper time τ, integrands in Eqs 8, 11 also become functions of τ, either through an explicit dependence, or via position and time dependent medium temperature (3). We numerically integrate these functions along the trajectory (parametrized by τ as x = x₀ + τ cos ϕ, y = y₀ + τ sin ϕ), starting from the origin at (x₀, y₀) and moving in small integration steps along the direction ϕ (in practice, 0.1 fm step is sufficiently small for most of the profiles). The integration is terminated when the medium temperature at the current parton’s position drops below T_c = 155 MeV [77], i.e., when the parton leaves the QGP phase. Also, we approximate that there are no energy losses before the initial time τ₀ (which is a parameter of the temperature profile evolution) and thus the first part of the trajectory, corresponding to τ < τ₀, is effectively skipped (i.e., τ₀ is taken as the lower limit of integration in Eqs 8, 11).

Once we, for a given trajectory, compute the integrals (8) and (11), we then perform the rest of procedure laid out by Eqs 8–15. Most of the computation time is spent on numerical integrations, in particular for evaluating integrals in Eqs 9, 10. While, in principle, n → ∞ in Eq. 9, in practice we show that n = 5 is sufficient for convergence in the case of quark jets, while for gluon jets n = 7 is needed. In general, the Quasi-Monte Carlo integration method turned out to be the most efficient and is used for all these integrals (as quasirandom numbers, we use precalculated and stored Halton sequences). The result of the integration (15) is the final hadron suppression $R_{AA}^{tr}(p_{\perp },H_Q)$ for the jet moving along the chosen trajectory, given as the function of its transversal momentum.

To obtain R_AA (p_⊥, ϕ, H_Q), we have to average this result over all production points (taking into account the provided jet production probability distribution) and repeat the procedure for many angles ϕ. In practice, this means that we must evaluate energy loss along a very large number of trajectories. This has significantly increased the computational complexity of the problem compared to DREENA-C and DREENA-B and required a number of optimisations.

2.3 Numerical optimisation of DREENA-A

We started by adapting optimisation methods that we successfully implemented in earlier versions. One useful approach was a tabulation and consequent interpolation of values for computationally expensive functions. In particular, this is crucial for the complicated integrals (4–7): while a two dimensional array is sufficient to tabulate $\frac{d{E}_{col}}{d\tau }$ (which is a function of T and p), values of $\frac{d^2{N}_{\mathrm{r}\mathrm{a}\mathrm{d}}}{dxd\tau }$ (depending on τ, T, p and x) must be stored in a four-dimensional array. Tabulating such functions is done adaptively, with the density of evaluated points varying, depending on the function behaviour (i.e., using a denser grid where the functions change rapidly and sparser where the behaviour is smooth). In the case of these two functions, not only that the consequent interpolation can significantly reduce the overall number of integral evaluations, but the corresponding tables (for each particle type) can be evaluated only once and then permanently stored and reused for all trajectories and even for different temperature profiles. To further optimise the algorithm, we also precalculate the integral $\int \frac{d^2{N}_{\mathrm{r}\mathrm{a}\mathrm{d}}}{dxd\tau }dx$ values and store a corresponding three-dimensional array (since it is a function of τ, T, and p).

When using this table-interpolation method, it is often necessary to make a function transformation before tabulation: e.g., it is more efficient and accurate to sample and later interpolate logarithm of a rapidly (nearly or approximately-exponentially) increasing function than the function itself (similarly, it is sometimes more optimal to tabulate ratio, or a product of functions than each of the functions separately). For example, it is much more optimal to tabulate and consecutively interpolate R_AAs (and other similarly behaving expressions) than the corresponding momentum distributions. This methodology is now extensively applied throughout DREENA-A (from some intermediate-level energy loss results to evaluating multi-dimensional integrals in the calculation of radiated gluon rates). Given the size of some of these tables and that many interpolations are needed, we ensured that the table lookup and interpolation algorithm are efficient.

As we encounter multiple numerical integrations at different stages of the computation, modifying their order was another type of optimisation, where the natural order (from the theoretical viewpoint) is not necessarily followed but is instead adapted to the particular function behaviour. Specifically, it turned out that a different order of integration (for radiative contribution) is optimal for heavy flavor particles compared to gluons. I.e., while it is natural, from the physical perspective, to start with the initial momentum distributions of partons and integrate over the radiative energy loss (see Eqs 9 and 10), it turned out that (for heavy flavors) the shape of the initial distributions necessitates a very high number of integration points to achieve the required computation precision. Reorganising the formulas and postponing the integration over initial distributions to the very end turned much more computationally optimal for heavy flavor. A similar procedure in the case of light quarks allowed much of the integration to be carried out jointly for all quarks, since their effective masses are the same, but initial p_⊥ distributions differ.

The crucial optimisation in DREENA-A is the method used for averaging over the particle trajectories. In suppression calculations, it is common to carry out the averaging over production points and directions by Monte Carlo (MC) sampling, but it turned out that the equidistant sampling of both jet production points and direction angles was here significantly more efficient. We initially implemented the Monte Carlo approach, randomly selecting both the origin coordinates and the angles of particle trajectories. The binary collision density was used as the probability density for coordinates of origins, while the angles were generated from a uniform distribution. Convergence of the results by using this method required a large number of sampled trajectories, as illustrated in Figure 1. The figure shows R_AA and v₂ results obtained by the DREENA-A algorithm for a different total number of trajectories (the computation was done for D meson traversing the temperature evolution generated using a Glauber initialised viscous hydrodynamic code [78], at 30–40% centrality class). The plots in the right column of Figure 1 show the magnitude of the deviation of the particular curve from the median curve, where the latter is the arithmetic mean of all curves in the plot (as the measure of deviation of a function f(p) from a reference function $\bar{f}(p)$ we use $|\delta f|=\frac{\int |f(p)-\bar{f}(p)|dp}{\int |\bar{f}(p)|dp}$). We see that R_AA convergence is easily achieved, where relative deviations of the order of 1% are obtained by taking into account only 2,500 trajectories (see Figure 1-A and Figure 1-A*). Computing the v₂ value requires much more trajectories, i.e., we see a substantial scattering of the Monte Carlo results with 2,500 trajectories, while $\sim 10^6$ trajectories are needed to reduce relative deviation below 1%. Note that a small number of sampled trajectories also causes a systematic error: the smaller the number of trajectories, the lower the averaged v₂.

FIGURE 1

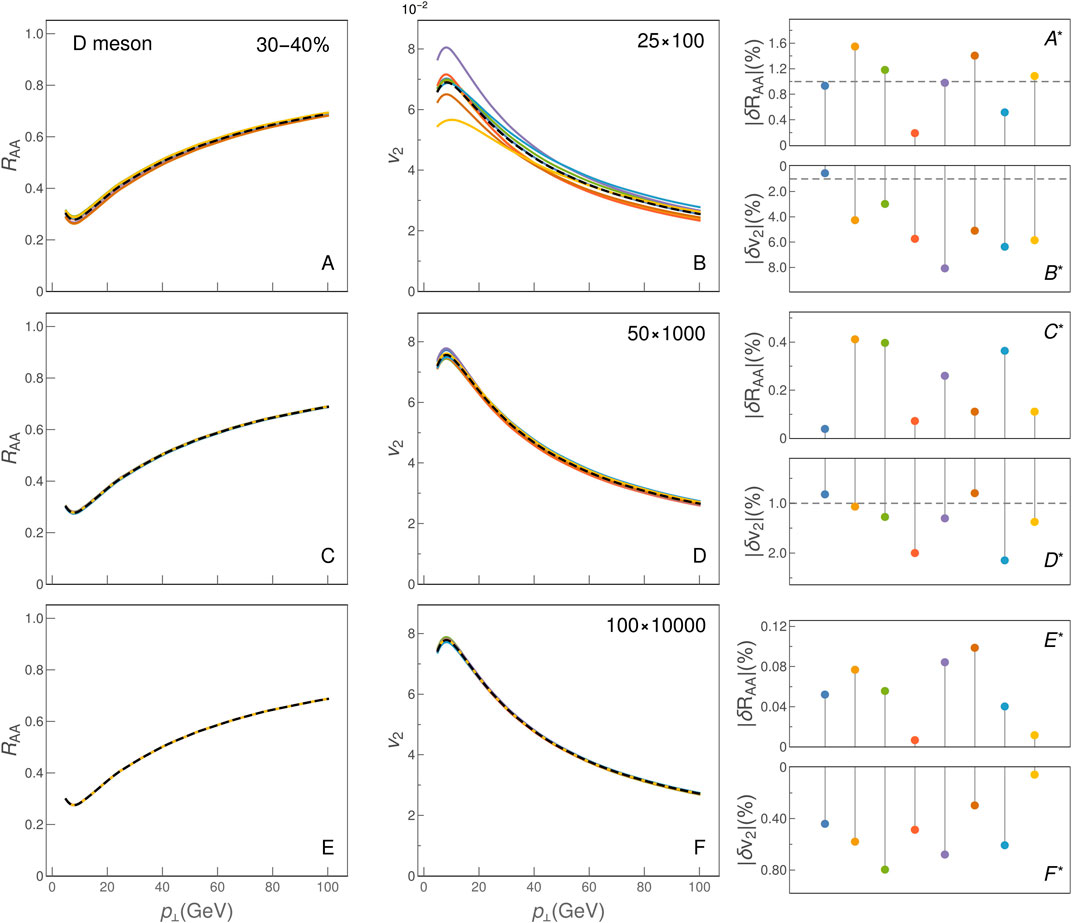
FIGURE 1. D meson R_AA (left) and v₂ (middle) at 30–40% centrality computed using different numbers of randomly generated trajectories (Monte Carlo approach), together with their deviations (right, scaled 1-norm was used as a metric) from the results averaged over the same ensemble of trajectories. The dashed horizontal line in rightmost panels indicates the threshold of 1% deviation. The top row depicts results obtained from sampling 25 trajectories at different angles originating from each of 100 randomly selected jet-production points; the middle row—50 angles from 1,000 points; the bottom row—100 angles from 10,000 points. Each panel shows the results of eight repeated computations (each with an independent ensemble of randomly generated trajectories), the dashed line representing the mean. M = 1.2 GeV. We use a single value μ_M/μ_E = 0.5 [67, 72] to make the figure clearer.

When using the equidistant sampling method instead of Monte Carlo, we divide the transverse plane into an equidistant grid, whose points are used as jet origins. Energy loss for each trajectory is then weighted with the jet production probability at each point, and summed up. As production probability, we used the binary collision density evaluated using the optical Glauber model. In Figure 2, we see that, for already ∼ 10.000 evaluated trajectories, the integral has converged within 1% of the estimated ‘proper’ value. This modification resulted in a more than two orders of magnitude reduction of the execution time. We also tested two hybrid variants: 1) where trajectory origins were randomly selected but directions equidistantly, and 2) where production points were equidistantly selected, but directions randomly sampled. The convergence of the two variants interpolated between the MC sampling and the equidistant sampling (Figures 1, 2, respectively).

FIGURE 2

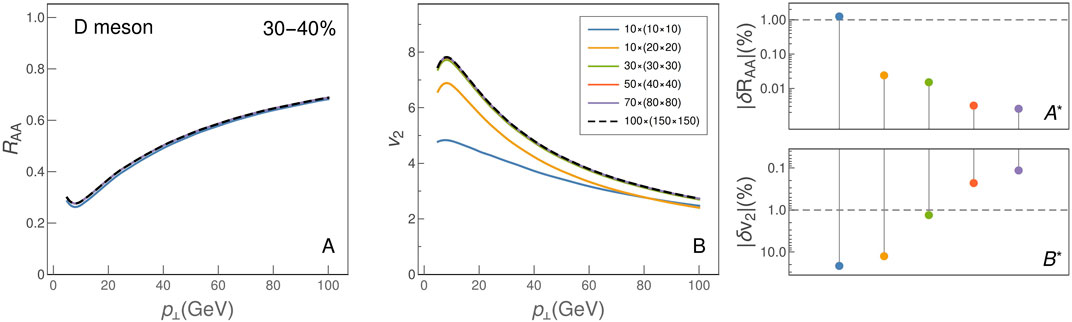
FIGURE 2. D meson R_AA (left) and v₂ (middle) at 30–40% centrality computed using different numbers of trajectories originating from equidistant points. Results are labeled by numbers n_ϕ × (n_x × n_y): jet directions are along n_ϕ uniformly distributed angles (from 0 to 2π) originating from each point of the n_x-by-n_y equidistant grid in the transversal plane. Deviation of each line from the baseline result (chosen as the outcome for 100 × (150 × 150) trajectories, dashed line) is shown in right panels. M = 1.2 GeV, μ_M/μ_E = 0.5.

2.4 Convergence test of different DREENA methods

Finally, as a consistency check for DREENA-A, we compared its predictions with DREENA-C and DREENA-B results. For this purpose, we generated artificial T profiles suitable for this comparison, illustrated in Figure 3. The results of the DREENA-A and DREENA-B comparison, for R_AA and v₂, are shown in the upper panels of Figure 4, respectively. Lower panels of Figure 4 show the comparison of all three frameworks on the hard-cylinder collision profile constant in time (for this comparison, we modified the DREENA-B code to remove temperature dependence on time). We see that all frameworks lead to consistent results (up to computational precision), supporting the reliability of the DREENA-A.

FIGURE 3

FIGURE 3. Temperature distribution (Pb + Pb collision, 30–40% centrality, mid-rapidity) for constant temperature [50] (A) and 1D Bjorken evolution [51] (B), at time (from left to right) τ = τ₀, 3, and five fm/c, represented by colour mapping. For constant temperature approximation, τ₀ = 0 fm. For 1D Bjorken approximation, τ₀ = 0.6 fm.

FIGURE 4

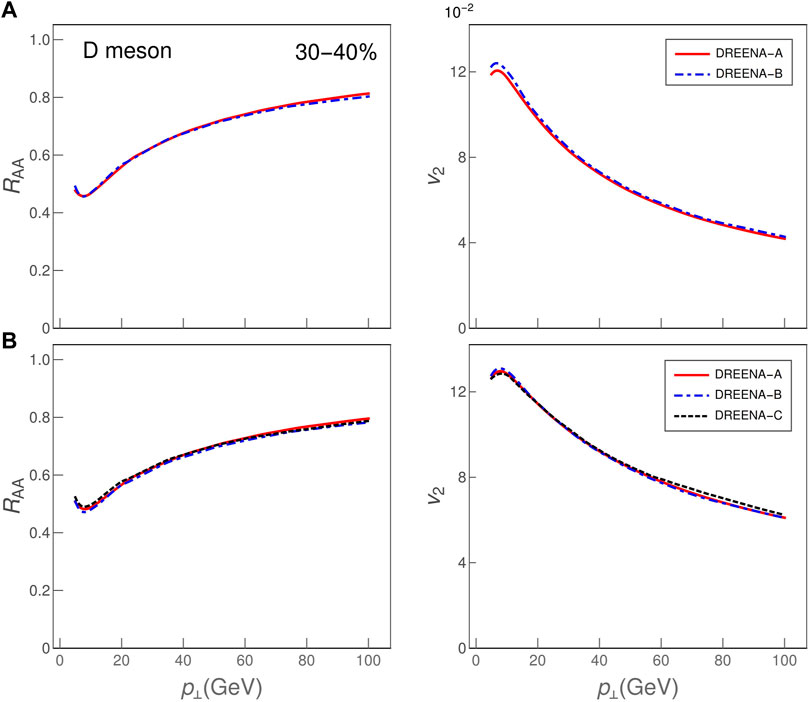
FIGURE 4. Comparison of different DREENA frameworks, for Bjorken medium evolution (A) and for constant medium temperature approximation (B), demonstrating inter-framework consistency. (A) show D meson R_AA (left) and v₂ (right) at 30–40% centrality computed using DREENA-A (supplied with temperature profiles representing Bjorken evolution) and DREENA-B. (B) show the same observables, computed using all three DREENA frameworks, when applied to the same constant temperature medium. M = 1.2 GeV, μ_M/μ_E = 0.5.

3 Results and discussion

To demostrate the utility of the DREENA-A approach, we generated temperature profiles for Pb + Pb collisions at the full LHC energy ($\sqrt{s_{\mathrm{N}\mathrm{N}}}=5.02$ TeV) and Au + Au collisions at the full RHIC energy ($\sqrt{s_{\mathrm{N}\mathrm{N}}}=200$ GeV) using three different initialisations of the fluid-dynamical expansion.

First, we used optical Glauber initialisation at initial time τ₀ = 1.0 fm without initial transverse flow. The evolution of the fluid was calculated using a 3+1D viscous fluid code from Ref. [78]. The parameters to describe collisions at the LHC energy were tuned to reproduce the low-p_⊥ data obtained in Pb + Pb collisions at $\sqrt{s_{\mathrm{N}\mathrm{N}}}=5.02$ TeV [32]. In particular, shear viscosity over entropy density ratio was constant η/s = 0.12, there was no bulk viscosity, and the equation of state (EoS) parametrisation was s95p-PCE-v1 [79]. For RHIC energy we used ‘LH-LQ’ parameters from Ref. [78], except that we used constant η/s = 0.16. Binary collision density from Glauber model was used as the probability distribution for the initial points of jets, while their directions were sampled from a uniform angular distribution.

Second, we used the EKRT initialisation [80–82], and evolved it using the same code we used to evolve the Glauber initialisation, but restricted to a boost-invariant expansion. In this case, the initial time was τ₀ = 0.2 fm, and parameters were the favoured values of a Bayesian analysis of the data from Pb + Pb collisions at $\sqrt{s_{\mathrm{N}\mathrm{N}}}=2.76$ and 5.02 GeV, and from Au + Au collisions at $\sqrt{s_{\mathrm{N}\mathrm{N}}}=200$ GeV using the EoS parametrisation s83s₁₈ [19]. In particular, there was no bulk viscosity and the minimum value of temperature-dependent η/s was 0.18. Origins of the high-p_⊥ particles were sampled using the binary collision density of Glauber model, while the distribution of their directions was uniform.

Our third option was the T_RENTo initialisation [83] evolved using the VISH2+1 code [84] as described in [85, 86]. To describe collisions at LHC, parameters were based on a Bayesian analysis of the data at the above mentioned two LHC collision energies [86], although the analysis was done event-by-event, whereas we carried out the calculations using simple event-averaged initial states. In particular, the calculation included free streaming stage until τ₀ = 1.16 fm, EoS based on the lattice results by the HotQCD collaboration [77], and temperature-dependent shear and bulk viscosity coefficients with the minimum value of (η/s)_min = 0.081 and maximum of (ζ/s)_max = 0.052. For RHIC, we used the “PTB” maximum a posteriori parameter values from Ref. [87], but changed the temperature-dependent shear viscosity coefficient (η/s) (T) to a constant η/s = 0.16. The initial event-by-event collision points were used to generate the spatial probability distribution for the initial coordinates of the high-p_⊥ particles, while their angular distribution was uniform.

All these calculations lead to an acceptable fit to measured charged hadron multiplicities, low-p_⊥ spectra, and p_⊥-differential v₂ in 10–20%, 20–30%, 30–40%, and 40–50% centrality classes. As we may expect, different initialisations and initial times lead to a visibly different temperature evolution. This is demonstrated in Figure 5 where we show the calculated temperature distributions in collisions at the LHC energy at various times. Looking at the profiles, it is easily noticeable that they evolve differently in space and time. Even if the initial anisotropy of the Glauber initialisation is lowest, later in time, its anisotropy is largest, since the very early start of EKRT initialisation, or the early free streaming of T_RENTo, dilute the spatial anisotropy very fast. That is, “Glauber” exhibits larger asymmetry throughout the QGP evolution compared to the other two profiles (though “EKRT” has larger asymmetry than “Trento”), which might accordingly translate to differences in high-p_⊥ v₂. Similarly, the early start of EKRT leads to a large initial temperature, which is expected to result in a smaller R_AA than the other two profiles.

FIGURE 5

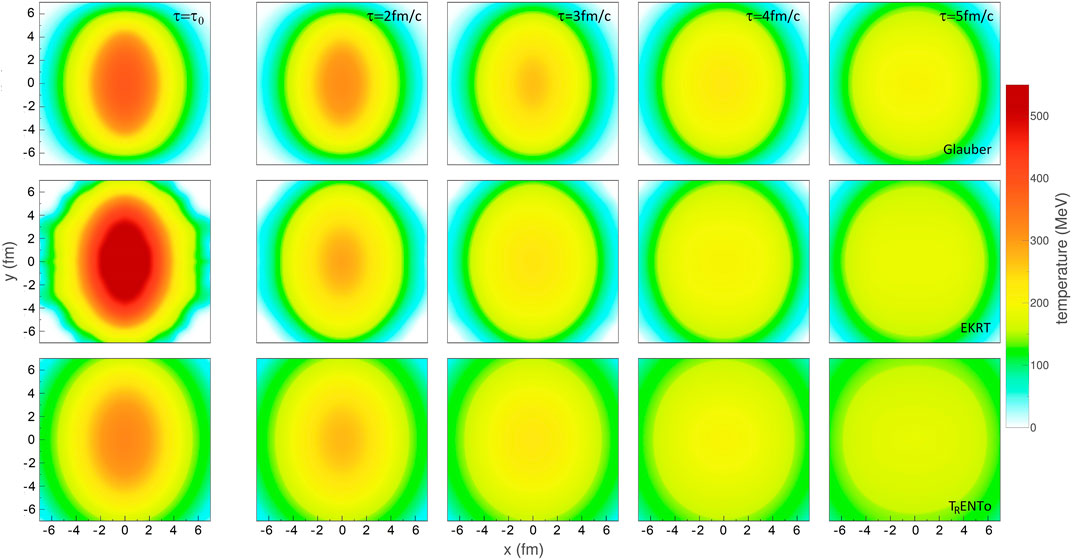
FIGURE 5. Temperature distribution (Pb + Pb collision, 30–40% centrality, mid-rapidity) for different medium evolution models, at time (from left to right) τ = τ₀, 2, 3, 4 and five fm/c, represented by colour mapping. First row: “Glauber”, τ₀ = 1 fm; second row: “EKRT”, τ₀ = 0.2 fm; third row: “T_RENTo”, τ₀ = 1.16 fm. Note that distributions in the first column correspond to different times.

To test if these visual differences can be quantified through high-p_⊥ data at the LHC and RHIC, we used these profiles as an input to the DREENA-A to generate high-p_⊥ R_AA and v₂ predictions for charged hadrons, D and B mesons. As can be seen in Figures 6, 7, both R_AA and v₂ show notable differences for both experiments and all types of flavor. For example, “EKRT” leads to the smallest R_AA, i.e., largest suppression, as can be expected based on the largest temperature. Similarly, the calculated high-p_⊥ v₂ depicts the same ordering as the system anisotropy during the evolution: “Glauber” leads to the largest, followed by “EKRT”, while T_RENTo leads to the lowest v₂. Consequently, the DREENA-A framework can differentiate between temperature profiles by corresponding differences in high-p_⊥ observables, where these differences agree with the qualitative observations from Figure 5. Since the differences in evolution are due to different initialisations, and different properties of the fluid (EoS and/or dissipative coefficients), R_AA and v₂ observables can be used to provide further constraints to the fluid properties. We note here that even low-p_⊥ data could be used to differentiate our three evolution scenarios, but such analysis would require evaluating χ² or a similar measure of the quality of the fit, or computing Bayes factors [87]. The high-p_⊥ observables, on the other hand, show clear differences visible by the naked eye.

FIGURE 6

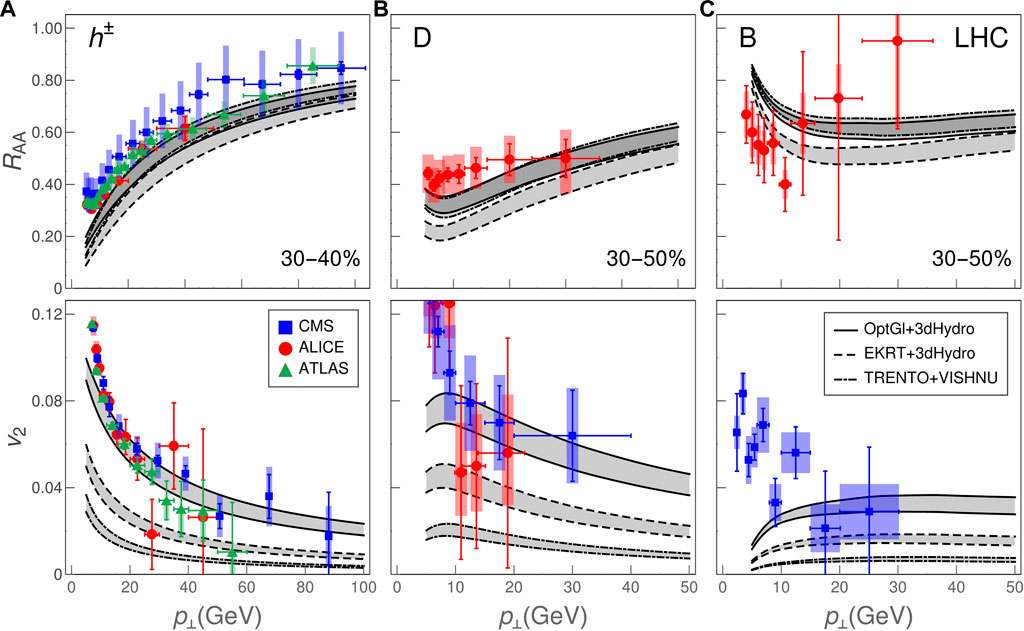
FIGURE 6. DREENA-A R_AA (top panels) and v₂ (bottom panels) predictions in Pb + Pb collisions at $\sqrt{s_{\mathrm{N}\mathrm{N}}}=5.02$ TeV are generated for different models of QGP medium evolution (indicated in the legend). Charged hadron (A) predictions are generated for 30–40% centrality, while D (B) and B (C) meson predictions are generated for 30–50% centrality region. For charged hadrons, the predictions are compared with the experimental data from CMS [88, 89], ALICE [90, 91] and ATLAS [92, 93]. For D mesons, the predictions are compared with ALICE [94, 95] and CMS [96] data. For B mesons predictions are compared with preliminary ALICE [97] and CMS [98]. The boundary of each gray band corresponds to 0.4 < μ_M/μ_E < 0.6 [67, 72].

FIGURE 7

FIGURE 7. DREENA-A R_AA (top panels) and v₂ (bottom panels) predictions in Au + Au collisions at $\sqrt{s_{\mathrm{N}\mathrm{N}}}=200$ GeV are generated for different models of QGP medium evolution (indicated in the legend). Charged hadron (A), D meson (B) and B meson (C) predictions are generated for 20–30% centrality region. The h^± predictions are compared with π⁰ data from PHENIX [99, 100] and h^± data from STAR [101, 102] - note that for v₂ 10–40% centrality data is shown for STAR. For D mesons, the predictions are compared with STAR [103, 104] data at 10–40% centrality and with PHENIX [105] data at 20–40%. B mesons predictions are compared with PHENIX [105] data at 20–40%. The boundary of each gray band corresponds to 0.4 < μ_M/μ_E < 0.6 [67, 72].

Moreover, from Figures 6, 7, we see that all types of flavor, at both RHIC and LHC, show apparent sensitivity to differences in medium evolution, making them equally suitable for exploring the bulk QGP properties with high-p_⊥ data. With the expected availability of precision data from the upcoming high-luminosity experiments at RHIC and LHC (see e.g. [106–108]), the DREENA-A framework provides a unique opportunity for exploring the bulk QGP properties. We propose that the adequate medium evolution should be able to reproduce high-p_⊥ observables in both RHIC and LHC experiments for different collision energies and collision systems, with reasonable accuracy. As demonstrated in this study, an equal emphasis should be given to light and heavy flavor, as they provide a valuable independent constraint for bulk medium evolution. Overall, DREENA-A provides a versatile tool to put large amounts of data generated at RHIC and LHC experiments to optimal use.

We also observe that none of the profiles analysed in Figures 6, 7 lead to satisfactory agreement with high-p_⊥ R_AA and v₂ data. However, we note that the goal of this study is not to get a good agreement with the experimental data, but to demonstrate that 1) different temperature profiles lead to different high-p_⊥ predictions, 2) high-p_⊥ data can provide an important further constraint in exploring the QGP properties. Finding suitable temperature profiles (i.e., QGP parameters) that would lead to a reasonable agreement with high-p_⊥ data is a highly non-trivial task which is left for further work.

4 Summary

We presented the DREENA-A computational framework for tomography of Quark-Gluon Plasma created in heavy-ion collisions at RHIC and the LHC. The tool is based on state-of-the-art energy loss calculation and can include arbitrary temperature profiles. This feature allows fully exploiting different temperature profiles as the only input in the framework. We showed that the calculated high-p_⊥ R_AA and v₂ exhibit notable sensitivity to the details of the temperature profiles, consistent with intuitive expectations based on the profile visualisation. The DREENA-A framework applies to different types of flavor, collision systems, and collision energies. It can, consequently, provide an efficient and versatile QGP tomography tool for further constraining the bulk properties of this extreme form of matter. To facilitate this, we also provided the fully optimized, publicly available software for generating DREENA-A predictions. The code allows straightforwardly generating high-p_⊥ predictions for diverse models of QGP evolution.

Data availability statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author. The source code of the DREENA-A algorithm (together with usage instructions and example data), can be found at https://github.com/DusanZigic/DREENA-A.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work is supported by the European Research Council, grant ERC-2016-COG: 725741, and by the Ministry of Science and Technological Development of the Republic of Serbia. PH was also supported by the program Excellence Initiative–Research University of the University of Wrocław of the Ministry of Education and Science.

Acknowledgments

We thank Marko Djordjevic, Bojana Ilic, and Stefan Stojku for useful discussions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹While it is challenging to implement further improvements into the analytical calculations while keeping all existing ingredients, some possible directions for advances include, e.g., flow velocity of the bulk medium and transverse gradients of temperature and density (see e.g. [45–48]).

²In earlier DREENA frameworks, this dependence was also present but was solely a consequence of the path-length distribution dependence on the angle.

³Note that, in Eq. 17, using R_AA(p_⊥, ϕ), instead of the hadron p_⊥ spectrum, is computationally more efficient since R_AA(p_⊥, ϕ) is a well-behaved function, and the number of p_⊥ points where we need to evaluate R_AA(p_⊥, ϕ) is significantly smaller.

References

1. Collins JC, Perry MJ. Superdense matter: Neutrons or asymptotically free quarks? Phys Rev Lett (1975) 34:1353–6. doi:10.1103/PhysRevLett.34.1353

CrossRef Full Text | Google Scholar

2. Baym G, Chin S. Can a neutron star be a giant mit bag? Phys Lett B (1976) 62:241–4. doi:10.1016/0370-2693(76)90517-7

CrossRef Full Text | Google Scholar

3. Shuryak EV. What RHIC experiments and theory tell us about properties of quark-gluon plasma? Nucl Phys A (2005) 750:64–83. doi:10.1016/j.nuclphysa.2004.10.022

CrossRef Full Text | Google Scholar

4. Shuryak E. Strongly coupled quark-gluon plasma in heavy ion collisions. Rev Mod Phys (2017) 89:035001. doi:10.1103/RevModPhys.89.035001

CrossRef Full Text | Google Scholar

5. Gyulassy M, McLerran L. New forms of QCD matter discovered at RHIC. Nucl Phys A (2005) 750:30–63. doi:10.1016/j.nuclphysa.2004.10.034

CrossRef Full Text | Google Scholar

6. Jacak B, Steinberg P. Creating the perfect liquid in heavy-ion collisions. Phys Today (2010) 63N5:39–43. doi:10.1063/1.3431330

CrossRef Full Text | Google Scholar

7. Muller B, Schukraft J, Wyslouch B. First results from Pb+Pb collisions at the LHC. Annu Rev Nucl Part Sci (2012) 62:361–86. doi:10.1146/annurev-nucl-102711-094910

CrossRef Full Text | Google Scholar

8. Stock R. The physics of dense nuclear matter from supernovae to quark gluon plasma. Nature (1989) 337:319–24. doi:10.1038/337319a0

CrossRef Full Text | Google Scholar

9. Stachel J. Has the quark-gluon plasma been seen? Int J Mod Phys A (2006) 21:1750–63. doi:10.1142/S0217751X06032733

CrossRef Full Text | Google Scholar

10. Kolb PF, Heinz UW. Hydrodynamic description of ultrarelativistic heavy ion collisions In: Quark–Gluon Plasma (2004) 3: 634–714. doi:10.1142/9789812795533_0010

CrossRef Full Text | Google Scholar

11. Romatschke P, Romatschke U. Viscosity information from relativistic nuclear collisions: How perfect is the fluid observed at RHIC? Phys Rev Lett (2007) 99:172301. doi:10.1103/PhysRevLett.99.172301

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Heinz U, Snellings R. Collective flow and viscosity in relativistic heavy-ion collisions. Annu Rev Nucl Part Sci (2013) 63:123–51. doi:10.1146/annurev-nucl-102212-170540

CrossRef Full Text | Google Scholar

13. Adams J, Aggarwal M, Ahammed Z, Amonett J, Anderson B, Arkhipkin D, et al. Experimental and theoretical challenges in the search for the quark gluon plasma: The STAR Collaboration’s critical assessment of the evidence from RHIC collisions. Nucl Phys A (2005) 757:102–83. doi:10.1016/j.nuclphysa.2005.03.085

CrossRef Full Text | Google Scholar

14. Adcox K, Adler S, Afanasiev S, Aidala C, Ajitanand N, Akiba Y, et al. Formation of dense partonic matter in relativistic nucleus-nucleus collisions at RHIC: Experimental evaluation by the PHENIX collaboration. Nucl Phys A (2005) 757:184–283. doi:10.1016/j.nuclphysa.2005.03.086

CrossRef Full Text | Google Scholar

15. Aad G, Abbott B, Abdallah J, Abdelalim AA, Abdesselam A, Abdinov O, et al. Observation of a centrality-dependent dijet asymmetry in lead-lead collisions at $\sqrt{s_{\mathrm{N}\mathrm{N}}}=2.76\mathrm{T}\mathrm{e}\mathrm{V}$ with the ATLAS detector at the LHC. Phys Rev Lett (2010) 105:252303. doi:10.1103/PhysRevLett.105.252303

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Aamodt K, Abrahantes Quintana A, Adamova D, Adare A, Aggarwal M, Aglieri Rinella G, et al. Suppression of charged particle production at large transverse momentum in central Pb–Pb collisions at $\sqrt{s_{\mathrm{N}\mathrm{N}}}$ = 2.76TeV. Phys Lett B (2011) 696:30–9. doi:10.1016/j.physletb.2010.12.020

CrossRef Full Text | Google Scholar

17. Chatrchyan S, Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Bergauer T, et al. Observation and studies of jet quenching in PbPb collisions at $\sqrt{s_{\mathrm{N}\mathrm{N}}}$ = 2.76TeV. Phys Rev C (2011) 84:024906. doi:10.1103/PhysRevC.84.024906

CrossRef Full Text | Google Scholar

18. Nagle JL, Bearden IG, Zajc WA. Quark-gluon plasma at RHIC and the LHC: Perfect fluid too perfect? New J Phys (2011) 13:075004. doi:10.1088/1367-2630/13/7/075004

CrossRef Full Text | Google Scholar

19. Auvinen J, Eskola KJ, Huovinen P, Niemi H, Paatelainen R, Petreczky P. Temperature dependence of η/s of strongly interacting matter: Effects of the equation of state and the parametric form of (η/s)(T). Phys Rev C (2020) 102:044911. doi:10.1103/PhysRevC.102.044911

CrossRef Full Text | Google Scholar

20. Orjuela Koop JD, Adare A, McGlinchey D, Nagle JL. Azimuthal anisotropy relative to the participant plane from a multiphase transport model in central p + Au , d + Au , and ³He + Au collisions at $\sqrt{s_{\mathrm{N}\mathrm{N}}}$ = 200 GeV. Phys Rev C (2015) 92:054903. doi:10.1103/PhysRevC.92.054903

CrossRef Full Text | Google Scholar

21. Auvinen J, Bernhard JE, Bass SA, Karpenko I. Investigating the collision energy dependence of η/s in the beam energy scan at the BNL Relativistic Heavy Ion Collider using Bayesian statistics. Phys Rev C (2018) 97:044905. doi:10.1103/PhysRevC.97.044905

CrossRef Full Text | Google Scholar

22. Kapusta JI. Finite temperature field theory. Cambridge: Cambridge Monographs on Mathematical Physics Cambridge University Press (1989).

Google Scholar

23. Bellac ML. Thermal field theory. Cambridge, UK: Cambridge Monographs on Mathematical Physics Cambridge University Press (2011).

Google Scholar

24. Djordjevic M. Collisional energy loss in a finite size QCD matter. Phys Rev C (2006) 74:064907. doi:10.1103/PhysRevC.74.064907

CrossRef Full Text | Google Scholar

25. Djordjevic M. Theoretical formalism of radiative jet energy loss in a finite size dynamical QCD medium. Phys Rev C (2009) 80:064909. doi:10.1103/PhysRevC.80.064909

CrossRef Full Text | Google Scholar

26. Djordjevic M, Heinz UW. Radiative energy loss in a finite dynamical QCD medium. Phys Rev Lett (2008) 101:022302. doi:10.1103/PhysRevLett.101.022302

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Stojku S, Ilic B, Djordjevic M, Djordjevic M. Extracting the temperature dependence in high-p_⊥ particle energy loss. Phys Rev C (2021) 103:024908. doi:10.1103/PhysRevC.103.024908

CrossRef Full Text | Google Scholar

28. Djordjevic M, Djordjevic M. Generalization of radiative jet energy loss to non-zero magnetic mass. Phys Lett B (2012) 709:229–33. doi:10.1016/j.physletb.2012.02.019

CrossRef Full Text | Google Scholar

29. Aurenche P, Gelis F, Zaraket H. A Simple sum rule for the thermal gluon spectral function and applications. J High Energ Phys (2002) 05:043. doi:10.1088/1126-6708/2002/05/043

CrossRef Full Text | Google Scholar

30. Peigne S, Peshier A. Collisional energy loss of a fast heavy quark in a quark-gluon plasma. Phys Rev D (2008) 77:114017. doi:10.1103/PhysRevD.77.114017

CrossRef Full Text | Google Scholar

31. Djordjevic M, Djordjevic M. LHC jet suppression of light and heavy flavor observables. Phys Lett B (2014) 734:286–9. doi:10.1016/j.physletb.2014.05.053

CrossRef Full Text | Google Scholar

32. Stojku S, Auvinen J, Djordjevic M, Huovinen P, Djordjevic M. Early evolution constrained by high-$p_{\perp }$ quark-gluon plasma tomography. Phys Rev C (2022) 105:L021901. doi:10.1103/PhysRevC.105.L021901

CrossRef Full Text | Google Scholar

33. Stojku S, Auvinen J, Zivkovic L, Huovinen P, Djordjevic M. Jet-temperature anisotropy revealed through high-p_⊥ data. Physics Letters B, in press (2022).

Google Scholar

34. Djordjevic M, Djordjevic M, Blagojevic B. RHIC and LHC jet suppression in non-central collisions. Phys Lett B (2014) 737:298–302. doi:10.1016/j.physletb.2014.08.063

CrossRef Full Text | Google Scholar

35. Djordjevic M, Djordjevic M. Predictions of heavy-flavor suppression at 5.1 TeV Pb + Pb collisions at the CERN large hadron collider. Phys Rev C (2015) 92:024918. doi:10.1103/PhysRevC.92.024918

CrossRef Full Text | Google Scholar

36. Djordjevic M. Heavy flavor puzzle at LHC: A serendipitous interplay of jet suppression and fragmentation. Phys Rev Lett (2014) 112:042302. doi:10.1103/PhysRevLett.112.042302

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Djordjevic M. Complex suppression patterns distinguish between major energy loss effects in Quark–Gluon Plasma. Phys Lett B (2016) 763:439–44. doi:10.1016/j.physletb.2016.10.077

CrossRef Full Text | Google Scholar

38. Baier R, Dokshitzer YL, Mueller AH, Peigne S, Schiff D. Radiative energy loss and $p_{\perp }$ broadening of high energy partons in nuclei. Nucl Phys B (1997) 484:265–82. doi:10.1016/S0550-3213(96)00581-0

CrossRef Full Text | Google Scholar

39. Zakharov BG. Fully quantum treatment of the Landau-Pomeranchik-Migdal effect in QED and QCD. JETP Lett (1996) 63:952–7. doi:10.1134/1.567126

CrossRef Full Text | Google Scholar

40. Zakharov BG. Radiative energy loss of high-energy quarks in finite size nuclear matter and quark - gluon plasma. JETP Lett (1997) 65:615–20. doi:10.1134/1.567389

CrossRef Full Text | Google Scholar

41. Armesto N, Salgado CA, Wiedemann UA. Medium induced gluon radiation off massive quarks fills the dead cone. Phys Rev D (2004) 69:114003. doi:10.1103/PhysRevD.69.114003

CrossRef Full Text | Google Scholar

42. Gyulassy M, Levai P, Vitev I. Reaction operator approach to nonAbelian energy loss. Nucl Phys B (2001) 594:371–419. doi:10.1016/S0550-3213(00)00652-0

CrossRef Full Text | Google Scholar

43. Arnold PB, Moore GD, Yaffe LG. Photon emission from ultrarelativistic plasmas. J High Energ Phys (2001) 11:057. doi:10.1088/1126-6708/2001/11/057

CrossRef Full Text | Google Scholar

44. Arnold PB, Moore GD, Yaffe LG. Photon emission from quark gluon plasma: Complete leading order results. J High Energ Phys (2001) 12:009. doi:10.1088/1126-6708/2001/12/009

CrossRef Full Text | Google Scholar

45. Li H, Liu F, Ma G, Wang XN, Zhu Y. Mach cone induced by γ-triggered jets in high-energy heavy-ion collisions. Phys Rev Lett (2011) 106:012301. doi:10.1103/PhysRevLett.106.012301

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Sadofyev AV, Sievert MD, Vitev I. Ab initio coupling of jets to collective flow in the opacity expansion approach. Phys Rev D (2021) 104:094044. doi:10.1103/PhysRevD.104.094044

CrossRef Full Text | Google Scholar

47. Antiporda L, Bahder J, Rahman H, Sievert MD. Jet drift and collective flow in heavy-ion collisions. Phys Rev D (2022) 105:054025. doi:10.1103/PhysRevD.105.054025

CrossRef Full Text | Google Scholar

48. Barata J, Sadofyev AV, Salgado CA. Jet broadening in dense inhomogeneous matter. Phys Rev D (2022) 105:114010. doi:10.1103/PhysRevD.105.114010

CrossRef Full Text | Google Scholar

49. Blagojevic B, Djordjevic M. Importance of different energy loss effects in jet suppression at the RHIC and the LHC. J Phys G: Nucl Part Phys (2015) 42:075105. doi:10.1088/0954-3899/42/7/075105

CrossRef Full Text | Google Scholar

50. Zigic D, Salom I, Auvinen J, Djordjevic M, Djordjevic M. DREENA-C framework: Joint R_AA and v₂ predictions and implications to QGP tomography. J Phys G: Nucl Part Phys (2019) 46:085101. doi:10.1088/1361-6471/ab2356

CrossRef Full Text | Google Scholar

51. Zigic D, Salom I, Auvinen J, Djordjevic M, Djordjevic M. DREENA-B framework: First predictions of R_AA and v₂ within dynamical energy loss formalism in evolving QCD medium. Phys Lett B (2019) 791:236–41. doi:10.1016/j.physletb.2019.02.020

CrossRef Full Text | Google Scholar

52. Wicks S, Horowitz W, Djordjevic M, Gyulassy M. Elastic, inelastic, and path length fluctuations in jet tomography. Nucl Phys A (2007) 784:426–42. doi:10.1016/j.nuclphysa.2006.12.048

CrossRef Full Text | Google Scholar

53. Djordjevic M, Gyulassy M, Vogt R, Wicks S. Influence of bottom quark jet quenching on single electron tomography of au+au. Phys Lett B (2006) 632:81–6. doi:10.1016/j.physletb.2005.09.087

CrossRef Full Text | Google Scholar

54. Kang ZB, Vitev I, Xing H. Nuclear modification of high transverse momentum particle production in p+A collisions at RHIC and LHC. Phys Lett B (2012) 718:482–7. doi:10.1016/j.physletb.2012.10.046

CrossRef Full Text | Google Scholar

55. Sharma R, Vitev I, Zhang BW. Light-cone wave function approach to open heavy flavor dynamics in QCD matter. Phys Rev C (2009) 80:054902. doi:10.1103/PhysRevC.80.054902

CrossRef Full Text | Google Scholar

56. Cacciari M, Frixione S, Houdeau N, Mangano ML, Nason P, Ridolfi G. Theoretical predictions for charm and bottom production at the LHC. J High Energ Phys (2012) 10:137. doi:10.1007/jhep10(2012)137

CrossRef Full Text | Google Scholar

57. Gyulassy M, Levai P, Vitev I. Jet tomography of Au+Au reactions including multigluon fluctuations. Phys Lett B (2002) 538:282–8. doi:10.1016/S0370-2693(02)01990-1

CrossRef Full Text | Google Scholar

58. Moore GD, Teaney D. How much do heavy quarks thermalize in a heavy ion collision? Phys Rev C (2005) 71:064904. doi:10.1103/PhysRevC.71.064904

CrossRef Full Text | Google Scholar

59. de Florian D, Sassot R, Stratmann M. Global analysis of fragmentation functions for pions and kaons and their uncertainties. Phys Rev D (2007) 75:114010. doi:10.1103/PhysRevD.75.114010

CrossRef Full Text | Google Scholar

60. Cacciari M, Nason P. Charm cross-sections for the tevatron run II. J High Energ Phys (2003) 09:006. doi:10.1088/1126-6708/2003/09/006

CrossRef Full Text | Google Scholar

61. Braaten E, Cheung K, Fleming S, Yuan TC. Perturbative QCD fragmentation functions as a model for heavy quark fragmentation. Phys Rev D (1995) 51:4819–29. doi:10.1103/PhysRevD.51.4819

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Kartvelishvili VG, Likhoded AK, Petrov VA. On the fragmentation functions of heavy quarks into hadrons. Phys Lett B (1978) 78:615–7. doi:10.1016/0370-2693(78)90653-6

CrossRef Full Text | Google Scholar

63. Braaten E, Thoma MH. Energy loss of a heavy fermion in a hot QED plasma. Phys Rev D (1991) 44:1298–310. doi:10.1103/PhysRevD.44.1298

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Selikhov A, Gyulassy M. Color diffusion and conductivity in a quark - gluon plasma. Phys Lett B (1993) 316:373–80. doi:10.1016/0370-2693(93)90341-E

CrossRef Full Text | Google Scholar

65. Selikhov AV, Gyulassy M. QCD Fokker-Planck equations with color diffusion. Phys Rev C (1994) 49:1726–9. doi:10.1103/PhysRevC.49.1726

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Peshier A. Running coupling and screening in the (s)QGP hep-ph/0601119 (2006).

Google Scholar

67. Nakamura A, Saito T, Sakai S. Lattice calculation of gluon screening masses. Phys Rev D (2004) 69:014506. doi:10.1103/PhysRevD.69.014506

CrossRef Full Text | Google Scholar

68. Field RD, Pines DA. Appl Perturbative QCD. Cambridge, Massachussetts: Perseus Books (1995).

69. Djordjevic M, Gyulassy M. Ter-Mikayelian effect on QCD radiative energy loss. Phys Rev C (2003) 68:034914. doi:10.1103/PhysRevC.68.034914

CrossRef Full Text | Google Scholar

70. Tanabashi M, Hagiwara K, Hikasa K, Nakamura K, Sumino Y, Takahashi F, et al. Review of particle physics. Phys Rev D (2018) 98:030001. doi:10.1103/PhysRevD.98.030001

CrossRef Full Text | Google Scholar

71. Beraudo A, Gossiaux P, Andronic A, Averbeck R, Masciocchi S. Extraction of heavy-flavor transport coefficients in QCD matter. Nucl Phys A (2018) 979:21–86. doi:10.1016/j.nuclphysa.2018.09.002

CrossRef Full Text | Google Scholar

72. Maezawa Y, Aoki S, Ejiri S, Hatsuda T, Ishii N, Kanaya K, et al. Electric and magnetic screening masses at finite temperature from generalized polyakov-line correlations in two-flavor lattice QCD. Phys Rev D (2010) 81:091501. doi:10.1103/PhysRevD.81.091501

CrossRef Full Text | Google Scholar

73. Djordjevic M. Heavy quark energy loss: Collisional vs radiative. Nucl Phys A (2007) 783:197–204. doi:10.1016/j.nuclphysa.2006.11.008

CrossRef Full Text | Google Scholar

74. Fickinger M, Ovanesyan G, Vitev I. Angular distributions of higher order splitting functions in the vacuum and in dense QCD matter. J High Energ Phys (2013) 07:059. doi:10.1007/JHEP07(2013)059

CrossRef Full Text | Google Scholar

75. Luzum M, Petersen H. Initial state fluctuations and final state correlations in relativistic heavy-ion collisions. J Phys G: Nucl Part Phys (2014) 41:063102. doi:10.1088/0954-3899/41/6/063102

CrossRef Full Text | Google Scholar

76. Bjorken JD. Highly relativistic nucleus-nucleus collisions: The central rapidity region. Phys Rev D (1983) 27:140–51. doi:10.1103/PhysRevD.27.140

CrossRef Full Text | Google Scholar

77. Bazavov A, Bhattacharya T, DeTar C, Ding HT, Gottlieb S, Gupta R, et al. Equation of state in (2+1)-flavor QCD. Phys Rev D (2014) 90:094503. doi:10.1103/PhysRevD.90.094503

CrossRef Full Text | Google Scholar

78. Molnar E, Holopainen H, Huovinen P, Niemi H. Influence of temperature-dependent shear viscosity on elliptic flow at backward and forward rapidities in ultrarelativistic heavy-ion collisions. Phys Rev C (2014) 90:044904. doi:10.1103/PhysRevC.90.044904

CrossRef Full Text | Google Scholar

79. Huovinen P, Petreczky P. QCD equation of state and hadron resonance gas. Nucl Phys A (2010) 837:26–53. doi:10.1016/j.nuclphysa.2010.02.015

CrossRef Full Text | Google Scholar

80. Eskola KJ, Kajantie K, Ruuskanen PV, Tuominen K. Scaling of transverse energies and multiplicities with atomic number and energy in ultrarelativistic nuclear collisions. Nucl Phys B (2000) 570:379–89. doi:10.1016/S0550-3213(99)00720-8

CrossRef Full Text | Google Scholar

81. Paatelainen R, Eskola KJ, Holopainen H, Tuominen K. Multiplicities and p_T spectra in ultrarelativistic heavy ion collisions from a next-to-leading order improved perturbative QCD + saturation + hydrodynamics model. Phys Rev C (2013) 87:044904. doi:10.1103/PhysRevC.87.044904

CrossRef Full Text | Google Scholar

82. Paatelainen R, Eskola KJ, Niemi H, Tuominen K. Fluid dynamics with saturated minijet initial conditions in ultrarelativistic heavy-ion collisions. Phys Lett B (2014) 731:126–30. doi:10.1016/j.physletb.2014.02.018

CrossRef Full Text | Google Scholar

83. Moreland JS, Bernhard JE, Bass SA. Alternative ansatz to wounded nucleon and binary collision scaling in high-energy nuclear collisions. Phys Rev C (2015) 92:011901. doi:10.1103/PhysRevC.92.011901

CrossRef Full Text | Google Scholar

84. Song H, Heinz UW. Causal viscous hydrodynamics in 2+1 dimensions for relativistic heavy-ion collisions. Phys Rev C (2008) 77:064901. doi:10.1103/PhysRevC.77.064901

CrossRef Full Text | Google Scholar

85. Bernhard JE. Bayesian parameter estimation for relativistic heavy-ion collisions. Ph.D. thesis. Duke U. arXiv:1804.06469 (2018).

Google Scholar

86. Bernhard JE, Moreland JS, Bass SA. Bayesian estimation of the specific shear and bulk viscosity of quark–gluon plasma. Nat Phys (2019) 15:1113–7. doi:10.1038/s41567-019-0611-8

CrossRef Full Text | Google Scholar

87. Everett D, Ke W, Paquet JF, Vujanovic G, Bass SA, Du L, et al. Multisystem Bayesian constraints on the transport coefficients of QCD matter. Phys Rev C (2021) 103:054904. doi:10.1103/PhysRevC.103.054904

CrossRef Full Text | Google Scholar

88. Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Asilar E, Bergauer T, et al. Charged-particle nuclear modification factors in PbPb and pPb collisions at $\sqrt{s_{\mathrm{N}\mathrm{N}}}=5.02\mathrm{T}\mathrm{e}\mathrm{V}$. J High Energ Phys (2017) 04:039. doi:10.1007/JHEP04(2017)039

CrossRef Full Text | Google Scholar

89. Sirunyan AM, Tumasyan A, Adam W, Asilar E, Bergauer T, Brandstetter J, et al. Azimuthal anisotropy of charged particles with transverse momentum up to 100 GeV/c in PbPb collisions at $\sqrt{s_{\mathrm{N}\mathrm{N}}}=5.02\mathrm{T}\mathrm{e}\mathrm{V}$. Phys Lett B (2018) 776:195–216. doi:10.1016/j.physletb.2017.11.041

CrossRef Full Text | Google Scholar

90. Acharya S, Acosta FT, Adamova D, Adolfsson J, Aggarwal MM, Aglieri Rinella G, et al. Transverse momentum spectra and nuclear modification factors of charged particles in pp, p-Pb and Pb-Pb collisions at the LHC. J High Energ Phys (2018) 11:013. doi:10.1007/JHEP11(2018)013

CrossRef Full Text | Google Scholar

91. Acharya S, Acosta FT, Adamova D, Adolfsson J, Aggarwal MM, Aglieri Rinella G, et al. Energy dependence and fluctuations of anisotropic flow in Pb-Pb collisions at $\sqrt{s_{\mathrm{N}\mathrm{N}}}=5.02\mathrm{T}\mathrm{e}\mathrm{V}$ and 2.76 TeV. J High Energ Phys (2018) 07:103. doi:10.1007/JHEP07(2018)103

CrossRef Full Text | Google Scholar

92.Measurement of nuclear modification factor R_AA in Pb+Pb collisions at $\sqrt{s_{\mathrm{N}\mathrm{N}}}=5.02\mathrm{T}\mathrm{e}\mathrm{V}$ with the ATLAS detector at the LHC ATLAS-CONF-2017-012 (2017).

Google Scholar

93. Aaboud M, Aad G, Abbott B, Abdinov O, Abeloos B, Abhayasinghe DK, et al. Measurement of the azimuthal anisotropy of charged particles produced in $\sqrt{s_{\mathrm{N}\mathrm{N}}}=5.02\mathrm{T}\mathrm{e}\mathrm{V}$ Pb+Pb collisions with the ATLAS detector. Eur Phys J C (2018) 78:997. doi:10.1140/epjc/s10052-018-6468-7

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Acharya S. Measurement of D⁰, D⁺, D*⁺ and D_s⁺ production in Pb-Pb collisions $\sqrt{s_{\mathrm{N}\mathrm{N}}}=5.02\mathrm{T}\mathrm{e}\mathrm{V}$. JHEP (2018) 10:174. doi:10.1007/JHEP10.174

CrossRef Full Text | Google Scholar

95. Acharya S, Adamova D, Adolfsson J, Aggarwal MM, Aglieri Rinella G, Agnello M, et al. D-meson azimuthal anisotropy in midcentral Pb-Pb collisions at $\sqrt{s_{\mathrm{N}\mathrm{N}}}=5.02\mathrm{T}\mathrm{e}\mathrm{V}$. Phys Rev Lett (2018) 120:102301. doi:10.1103/PhysRevLett.120.102301

PubMed Abstract | CrossRef Full Text | Google Scholar

96. Sirunyan AM, Tumasyan A, Adam W, Ambrogi F, Asilar E, Bergauer T, et al. Measurement of prompt D⁰ meson azimuthal anisotropy in Pb-Pb collisions at $\sqrt{s_{\mathrm{N}\mathrm{N}}}=5.02\mathrm{T}\mathrm{e}\mathrm{V}$. Phys Rev Lett (2018) 120:202301. doi:10.1103/PhysRevLett.120.202301

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Peng X. Beauty production in heavy-ion collisions with ALICE at the LHC, arXiv:2207.10259 (2022).

Google Scholar

98. Kim Y. Highlights from the CMS experiment. In: Plenary talk at Quark Matter 2022 conference (2022).

Google Scholar

99. Adare A, Afanasiev S, Aidala C, Ajitanand NN, Akiba Y, Al-Bataineh H, et al. Neutral pion production with respect to centrality and reaction plane in Au+Au collisions at $\sqrt{s_{\mathrm{N}\mathrm{N}}}=200\mathrm{G}\mathrm{e}\mathrm{V}$. Phys Rev C (2013) 87:034911. doi:10.1103/PhysRevC.87.034911

CrossRef Full Text | Google Scholar

100. Adare A, Afanasiev S, Aidala C, Ajitanand NN, Akiba Y, Al-Bataineh H, et al. Azimuthal anisotropy of ${\pi }^0$ Production in $\mathrm{A}\mathrm{u}+\mathrm{A}\mathrm{u}$ Collisions at $\sqrt{s_{NN}}=200\mathrm{G}\mathrm{e}\mathrm{V}$: Path-length dependence of jet quenching and the role of initial geometry. Phys Rev Lett (2010) 105:142301. doi:10.1103/PhysRevLett.105.142301

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Adams J, Adler C, Aggarwal MM, Ahammed Z, Amonett J, Anderson BD, et al. Transverse-momentum and collision-energy dependence of High-$p_T$ Hadron Suppression in $\mathrm{A}\mathrm{u}+\mathrm{A}\mathrm{u}$ Collisions at ultrarelativistic Energies. Phys Rev Lett (2003) 91:172302. doi:10.1103/PhysRevLett.91.172302

PubMed Abstract | CrossRef Full Text | Google Scholar

102. Abelev BI, Aggarwal MM, Ahammed Z, Anderson BD, Arkhipkin D, Averichev GS, et al. Centrality dependence of charged hadron and strange hadron elliptic flow from $\sqrt{s_{\mathrm{N}\mathrm{N}}}=200\mathrm{G}\mathrm{e}\mathrm{V}$. Phys Rev C (2008) 77:054901. doi:10.1103/PhysRevC.77.054901

CrossRef Full Text | Google Scholar

103. Adamczyk L, Adkins J, Agakishiev G, Aggarwal M, Ahammed Z, Alekseev I, et al. Observation of D⁰ meson nuclear modifications in Au+Au collisions at $\sqrt{s_{\mathrm{N}\mathrm{N}}}=200\mathrm{G}\mathrm{e}\mathrm{V}$. Phys Rev Lett (2014) 113:142301. [Erratum: Phys.Rev.Lett. 121, 229901 (2018)]. doi:10.1103/PhysRevLett.113.142301

PubMed Abstract | CrossRef Full Text | Google Scholar

104. Adamczyk L, Adkins J, Agakishiev G, Aggarwal M, Ahammed Z, Ajitanand N, et al. Measurement of D⁰ azimuthal anisotropy at midrapidity in Au+Au collisions at $\sqrt{s_{\mathrm{N}\mathrm{N}}}=200\mathrm{G}\mathrm{e}\mathrm{V}$. Phys Rev Lett (2017) 118:212301. doi:10.1103/PhysRevLett.118.212301

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Hachiya T. Charm and Bottom quark energy loss and flow measurements in Au+Au collisions by the PHENIX experiment. In: Plenary talk at Quark Matter 2022 conference (2022).

PubMed Abstract | Google Scholar

106.sPHENIX beam use proposal (2021). https://indico.bnl.gov/event/11884/attachments/34524/56472/sPHENIX_BUP_2021.pdf.

Google Scholar

107.BUR Committee. The STAR beam use request for run-22 and data taking in 2023-25 (2021). https://drupal.star.bnl.gov/STAR/files/STAR_Beam_Use_Request_Runs22_25.pdf.

Google Scholar

108. Fartoukh S. LHC configuration and operational scenario for run 3 (2021). CERN-ACC-2021-0007.

Google Scholar