Dual solutions for double diffusion and MHD flow analysis of micropolar nanofluids with slip boundary condition

The present communication is designed to elucidate the flow attributes of micro-polar non-Newtonian liquid over stretching/shrinking surfaces. In addition, we have observed the stagnation aspect along with the velocity slip condition on the momentum field. The Fourier law of heat conduct, along with a physical aspect of stratified and heat generation absorption, are then used to model the temperature equation. The Buongiorno nanofluid model is used to study additional transport features. After a discussion of PDEs using similarity transformation, mathematical formulations of the given problem are supported in the form of an ordinary differential system. The solution of modeled governing equations containing physical effects is simulated by using the shooting method in conjunction with RK- Method. The significant effects of flow parameters that are associated with velocity, temperature, and concentration distribution for low and upper branch solutions are revealed through graphs and tables. Quantities of engineering concerns like skin friction coefficient and Nusselt number are also compared with previous results of critical values. Furthermore, it should be considered that as the micro-pole parameters are increased, the local skin friction coefficient and the local Nusselt number amplitude also rise.

1 Introduction

Magnetic fluid dynamics is the foundation for improving the progression of high conductivity fluids in the direction of the magnetic field. The study of magnetic field flows, both Newtonian and non-Newtonian, has an extensive variety of applications in industry and engineering. The cooling system fluid metal, MHD generators, liquid beads and sprays, accelerators, atomic reactors, nutrient preparation, the oil industry, microelectronics equipment, geothermal energy extraction equipment, and so on are all examples of MHD applications. Many scientists believe that it has great uses in micro-skipping and slip velocities explored the fluid analysis of small horizontal heat shifts. Sliding flow plays a key role in small-scale instruments, hard disk scale valves, and micro-scale wells. [1] explain the two parallel bands between the secondary fluid magnetic flow force serialized stream. [2] the semi-inverse solution of nanometer uniform magnetic flow on the stretched surface of the secondary fluid was studied. [3] observed an irregular magnetic-fluid-dynamic hybrid convector of a secondary nanofluid caused by thermal radiation in a stretched plane. Recently, [4] analysis of the magnetic flow of the two nanofluids due to non-linear stretching of the surface. [5] examines the magnetic flow of nanofluids in tubes. [6] considered the entropy generation of nanofluids and MHD streams on non-linear stretched surfaces was studied. [7] discuss the rotational flow of water-based nanofluids in parallel plates. [8] analyzed the influence of pseudoplastic fluids loaded with antiparticles on the heat transfer of MHD flow. [9] a three-dimensional MHD stream of Maxwell nanoflow was analyzed by convection boundary. [10] speculate on the magnetic flow of the secondary fluid above the stretching plane. [4] the magnetic fluid dynamics of the secondary nanofluid were analyzed due to the non-linear stretching of the surface. [11] also studied the computational aspects of MHD streams near rotating disks. Many comparative investigations are considering the significance of fluid motion through various physical phenomena that can be found in [12–14].

Thermal rays play an important role in space technology and high-temperature operations. When the temperature changes greatly, the linear thermal radiation can cause significant errors. To overcome this inaccuracy, non-linear thermal radiation was taken into account. The chattels of chemical processes and the flow of thermal radiation to the externally stretched surface were explored by [15]. Many scientists have conducted several studies to emphasize the significance of thermal radiation [16–18].

Natural convection and forced convection combine to form mixed convection, which is among the transmitting phenomena. Mixed convection occurs in many natural and engineering applications during transport. Industrial and technological processes, including exposure to the wind in the solar central receiver, fan-cooled electronics, and cooling of nuclear reactors in the event of downtime. [19] check past mass exchange and Hall effects semi-infinite vertical band magnetic fluid free heat transfer flow. [20] studied the influence of conical micro-polar fluid flow on the stretched surface. Micro-polar fluids are those that contain micro-components that can be rotated, and whose appearance can affect the flow of fluid power so that it can be non-Newtonian. Different types of non-ideal fluids can be seen in regular life, such as macromolecules, animal blood, and shampoos.

Analysis of Dual Solutions in MHD Fluid Flow with Heat and Mass Transfer Past an Exponentially Shrinking/Stretching Surface in a Porous Medium was studied by [21]. Using a conducting fluid to pass through a sheet that was simultaneously stretching and contracting exponentially, researchers examined the nature of dual solutions in the hydromagnetic boundary layer. Investigation of the combined effects of the electrically conducting water-based nanofluid parameters, thermal radiation, the porous medium, convective heating, viscous dissipation, magnetic field, and the nanofluid on the dimensionless velocity, temperature, and rescaled nanoparticle volume frame is the aim of the current work. Readers are directed to [22–34] and any cited references therein for more information.

This study’s objective is to numerically investigate micropolar nanofluid flow with slip boundary conditions. The first step in this is mathematical modeling for the MHD nanofluid flow with a nonlinear condition. Finally, use a shooting scheme to solve numerical results. The remaining sections of the document are arranged as follows; in Section 2, flow configuration and governing equations are described. The numerical scheme is carried out in Section 3. Section 4 conducts a thorough analysis of the findings. Section 5 also discusses the conclusion.

2 Flow analysis and development

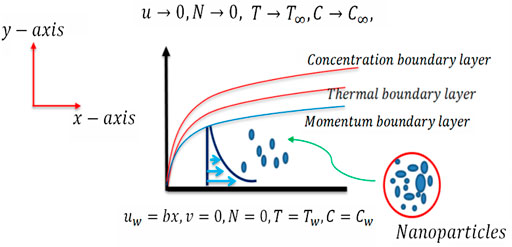
This study investigates the steady, 2D, and double stratified flow of an electrically conductive micropolar nanoparticle on a stretching/shrinking surface. It is worth noting that the heat and mass transport phenomena are investigated when velocity slip and thermal generation/absorption are considered (see Figure 1).

FIGURE 1

FIGURE 1. An illustration of flow analysis.

The following are the governing equations for heat and mass transfer:

$\frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}=0,(1)$

$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\left({\nu }_f+\frac{k_f}{{\rho }_f}\right)\frac{\partial ²u}{\partial y^2}+\frac{k_f}{{\rho }_f}\frac{\partial N}{\partial y}-\frac{\sigma B_0^2}{{\rho }_f}\left(u-u_{\infty }\right)+u_{\infty }\frac{d{u}_{\infty }}{du},(2)$

$u\frac{\partial N}{\partial x}+v\frac{\partial N}{\partial y}=\frac{{\gamma }_f}{{\left(j\rho \right)}_f}\frac{{\partial }^{2}N}{\partial y^2²}+\frac{k_f}{{\left(j\rho \right)}_f}\left\{2N+\frac{\partial u}{\partial y}\right\},(3)$

$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k_f}{{\left(\rho c_p\right)}_f}\frac{{\partial }^2²T}{\partial y^2²}+\frac{{\left(\rho c_p\right)}_p}{{\left(\rho c_p\right)}_f}\left\{D_B\frac{\partial C}{\partial y}\frac{\partial T}{\partial x}+\frac{D_T}{T_{\infty }}{\left(\frac{\partial T}{\partial y}\right)}^2\right\}+\frac{Q^{*}}{{\left(\rho c_p\right)}_f}\left(T-T_{\infty }\right),(4)$

$u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=D_B\frac{\partial ²C}{\partial y^2}+\frac{D_T}{T_{\infty }}\frac{{\partial }^2²T}{\partial y^2²}.(5)$

The associated practical boundary condition is given as

$\begin{array}{l}\text{At}y=0,u=u_w\left(x\right)+u_{slip},v=0,N=-n\frac{\partial u}{\partial y},T=T_w\left(x\right)=T_0+m_{1}x,C=C_w\left(x\right)=C_0+n_{1}x\\ \text{As}y\to \infty ,u\to u_{\infty }=bx,N=-n\frac{\partial u}{\partial y},T=T_{\infty }=T_0+m_{2}x,C=C_{\infty }=C_0+n_{2}x\end{array}(6)$

where

$u_w\left(x\right)=bx,u_{slip}=L^{*}\left[\left(\mu +k\right)\frac{\partial u}{\partial y}+kN\right].(7)$

While using the similarity transformation

$\begin{array}{l}\eta ={\left(\frac{b}{{\nu }_f}\right)}^{\frac{1}{2}}y,u=ax{f}^{\prime }\left(\eta \right),v={\left(b{\nu }_f\right)}^{\frac{1}{2}}f\left(\eta \right),N={\left(\frac{b^3³}{{\nu }_f}\right)}^{\frac{1}{2}}xg\left(\eta \right),\\ \theta \left(\eta \right)\left(T_w-T_{\infty }\right)=\left(T-T_{\infty }\right),\phi \left(\eta \right)\left(C_w-C_{\infty }\right)=\left(C-C_{\infty }\right).\end{array}(8)$

Using Eq. into Eqs 2–5 we have

$\left(1+K\right)f^{‴}+f{f}^{″}-f^{\prime 2}+M\left(1-f^{\prime }\right)+K{g}^{\prime }+1=0,(9)$

$\left(1+\frac{K}{2}\right)g^{″}+f{g}^{\prime }-f^{\prime }g-K\left(2g+f^{″}\right)=0,(10)$

${\theta }^{″}-\mathrm{Pr}\left(f^{\prime }\theta -{\theta }^{\prime }f+{\in }_1{f}^{\prime }\right)+\mathrm{Pr}{N}_b{\theta }^{\prime }{\phi }^{\prime }+\mathrm{Pr}{N}_t{\theta }^{\prime 2}+\mathrm{Pr}Q\theta =0,(11)$

${\phi }^{″}+Sc\left(f^{\prime }\phi -f{\phi }^{\prime }+{\in }_2{f}^{\prime }\right)+\frac{N_t}{N_b}{\theta }^{″}=0.(12)$

The corresponding non-dimensional boundary conditions are expressed as follows:

$\begin{array}{l}f\left(0\right)=0,f^{\prime }\left(0\right)=\lambda +\alpha \left[1+K\left(1-n\right)\right]f^{″}\left(0\right),g\left(0\right)=-n{f}^{″}\left(0\right),\\ \theta \left(0\right)=1-{\in }_1\phi \left(0\right)=1-{\in }_2,f^{\prime }\left(\infty \right)=1,g\left(\infty \right)=0,\theta \left(\infty \right)=0,\phi \left(\infty \right)=0.\end{array}(13)$

The material parameter, magnetic parameter, Eckert number, Schmidt number, Brownian motion number, Prandtl number, thermophoresis number, thermal stratification, and solutal stratification are among the non-dimensional parameters used in our analysis. The mathematically defined as:

$\begin{array}{l}K=\frac{k_f}{{\mu }_f},M=\frac{\sigma B_0^2}{\rho b},\mathrm{Pr}=\frac{C_p\mu }{k},Sc=\frac{\nu }{D},Ec=\frac{u_w^2}{C_p\left(T_w-T_{\infty }\right)},{\in }_1=\frac{m_2}{m_1},\\ N_b=\frac{{\left(\rho c_p\right)}_p{D}_B\left(C_w-C_{\infty }\right)}{{\left(\rho c_p\right)}_f{\nu }_f},N_t=\frac{{\left(\rho c_p\right)}_p{D}_T\left(T_w-T_{\infty }\right)}{{\left(\rho c_p\right)}_f{\nu }_f{T}_{\infty }},{\in }_2=\frac{n_2}{n_1}.\end{array}(14)$

3 Physical quantities

The surface shear stress is determined by

${\tau }_w={\left(\left(\mu +k\right)\frac{\partial u}{\partial y}+KN\right)}_{y=0}.(15)$

Skin friction is defined as

$C_f=\frac{{\tau }_w}{{\rho }_f{u}_w^2}.(16)$

Using eqs. (8)-(10) into eqs. (15)-(16), we have

$\sqrt{\text{Re}}{C}_f=\left[1+K\left(1-n\right)\right]f^{″}\left(0\right).(17)$

and the heat transfer rate is given by

$q_w\left(x\right)=-k_f{\left(\frac{\partial T}{\partial y}\right)}_{y=0}.(18)$

after using similarity transformation we have

$q_w\left(x\right)=-k_f{m}_1\sqrt{\frac{b}{v_f}}x{\theta }^{\prime }\left(\eta \right).(19)$

and local Nusselt number written as

$N{u}_x=\frac{x{q}_w}{k_f\left(Tw-T_{\infty }\right)}.(20)$

by using similarity transformation, we have

$N{u}_x=\frac{-1}{1-{\in }_1}{\theta }^{\prime }\left(0\right).(21)$

where ${\in }_1=\frac{m_2}{m_1}$

4 Numerical scheme

Finding a precise solution to the current governance model equations’ problems is challenging due to their complexity and high nonlinearity. Therefore, the bvp4c method is used to calculate a numerical solution for the ode under boundary conditions. In this case, we first defined the new variables in accordance with the control equations’ order and changed the PDE system into a first-order ode. To adapt to the First-Order system, we use the following variables.

$f=y_1,f^{\prime }=y_2,f^{″}=y_3,g=y_4,g^{\prime }=y_5,\theta =y_6,{\theta }^{\prime }=y_7,\phi =y_8,{\phi }^{\prime }=y_9.(22)$

Thus, the reduced system of First-Order differential equations becomes:

$y_1^{\prime }=y_{2,}{y}_2^{\prime }=y_3,(23)$

$\left(1+K\right)y_3^{\prime }+y_1{y}_3-y_2^2+K{y}_5+M\left(1-y_2\right)+1=0,(24)$

$y_3^{\prime }=\frac{1}{1+K}\left[-y_1{y}_3+y_2^2-K{y}_5-M\left(1-y_2\right)-1\right],(25)$

$y_4^{\prime }=y_5,$

$\left(1+\frac{K}{2}\right)y_5^{\prime }+y_1{y}_5-y_2{y}_4-K\left(2y_4+y_3\right)=0,(26)$

$y_5^{\prime }=\frac{1}{1+\frac{K}{2}}\left[-y_1{y}_5+y_2{y}_4+K\left(2y_4+y_3\right)\right],(27)$

$y_6^{\prime }=y_7,(28)$

$y_7^{\prime }+\mathrm{Pr}{y}_1{y}_7-\mathrm{Pr}{y}_2{y}_6-\mathrm{Pr}{\in }_1{y}_2+\mathrm{Pr}{N}_b{y}_7{y}_9+\mathrm{Pr}{N}_t{y}_7^2+\mathrm{Pr}Q{y}_6=0,(29)$

$y_7^{\prime }=-\mathrm{Pr}{y}_1{y}_7+\mathrm{Pr}{y}_2{y}_6+\mathrm{Pr}{\in }_1{y}_2-\mathrm{Pr}{N}_b{y}_7{y}_9-\mathrm{Pr}{N}_t{y}_7^2-\mathrm{Pr}Q{y}_6,(30)$

$y_8^{\prime }=y_9,(31)$

$y_9^{\prime }=Sc{y}_2{y}_6-Sc{y}_1{y}_9+Sc{\in }_2{y}_2-\frac{N_t}{N_b}{y}_7^{\prime },(32)$

And the boundary conditions are

$\begin{array}{l}{y}_0\left(0\right)=0,y_0\left(2\right)=\lambda +\alpha \left[1+K\left(1-n\right)\right]y_0\left(3\right),y_0\left(4\right)=-n{y}_0\left(3\right),\\ y_0\left(6\right)=1-{\in }_1,y_0\left(8\right)=1-{\in }_2,y_{\infty }\left(2\right)=1,y_{\infty }\left(4\right)=0,y_{\infty }\left(6\right)=0,y_{\infty }\left(8\right)=0.\end{array}(33)$

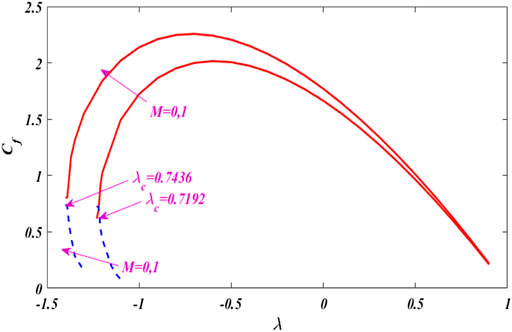
This is a very effective numerical procedure for handling BVP problems. This scheme uses a finite difference code to perform a Level 3 Lobatto IIIa formula. In this approach, we have to select an appropriate finite value of, say between 10 and 35. On the other hand, the grid is chosen and error control depends on the residue of the continuous solution. The current findings are compared to those found in the literature [21] for validation, as shown in Table 1.

TABLE 1

TABLE 1. Skin friction comparison with [21].

5 Result and discussion

This section analyzes the computational findings in terms of nondimensional velocities, $f^{\prime }\left(\eta \right)$, $g\left(\eta \right)$, concentration $\varphi \left(\eta \right)$, temperature $\theta \left(\eta \right)$, skin friction coefficient_, and rate of heat transfer with distinct values Prandtl number$\mathit{Pr}$, the material parameter K, slip parameter $\alpha$, stratification parameter $\lambda$, Eckert number Ec, magnetic number M, Brownian motion number $N_b$, thermophoresis number$N_t$, Schmidt number $Sc$, Temperature proportion ratio parameter$Q$.

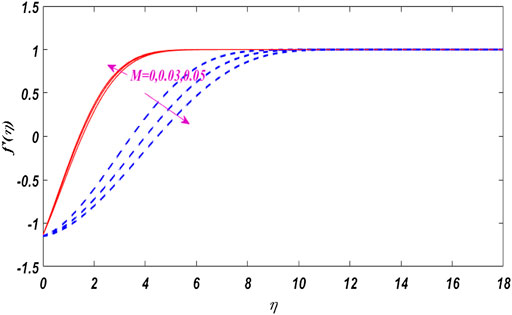
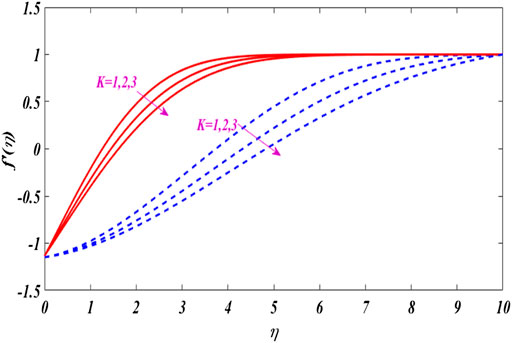
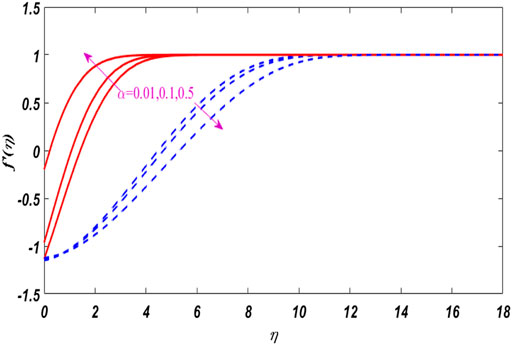
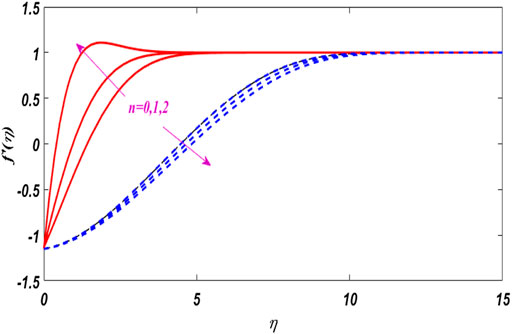
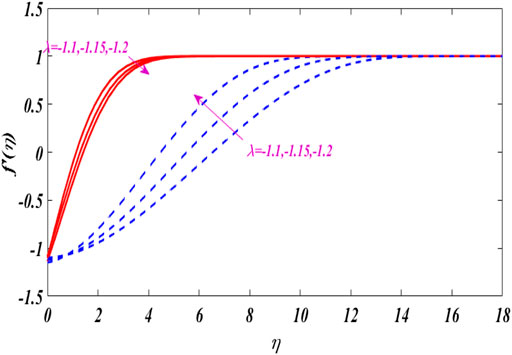
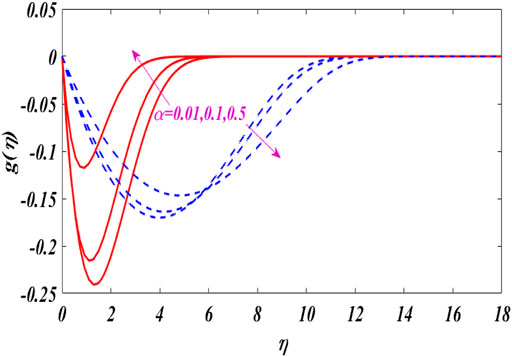
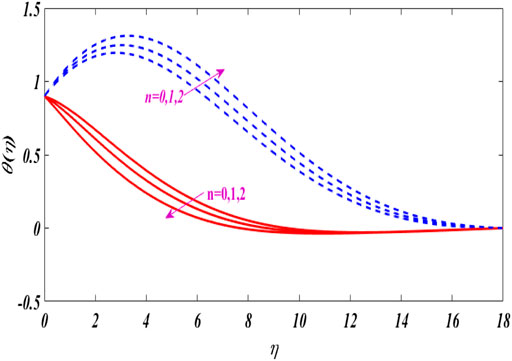
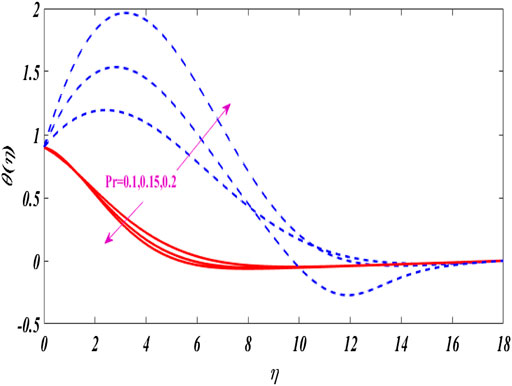
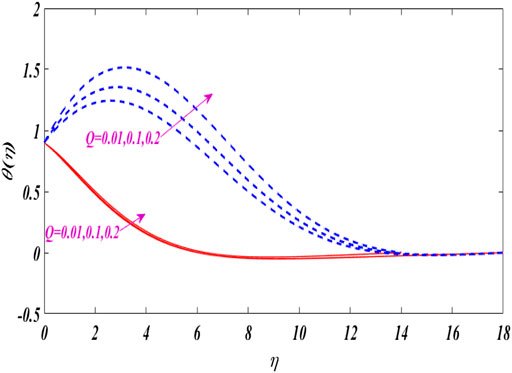
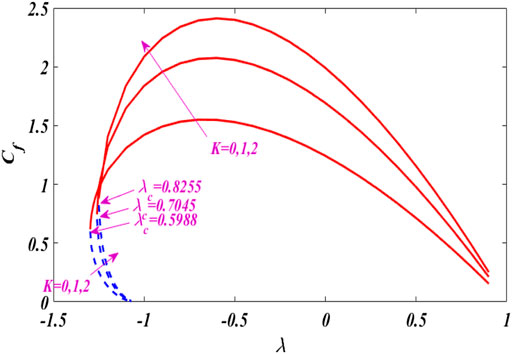
Figures 2–6 show the relationship between boundary layer thickness and velocity $f^{\prime }\left(\eta \right)$ against the M, K, and n, while the other parameter remains constant. Figure 2 is drawn to witness the impact of magnetic parameters on the dimensionless velocity distribution $f^{\prime }\left(\eta \right)$. Curves show that when the magnetic parameter is increasing, the profiles of velocity distributions in the first solution are increasing but they have opposite behavior in the second solution. The significant effect of material parameters on dimensionless velocity is shown in Figure 3. A significant decline in the profiles of the first solution as well as in the second solution when a suitable enhancement happens in the values of a material parameter. The velocity distribution for various values of slip constraint is shown in Figure 4. The graphs show that a dual solution for shrinking flow inside the boundary layer region exists. In the first solution, growing the value of the slip parameter improves velocity profiles, whereas the second solution has the opposite effect. Figure 5 describes the disparity of velocity distribution with changing values of stratification parameters. We note that as the stratification parameter rises, there a decline happens in the upper branch solutions but the outcomes are fairly reversed for the second solution. Figure 6 shows the comparison of both solutions for different values of $n$. It is clear that for the upper branch solution, with the growth in $f^{\prime }\left(\eta \right)$, dimensionless velocity profile upsurges, while the effect is different for the second solution.

FIGURE 2

FIGURE 2. Dual solutions impact on for several M.

FIGURE 3

FIGURE 3. Dual solutions impact on for several K.

FIGURE 4

FIGURE 4. Dual solutions impact on $f^{\prime }\left(\eta \right)$for several.

FIGURE 5

FIGURE 5. Dual solutions impact on for several n.

FIGURE 6

FIGURE 6. Dual solutions impact on for several.

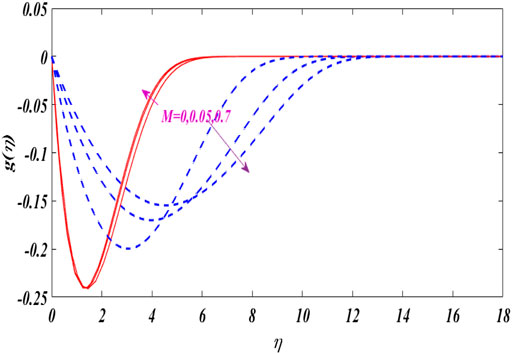
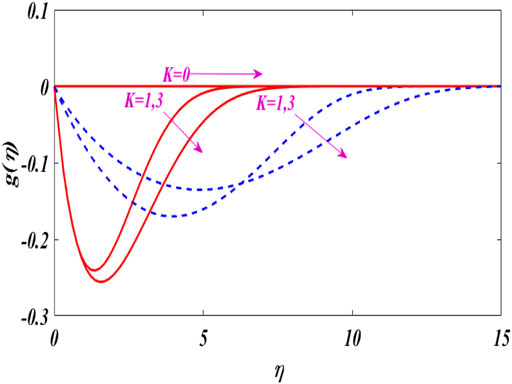
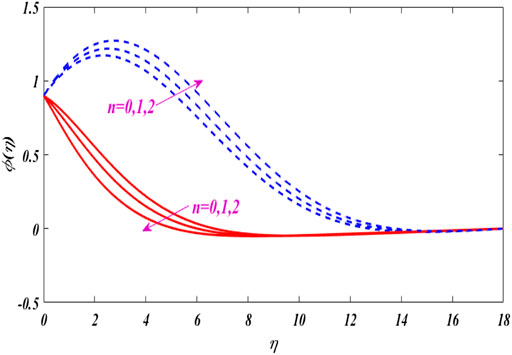
The characteristics of angular velocity distribution $g\left(\eta \right)$ are illustrated graphically through Figures 7–11 for numerous quantities of physical parameters $M,K,\alpha ,\lambda$ and $n$. In each Fig, we observe the dual nature of angular velocity distribution for shrinking flow. The influence of magnetic parameters on dimensionless angular velocity inside the boundary layer is displayed in Figure 7. As expected, the angular velocity curves show an increasing behavior with an uplifting value of the magnetic parameter in the first solution, while in the second solution, the profiles show a decreasing behavior when we grow the value of the M. The computed result of $g\left(\eta \right)$ for numerous values of the $K$ is illustrated in Figure 8. According to this figure, a straight line is displayed on a graph when $K$ = 0, for both the solution, but when $K$ = 1, 3 there is a comparison made for dimensionless angular velocity distributions. It is seen that dimensionless angular velocity profiles decrease in the case of the first solution due to the magnetic effect and the results are the same for the second solution. Figure 9 reveals the outcomes of the slip parameter on angular velocity distribution. As you have seen, the $\alpha$significantly affects the angular velocity curves and shows an increasing trend for an upper solution but the results are different in the lower solution. Figure 10 display the variation of dimensionless angular velocity profiles within the boundary layer for numerous values of stratification parameters. It is seen from this figure that all curves approach the far-field boundary conditions asymptotically. From the curves, a comparison is made for dimensionless angular velocity profiles with different values of stratification parameters. In the case of the first solution with a magnetic effect, the angular velocity profile increases but the results are quite opposite in the case of the second solution. Figure 11 illustrates the dual $g\left(\eta \right)$for different $\alpha$. Again, we notice a similar behavior in both solutions with uplifting values of $g\left(\eta \right)$.

FIGURE 7

FIGURE 7. Dual solutions impact on for several M.

FIGURE 8

FIGURE 8. Dual solutions impact on for several K.

FIGURE 9

FIGURE 9. Dual solutions impact on for several.

FIGURE 10

FIGURE 10. Dual solutions impact on for several n.

FIGURE 11

FIGURE 11. Dual solutions impact on for several.

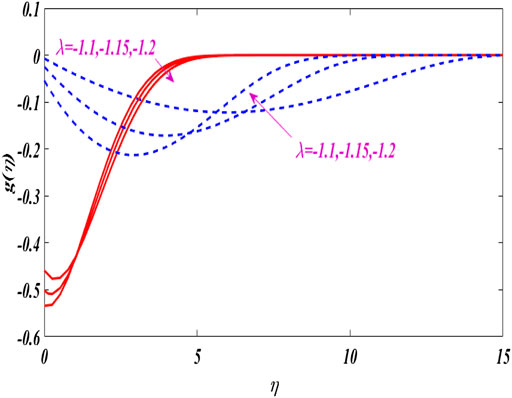
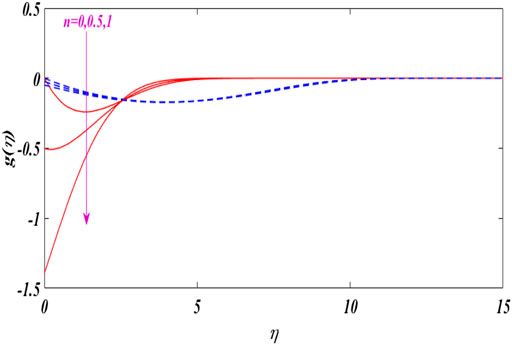
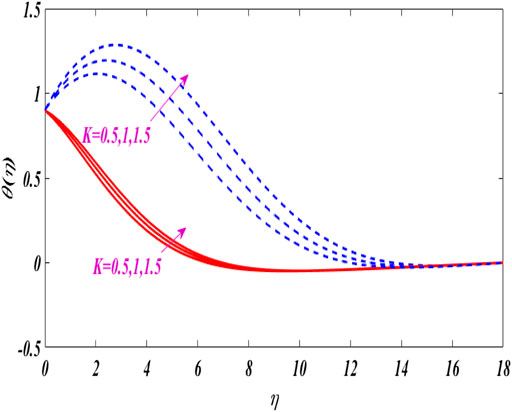
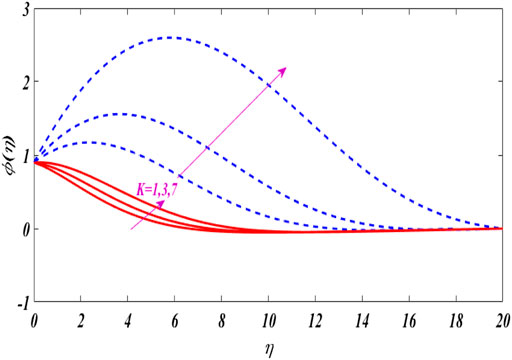
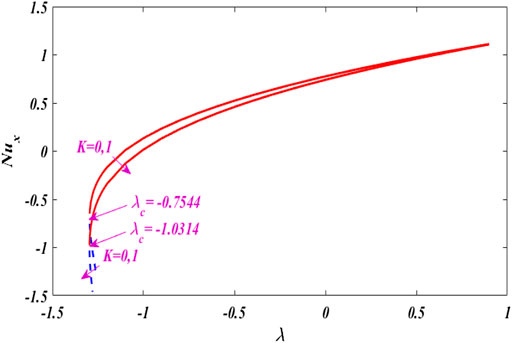
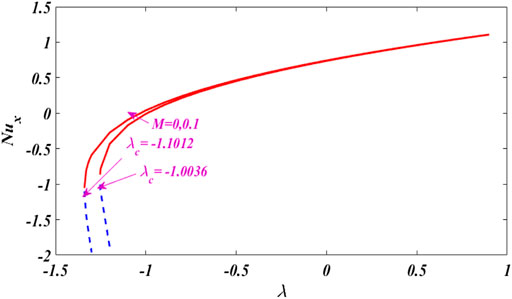
Figures 12–16 portray the characteristics of $\theta \left(\eta \right)$ are illustrated graphically for several values of physical parameters $M,K,n,\mathit{Pr}$ and $Q$ Figure 12 reveals the dual $\theta \left(\eta \right)$ for different $M$. As expected, a decline in temperature profile is seen for growing values of $\theta \left(\eta \right)$ in the first solution, while an inverse is noted in the second solution. The temperature distribution $\theta \left(\eta \right)$ with different $K$are is demonstrated in Figure 13, which displays that as the material parameter boosts the $\theta \left(\eta \right)$show an increasing trend in both solutions. The effects of various n values on temperature profiles, for shrinking cases, are shown in Figure 14. Furthermore, the first solution’s curves demonstrate a decline in energy distribution as n increases, but the results for the second solution, which promotes a higher thermal flow rate between the surface and fluid, are noticeably different. The dual $\theta \left(\eta \right)$for specific entries of the Prandtl number $\mathit{Pr}$are shown in Figure 15. With the rise of $\theta \left(\eta \right)$, a decline is seen in the upper branch solution, while the inverse behavior happens in the case of the lower branch solution. The variation of dual $\theta \left(\eta \right)$ for changing values temperature proportion $Q$ is plotted in Figure 16. We analyzed that, as the $Q$ is upsurges the temperature distribution increases in both solutions.

FIGURE 12

FIGURE 12. Dual solutions impact on for several M.

FIGURE 13

FIGURE 13. Dual solutions impact on for several K.

FIGURE 14

FIGURE 14. Dual solutions impact on for several n.

FIGURE 15

FIGURE 15. Dual solutions impact on for several.

FIGURE 16

FIGURE 16. Dual solutions impact on for several Q.

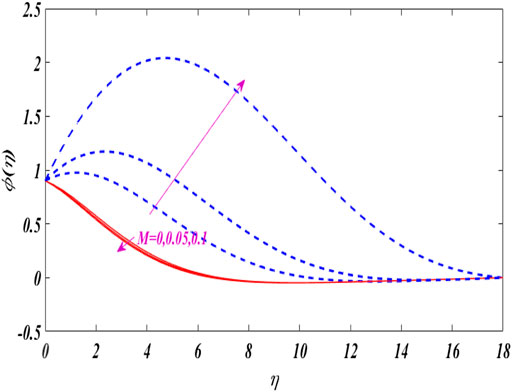
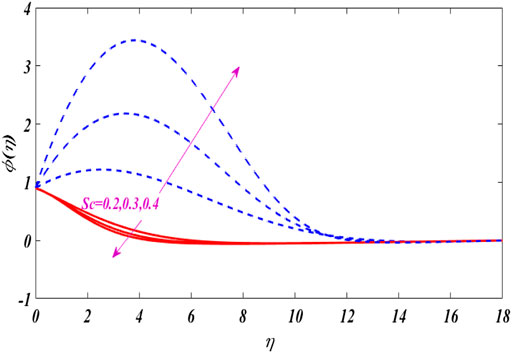
The dual concentration distributions are displayed in Figures 17–20 for different values of parameters $Q$ and Sc. The impact of M and K on concentration profiles is demonstrated in Figures 17, 18 by other parameters keeping fixed. We observed that the larger M gives the decline of $Q$ in the case of the first solution. Furthermore, we see a growing trend in concentration distribution $\varphi \left(\eta \right)$ or larger M. In addition, it is extracted from Figure 18 that the concentration profiles increase by uplifting values of material parameter K in both solutions. The variation of nondimensional concentration distributions $\varphi \left(\eta \right)$ along with numerous values of n and Sc are illustrated in Figures 19, 20 respectively. It is found in Figure 19 that the $\varphi \left(\eta \right)$decline with the growing values of n for the first solution. However, an inverse behavior is noted for the second solution. Similarly, the same behavior is noticed in concentration distributions for various values of Schmidt number Sc, as shown in Figure 20. Moreover, Figures 21, 22 are drawn with different values of M and K. Figure 21 draws to witness the effect of M on wall shear stress. A massive enhancement in critical values is noted with larger values of M which enhances the existence domain of dual solution. The impact of K on skin friction $\varphi \left(\eta \right)$against the stratification parameter is exhibited in Figure 22. Moreover, we described the existence of a dual solution in the case of shrinking flow. As the K is increased, the magnitude of critical values grows. Furthermore, a substantial enhancement in skin-friction coefficient is examined for growing values of K, as depicted in Figure 23. The variation in heat transfer rate at the surface $\varphi \left(\eta \right)$against shrinking parameters for numerous values of K and M are demonstrated through Figures 23, 24.

FIGURE 17

FIGURE 17. Dual solutions impact on for several M.

FIGURE 18

FIGURE 18. Dual solutions impact on for several K.

FIGURE 19

FIGURE 19. Dual solutions impact on for several

FIGURE 20

FIGURE 20. Dual solutions impact on for several Sc.

FIGURE 21

FIGURE 21. Dual solutions impact on against for several M.

FIGURE 22

FIGURE 22. Dual solutions impact on against for several K.

FIGURE 23

FIGURE 23. Dual solutions impact on against for several K.

FIGURE 24

FIGURE 24. Dual solutions impact on against for several M.

6 Conclusion

In this research work, we erect a dual solution close to the stagnation point of the micro-polar fluid under the action of nonlinear tensile/shrinkage sheet magnetics. Graphical results and discussion for fluid particles micro-floating, tensile/contraction parameters, and magnetic parameters invoke the thermal flow rate. For computational purposes, using MATLAB bvp4c scheme. As can be seen, MATLAB bvp4c is time-saving, efficient, durable, and fast convergence, and has good consistency with earlier studies. It should also be esteemed that the local skin friction coefficient and the local Nusselt number amplitude increase with increasing micro-pole parameters. The range of skin friction and solution is expanded by the application of magnetic force. The fluid moves more quickly when nonlinear stretching and contracting parameters are used. As the material parameter K rises, resistance close to the surface increases.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

YK: funding; AA computed the results; AM and MR wrote the original draft; HS wrote the review draft; HS: modeling; Conceptualization, YK and Validation, YK, AM, and MR.

Funding

This research work was funded by institutional fund projects under no. (IFP-A- 2022-2-5-24). Therefore, the authors gratefully acknowledge technical and financial support from the ministry of education and the University of Hafr Al Batin, Saudi Arabia.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Hayat T, Yousaf A, Mustafa M, Obaidat S. MHD squeezing flow of second-grade fluid between two parallel disks. Int J Numer Methods Fluids (2012) 69:399–410. doi:10.1002/fld.2565

CrossRef Full Text | Google Scholar

2. Ahmad A, Afzal S, Ashgar S. Semi-inverse solution for transient MHD flow of a second-grade fluid past a stretching surface. AIP Adv (2015) 10:127140. doi:10.1063/1.4939572

CrossRef Full Text | Google Scholar

3. Ramzan M, Bilal M. Time dependent MHD nano-second grade fluid flow induced by permeable vertical sheet with mixed convection and thermal radiation. PLoS ONE (2015) 64:e0124929. doi:10.1371/journal.pone.0124929

CrossRef Full Text | Google Scholar

4. Hayat T, Aziz A, Muhammad T, Ahmad B. On magnetohydrodynamic flow of second grade nanofluid over a nonlinear stretching sheet. J Magnetism Magn Mater (2016) 408:99–106. doi:10.1016/j.jmmm.2016.02.017

CrossRef Full Text | Google Scholar

5. Ellahi R. The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe: Analytical solutions. Appl Math Model (2013) 3:1451–67. doi:10.1016/j.apm.2012.04.004

CrossRef Full Text | Google Scholar

6. Govindaraju M, Ganesh NV, Ganga B, Hakeem AA. Entropy generation analysis of MHD flow of a nanofluid over a stretching sheet. Egypt Math Soc (2015) 2:429–34.

CrossRef Full Text | Google Scholar

7. Sheikholeslami M, Hatami T, Ganji DD. Nanofluid flow and heat transfer in a rotating system in the presence of a magnetic field. J Mol Liquids (2014) 190:112–20. doi:10.1016/j.molliq.2013.11.002

CrossRef Full Text | Google Scholar

8. Lin Y, Zheng L, Zhang X, Ma L, Chen G. MHD pseudo-plastic nanofluid unsteady flow and heat transfer in a finite thin film over stretching surface with internal heat generation. Int J Heat Mass Transfer (2015) 84:903–11. doi:10.1016/j.ijheatmasstransfer.2015.01.099

CrossRef Full Text | Google Scholar

9. Hayat T, Muhammad T, Shehzad SA, Chen GQ, Abbas IA. Interaction of magnetic field in flow of Maxwell nanofluid with convective effect. J Magnetism Magn Mater (2016) 389:48–55. doi:10.1016/j.jmmm.2015.04.019

CrossRef Full Text | Google Scholar

10. Ahmad A, Asghar S. Flow of a second grade fluid over a sheet stretching with arbitrary velocities subject to a transverse magnetic field. Appl Math Lett (2016) 24:1905–9. doi:10.1016/j.aml.2011.05.016

CrossRef Full Text | Google Scholar

11. Ariel PD. On computation of MHD flow near a rotating disk. Z Angew Mathematik Mechanik (2002) 82:235. doi:10.1002/1521-4001(200204)82:4<235::aid-zamm235>3.0.co;2-l

CrossRef Full Text | Google Scholar

12. Ahmad R, Mustafa M, Hayat T, Alsaedi A. Numerical study of MHD nanofluid flow and heat transfer past a bidirectional exponentially stretching sheet. J Magnetism Magn Mater (2016) 407:69–74. doi:10.1016/j.jmmm.2016.01.038

CrossRef Full Text | Google Scholar

13. Sheikholeslami M, Hayat T, Alsaedi A. MHD free convection of Al2O3–water nanofluid considering thermal radiation: A numerical study. Int J Heat Mass Transfer (2016) 96:513–24. doi:10.1016/j.ijheatmasstransfer.2016.01.059

CrossRef Full Text | Google Scholar

14. Sheikholeslami M, Vajravelu K, Rashidi MM. Forced convection heat transfer in a semi annulus under the influence of a variable magnetic field. Int J Heat Mass Transfer (2016) 92:339–48. doi:10.1016/j.ijheatmasstransfer.2015.08.066

CrossRef Full Text | Google Scholar

15. Krishna PM, Sandeep N, Sugunamma V. Effects of radiation and chemical reaction on MHD convection flow over a permeable stretching surface with suction and heat generation. Web J Sci Tech (2015) 12:831–47.

Google Scholar

16. Abbas Z, Naveed M, Sajid M. Hydromagnetic slip flow of nanofluid over a curved stretching surface with heat generation and thermal radiation. J Mol Liquids (2016) 215:756–62. doi:10.1016/j.molliq.2016.01.012

CrossRef Full Text | Google Scholar

17. Haq RU, Nadeem S, Khan ZH, Akbar NS. Thermal radiation and slip effect on MHD stagnation point flow of nanofluid over a stretching sheet. Phys E (2015) 65:17–23. doi:10.1016/j.physe.2014.07.013

CrossRef Full Text | Google Scholar

18. Sheikholeslami M, Ganji DD, Javed MY, Ellahi R. Effect of thermal radiation on magnetohydrodynamics nanofluid flow and heat transfer by means of two phase model. J Magnetism Magn Mater (2015) 374:36–43. doi:10.1016/j.jmmm.2014.08.021

CrossRef Full Text | Google Scholar

19. Abo-Eldahab EM, Elbrabary ME. Hall current effect on magnetohydrodynamic free-convection flow past a semi-infinite vertical plate with mass transfer. Int J Eng Sci (2001) 60:1641–52. doi:10.1016/s0020-7225(01)00020-9

CrossRef Full Text | Google Scholar

20. Abo-Eldahab EM, Aziz MA. Hall current and Ohmic heating effects on mixed convection boundary layer flow of a micropolar fluid from a rotating cone with power-law fluid at a stretching surface. Int Commun Heat Mass Transfer (2004) 31:751–62. doi:10.1016/s0735-1933(04)00062-4

CrossRef Full Text | Google Scholar

21. Dey D, Makinde OD, Borah R. Analysis of dual solutions in MHD fluid flow with heat and mass transfer past an exponentially shrinking/stretching surface in a porous medium. Int J Appl Comput Math (2022) 8(2):66. doi:10.1007/s40819-022-01268-7

CrossRef Full Text | Google Scholar

22. Tadesse FB, Makinde OD, Enyadene LG. Mixed convection of a radiating magnetic nanofluid past a heated permeable stretching/shrinking sheet in a porous medium. Math Probl Eng (2021) 2021:21. doi:10.1155/2021/6696748

CrossRef Full Text | Google Scholar

23. Jumana SA, Murtaza MG, Ferdows M, Makinde OD, Zaimi K. Dual solutions analysis of melting phenomenon with mixed convection in a nanofluid flow and heat transfer past a permeable stretching/shrinking sheet. j nanofluids (2020) 9(4):313–20. doi:10.1166/JON.2020.1761

CrossRef Full Text | Google Scholar

24. Tshivhi KS, Makinde OD. Magneto-nanofluid coolants past heated shrinking/stretching surfaces: Dual solutions and stability analysis. Results Eng (2021) 10:100229. doi:10.1016/j.rineng.2021.100229

CrossRef Full Text | Google Scholar

25. Tadesse FB, Makinde OD, Enyadene LG. Hydromagnetic stagnation point flow of a magnetite ferrofluid past a convectively heated permeable stretching/shrinking sheet in a Darcy–Forchheimer porous medium. Sadhana (2021) 46(3):115. doi:10.1007/s12046-021-01643-y

CrossRef Full Text | Google Scholar

26. Sher Akbar N, Maraj EN, Noor NFM, Habib MB. Exact solutions of an unsteady thermal conductive pressure driven peristaltic transport with temperature-dependent nanofluid viscosity. Case Stud Therm Eng (2022) 35:102124. doi:10.1016/j.csite.2022.102124

CrossRef Full Text | Google Scholar

27. Akrama J, Akbar NS, Tripathi D. “Entropy generation in electroosmotically aided peristaltic pumping of MoS2 Rabinowitsch nanofluid. Fluid Dyn Res (2022) 54:015507. doi:10.1088/1873-7005/ac4e7b

CrossRef Full Text | Google Scholar

28. Akrama J, Akbar NS, Tripathi D. “Entropy generation in electroosmotically aided peristaltic pumping of MoS2 Rabinowitsch nanofluid. Fluid Dyn Res (2022) 54:015507. doi:10.1088/1873-7005/ac4e7b

CrossRef Full Text | Google Scholar

29. Butt WA, Akbar NS, Mir AN. “Heat transfer analysis of peristaltic flow of a Phan-Thien-Tanner fluid model due to metachronal wave of cilia. Biomech Model Mechanobiol (2020) 19:1925–33. doi:10.1007/s10237-020-01317-4

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Akrama J, Akbar NS, Maraj E. Chemical reaction and heat source/sink effect on magnetonano Prandtl-Eyring fluid peristaltic propulsion in an inclined symmetric channel. Chin J Phys (2020) 65:300–13. doi:10.1016/j.cjph.2020.03.004

CrossRef Full Text | Google Scholar

31. Akrama J, Akbar NS. Biological analysis of Carreau nanofluid in an endoscope with variable viscosity. Phys Scr (2020) 95:055201. doi:10.1088/1402-4896/ab74d7

CrossRef Full Text | Google Scholar

32. Jagadeesha RD, Prasanna BMR, Sankar M. Double diffusive convection in an inclined parallelogrammic porous enclosure. Proced Eng (2015) 127:1346–53. doi:10.1016/j.proeng.2015.11.493

CrossRef Full Text | Google Scholar

33. Sankar M, Reddy NK, Do Y. Conjugate buoyant convective transport of nanofluids in an enclosed annular geometry. Sci Rep (2021) 11(1):17122. doi:10.1038/s41598-021-96456-8

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Sankar M, Kemparaju S, Prasanna BMR, Eswaramoorthi S. Buoyant convection in porous annulus with discrete sources-sink pairs and internal heat generation. J Phys : Conf Ser (2018) 1139(1):012026. doi:10.1088/1742-6596/1139/1/012026

CrossRef Full Text | Google Scholar