Propagation properties and radiation forces of partially coherent self-shifting cosine-Gaussian beams

In the ABCD optical system, the propagation properties and the radiation forces are obtained by studying the cross spectral density of partially coherent self-shifting cosine-Gaussian beams. A self-shifting phenomenon occurs when the beams propagate in the strongly nonlocal nonlinear medium. The shifting parameters could influence the bend characteristics of the propagation trajectory and the beam center, while the power ratio affects the periods of the parabolic trajectory. Furthermore, the radiation forces on a Rayleigh particle in the focusing optical system are studied, and the obtained force distributions depend on the refractive index, the shifting parameters, and the coherence widths. What we report here has potential applications in optical communication and optical tweezing.

1 Introduction

The study of novel partially coherent related structured light fields and their generation, transmission, and regulation is a hot research topic in the international optical field [1, 2]. Partially coherent sources are common in practice. Compared with completely coherent beams, partially coherent beams are less affected by disturbance [3]. The cross spectral density (CSD) is a significant physical quantity in partially coherent beams. It should satisfy the quasi-Hermiticity and the non-negative definiteness [4–6]. The experimentally produced partially coherent beams with various complex degrees of coherence was obtained by Wang et al. [7]. Due to the wide applications in ghost imaging, free space optical communications, particle trapping, and optical scattering [6–10], partially coherent beams have attracted intensive attention.

In nonlocal nonlinear media, various beams of different degrees have been reported in many aspects [11–18]. In the case of nonlocal nonlinearity, the nonlinear responses of the medium under the optical field are related to both the point and optical fields around it. Among which, the phenomenological model under strong nonlocal conditions is Snyder-Mitchell model [11]. The lead glass and nematic liquid crystals are strongly nonlocal nonlinear media (SNNM), which have been demonstrated by some experimental results [19, 20]. Deng et al. reported the stable propagation of different types of soliton and beams in SNNM [11, 12]. Analytical expressions of the corresponding characteristic parameters for example the beam size, the center of gravity, the curvature radius, and linear momentum of Airy beams propagating in SNNM have been studied [21]. Under the framework of fractional nonlinear Schrödinger equation, Zhang et al. analyzed the attractive and repulsion forces between abnormal Airy beams [22], revealing a new situation of the interaction of Airy beams and providing an alternative mechanism to control the generation of breathing solitons. Different types of spatiotemporal self-accelerating wave packets in SNNM are also studied. The numerical simulation findings consistent with their theoretical findings in the strongly nonlocal requirement, and the numerical simulation under different perturbation conditions is discussed [23, 24].

With the development of science and technology, people are no longer satisfied with the observation of microscopic particles, how to manipulate and control the studied particles put forward more profound questions, and are committed to exploring new research methods [25–28]. Piconewton-level forces optical trapping and manipulating particles with micrometer-size, while simultaneously measuring displacement with nanometer-level precision have been extensively studied [27, 29]. Trapping particles by radiation pressures in a succession of groundbreaking papers were reported by Ashkin et al. [25–27]. Without losing of generality, the optical force is decomposed into the scattering force and the gradient force. Gradually, optical trapping techniques continued to improve, then become better established, and finally have emerged as a formidable tool with extensive and far-reaching applications. Nowadays, optical trapping produced by various beams [30–33] such as Laguerre–Gaussian beams, twist beams, and rotating beams are reported by many researchers. Guo et al. investigated the radiation forces on a Rayleigh dielectric particle induced by a highly focused parabolic scaling Bessel beam [34], the findings indicate that this beam can trap high-index particles at the focus and near the focus. Combined with the new light field, the realization of specific manipulation of nonabsorbing nanoparticles is a significant development trend of optical tweezers.

Therefore, we concentrate on the propagation properties and radiation forces of the partially coherent self-shifting cosine-Gaussian beams (PCSCBs) in the ABCD optical system. The power factors, the shifting parameters, and the beam order that influence the propagation characteristics in SNNM are discussed in detail. PCSCBs with a self-shifting effect are beneficial for trapping particles. Therefore, we analyze the radiation forces of such focused beams with different refractive indexes, shifting parameters, and coherence widths.

2 Theoretical model of PCSCBs in ABCD matrix

Here, we choose the PCSCBs [2, 6, 35], which meet the requirements of Fourier transformability, even magnitude, and odd phase. In the initial plane (z = 0), its CSD function can be written as

$\begin{array}{cc}\hfill W_0\left(r_1^{\prime },r_2^{\prime }\right)& =\exp \left(-\frac{x_1^{\prime 2}+x_2^{\prime 2}}{{\sigma }_x^2}-\frac{y_1^{\prime 2}+y_2^{\prime 2}}{{\sigma }_y^2}\right)\cos \left[C_x\left(x_1^{\prime }-x_2^{\prime }\right)\right]\cos \left[C_y\left(y_1^{\prime }-y_2^{\prime }\right)\right]\hfill \\ \hfill & \times \exp \left[-\frac{{\left(x_1^{\prime }-x_2^{\prime }\right)}^2}{2{\delta }_x^2}-\frac{{\left(y_1^{\prime }-y_2^{\prime }\right)}^2}{2{\delta }_y^2}\right]\exp \left[ia\left(x_1^{\prime }-x_2^{\prime }\right)+ib\left(y_1^{\prime }-y_2^{\prime }\right)\right],\hfill \end{array}(1)$

where σ_x and σ_y are the transverse intensity widths along the x and y directions, δ_x and δ_y are the coherent length, a and b are the shifting parameters, $C_x=\sqrt{2\pi }n/{\delta }_x$, $C_y=\sqrt{2\pi }n/{\delta }_y$, n is the beam order. When n = 0, the cosine-Gaussian functions reduce to the Gaussian functions. The paraxial approximation, namely the small-angle approximation, requires light travelling through the optical system with a small angle to the optical axis of the system. Therefore, in the paraxial form, based on the extended Huygens-Fresnel principle, the CSD at z > 0 can be expressed as

$W\left(r_1,r_2,z\right)=\iint W_0\left(r_1^{\prime },r_2^{\prime }\right)H_z^{\ast }\left(r_1,r_1^{\prime }\right)H_z\left(r_2,r_2^{\prime }\right)d^2{r}_1^{\prime }{d}^2{r}_2^{\prime },(2)$

where H_z is based on the ABCD matrix,

$H_z\left(r,r^{\prime }\right)=-\frac{ik{e}^{\mathit{ikz}}}{2\pi B}\exp \left[\frac{ik}{2B}\left(A{r}^2-2r{r}^{\prime }+D{r}^{\prime 2}\right)\right].(3)$

When r₁ = r₂ = r, the spectral density and the CSD of the PCSCBs at the output plane are associated by the formula as

$I\left(r,z\right)=W\left(r,r,z\right).(4)$

After substituting Eqs 1–3 into Eq. 4, we can express the spectral density as

$\begin{array}{ll}\hfill I\left(r,z\right)& =\frac{k^2}{16a_1{a}_2{a}_3{a}_4{B}^2}\left\{\exp \left[{\left(\frac{iaB+iB{C}_x+ikx}{2a_{1}B}\right)}^2+{\left(\frac{ibB+iB{C}_y+iky}{2a_{2}B}\right)}^2+\frac{B_1^2}{2a_3}+\frac{B_2^2}{2a_4}\right]\right.\hfill \\ \hfill & +\exp \left[{\left(\frac{iaB+iB{C}_x+ikx}{2a_{1}B}\right)}^2+{\left(\frac{ibB-iB{C}_y+iky}{2a_{2}B}\right)}^2+\frac{B_1^2}{2a_3}+\frac{B_4^2}{2a_4}\right]\hfill \\ \hfill & +\exp \left[{\left(\frac{iaB-iB{C}_x+ikx}{2a_{1}B}\right)}^2+{\left(\frac{ibB+iB{C}_y+iky}{2a_{2}B}\right)}^2+\frac{B_3^2}{2a_3}+\frac{B_2^2}{2a_4}\right]\hfill \\ \hfill & \left.+\exp \left[{\left(\frac{iaB-iB{C}_x+ikx}{2a_{1}B}\right)}^2+{\left(\frac{ibB-iB{C}_y+iky}{2a_{2}B}\right)}^2+\frac{B_3^2}{2a_3}+\frac{B_4^2}{2a_4}\right]\right\},\hfill \end{array}(5)$

where $a_1^2=\frac{1}{{\sigma }_x^2}+\frac{1}{2{\delta }_x^2}+\frac{ikA}{2B}$, $a_2^2=\frac{1}{{\sigma }_y^2}+\frac{1}{2{\delta }_y^2}+\frac{ikA}{2B}$, $a_3^2=\frac{1}{{\sigma }_x^2}+\frac{1}{2{\delta }_x^2}-\frac{ikA}{2B}-\frac{1}{4a_1{\delta }_x^4}$, $a_4^2=\frac{1}{{\sigma }_y^2}+\frac{1}{2{\delta }_y^2}-\frac{ikA}{2B}-\frac{1}{4a_3{\delta }_y^4}$, $B_1=(ia+i{C}_x+\frac{ikx}{B})[\frac{1}{2a_1{\delta }_x^2}-1]$, $B_2=(ib+i{C}_y+\frac{iky}{B})[\frac{1}{2a_3{\delta }_y^2}-1]$, $B_3=(ia-i{C}_x+\frac{ikx}{B})[\frac{1}{2a_1{\delta }_x^2}-1]$, $B_4=(ib-i{C}_y+\frac{iky}{B})[\frac{1}{2a_3{\delta }_y^2}-1]$.

In Eq. 5, the exact analytical solution is based on the ABCD matrix. Now we can analyze the propagation properties in SNNM and the radiation forces in the focusing system, respectively.

3 Propagation properties of PCSCBs in SNNM

In the nonlinear media, the propagation of PCSCBs obeys the nonlinear Schrödinger equation [12,32]

$2ik\frac{\partial I}{\partial z}+\frac{{\partial }^{2}I}{\partial x^2}+\frac{{\partial }^{2}I}{\partial y^2}+2k^2\frac{\mathrm{\Delta }n}{n_0}I=0,(6)$

where Δn = n₁ ∫N (r − r′)|I (r′, z)|²d²r′ is the nonlinear perturbation of the refraction index, n₁ is the nonlinear index coefficient, n₀ is the linear refractive index of the medium, and N is the symmetrical real spatial response function of the medium [24]. In addition, the Gaussian function $w_0^2/(2\pi w_m^2)\exp [-r^2/(2w_m^2)]$ is selected as the nonlocal response function [13, 24], where w_m is the characteristic length of the response. In the strong nonlocality condition [13], w_m → ∞, the length of the beam is very short when compared with the length of the response function, Eq. 1 can be written as the Snyder–Mitchell model [11–13].

$2ik\frac{\partial I}{\partial z}+\frac{{\partial }^{2}I}{\partial x^2}+\frac{{\partial }^{2}I}{\partial y^2}-k^2{\beta }^2\left(x^2+y^2\right)I=0,(7)$

where $\beta =\sqrt{n_1\gamma P_0/n_0}$ is related to the power ratio, the input power at the initial plane is P₀, γ represents the material parameter associated with N [13]. When the degrees of nonlocality approaching infinity, Eq. 7 is in the case of the nonlinearity limit, the field can change the refractive index of the medium while propagating, this produce a structure similar to the graded-index fiber. The ABCD matrix for this system is

$\left(\begin{array}{cc}\hfill A\hfill & \hfill B\hfill \\ \hfill C\hfill & \hfill D\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill \cos \left(\beta z\right)\hfill & \hfill \sin \left(\beta z\right)/\beta \hfill \\ \hfill -\beta \sin \left(\beta z\right)\hfill & \hfill \cos \left(\beta z\right)\hfill \end{array}\right).(8)$

After substituting Eq. 8 into Eq. 5, we can obtain the spectral density of PCSCBs. We set the parameters in SNNM as σ_x = 1mm, σ_y = 0.3mm, δ_x = 1mm, δ_y = 0.3mm, and a = b.

In SNNM, Figure 1 displays the change of the spectral density for PCSCBs with the propagation distance in different shifting parameters and beam orders. The transverse distributions of the PCSCBs change from unimodal distribution to bimodal distribution, and with the increase of propagation distance z, the center peak decreases. We notice that positive shifting parameters in Figures 1B,D bring negative linear shifting along the x direction, while the negative one in Figures 1A,C behaves in the opposite direction. It is found that the larger the beam order is, the faster the spectral density decays.

FIGURE 1

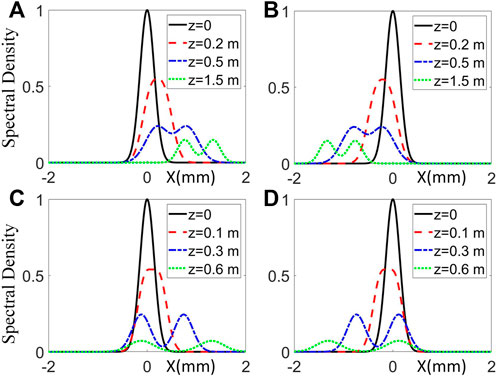
FIGURE 1. The distributions of the spectral density at the selected propagation distances in SNNM with β = 1. (A) n = 1, a = −10mm⁻¹, (B) n = 1, a = 10mm⁻¹, (C) n = 2, a = −10mm⁻¹, and (D) n = 2, a = 10mm⁻¹.

Figure 2 illustrates that the trajectory evolution of the PCSCBs changes periodically in SNNM, and the period is L = 2π. Different shifting parameters change the structure of the trajectory bending trend. The evolution initially broadens because beam diffraction initially overcomes beam-induced refraction. Different beam orders do not affect the trajectory evolution period, but the trajectory profiles behave differently.

FIGURE 2

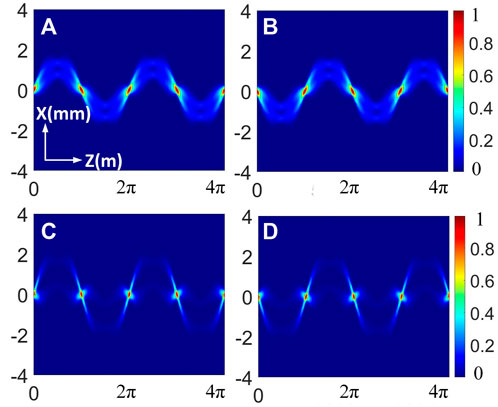
FIGURE 2. Propagation trajectory of the PCSCBs in SNNM with β = 1. (A) n = 1, a = −10 mm⁻¹, (B) n = 1, a = 10 mm⁻¹, (C) n = 2, a = −10 mm⁻¹, and (D) n = 2, a = 10 mm⁻¹.

To further discover the effect of the shifting parameters, we discuss the beam center [29], which can be given as

$<x>={\iint }_{-\infty }^{\infty }x\mid I\left(x,y,z\right){\mid }^{2}dxdy/{\iint }_{-\infty }^{\infty }\mid I\left(x,y,z\right){\mid }^{2}dxdy,(9)$

$<y>={\iint }_{-\infty }^{\infty }y\mid I\left(x,y,z\right){\mid }^{2}dxdy/{\iint }_{-\infty }^{\infty }\mid I\left(x,y,z\right){\mid }^{2}dxdy.(10)$

In Figure 3, the beam center distributions undergo a parabolic trajectory. The beam center changes vividly with different β, the period is L = 2π with β = 1, and L = π with β = 0.5. Though the beam center undergoes a parabolic profile, the shifting parameters change their bends characteristics. As the PCSCBs behave with interesting features, it is meaningful to explore the potential applications in optical trapping. Thus, we discuss the radiation forces generated by the focused PCSCBs next.

FIGURE 3

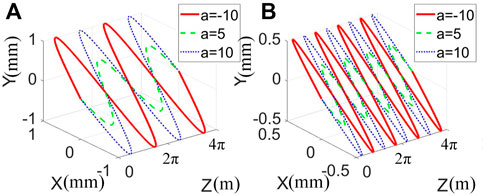
FIGURE 3. The numerical demonstrations of the beam center in SNNM with different shifting parameters. (A) β = 1, (B) β = 0.5.

4 Radiation forces produced by the focused PCSCBs

The research of the optical radiation force has a profound impact on many micro manipulation technologies [25, 28]. In the following, the radiation forces of the PCSCBs acting on a nonabsorbent Rayleigh dielectric particle are studied. When the particle radius r₀ is sufficiently small compared with the wavelength (i.e., r₀ ≤ λ/20), it can be seen as a point dipole in the light field. Considering the propagation of the PCSCBs through a lens system, where z is the distance from the input plane to the output plane, f is the focal length, and z₁ is the axial distance from the focal plane to the output plane, the ABCD matrix for this focusing system [30] is

$\left(\begin{array}{cc}\hfill A\hfill & \hfill B\hfill \\ \hfill C\hfill & \hfill D\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill 1\hfill & \hfill z\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right)\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill -1/f\hfill & \hfill 1\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill 1-z/f\hfill & \hfill z\hfill \\ \hfill -1/f\hfill & \hfill 1\hfill \end{array}\right).(11)$

After substituting Eq. 11 into Eq. 5, we can got the intensity of the PCSCBs in the focusing system. Light forces depend not only on the physical properties of the particle but also on the properties of the light field (e.g., amplitude, phase, polarization, etc.) are closely related. In this paper, the scattering force component is proportional to the distribution of the intensity, while the gradient force distribution is given on the basis of its electric field amplitude. Assuming that the particle is under a steady state, the scattering force and the gradient force [28, 32] can be expressed as

${\vec{F}}_{\mathit{scat}}\left(x,y,z\right)=\frac{n_m{\zeta }_0}{c}I\left(x,y,z\right){\vec{e}}_z,(12)$

${\vec{F}}_{grad}\left(x,y,z\right)=\frac{2\pi n_m{\rho }_0}{c}\nabla I\left(x,y,z\right),(13)$

where ${\vec{e}}_z$ is a unity vector along the beam propagation, ${\zeta }_0=(128{\pi }^5{r}_0^6/3{\lambda }^4){[({\eta }^2-1)/{\eta }^2+2\left.\right)]}^2,{\rho }_0=r_0^3({\eta }^2-1)/({\eta }^2+2),\eta =n_p/n_m$ is the relative refraction index of the particle, r₀ = 15nm, n_m = 1.332 (water) is the refractive index of the medium. n_p = 1 (air bubble, η < 1) or n_p = 1.59 (glass, η > 1) is the refractive index of the particle. Both the gradient force and the scattering force can be affected by the refraction index η, the shifting parameter a, the coherence width δ. We set the parameters in the focusing system as f = 10mm, σ_x = 10mm, σ_y = 4mm, δ_x = 10mm, δ_y = 4mm, and a = b = 0.01mm⁻¹.

Figure 4 gives information on the radiation forces produced by the focused PCSCBs on the high-index particle (η > 1) and the low-index particle (η < 1) on the trapped plane. To achieve stable trapping, the gradient forces need to be larger than scattering forces. Because the scattering forces push the Rayleigh particles along the propagation direction, while the gradient forces pull the Rayleigh particles toward the maximum of the transverse optical field. That is to say, R = F_grad,z/F_scat ≥ 1, where the ratio R represents the stability standard. One can find stable equilibrium points in Figures 4A,B,D, where the refractive index the Rayleigh particle is smaller than the refractive index of the ambient, the particle can be trapped at the focus point by the partially coherent PCSCBs. Near the focal plane, the scattering force is smaller than the longitudinal gradient force. However, in Figure 4C, the high-index particle can be trapped at the focus (z₁ = 0) when x = ±0.3 μm. These two kind of particles can be trapped in the mean time at different x positions of the trapped plane.

FIGURE 4

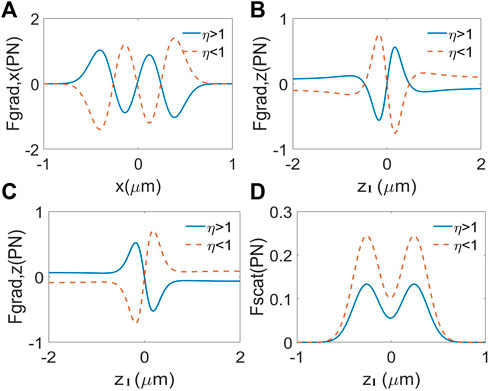
FIGURE 4. Effects of the refraction index on the radiation forces. The high-index particle (η > 1) in solid lines, the low-index particle (η < 1) in dashed lines. (A), (B) and (D) at the focus, x = 0 μm, (C) at the points of x = ±0.3 μm.

Furthermore, we investigate the effect of the shifting parameter a and the coherent length δ on radiation forces acting on the low-index particle η < 1 (see Figure 5), respectively. It is shown in Figures 5A1,A3 that the bigger shifting parameters bring the stronger scattering forces and gradient forces along x direction. However, in Figure 5A2, the gradient forces along the z direction become weaker as a increases. Nevertheless, it needs to be noted that the gradient force along the z direction is still bigger than the scatting force with the same a. In Figures 5B1–B3, one could see that the gradient force and the scattering force grow up with the increase of the coherence width, meaning that the trapping stiffness becomes higher. Moreover, the peak position moves far away from the focus point as δ increases. We also note that the shifting parameter and the coherent length do not have an influence on the position where the PCSCBs capture the particles.

FIGURE 5

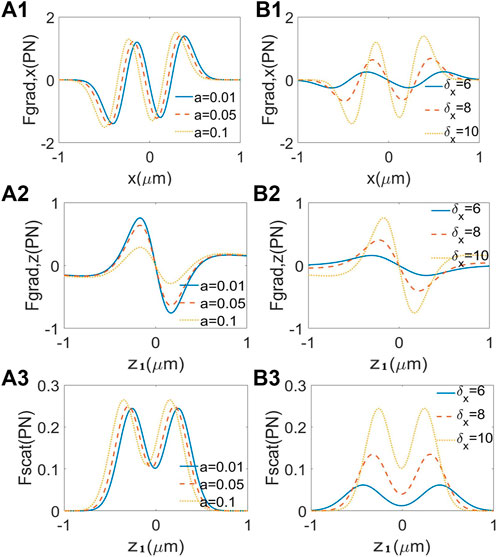
FIGURE 5. Effects of the shifting parameter a and the coherent length δ on the radiation forces for the low-index particle at the focal plane. (A1–A3) σ_x = 10 mm, σ_y = 4 mm, δ_x = 10 mm, δ_y = 4 mm. (B1–B3) a = 0:01 mm⁻¹.

5 Conclusion

To summarize, we have investigated the CSD of the partially coherent PCSCBs, studied propagation properties through the SNNM, and researched the radiation forces on a nonabsorbing nanoparticle in the focusing optical system. In SNNM, the PCSCBs is transverse self-shifting in different directions as various shifting parameters. While propagating, we observed that the spectral density decreases faster as the beam order increases. The propagation trajectory and the beam center change periodically. The power factors affect the periods, and the shifting parameters influence the bend characteristics.

In the focusing optical system, the optical force on a nonabsorbent Rayleigh dielectric particle has been decomposed into the scattering force and the gradient force. The radiation forces generated by the focused PCSCBs on the high-index particle (η > 1) and the low-index particle (η < 1) are discussed. These two kinds of particles can be trapped in the mean time at different x positions on the trapped plane. Specifically, the low-index particle is trapped at the focus point, while the high-index particle is trapped at the focus at x = ±0.3 μm. It is worthy to note that variation of the shifting parameter and the coherent length will cause the radiation force distributions to change but not affect the position where the PCSCBs capture the particles.

With all of these magnificent properties, the theoretical and numerical outcomes delivered in this paper could help understand the behavior of PCSCBs in the SNNM and the focusing optical system. The results indicate their potential applications in optical communication and optical trapping nonabsorbent nanoparticles.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

XP and DZ proposed the idea. XP wrote the original manuscript. SH and DD gave suggestions in numerical simulation. YH, DD, and DZ supervised the project. All authors contributed to the revision of the manuscript and approved the final version.

Funding

Postdoctoral Research Program of Zhejiang Province (ZJ2021034); National Natural Science Foundation of China (12004081, 12174122, 12174338, 62175042); Talent Introduction Project Foundation of Guangdong Polytechnic Normal University (2021SDKYA142).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Wolf E. Introduction to the theory of coherence and polarization of light. Cambridge: Cambridge University Press (2007).

Google Scholar

2. Mei Z, Korotkova O, Zhao D, Mao Y. Self-focusing vortex beams. Opt Lett (2021) 46:2384. doi:10.1364/ol.423220

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Collett E, Wolf E. Partially coherent sources which produce the same far-field intensity distribution as a laser. Opt Commun (1978) 25:293–6. doi:10.1016/0030-4018(78)90131-1

CrossRef Full Text | Google Scholar

4. Cai Y, Chen Y, Yu J, Liu X, Liu L. Generation of partially coherent beams. Prog Opt (2017) 62:157–223.

CrossRef Full Text | Google Scholar

5. Cai Y, Chen Y, Wang F. Generation and propagation of partially coherent beams with nonconventional correlation functions: A review [invited]. J Opt Soc Am A (2014) 31:2083. doi:10.1364/josaa.31.002083

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Korotkova O, Chen X. Phase structuring of the complex degree of coherence. Opt Lett (2018) 43:4727. doi:10.1364/ol.43.004727

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Wang F, Liang C, Yuan Y, Cai Y. Generalized multi-Gaussian correlated Schell-model beam: From theory to experiment. Opt Express (2014) 22:23456. doi:10.1364/oe.22.023456

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Zhao C, Cai Y. Trapping two types of particles using a focused partially coherent elegant Laguerre-Gaussian beam. Opt Lett (2011) 36:2251. doi:10.1364/ol.36.002251

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Korotkova O, Andrews L, Phillips R. Model for a partially coherent Gaussian beam in atmospheric turbulence with application in Lasercom. Opt Eng (2004) 43:330. doi:10.1117/1.1636185

CrossRef Full Text | Google Scholar

10. Liu L, Wang H, Liu L, Dong Y, Wang F, Hoenders B, et al. Propagation properties of a twisted Hermite-Gaussian correlated schell-model beam in free Space. Front Phys (2022) 10:847649. doi:10.3389/fphy.2022.847649

CrossRef Full Text | Google Scholar

11. Snyder A, Mitchell D. Accessible solitons. Science (1997) 276:1538–41. doi:10.1126/science.276.5318.1538

CrossRef Full Text | Google Scholar

12. Deng D, Guo Q, Hu W. Complex-variable-function Gaussian beam in strongly nonlocal nonlinear media. Phys Rev A (2009) 79:023803. doi:10.1103/physreva.79.023803

CrossRef Full Text | Google Scholar

13. Deng D, Guo Q. Ince-Gaussian solitons in strongly nonlocal nonlinear media. Opt Lett (2007) 32:3206. doi:10.1364/ol.32.003206

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Bekenstein R, Segev M. Self-accelerating optical beams in highly nonlocal nonlinear media. Opt Express (2011) 19:23706. doi:10.1364/oe.19.023706

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Mihalache D, Mazilu D, Crasovan L, Towers I, Buryak A, Malomed B, et al. Stable spinning optical solitons in three dimensions. Phys Rev Lett (2002) 88:073902. doi:10.1103/physrevlett.88.073902

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Ou J, Plum E, Zhang J, Zheludev N. Giant nonlinearity of an optically reconfigurable plasmonic metamaterial. Adv Mater (2015) 28:729–33. doi:10.1002/adma.201504467

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Xu J, Plum E. Defect-induced nonlinearity in 2D nanoparticles. Opt Express (2022) 30:7162. doi:10.1364/oe.443977

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Xu J, Plum E, Savinov V, Zheludev N. Second harmonic generation in amorphous silicon-on-silica metamaterial. APL Photon (2021) 6:036110. doi:10.1063/5.0037428

CrossRef Full Text | Google Scholar

19. Conti C, Peccianti M, Assanto G. Observation of optical spatial solitons in a highly nonlocal medium. Phys Rev Lett (2004) 92:113902. doi:10.1103/physrevlett.92.113902

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Rotschild C, Cohen O, Manela O, Segev M, Carmon T. Solitons in nonlinear media with an infinite range of nonlocality: First observation of coherent elliptic solitons and of vortex-ring solitons. Phys Rev Lett (2005) 95:213904. doi:10.1103/physrevlett.95.213904

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Zhou G, Chen R, Ru G. Propagation of an Airy beam in a strongly nonlocal nonlinear media. Laser Phys Lett (2014) 11:105001. doi:10.1088/1612-2011/11/10/105001

CrossRef Full Text | Google Scholar

22. Zhang L, Zhang X, Wu H, Li C, Pierangeli D, Gao Y, et al. Anomalous interaction of Airy beams in the fractional nonlinear Schrödinger equation. Opt Express (2019) 27:27936. doi:10.1364/oe.27.027936

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Peng X, He S, He Y, Deng D. Propagation of self-accelerating Hermite complex-variable-function Gaussian wave packets in highly nonlocal nonlinear media. Nonlinear Dyn (2020) 102:1753–60. doi:10.1007/s11071-020-06003-9

CrossRef Full Text | Google Scholar

24. Peng X, He Y, Deng D. Three-dimensional chirped Airy Complex-variable-function Gaussian vortex wave packets in a strongly nonlocal nonlinear medium. Opt Express (2020) 28:1690. doi:10.1364/oe.384852

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Ashkin A. Acceleration and trapping of particles by radiation pressure. Phys Rev Lett (1970) 24:156–9. doi:10.1103/physrevlett.24.156

CrossRef Full Text | Google Scholar

26. Ashkin A, Dziedzic J, Bjorkholm J, Chu S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt Lett (1986) 11:288. doi:10.1364/ol.11.000288

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Ashkin A, Dziedzic J. Optical trapping and manipulation of viruses and bacteria. Science (1987) 235:1517–20. doi:10.1126/science.3547653

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Harada Y, Asakura T. Radiation forces on a dielectric sphere in the Rayleigh scattering regime. Opt Commun (1996) 124:529–41. doi:10.1016/0030-4018(95)00753-9

CrossRef Full Text | Google Scholar

29. Wang H, Sun C, Tu J, Zhen W, Deng D. Propagation dynamics and radiation forces of autofocusing circle Bessel Gaussian vortex beams in a harmonic potential. Opt Express (2021) 29:28110. doi:10.1364/oe.435588

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Peng X, Chen C, Chen B, Peng Y, Zhou M, Yang X, et al. Optical trapping Rayleigh particles by using focused partially coherent multi-rotating elliptical Gaussian beams. Chin Opt Lett (2016) 14:011405.

Google Scholar

31. Zhang Y, Yan H, Zhao D. Optical trapping Rayleigh particles with a twist effect. Opt Lasers Eng (2020) 130:106101. doi:10.1016/j.optlaseng.2020.106101

CrossRef Full Text | Google Scholar

32. Zhou Y, Zhao D. Research on statistical properties and application of Off-Axis Gaussian Schell-Model beams. Ann Phys (2021) 533:2100017. doi:10.1002/andp.202100017

CrossRef Full Text | Google Scholar

33. Guo M, Zhao D. Radiation forces on a Rayleigh dielectric sphere produced by highly focused parabolic scaling Bessel beams. Appl Opt (2017) 56:1763. doi:10.1364/ao.56.001763

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Guo M, Zhao D. Changes in radiation forces acting on a Rayleigh dielectric sphere by use of a wavefront-folding interferometer. Opt Express (2016) 24:6115. doi:10.1364/oe.24.006115

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Liang C, Wang F, Liu X, Cai Y, Korotkova O. Experimental generation of cosine-Gaussian-correlated Schell-model beams with rectangular symmetry. Opt Lett (2014) 39:769. doi:10.1364/ol.39.000769

PubMed Abstract | CrossRef Full Text | Google Scholar