Predicting beam transmission using 2-dimensional phase space projections of hadron accelerators

We present a method to compress the 2D transverse phase space projections from a hadron accelerator and use that information to predict the beam transmission. This method assumes that obtaining at least three projections of the 4D transverse phase space is possible and that an accurate simulation model is available for the beamline. Using a simulated model, we show that—a computer can train a convolutional autoencoder to reduce phase-space information which can later be used to predict the beam transmission. Finally, we argue that although using projections from a realistic nonlinear distribution produces less accurate results, the method still generalizes well.

1 Introduction

A challenging problem in obtaining high beam power in hadron linacs, such as ATLAS, SNS, and FRIB, is understanding and minimizing uncontrolled beam loss—a significant unexpected loss of the beam within the beamline. [1]. In the low energy beam transport lines (LEBT), the machine must carefully control the beam to minimize downstream beam loss. The beam describes a collection of particles in six-dimensional space; three positions and three momentum coordinates. For the DC beam in the LEBT, the longitudinal coordinates are not involved in the dynamics but appear as parameters. Therefore, each charged particle is described by its location in the four-dimensional (4D) transverse phase space (x, x′, y, y′), where primed coordinates are derivatives with respect to the longitudinal direction.

In the LEBT, multiple beam measurement devices such as Alison Scanners [2], Pepper-Pot emittance meters [3], wire scanners [4], and viewers, are used to capture one-dimensional (1D) or two-dimensional (2D) profile measurements. These are projections of the four-dimensional (4D) transverse phase space. Inferring the 4D distribution from this projected 1D and 2D information is referred to as 4D tomography. Mathematical and physical methods, such as the maximum entropy principle [5, 6], have been successfully demonstrated to realize the 4D tomography in accelerators. However, there are still challenges in combining 1D or 2D information from different locations. The optics deviation, when the machine deviates from the model, for example, will affect the accuracy of the 4D tomography.

In this paper, we tested a data-driven approach to predict the beam loss using 4D phase space distribution information encoded in a low-dimensional vector from 2D projection measurements. The data was generated from virtual diagnostic instruments simulated using the beam dynamics code TRACK. The simulation is of a test lattice adopted from the LEBT of the ATLAS accelerator, which consists of six quadrupoles and five virtual diagnostic instruments. The simulation results were used to develop a convolutional autoencoder to encode the data into a meaningful lower-dimensional representation, which the model will then use to relate the phase-space information to the beam loss.

2 Methods

2.1 ATLAS lattice

The presented study used data generated from the simulation of ATLAS’s LEBT. The lattice consists mainly of a multi-harmonic buncher, nine quadrupole magnets—six of which are being used to tune the lattice—and five virtual diagnostic instruments. The virtual diagnostic instruments capture the 4D phase space of the beam, providing information on the 2D projections and beam transmission for use later. This amount of data is currently hard to achieve in an actual accelerator, but it is used to study the method’s feasibility, giving the initial model a higher chance to succeed.

Figure 1 shows the location of the virtual diagnostic instruments. The measurements were recorded at five locations: beginning, end, and after quadrupoles 2, 4, and 6.

FIGURE 1

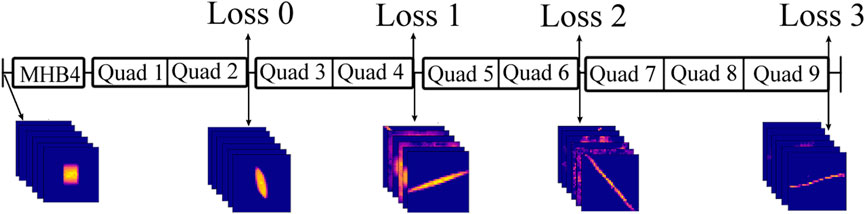
FIGURE 1. Cartoon of accelerator and beam measurements. The image shows where the model collected each beam measurement.

2.2 Generating data using TRACK

TRACK is a ray-tracing or particle-tracking code that can:

1) represent external fields accurately within the aperture.

2) calculate the particle coordinate at any point in the space.

3) determine to calculate beam loss in both the ideal case and in the presence of complex field errors and device misalignments [7].

Since machine time is costly, the TRACK simulation was used to gather data. It was generated on Michigan State University’s high-performance computing cluster for a week, producing over a million data points. As will be covered in a later section, a significant amount of data will be required for training autoencoders to high fidelity. The model varied the parameters for these simulations according to Table 1. The model chose these parameters within a small range to interpolate well. Once the model collected the data, it was filtered so that the initial beam distributions were contained within the beam aperture, resulting in a final data set of around 430,000 simulation points.

TABLE 1

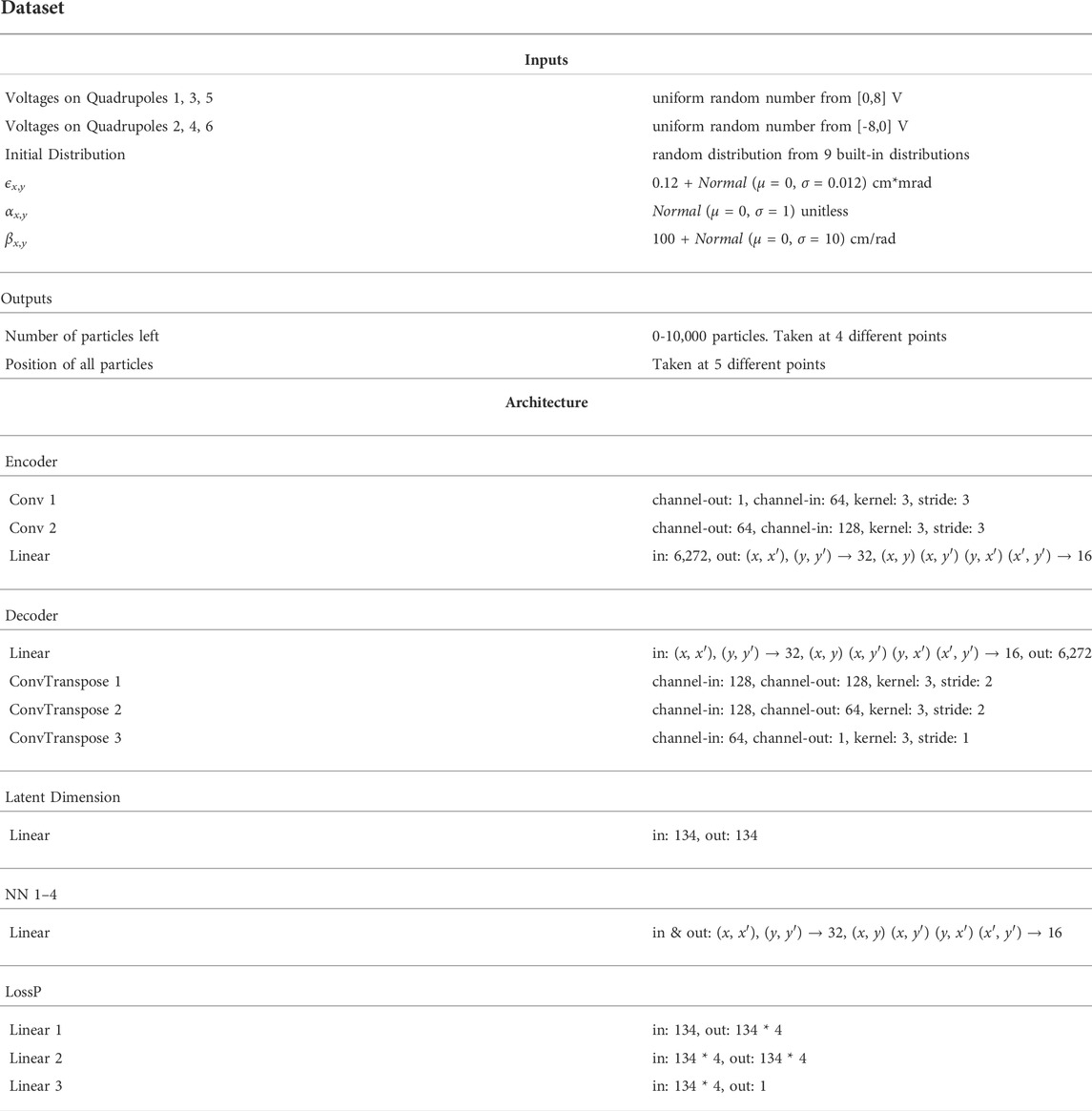
TABLE 1. Inputs: Parameter range used to generate a dataset of the initial beam distributions and quadrupole settings. Architecture: Description of some blocks used in the architecture. Each projection was given a separate encoder and decoder block where the latent dimension differ for the $(x, x′)$ and $(y, y′)$ projections.

2D phase-space projections from the 4D phase space were created by having all the particles deposited onto an n × n grid using pairs of the coordinates axes, (x, x′, y, y′). This method resulted in 6 independent projections.

2.2.1 Non-linear field

Another data set was created to test the model’s generalizability, which will be explained later. This was done with a perturbation to the initial distribution. The distribution was created at the beginning of the simulation by using a nonlinear magnetic field, such as a sextupole. All other generative settings were kept the same. This simulates the realistic case of ECR beams which experience a sextupole field inside the source.

2.3 Autoencoder

An autoencoder is a nonlinear data reduction algorithm used in machine learning. It is composed of two parts, an encoder and a decoder. The encoder takes a significant input and reduces it into a lower dimension, known as a latent dimension, while the decoder attempts to reconstruct the latent dimension back into the original input. The error, which is the difference between the original and reconstructed data, quantifies how well the latent dimension explains the initial input. The advantage of compressing the data into a meaningful representation [8] makes it more efficient to train a neural network model on the reduced data.

In the model, a convolutional autoencoder was implemented in PyTorch [9] to reduce the dimension of the 2D projections of the phase space. A convolutional autoencoder uses a convolutional neural network as the encoder and decoder. A convolutional neural network is a type of neural network used to analyze visual information [10, 11]. This network has the advantage over principal component analysis [12], another data reduction algorithm, in that it includes spatial information and can account for nonlinear effects by using nonlinear activation functions in the network. Activation functions take the summed weighted inputs of a layer inputs of a layer and map it onto a set range. It was found that the ReLU activation function and the ELU activation function were the best activation functions to use [13] in this case, it helps the model to train fast and be less likely to fail during training.

Each of the six 2D projections was given its own autoencoder. The decoder reproduces all the original projections reasonably, verifying that the model effectively encoded the projections into a latent dimension. The latent dimensions sizes used for this paper were 32 for the (x, x′), and (y, y′) projection, and 16 for the rest. Given that the code made the original images to be 33 × 33, the model significantly reduced the inputs.

2.4 Modeling

A neural network was used to create a surrogate model of the ATLAS front-end, as shown in Figure 2. A more detailed description of each block is described in Table 1, and the full detail can be seen in the code¹. The architecture is composed of an encoder-decoder block to reduce each of the six phase-space projections into lower latent dimensions and then concatenate them together. The quad settings were also joined onto this vector and processed through fully connected layers. Each fully connected layer attempts to model the phase space changes by transforming the latent variables into a different set of latent variables describing the new 4D phase space. This new vector would be the input into the next fully connected layer to model the following transformation, a decoder block to reconstruct the distribution as 2D phase-space projections at that location, and another fully connected layer to predict the beam transmission represented by the number of particles left.

FIGURE 2

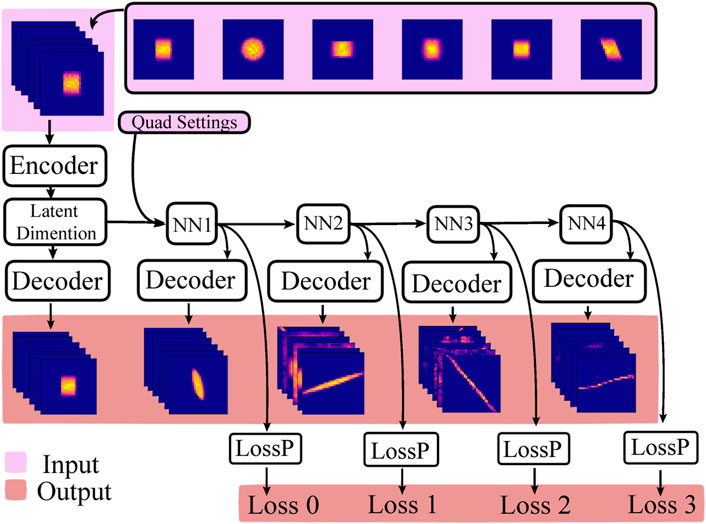
FIGURE 2. Cartoon of architecture. During training, the model takes all the 2D projections and loss value as input into the training. Only the initial 2D projections were given during testing, and the model predicts the loss values and 2D projections in addition.

The encoder-decoder block uses a convolutional autoencoder, as described in the previous section. The decoder was built similarly to the encoder, the only difference being that some adjustments were made to match the original dimensions. A decoder was not trained for every location but was combined for each projection. This method saves limited GPU memory and produces a more generalized decoder.

The model used a two-layer, fully connected network to calculate the number of particles left. Again, the model did not train the network at every location, but it was combined to make a generalized particle loss predictor for the same reasons stated above.

2.5 Training

Overall, the model encodes each initial phase-space projection into separate latent dimensions, then attempts to recreate the phase-space forecast and predict the beam transmissions at the other 4 locations, and then compares them to the ground truth from the dataset. Using both results in a training loop, the model will update itself using gradient descent [10] to recreate the image in the next iteration better. Gradient descent is performed using backpropagation on PyTorch computational map. The basic idea is that parameters in the network will be adjusted using the gradient information in the direction that will result in the final output closer to the actual values. The size of the step taken is related to the learning rate.

The model used a loss function to quantify the difference between the predicted and ground truth results. Commonly, mean square error loss is used because it punishes large deviations; however, this results in an overflow—an error that occurs when a computer produces a number more significant than it can represent, in the gradient calculation during training. This could have be resolved by normalizing the inputs and outputs, but a non-normalized dataset was used since that gave a better convergence. The model used absolute loss (L1 Loss) in these cases. This could also have been resolved by using a double or a long float, but this would use up valuable memory on the GPU.

To also aid in training, frozen layers were implemented to decrease training time and prevent gradient overflow. Frozen layers are layers where the gradient information was disconnected, thus preventing changes to that layer during training. This method was implemented in the following three-step training procedure:

1. LossP blocks were frozen and trained with a learning rate of 0.01. Everything else was trained for 20 epochs.

2. LossP blocks were unfrozen, and everything else was frozen; thus, only LossP was trained for 10 epochs. The learning rate was also 0.01

3. Everything was unfrozen and trained for 5 epochs at a lower learning rate of 0.001.

A problem that arises from using simulation is overfitting, which is a state where the model memorizes the training data rather than generalizing it. Because simulation generally differs from the actual machine due to installation and operation errors, if the model is not generalized or adjusted enough, it will perform poorly on the actual device.

The model used the last step of the training procedure to better merge the LossP block with the whole model. This also helps to prevent overfitting. A lower learning rate than the previous two steps discourages radical changes that may destroy the learned model in the first two steps.

2.6 Results

The model was tested on a newly generated dataset using the original parameters and a nonlinear dataset generated using a sextupole. Only the initial distributions were given, but the model would still predict the 2D projections and beam transmission at the other locations downstream. Then, to test the model’s generalization, a nonlinear field in the form of a sextupole [14] was added to the beginning of the simulation to generate a distinct subset of inputs.

An error of less than 1% for results within two standard deviations from the mean would be sufficiently good for predicting the loss on ATLAS since it is a low-power machine. For the rest of the paper, the percentage refers to a two standard deviation bound. The error is defined as the absolute difference between the ground truth and the predicted values divided by the total number of particles. The obtained values were plotted as a correlation graph in Figure 3A. If there were no errors, there would be a straight line. Given that we have 10⁴ particles, the error for the original data set using six projections would be 3%.

FIGURE 3

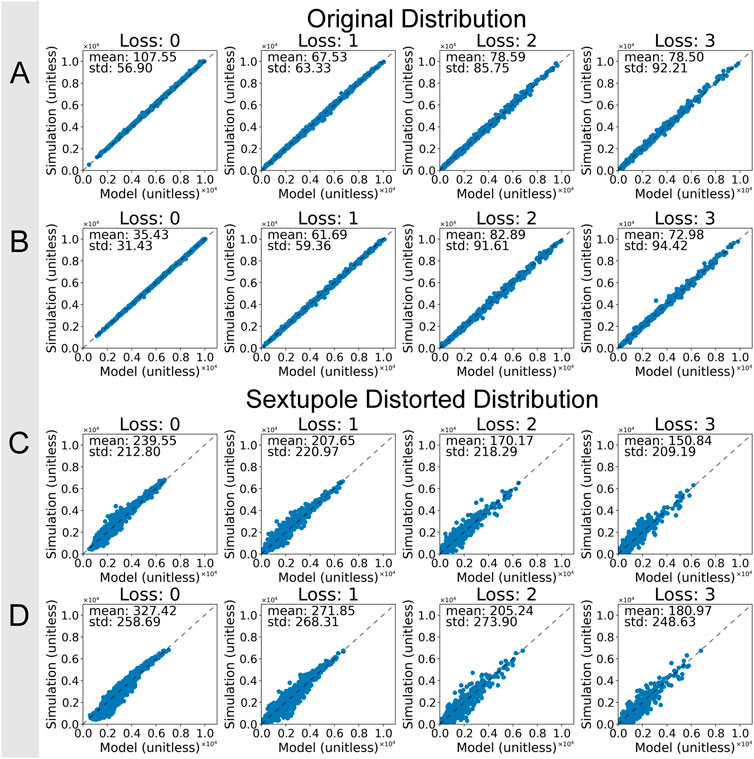
FIGURE 3. (A) Histogram of original data set using six projections (B) and same model but using three projections. (C) Histogram of original data set using six projections, (D) and same model but using three projections.

This was then tested on the nonlinear sextupole distribution with fair results, an error of 5.5% as shown in Figure 3C. The model was able to generalize reasonably well; however, it is still far from the ideal case. In this case, a machine learning model mainly interpolates the results, so the accuracy of a model depends on how much training data it is given. The more data points a model has, the better the interpolation.

Due to the nature of hadron accelerators, many quadrupole configurations would produce a high particle loss because only a few configurations would allow most particles to pass. Thus, most of the dataset would be skewed towards high loss, resulting in higher accuracy since there is more data in those cases. The dataset was split into bins, and as expected, the bin of particle loss between 9,000–10,000 has an error around 2.5%, and for the bin of particle loss between 0–1,000, the error was as high as 5%.

2.6.1 Testing on a smaller data set

The same model was tested again, but with the (x, y′) (x′, y′), and (y, x′) projections removed. In Figure 3B, the error predictions from the original data set show an improvement in the accuracy for “Loss: 0”, while it has around the same error for the other losses. This difference in error is likely due to overfitting as the predictions from the nonlinear data set show a loss of accuracy overall, as seen in Figure 3D; however, the model was shown to work with half the image data used, making this model more practical.

3 Discussion

A proof-of-principle machine learning-based model has been reported to test an ML-based 4D tomography using its 2D projections and the capability to predict beam transmission. The result shows that if given only three projections of the 4D phase space, the model can reduce the projections into a smaller latent dimension that contains the core information, which the model can then use to predict the beam transmission downstream. If the model used fewer projections, the model would not have enough information to describe the entire 4D phase space. The latent dimension was verified to have contained the core information through a decoder that correctly reconstructed the encoded images. This method generalizes reasonably well to initial beam distributions with nonlinear perturbations, showing robustness and the potential for modeling the real machine.

Before bringing this to a real machine, it should be noted that this is a simplified model of an actual accelerator, with considerable differences to consider. This model assumes that a single parameter can model the accelerator elements; therefore, more complicated effects, such as misalignment of the magnets and the longitudinal overlapping of transverse magnets, are not considered. The model also assumes no space charge, neglects the profile’s beam-to-beam fluctuation, and overlooks the longitudinal components of the beam distribution.

It requires at least three projections to make the prediction, but this is not always available. In addition, it assumes perfect accuracy in the measurements. The prediction accuracy will also depend on the accuracy of the projections and beam loss monitors, but one method to reduce measurement error at various locations can be to use multiple measurements with different optics. The current model cannot predict fractional beam loss over the entire length of the accelerator at the level of 1e-06 to 1e-08 per meter, which would be desirable for future works, but methods such as adaptive tuning and physics-informed learning may prove helpful to make the model more robust and accurate and eventually reach that goal.

The beam loss value is represented by the percentage of the total beam intensity. Accuracy of a few percent beam loss has been demonstrated with this simplified model; however, characterizing the beam loss with a certain percentage of the total power results in a very different threshold for accelerators with another goal of beam power. Therefore, the absolute power loss should be used in later applications for real accelerators.

The traditional approach to evaluating beam loss would be to use simulations or beam loss monitors. The simulation requires an accurate lattice model with boundary data information where beam halo information is usually absent. Other methods, such as beam loss monitors, are physical devices used to measure beam loss, whereas some standard devices are ion chambers and photomultipliers. In choosing the suitable machine, there are various considerations such as sensitivity, cost, size, dynamic range, and radiation hardness [15].

The model could be trained using data from a real machine, but collecting a large amount of data is expensive and time-consuming. Thus, models will have to be introduced on realistic simulation models and then transferred to the actual machine. Methods known as “transfer learning” allow knowledge learned from the source dataset to be transferred to a target dataset [10]. This could be done, for example, by freezing the model, adding another layer to the encoder and decoder, and training that layer on the distribution from the machine to adapt the model to the machine. Then, the rest of the model can be unfrozen and trained with a much lower learning rate to fine-tune the model. Further studies will allow models to be trained first with simulations and then transferred to machines.

Machine learning has various advantages and disadvantages. Machine learning has an advantage since it can make a data-driven model with no lattice information at the expense of a large data set. Two disadvantages are that the model will need high-fidelity data to reach high accuracy and that the model will constantly need to be calibrated to the current machine. Future research will study ways to combine machine learning with physics to make a more sample-efficient and robust model. One way this could be done is by encoding constraints in the loss function during model training or by incorporating domain knowledge by including the transfer matrices in the calculation. The positive results of this work give hope that incorporating this knowledge may increase sample efficiency and further reduce the beam transmission error.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

AT did the data generation, the analysis, and the writing of this paper. YH advised AT along the way and revised the paper. BM helped revise the paper for better understanding. JM created the initial wrapper to run TRACK in python.

Funding

This work was supported by the U.S. Department of Energy, under Contract No. DE-AC02-06CH11357. This research used the ATLAS facility, which is a DOE Office of Nuclear Physics User Facility. Funded through a “Data, Artificial Intelligence, and Machine Learning at DOE Scientific User Facilities” Grant from the DOE’s Office of Nuclear Physics.

Acknowledgments

I acknowledge Jaturong Kongmanee for multiple discussions related to machine learning.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹The code is available upon request.

References

1. Aleksandrov A, Shishlo A. Path to beam loss reduction in the sns linac using measurements, simulation and collimation. In: 57th ICFA Advanced Beam Dynamics Workshop on High-Intensity, High Brightness and High Power Hadron Beams; Malmö, Sweden (2016).

Google Scholar

2. Allison PW, Sherman JD, Holtkamp DB. An emittance scanner for intense low-energy ion beams. IEEE Trans Nucl Sci (1983) 30:2204–6. doi:10.1109/tns.1983.4332762

CrossRef Full Text | Google Scholar

3. Pikin A, Kponou A, Ritter J, Zajic V. Pepper pot emittance meter. In: Tech. rep. Upton, NY, United States: Brookhaven National Lab. (BNL) (2006). Relativistic Heavy.

Google Scholar

4. Koziol H. Beam diagnostics for accelerators. In: Tech. rep. Meyrin, Switzerland: CERN (2001).

Google Scholar

5. Reggiani D, Seidel M, Allen C. Transverse phase-space beam tomography at psi and sns proton accelerators. In: Proceedings of IPAC10; Kyoto, Japan (2010).

Google Scholar

6. Wong JC, Shishlo A, Aleksandrov A, Liu Y, Long C. 4d transverse phase space tomography of an operational hydrogen ion beam via noninvasive 2d measurements using laser wires. Phys Rev Accel Beams (2022) 25:042801. doi:10.1103/physrevaccelbeams.25.042801

CrossRef Full Text | Google Scholar

7. Aseev V, Ostroumov P, Lessner E, Mustapha B. Track: The new beam dynamics code. In: Proceedings of the 2005 Particle Accelerator Conference (2005). p. 2053–5. doi:10.1109/PAC.2005.1591006

CrossRef Full Text | Google Scholar

8. Bank D, Koenigstein N, Giryes R. Autoencoders (2020). arXiv preprint arXiv:2003.05991.

Google Scholar

9. Paszke A, Gross S, Massa F, Lerer A, Bradbury J, Chanan G, et al. Pytorch: An imperative style, high-performance deep learning library. Adv Neural Inf Process Syst (2019) 32.

Google Scholar

10. Zhang A, Lipton ZC, Li M, Smola AJ. Dive into deep learning (2021). arXiv preprint arXiv:2106.11342.

Google Scholar

11. Scheinker A. Adaptive machine learning for time-varying systems: Low dimensional latent space tuning. J Instrum (2021) 16:P10008. doi:10.1088/1748-0221/16/10/p10008

CrossRef Full Text | Google Scholar

12. Abdi H, Williams LJ. Principal component analysis. Wires Comp Stat (2010) 2:433–59. doi:10.1002/wics.101

CrossRef Full Text | Google Scholar

13. Ding B, Qian H, Zhou J. Activation functions and their characteristics in deep neural networks. In: 2018 Chinese control and decision conference (CCDC). Shenyang, China: IEEE (2018). p. 1836–41.

CrossRef Full Text | Google Scholar

14. Lee SY. Accelerator physics. Singapore: World Scientific Publishing Company (2018).

Google Scholar

15. Wittenburg K. Beam loss monitoring and control. In: Proceedings of EPAC (2002). p. 109–13.

Google Scholar