Component characterization and commissioning of a gamma-PET prototype detector system

Hybrid imaging systems, comprising PET and Compton camera modules, have recently gained in interest, due to their capability to simultaneously detect positron annihilation photons and γ-rays from single-photon emitting sources as also used in SPECT. A unique feature of such systems, however, is the capability to also be operated in a so called γ-PET mode. Here, specific β⁺- emitting radioisotopes (such as ⁴⁴Sc, ¹°C or ¹⁴O) are used to detect triple-coincidences between two annihilation γ-rays (in PET imaging) and a third, prompt photon (in Compton imaging), that is emitted by the deexcitation of the decay’s daughter nucleus. Consequently, an intersection between the line-of-response (LOR) and the Compton cone can be determined, which (in principle) allows to localize the photons’ emission vertices on a single decay basis. In practice, however, a few tens of events are required to localize a point source, which still results in a considerable sensitivity improvement compared to conventional PET imaging.

For a proof-of-principle study, we used a pixelated GAGG crystal array (16 × 16 crystals; 1.45 × 1.45 × 6 mm³ crystal volume; 25 μm SPAD SiPMs as readout) as Compton camera scatterer and PET detectors, and a three-layered LYSO crystal array (1.2 × 1.2 × 6.66 mm³ crystal volume; 50 μm SPAD SiPMs as readout) as Compton camera absorber. We characterized the individual detector components with regard to their energy resolution and the capability to identify the various scintillator array’s individual crystals. Our first γ-PET prototype was tested in PET-only and Compton-only imaging mode, in which spatial resolutions of 3.2–3.5 mm FWHM (PET-only mode) and 14.4–19.3 mm FWHM (Compton-only mode at 1,274 keV) were achieved, respectively, using a²²Na point source and 10 iterations of an ML-EM reconstruction algorithm. By using triple-coincidences in a γ-PET mode (event-wise intersection of the LOR and the Compton cone), we could demonstrate the capability of the prototype to perform a full 3D point source reconstruction using only 77 events.

Introduction

Hybrid γ-ray imaging systems combining positron-emission tomography (PET) and a Compton camera result in a so-called γ-PET system, also referred to as Compton-PET or Whole-Gamma Imaging (WGI) [1–3]. Such a combined Compton- and PET scanner is capable to detect annihilation photons in a PET-only mode, photons from a single γ ray emitting nucleus (Compton-mode) or, if suitable radioisotopes are used, a triple - coincidence (β⁺- γ coincidence) between two annihilation photons and a third gamma (γ-PET) that is emitted due to the deexcitation of the daughter nucleus following the β⁺ decay. Prominent examples of isotopes that provide such decay characteristics are ⁴⁴Sc, ¹°C and ¹⁴O [1]. From their decay characteristics (⁴⁴Sc to ⁴⁴Ca: 1,157 keV, t_1/2 = 2.71 ps, ¹°C to ¹⁰B: 718 keV, t_1/2 = 0.7 ns, ¹⁴O to ¹⁴N: 2,312 keV, t_1/2 = 68 fs) it becomes clear that the β⁺γ triple coincidence in γ-PET mode occurs simultaneously from a practical perspective. Especially ¹°C and ¹⁴O are promising candidates for γ-PET in the context of online dose delivery control and range verification in particle therapy, since these isotopes are, among others, products of beam induced fragmentation processes in human tissue.

The limitations of PET, which requires β⁺ emitters, and Compton cameras, which suffer from low sensitivity and spatial resolution, especially when the source-to-detector distances increase, may be overcome by the detection of triple coincidences [1, 2]. This method allows to intersect a LOR with a Compton cone. Other than in the individual imaging methods, where emission centers can only be reconstructed using the intersection of multiple LORs and Compton cones, respectively, the triple coincidence in principle allows to localize the emission on a single event basis, resulting in a sensitivity improvement compared to the individual imaging techniques and therefore has the potential for achieving a more favorable tradeoff between image quality and number of detected events. Lang et al. could show in a simulation study that already 40 detected triple-coincidences are sufficient to reliably image a sub-millimeter point source [3, 4]. This increase in sensitivity may help to counterbalance the loss in efficiency compared to conventional PET caused by the requirement of the detection of γ-rays in triple coincidence. The principle of the γ-PET technique is exemplarily shown in Figure 1, where one Compton camera arm and two opposing PET detectors are indicated.

FIGURE 1

FIGURE 1. Schematic illustration of a γ-PET setup as commissioned in this work.

Based on numerical simulations, various groups have studied such imaging techniques based on the detection of 3γ and/or β⁺-γ coincidences [5–13]. In 2020 Shimazoe et al. presented a system for simultaneous PET and Compton imaging. The system, however, did not rely on the detection of triple coincidences in a γ-PET mode, but instead featured a dual imaging mode to simultaneously monitor positron and individual γ-ray emitters [14–16]. The experimental demonstration of imaging in a triple−γ mode was given by Yoshida et al. also in 2020 [1].

We developed a prototype of a detector system that is based on scintillation crystals with silicon photomultiplier (SiPM) readout and is capable of detecting β⁺-γ coincidences. In this work, we present a characterization of the individual detector components and first results of the full system operated in γ-PET mode.

Materials and methods

The Compton camera scatterer and the PET detector arrangement was assembled using the same type of scintillation detectors. The scintillator, a 16 × 16 GAGG (Gadolinium Aluminium Gallium Garnet, (Ce:Gd₃Al₂Ga₃O₁₂)) crystal array (1.45 × 1.45 × 6 mm³ active crystal volume, 1.6 mm crystal pitch), resulting in a detector area of 25.6 × 25.6 mm², was optically coupled to a Broadcom AFBR-S4K33P6425B (formerly from KETEK known as PA3325WB-0808) SiPM array (8 × 8 channels, 25 μm microcell size) [17, 18] using optical grease (∼100 μm thickness). In this readout configuration the GAGG crystal array provided the best relative energy resolution at 662 keV among three evaluated SiPM arrays with 15 μm, 25 and 50 μm SPAD pitch (former WB series of KETEK (now Broadcom)) and a HAMAMTSU MPPC array with 50 μm SPAD pitch, while the spatial resolution (given as the ability to distinguish the individual crystal response in the flood map) was of comparable quality for all investigated arrays [19]. The individual GAGG crystals of the array were optically isolated by using 150 μm thick BaSO₄ powder. The Compton camera absorber was a three-layered, staggered LYSO block built from 1.2 × 1.2 × 6.66 mm³ crystals and a crystal pitch of 1.28 mm. In-between the crystals, a 80 μm of ESR (enhanced specular reflector) film was used for optical isolation. The number of crystals in the first (top), second (middle) and third (bottom) layer are 16 × 17, 17 × 18 and 18 × 18, respectively. The LYSO block was optically coupled to a HAMAMATSU S14161-3050HS-08 MPPC array (8 × 8 channels, 50 μm microcell size) [20] using a 1 mm thick room-temperature vulcanizing (RTV) silicon rubber sheet as light guide.

The SiPM signal readout and processing were performed using the PETsys TOFPET v2c ASIC [21]. For the characterization of the PET assembly (Compton camera), the source-to-detector distance was 50 mm (11 and 50 mm, respectively).

The γ-PET prototype was commissioned as shown in Figure 2 (with a source-to-scatterer distance of 55 mm). The two PET detectors were placed face-to-face with their centers at y = z = 0 mm and x = 50/−50 mm for detectors PET 1 and PET 2. The Compton camera was placed perpendicular to the PET arrangement with the scatter detector located in a distance to the system center of z = 55 mm. The distance between the scatter and absorber component was chosen to be 43 mm. For an off-center position measurement (in the PET system) with 5 mm in the x and z dimension, respectively, the distance to the Compton camera scatterer was therefore 50 mm, as also in the Compton camera characterization. A geometry with the absorber placed in-line relative to the scatterer was chosen due to an expected increased geometrical efficiency compared to an out-of-line geometry. The reason is that at the relevant γ-ray energies for the third γ ray, according to the Klein-Nishina formula, already a sizable forward boost can be observed [22].

FIGURE 2

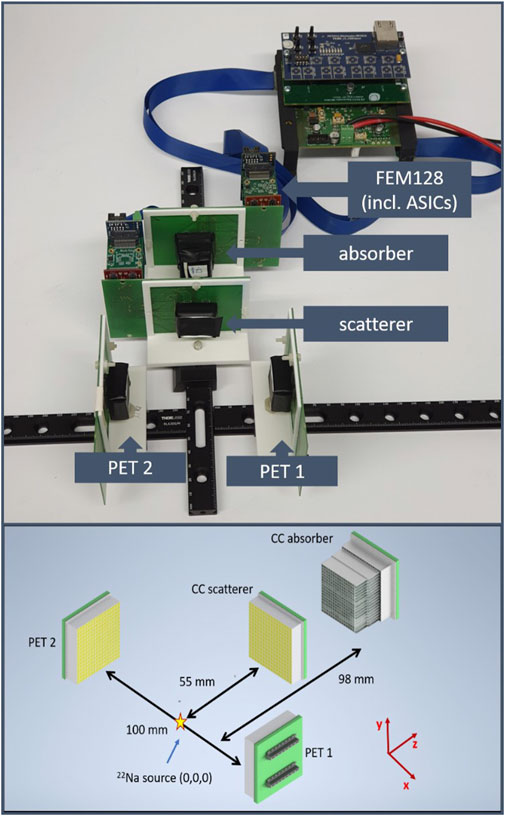
FIGURE 2. Photograph of the γ-PET setup (top) and related schematics including the dimensions and distances (bottom).

The setup was used to image a 140 kBq ²²Na point source (511 and 1,274 keV) at various positions in PET-only (600 s), Compton-only and γ-PET mode (each 5,400 s). In order to obtain β⁺-γ coincidences, the ²²Na point source was placed at an off-center position (x = 5 mm, y = 5 mm, z = 5 mm. To search for the triple coincidences between the two 511 keV annihilation γ rays and the 1,274 keV photon, two trigger regions were defined. One contained the two PET detectors, the other one the two components of the Compton camera. Within these two trigger regions the triggered ASIC channels were treated as a group of hits originating from a single γ-ray hit. Only events that triggered at least one detector in both trigger regions (3 ns coincidence window) were taken for a second post-processing step. This second step looped through all detected coincidences and used the ASIC channel identifier (channel-ID) to relate the triggered hits to one of the two detectors within the respective region.

If an initial γ−ray hit was detected in both trigger regions and, furthermore, also registered in both detectors in each of the trigger regions, it was considered as a valid triple coincidence, to which, subsequently, an energy gate was applied such that only fully absorbed 511 keV annihilation photons were considered in the PET detector pair and the total detected photon energy in the Compton camera corresponded to 1,274 keV.

The image reconstruction was based on the Maximum Likelihood Expectation Maximization method and performed using the MEGAlib toolkit [23–25]. For the characterization of the individual setups (PET and Compton camera) 10 iterations were used for the reconstruction, while in γ-PET mode only 3 iterations were used. 10 iterations were chosen as a suitable number of iterations, providing a reasonable compromise between spatial resolution and image noise. The increasing image noise for higher numbers of iterations on data with only a very limited number of events was the reason to use only 3 iterations for the γ-PET data.

Results

A. component characterization

Firstly, in order to prepare for measurements in the γ-PET mode, the individual detector performances were evaluated (Compton camera absorber and scatterer and two PET detectors). By inspecting the flood maps, the alignment of the GAGG scintillator arrays relative to their readout SiPM arrays was confirmed (Figure 3).

FIGURE 3

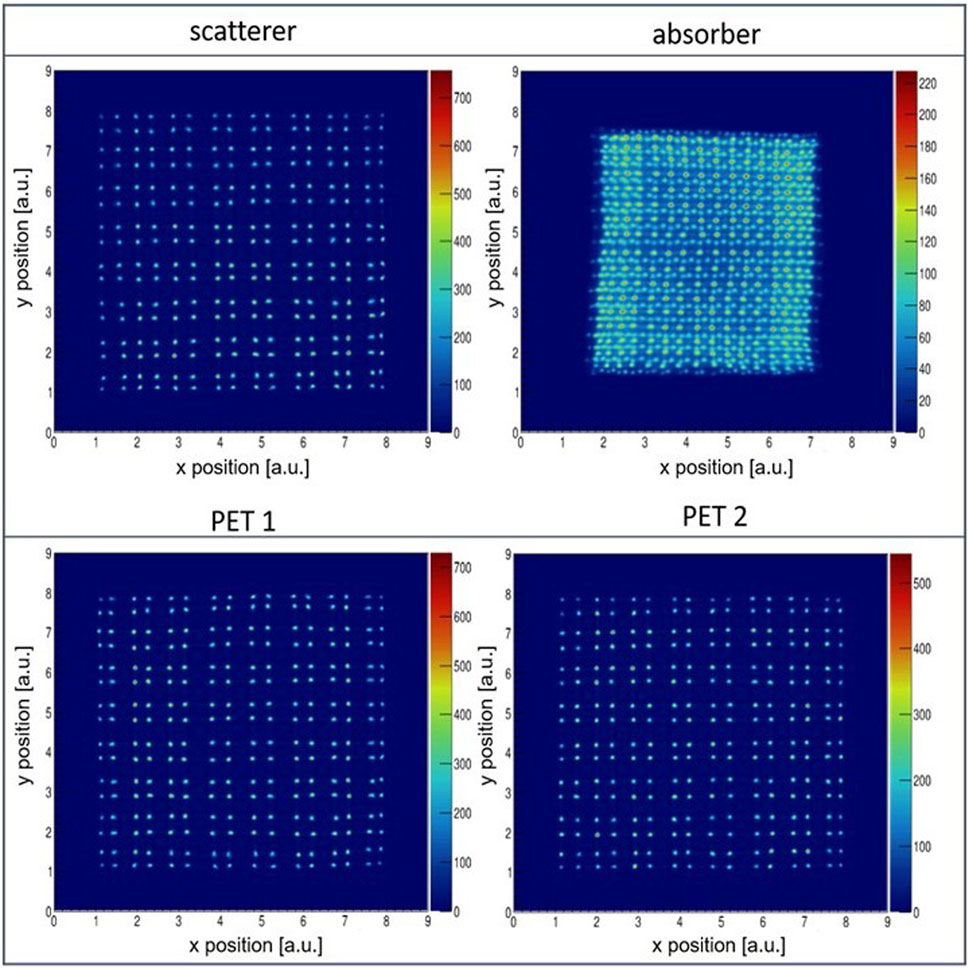
FIGURE 3. Flood maps obtained from the four detectors of the γ-PET prototype acquired using an irradiation with a¹³⁷Cs point source (662 keV).

For the three GAGG crystal arrays all crystals can be clearly identified without overlap and with only negligible distortions. For the three-layered LYSO (absorber) scintillator, crystals in the central area (10 × 12 crystals) can be well separated from each other. At the edges, however, some crystals show an overlap with neighboring crystals of other layers.

Secondly, the energy resolution of the four detectors in this specific assembly was measured from an inclusive energy spectrum of all crystals (of a layer) at a γ-ray energy of 662 keV (from a¹³⁷Cs point source). The obtained relative energy resolution of the scatterer was ΔE/E = 10.4 ± 0.2%, while for the absorber energy resolutions of ΔE/E = 12.8 ± 0.1% (12.4 ± 0.1%) [15.0 ± 0.1%] were determined for the first (second) [third] layer. The inferior energy resolution of the third layer is likely attributed to inter-crystal scattering (ICS) [26–28]. For the two PET detector assemblies an energy resolution of 10.0 ± 0.1% (PET1) and 10.7 ± 0.1% (PET2) was obtained (Figure 4).

FIGURE 4

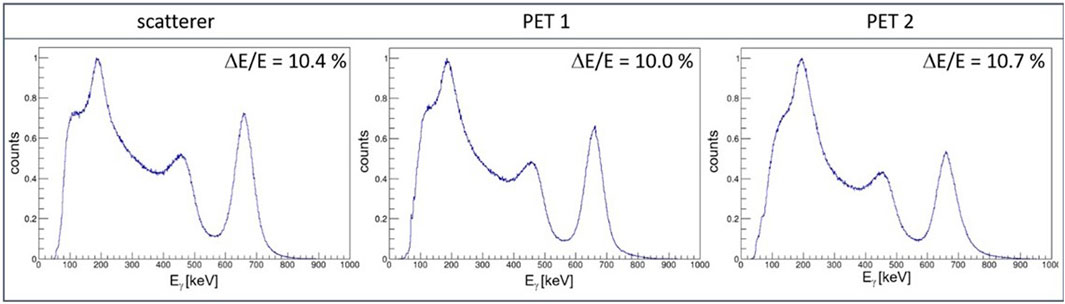
FIGURE 4. Inclusive energy spectrum of all 256 individual crystals obtained from a¹³⁷Cs point source acquired using the scatter (left), PET detector 1 (center) and PET detector 2 (right).

Next, both imaging systems, the Compton camera and the PET assembly, were characterized in dedicated single-mode measurements.

For the Compton camera at a source-to-scatterer distance of 50 mm, geometrically scattering angles between 0 and 39 (36) [34] degrees can be detected if the photon is detected in first (second) [third] layer of the absorber (assuming that both interactions - scattering and absorption - take place in the center if the respective crystal). However, the minimum energy deposit that can be detected (varies from crystal to crystal) of about 50–70 keV also sets a lower limit on detectable scattering angles that is a function of the incoming γ-ray’s energy.

From measurements using only the Compton camera an angular resolution measure (ARM) of 15.7° and 8.2° (at 1,274 keV) was obtained for source-to-scatterer distances of 11 and 50 mm, respectively. The corresponding spatial resolution along the x- and y-dimensions was SR_x/y = 3.7/3.6 mm (for 11 mm distance) and SR_x/y = 6.0/6.1 mm (for 50 mm distance). A source-to-scatterer distance of 50 mm was used in the γ-PET configuration for a point source measurement with the source at an off-center position. The number of reconstructed events was in between 10⁵ and 10⁶ and the image reconstruction was performed using 10 iterations of an ML-EM algorithm. The results of the Compton camera characterization are summarized in Table 1.

TABLE 1

TABLE 1. Summary of the performance characterization (FWHM values) of the Compton camera.

The covered solid angle of the Compton camera is 2.1% and the calculated efficiency (central source position, at 1,274 keV, 50 mm source-to-scatterer) is 2.9 × 10^–5.

Figure 5 displays the observed point spread function of a²²Na point source (1,274 keV) placed at a central position (0,0) and a distance to the scatterer of 11 and 50 mm, respectively.

FIGURE 5

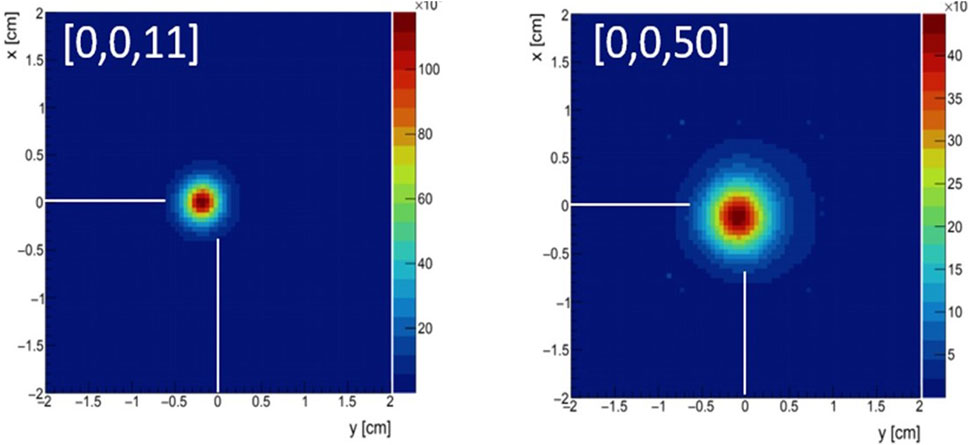
FIGURE 5. Reconstructed images of a²²Na point source located at a distance to the scatterer’s front surface of 11 mm (left) and 50 mm (right). The source was placed centrally along the x and y-dimension (detector plane).

The two GAGG detectors forming the PET detector arrangement was characterized using 511 keV annihilation photons (from a²²Na point source) and the achievable spatial resolution was found to be 2.0 mm using a simple back-projection, and 1.0 mm using 10 iterations of an ML-EM method for image reconstruction.

The PET assembly efficiency (for central source position, after energy selection) was measured to be 1.6 × 10^–4. The solid angle covered by the two GAGG detectors was 2.1%.

B. γ-PET imaging mode

From the 5,400 s measurement of the γ-PET mode only one event could be found after applying all post-processing conditions. Therefore, triple coincidences were synthetically formed by an event-wise combination of Compton and PET events for a proof-of-principle study. This method is only valid for point-like radiation sources and it is ensured that the γ−ray vertices of all emitted photons are identical (within the range a positron can drift before it is thermalized and annihilates). Thus, the dataset used for event reconstruction in γ−PET mode contained four energy values and four 2D position values of γ−ray hits that originated from within the point source volume, but did not necessarily correlate in time (between PET and Compton events).

Point spread functions were reconstructed using PET-only, Compton-only and the γ−PET mode. The width (sigma) of the line-of-response (LOR) was set to 1.6 mm (crystal pitch) and the Compton cone’s width was set to 8.2^°. The number of iterations was reduced compared to the individual PET and Compton camera measurements due to the reduced number of used events and the therefore resulting increase in noise at higher numbers of iterations. All images were reconstructed using three iterations of the ML-EM method.

Using 419 events (i.e. the available number of events after applying the energy cuts) in PET-only mode, a circular point spread function along the y- and z-dimension (PET plane) and a spatial resolution of SR_y = 3.5 mm and SR_z = 3.2 mm (FWHM) was found. Along the x-dimension the PET detector pair is not capable to resolve the point source position due to its limited solid angle coverage and the resulting small angles with which the individual LORs intersect. Figure 6 shows the reconstructed point spread function in the yz-plane and the xy-plane, respectively. Slices through the image along the individual dimensions are shown below. The red lines mark the bin which is plotted below as slice of the plane. The white lines indicate the actual point source position.

FIGURE 6

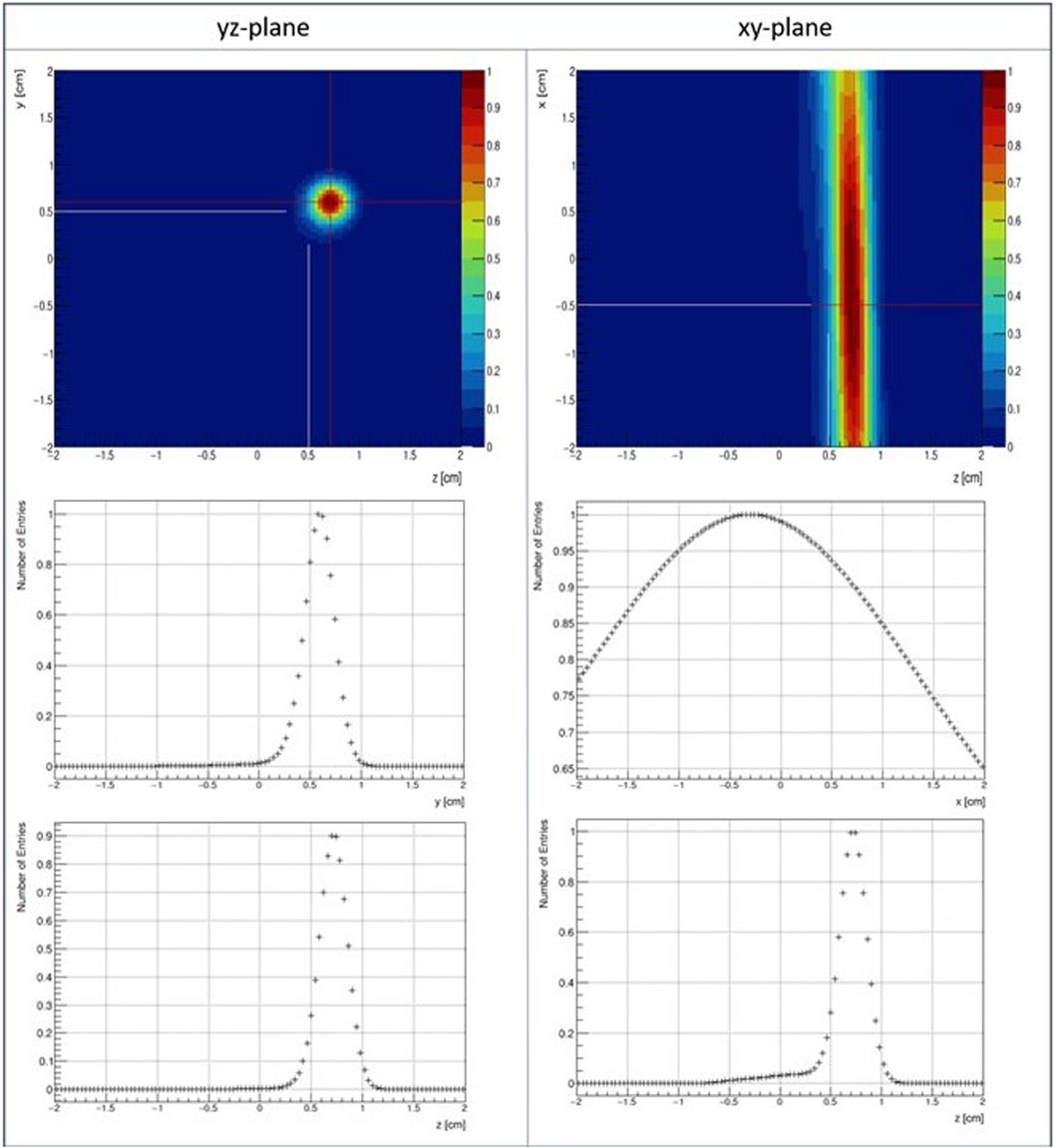
FIGURE 6. Point spread functions of a²²Na point source placed at x = −5 mm, y = 5 mm and z = 5 mm and reconstructed in PET-only mode (top row) and a slice though one bin (indicated by the red lines) along the two respective dimensions (central, bottom row). The intersection of the (extrapolated) white lines indicates the actual source position.

In Compton-only mode around 2000 events were used for the reconstruction (Figure 7). Along the x- and y-dimension (Compton plane) a spatial resolution (FWHM) of SR_x = 14.4 mm and SR_y = 19.3 mm was obtained, respectively. Without detailed knowledge of the Compton camera’s full system matrix no spatial resolution can be obtained along the z-dimension (that marks the distance of the source to the camera).

FIGURE 7

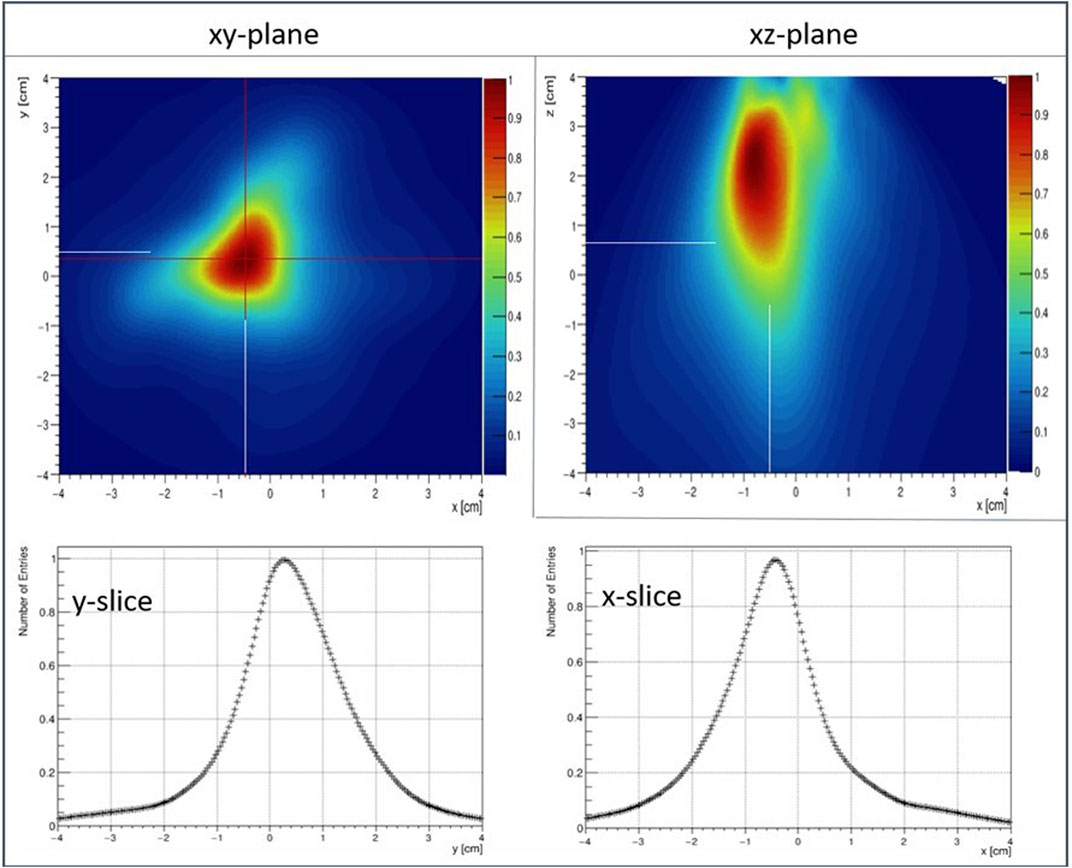
FIGURE 7. Point spread functions of a²²Na point source placed at x = −5 mm, y = 5 mm and z = 5 mm reconstructed in Compton-only mode (top row) and a slice through one bin (indicated by the red lines) along the two respective dimensions (central, bottom row). The intersection of the (extrapolated) white lines indicates the actual source position.

In γ-PET reconstruction mode, the point source could be localized in 3D using only 77 events.

The amount of 77 γ-PET events was used in the present study to characterize the γ-PET imaging performance, however, without performing a systematic study of the tradeoff between event numbers and reconstruction performance.

The obtained spatial resolution was 12.9, 3.9 and 3.3 mm along the x-, y- and z-dimension, which indicates a similar spatial resolution as in PET-only mode (using 418 events) in the PET plane and an improvement of 1.5 mm in the x-dimension. The reconstruction accuracy (distance of reconstructed—true source position) was found to be 2.1 mm (x-dimension), 0.1 mm (y-dimension) and 1.2 mm (z-dimension). Figure 8 shows the reconstructed images of the ²²Na point source in γ-PET mode in the xz- (left), xy- (center) and yz-plane (right). Below the 2D point spread functions, a cut through the bin that contains the distributions’ maximum (indicated by the red lines) is shown for the two respective dimensions.

FIGURE 8

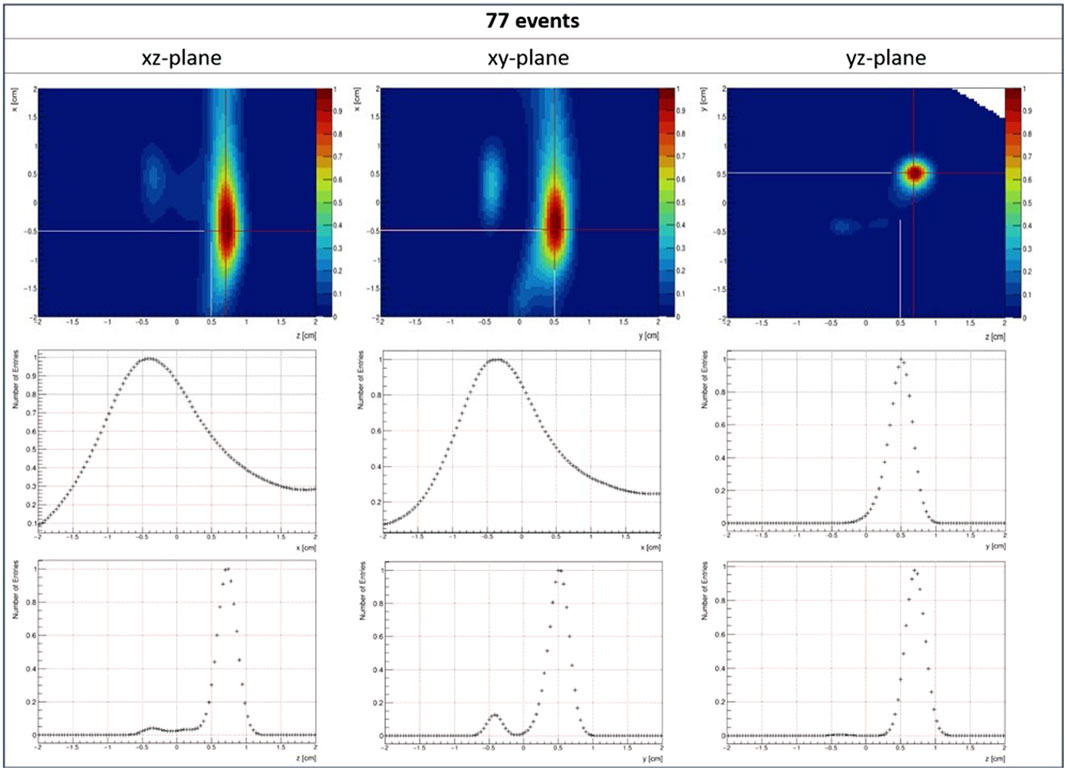
FIGURE 8. Reconstructed image of a²²Na point source located at an off-center position (x = 5 mm, y = −5 mm, z = −5 mm) in the xz-(left), xy-(center) and yz-plane (right). The intersection of the (extrapolated) white lines indicates the source position and the red lines represent the bin for which the 1D projection is shown in the center and bottom row. Furthermore, an artefact that corresponds to the second intersection of the LOR and the Compton cone is visible at the inverse source position (x = 5 mm, y = −5 mm, z = −5 mm) in all three 2D images.

Furthermore, in all image reconstructions in γ−PET mode an artefact at the exact inverse source position (x = 5 mm, y = -5 mm, z = -5 mm) can be observed (see Figure 8), which does not reduce with an increasing number of events used for image reconstruction. Therefore, it is unlikely to originate from noise arising from a too high number of iterations of the ML-EM method, since such an image fragmentation would have to reduce with an increasing number of events. However, it is very likely to be caused by the second intersection of the LOR with the Compton cone. There is only a limited amount of detector combinations in this tight geometry of the prototype camera that can detect PET coincidences of a point source in an off-center position. Also, the orientation of the Compton cones would be very similar. Consequently, a considerable amount of LOR-Compton cone intersections are found in a region which happens to be at [x,y,z] = [5 mm, 5 mm, - 5 mm], corresponding to the inverse source position.

Table 2 summarizes the findings on the image reconstruction in γ−PET mode.

TABLE 2

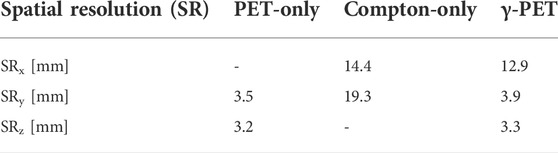
TABLE 2. Summary of the achieved spatial resolution values [FWHM] along the x, y and z-dimension in PET-only, Compton-only and γ-PET imaging mode.

Discussion

The study presented in this work is meant as a first proof-of-concept study that demonstrates the general suitability of the used (SiPM read-out, pixelated scintillator) detector components to be used in a γ-PET prototype. As such it paves the road for more detailed studies in the future, where an upscaling of the number of Compton camera arms is envisaged to mitigate the presently rather limited efficiency. The current accuracy of the positioning of the radioactive point (-like) source of approx. 1 mm can account at least for parts of the observed deviations between the reconstructed and the true source positions. Still, the setup allowed for a test of dedicated image reconstruction algorithms for γ-PET imaging. Here, in order to obtain a detailed understanding of image quality improvements, such as signal-to-noise ratio or reconstruction time (e.g. by the number of iterations), further investigations are needed and were beyond the scope of this work.

The Compton camera of the prototype configuration was designed in an in-line arrangement in order to increase the number of detected photons, which will primarily be scattered in forward angles at energies around 1 MeV. However, an increased ratio of the detector areas between absorber and scatterer of, e.g., 4:1, would result in an increased range of detectable scattering angles. In future studies towards a ring- or sphere-like setup, there are plans to evaluate such area ratios and their impact on the image quality.

Also, an overall increase of the solid angle coverage by the detector arrangement will result in an increased geometrical efficiency, thus allowing to detect suitable rates of true triple-coincidences.

The reconstruction accuracy in the presented prototype also suffers from an imperfect manual source positioning. In an improved system, the authors plan to use a motorized precision stage to position the point source relative to the detector, allowing for higher positioning accuracy (and the ability to apply a line source via a moving point source). The accuracy, however, has no influence on the image resolution (which is given as the FWHM of the point spread function) and the validity of the general proof-of-concept.

The added value of the γ-PET imaging modality can be seen in the capability provided to exploit the full information contained in the emitted photon radiation when using a suitable detection system. Individual (prompt) photons (Compton imaging), coincident photon pairs (PET) or triple coincidences (γ-PET) will allow for deriving a maximum of imaging information from a given emission scenario.

Summary and conclusion

In conclusion, a proof-of-principle study of a γ-PET prototype consisting of 3 segmented GAGG scintillator arrays used as PET detectors and Compton-camera scatterer and a 3-layer depth-of-interaction (DOI)-capable LYSO detector block as Compton-camera absorber was conducted and 3D point source images could be reconstructed using only 77 events.

The low solid angle coverage of the γ−PET system resulted in a triple-coincidence count rate (after energy selection) of only 1—2 count/h. Therefore, events obtained from a single measurement, but triggered in PET-only and Compton-only mode in the post-processing, were combined to obtain a sufficient amount of synthetic triple-coincidence events. Using only 77 events reconstructed in γ−PET mode (via event-wise intersection of the line-of-response and the Compton cone) resulted in a full 3D imaging capability with a spatial resolution similar to the one obtained in PET-only mode (3.9 mm in y-dimension and 3.3 mm in z-dimension) when looking at the PET plane (y-z plane) and 12.9 mm along the x-dimension (i.e. dimension between the two PET detectors). In order to allow for the acquisition and reconstruction of true triple-coincidence events, the here studied γ-PET prototype detector arrangement has to be upgraded by implementing more (at least in total four) Compton camera arms to improve the overall geometrical efficiency.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

TMB performed the measurements and data analysis, assisted and supervised by PGT and KP. VA, MN, GD, MJS, AZ contributed to the image reconstruction. HGK, MN and TY contributed to the DOI detector design. KK provided the GAGG arrays. TMB and PGT prepared the manuscript with contributions from all coauthors.

Funding

This work was supported by the Bayerische Forschungsstiftung, the Alexander von Humboldt Foundation, the ERC Consolidator Grant 725539 SIRMIO, the European Union’s Marie-Skłodowska-Curie Actions Individual Fellowship HIPPOCRATE and the Bavaria California Technology Center (BaCaTec).

Conflict of interest

Author KK is employed by C and A Corporation, Sendai, Japan.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Yoshida E, Tashima H, Nagatsu K, Tsuji AB, Kamada K, Parodi K, et al. Whole gamma imaging: A new concept of PET combined with Compton imaging. Phys Med Biol (2020) 65:125013. doi:10.1088/1361-6560/ab8e89

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Nakano T, Sakai M, Torikai K, Suzuki Y, Takeda S, Noda S, et al. Imaging of ^99mTc-DMSA and ¹⁸F-FDG in humans using a Si/CdTe Compton camera. Phys Med Biol (2020) 65:05LT01. doi:10.1088/1361-6560/ab33d8

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Lang C, Habs D, Parodi K, Thirolf PG. Sub-millimeter nuclear medical imaging with high sensitivity in positron emission tomography using β⁺γ coincidences. J Instrum (2014) 9:P01008. doi:10.1088/1748-0221/9/01/P01008

CrossRef Full Text | Google Scholar

4. Lang C. Design of a Compton camera for medical imaging and characterization of its components. Germany: LMU Munich (2015). Doctoral Dissertation.

5. Grignon C, Barbet J, Bardies M, Carlier T, Chatal J, Couturier O, et al. Nuclear medical imaging using β⁺-γ coincidences from ⁴⁴Sc radio-nuclide with liquid xenon as detection medium. Nucl Instr Methods Phys Res (2007) 571:142–5. doi:10.1016/j.nima.2006.10.048

CrossRef Full Text | Google Scholar

6. Garcia AD, Rubio Rodríguez JA, Pérez Morales JM, Dubois PA, Morales OV, Romeu EA, et al. PET-Compton system comparative evaluation with PET system using Monte Carlo simulation. Nucleus (2012) 51:6–13.

Google Scholar

7. Oger T, Chen WT, Cussonneau JP, Donnard J, Duval S, Lamblin J, et al. A liquid xenon TPC for a medical imaging Compton telescope. Nucl Instr Methods Phys Res Section A: Acc Spectrometers Detectors Associated Equipment (2012) 695:125–8. doi:10.1016/j.nima.2011.12.004

CrossRef Full Text | Google Scholar

8. Donnard J, Chen WT, Cussonneau JP, Duval S, Lamblin J, Lemaire O, et al. Compton imaging with liquid xenon and 44Sc: Recent progress toward 3 gamma imaging nucl. Med Rev (2012) 15:64. doi:10.5603/NMR.2012.0003

CrossRef Full Text | Google Scholar

9. Thirolf PG, Lang C, Parodi K. Perspectives for highly-sensitive PET-based medical imaging using β⁺-γ coincidences. Acta Phys Pol A (2015) A127:1441–4. doi:10.12693/aphyspola.127.1441

CrossRef Full Text | Google Scholar

10. Yamaya T, Yoshida E, Tashima H, Tsuji A, Nagatsu K, Yamaguchi M, et al. Whole gamma imaging (WGI) concept: Simulation study of triple-gamma imaging. J Nucl Med (2017) 58(1):152.

Google Scholar

11. Tashima H, Yoshida E, Wakizaka H, Takahashi M, Nagatsu K, Tsuji AB, et al. 3D Compton image reconstruction method for whole gamma imaging. Phys Med Biol (2020) 65:225038. doi:10.1088/1361-6560/abb92e

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Jin Y, Tanton P, Streicher M, Yang H, Brown S, He Z, et al. Experimental evaluation of a prototype combined PET-Compton imaging system based on 3D position-sensitive CZT detectors for dedicated breast cancer imaging. J Nucl Med (2021) 62(Supplement 1):1129.

Google Scholar

13. Kowalski P, Moskal P, Wislicki W, Raczynski L, Bednarski T, Bialas P, et al. Multiple scattering and accidental coincidences in the J-PET detector simulated using GATE package. Acta Phys Pol A (2015) 127:1505–12. doi:10.12693/APhysPolA.127.1505

CrossRef Full Text | Google Scholar

14. Shimazoe K, Yoshino M, Ohshima Y, Uenomachi M, Oogane K, Orita T, et al. Development of simultaneous PET and Compton imaging using GAGG-SiPM based pixel detectors. Nucl Instr Methods Phys Res (2020) 954:161499. doi:10.1016/j.nima.2018.10.177

CrossRef Full Text | Google Scholar

15. Ogane K, Uenomachi M, Shimazoe K, Kamada K, Takahashi M, Momose T, et al. Development of Compton-PET hybrid imaging of diagnostic and therapeutic nuclides for theranostics. J Nucl Med (2020) 61(Supplement 1):1515.

Google Scholar

16. Uenomachi M, Takahashi M, Shimazoe K, Takahashi H, Kamada K, Orita T, et al. Simultaneous in vivo imaging with PET and SPECT tracers using a Compton-PET hybrid camera. Sci Rep (2021) 11:17933. doi:10.1038/s41598-021-97302-7

PubMed Abstract | CrossRef Full Text | Google Scholar

17.Broadcom Inc. Data sheet - AFBR-S4K33P6425B series (2021).

Google Scholar

18.Broadcom Inc. Data sheet - AFBR-S4K33C025B series (2022). Available at: https://docs.broadcom.com/doc/AFBR-S4K33C0125B-SiPM-DS (Accessed May 18, 2022).

Google Scholar

19. Fitzpatrick T. A Compton camera prototype with gamma-PET imaging capability: From component evaluations to online tests. Germany: LMU Munich (2021). Doctoral Thesis.

20.Hamamatsu Photonics. MPPC (Multi-Pixel photon counter), S14160/14161 series datasheet (2020). Available under: https://www.hamamatsu.com/resources/pdf/ssd/s14160\_s14161\_series\_kapd1064e.pdf (Accessed November, 2021).

Google Scholar

21.PETsys Electronics SA. TOFPET 2c SiPM readout ASIC datasheet (Rev 10) (2019).

Google Scholar

22. Klein O, Nishina Y. Über die Streuung von Strahlung durch freie Elektronen nach der neuen relativistischen Quantendynamik von Dirac. Z Physik (1929) 52:853–68. doi:10.1007/BF01366453

CrossRef Full Text | Google Scholar

23. Zoglauer AC. First light for the next generation of Compton and pair telescopes. Germany: Technical University of Munich (2005). Doctoral Dissertation.

24. Zoglauer AC, Andritschke R, Boggs SE, Schopper F, Weidenspointner G, Wunderer CB. MEGAlib - simulation and data analysis for low-to-medium-energy gamma-ray telescopes. Proc SPIE Int Soc Opt Eng (2008) 7011:70113F. doi:10.1117/12.789537

CrossRef Full Text | Google Scholar

25. Zoglauer AC. MEGAlib - the medium-energy gamma-ray astronomy library website (2021). Available at: https://megalibtoolkit.com/documentation.html (Accessed September, 2021).

Google Scholar

26. Binder T, Kang HG, Nitta M, Schneider F, Yamaya T, Parodi K, et al. Performance evaluation of a staggered three-layer DOI PET detector using a 1 mm LYSO pitch with PETsys TOFPET2 ASIC: Comparison of HAMAMATSU and KETEK SiPMs. Phys Med Biol (2021) 66:125016. doi:10.1088/1361-6560/abfbf3

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Kang HG, Nishikido F, Yamaya T. A staggered 3-layer DOI PET detector using BaSO4 reflector for enhanced crystal identification and inter-crystal scattering event discrimination capability. Biomed Phys Eng Express (2021) 7:035018. doi:10.1088/2057-1976/abf6a8

CrossRef Full Text | Google Scholar

28. Kang HG, Tashima H, Nishikido F, Akamatsu G, Wakizaka H, Higuchi M, et al. Initial results of a mouse brain PET insert with a staggered 3-layer DOI detector. Phys Med Biol (2021) 66:215015. doi:10.1088/1361-6560/ac311c

PubMed Abstract | CrossRef Full Text | Google Scholar