Spatial opinion dynamics incorporating both positive and negative influence in small-world networks

When we consider tipping points of political and social opinions in groups, we often rely on a physics-based opinion dynamics approach. Despite the many studies on simple models, studies on more realistic situations have yet to be done. In this paper, we extend the basic model of opinion dynamics in two ways. The first extension incorporates negative influence between individuals. The second arranges individuals in a small-world network and fixes them in neighborhoods to consider their relationships. Our results show that a consensus tends to result with a higher positive trust ratio in the network, a denser network, and a milder degree of trust between individuals. In a real society, the development of consensus opinions depends on frequent communication, reliable people, and mild opinions. Moreover, we explore the conditions for merging the majority with a minority of individuals who are strongly connected. Our dense city model shows that the opinions of two parties connecting in dense interactions will gradually attract each other, and when a certain threshold is exceeded, those opinions will be integrated at once like a phase transition.

1 Introduction

Opinion dynamics uses social physics techniques to explain how the distribution of different opinions in a group of individuals changes over time. This simple and abstract setting for capturing changing opinions provides a possible theoretical model for many of the challenges facing modern society, from polarized political opinion mechanisms to information diffusion mechanisms in the Internet age.

Research on opinion dynamics forms a major area of sociological research on social influence. [1] mentioned that identifying consensus, diversity, and polarization mechanisms in the dynamics of large-scale social impact is a major scientific issue with a long tradition of lively debate. [2] also added the issue of group polarization and diversification to their list of important open issues in sociology. Flasche et al.’s review study [3] categorized social influence into three models. The first model considers assimilative social influence reproducing consensus, and the second model considers similarity biased influence reproducing clusters or fragmentation. The third one considers repulsive influence showing bi-polarization. In summary, a theoretical approach to social impact can be seen as a journey of finding a turning point in the dynamics of opinion.

There have been many theoretical studies on the dynamics of opinion in recent decades [4–8]. Models of opinion expression have ranged from simple binary models such as the voter model [9–11] to a rich definition space using multi-dimensional continuous approaches [12, 13]. Several features of dynamics have been discovered, such as homogeneity, bipolarity, and polymorphism [4]. [14] theoretically showed the emergent properties of phase transitions and tipping points by focusing on the phase diagram of the opinion dynamics model.

Connections with neighboring disciplines include relationships with external information (mainly in the form of mass media broadcasts) [15], influence and confirmation bias [16], and social psychology topics such as conformity and independence [17]. Although the importance of incorporating real data has been pointed out, the research is still ongoing. For example, a simulation study [18] revealed that filtering leads to strengthening of the echo chamber, while keeping in mind the reality of information society.

Some researchers have focused on the interaction structure of a population in the dynamics of opinion. [19] showed that the time to reach consensus depends on the moments of the degree distribution using the non-conservative analytical framework of the magnetization of a voter model. [20] mentioned that a voter model for a small-world network states that the opinion dynamics settles in a steady state where opinions with different lifespans coexist depending on the size of the system. Thus, their results support the idea that important connection patterns lead to the counter-intuitive conclusion that long-distance connections impede the ordering process.

Under such circumstances, opinion dynamics analysis with consideration of network structures has broken away from the model that assume a complete graph, in which all individuals can freely communicate with each other [21, 22]. These analyses have shown that, unlike in the case of a complete graph, the opinion dynamics operates differently depending on the network structure. Although a simple analytical model of opinion dynamics is sometimes quite important, it often requires careful consideration for application to real-life situations. In particular, when examining the opinion dynamics for people who have various communication channels because of the development of the Internet, it is essential to analyze spatial opinion dynamics. [23] analyzed the effects of interaction structures with a two-dimensional lattice model on homogeneity, polarization, and deadlock via a differential equation using the mean-field approximation, and the results showed the effects of rearrangement and telephoning (i.e., nonlocal interaction).

Here we extend Baumgaertner’s idea to a more realistic situation. We assume that he adopted a two-dimensional lattice graph to imitate physical contact among people in their daily lives. On the other hand, people also have non-physical channels like the Internet to contact others. A random graph is a suitable topology to model that kind of communication style. We believe that real situations lie between these two extreme cases of a lattice graph and a random graph [24]. While we think that a comparison of the two extreme cases is worthwhile, an analysis of the middle case is also important for consideration of more realistic situations. Therefore, in this paper, we consider three types of graphs: a random graph, a two-dimensional lattice graph, and a beta model of a small-world network that was developed by [25].

The degree of other individuals’ influence on one’s opinion is also an important component in the analysis of opinion dynamics. A typical example is the formulation by [26], which simply normalizes the total effect of others on each person to 1 and determines an individual’s own opinion according to the relative degree of influence and the opinions of others. However, their theoretical bounded confidence model always converges over an infinite amount of time, so an-other extension is needed to capture the phenomenon of polarization and divergence [27]. In sociology, many theories have been developed on structures of trust, including Haider’s balance theory [28], which considers not only positive trust relationships but also the effects of negative trust relationships. While traditional opinion dynamics has primarily aimed to capture the dynamism of opinion convergence, the incorporation of negative trust is also quite important for capturing polarized opinions. The effects of negative trust relationships on opinion dynamics have been considered through both agent-based simulation [29] and experimental approaches [30, 31]. [32] built the Trust-Distrust Model to focus on this point and analyzed the effects of distrust on opinion dynamics [33, 34].

In this study, we focus on some specific parameters to analyze opinion dynamics. First, we assume that society involves frequent communication between individuals, and we are thus interested in the effects on opinion dynamics of increased opportunities to communicate with others. Hence, we model a network density parameter (γ) to capture this situation. Second, we also analyze a trust structure characterized by two parameters (δ, θ), where δ indicates the degree of trust and θ indicates the ratio of trustful human relationships.

We adopted an agent-based approach, as in many previous studies [4, 6, 7, 18, 24, 26, 27], because this approach can capture rich network structures and obtain clear results.

As described above, many extensions have been applied to simple theoretical opinion dynamics to handle real-world situations. In this paper, we consider an ex-tended approach to trust structures and spatial applications. Specifically, these two extensions enable analysis of the dynamics in a polarized opinion space. We believe that this extension is essential for capturing real-world phenomena of social divisions.

2 Models

Let us consider a finite number of individuals in a group and let denote that set as N. At a discrete time t, an individual p ∈ N has a one-dimensional opinion I_p(t). The opinion at t = 0 is called the initial opinion. The initial distribution of opinions, I (0), is homogeneous. That is, for all p ∈ N, I_p(0) is obtained from a probability distribution consisting of a uniform finite interval set [ − κ, κ].

Each individual’s opinion changes through interaction with other people at each time. Accordingly, we model the interaction structure between individuals. Let L_pq = 1 indicate that individual p is influenced by individual q, whereas L_pq = 0 indicates no influence of q on p. Note that the interaction structure does not guarantee the symmetry property; that is, in our model, L_pq = L_qp does not always hold for any p, q ∈ N [24]. In addition, let L_pp = 0. For the individuals in N, their opinions change according to the degree of trust between interacting individuals. The degree of trust represents the strength of influence that changes an opinion, and it is denoted as $T_{pq}\in \mathfrak{R}$ for any p, q ∈ N. If T_pq > 0, then individual p trusts individual q, and it is easier for p’s opinion to approach q’s opinion. On the other hand, our model also considers the case of T_pq < 0. In this case, individual p distrusts individual q, and p’s opinion is more likely to deviate from qes opinion. In this model, L = (L_pq) and T = (T_pq) are invariant through time. The values of T_pq are independently and identically distributed. For all p, q ∈ N, T_pq denotes the degree to which p trusts q, and it is obtained from a probability distribution consisting of a uniform finite interval set [0, δ] with probability θ or [ − δ, 0] with probability 1 − θ. In our approach, we investigate the existence of distrust and the effect of the interaction structure on the system by comparing models with different definitions of T and L.

The opinion dynamics of individual p at time t + 1 is expressed by

$I_p\left(t+1\right)=I_p\left(t\right)+\mathrm{\Delta }{I}_p\left(t\right),(1)$

where

$\begin{array}{ccc}\hfill \mathrm{\Delta }{I}_p\left(t\right)& =\hfill & \mathrm{\Sigma }{L}_{pq}{R}_{pq}\left(t\right),\hfill \\ \hfill R_{pq}\left(t\right)& =\hfill & T_{pq}\mathrm{\Theta }\left(I_q\left(t\right)-I_p\left(t\right)\right)\left(I_q\left(t\right)-I_p\left(t\right)\right),\text{\hspace{0.17em}and\hspace{0.17em}}\hfill \\ \hfill \mathrm{\Theta }\left(x\right)& =\hfill & 1/\left(1+\exp \left\{\alpha \left(|x|-\beta \right)\right\}\right).\hfill \end{array}(2)$

The sigmoid function Θ is used here to eliminate the effect of an opinion gap that is too large [19, 26]. The parameters α and β must be positive. The parameter β is related to the magnitude of the distance between opinions: the larger this value is, the more distant opinions can influence each other.

First, we consider the following three graphs for the interaction structure.

L_r(γ): A random graph, in which Prob (L_pq = 1) = γ for all p, q ∈ N.

L₂: A two-dimensional lattice graph, in which individuals are fixedly arranged on a torus-shaped two-dimensional lattice such that L_pq = 1 between individuals in a Von Neumann neighborhood and L_pq = 0 otherwise.

L_s(β^SW): A small-world network that is initially equivalent to L₂. Then, for each link in the graph, its end node is changed randomly with a probability of β^SW.

Note that the third graph effectively includes the other two graphs, because L_s (0) corresponds to L₂ and L_s (1) almost corresponds to L_r (4/(N − 1)). Precisely, each node of L_s (1) has four outbound links, while the expected number of outbound links for each node in L_r (4/(n − 1)) is four. By analyzing a small-world network, we may obtain results that apply to more realistic situations, as well as the two extreme cases of a random graph and a lattice graph.

The analysis of behavior in polarized systems is very interesting because a spatial structure is introduced into opinion dynamics. Here, we analyze the opinion dynamics when a majority having larger opinion distributions is mixed with a minority that is spatially strongly connected. Let us consider the following dense city model.

L_c: A dense city model with a group consisting of individuals (i.e., inhabitants on the city) that are fixedly arranged in a square two-dimensional lattice, along with other individuals (i.e., those outside the city). Let N′ be the set of inhabitants on the city. For any individuals p, q ∈ N′ between individuals in a Von Neumann neighborhood, Prob (L_pq = 1) = 1 and T_pq = δ′; otherwise, Prob (L_pq = 1) = γ and the confidence structure is T (θ, δ), which is of the L_r type. The initial opinion distribution, I (0) follows a probability distribution consisting of a uniform finite interval set of [κ₁, κ₂] when p ∈ N′, or [ − κ, κ] otherwise.

3 Results

In opinion dynamics, the notion of whether various initial distributions of opinions converge or diverge is an important, basic indicator. Accordingly, we consider the transition of the degree of convergence, C_t = ΣΣ|I_p(t) − I_q(t)|/ΣΣ|I_p(0) − I_q (0)|, at time t.

As shown in Figure 1, depending on the parameters, our model captures both (a) the case of diverging opinions and (b) the case of converging opinions, in which a consensus is formed.

FIGURE 1

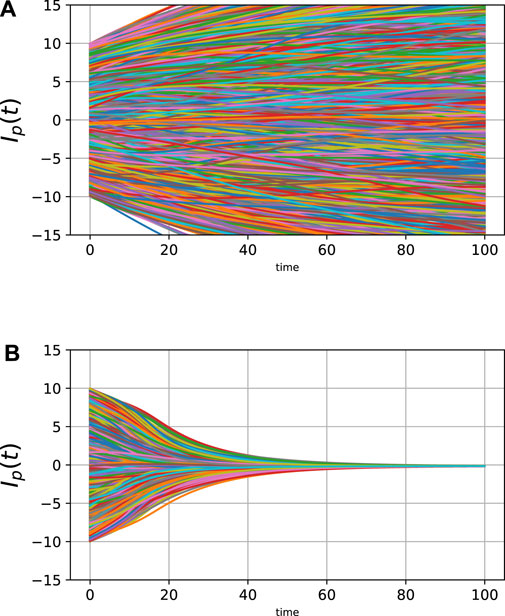
FIGURE 1. Two examples of changes in an opinion distribution: (A) opinions diverge and a consensus is not built, and (B) opinions converge and a consensus is built. Each panel shows the changes in the values of all individuals’ opinions in a particular simulation result using the L_r type (random graph) of interaction structure. The horizontal axis indicates the simulation time, and the vertical axis indicates the opinion value. Here, we set the parameters as (|N|, α, β, δ, γ, κ) = (1,600, 1, 10, 0.002, 0.1, 10), with θ = 0.3 in (A) and θ = 0.8 in (B).

Figure 2 shows the degree of convergence of opinions in the random graph. Basically, it can be seen that the higher the ratio of positive trust (favorability) relationships in the trust structure, the easier it is for opinions to converge and a consensus to be reached. Simply put, the divergence or convergence of opinions can almost be predicted by whether the value of C₁₀₀ exceeds or falls below 1, respectively. In other words, if the value is below 1, the opinion dynamics converge eventually, and they diverge otherwise. We thus regard the value of 1 as a tipping point or critical point of the system.

FIGURE 2

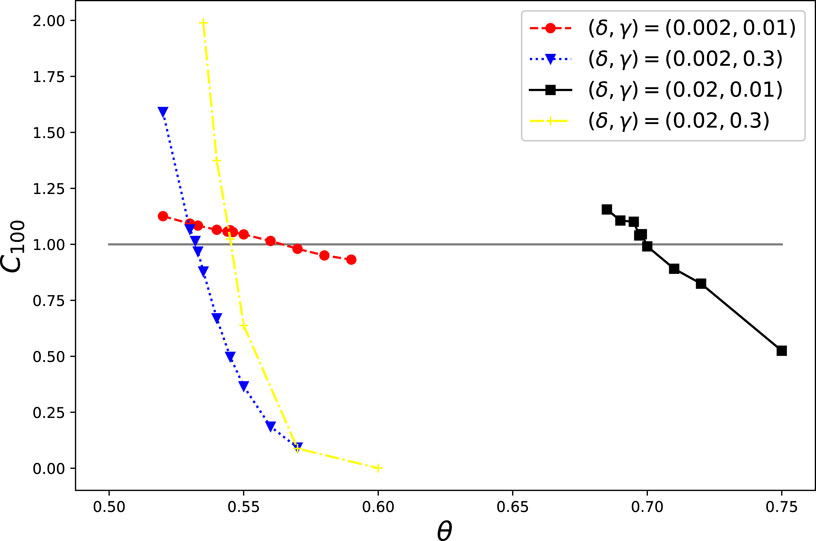
FIGURE 2. Effects of the network density (γ) and trust structure (θ, δ) on the convergence of opinions in the L_r type (random graph) of interaction structure. Here, the parameters were (|N|, α, β, κ) = (1,600, 1, 10, 10), and the four cases of (γ, δ) = (0.01, 0.002) (0.3, 0.002) (0.01, 0.02), and (0.3,0.02) are shown. The horizontal axis indicates the value of θ, while the vertical axis indicates the average value of C₁₀₀ for 10 trials with different random seeds.

Figure 2 shows that opinion convergence depends on the interaction effect of the network density and the initial opinion distribution. When the initial opinion distribution is mild (δ = 0.002), a denser network (higher γ) makes it easier for opinions to converge. This tendency keeps the case with extreme initial opinion distribution (δ = 0.02). Additionally, in a constant-density network, a milder initial opinion distribution (smaller δ) makes it easier for opinions to converge. To summarize these features, we can extract two conditions for convergence and consensus formation: 1) a high proportion of positive trust relationships in the trust structure, 2) a denser network, and 3) a mild initial opinion distribution. Regarding the reasons for these conditions, if the initial opinion distribution is mild, opinions between any two individuals are close, and convergence is easy. Moreover, if the network is dense, individuals promote more active exchange of opinions, which may increase the likelihood of convergence.

Next, we observe the effect on convergence of increasing or decreasing the level of positive trust relationships in the trust structure. By focusing on the slope of each case shown in Figure 2, it can be seen that the denser the network, the greater the influence of a slight increase or decrease in the level of trust relationships on the degree of convergence. Interestingly, the convergence lines for denser networks (the blue and yellow plots in Figure 2) cut across the tipping point (= 1.0) on the smaller value of the rate of positive trust relationships (σ) at a steep angle. Concretely, in the case of δ = 0.002, the values across the tipping point are about 0.57 and 0.53 for γ = 0.01 and 0.3, respectively. Moreover, in the latter case, the convergence degree drastically declines to below 0.7 when σ changes to 0.54 from 0.53. These results show that it is easier for a denser network to reach opinion convergence even with a low rate of positive trust relationships, if a small number of relationships can be made positive.

As in the above discussion, it can be inferred that a dense network structure tends to cause attraction between people with similar opinions and repulsion between people with disagreements. From this result, we obtain a fourth condition for opinion convergence: 4) the denser the network structure, the greater the impact that a slight change in positive trust relationships in the trust structure has on whether the system saturates or diverges. Accordingly, the level of positive trust relationships has a strong influence on whether opinions converge.

Next, we analyze the effect of the interaction structure on the degree of opinion convergence. Figure 3 shows the degree of opinion convergence in two graphs having almost the same expected number of links but different topologies. When the initial opinion distribution is mild (δ = 0.002), the results are almost the same between the random graph and the two-dimensional lattice graph. This indicates that the degree effect (the number of interactions between individuals) has a greater effect than the network structure on opinion convergence. This tendency does not change if the initial opinion distribution becomes larger, unless it becomes extreme (δ = 0.02, 0.04), in which case the interaction structure’s effect becomes non negligible. Specifically, the two-dimensional lattice graph tends to have stricter conditions for convergence (ratio of positive trust relationships) in the extreme cases. In this graph, interaction relationships exist only between adjacent individuals, so the distance between two individuals strongly depends on their positional relationship in the graph. Accordingly, the distance between any two individuals is likely to be shorter in a random graph than in a two-dimensional lattice graph and we can infer that the latter graph is a disadvantageous environment for opinion convergence.

FIGURE 3

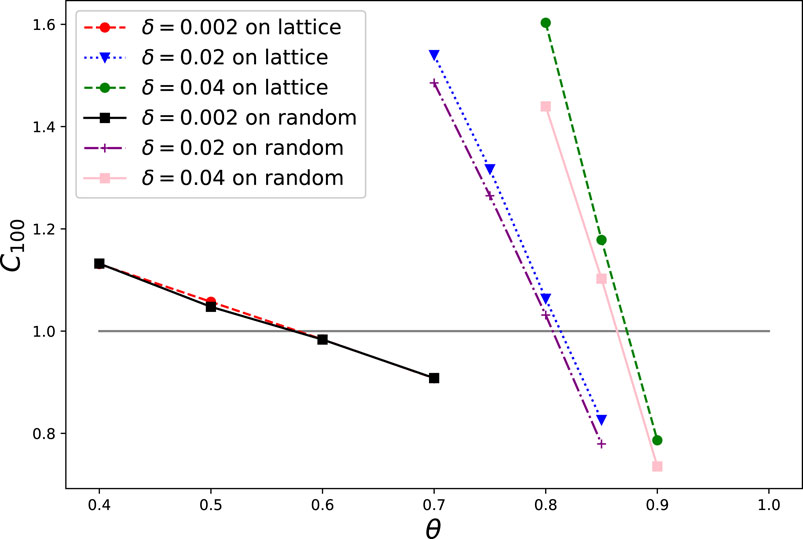
FIGURE 3. Effect of the confidence structure (θ, δ) on the convergence of opinions in the L₂ (two-dimensional lattice graph) and L_r (random graph) types of interaction structure. Because the degree of each individual in the L₂ graph is 4, the parameters were adjusted so that the expected degree in the L_r was also 4. Here, the parameters were (|N|, α, β, κ, γ) = (1,600, 1, 10, 10, 0.0025). The cases of δ = 0.002, 0.02, and 0.04 are shown for each structure type. The horizontal axis indicates the value of θ, and the vertical axis indicates the average value of C₁₀₀ for 10 trials with different random seeds.

For application to more realistic situations, we analyze a small-world network. Figure 4 shows boxplots of C₁₀₀ with different values of β^SW, indicating that the degree of convergence monotonically decreases with β^SW. This result suggests that the effects of the small-world topology lie between those of a random graph and a lattice graph. Note that the influence of the random seeds in the simulation was nonnegligible. The parameter settings were carefully tuned around the tipping point (= 1.0), and thus a slight change in either the trust relationship or the initial opinion distribution may have an essential influence on the opinion dynamics.

FIGURE 4

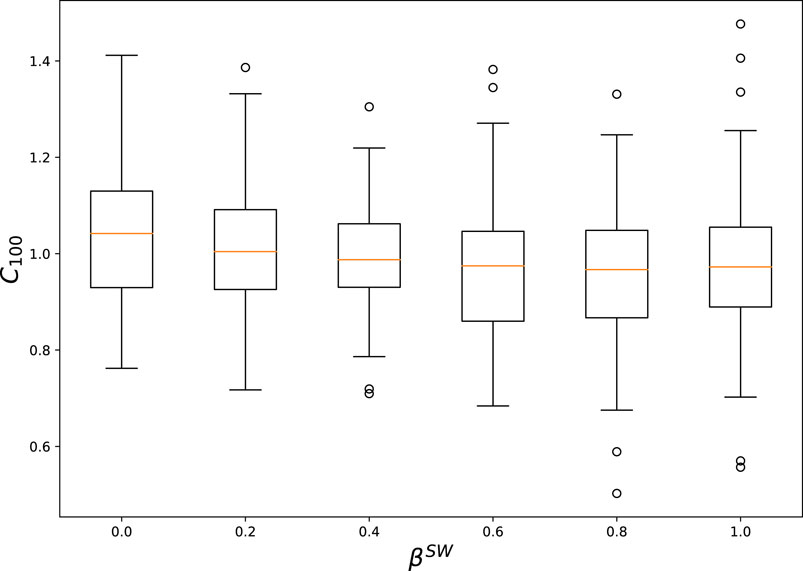
FIGURE 4. Boxplots of the degree of convergence, C₁₀₀ for different values of β^SW. Each boxplot represents 100 trials with different random seeds. Here, the parameters were (|N|, α, β, κ, θ, δ) = (400, 1, 10, 5, 0.86, 0.04). For the difference between the population means with β^SW = 0 and β^SW = 1, the level of significance from Student’s t-test was 0.001243, indicating 1% significance.

Figure 5 shows the simulation results for the dense city model, which show how consensus building occurs when the size of the city and the minority opinion distribution are fixed. If the effect of the random network is low ((a), γ = 0.01), the opinions of the majority outside the city do not converge but instead diverge, while the opinions of the minority on the city do not change. The behavior varies with the effect of the random network. When the effect is moderate ((b), γ = 0.2 and (c), γ = 0.5), the majority gradually becomes closer to the minority while remaining diverged, and the minority also becomes closer to the majority. Because our master equation uses a sigmoid function, when the cutoff effect due to the dissociation of opinions is canceled, it can be seen that the opinions converge at once like a phase transition. For example, consider the performance at time from around 200 to 300 in the left graph of panel (b): the opinions of several citizens outside the island become close to those of the island’s inhabitants. This mechanism is a key factor to understand. When the effect of the random network is high ((c), γ = 0.5), the majority opinions converge first, but the majority and the minority are attracted to each other over a long period of time and eventually converge. This result reveals interesting insights into the case of a consensus reached between polarized populations. If there is a trust structure or interaction structure that attracts the opinions of both parties to some extent, the centers of gravity of each party will gradually attract each other, and when a certain threshold is exceeded, the opinions of the group will be integrated at once like a phase transition.

FIGURE 5

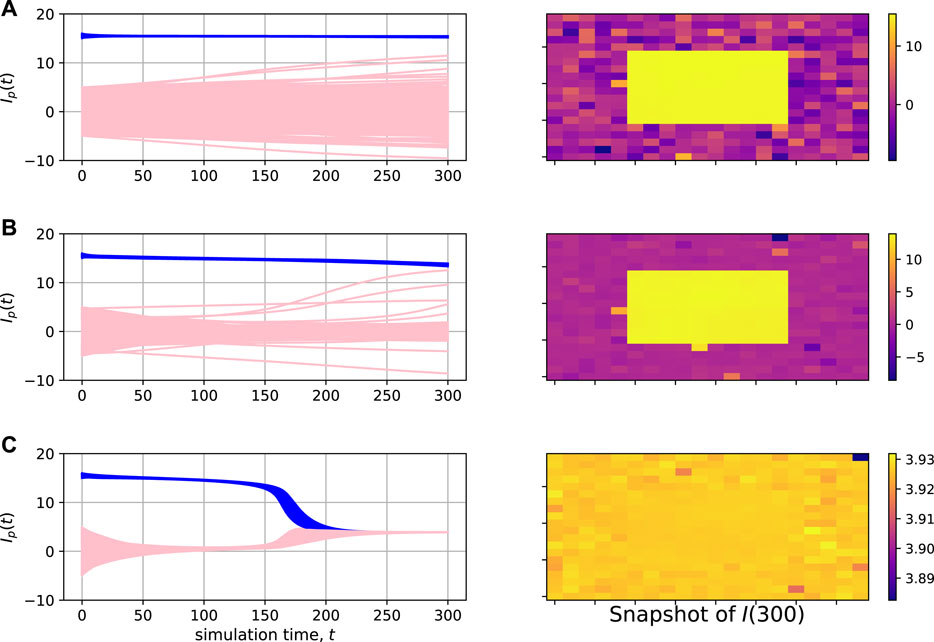
FIGURE 5. Opinion dynamics in the dense city model. Each panel shows the result of a simulation trial. The panels on the left show the changes in the opinions of all individuals over the 300 periods. The opinions of the city inhabitants are plotted in blue, while those of the individuals are plotted in pink. The panels on the right show snapshots of the opinions of individuals mapped in a two-dimensional grid at the 300th period. Here, the parameters were (|N|, α, β, θ, δ) = (400, 1, 10, 0.7, 0.002) and (|N′|, κ, κ₁, κ₂, δ′) = (100, 5, 15, 16, 0.04), with (A) γ = 0.01, (B) γ = 0.2, and (C) γ = 0.5.

It is trivial that a group’s opinions converge after an infinite amount of time, even in a polarized, if the group has a trust relationship in which opinions are attracted to each other. This has been pointed out since the study of the bounded confidential model [26], but it is not always obvious what kind of dynamics will appear until the opinions converge. Hence, Figure 6 shows the effect of a particular parameter (β) on the convergence time. Basically, when the opinions of both parties are too far apart, they have little effect on each other regardless of the trust relationship, but the influence is not zero. As the tolerance becomes smaller (β), it takes exponentially longer for the system to reach convergence. This suggests that even a polarized population may be in a pseudo-stable state in the middle of a long convergence process. Of course, we must note that this result a consequence of the simple assumptions of our theoretical model; in reality, it might be natural that an event causes the parameter value to change over a long simulation time.

FIGURE 6

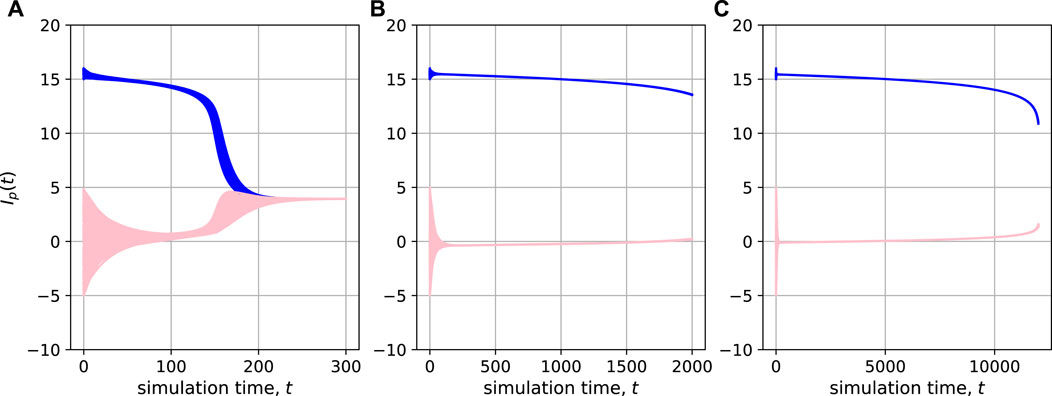
FIGURE 6. Effect of the distance of opinions on the opinion dynamics in the dense city model. Each panel shows the result of a simulated time series of the opinions of all individuals during the simulation period. The opinions of the city inhabitants are plotted in blue, while those of the individuals outside the city are plotted in pink. Note that the simulation period is different for each panel. Here, the parameters were (|N|, α, θ, δ, γ) = (400, 1, 0.7, 0.002, 0.5) and (|N′|, κ, κ₁, κ₂, δ′) = (100, 5, 15, 16, 0.04), with (A) β = 10, (B) β = 8, and (C) β = 6.

4 Discussion

In this paper, we relaxed the basic assumptions of opinion dynamics and conducted an analysis closed to real-world social structures like the internet society. For this analysis, we extended from an interaction structure such as a simple complete graph and examined a two-dimensional lattice graph and a small-world network. We also extended the trust structure from a model dealing only with positive trust to allow negative trust, as well.

Through simulation with the models, we gained the following insights. First, we extracted the basic conditions under which consensus building is likely to occur. A consensus tends to result with a higher positive trust ratio in the network (θ), a denser network (γ), and a milder degree of trust between individuals (δ). Equivalently, in a real society, the development of consensus opinions depends on reliable people, frequent communication, and mild opinions. These findings make intuitive sense and are supported by empirical and theoretical evidence. For example, the social influence theory of ([35]) assumed that the degree of social influence corresponds to the number of other influencers. [36] showed that the participants in his experiment were more susceptible to the influence of more trusted advisors, and that the weight of the advice decreased with increasing distance from the initial opinion. The experiment of [37] showed the effect of social influences in promoting convergence of opinion.

It is important to distinguish whether a system of opinion dynamics converges and forms a consensus or diverges. In that regard, for a complete graph, [32] hypothesized that the proportion of positive trust relationships in a trust structure converges when a threshold is exceeded and diverges otherwise. They estimated a threshold of 55%. In our simulation analysis, we could systematically understand what parameters are required and how the threshold changes in various networks including a random graph, a lattice graph, and a graph of a small-world network.

Compared with the two extreme cases of a random graph and a lattice graph, the topology of the small-world network seems to reflect a realistic situation. People communicate both within their neighborhoods and with more distant people. However, Figure 4 shows that the degree of convergence of the opinion dynamics is estimated to lie between the two extreme cases, regardless of the value of β^SW in a real situation.

By using the spatial opinion dynamics model, it is possible to perform dynamic analysis of groups whose opinions are polarized. Here, we assumed that a minority group was located on a dense city and had a lattice structure with opinions that were far from those of the majority then, we simulated how that group and the majority changed their opinions. Our results show that if there is a trust structure or interaction structure that attracts the opinions of both parties to some extent, then the centers of gravity of each group’s opinions will gradually attract each other; furthermore, when a certain threshold is exceeded, the groups’ opinions will be drastically integrated like a phase transition.

As several studies have shown, a positive-negative influence model may promote so-called bipolarization [38, 39]. In our current analysis, we sought to show more fundamental phenomena with respect to opinion dynamics by introducing negative influence and structural situations; thus, analysis of bipolarization will be a future extension.

Here, however, we mention several important aspects that point to that future work. [38] revealed that the introduction of negative interactions eventually facilitates balance as taught by balance theory, after an initial unbalanced state. Negative relationships are not favored in sustainable interactions, and thus, such interactions may be drastically diminished sooner or later by disconnecting a relationship or reaching a far distance of opinion. In our model, the trust relationship between agents is set randomly and then fixed, making it hard for our simulation to reproduce a bipolarization phenomenon. Generally, however, a trust relationship between people may change, especially when it strongly depends on the frequency of interactions. If we extend our model in such a direction, we will find a bipolarization that is implied by the current model, as shown in Figure 6. In addition, as [39] mentioned, the formalization of bi-polarization during opinion evolution will require a novel model for networks of agents with bi-directional bounded thresholds for studying the evolution of opinion dynamics.

Because our analysis was based on a specific parameter set, a more systematic study will be an important research topic in the future. Moreover, some of the time-invariant model parameter settings will provide meaningful extensions. Figure 6 shows the effect of changes in a certain parameter on the convergence time, but it will be necessary to consider other parameter changes, as well. For example, the variable T = (T_pq) indicating the trust structure was given as a constant in this paper. However, it may be natural that interactions and changes in opinion are affected by certain events, and it would thus be useful to analyze the coevolution of trust dynamics as well as opinion dynamics.

We analyze small-world networks to apply them to more realistic situations, but these networks have some limitations. One is that each node has essentially the same number of links. We estimate that heterogeneity of link size has a significant impact on simulation performance. We do not apply flexibility in this regard because our focus is on the mobility of real people’s links, like in a small-world network. In the real world, however, influencers form hubs with many links, while others are isolated in the network. To address this issue, we will need to consider other topologies, including a scale-free network, and future extensions will be welcome.

In this study, we use a simple opinion space to ensure that we can analyze the mechanisms of our simulation results. Whereas this model covers the convergence and divergence of two different opinions, real opinions that emerge in society result from integration of multifaceted value judgments which often causes two or more opinions to become divided. In this model, however, opinion is polarized in one dimension, which is too simplistic to reflect reality. This point will also require expansion in the future.

Analysis of the same model with a differential equation system will be another future extension. Because we adopted an agent-based approach, our model used a difference equation system. However, human opinion dynamics is asynchronous in real cases. Although we think that this asynchronicity is not crucial, it will be necessary to confirm this point.

Because we do not perform sensitivity analysis here, we have shown just a few cases with specific parameters. However, this is an abstract model, so the numbers themselves are not especially meaningful. Accordingly, we show the results for general characteristics such as the slope of the graph, and we think that the current version is sufficient for testing such general findings. Of course, a more rigorous analysis will be welcome in the future.

The objective of this paper was to explore conditions with respect on convergence and divergence using an extended opinion dynamics model considering the effects of untrustful human relationship and spatial interaction structure. To do so, we introduced several parameters including a network density parameter (γ), two trust structure parameters (δ: the degree of trust, θ: the ratio of trustful human relationships), and an interaction structure parameter (β^SW). According to our agent-based simulations, a consensus tends to result with a higher positive trust ratio in the network, a denser network, and a milder degree of trust between individuals. Especially, the degree of consensus is highly sensitively affected by the degree of trust. Moreover, we show that the opinions of two parties connecting in dense interactions will gradually attract each other, and when a certain threshold is exceeded, those opinions will be integrated at once like a phase transition. We conclude that our extended model is a useful tool for exploring convergence conditions on opinion dynamics.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

All authors conceived the study, developed the model, analysed the results, and discussed the results. IO wrote the manuscript.

Funding

This research was funded by JSPS KAKENHI Grant Numbers 19H02376, 20K20651, 21H01568, and 21KK0027.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Mason WA, Conrey FR, Smith ER. Situating social influence processes: Dynamic, multidirectional flows of influence within social networks. Pers Soc Psychol Rev (2007) 11(3):279–300. doi:10.1177/1088868307301032

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Bonacich P, Lu P. Princeton and Oxford. Princeton University Press (2012).

Google Scholar

3. Flache A, Mäs M, Feliciani T, Chattoe-Brown E, Deffuant G, Huet S, et al. Models of social influence: Towards the next frontiers. J Artif Soc Soc Simul (2017) 20(4):2. doi:10.18564/jasss.3521

CrossRef Full Text | Google Scholar

4. Jager W, Amblard F. Uniformity, bipolarization and pluriformity captured as generic stylized behavior with an agent-based simulation model of attitude change. Comput Math Organ Theor (2005) 10:295–303. doi:10.1007/s10588-005-6282-2

CrossRef Full Text | Google Scholar

5. Salzarulo L. A continuous opinion dynamics model based on the principle of meta- contrast. J Artif Societies Soc Simulation (2009) 9(1):13.

Google Scholar

6. Kondrat G, Sznajd-Weron K. Spontaneous reorientations in a model of opinion dynamics with anticonformists. Int J Mod Phys C (2010) 21(4):559–66. doi:10.1142/s0129183110015312

CrossRef Full Text | Google Scholar

7. Sîrbu A, Loreto V, Servedio V, Tria F. Opinion dynamics with disagreement and modulated information. J Stat Phys (2013) 151(1-2):218–37. doi:10.1007/s10955-013-0724-x

CrossRef Full Text | Google Scholar

8. Sîrbu A, Loreto V, Servedio V, Tria F. Opinion dynamics: Models, extensions and external effects. In: L Vea, editor. Participatory sensing, opinions and collective awareness, understanding complex systems. Cham: Springer (2017). p. 363–401.

Google Scholar

9. Frachebourg L, Krapivsky PL. Exact results for kinetics of catalytic reactions. Phys Rev E (1996) 53(4):R3009–12. doi:10.1103/physreve.53.r3009

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Biswas S, Sen P. Model of binary opinion dynamics: Coarsening and effect of disorder. Phys Rev E (2009) 80:027101. doi:10.1103/physreve.80.027101

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Nyczka P, Sznajd-Weron K, Cis J. Phase transitions in theq-voter model with two types of stochastic driving. Phys Rev E (2012) 86(1):011105. doi:10.1103/physreve.86.011105

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Pineda M, Toral R, Hernández-García E. Noisy continuous-opinion dynamics. J Stat Mech (2009) 2009:P08001. doi:10.1088/1742-5468/2009/08/p08001

CrossRef Full Text | Google Scholar

13. Vaz Martins T, Pineda M, Toral R. Mass media and repulsive interactions in continuous-opinion dynamics. EPL (2010) 91(4):48003. doi:10.1209/0295-5075/91/48003

CrossRef Full Text | Google Scholar

14. Galam S, Cheon T. Tipping points in opinion dynamics: A universal formula in five dimensions. Front Phys (2020) 8:566580. doi:10.3389/fphy.2020.566580

CrossRef Full Text | Google Scholar

15. Pineda M, Buendia G. Mass media and heterogeneous bounds of confidence in continuous opinion dynamics. Physica A: Stat Mech its Appl (2015) 420(15):73–84. doi:10.1016/j.physa.2014.10.089

CrossRef Full Text | Google Scholar

16. Allahverdyan A, Galstan A. Opinion dynamics with confirmation bias. PLoS ONE (2014) 9(7):e99557. doi:10.1371/journal.pone.0099557

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Sznajd-Weron K, Tabiszewski M, Timpanaro A. Phase transition in the sznajd model with independence. EPL (2011) 96(4):48002. doi:10.1209/0295-5075/96/48002

CrossRef Full Text | Google Scholar

18. Perra N, Rocha L. Modelling opinion dynamics in the age of algorithmic personalisation. Sci Rep (2019) 9:7261. doi:10.1038/s41598-019-43830-2

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Sood V, Redner S. Voter model on heterogeneous graphs. Phys Rev Lett (2005) 94(17):178701. doi:10.1103/physrevlett.94.178701

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Castellano C, Vilone D, Vespignani A. Incomplete ordering of the voter model on small-world networks. Europhys Lett (2003) 63(1):153–8. doi:10.1209/epl/i2003-00490-0

CrossRef Full Text | Google Scholar

21. Benczik I, Benczik S, Schmittmann B, Zia R. Opinion dynamics on an adaptive random network. Phys Rev E (2009) 79:046104. doi:10.1103/physreve.79.046104

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Oestereich A, Pires M, Crokidakis N. Three-state opinion dynamics in modular networks. Phys Rev E (2019) 100:032312. doi:10.1103/physreve.100.032312

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Baumgaertner B, Fetros P, Krone S, Tyson R. Spatial opinion dynamics and the effects of two types of mixing. Phys Rev E (2018) 98:022310. doi:10.1103/physreve.98.022310

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Gandica Y, del Castillo-Mussot M, Vázquez G, Rojas S. Continuous opinion model in small world directed networks. Physica A: Stat Mech its Appl (2010) 389:5864–70. doi:10.1016/j.physa.2010.08.025

CrossRef Full Text | Google Scholar

25. Watts DJ, Strogatz SH. Collective dynamics of ’small-world’ networks. Nature (1998) 383(6684):440–2. doi:10.1038/30918

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Hegselmann R, Krause U. Opinion dynamics and bounded confidence models, analysis, and simulation. J Artif Societies Soc Simulation (2002) 5(3):2.

Google Scholar

27. Kurmyshev E, Juàrez H, González-Silva R. Dynamics of bounded confidence opinion in heterogeneous social networks: Concord against partial antagonism. Physica A: Stat Mech its Appl (2011) 390(16):2945–55. doi:10.1016/j.physa.2011.03.037

CrossRef Full Text | Google Scholar

28. Heider F. Attitudes and cognitive organization. J Psychol (1946) 21:107–12. doi:10.1080/00223980.1946.9917275

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Radillo-Díaz A, Pérez L, Del Castillo-Mussot M. Axelrod models of social influence with cultural repulsion. Phys Rev E (2009) 80(6):066107. doi:10.1103/physreve.80.066107

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Takács K, Flache A, Mäs M. Discrepancy and disliking do not induce negative opinion shifts. PLoS ONE (2016) 11(6):e0157948. doi:10.1371/journal.pone.0157948

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Flache A. About renegades and outgroup haters: Modeling the link between social influence and intergroup attitudes. Adv Complex Syst (2018) 21:1850017. doi:10.1142/s0219525918500170

CrossRef Full Text | Google Scholar

32. Ishii A, Kawahata Y. Opinion dynamics theory for analysis of consensus formation and division of opinion on the internet. In: Proceedings of the 22nd asia pacific symposium on intelligent and evolutionary systems (IES2018) (2018). p. 71–6.

Google Scholar

33. Ishii A. Opinion dynamics theory considering trust and suspicion in human relations. In: D Morais, A Carreras, A De Almeida, and R Vetschera, editors. Lecture notes in business information processing 351, group decision and negotiation: Behavior, models, and support. Springer (2019). p. 193–204.

CrossRef Full Text | Google Scholar

34. Ishii A, Okano N, Nishikawa M. Social simulation of intergroup conflicts using a new model of opinion dynamics. Front Phys (2021) 9:640925. doi:10.3389/fphy.2021.640925

CrossRef Full Text | Google Scholar

35. Latané B. The psychology of social impact. Am Psychol (1981) 36(4):343–56. doi:10.1037/0003-066x.36.4.343

CrossRef Full Text | Google Scholar

36. Yaniv I. Receiving other people’s advice: Influence and benefit. Organizational Behav Hum Decis Process (2004) 93(1):1–13. doi:10.1016/j.obhdp.2003.08.002

CrossRef Full Text | Google Scholar

37. Lorenz J, Rauhut H, Schweitzer F, Helbing D. How social influence can undermine the wisdom of crowd effect. Proc Natl Acad Sci U S A (2011) 108:9020–5. doi:10.1073/pnas.1008636108

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Aghbolagh HD, Zamani M, Chen PZS. Balance seeking opinion dynamics model based on social judgment theory. Physica D: Nonlinear Phenomena (2020) 403:132336. doi:10.1016/j.physd.2020.132336

CrossRef Full Text | Google Scholar

39. Liu S, Guan X, Luo S, Xia H. Consensus, bi-polarization and multiformity in opinion dynamics with bidirectional thresholds, 2005 (2020). p. 04948. arXiv preprint.

Google Scholar