Generation of the Anomalous Vortex Beam by Spiral Axicon Implemented on Spatial Light Modulator

The anomalous vortex beam (AVB), whose paraxial local topological charge varies with propagation, has potential applications in quantum information, laser beam shaping, and other fields. However, there are currently no efficient optical devices to generate AVBs. In this paper, we propose an efficient pure-phase device called spiral axicons. We theoretically analyze the spiral axicon, and then experimentally verify its performance by implementing a spiral axicon on spatial light modulator. Our work provides an alternative method for generating AVB, which will facilitate its application in different fields.

1 Introduction

An axicon refers to a cone-shaped optical element with central rotational symmetry. It was first proposed to generate a Bessel beam with quasi-non-diffraction properties [1–4]. Due to its excellent properties, it is widely used in optical shaping [5], laser capture [6] and other fields [7, 8].

The vortex beam refers to the beam with the phase factor e^ilϕ, and carries lℏ orbital angular momentum per photon [9]. Here ϕ is the azimuthal angle and l is the topological charge. The vortex beam has been extensively studied over the past 30 years [10–17], and has significant applications in optical communications [18–20], optical micro-manipulation [21, 22], optical trapping [23, 24], and so on. The most common vortex beams, such as Laguerre Gaussian beams [25–27], Bessel Gaussian beams [28–30] and perfect optical vortex beams [31–33], have fixed paraxial local topological charge (PLTC) during propagation.

Different from the above vortex beams, the PLTC of the AVB can vary with propagation. Therefore, this beam has unique advantages in many fields including optical shaping, optical communications, and optical micro-manipulation [5, 20, 22]. Research on AVBs started late thus the method generated AVBs efficiently is still lacking. Recently, many efforts have been made on the AVB [34–39]. Dorrah et al. [34] used nondiffracting frozen waves to control the sign and value of the PLTC of the beam along the propagation direction. But the method can only non-continuously change the PLTC of the beam in integer orders. Moreover, using a spiral slit to generate a vortex beam whose PLTC continuously decreases with propagation has also been proposed [36]. Since only the beam that passes through the spiral slit can be utilized, the generation efficiency is low. The lack of efficient methods to generate the AVB limits its applications.

In this paper, we propose an efficient pure-phase device called spiral axicons to generate AVBs. First, we introduce the structure and principle. Then we verify that spiral axicon can efficiently generate AVBs whose PLTC varies linearly and continuously with propagation both in simulations and experiments. Furthermore, we analyze how the generated AVB changes when the parameters of the spiral axicon are changed.

2 Spiral Axicon

The mathematical form of the Bessel beam can be explained as the superposition of plane waves, and the wave vectors of these plane waves are distributed on a cone. Therefore, Graeme Scott et al. [2] realized the efficient generation of Bessel beams through an axicon for the first time. However, the Bessel beam generated by the axicon does not have the property that the PLTC varies with propagation. Inspired by Yang et al. [36], they turned a circular slit that generates a Bessel beam into a spiral slit to generate an anomalous Bessel beam, we propose the spiral axicon to effectively generate the AVB. The AVB in cylindrical coordinate can be expressed as:

$E\left(r,\varphi ,z\right)=E_0{e}^{il\varphi },(1)$

$l=\mathrm{C}\frac{z}{\lambda },(2)$

where r is used to refer to the radial coordinates and ϕ to the azimuthal coordinates. E₀ is the amplitude, and l is the PLTC, λ is the wavelength. Eq. 2 indicates that for a certain wavelength, the l increases linearly with the increase of propagation distance z, and C is the device parameter that determines the l variation. In addition, spiral axicon responds differently to beams of different wavelengths. At the same propagation distance, the longer the wavelength, the smaller the PLTC of the generated AVB.

We theoretically analyze how spiral axicon generates the AVB. The structure of the spiral axicon is first described. As shown in Figure 1A, the spiral axicon has a spiral bottom and a fixed central height. On the spiral bottom surface, r₀ is the initial radius at azimuthal coordinate ϕ = 0° and r_ϕ is the radius at any angle ϕ. In the spiral axicon, α₀ is the initial base angle at ϕ = 0° and α_ϕ is the base angle at ϕ. To convey the structure more clearly, a video is also provided as supplementary material. And Figure 1B shows the phase diagram of the spiral axicon. The fixed center height is r₀ tan α₀, so that the spiral bottom surface radius can be expressed as

$r_{\varphi }=\frac{r_0\tan {\alpha }_0}{\tan {\alpha }_{\varphi }}.(3)$

As long as the base angle α_ϕ is calculated, the structure of the spiral axicon can be determined. The α_ϕ is obtained by calculating the propagation of the plane wave through the spiral axicon to generate the AVB.

FIGURE 1

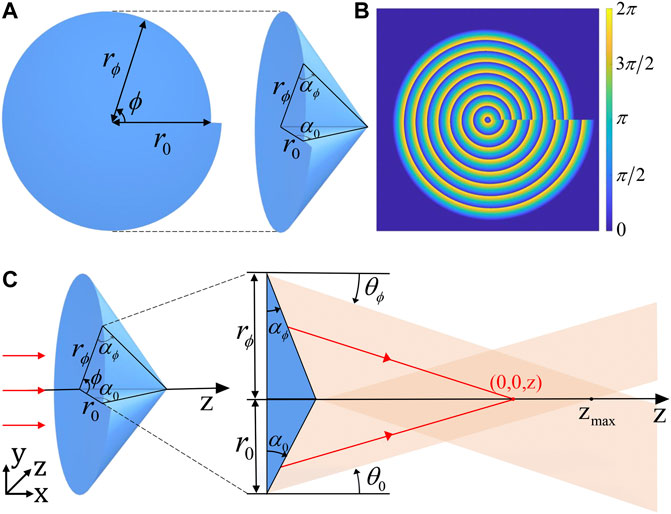
FIGURE 1. (A) Schematic diagram of the spiral axicon: it has a spiral bottom and a fixed central height, and a clearer structure is shown in the supplementary material; (B) phase diagram of the spiral axicon; (C) analysis diagram of beam propagation through spiral axicon.

As shown in Figure 1C, we analyze the propagation by geometrical optics. Based on the propagation law of the axicon, the angle of refraction after passing through the axicon is θ = (n − 1)α for a given base angle α, where n is the refractive index of the axicon. The maximum non-diffraction distance z_max = r/(n − 1)α, where r is the radius of the axicon. Thus, in the spiral axicon, the angle of refraction can be described as

${\theta }_{\varphi }=\left(n-1\right){\alpha }_{\varphi },(4)$

where n is the refractive index of the spiral axicon. The maximum effective propagation distance can be obtained as

$z_{\max }=\frac{\min \left(r_{\varphi }\right)}{\left(n-1\right)\max \left({\alpha }_{\varphi }\right)}.(5)$

The spiral axicon lies in the plane z = 0, and a plane wave passes through the spiral axicon as incident light. At any observation plane z, the optical path in the small neighborhood (Δr, ϕ, z) of the center of the plane is z/cos θ_ϕ, where Δr tends to zero. Therefore, the optical path difference between (Δr, ϕ, z) and (Δr, 0, z) can be calculated as

${\int }_0^{\varphi }\frac{z}{\cos {\theta }_{\varphi +\mathrm{\Delta }\varphi }}-\frac{z}{\cos {\theta }_{\varphi }}d\varphi =\frac{z}{\cos {\theta }_{\varphi }}-\frac{z}{\cos {\theta }_0}.(6)$

The optical path difference can be written as lλ, where l is a constant for the determined propagation position z. The phase change of the vortex beam along with the azimuthal coordinates ϕ should be uniform, so we can obtain

$\frac{z}{\cos {\theta }_{\varphi }}-\frac{z}{\cos {\theta }_0}=\frac{\varphi }{2\pi }l\lambda ,(7)$

when ϕ = 2π, the optical path difference of one circle change in azimuthal coordinates is lλ with the phase change 2πl. Thus an AVB, whose PLTC l related to the propagation distance z, is generated in the paraxial region.

Based on the above analysis, bring Eq. 2 and Eq. 4 into Eq. 7 can obtain

${\alpha }_{\varphi }=\frac{1}{n-1}\arccos \frac{2\pi \cos \left(n-1\right){\alpha }_0}{2\pi +C\varphi \cos \left(n-1\right){\alpha }_0},(8)$

the structure of the spiral axicon is determined. Its three-dimensional structure can be clearly expressed by the sag:

$H\left(r,\varphi \right)=\left\{\begin{array}{cc}\hfill \left(r_{\varphi }-r\right)\tan {\alpha }_{\varphi }\hfill & \hfill \left(0\le r\le r_{\varphi }\right)\hfill \\ \hfill 0\hfill & \hfill \left(r>r_{\varphi }\right)\hfill \end{array}\right.,(9)$

where

$r_{\varphi }=\frac{r_0\tan {\alpha }_0}{\tan {\alpha }_{\varphi }},{\alpha }_{\varphi }=\frac{1}{n-1}\arccos \frac{2\pi \cos \left(n-1\right){\alpha }_0}{2\pi +C\varphi \cos \left(n-1\right){\alpha }_0}.$

To give the simulation results, diffraction theory is used to calculate the propagation of a plane wave through a spiral axicon. Under paraxial approximation, the complex amplitude of the beam at z can be calculated through the Huygens-Fresnel diffraction integral:

$E\left(r^{\prime },{\varphi }^{\prime },z\right)=\frac{e^{ikz}}{i\lambda z}{e}^{i\frac{k}{2z}{r}^{\prime 2}}{\int }_0^{\infty }{\int }_0^{2\pi }T\left(r,\varphi \right)e^{i\frac{k}{2z}{r}^2}{e}^{i\frac{k}{z}{r}^{\prime }r\cos \left(\varphi -{\varphi }^{\prime }\right)}rdrd\varphi ,(10)$

where r′, ϕ′ are expressed as the radial coordinates and azimuthal coordinates on the observation plane respectively. k = 2π/λ is the wave vector. T (r, ϕ) is the transmission function of the spiral axicon, for the thin spiral axicon:

$T\left(r,\varphi \right)=\left\{\begin{array}{cc}\hfill \exp \left(-ik\left(n-1\right)r{\alpha }_{\varphi }\right)\hfill & \hfill \left(0\le r\le r_{\varphi }\right)\hfill \\ \hfill 0\hfill & \hfill \left(r>r_{\varphi }\right)\hfill \end{array}\right..(11)$

3 Experiments and Results

We conduct a proof-of-principle experimental demonstration following the above analysis. The experimental setup is shown in Figure 2. The laser source is a He-Ne laser running at 632.8 nm. The Gaussian beam from the laser passes through a half-wave plate (HWP) and a polarized beam splitter (PBS), which are used to adjust the intensity of the beam to avoid overexposure during measurement. The beam then passes through a 4f system composed of lens pair L1 (f₁ = 100 mm) and L2 (f₂ = 500 mm) for beam expansion. The expanded beam has a beam radius of 5 mm, which can cover the screen of a reflective liquid crystal pure phase spatial light modulator (SLM, UPOLabs, HDSLM80 R). The inset shows the phase holograms of the spiral axicon loaded on the SLM. Due to the reflectivity of the SLM, the PLTC of the experimentally generated AVB is opposite to that transmitted in the theoretical analysis. A CMOS camera (Basler ace acA4112-20 μm, 4,096 × 3,000 pixels, pixel size of 3.45 μm × 3.45 μm) is used to detect modulated beams at different distances, and the detecting distance is calculated from the position of the SLM. We measure the phase of the vortex beam by the interference method mentioned in Ref. [40], the signal light interferes with four reference plane waves Ae^isπ/2 (where A is the amplitude, s = 1, 2, 3, 4). The reference beam is also loaded on the SLM, so the SLM is loaded with the phase hologram calculated by T (r, ϕ) + Ae^isπ/2. The phase-shifted interferogram is obtained by changing the phase of the interference beam. Therefore, the phase of the signal light is

$\phi \left(r^{\prime },{\varphi }^{\prime }\right)=\arg \left(\sum _{s=1}^{4}A{e}^{is\pi /2}{I}_s\right),(12)$

where I_s the interferograms measured.

FIGURE 2

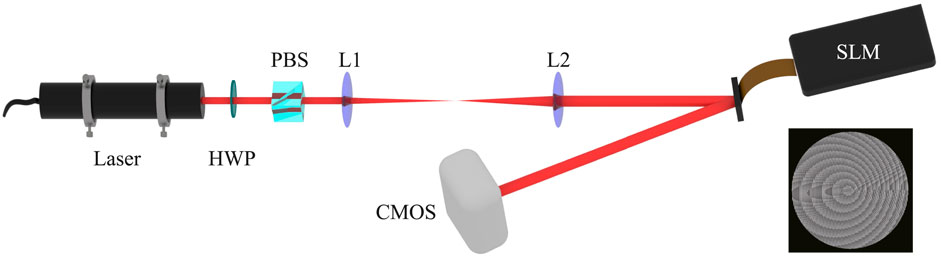
FIGURE 2. Schematic of the experimental setup. The inset is the phase hologram of the spiral axicon loaded on the SLM. HWP, half-wave plate; PBS, polarized beam splitter; L, Lens; SLM, spatial light modulator. HWP, PBS, L1, and L2 are used to control the intensity and radius of the beam. The SLM implements a spiral axicon to produce the AVB. The CMOS detects the generated AVB.

The experimental parameters of the spiral axicon are set to α₀ = 0.2°, r₀ = 6 mm, C/632.8 nm = 2 m⁻¹, n = 1.5, λ = 632.8 nm. In the experiments, only the region with a radius of 3 mm in the middle of the spiral axicon is used, so the maximum effective propagation distance of the beam is

$z_{\max }=\frac{0.003}{\left(n-1\right)\max \left({\alpha }_{\varphi }\right)}=1.71\mathrm{m}.(13)$

Figure 3 shows the intensity and phase patterns at different propagation distances z. The PLTC increases linearly with propagation, and the intensity of the fractional-order beam does not exhibit rotational symmetry. According to Eq. 2, it can be calculated that l/z = C/λ = 2 m⁻¹, so within the effective propagation distance, the absolute value of the topological charge is twice the propagation distance under the International System of Units. When the propagation distance increases from 0.5 m to 1.5 m, the absolute value of the topological load of the AVB also increases from 1 to 3. The plane wave passing through the clockwise spiral axicons should generate an AVB with a positive topological charge, and the negative topological charge is due to the SLM caused by reflection. Figure 3A shows the result of the experimental measurement, and Figure 3B shows the result of the simulation by Eqs. 10 and 11. The experimental results and the simulation results are in good agreement.

FIGURE 3

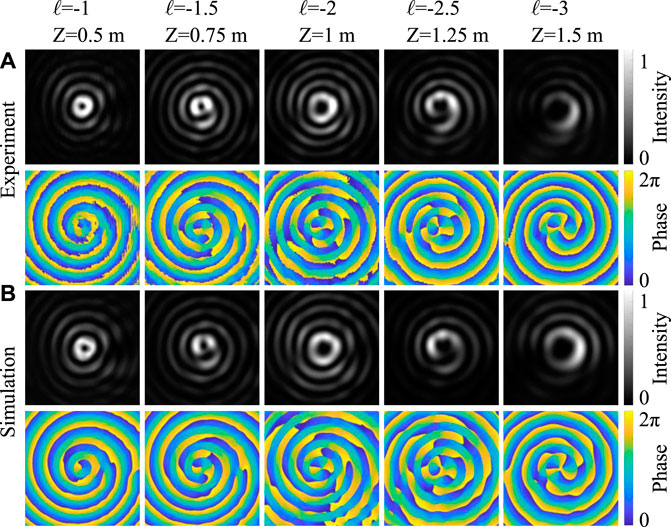
FIGURE 3. Intensity and phase patterns of anomalous vortices generated by a beam of 632.8 nm through a clockwise spiral axicon at different distances z. (A) Experimental results; (B) simulation results. The top of the figure is marked with the PLTC l of the corresponding propagation distance z calculated by Eq. 2.

Figure 4 shows the simulation and experimental results corresponding to different experimental parameters at z = 1 m. According to Eq. 2, when the device parameter C or the wavelength λ changes, the PLTC l changes. By comparing Figure 4(C1) and Figure 4(C2), it can be seen that when λ is fixed but C decreases, the l of the beam at the same position z decreases. By comparing Figure 4(C1) and Figure 4(C3), it can be known that when C is fixed but the wavelength increases, the PLTC of the beam at the same position z also decreases. It is consistent with the analysis result of Eq. 2. In addition, it is obvious that when the spiral direction of the bottom surface of the spiral axicon changes, the PLTC sign of the corresponding beam also changes. Using a plane wave as the incident light, when the bottom surface spiral direction of the spiral axicon load on the SLM is clockwise, the PLTC of the produced AVB decreases with propagation. When the bottom surface spiral direction of the spiral axicon is counterclockwise, the PLTC of the produced AVB increases with propagation. This can be demonstrated by comparing Figure 4(C4) with Figure 4(C1). Figure 4(C4) shows the counterclockwise spiral axicon situation. Compared with Figure 4(C1), the absolute value of the AVB PLTC still conforms to the theoretical analysis result, but its sign changes to plus.

FIGURE 4

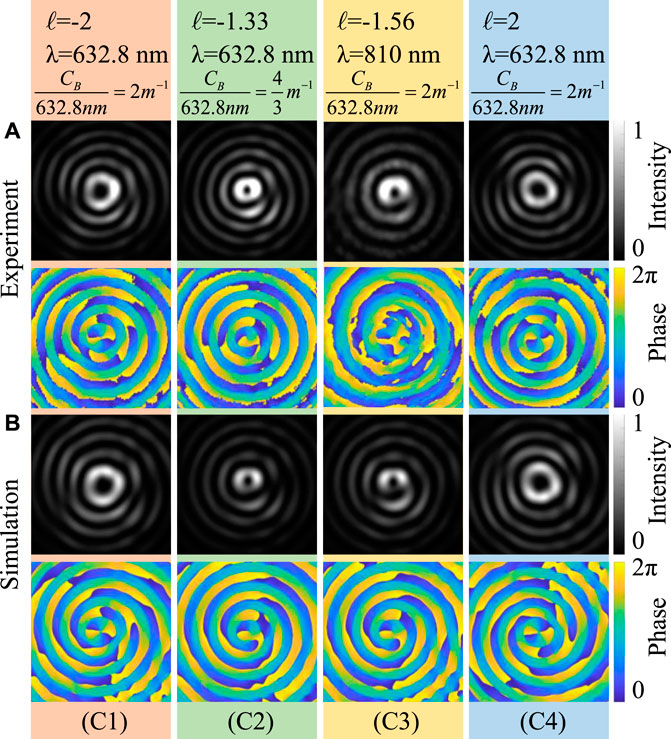
FIGURE 4. Intensity and phase patterns of the AVB generated by different parameters of spiral axicon at z = 1 m. (A) Experimental results; (B) simulation results. The results of the clockwise spiral axicon whose parmeters are set to (C1) λ = 632.8 nm, C/632.8 nm =2 m⁻¹; (C2) λ = 632.8 nm, C/632.8 nm = 4/3 m⁻¹; (C3) λ = 810 nm, C/632.8 nm = 2 m⁻¹. (C4) The result of the counterclockwise spiral axicon whose parameters are set to λ = 632.8 nm, C/632.8 nm = 2 m⁻¹. The top of the figure is marked with the PLTC l of the corresponding propagation distance z calculated by Eq. 2.

4 Conclusion

In summary, we have proposed an efficient pure-phase device that can simply and efficiently generate AVB whose PLTC increases linearly with propagation. Using a SLM, we have experimentally demonstrated the performance of spiral axicon. By changing the parameters of the spiral axicon, we can control the PLTC variation of the AVB. Our work provides a new method to generate AVB, which is expected to promote its application in quantum information, laser beam shaping, and other fields.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

XH, XZ and PZ proposed the idea. XH, ZC and YZ performed the experiment. XH organized the database. XH, ZC and YW wrote the first draft of the manuscript. PZ and XZ supervised the project. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (NSFC) (Grant No. 51905412, 12174301, and 91736104).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.951516/full#supplementary-material

References

1. Durnin J, Miceli JJ, Eberly JH. Diffraction-free Beams. Phys Rev Lett (1987) 58:1499–501. doi:10.1103/physrevlett.58.1499

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Scott G, McArdle N. Efficient Generation of Nearly Diffraction-free Beams Using an Axicon. Opt Eng (1992) 31:2640–3. doi:10.1117/12.60017

CrossRef Full Text | Google Scholar

3. Zhai Z, Zhao B. Diffraction Intensity Distribution of an Axicon Illuminated by Polychromatic Light. J Opt A Pure Appl Opt (2007) 9:862–7. doi:10.1088/1464-4258/9/10/015

CrossRef Full Text | Google Scholar

4. Wei Z, Yuan Q, Ma X, Hu J, Zeng A, Huang H. Measurement of Base Angle of an Axicon Lens Based on Auto-Collimation Optical Path. Opt Commun (2019) 434:23–7. doi:10.1016/j.optcom.2018.10.034

CrossRef Full Text | Google Scholar

5. Woerdemann M, Alpmann C, Esseling M, Denz C. Advanced Optical Trapping by Complex Beam Shaping. Laser Photon Rev (2013) 7:839–54. doi:10.1002/lpor.201200058

CrossRef Full Text | Google Scholar

6. Shao B, Esener SC, Nascimento JM, Botvinick EL, Berns MW. Dynamically Adjustable Annular Laser Trapping Based on Axicons. Appl Opt (2006) 45:6421–8. doi:10.1364/AO.45.006421

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Jarutis V, Paškauskas R, Stabinis A. Focusing of Laguerre-Gaussian Beams by Axicon. Opt Commun (2000) 184:105–12. doi:10.1016/s0030-4018(00)00961-5

CrossRef Full Text | Google Scholar

8. Dudutis J, Pipiras J, Schwarz S, Rung S, Hellmann R, Račiukaitis G, et al. Laser-fabricated Axicons Challenging the Conventional Optics in Glass Processing Applications. Opt Express (2020) 28:5715–30. doi:10.1364/oe.377108

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital Angular Momentum of Light and the Transformation of Laguerre-Gaussian Laser Modes. Phys Rev A (1992) 45:8185–9. doi:10.1103/PhysRevA.45.8185

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Shen Y, Wang X, Xie Z, Min C, Fu X, Liu Q, et al. Optical Vortices 30 Years on: Oam Manipulation from Topological Charge to Multiple Singularities. Light Sci Appl (2019) 8:697. doi:10.1038/s41377-019-0194-2

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Yao AM, Padgett MJ. Orbital Angular Momentum: Origins, Behavior and Applications. Adv Opt Photon (2011) 3:161–204. doi:10.1364/AOP.3.000161

CrossRef Full Text | Google Scholar

12. Padgett MJ, Miatto FM, Lavery MPJ, Zeilinger A, Boyd RW. Divergence of an Orbital-Angular-Momentum-Carrying Beam upon Propagation. New J Phys (2015) 17:023011. doi:10.1088/1367-2630/17/2/023011

CrossRef Full Text | Google Scholar

13. Barnett SM, Allen L. Orbital Angular Momentum and Nonparaxial Light Beams. Opt Commun (1994) 110:670–8. doi:10.1016/0030-4018(94)90269-0

CrossRef Full Text | Google Scholar

14. Beijersbergen MW, Allen L, Van der Veen HELO, Woerdman JP. Astigmatic Laser Mode Converters and Transfer of Orbital Angular Momentum. Opt Commun (1993) 96:123–32. doi:10.1016/0030-4018(93)90535-d

CrossRef Full Text | Google Scholar

15. Yang Y, Dong Y, Zhao C, Cai Y. Generation and Propagation of an Anomalous Vortex Beam. Opt Lett (2013) 38:5418–21. doi:10.1364/ol.38.005418

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Liu R, Long J, Wang F, Wang Y, Zhang P, Gao H, et al. Characterizing the Phase Profile of a Vortex Beam with Angular-Double-Slit Interference. J Opt (2013) 15:125712. doi:10.1088/2040-8978/15/12/125712

CrossRef Full Text | Google Scholar

17. Zhu J, Zhang P, Li Q, Wang F, Wang C, Zhou Y, et al. Measuring the Topological Charge of Orbital Angular Momentum Beams by Utilizing Weak Measurement Principle. Sci Rep (2019) 9:7993–6. doi:10.1038/s41598-019-44465-z

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Barreiro JT, Wei TC, Kwiat PG. Beating the Channel Capacity Limit for Linear Photonic Superdense Coding. Nat Phys (2008) 4:282–6. doi:10.1038/nphys919

CrossRef Full Text | Google Scholar

19. Wang J, Yang J-Y, Fazal IM, Ahmed N, Yan Y, Huang H, et al. Terabit Free-Space Data Transmission Employing Orbital Angular Momentum Multiplexing. Nat Photon (2012) 6:488–96. doi:10.1038/nphoton.2012.138

CrossRef Full Text | Google Scholar

20. Willner AE, Huang H, Yan Y, Ren Y, Ahmed N, Xie G, et al. Optical Communications Using Orbital Angular Momentum Beams. Adv Opt Photon (2015) 7:66–106. doi:10.1364/AOP.7.000066

CrossRef Full Text | Google Scholar

21. Paterson L, MacDonald MP, Arlt J, Sibbett W, Bryant PE, Dholakia K. Controlled Rotation of Optically Trapped Microscopic Particles. Science (2001) 292:912–4. doi:10.1126/science.1058591

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Padgett M, Bowman R. Tweezers with a Twist. Nat Photon (2011) 5:343–8. doi:10.1038/nphoton.2011.81

CrossRef Full Text | Google Scholar

23. Yang Y, Ren Y, Chen M, Arita Y, Rosales-Guzmán C. Optical Trapping with Structured Light: A Review. Adv Photon (2021) 3:034001. doi:10.1117/1.ap.3.3.034001

CrossRef Full Text | Google Scholar

24. Zhang D, Yang Y. Radiation Forces on Rayleigh Particles Using a Focused Anomalous Vortex Beam under Paraxial Approximation. Opt Commun (2015) 336:202–6. doi:10.1016/j.optcom.2014.10.034

CrossRef Full Text | Google Scholar

25. Long J, Liu R, Wang F, Wang Y, Zhang P, Gao H, et al. Evaluating Laguerre-Gaussian Beams with an Invariant Parameter. Opt Lett (2013) 38:3047–9. doi:10.1364/ol.38.003047

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Fu D, Chen D, Liu R, Wang Y, Gao H, Li F, et al. Probing the Topological Charge of a Vortex Beam with Dynamic Angular Double Slits. Opt Lett (2015) 40:788–91. doi:10.1364/ol.40.000788

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Fontaine NK, Ryf R, Chen H, Neilson DT, Kim K, Carpenter J. Laguerre-gaussian Mode Sorter. Nat Commun (2019) 10:1865–7. doi:10.1038/s41467-019-09840-4

PubMed Abstract | CrossRef Full Text | Google Scholar

28. McGloin D, Dholakia K. Bessel Beams: Diffraction in a New Light. Contemp Phys (2005) 46:15–28. doi:10.1080/0010751042000275259

CrossRef Full Text | Google Scholar

29. Mitri F. High-order Bessel Nonvortex Beam of Fractional Type α. Phys Rev A (Coll Park) (2012) 85:025801. doi:10.1103/physreva.85.025801

CrossRef Full Text | Google Scholar

30. Chen WT, Khorasaninejad M, Zhu AY, Oh J, Devlin RC, Zaidi A, et al. Generation of Wavelength-independent Subwavelength Bessel Beams Using Metasurfaces. Light Sci Appl (2017) 6:e16259. doi:10.1038/lsa.2016.259

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Ostrovsky AS, Rickenstorff-Parrao C, Arrizón V. Generation of the "perfect" Optical Vortex Using a Liquid-crystal Spatial Light Modulator. Opt Lett (2013) 38:534–6. doi:10.1364/ol.38.000534

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Vaity P, Rusch L. Perfect Vortex Beam: Fourier Transformation of a Bessel Beam. Opt Lett (2015) 40:597–600. doi:10.1364/ol.40.000597

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Zhao Y, Huang X, Chang Z, Wang X, Zhang P. Measure the Arbitrary Topological Charge of Perfect Optical Vortex Beams by Using the Dynamic Angular Double Slits. Opt Express (2021) 29:32966–72. doi:10.1364/oe.439031

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Dorrah AH, Zamboni-Rached M, Mojahedi M. Controlling the Topological Charge of Twisted Light Beams with Propagation. Phys Rev A (2016) 93:063864. doi:10.1103/PhysRevA.93.063864

CrossRef Full Text | Google Scholar

35. Davis JA, Moreno I, Badham K, Sánchez-López MM, Cottrell DM. Nondiffracting Vector Beams where the Charge and the Polarization State Vary with Propagation Distance. Opt Lett (2016) 41:2270–3. doi:10.1364/ol.41.002270

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Yang Y, Zhu X, Zeng J, Lu X, Zhao C, Cai Y. Anomalous Bessel Vortex Beam: Modulating Orbital Angular Momentum with Propagation. Nanophotonics (2018) 7:677–82. doi:10.1515/nanoph-2017-0078

CrossRef Full Text | Google Scholar

37. Wang H, Liu L, Zhou C, Xu J, Zhang M, Teng S, et al. Vortex Beam Generation with Variable Topological Charge Based on a Spiral Slit. Nanophotonics (2019) 8:317–24. doi:10.1515/nanoph-2018-0214

CrossRef Full Text | Google Scholar

38. Yang B, Su M, Lu L, Liu J, Chai G. Generation of Anomalous Vector Bessel Beams with Varying Polarization Order along the Propagation Direction. Optik (2021) 232:166578. doi:10.1016/j.ijleo.2021.166578

CrossRef Full Text | Google Scholar

39. Fang J, Zhou C, Mou Z, Wang S, Yu J, Yang Y, et al. High Order Plasmonic Vortex Generation Based on Spiral Nanoslits. New J Phys (2021) 23:033013. doi:10.1088/1367-2630/abe72c

CrossRef Full Text | Google Scholar

40. Lai S, King B, Neifeld MA. Wave Front Reconstruction by Means of Phase-Shifting Digital In-Line Holography. Opt Commun (2000) 173:155–60. doi:10.1016/S0030-4018(99)00625-2

CrossRef Full Text | Google Scholar