Simulation and Analysis of Multiphase Flow in a Novel Deepwater Closed-Cycle Riserless Drilling Method With a Subsea pump+gas Combined Lift

Recently, deepwater resource exploration has grown rapidly. Because the conditions of marine environment and seabed geology are more complex, deepwater drilling needs to numerous confront challenges, such as more complicated wellbore situations, low drilling efficiency, and high cost. Advanced novel drilling methods serve as significant impetus to facilitate the rapid advancement in deepwater oil-and-gas exploration and development. However, adopting riserless drilling methods may pollute marine environment and yield poor wall protective effects, while drilling methods with risers may suffer from relatively high cost and risk. Based on these dilemmas, in this study, a novel deepwater closed-cycle riserless drilling method with a subsea pump + gas combined lift is proposed. The proposed novel closed-cycle method has also established a multiphase flow drilling model and analyzed the effects of drilling fluid displacement, gas injection displacement, gas injection site and seawater depth on the multiphase flow in the wellbore. The simulation results revealed the following: As the gas migrates upward along the pipeline, its flow velocity first increases slowly and then rapidly owing to the volume expansion of gas. Larger displacement of drilling fluid demands greater working power of the subsea lifting pump, which is characterized by a nonlinear relationship. The gas injection displacement can effectively mitigate the load-bearing capacity of the pump, and increasing gas injection displacement leads to a decreased subsea lifting pump working power requirement; the decreasing effect on pump power load is more significant in the case of low gas injection displacement. Increasing the depth of gas injection sites reduces the subsea pump working with a decreasing slope with respect to the power descent. Finally, the subsea pump lifting power demand increases approximately linearly with an increasing seawater depth. Subsequently, an optimization method of hydraulic parameters for deepwater closed-cycle riserless drilling was proposed, which provides a theoretical foundation for the selection of subsea pumping power as well as the optimization of gas injection sites and displacement.

1 Introduction

70% of the earth is covered by sea. In the future, 40% of global gas-and-oil reserves are projected to come from deepwater; moreover, the foreseeable alternative energy “natural gas hydrate” mainly originates from deepwater as well. Consequently, deepwater study has become a Frontier field to explore essential scientific problems such as the origins of multicellular life, evolution of the earth, and climate change. Offshore drilling is the most intuitive approach to acquiring subsea stratigraphic information, which is also a leading method of marine resource exploration.

In Offshore drilling, the drilling equipment must meet high safety and reliability because it can withstand the effects of wind, wave and current, gas hydrate, strong tropical storm and the corrosion damage of marine environment to the equipment. At present, two mature deepwater drilling units have been developed: deepwater drilling ship and deepwater semi submersible drilling platform [1, 2]. Drilling ship is one of the most mobile drilling units. It has the advantages of flexible movement, simple berthing and wide range of water depth, and is especially suitable for drilling in deep water or deeper water. Drilling ships are mainly active in the waters of Brazil, the Gulf of Mexico and West Africa. Since the emergence of semi submersible drilling platform in the 1960s, it has experienced six generations of development. The sixth generation semi submersible drilling platform appeared at the beginning of the 21st century. With dynamic positioning, the hull structure is more optimized and the quality is reduced. It is equipped with automatic control system, with larger variable load, operating water depth of more than 3,000 m, maximum drilling depth of 12,000 m, strong derrick bearing capacity and high power of drilling winch.

With advancements in offshore oil drilling, deepwater drilling technology has been developing consistently, which has promoted the development of conductor jetting, dynamic killing, well logging while-drilling and pressure while-drilling techniques [1]. However, the exploration and development of deepwater resources still suffer from many challenges, which mainly span following three aspects [3–8]. First, if a riser is adopted during operation, riser length must grow with increasing water depth, yielding a heavy and cumbersome structure, especially for the upper riser, which must bear a larger tension. Second, difficulties arise during advancing in the horizontal section; when drilling in the horizontal section, it is difficult for the drilling fluid to carry the rocks. Moreover, the borehole friction increases rapidly, resulting in extra weight constraints. Third, owing to the narrow pore-fraction pressure window, a precise control of wellbore pressure is required for formations with severe leakage, reservoir pressure failure, and high sulfur content. Therefore, focusing on a series of challenges in deepwater drilling, a subsea closed-cycle riserless drilling method with pump + gas combined lift is proposed in this study, providing the theoretical foundation and design basis for efficient, economical, and safe subsea drilling applications.

In this work, the advantages of closed-cycle riserless drilling method using a pump + gas combined lift are analyzed and its multiphase flow drilling model is proposed. By solving the model, the influence of drilling fluid displacement, gas injection displacement, gas injection site and seawater depth on drilling hydraulic parameters can be obtained. The optimization hydraulic parameters design method of closed-cycle riserless drilling method with a subsea pump + gas combined lift is proposed.

2 Advantages of the Novel Subsea Closed-Cycle Riserless Drilling Method Using a pump + gas Combined Lift in Deepwater Drilling

In 2001, a Norwegian company called AGR developed a riserless mud recovery (RMR) drilling technology based on its cutting transportation system (CTS). The principle of this technology is to pump mud subsea to the drilling platform by leveraging the mud suction module at the wellhead, subsea mud lifting pump, as well as mud return pipeline, thereby forming a closed-cycle of drilling fluid. The practice costs and risks are significantly lower than that of methods using risers [9]. First, RMR was merely adopted for shoal-water oil-and-gas exploitation, which is mainly targeted to solve the drilling challenges concerning complex subsea conditions and shallow risks and ensures a smooth borehole drilling operation on the surface layer. In 2003, the first commercial RMR application was performed in the Caspian Sea. As the technology developed, the closed-cycle riserless drilling system has been advancing from shallow sea to deep sea applications. The issues restricting the application of deepwater closed-cycle drilling methods with risers mainly stem from the lifting capacity of mud lifting pump and strength of mud return pipeline. Therefore, AGR, together with Shell, BP America, and DEMO2000, formed an industrial project team to develop the so-called deepwater RMR system, and successfully conducted a field test in the South China Sea (Malaysia) at a depth of 1,419 m in September 2008. The test has proved the feasibility of this technology in deepwater drilling applications and its advantages for drilling in the South China Sea, such as safe drilling in strata with shallow risk, overcoming the mud logging restrictions, extending the setting depth of surface casing, etc. In 2008, the RMR drilling system has been adopted for a drilling operation with self-elevating platform for the first time, which achieved favorable results. The deepwater RMR system is illustrated in Figure 1.

FIGURE 1

FIGURE 1. Deepwater RMR system.

Compared with the conventional riserless mud lifting systems, this system has introduced an innovative gas lifting process by adopting a gas + pump combined lifting scheme. This design can effectively decrease the subsea pump working power, enhance the lifting head, reduce the cost and difficulty of construction, improve the reliability of lifting systems, and enable the application of closed-cycle riserless drilling in offshore applications with higher depth. The gas + pump combined lifting system is illustrated in Figure 2.

FIGURE 2

FIGURE 2. Schematic of the gas + pump combined lifting system.

Major advantages of this novel subsea closed-cycle riserless drilling method with a subsea pump + gas combined lift in deepwater drilling are as follows:

(1) Riserless drilling: Conventional offshore drilling adopts risers to isolate seawater inside the drilling fluid system. The dual-channel drill pipeline exposed to seawater replaces the cumbersome riser system and its components, thereby reducing the amount of drilling fluid and number of drilling pumps required, as well as the bearing capacity and space requirements for drilling rig deck. Moreover, it can reduce the quantity of casing, optimize the structure along well depth, and obtain a wellbore with a single diameter.

(2) Closed-cycle system: When a subsea pump + gas combined lift is used, drilling fluid is pumped to the well bottom through the inner pipe of the drilling pipeline; then, it impacts the rock stratum via jet from the drill bit. The fluid, carrying rock debris cut by the drilling bit, is then lifted to the subsea mud pipeline along the annular channel formed between the wellbore and drilling pipe. Exploiting the drilling fluid return pipeline, rock debris are carried to the drilling platform via the subsea pump + gas combined lift. Closed-cycle serves as the basis for the implementation of deepwater drilling technology with pressure control. Via precise control of bottom hole pressure and drilling fluid flow, this technique can address the narrow safety density window issue in deepwater drilling, while reducing down-time and well control risks.

(3) High cutting carrying efficiency: In conventional offshore drilling applications, the drilling fluid is pumped in via drill pipe and returned through the borehole annulus and riser annulus after carrying the cuttings. By leveraging the subsea pump + gas combined lift, carried drilling fluid cuttings return to the wellhead via the drilling fluid return pipeline. The drilling fluid is not required to be transported at high velocities for carrying cuttings to the wellhead, which reduces the scouring of the borehole wall, which is greatly applicable to wells with large displacement and horizontal wells.

(4) Enlarging the working water depth of third- and fourth-generation drilling rigs: deepwater and ultra-deepwater operations mandate significant load-bearing requirements on drilling rigs and deck space. Hence, for conventional offshore drilling, fifth-, sixth- or seventh-generation drilling rigs are required. The novel closed-cycle riserless drilling method using a subsea pump + gas lift alleviates the load-bearing capacity and space requirements on the drilling rig deck. Consequently, third- and fourth-generation drilling rigs can be adopted for such drilling operations, which reduces the daily running costs of drilling rigs and increases their working water depth.

3 Multiphase Flow Patterns in the Proposed Novel Closed-Cycle Riserless Drilling Method With a Subsea pump + gas Combined Lift

This technology aims to optimize the hydraulic parameters in deepwater drilling. The hydraulic parameter accuracy directly affects the safety and efficiency of drilling. Significant discrepancies exist between the novel closed-cycle riserless drilling with a subsea pump + gas combined lift and conventional deepwater drilling applications, which are mainly observed in the calculation of gas-liquid-solid three-phase flow in the upper return pipeline, wellbore pressure, and cutting carrying efficiency when subsea pump is online. The wellbore multiphase flow model states the fundamental theory for calculating the hydraulic parameters of the novel closed-cycle riserless drilling with a subsea pump + gas combined lift.

The foremost multiphase flow simulation of the well kick adopts homogeneous flow models. Leblanc and Leuis (1968) established the first multiphase flow model of a well kick suitable for gas overflow [10]. This model assumes that the overflowing gas exists as a continuous column inside the wellbore; then, performs simple calculations regarding the pressure change in the annulus during overflow without considering the mutual slippage between gas and liquid phases. Similarly, based on the concept of homogeneous flow, Horberock and Stanbery (1981) calculated the average value of gas-liquid characteristic parameters [11]; then, they established the continuity and momentum conservation equations of the homogeneous fluid in vertical pipeline. Subsequently, they simulated the pressure change in the wellbore. Santos (1982) established a relatively comprehensive multiphase flow model of deepwater kick by assuming a bubbly status in the wellbore during overflow [12]. In their model, they introduced the void fraction concept, as well as the effects of gas-liquid slippage and friction pressure losses in two-phase flows. Nickens (1987) considered the velocity slippage between different phases as well as the friction pressure loss of single and multiple flows. By numerically solving the dynamic equations of mass conservation for gas and liquid phases simultaneously, a comprehensive multiphase flow model in the wellbore has been established [13]. However, many factors, such as temperature variation, gas dissolution, etc., were not considered in this model. Adopting the established model, the effects of wellbore shape and hydraulic parameters of drilling assembly on the borehole pressure distribution were investigated. Moreover, many scholars, such as White and Walton (1990), Van Slyke and Huang (1990), Szczepanski et al. (1998), Nunes et al. (2002), and Velmurugan et al. (2016), applied the classic model of gas-liquid two-phase flow during well kick to analyze the multiphase flow pattern in the wellbore under different working conditions, namely, varying mud types [14, 15], overflowing gas composition, and deepwater drilling [16–18]. Sun et al. (2017, 2022) integrated the hydrate phase balance equilibrium and phase transition rate models with the multiphase flow model of deepwater well kick [19, 20]. Based on their analysis, they discovered that during well kick, the phase transition of hydrate would lead to concealment in the early stage and burstiness in the later stage. Fu et al. (2020, 2022) revealed that the hydrate formation makes drilling fluid exhibit the shear-thinning at low shear rate condition and the shear-thickening at high shear rate condition. The corresponding rheological model of drilling fluid is developed incorporating hydrate concentration, shear rate and additive concentration, which has an important contribution to improvement of the multiphase flow [21–23].

Because the novel closed-cycle riserless drilling method with a subsea pump + gas combined lift is still in its initial stage globally, current research on the multiphase flow pattern in wellbore is mainly based on the working conditions of deepwater drilling applications with risers. The multiphase flow patterns in wellbore that are affected by multiple factors, such as subsea pump and gas injection, are rarely reported. Hence, the existing theoretical model is difficult to apply in most cases.

3.1 Multiphase Flow Model of the Novel Deepwater Closed-Cycle Riserless Drilling Method With a Subsea pump + gas Combined Lift

When using the novel deepwater closed-cycle riserless drilling with a subsea pump + gas combined lift, gas lifting module enters wellbore through the mud return pipeline and changes the flow patterns of drilling fluid from liquid-solid two-phase flow to complex three-phase flow comprising gas, liquid, and solid. The selection process of pump + gas combined lifting parameters is constrained by various restrictions, such as borehole cleanliness, mud pump capacity, formation stability, rated power of lifting pump, etc. The following requirements should be fulfilled:

(1) The cutting carrying capacity of the wellbore must be ≥ 50%.

(2) The cutting bed height in inclined and horizontal sections must be smaller than 10% of the pipe size.

(3) The cutting concentration in the pipeline must be < 9%.

(4) The bottom hole pressure must be maintained between the fracture pressure and pore pressure of weak formation.

(5) The power of mud pump and subsea lifting pump must be within the rated power requirements.

3.1.1 Multiphase Flow Model of Closed-Cycle Riserless Drilling

The drilling fluid return pipeline is divided into two sections, namely, sections a and b. Along the drilling fluid return pipeline, the section from the subsea lifting pump to the intersection of gas injection pipeline and drilling fluid return pipeline is named section a of the return pipeline (as shown in Figure 2). Accordingly, the section from subsea lifting pump to the intersection of the gas injection pipeline and drilling fluid return pipeline to the drilling ship is named section b of return pipeline. The multiphase flow equations of sections a and b are established. No gas phase exists in section a of drilling fluid return pipeline. By considering only the liquid and cutting phases, the multiphase flow equations in section a of drilling fluid return pipeline are stated as follows:

① Continuity equations: Eq. 1

Liquid phase:

$\frac{\partial }{\partial t}\left(A{\rho }_l{E}_l\right)+\frac{\partial }{\partial s}\left(A{\rho }_l{v}_l{E}_l\right)=0(1)$

Cutting phase: Eq. 2

$\frac{\partial }{\partial t}\left(A{\rho }_c{E}_c\right)+\frac{\partial }{\partial s}\left(A{\rho }_c{v}_c{E}_c\right)=0(2)$

②Momentum equation: Eq. 3

$\begin{array}{l}\frac{\partial }{\partial t}\left(A{E}_l{\rho }_l{v}_l+A{E}_{\text{c}}{\rho }_{\text{c}}{v}_c\right)+\frac{\partial }{\partial s}\left(A{E}_l{\rho }_l{v}_l^2+A{E}_{\text{c}}{\rho }_{\text{c}}{v}_c^2\right)\\ +Ag\cos \alpha \left(E_l{\rho }_l+E_{\text{c}}{\rho }_{\text{c}}\right)+\frac{d\left(Ap\right)}{ds}+\frac{d\left(A{f}_r\right)}{ds}=0\end{array}(3)$

③Energy equation: Eq. 4

$\frac{\partial }{\partial t}{\rho }_l{E}_l\left(h+\frac{1}{2}{v}^2-g\cdot s\cdot \cos \alpha \right)-\frac{\partial \left(w_l\left(h+\frac{1}{2}{v}^2-g\cdot s\cdot \cos \alpha \right)\right)}{\partial s}=2\left[\frac{1}{A^{\prime }}\left(T_{ei}-T_t\right)\right](4)$

Of which, Eq. 5

$A^{\prime }=\frac{1}{2\pi }\left[\frac{k_e+r_{c\text{o}}{U}_a{T}_D}{r_{c\text{o}}{U}_a{k}_e}\right](5)$

where A denotes the sectional area of annulus (m²);E_l and E_c denote the volume fraction of drilling fluid and cutting phases, respectively (dimensionless); v_c and v_l denote the velocity of cutting and drilling fluid phases (m/s); ρ_c and ρ_l denote the density of cutting and drilling fluid phases, respectively, (kg/m³); q_c denotes the generation rate of cuttings (kg/s); f_r denotes the on-way friction pressure drop (Pa); s is the coordinate along the flow direction (m); α is the deviation angle of the well (°); p denotes the pressure (Pa); T_a is fluid temperature in the drilling fluid return pipeline (°C); k_e is the thermal conductivity of seawater (W/(m°C)); r_co is the outer diameter of drilling fluid return pipeline (m); w_c is the mass flow rate of cuttings (kg/s); w_l is the mass flow of drilling fluid (kg/s); C_pg is the specific heat of gas phase (J/kg°C); T_ei and T_t denote the temperatures of seawater and drilling fluid, respectively, in return pipeline (°C); U_a is the total heat transfer coefficient between fluid in drilling fluid return pipeline and seawater (W/(m²·°C)); T_D is the transient heat transfer coefficient; g is the gravitational acceleration (m/s²); h is the well depth at a certain point (m); A′ is an intermediate parameter.

The gas lifting system injects gas into the drilling fluid return pipeline, which alters the flow characteristics of drilling fluid from the original liquid-solid two-phase flow to the more complex gas-liquid-solid three-phase flow. Consequently, the multiphase flow equations in section b of drilling fluid return pipeline are stated as follows:

① Continuity equations:

Gas phase: Eq. 6

$\frac{\partial }{\partial t}\left(A{\rho }_g{E}_g\right)+\frac{\partial }{\partial s}\left(A{\rho }_g{v}_g{E}_g\right)=0(6)$

Liquid phase: Eq. 7

$\frac{\partial }{\partial t}\left(A{\rho }_l{E}_l\right)+\frac{\partial }{\partial s}\left(A{\rho }_l{v}_l{E}_l\right)=0(7)$

Cutting phase: Eq. 8

$\frac{\partial }{\partial t}\left(A{\rho }_c{E}_c\right)+\frac{\partial }{\partial s}\left(A{\rho }_c{v}_c{E}_c\right)=0(8)$

②Momentum equation: Eq. 9

$\begin{array}{l}\frac{\partial }{\partial t}\left(A{E}_{\text{g}}{\rho }_{\text{g}}{v}_g+A{E}_l{\rho }_l{v}_l+A{E}_{\text{c}}{\rho }_{\text{c}}{v}_c\right)+\frac{\partial }{\partial s}\left(A{E}_g{\rho }_g{v}_g^2+A{E}_l{\rho }_l{v}_l^2+A{E}_{\text{c}}{\rho }_{\text{c}}{v}_c^2\right)\\ +Ag\cos \alpha \left(E_g{\rho }_g+E_l{\rho }_l+E_{\text{c}}{\rho }_{\text{c}}\right)+\frac{d\left(Ap\right)}{ds}+\frac{d\left(A{f}_r\right)}{ds}=0\end{array}(9)$

③Energy equation: Eq. 10

$\begin{array}{l}\frac{\partial }{\partial t}\left[\left({\rho }_l{E}_l\left(h+\frac{1}{2}{v}^2-g\cdot s\cdot \cos \alpha \right)\right)+\left({\rho }_{\text{g}}{E}_{\text{g}}\left(h+\frac{1}{2}{v}^2-g\cdot s\cdot \cos \alpha \right)\right)\right]\\ -\left[\frac{\partial \left(w_l\left(h+\frac{1}{2}{v}^2-g\cdot s\cdot \cos \alpha \right)\right)}{\partial s}+\frac{\partial \left(w_g\left(h+\frac{1}{2}{v}^2-g\cdot s\cdot \cos \alpha \right)\right)}{\partial s}\right]\\ =2\left[\frac{1}{A^{\prime }}{\left(T_{ei}-T\right)}_t\right]\end{array}(10)$

where E_g is the volume fraction of gas (dimensionless); v_g denotes the gas velocity (m/s); ρ_g denotes the gas density (g/m³); q_g is the gas injection rate (kg/s); w_g is the mass flow of gas (kg/s).

3.1.2 Auxiliary Equations and Boundary Conditions

(1) Auxiliary equations

To solve control equations of multiphase flow, it is necessary to combine the calculation equations of gas phase volume fraction, drilling fluid rheology, distribution coefficient, and drift velocity[19].

The gas phase volume fraction, E_g, is calculated using Eq. 11; gas distribution coefficient, C₀, is calculated using Eq. 12; drift velocity, V_gr, is calculated using Eq. 13; rheological properties of drilling fluid in the pipeline are calculated using Eq. 13, including the apparent viscosity, plastic viscosity, and dynamic shear force of the drilling fluid: Eq. 14

$E_g=\frac{V_{sg}}{C_0{V}_m+V_{gr}}(11)$

$C_0=\frac{2}{1+{\left(\frac{{\mathrm{Re}}_{tp}}{1000}\right)}^2}+\frac{1.2-0.2{\theta }^4}{1+1+{\left(\frac{1000}{{\mathrm{Re}}_{tp}}\right)}^2}(12)$

$V_{gr}=1.53{\left(\frac{g\sigma \left({\rho }_l-{\rho }_g\right)}{{\rho }_l^2}\right)}^{0.25}+0.35\sqrt{\frac{g{D}_0\left({\rho }_l-{\rho }_g\right)}{{\rho }_l}}\theta {\left(1-\theta \right)}^{0.25}(13)$

$f\left(p,T\right)=f\left(p_0,T_0\right)e^{\left[A\left(T-T_0\right)+B\left(p-p_0\right)+C\left(T-T_0\right)\left(p-p_0\right)+D{\left(T-T_0\right)}^2\right]}(14)$

where V_sg denotes the apparent flow velocity of gas (m/s); V_m denotes the mixing flow velocity of drilling fluid and cuttings (m/s); σ is the surface tension (Pa); C₀ is the distribution coefficient (dimensionless); D₀ is the pipe diameter (m); Re_tp is the two-phase Reynolds number (dimensionless); θ is the average sectional void fraction (dimensionless); f (p,T) represents μ_a (p,T), μ_p (p,T), and τ_a (p,T), respectively, namely, apparent viscosity, plastic viscosity, and dynamic shear force under pressure p and temperature T; p₀ is the atmospheric pressure (MPa); T₀ is the ambient temperature (°C); A, B, C, and D denote the characteristic constants of drilling fluid, whose values are related to the composition of drilling fluid.

The equation to calculate the sinking velocity of cuttings in the pipe is as follows: Eq. 15

$\begin{array}{l}{v}_s=\frac{k_1{d}_p^2\left({\rho }_s-{\rho }_f\right)}{{\mu }_e}{N}_R\le 10\\ v_s=\frac{k_2{d}_p^2{\left({\rho }_s-{\rho }_f\right)}^{0.6667}}{{\left({\rho }_f{\mu }_e\right)}^{0.3333}}10\text{<}{N}_R\le 100\\ v_s=\frac{k_3{\left[d_p\left({\rho }_s-{\rho }_f\right)\right]}^{0.5}}{{\left({\rho }_f\right)}^{0.5}}{N}_R>100\end{array}(15)$

where k₁, k₂, and k₃ are experimental coefficients, whose values are 0.3268, 0.07068, and 0.0813, respectively; N_R is the sinking Reynolds number of particles; μ_e is the plastic viscosity of drilling fluid (mPa·s); ρ_f and ρ_s are the density of drilling fluid and cuttings, respectively (g/cm³).

The power outputs for mud and subsea lifting pumps are calculated using Eqs 16, 17, respectively:

$P_s=p_{s}Q(16)$

$P_o=p_{o}Q(17)$

where, P_s is the power output of the mud pump (W); P_o is the power output of the subsea lifting pump (W); Q is displacement of drilling fluid (m³/s).

Because PR equation has high accuracy in estimating liquid density and describing the phase behavior of high-pressure system, and is widely used in practical engineering, the state of gas in this paper is mainly calculated by PR equation (24).

Equation 18–23

$p=\frac{RT}{V-b}-\frac{a}{V\left(V+b\right)+b\left(V-b\right)}(18)$

$a=a_c\cdot \alpha \left(T_r\right)(19)$

$b=\frac{0.07780R{T}_c}{p_c}(20)$

$a_c=\frac{0.45724R^2{T}_c^2}{p_c}(21)$

$\alpha \left(T_r\right)={\left[1+m\left(1-T_r^{0.5}\right)\right]}^2(22)$

$m=0.37464+1.5226w-0.26992w^2(23)$

Where, p is the environmental pressure (Pa); T is the environmental temperature (°C); p_c is the critical pressure of gas (Pa); T_c is the critical temperature of gas (°C); w is the eccentricity factor of gas, dimensionless; V is molar volume (m³/kmol); Z is the compression factor, dimensionless.

(2) Boundary conditions

The temperature and pressure of drilling fluid inside the return pipeline on sea surface are measured using thermometer and pressure gauges at the wellhead. The displacement of drilling fluid is calculated based on the mud pump readings. The air injection displacement is measured according to the gas flowmeter, and the cutting displacement is calculated based on the mechanical drilling speed.

The boundary conditions of well section b are as follows: Eq. 24

$\{\begin{array}{l}P\left(0,t\right)=P_0\\ T\left(0,t\right)=T_0\\ q_g\left(h_1,t\right)=q_0\\ q_c\left(0,t\right)=q_c\\ q_l\left(0,t\right)=q_l\end{array}(24)$

Well section a adapts to well section b, when only the liquid-solid two phases are considered. The initial conditions are Eqs 25–27

$E_g\left(h_1,0\right)=0(25)$

$E_c\left(h_1,0\right)=\frac{V_{sc}\left(h_1,0\right)}{C_c{V}_{sl}\left(h_1,0\right)+V_{cr}\left(h_1,0\right)}(26)$

$E_m=1-E_c(27)$

where V_sc, V_sl, and V_cr are the drift velocity of cuttings, liquid phase, and cutting settlement, respectively (kg/m³), and h₁ is the insertion depth of gas injection pipeline (m).

A method similar to the so-called SIMPLE method is adopted to solve the multiphase flow equations. When solving the equations, the first-order backward difference is used for the time partial derivation. Taking the mass conservation equation of gas phase as an example, the difference scheme of its time partial derivative is described as follows: Eq. 28

$\frac{{\left(E_g{\rho }_g\right)}^j-{\left(E_g{\rho }_g\right)}^{j-1}}{\mathrm{\Delta }t}+\frac{\partial {\left(E_g{\rho }_g{v}_g\right)}^j}{\partial s}=0(28)$

For the spatial partial derivative, the finite volume method of a staggered grid is used for calculating the difference. The scalar variables (pressure, void fraction, liquid holdup, liquid density, and gas density) are located in the center of the control unit, while the vector variables (liquid velocity and gas velocity) are located at the boundaries.

The first-order upwind differential scheme is adopted for the mass and momentum conservation equations. Taking the mass conservation equation as an example, the differential scheme of its convection term is described as follows: Eq. 29

${\frac{\partial \left(E_g{\rho }_g{v}_g\right)}{\partial s}|}_i=\frac{1}{\mathrm{\Delta }s}\left[{\left(E_g{\rho }_g{v}_g\right)}_{\frac{i+1}{2}}-{\left(E_g{\rho }_g{v}_g\right)}_{\frac{i-1}{2}}\right](29)$

where I and j are the time and space nodes, respectively, and Δs and Δt are the space and time steps, respectively. Basic parameters obtained in step 1 are substituted into the discrete formula to calculate the gas injection displacement of current step, q_g, as well as the pressure, gas velocity, drilling fluid return velocity, cutting return velocity, and cutting concentration distribution along the drilling fluid return pipeline at a depth of h₁ for the gas injection pipeline.

3.2Analysis of Simulation Results

The basic simulation parameters are the actual parameters of a wellbore in the South China Sea, which include a well depth of 3,918 m, water depth of 1,340 m, drilling fluid density of 1,200 kg/m³, mechanical rate of penetration of 40 m/h, injection pipe depth of 400 m, diameter of 50 mm, injection gas flow of 120 m³/h, and inner diameter of drilling fluid return pipeline of 80 mm.

3.2.1 Effect of Drilling Fluid Displacement on the Multiphase Flow Inside the Wellbore

With the same pumping parameters, the drilling fluid displacement varies from 5 L/s to 40 L/s with 5 L/s increments. The multiphase flow model for the closed-cycle riserless drilling is used during the analysis, and the influence of subsea pump displacement on the multiphase flow in the return pipeline is examined, as demonstrated in Figure 3. The simulation results indicate that in the section mudline, the pressure along depth inside the return pipeline increases with increasing drilling fluid displacement values; moreover, in the section below mudline, the pressure along depth inside the return pipeline decreases with increasing drilling fluid displacement. This is because the subsea pump is located at the mudline level. In the section above the mudline, increasing the liquid phase displacement will result in higher subsea pump discharge pressure and larger fluid kinetic energy in the pipeline. Hence, the pressure inside the pipe increases. In the section below mudline, as the fluid in the pipeline is not affected by the subsea pump, the well bottom pressure decreases with an increasing drilling fluid displacement, decreasing the pressure inside the pipeline.

FIGURE 3

FIGURE 3. Effect of drilling fluid displacement on the pressure in the return pipeline.

As illustrated in Figure 4, the variation in drilling fluid displacement affects the cutting distribution inside the return pipeline. Higher displacement yields smaller volume fraction of cuttings in the pipeline. Affected by the gas injection in the pipeline at 400 m, the volume fraction of cuttings gradually decreases along the return pipeline and eventually becomes consistent. Gas injection will enhance the turbulence intensity of the fluid in the pipeline, which increases the fluid flow velocity and decreases the sectional volume fraction of cuttings. Therefore, migrating cuttings to the wellhead becomes easier.

FIGURE 4

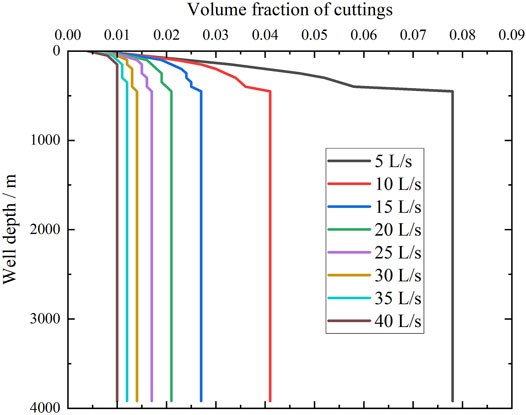
FIGURE 4. Effect of drilling fluid displacement on the volume fraction of cuttings inside the return pipeline.

Effect of drilling fluid displacement on gas volume fraction inside the return pipeline is calculated and demonstrated in Figure 5. As the gas migrates from the gas injection point at a depth of 400 m, the gas volume fraction decreases with increasing drilling fluid displacement. When the drilling fluid displacement is 5 L/s, 10 L/s, 15 L/s, 20 L/s, 25 L/s, 30 L/s, 35 L/s, and 40 L/s, the gas volume fraction returning to the wellhead is 0.913, 0.846, 0.787, 0.737, 0.692, 0.653, 0.617, and 0.586, respectively. Lowering the subsea pump displacement will result in a larger sectional gas volume fraction in the pipeline, which significantly increases effects of gas injection on cutting migration. As shown in Figure 6, during the upward migration of gas along the pipeline, the flow velocity first increases slowly and then rapidly owing to the gas volume expansion. The gas velocity in gas injection section increases gradually with an increasing drilling fluid displacement. The effects of a fluid displacement lower than 15 L/s are more significant compared with those of other setpoints.

FIGURE 5

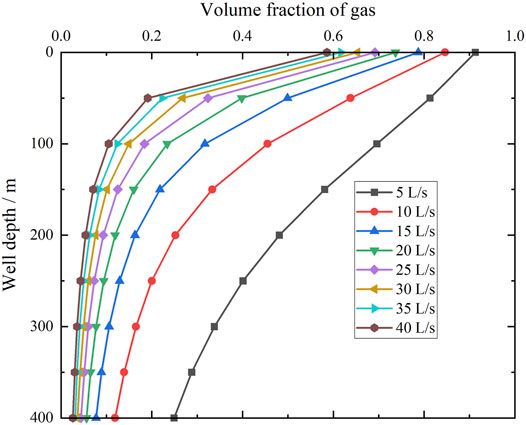
FIGURE 5. Effect of drilling fluid displacement on the gas volume fraction inside the return pipeline.

FIGURE 6

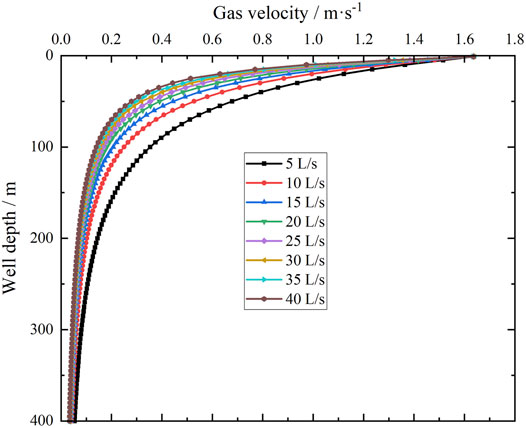
FIGURE 6. Gas velocity distribution in the wellbore with respect to different drilling fluid displacements.

The drilling fluid displacement is closely associated with pump lifting power. As illustrated in Figure 7, the results of calculating the drilling fluid displacement effect on pump lifting power indicate that a higher drilling fluid displacement results in a higher subsea pump working power, which exhibits a nonlinear relationship. During the actual riserless drilling process, considering the power configuration of drilling platform or drilling ship, the subsea pumps should be selected to combine the effects of sites and amount of gas injection. Moreover, to optimize cutting carrying efficiency, a minimum drilling fluid displacement is obtained for selecting the corresponding pump power, which serves as a theoretical basis for selecting the proper subsea pumps.

FIGURE 7

FIGURE 7. Effect of drilling fluid displacement on pump lifting power.

3.2.2 Effect of Gas Injection Displacement on the Multiphase Flow Inside the Wellbore

The most prominent characteristic of novel riserless drilling is the combination of gas injection and subsea pump lift processes. The variations in the gas injection displacement has great impact on the pressure and volume fraction in the pipeline as well as the subsea pump power. By setting the gas injection displacement to 60 m³/h, 80 m³/h, 100 m³/h, 120 m³/h, 140 m³/h, 160 m³/h, 180 m³/h, and 240 m³/h, the effect of gas injection displacement on the multiphase flow in wellbore can be calculated.

As shown in Figure 8, the pressure along depth inside the return pipeline decreases with increasing gas injection displacement values above the mudline level. In the section below the mudline, the gas injection displacement has no effect on pressure in the pipeline is shown. Therefore, in this study, only pressure simulation results in the section above mudline are considered. Affected by gas injection displacement, the discharge pressure of the subsea pump fluctuates greatly. When the gas injection displacement changes from 60 m³/h to 240 m³/h, the pump discharge pressure decreases from 17.288 to 5.527 MPa. A higher gas injection displacement results in smaller pressure losses in the return pipeline and a higher pressure in the pipeline with the same depth.

FIGURE 8

FIGURE 8. Effect of gas injection displacement on pressure in return pipeline.

Gas injection displacement is crucial for ensuring the efficient migration of cuttings and enhance the pumping capacity. Figure 9 demonstrates the effect of varying gas injection displacement using an injection site at 400 m on the gas volume fraction in the return pipeline. A larger gas injection displacement results in a higher gas proportion and fluid kinetic energy throughout the section inside the pipeline; therefore, cuttings can be carried to the wellhead more easily. From the calculation procedure depicted in Figure 10, the gas flow velocity increases with increasing gas injection displacement; its cutting carrying capacity is enhanced significantly as well. When the gas injection displacement elevates from 60 m³/h to 240 m³/h, the gas flow velocity at the wellhead increases from 0.8182 m/s to 3.273 m/s.

FIGURE 9

FIGURE 9. Effect of gas injection displacement on gas volume fraction in the return pipeline.

FIGURE 10

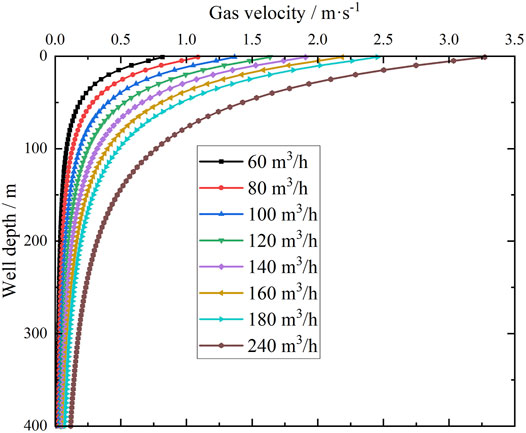
FIGURE 10. Gas velocity distribution in the wellbore with different gas injection displacement values.

The effect of gas injection displacement on pump power is analyzed, which can greatly decrease the load-bearing capacity of pump. By increasing gas injection displacement, the subsea lifting pump power decreases (see Figure 11). Especially in the case of low gas injection displacement, its effect on pump power is more significant. As gas injection displacement elevates from 60 m³/h to 120 m³/h, the pump power decreases by 8.28 kW. In the case of high gas injection displacement, as gas injection displacement increases from 180 m³/h to 240 m³/h, the pump power decreases by 6.01 kW. Therefore, the subsea pump and gas lifting equipment cannot be operated at a high operation efficiency simply by constantly increasing the gas injection displacement. Consequently, in the design stage, the lifting capacity of subsea pump and optimal gas injection displacement should be thoroughly considered.

FIGURE 11

FIGURE 11. Effect of gas injection displacement on pump lifting power.

3.2.3 Effect of Gas Injection Site on the Subsea Pump Lifting Power

Gas injection displacement and sites are the key parameters of gas lifting. Properly selecting the gas injection sites significantly affects the subsea pump power requirements. The interaction between the depth of gas injection sites and pump lifting power is calculated as shown in Figure 12. Keeping the gas injection displacement constant, as the depth of gas injection sites increases, the subsea pump power requirement is reduced with a decreasing slope. As the gas injection site depth changes from 100 to 400 m, the pump power decreases from 57.255 to 49.14 kW, an 8.115 kW reduction. As the gas injection site depth changes from 400 to 700 m, the pump power is reduced by 2.903 kW. A deeper gas injection site results in higher requirements for the air compressor on the platform. Based on the conditions of this example, the recommended depth of gas injection site is 400 m.

FIGURE 12

FIGURE 12. Effect of gas injection depth on pump lifting power.

3.2.4 Effect of Seawater Depth on the Subsea Pump Lifting Power

During deepwater drilling, as seawater depth increases, the requirements regarding drilling equipment and engineering risks will increase as well. The subsea pumping power variations with respect to different seawater depths are calculated as illustrated in Figure 13. The calculation results exhibit that as seawater depth increases, the subsea pump lifting power increases almost linearly. The subsea pump power requirements increase with an increasing depth, during which the effect of gas lifting increases as well. Based on the conditions of this example, subsea pump power increases by 4.97 kW for every additional 100 m in seawater depth.

FIGURE 13

FIGURE 13. Effect of seawater depth on pump lifting power.

4 Optimization of Hydraulic Parameters in the Novel Deepwater Closed-Cycle Riserless Drilling Method With a Subsea pump + gas Combined Lift

The novel deepwater closed-cycle riserless drilling method with a subsea pump + gas combined lift aims to address the marine environment pollution and poor wall protection issues caused by open-cycle drilling operation, while avoiding the high costs and risks associated with drilling operations that use risers. In a conventional closed-cycle riserless drilling system, the return of mud is only powered by the subsea lifting pump. Therefore, the flow rate and cutting carrying effect of mud return can be solely controlled by adjusting the lifting pump. For the novel deepwater closed-cycle riserless drilling method with a subsea pump + gas combined lift, the interaction between process parameters of gas lift and flow pattern of mud return, as well as the coupling between each process parameter during pump + gas combined lifting, should be considered to achieve efficient cutting carrying.

In a fixed deepwater drilling block, given the drilling depth, seawater depth, and other drilling parameters, the minimum return velocity of cutting carrying and its corresponding subsea pump rated power with gas lifting can be calculated. By designing orthogonal experiments, the subsea pump power can be simulated and calculated, which can fulfill the cutting carrying requirements with respect to different gas injection depths of gas injection pipeline, gas injection displacements, and drilling fluid displacements. The minimum subsea pump power is selected to optimize and maximize the cutting carrying efficiency by gas injection. In the block with large seawater depth, it might be preferred to first increase gas injection displacement and then increase the depth of gas injection sites. Consequently, the subsea pump load can be decreased as much as possible; in other words, a high-efficiency deepwater drilling process with a low-power subsea pump can be achieved.

5 Conclusion

The multiphase flow model of the deepwater closed-cycle riserless drilling with a subsea pump + gas combined lift has been proposed to analyze the effects of drilling fluid displacement, gas injection displacement, gas injection site, and seawater depth on the multiphase flow in the novel closed-cycle riserless drilling wellbore. Subsequently, the following conclusions are obtained:

(1) With increasing drilling fluid displacement, the volume fraction of cuttings in the pipeline decreases; whereas, the gas velocity in gas injection pipeline increases gradually. When the drilling fluid displacement is lower than 15 L/s, the effects are more prominent.

(2) With increasing gas injection displacement, it is easier to carry the cuttings and return them to the wellhead, which reduces the subsea lifting pump power requirement.

(3) With an increasing depth of gas injection sites, the subsea pump power requirement is reduced with a decreasing slope.

(4) Greater seawater depths result in higher power requirements for the subsea pump; accordingly, the lifting power increases almost linearly.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

JW Overall structure design and numerical simulation. JS: Multiphase flow model of closed-cycle riserless drilling biulding. WX: Advantages of the novel subsea closed-cycle riserless drilling method using a pump + gas combined lift in deep-sea drilling analysis. HC: Mesh generation and solution of multiphase flow model. CW: Effect of gas injection site on the subsea pump lifting power analysis and language check. YY: Effect of seawater depth on the subsea pump lifting power analysis. RQ: Optimization of hydraulic parameters analysis.

Funding

This work was supported by the Key Special Project for Introduced Talents Team of Southern Marine Science and Engineering Guangdong Laboratory (Guangzhou) (GML2019ZD0501), the National Key Research and Development Program of China (2021YFC2800803).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Peter A. Deepwater Drilling: Well Planning, Design, Engineering, Operations, and Technology Application. Houston, Texas: Gulf Professional Publishing (2019).

Google Scholar

2. Yang X, Sun J, Zhang Z, Xu L, Wang C, Liu Z, et al. Design and Application of Drilling System Digital Prototype for deepwater Drilling Platform. IOP Conf Ser Mater Sci Eng (2020) 964:012027. doi:10.1088/1757-899x/964/1/012027

CrossRef Full Text | Google Scholar

3. Meng X, Zhu J, Chen G, Shi J, Li T, Song G. Dynamic and Quantitative Risk Assessment under Uncertainty during deepwater Managed Pressure Drilling. J Clean Prod (2022) 334:130249. doi:10.1016/j.jclepro.2021.130249

CrossRef Full Text | Google Scholar

4. Li H, Zhang M, Lau HC, Fu S. China's deepwater Development: Subsurface Challenges and Opportunities. J Pet Sci Eng (2020) 195:107761. doi:10.1016/j.petrol.2020.107761

CrossRef Full Text | Google Scholar

5. Huang Y, Lan H, Hong Y-Y, Wen S, Yin H. Optimal Generation Scheduling for a Deep-Water Semi-submersible Drilling Platform with Uncertain Renewable Power Generation and Loads. Energy (2019) 181:897–907. doi:10.1016/j.energy.2019.05.157

CrossRef Full Text | Google Scholar

6. Tian D, Fan H, Leira BJ, Sævik S. Study on the Static Behavior of Installing a Deep-Water Drilling Riser on a Production Platform. J Pet Sci Eng (2020) 185:106652. doi:10.1016/j.petrol.2019.106652

CrossRef Full Text | Google Scholar

7. Gao Y, Chen Y, Zhao X, Wang Z, Li H, Sun B. Risk Analysis on the Blowout in deepwater Drilling when Encountering Hydrate-Bearing Reservoir. Ocean Eng (2018) 170:1–5. doi:10.1016/j.oceaneng.2018.08.056

CrossRef Full Text | Google Scholar

8. Xu Y, Jin Y, Guan Z, Liu Y, Wang X, Zhang B, et al. Evolution of Gas Kick and Overflow in Wellbore during deepwater Drilling and Advantage Analysis of Early Gas Kick Detection in Riser. J China Univ Pet (Edition Nat Science) (2019) 43(1):60–7.

Google Scholar

9. Li X, Zhang J, Tang X, Mao G, Wang P. Study on Wellbore Temperature of Riserless Mud Recovery System by CFD Approach and Numerical Calculation. Petroleum (2020) 6(2):163–9. doi:10.1016/j.petlm.2019.06.006

CrossRef Full Text | Google Scholar

10. Leblanc JL, Leuis RL. A Mathematical Model of a Gas Kick. J Pet Tech (1968) 20(4):888–98. doi:10.2118/1860-pa

CrossRef Full Text | Google Scholar

11. Hoberock LL, Stanbery SR. Pressure Dynamics in wells during Gas Kick: Part 1-fluid Lines Dynamics. J Pet Tech (1981) 33(6):1357–66. doi:10.2118/9256-pa

CrossRef Full Text | Google Scholar

12. Santos OLA. A Mathematical Model of a Gas Kick when Drilling in Deep Waters. Golden: Colorado School of Mines (1982).

Google Scholar

13. Nickens HV. A Dynamic Computer Model of a Kicking Well. SPE Drilling Eng (1987) 2(02):159–73. doi:10.2118/14183-pa

CrossRef Full Text | Google Scholar

14. White DB, Walton IC. A Computer Model for Kicks in Water- and Oil-Based Muds. In: IADC/SPE Drilling Conference; February 1990; Houston, Texas (1990). SPE-19975.

CrossRef Full Text | Google Scholar

15. Van Slyke DC, Huang ETS. Predicting Gas Kick Behavior in Oil-Based Drilling Fluids Using a Pc-Based Dynamic Wellbore Model. In: IADC/SPE Drilling Conference; February 1990; Houston, Texas (1990). SPE 19972.

CrossRef Full Text | Google Scholar

16. Szczepanski R. Differences between Methane and Condensate Kicks-A Simulation Study. SPE drilling & completion (1998) 13(1):36–41. doi:10.2118/37366-pa

CrossRef Full Text | Google Scholar

17. Nunes JOL, Bannwart AC, Ribeiro PR. Mathematical Modeling of Gas Kicks in Deep Water Scenario. In: IADC/SPE Asia Pacific Drilling Technology; September 2002; Jakarta, Indonesia (2002). SPE 77253.

CrossRef Full Text | Google Scholar

18. Velmurugan N, Godhavn JM, Hauge E. Dynamic Simulation of Gas Migration in marine Risers. In: SPE Bergen One Day Seminar; April 20, 2016; Bergen, Norway (2016). SPE 180022. doi:10.2118/180022-ms

CrossRef Full Text | Google Scholar

19. Sun B, Sun X, Wang Z, Chen Y. Effects of Phase Transition on Gas Kick Migration in deepwater Horizontal Drilling. J Nat Gas Sci Eng (2017) 46:710–29. doi:10.1016/j.jngse.2017.09.001

CrossRef Full Text | Google Scholar

20. Zhang Z, Sun B, Wang Z, Pan S, Lou W, Sun D. Intelligent Well Killing Control Method Driven by Coupling Multiphase Flow Simulation and Real-Time Data. J Pet Sci Eng (2022) 213:110337. doi:10.1016/j.petrol.2022.110337

CrossRef Full Text | Google Scholar

21. Fu W, Chen B, Zhang K, Liu J, Sun X, Huang B, et al. Rheological Behavior of Hydrate Slurry with Xanthan Gum and Carboxmethylcellulose under High Shear Rate Conditions. Energy Fuels (2022) 36(6):3169–83. doi:10.1021/acs.energyfuels.1c04359

CrossRef Full Text | Google Scholar

22. Fu W, Wang Z, Chen L, Sun B. Experimental Investigation of Methane Hydrate Formation in the Carboxmethylcellulose (CMC) Aqueous Solution. SPE J (2020) 25(3):1042–56. doi:10.2118/199367-pa

CrossRef Full Text | Google Scholar

23. Fu W, Wang Z, Sun B, Xu J, Chen L, Wang X. Rheological Properties of Methane Hydrate Slurry in the Presence of Xanthan Gum. SPE J (2020) 25(5):2341–52. doi:10.2118/199903-pa

CrossRef Full Text | Google Scholar

24. Peng D-Y, Robinson DB. A New Two-Constant Equation of State. Ind Eng Chem Fund (1976) 15(1):59–64. doi:10.1021/i160057a011

CrossRef Full Text | Google Scholar