Scaling Analysis of Shear Thickening Suspensions

Dense suspensions of particles in viscous liquid often demonstrate the striking phenomenon of abrupt shear thickening, where their viscosity increases strongly with increase of the imposed stress or shear rate. In this work, discrete-particle simulations accounting for short-range hydrodynamic, repulsive, and contact forces are performed to simulate flow of shear thickening bidisperse suspensions, with the packing parameters of large-to-small particle radius ratio δ = 3 and large particle fraction ζ = 0.15, 0.50, and 0.85. The simulations are carried out for volume fractions 0.54 ≤ ϕ ≤ 0.60 and a wide range of shear stresses. The repulsive forces, of magnitude F_R, model the effects of surface charge and electric double-layer overlap, and result in shear thinning at small stress, with shear thickening beginning at stresses σ ∼ F_Ra⁻². A crossover scaling analysis used to describe systems with more than one thermodynamic critical point has recently been shown to successfully describe the experimentally-observed shear thickening behavior in suspensions. The scaling theory is tested here on simulated shear thickening data of the bidisperse mixtures, and also on nearly monodisperse suspensions with δ = 1.4 and ζ = 0.50. Presenting the viscosity in terms of a universal crossover scaling function between the frictionless and frictional maximum packing fractions collapses the viscosity for most of the suspensions studied. Two scaling regimes having different exponents are observed. The scaling analysis shows that the second normal stress difference N₂ and the particle pressure Π also collapse on their respective curves, with the latter featuring a different exponent from the viscosity and normal stress difference. The influence of the fraction of frictional contacts, one of the parameters of the scaling analysis, and its dependence on the packing parameters are also presented.

1 Introduction

Suspensions of solid particles in liquids, under highly concentrated or ‘dense’ conditions in which the volume fraction ϕ approaches the jamming fraction, can exhibit strong shear thickening. This is seen as an abrupt increase in apparent viscosity η with increasing shear stress σ or shear rate $\dot{\gamma }$ [1–5]. Strong shear thickening has been linked to a shear-induced transition from lubricated or ‘frictionless’ particle interactions at low shear stress, where the interaction between the particles is hydrodynamic, to predominately contact interactions at high shear stress [6–9], with the critical stress determined by interparticle repulsive forces that tend to maintain the lubricated state at low stress [10–12].

Based on the lubrication-to-frictional transition scenario [12], Wyart and Cates (WC) [10] developed a model where shear thickening viscosity η is controlled by divergences at two jamming volume fractions: ${\varphi }_J^0$ for the frictionless regime at low shear stress (in monodisperse systems, corresponding to random close packing ${\varphi }_J^0={\varphi }_{\mathit{RCP}}\sim 0.64$ [13]) and ${\varphi }_J^{\mu }<{\varphi }_J^0$ for the frictional regime at high shear stress. The suspension viscosity was expressed as $\eta \sim {({\varphi }_J-\varphi )}^{-2}$, with the transition between ${\varphi }_J^0$ and ${\varphi }_J^{\mu }$ implying a stress-dependent jamming fraction ϕ_J(σ). This was modeled using a parameter f, the fraction of close-pair interactions that are frictional, as ${\varphi }_J(\sigma )={\varphi }_J^0(1-f(\sigma ))+{\varphi }_J^{\mu }f(\sigma )$. Here, 0 ≤ f ≤ 1, with f = 0 when neighboring particles have lubricated (frictionless) interactions at low stress, and f → 1 when the neighboring particles are predominately in the frictional state at high stress. In their work, f was described as a function of the particle pressure Π; since Π and σ for non-colloidal suspensions are related by an O (1) factor, μ_B = σ/Π [14], f can be written in terms of shear stress f(σ). Mari et al. [11] have validated elements of the WC theory by carrying out simulations of nearly monodisperse suspensions with particle size ratio δ = 1.4, where they have described f as f(σ) = exp (σ*/σ). Singh et al. [15] adopted this expression and extended the model to develop a constitutive description for simple shear flow. This provides a description of relative viscosity η/η₀ (η₀ is the suspending fluid viscosity), the second normal stress difference N₂, and the particle pressure Π as a function of parameters ϕ, σ, and interparticle friction coefficient μ. As seen in other work [16], the first normal stress difference N₁ = Σ₁₁ − Σ₂₂ was found to change sign from negative to positive with increasing ϕ and σ and was not well-described. We confine our consideration of the normal stress response to N₂ = Σ₂₂ − Σ₃₃ and Π = −(Σ₁₁ + Σ₂₂ + Σ₃₃)/3, where 1, 2, and 3 (or x, y, and z) are, respectively, the flow, gradient, and vorticity directions of a viscometric flow. We study only simple shear here, of form $u_x=\dot{\gamma }y$.

Rheological experiments were carried out by Guy et al. [17] on monodisperse suspensions of poly-methylmethacrylate particles sterically stabilized by poly-12-hydroxystearic acid, where the data are shown to be fitted by the WC model. This model’s predictions were, however, found [18] to exhibit significant discrepancies from the experimental data for binary mixtures of spheres with large-to-small particle size ratio δ = 4. This was especially pronounced for cases with a predominance of particle volume from the large particles. Unlike monodisperse systems, where there is only one type of frictional contact, the bidisperse systems have three different types of frictional contact coming from the large-large, the large-small, and the small-small particles contact that contribute to stress development differently. This motivates our consideration of suspensions with significant bidispersity.

A recent study [19] showed that the WC model can be framed in the language of crossover scaling. Specifically, the shear thickening transition was described in terms of a crossover between two critical points, at each of which the viscosity diverges, the frictionless ${\varphi }_J^0$ and the frictional ${\varphi }_J^{\mu }$ maximum packing fractions. In this scaling analysis, the viscosity was expressed as a function of the fraction of frictional contacts f(σ) and the distance to the frictionless maximum packing fraction,

${\eta }_r{\left({\varphi }_J^0-\varphi \right)}^2\sim {\mathcal{F}}_{WC}\left(\frac{f\left(\sigma \right)}{{\varphi }_J^0-\varphi }\right),{\mathcal{F}}_{WC}\sim {\left(\frac{1}{{\varphi }_J^0-{\varphi }_J^{\mu }}-\frac{f\left(\sigma \right)}{{\varphi }_J^0-\varphi }\right)}^{-2},(1)$

where the scaling variable $x_{WC}=f(\sigma )/({\varphi }_J^0-\varphi )$ is the part of the scaling function associated with the frictionless jamming critical point, and $x_c=1/({\varphi }_J^0-{\varphi }_J^{\mu })$ is its critical value at which there is a divergence of the scaling function ${\mathcal{F}}_{WC}$. More generally, the scaling may be written

${\eta }_r{\left({\varphi }_J^0-\varphi \right)}^2\sim \mathcal{F}\left(\frac{g\left(\sigma ,\varphi \right)}{{\varphi }_J^0-\varphi }\right),(2)$

with g allowing dependence on variables beyond the stress dependence of f(σ), and ${\mathcal{F}}_{WC}$ a particular form of $\mathcal{F}(x)$. With these generalizations, an excellent collapse to a single universal curve was achieved for experimental viscosity data for both cornstarch and silica particle suspensions measured over a wide range of volume fractions and shear stresses. In our work, we will not make allowance for ϕ-dependence in g, but will consider the scaling based on the WC scaling variable, x_WC, with f(σ) describing the microscopic interaction state, and identify any limitations of the generalized scaling function, $\mathcal{F}(x_{WC})$, with regard to describing the bidisperse suspension rheology.

The scaling of the viscosity presented in Eq. 2 resembles a well-known form called crossover scaling. An alternative way of representing this scaling, which is better suited to identifying any change in the nature of the divergence with g (σ, ϕ) is the Cardy scaling form [20]. Cardy scaling is typically applied in study of critical points and phase transitions in thermal equilibrium systems, among which a well-known example is that of magnetic systems described by Heisenberg and Ising models. These differ in their symmetry properties [21], as the Heisenberg model is isotropic, whereas the Ising model has uniaxial symmetry as it considers a single component of the vector spin. Based on these different symmetry properties, the two models for magnetic systems show different universality classes characterized by different critical exponents and scaling functions [22], and a crossover in the dominant singularity may be observed. Analogously, the dense suspension that undergoes shear thickening by the lubricated-to-frictional mechanism also consists of different states, namely frictionless and frictional. Note that the function g (σ, ϕ) plays the same role as the uniaxial anisotropy plays in the Heisenberg-Ising crossover, but the suspension crossover does not involve a clear change of symmetry. Ramaswamy et al. [19] expressed the scaling function for the viscosity in the Cardy scaling form

${\eta }_r{g}^2\left(\sigma ,\varphi \right)\sim \mathcal{H}\left(|1/x_c-1/x|\right),(3)$

where $\mathcal{H}$ is a scaling function. The authors found that the viscosity divergence weakened to a -3/2 exponent, i.e., $\mathcal{H}\sim |1/x_c-1/x{|}^{-3/2}$, in the frictional regime, distinctly different from $\mathcal{H}\sim |1/x_c-1/x{|}^{-2}$ in the frictionless limit. The two divergences of $\mathcal{F}$ suggest critical points of different universality classes.

In this work, we apply the scaling approach presented in Ramaswamy et al. [19] to dense suspension rheological data obtained from numerical simulation. We consider nearly-monodisperse systems, as well as more strongly bidisperse systems of varying large particle fraction. The analyses of the simulation data are carried out by two different approaches. We first consider the critical exponents and scaling functions. Following this, we implement Cardy scaling to study the crossover behavior.

2 Methods

Shear thickening has been observed in molecular dynamics simulations [23], including approaches which also introduce friction to the particle interactions [24]. Here, we prefer to consider the viscous fluid effects, but in a simplified fashion relative to the more rigorous Stokesian Dynamics [25, 26]. To this end, we use the lubrication flow-discrete element model (LF-DEM) [6] to simulate shear flow of dense suspensions of non-Brownian frictional spheres immersed in a viscous Newtonian fluid under an imposed shear stress σ. With a repulsive interaction and contact forces including friction, this method has been found to successfully describe the flow of dense suspensions [11], and to closely reproduce essential features of DST and shear jamming seen experimentally [5]. Recent work [27] has extended this approach to include a rolling friction [28], but here we consider only frictional resistance to slipping of the contact.

Our typical simulation is performed using 1,000 particles in a cubic box with periodic boundary conditions, to mimic an infinite system. Shear flow is imposed using Lees-Edwards boundary conditions. The suspensions studied in this work are bidisperse with a_s and a_l as the radii of the smaller and larger particles, respectively, with the size ratio defined as δ ≡ a_l/a_s. The motion of particles is considered inertialess, i.e. to be at particle Reynolds number $\mathrm{R}\mathrm{e}=\rho \dot{\gamma }{a}^2/{\eta }_0\to 0$. The equation of motion is hence simply the force/torque balance 0 = F_H + F_R + F_C, where F_H is the finite-range hydrodynamic force/torque, F_R is the repulsive force, and F_C is the contact force/torque.

The hydrodynamic forces are of the form F_H = −R_FU ⋅ (U − U^∞) + R_FE: E^∞, where U is the particle translational and angular velocity, ${\mathit{U}}^{\infty }=\dot{\gamma }y{\widehat{\mathit{e}}}_x$ is the flow due to imposed shear, and ${\mathit{E}}^{\infty }=({\widehat{\mathit{e}}}_x{\widehat{\mathit{e}}}_z+{\widehat{\mathit{e}}}_z{\widehat{\mathit{e}}}_x)\dot{\gamma }/2$ is the rate-of-strain tensor. The resistance matrices R_FU and R_FE contain single-particle Stokes drag and the leading terms of the pairwise hydrodynamic interaction corresponding to short-range lubrication forces [29]. The divergence of the resistance matrix at vanishing dimensionless interparticle gap h = 2 (r − a_i − a_j)/(a_i + a_j) is regularised to allow contact: the squeeze mode resistance is proportional to (h + ϵ)⁻¹ and shear mode resistance is proportional to log [(h + ϵ)⁻¹], where ϵ = 10⁻³a_s. Including ϵ allows the lubrication resistance to be finite at contact (h = 0), which could be interpreted as representing the influence of particle surface roughness.

A repulsive electrical double layer (EDL) force maintains the particle surface separation at low stress. The force decays exponentially with the interparticle gap h over the length scale defined by Debye length κ⁻¹ as $F_R=F_R^0{e}^{-\kappa h}$. For this work, based on prior experience [11], the Debye length is taken as κ⁻¹ = 0.05a_s. The repulsive force introduces a stress scale of ${\sigma }_0=F_R/6\pi a_s^2$. This form of the simulation is called the electrostatic repulsion model (ERM) [11]. The contact between the particles occurs when the applied stress overcomes the repulsive forces. The contact force is modeled by linear springs in both normal and tangential directions; the friction prohibits slipping at the contact if the force components satisfy the Coulomb friction law, F_C, tan ≤ μF_C,nor, where μ is the interparticle friction coefficient. When the particles make contact, the friction is activated. The friction coefficient is fixed at μ = 1 for this work.

The repulsive force sets the level of the critical stress, such that when the applied stress σ ≪ σ₀, the interactions between the particles are lubricated (frictionless). When σ ≫ σ₀, the interactions are predominately frictional contacts. At each time step, we evaluate F_R and F_C and solve the equation of motion for the particle velocities, $\mathit{U}-{\mathit{U}}^{\infty }={\mathit{R}}_{\text{FU}}^{-1}\cdot ({\mathit{R}}_{\text{FE}}:{\mathit{E}}^{\infty }+{\mathit{F}}_{\text{R}}+{\mathit{F}}_{\text{C}})$. The flow, velocity gradient, and vorticity directions are x, z, and y, respectively. We do not consider Brownian motion, i.e. the Péclet number $Pe={\eta }_0\dot{\gamma }{a}^3/kT\to \infty$.

The stress-controlled simulations were performed over a range of dimensionless shear stresses of 0.3 ≤ σ/σ₀ ≤ 562. Each simulation was run to $\dot{\gamma }t=30$ strain units. The results of the transient period were not included, as we discard the initial five strain units. We report the suspension viscosity in the form of the relative viscosity η_r = η/η₀, and for scaling purposes we will use the particle interaction viscosity η′ = η_r − (1 + 2.5ϕ), where (1 + 2.5ϕ) is the correction for the Einstein viscosity. The reported shear stresses and shear rates will be nondimensionalized by ${\sigma }_0=F_R/6\pi a_s^2$ and $\dot{{\gamma }_0}=F_R/6\pi {\eta }_0{a}_s^2$, respectively. The bidisperse suspensions in this study are in the range of total solid volume fraction of 0.54 ≤ ϕ ≤ 0.60, with particle size ratio of δ = a_l/a_s = 1.4 and 3. For δ = 3, the large particle fraction of the total volume fraction is varied by taking ζ = ϕ_l/ϕ = 0.15, 0.50, and 0.85.

3 Results

We present the results of the scaling analysis for all suspensions studied, first applying it to prior work on nearly monodisperse suspensions [15] with δ = 1.4 and ζ = 0.50 for volume fractions 0.52 ≤ ϕ ≤ 0.63 and shear stresses 0.1 ≤ σ/σ₀ ≤ 100. For brevity, we call these suspensions monodisperse, as the slight bidispersity avoids the layering or string ordering of particles subjected to shear flow [30] but the shear thickening at δ = 1.4 is found to differ little from smaller δ = 1.2 [11]. We then present the scaling analysis applied to our rheological property data for bidisperse suspensions with δ = 3 and varying ζ = 0.15, 0.50, and 0.85 for 0.54 ≤ ϕ ≤ 0.60 and 0.3 ≤ σ/σ₀ ≤ 562. Unless otherwise stated, we model the fraction of frictional contacts as $f(\sigma )=e^{-{\sigma }^{*}/\sigma }$, with σ*/σ₀ = 1.45 based on previous work [11, 15, 31]. The rheology data that is considered in the scaling analysis, for both the monodisperse and bidisperse suspensions, is shown in Figure 1. Note that we do not consider data for cases where the viscosity is shear thinning, and thus for the monodisperse case we use data σ/σ₀ ≥ 0.2 and for the bidisperse suspensions σ/σ₀ ≥ 0.32, data which is to the right of the dashed lines shown in Figures 1A,G. This figure provides the relative viscosity η_r, normal stress difference as ${\widehat{N}}_2=N_2/{\eta }_0\dot{\gamma }$, and particle pressure as $\widehat{\mathrm{\Pi }}=\mathrm{\Pi }/{\eta }_0\dot{\gamma }$; plotting the normal stresses normalized by ${\eta }_0\dot{\gamma }$ produces a property analogous to the viscosity and proportional to the well-known ‘normal stress viscosity’ [14]. All quantities are shown as functions of the dimensionless shear stress σ/σ₀. As noted, we do not consider the first normal stress difference in the scaling analysis.

FIGURE 1

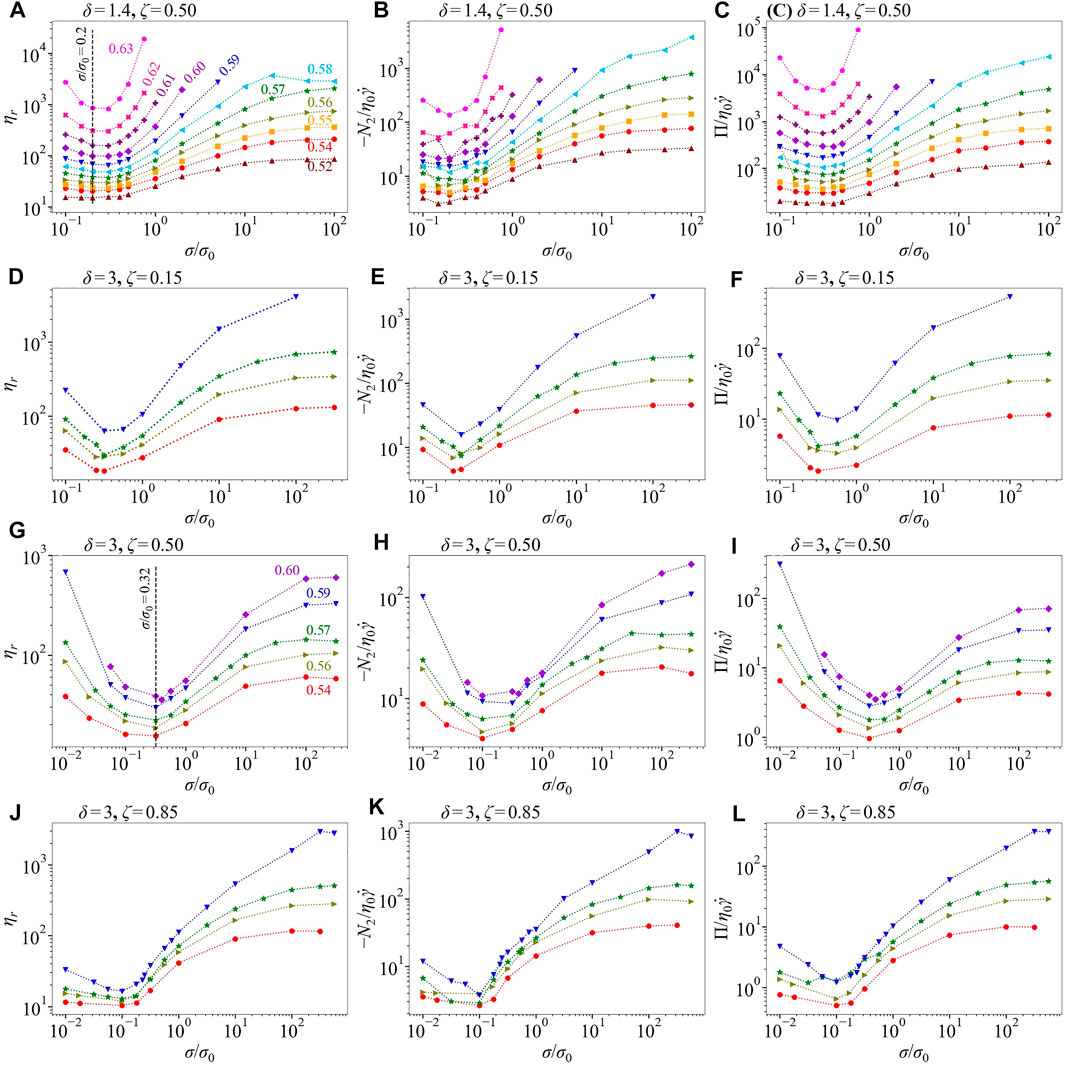
FIGURE 1. Rheology of simulated suspensions as a function of dimensionless shear stress. Row 1: Nearly monodisperse suspensions, δ = 1.4 and ζ = 0.50; rows 2–4: bidisperse suspensions. Row 2: δ = 3 and ζ = 0.15; row 3: δ = 3 and ζ = 0.50; row 4: δ = 3 and ζ = 0.85 (A) (D) (G) (J): relative viscosity η_r (B) (E) (H) (K): the second normal stress difference plotted as $N_2/{\eta }_0\dot{\gamma }$ (C) (F) (I) (L) : particle pressure plotted as $\mathrm{\Pi }/{\eta }_0\dot{\gamma }$. Data in (A–C) are from the work of Singh et al. [15]. Legends of panels A and G apply to (A–C) and to (D–L), respectively. For the scaling analysis, we do not consider shear thinning data, and thus consider data to the right of the dashed lines shown in panels A and G as examples.

As the two scaling methods we apply in this work have not previously been applied to simulated suspension rheology data, we provide some guidance before presenting our results. The two methods (which we will call crossover and Cardy scaling) have the same content, but the insights gained from the two are different. In the crossover scaling analysis (presented in Figure 2, and 4–6), the scaling approach can be seen based on the WC [10] form of the viscosity ${\eta }_r\sim {({\varphi }_J(\sigma )-\varphi )}^{-2}$ with ${\varphi }_J(\sigma )=f(\sigma ){\varphi }_J^{\mu }+(1-f(\sigma )){\varphi }_J^0$ using the fraction of frictional contacts f. This yields

${\eta }_r\sim {\left[f{\varphi }_J^{\mu }+\left(1-f\right){\varphi }_J^0-\varphi \right]}^{-2}={\left({\varphi }_J^0-\varphi \right)}^{-2}{\left[1-x/x_c\right]}^{-2}$

where, as defined previously,

$x=f/\left({\varphi }_J^0-\varphi \right)\mathrm{a}\mathrm{n}\mathrm{d}{x}_c=1/\left({\varphi }_J^0-{\varphi }_J^{\mu }\right).$

FIGURE 2

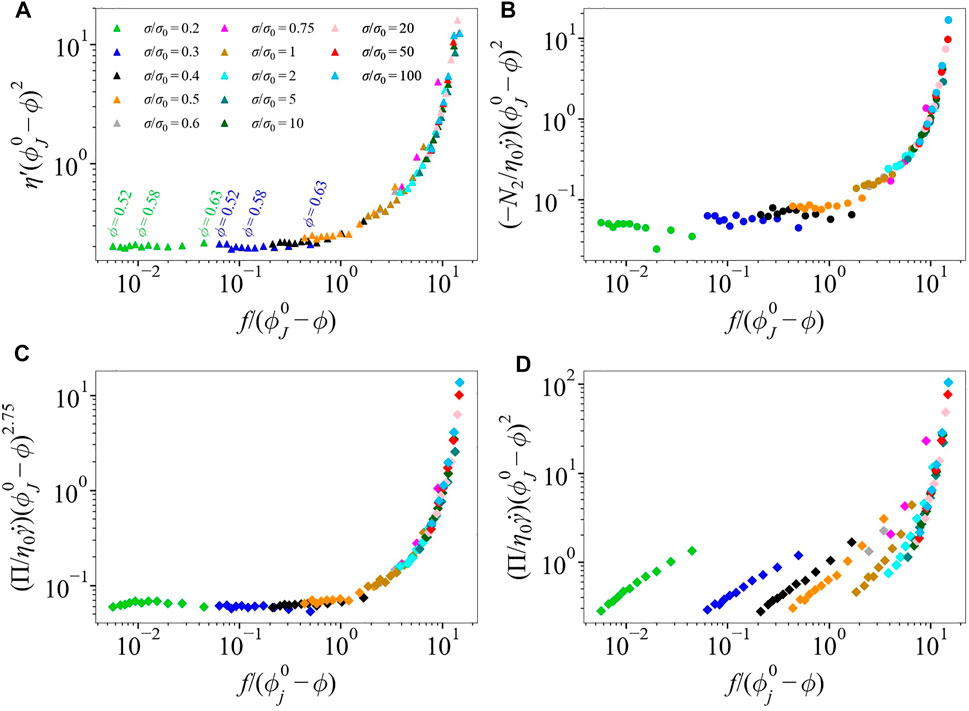
FIGURE 2. The scaling functions (A) ${\mathcal{F}}_{\eta }$, (B) ${\mathcal{F}}_{N_2}$, and (C) ${\mathcal{F}}_{\mathrm{\Pi }}$ as a function of the scaling variable $x=f/({\varphi }_J^0-\varphi )$ for simulated suspensions at δ = 1.4 and ζ =0.50 for 0.52≤ ϕ ≤0.63. Note that in (A,B), ${\eta }^{\prime }{({\varphi }_J^0-\varphi )}^2$ and $(N_2/{\eta }_0\dot{\gamma }){({\varphi }_J^0-\varphi )}^2$ collapse, while in (C) $(\mathrm{\Pi }/{\eta }_0\dot{\gamma }){({\varphi }_J^0-\varphi )}^{2.75}$ collapses whereas in (D) $(\mathrm{\Pi }/{\eta }_0\dot{\gamma }){({\varphi }_J^0-\varphi )}^2$ does not collapse. Data are adapted from Singh et al. [15] and $f(\sigma )=e^{({\sigma }^{*}/\sigma )}$ with σ*= 1.45.

Thus we see that if x → x_c, there are two possible divergences. From the crossover scaling analysis we find the data presented as ${\eta }^{\prime }{({\varphi }_J^0-\varphi )}^2$ as a function of x collapse to the generalized scaling form, $\mathcal{F}$ of Eq. 2 (not necessarily the precise form of WC), and confirm the presence of a second divergence, i.e. a divergence in the scaled data. Note that η′ is the singular part of the viscosity, which will be defined in the following paragraph. The form of the second divergence, at the frictional jamming fraction, revealed by crossover scaling and assumed to have exponent -2 in the WC form, is more effectively probed by Cardy scaling. For this purpose, we manipulate the expressions of the viscosity and other rheological functions differently, again using the WC form for concreteness,

${\eta }_r\sim {\left[f{\varphi }_J^{\mu }+\left(1-f\right){\varphi }_J^0-\varphi \right]}^{-2}=f^{-2}{\left[\left({\varphi }_J^0-\varphi \right)/f-\left({\varphi }_J^0-{\varphi }_J^{\mu }\right)\right]}^{-2}=f^{-2}{\left(x^{-1}-x_c^{-1}\right)}^{-2}.$

Plotting η′f² as a function of $|x_c^{-1}-x^{-1}|$ (as indicated by Eq. 3 with the more general g in place of f), a change in slope of the curve provides insight to whether the two divergences have the same exponent. In fact, we find evidence they are different.

3.1 Monodisperse Suspensions

We first consider the scaling of data for δ = 1.4. This data was previously fitted [15] to the forms proposed by Wyart and Cates [10], with $\eta \sim {(1-\varphi /{\varphi }_J(\sigma ))}^{-2}$, and has not previously been studied by the scaling approach presented here. In Figure 2 we plot the scaling function $\mathcal{F}$ specific to each rheological property as a function of the scaling variable $x=f(\sigma )/({\varphi }_J^0-\varphi )$ using ${\varphi }_J^0=0.646$ reported in [15]. We scale viscosity, following Eq. 1, as ${\mathcal{F}}_{\eta }={\eta }^{\prime }{({\varphi }_J^0-\varphi )}^2$ (Figure 2A) and find the entire range of monodisperse data show an excellent collapse on a single universal curve. Note that η′ = η_r − (1 + 5ϕ/2), in which the nonsingular Einstein contribution due to individual particles is removed, is the particle interaction contribution to the relative viscosity; as N₂ and Π require particle interactions, this places all properties on a similar footing. The monotonic nature of the curves in Figure 2 relative to the ‘U-shape’ curve of Figure 1 is due to the noted exclusion of shear-thinning data in the scaling analysis. To aid the reader, in Figure 2A, points in the first two sets of data, for σ/σ₀ = 0.2 and 0.3 and appearing at the left of the plot, are labeled with their respective ϕ values, showing that as σ/σ₀ or ϕ increases, we move from left to right on the curve.

At small values of $x=f(\sigma )/({\varphi }_J^0-\varphi )$, ${\mathcal{F}}_{\eta }$ is a constant and increases as x increases, then eventually diverges at $x=x_c={({\varphi }_J^0-{\varphi }_J^{\mu })}^{-1}\approx 16.13$. When we adapt Eq. 1 for the second normal stress difference, the scaling function ${\mathcal{F}}_{N_2}=-{\widehat{N}}_2{({\varphi }_J^0-\varphi )}^2$ behaves in a similar manner, but with more scatter for small values of x (Figure 2B). Scatter at small values of the scaling variable, i.e., at conditions far from the controlling singularity, is not unexpected.

For the particle pressure, $\widehat{\mathrm{\Pi }}{({\varphi }_J^0-\varphi )}^2\sim x$ does not produce a data collapse as seen by Figure 2D. Strikingly, we find the scaling function must have a significantly different exponent, and ${\mathcal{F}}_{\mathrm{\Pi }}=\widehat{\mathrm{\Pi }}{({\varphi }_J^0-\varphi )}^{2.75}$ is shown in Figure 2C to exhibit a good collapse. In fact, the collapse is arguably better near the divergence at x_c than seen for the viscosity and N₂, but we can not presently offer a mechanistic basis for this difference in the exponent.

We treat the same data shown in Figure 2 using the Cardy scaling approach, as described by Eq. 3 with f(σ) in place of g (σ, ϕ). The two scaling forms have the same physical content, but the Cardy scaling proves better for understanding the precise form of the divergence at the second critical point where f(σ) is large and x ∼ x_c. Therefore, it is better at identifying changes in the nature of the divergence (change in exponents) from the frictionless, f(σ) = 0, viscosity divergence to the frictional one. In the Cardy scaling, the viscosity scaling function is ${\eta }^{\prime }{f}^2(\sigma )\sim {\mathcal{H}}_{\eta }(1/x_c-1/x)$. We use this scaling form for the normal stresses, as well.

In Figure 3, we plot the scaling function $\mathcal{H}$ as a function of |1/x − 1/x_c| for η′, ${\widehat{N}}_2$, and $\widehat{\mathrm{\Pi }}$. The scaling functions ${\mathcal{H}}_{\eta }={\eta }^{\prime }{f}^2$ and ${\mathcal{H}}_{N_2}=-\widehat{N}{f}^2$ have qualitatively similar behavior. Both datasets collapse on their respective lines having slope of −2 at small values of x. As x approaches x_c, the slope decreases in magnitude. The value is near −1.5, but the range of data is rather limited for any conclusions. The particle pressure data again have a distinctly different behavior, shown by Cardy scaling to be ${\mathcal{H}}_{\mathrm{\Pi }}\sim |1/x_c-1/x{|}^{-2.75}$ at small x, with the slope decreasing significantly at larger x (i.e. at small |1/x − 1/x_c|). For all three rheological properties, the change in slope, or crossover, occurs at |1/x_c − 1/x| in the range of 10^–1 to 10^–2. Importantly, this change in exponent suggests that the frictionless regime (small x) and the frictional regime (large x) are qualitatively different and belong to different universality classes. This agrees with the scaling of experimental data by Ramaswamy et al. [19], where a reduction in the exponent for viscosity divergence in the high stress regime was observed, with the change in exponent occurring in a similar range of |1/x − 1/x_c|.

FIGURE 3

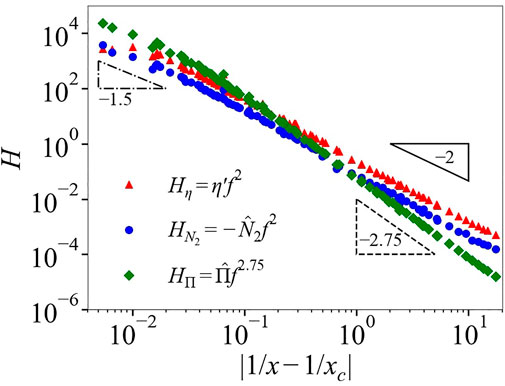
FIGURE 3. Scaling functions ${\mathcal{H}}_{\eta }$ (red triangles), ${\mathcal{H}}_{N_2}$ (blue circles), and ${\mathcal{H}}_{\mathrm{\Pi }}$ (green diamonds) versus |1/x_c −1/x| for simulated suspensions at δ = 1.4 and ζ = 0.50 for 0.52 ≤ ϕ ≤0.63 for exponential form $f(\sigma )=e^{({\sigma }^{*}/\sigma )}$. The black solid triangle shows the slope of −2, the dashed black triangle of −2.75, the black dash-dotted triangle of −1.5. Data for δ = 1.4 are adapted from Singh et al. [15].

3.2 Bidisperse Suspensions

In this section, we test the scaling of Eq. 1 on our simulation data from bidisperse suspensions. These are at δ = 3 and ζ = 0.15, 0.50, and 0.85 for 0.54 ≤ ϕ ≤ 0.60 and 0.32 ≤ σ/σ₀ ≤ 562. Based on the scaling procedure, we find that the data collapse requires frictionless maximum packing fractions of ${\varphi }_J^0=0.65$, 0.70, and 0.71 for ζ = 0.15, 0.50, and 0.85, respectively. These values are slightly lower than those determined in our previous work [32] using the least-square error method, with ${\varphi }_J^0$ being the best fitting parameter in ${\eta }_r(\varphi )={(1-\varphi /{\varphi }_J^0)}^{-2}$ at low shear stress σ/σ ≤ 0.32. In contrast, in the present work, we use a single ${\varphi }_J^0$ value for each value of ζ across the entire range of shear stresses 0.32 ≤ σ/σ₀ ≤ 562.

In Figure 4 we plot the viscosity scaling function ${\mathcal{F}}_{\eta }={\eta }^{\prime }{({\varphi }_J^0-\varphi )}^2$ as a function of the scaling parameter $x=f/({\varphi }_J^0-\varphi )$. The scaling collapse holds for bidisperse suspensions for each ζ. Due to different ${\varphi }_J^0$ for each ζ, each data curve diverges at different $x_c=1/({\varphi }_J^0-{\varphi }_J^{\mu })$: at x_c = 18.18 for ζ = 0.15 (Figure 4A), x_c = 13.51 for ζ = 0.50 (Figure 4B) and x_c = 9.26 for ζ = 0.85 (Figure 4C). The scaling function ${\mathcal{F}}_{N_2}$ (Figure 5) shows a good collapse at large x, but the data exhibit scatter at small x. Similar to what was found for the monodisperse suspensions, the bidisperse particle pressure does not produce a single curve when scaled as $\widehat{\mathrm{\Pi }}{({\varphi }_J^0-\varphi )}^2$ and plotted as a function of x. We again find that $\widehat{\mathrm{\Pi }}{({\varphi }_J^0-\varphi )}^{2.75}$ yields a good collapse (Figure 6). See Supplemental Material showing $\widehat{\mathrm{\Pi }}{({\varphi }_J^0-\varphi )}^2\sim x$ not collapsing on a single curve.

FIGURE 4

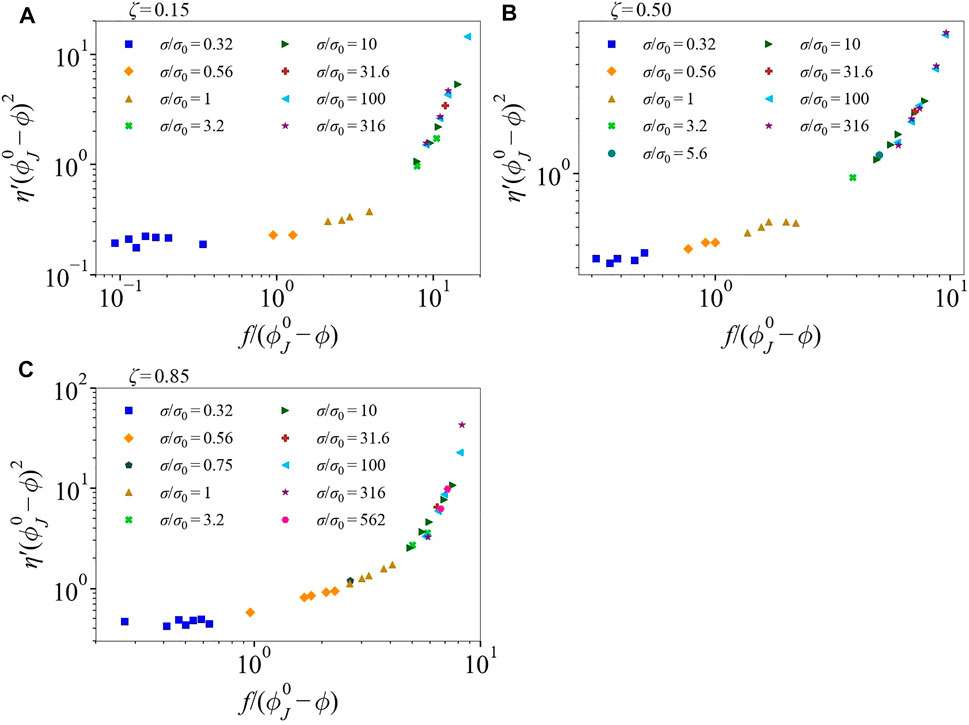
FIGURE 4. The scaling function ${\mathcal{F}}_{\eta }={\eta }^{\prime }{({\varphi }_J^0-\varphi )}^2$ plotted as a function of the scaling variable x = f/(ϕ₀ − ϕ) for bidisperse suspensions at δ = 3 and varying large particle fraction (A) ζ = 0.15 (B) ζ = 0.50, (C) ζ = 0.85 over 0.54 ≤ ϕ ≤ 0.60 and 0.32 ≤ σ/σ₀ ≤ 562. For ζ = 0.15, the form of f is exponential f(σ) = exp (σ*/σ) with σ* = 1.45, for ζ = 0.50 and 0.85, it is fitted manually f = f_fit.

FIGURE 5

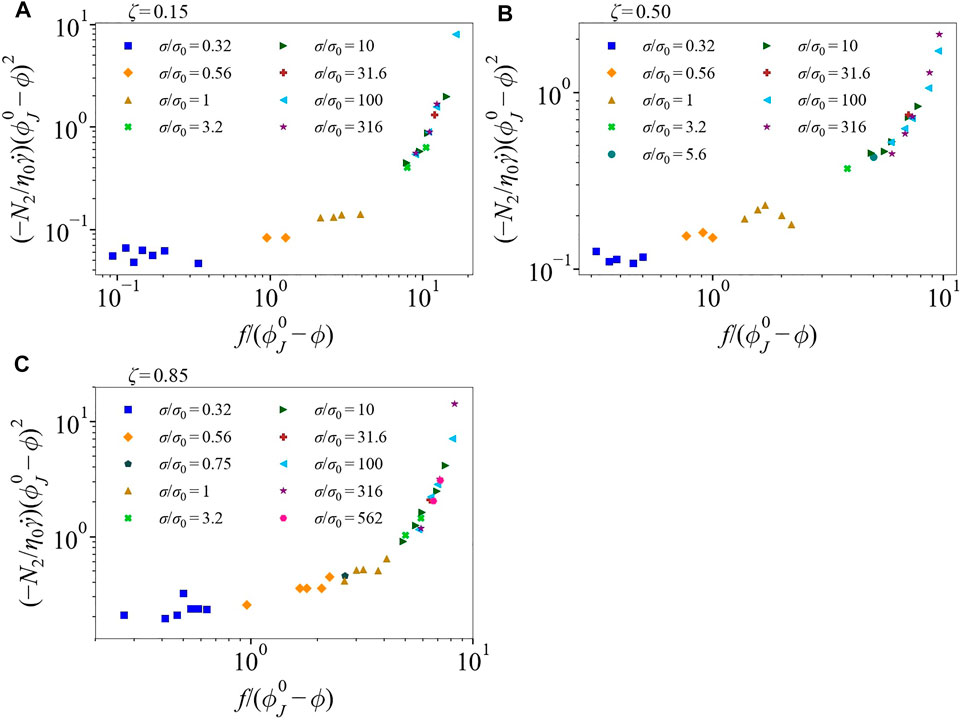
FIGURE 5. The scaling function ${\mathcal{F}}_{N_2}=-{\widehat{N}}_2{({\varphi }_J^0-\varphi )}^2$ plotted as a function of the scaling variable x = f/(ϕ₀ − ϕ) for bidisperse suspensions at δ = 3 and varying large particle fraction (A) ζ = 0.15 (B) ζ = 0.50, (C) ζ = 0.85 over 0.54 ≤ ϕ ≤ 0.60 and 0.32 ≤ σ/σ₀ ≤ 562. For ζ = 0.15, the form of f is exponential f(σ) = exp (σ*/σ) with σ* = 1.45; for ζ = 0.50 and 0.85, it is fitted manually f = f_fit.

FIGURE 6

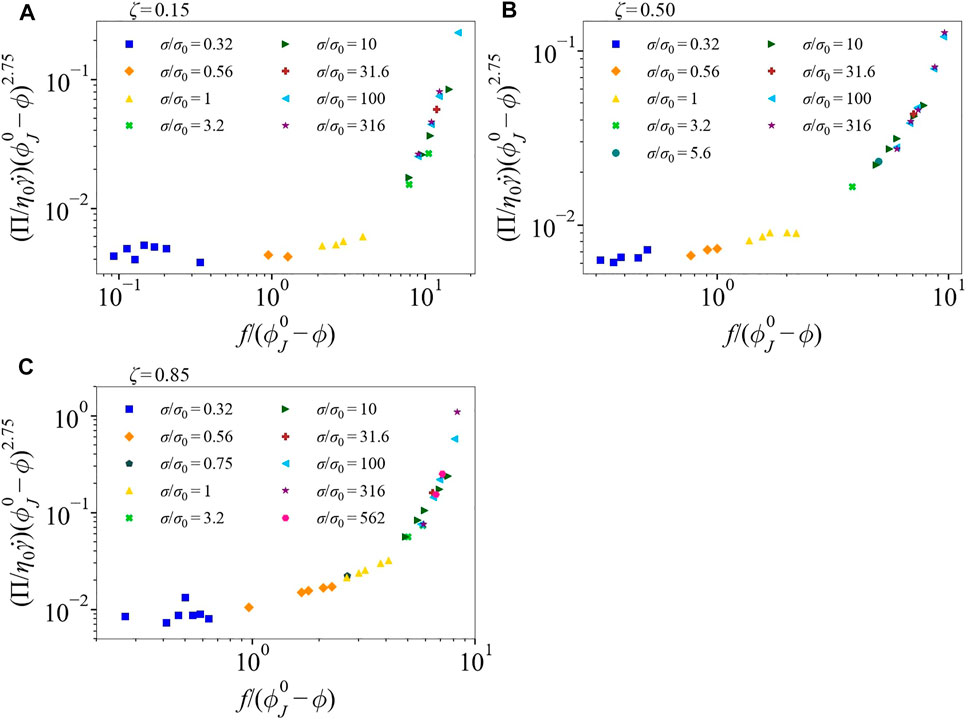
FIGURE 6. The scaling function ${\mathcal{F}}_{\mathrm{\Pi }}=\widehat{\mathrm{\Pi }}{({\varphi }_J^0-\varphi )}^{2.75}$ (note the different exponent relative to ${\mathcal{F}}_{\eta }$ and ${\mathcal{F}}_{N_2}$ in the prior two figure) plotted as a function of the scaling variable x = f/(ϕ₀ − ϕ) for bidisperse suspensions at δ = 3 and varying large particle fraction (A) ζ = 0.15 (B) ζ = 0.50, (C) ζ = 0.85 over 0.54 ≤ ϕ ≤ 0.60 and 0.32 ≤ σ/σ₀ ≤ 562. For ζ = 0.15, the form of f is exponential f(σ) = exp (σ*/σ) with σ* = 1.45; for ζ = 0.50 and 0.85, it is fitted manually f = f_fit.

For ζ = 0.15, we use f(σ) = exp (σ*/σ), as done for the monodisperse suspension data. For ζ = 0.50 and 0.85, however, we have to modify the expression. To do so, we fit the function manually, calling the result f_fit, in order that the data collapse to their respective curves. The selected values are the same for any fixed value of σ/σ₀, consistent with f = f_fit being a function only of σ and independent of ϕ. It is important to highlight that the ζ = 0.15 suspension consists of mostly small particles. This makes the suspension very similar to the monodisperse case with just a few large particles, thus creating no issues with using f(σ) = exp (σ*/σ); note that the dominant fraction is truly monodisperse in this mixture.

To illustrate the form of f_fit and how it differs from the exponential f(σ) = exp (σ*/σ), in Figure 7 we plot both forms as a function of dimensionless shear stress σ/σ₀. There are significant differences, and these depend on the packing parameters. For ζ = 0.85, f_fit is larger compared to the exponential f, with df/dσ being more gradual at low shear stresses σ/σ₀ ≤ 3. As shear stress increases, f_fit crosses the exponential f and eventually saturates at high shear stress but slightly slower than its counterpart. For ζ = 0.50, f_fit is slightly larger than the exponential f at low stresses, but becomes gradually smaller after σ/σ₀ ≥ 6 and requires larger stress to saturate. The difference between the forms of f raises the question of how f is related to frictional contacts of different types of particles, i.e. between small-small, small-large, and large-large particles. Note that in the work of Ramaswamy et al. [19], it was found necessary to allow a modification of the function related to the fraction of frictional contacts, g (σ, ϕ) to allow data collapse; in the current work, the added dependence is not on ϕ but on packing parameters.

FIGURE 7

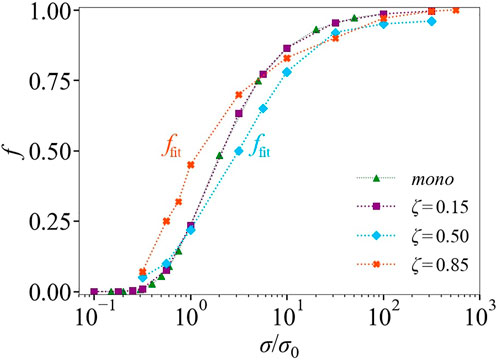
FIGURE 7. Fraction of frictional contacts f and f_fit as a function of dimensionless shear stress σ/σ₀ for monodisperse suspension δ = 1.4 ζ = 0.50 and bidisperse suspensions δ =3 for ζ = 0.15, 0.50 0.85. For δ = 1.4 with ζ = 0.50 and δ = 3 with ζ = 0.15, the form of f is exponential f(σ) = exp (σ*/σ) with σ* = 1.45. For ζ = 0.50 and 0.85, it is fitted manually f = f_fit.

To provide an essentially similar form for each rheological function across all cases, we normalize the scaled data. Scaling each $\mathcal{F}$ by its baseline value and plotting the result as a function of x/x_c, we see that ${\mathcal{F}}_{\eta }={\eta }^{\prime }{({\varphi }_J^0-\varphi )}^2$ shows an excellent scaling collapse (Figure 8). ${\mathcal{F}}_{\mathrm{\Pi }}=\widehat{\mathrm{\Pi }}{({\varphi }_J^0-\varphi )}^{2.75}$ also shows good scaling collapse for x/x_c > 10⁻¹, but there is significant scatter for smaller x/x_c. For ${\mathcal{F}}_{N_2}=-{\widehat{N}}_2{({\varphi }_J^0-\varphi )}^2$ a common curve emerges as x/x_c → 1, but the general collapse is poorer than we find for the other $\mathcal{F}$-functions.

FIGURE 8

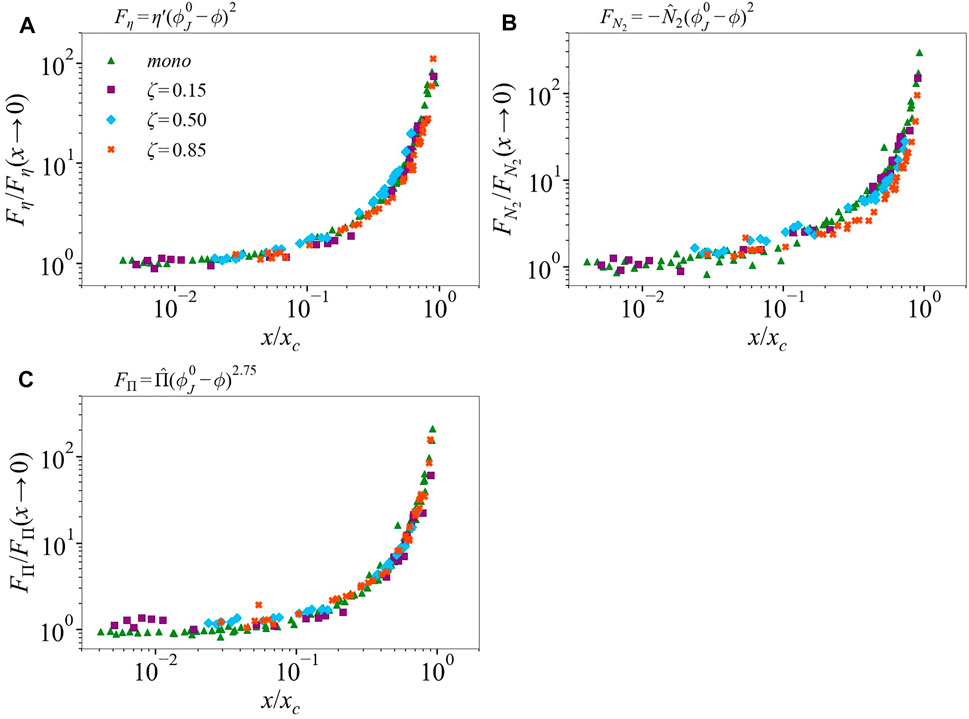
FIGURE 8. Scaling functions (A) ${\mathcal{F}}_{\eta }$, (B) ${\mathcal{F}}_{N_2}$, and (C) ${\mathcal{F}}_{\mathrm{\Pi }}$, normalized by their baseline values, versus the scaling variable x/x_c for simulated monodisperse (δ = 1.4 and ζ = 0.50 over 0.52 ≤ ϕ ≤ 0.63) and bidisperse (δ = 3 for ζ = 0.15, 0.50, 0.85 over 0.54 ≤ ϕ ≤ 0.60) suspensions, where $x=f/({\varphi }_J^0-\varphi )$ and $x_c=1/({\varphi }_J^0-{\varphi }_J^{\mu })$. For monodisperse suspension and bidisperse suspension at ζ = 0.15 the form of f is $f(\sigma )=e^{-{\sigma }^{*}/\sigma }$. For bidisperse suspensions at ζ = 0.50 and 0.85 it is f_fit. The legend in panel (A) is used in all plots.

Cardy scaling: We now apply the Cardy scaling to the bidisperse suspension data. We plot the scaling functions $\mathcal{H}$ against |1/x − 1/x_c| in Figure 9 for η′, ${\widehat{N}}_2$, and $\widehat{\mathrm{\Pi }}$. Recall that ${\mathcal{H}}_{\eta }={\eta }^{\prime }{f}^2$ and ${\mathcal{H}}_{N_2}=-{\widehat{N}}_2{f}^2$, while the particle pressure differs in the exponent of f and is given by ${\mathcal{H}}_{\mathrm{\Pi }}=\widehat{\mathrm{\Pi }}{f}^{2.75}$.

FIGURE 9

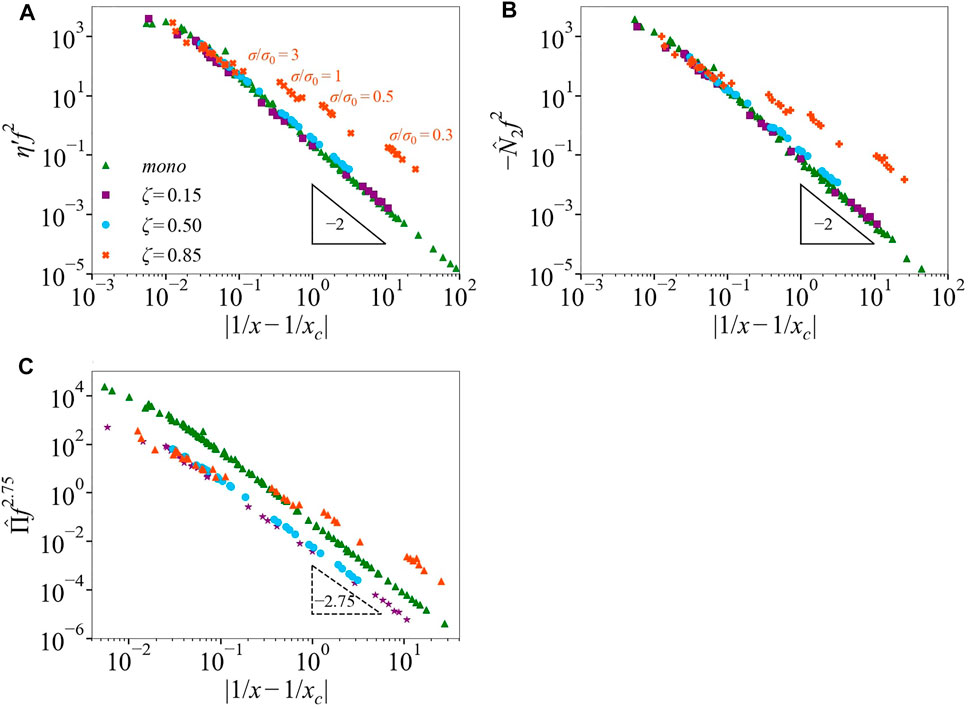
FIGURE 9. The scaling functions (A) ${\mathcal{H}}_{\eta }={\eta }^{\prime }{(f(\sigma ))}^2$, (B) ${\mathcal{H}}_{N_2}=-{\widehat{N}}_2{(f(\sigma ))}^2$, (C) ${\mathcal{H}}_{\mathrm{\Pi }}=\widehat{\mathrm{\Pi }}{(f(\sigma ))}^2$ versus |1/x_c − 1/x| for monodisperse suspensions with δ = 1.4, ζ = 0.50 and bidisperse suspensions with δ = 3 and varying ζ = 0.15, 0.50, 0.85 over 0.54 ≤ ϕ ≤ 0.60 for $f(\sigma )=e^{({\sigma }^{*}/\sigma )}$ and f_fit. Each set of data for ζ = 0.85 belongs to a specific shear stress (labeled) but varying ϕ. The black solid triangles in (A) and (B) indicate the slope of −2, the black dashed triangle in (C) indicates the slope of −2.75.

For ζ = 0.15, an excellent collapse on the same curve as the monodisperse data is found over almost five orders of magnitude in the scaling variable for η′ and ${\widehat{N}}_2$ in Figures 9A,B, respectively; for ζ = 0.50, the collapse to this same line is equally good for small |1/x − 1/x_c| (approaching frictional jamming) but there is some evidence of departure from the scaling at |1/x − 1/x_c| > 10^–1. At larger values of |1/x − 1/x_c|, the behavior is governed for both by $\mathcal{H}\sim |1/x-1/x_c{|}^{-2}$, i.e., the line has slope of −2. However, this slope changes to a smaller magnitude at small |1/x_c − 1/x|, with the crossover occurring at |1/x_c − 1/x| between 10^–2 and 10^–1. For bidisperse suspensions with ζ = 0.85, the data lay off the collapse curve for |1/x − 1/x_c|≳ 10^–1, with each separate set of data corresponding to one shear stress in the range between 0.3 ≤ σ/σ₀ ≤ 3; the points in each set labeled by stress level are at different volume fraction. The higher stress data, σ/σ₀ > 3, eventually collapse on the main line at |1/x − 1/x_c|≲ 10^–1. The ζ = 0.85 suspension data not lining up with the rest of the data highlights the fact that f used to collapse the data in Figures 4–6 and Figure 8, fails in Cardy scaling. This leads us to think that defining f as a function of shear stress only is not accurate, perhaps because the frictional contacts between different types of particles, small-small, small-large, and large-large, are not equal in their influence on the bulk stress, as was suggested by Guy et al. in their analysis of the Wyart and Cates [10] approach when applied to experimental data at δ = 4 [18].

The Cardy scaling of bidisperse particle pressure data shows two notable features. First is that the scaling requires the different dependence of f^2.75 to achieve collapse, and the data for the bidisperse cases do not fall on the line with the nearly monodisperse data, but both have power law scaling with an exponent of −2.75 at larger values of |1/x − 1/x_c| (lower stress). Similar to η′ and ${\widehat{N}}_2$, the exponent changes to a slightly smaller value at |1/x − 1/x_c| < 10⁻¹. Again, the data for ζ = 0.85 do not collapse well, except as |1/x − 1/x_c| → 0.

The crossover behavior for both monodisperse and bidisperse suspensions is in line with the findings from experimental work of Ramaswamy et al. [19] carried out for two different suspensions, cornstarch in glycerol and silica particles in glycerol-water mixtures. On the other hand, this appears to disagree with the previous simulation work [32], where the monodisperse (δ = 1.4, ζ = 0.50) and bidisperse (δ = 3 and four for ζ = 0.15, 0.50, 0.85) viscosity data were shown to diverge with a single exponent as $\eta \sim {({\varphi }_J-\varphi )}^{-2}$, where ϕ_J is the maximum packing fraction that decreases its value with the increase of σ. In that work, the high-ϕ data at large σ lay off the power law curve, which was suggested as potentially being due to underestimation of the maximum packing fraction. In light of the current work, this discrepancy suggests that a more sophisticated form of scaling than was used in [32] is needed to account for the diverging viscosity on approach to ${\varphi }_J^{\mu }$.

4 Conclusion

We have carried out a scaling analysis on the rheology determined from simulations of shear-thickening suspensions. This is the first application of the crossover and Cardy scaling to simulated suspension rheology data. Our analysis includes nearly monodisperse suspensions studied in prior work [15] and bidisperse suspensions with particle size ratio δ = 3 for fractions of the particle volume occupied by large particles given by ζ = 0.15, 0.50, and 0.85. We considered first a critical exponent approach and then Cardy scaling. We showed that the singular part of the suspension relative viscosity given by η′ = η_r − (1 + 5ϕ/2) exhibits critical scaling, with the data collapsing to a universal curve when plotted as ${\eta }^{\prime }{({\varphi }_J^0-\varphi )}^2$ as a function of $f/({\varphi }_J^0-\varphi )$ for both monodisperse and bidisperse suspensions studied. Here, ${\varphi }_J^0$ is the frictionless (or low stress) jamming fraction, and the fraction of frictional contacts f(σ) plays a key role. Note that while the data collapses with that of the monodisperse case for the smaller ζ bidisperse suspensions and the flow state diagrams [5, 10, 15] would be qualitatively similar, the forms would differ quantitatively because jamming fractions and the separation between them differ with the packing parameters δ and ζ.

The normal stress response was also found to follow the scaling, albeit with more scatter. Adapting Eq. 1 for ${\widehat{N}}_2=N_2/{\eta }_0\dot{\gamma }$, $-{\widehat{N}}_2{({\varphi }_J^0-\varphi )}^2$ showed reasonably good collapse. The particle pressure, however, exhibited a different exponent in order for the data to achieve a collapse, namely $\widehat{\mathrm{\Pi }}{({\varphi }_J^0-\varphi )}^{2.75}$ collapsed the data, again as a function of $f/({\varphi }_J^0-\varphi )$; we cannot at present offer a mechanistic basis for this difference in form for the particle pressure. All functions plotted in this fashion had a divergence at $x_c=1/({\varphi }_J^{\mu }-{\varphi }_J^0)$, with ${\varphi }_J^{\mu }$ the frictional or high stress jamming fraction. As noted, ${\varphi }_J^{\mu }-{\varphi }_J^0$ differs depending upon the packing parameters.

The Cardy scaling analysis revealed a change in the exponent for the divergences of η′, ${\widehat{N}}_2$, and $\widehat{\mathrm{\Pi }}$. We find the frictionless limit to have a −2 exponent for η′ and ${\widehat{N}}_2$ and −2.75 for $\widehat{\mathrm{\Pi }}$, and the magnitude decreases to an exponent of $\approx 1.5$ as frictional jamming is approached. The change in slope occurred in the range |1/x_c − 1/x| of 10⁻¹ to 10⁻², similar to the location of the slope change observed in the experimental work of Ramaswamy et al. for two different systems. In essence, we demonstrated that all viscosity data, as well as N₂ and Π data could be related to each other through the scaling parameter $x=f/({\varphi }_J^0-\varphi )$.

We have also demonstrated that the fraction of frictional contacts f necessary to obtain collapse differs in form depending on the suspension packing parameters. Specifically, for monodisperse suspensions and the bidisperse ζ = 0.15-suspensions, f follows the exponential form $f(\sigma )=e^{({\sigma }^{*}/\sigma )}$ which has been previously described [15]. In order to achieve a collapse for the bidisperse ζ = 0.50 and 0.85 suspensions, however, we found that f had to be modified and this was done by fitting the function manually for each set of packing parameters (δ and ζ), but otherwise retaining only stress dependence, such that a scaling collapse could be obtained. This was due in part to the fact that the different size particles are driven into contact across a range of stresses, such that the single critical stress is incomplete. However, consistent with the arguments of Guy et al. [18], the need for different forms of f depending on ζ appears to also arise from the different contributions to the stress of frictional contacts between different types of particles, i.e. small-small, small-large, or large-large particle interaction, and this topic warrants further investigation.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

NM performed the simulations. NM, AS, and JM analyzed the data. BC conceived the scaling analysis approach for the system under study and oversaw its application. JM developed the simulation approach and designed the study of the bidisperse suspensions. All authors wrote the manuscript.

Funding

This work was supported by a collaborative grant, NSF CBET-1916877 (BC) and NSF CBET- 1916879 (JM). Computations resulting in this work were supported, in part, under the NSF grants CNS-0958379, CNS-0855217, and ACI-1126113 to the City University of New York High Performance Computing Center at the College of Staten Island.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors are grateful to Abhinendra Singh (University of Chicago) for providing data for the δ = 1.4 suspension. We are grateful for support in the simulation effort from Romain Mari (CNRS, Grenoble).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.946221/full#supplementary-material

References

1. Barnes HA. Shear Thickening ("Dilatancy") in Suspensions of Nonaggregating Solid Particles Dispersed in Newtonian Liquids. J Rheol (1989) 33(2):329–66. doi:10.1122/1.550017

CrossRef Full Text | Google Scholar

2. Wagner NJ, Brady JF. Shear Thickening in Colloidal Dispersions. Phys Today (2009) 62(10):27–32. doi:10.1063/1.3248476

CrossRef Full Text | Google Scholar

3. Peters IR, Majumdar S, Jaeger HM. Direct Observation of Dynamic Shear Jamming in Dense Suspensions. Nature (2016) 532(7598):214–7. doi:10.1038/nature17167

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Brown E, Jaeger HM. Shear Thickening in Concentrated Suspensions: Phenomenology, Mechanisms and Relations to Jamming. Rep Prog Phys (2014) 77(4):046602. doi:10.1088/0034-4885/77/4/046602

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Morris JF. Shear Thickening of Concentrated Suspensions: Recent Developments and Relation to Other Phenomena. Ann Rev Fluid Mech (2020) 52, 121. doi:10.1146/annurev-fluid-010816-060128

CrossRef Full Text | Google Scholar

6. Seto R, Mari R, Morris JF, Denn MM. Discontinuous Shear Thickening of Frictional Hard-Sphere Suspensions. Phys Rev Lett (2013) 111(21):218301. doi:10.1103/physrevlett.111.218301

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Lin NYC, Guy BM, Hermes M, Ness C, Sun J, Poon WCK, et al. Hydrodynamic and Contact Contributions to Continuous Shear Thickening in Colloidal Suspensions. Phys Rev Lett (2015) 115(22):228304. doi:10.1103/physrevlett.115.228304

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Lootens D, Van Damme H, Hémar Y, Hébraud P. Dilatant Flow of Concentrated Suspensions of Rough Particles. Phys Rev Lett (2005) 95(26):268302. doi:10.1103/physrevlett.95.268302

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Brown E, Jaeger HM. Dynamic Jamming point for Shear Thickening Suspensions. Phys Rev Lett (2009) 103(8):086001. doi:10.1103/PhysRevLett.103.086001

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Wyart M, Cates ME. Discontinuous Shear Thickening without Inertia in Dense Non-brownian Suspensions. Phys Rev Lett (2014) 112(9):098302. doi:10.1103/PhysRevLett.112.098302

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Mari R, Seto R, Morris JF, Denn MM. Shear Thickening, Frictionless and Frictional Rheologies in Non-brownian Suspensions. J Rheol (2014) 58(6):1693–724. doi:10.1122/1.4890747

CrossRef Full Text | Google Scholar

12. Morris JF. Lubricated-to-frictional Shear Thickening Scenario in Dense Suspensions. Phys Rev Fluids (2018) 3(11):110508. doi:10.1103/physrevfluids.3.110508

CrossRef Full Text | Google Scholar

13. O'Hern CS, Silbert LE, Liu AJ, Nagel SR. Jamming at Zero Temperature and Zero Applied Stress: The Epitome of Disorder. Phys Rev E Stat Nonlin Soft Matter Phys (2003) 68(1):011306. doi:10.1103/PhysRevE.68.011306

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Morris JF, Boulay F. Curvilinear Flows of Noncolloidal Suspensions: The Role of normal Stresses. J Rheol (1999) 43(5):1213–37. doi:10.1122/1.551021

CrossRef Full Text | Google Scholar

15. Singh A, Mari R, Denn MM, Morris JF. A Constitutive Model for Simple Shear of Dense Frictional Suspensions. J Rheol (2018) 62(2):457–68. doi:10.1122/1.4999237

CrossRef Full Text | Google Scholar

16. Royer JR, Blair DL, Hudson SD. Rheological Signature of Frictional Interactions in Shear Thickening Suspensions. Phys Rev Lett (2016) 116(18):188301. doi:10.1103/physrevlett.116.188301

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Guy BM, Hermes M, Poon WCK. Towards a Unified Description of the Rheology of Hard-Particle Suspensions. Phys Rev Lett (2015) 115(8):088304. doi:10.1103/physrevlett.115.088304

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Guy BM, Ness C, Hermes M, Sawiak LJ, Sun J, Poon WCK. Testing the Wyart-Cates Model for Non-brownian Shear Thickening Using Bidisperse Suspensions. Soft Matter (2020) 16(1):229–37. doi:10.1039/c9sm00041k

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Ramaswamy M, Griniasty I, Liarte DB, Shetty A, Katifori E, Del Gado E, et al. Universal Scaling of Shear Thickening Transitions. arXiv preprint arXiv:2107.13338 (2021).

Google Scholar

20. Cardy J. Scaling and Renormalization in Statistical Physics. Cambridge: Cambridge University Press (1996).

Google Scholar

21. Greiner W, Neise L, Stöcker H. The Models of Ising and Heisenberg. In: Thermodynamics and Statistical Mechanics. New York: Springer (1995). p. 436–56. doi:10.1007/978-1-4612-0827-3_18

CrossRef Full Text | Google Scholar

22. Kadanoff LP. Critical Behavior. Universality and Scaling. In: MS Green, editor. Proceedings of the International School of Physics ’Enrico Fermi’ Course LI. New York: Italian Physical Society, Academic Press (1971). p. 100–17.

Google Scholar

23. Loose W, Hess S. Rheology of Dense Model Fluids via Nonequilibrium Molecular Dynamics: Shear Thinning and Ordering Transition. Rheol Acta (1989) 28(2):91–101. doi:10.1007/bf01356970

CrossRef Full Text | Google Scholar

24. Heussinger C. Shear Thickening in Granular Suspensions: Interparticle Friction and Dynamically Correlated Clusters. Phys Rev E Stat Nonlin Soft Matter Phys (2013) 88(5):050201. doi:10.1103/PhysRevE.88.050201

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Sierou A, Brady JF. Rheology and Microstructure in Concentrated Noncolloidal Suspensions. J Rheol (2002) 46(5):1031–56. doi:10.1122/1.1501925

CrossRef Full Text | Google Scholar

26. Jamali S, Brady JF. Alternative Frictional Model for Discontinuous Shear Thickening of Dense Suspensions: Hydrodynamics. Phys Rev Lett (2019) 123(13):138002. doi:10.1103/physrevlett.123.138002

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Singh A, Ness C, Seto R, de Pablo JJ, Jaeger HM. Shear Thickening and Jamming of Dense Suspensions: The “Roll” of Friction. Phys Rev Lett (2020) 124(24):248005. doi:10.1103/physrevlett.124.248005

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Estrada N, Azéma E, Radjai F, Taboada A. Identification of Rolling Resistance as a Shape Parameter in Sheared Granular media. Phys Rev E Stat Nonlin Soft Matter Phys (2011) 84(1):011306. doi:10.1103/PhysRevE.84.011306

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Ball RC, Melrose JR. A Simulation Technique for many Spheres in Quasi-Static Motion under Frame-Invariant Pair Drag and Brownian Forces. Physica A (1997) 247(1-4):444–72. doi:10.1016/s0378-4371(97)00412-3

CrossRef Full Text | Google Scholar

30. Ackerson BJ. Shear Induced Order and Shear Processing of Model Hard Sphere Suspensions. J Rheol (1990) 34(4):553–90. doi:10.1122/1.550096

CrossRef Full Text | Google Scholar

31. Ness C, Sun J. Shear Thickening Regimes of Dense Non-brownian Suspensions. Soft Matter (2016) 12(3):914–24. doi:10.1039/c5sm02326b

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Malbranche N, Chakraborty B, Morris JF. Shear Thickening in Dense Bidisperse Suspensions. J Rheol (2022). Submitted.

Google Scholar