
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Phys., 18 October 2022
Sec. Nuclear Physics
Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.944339
This article is part of the Research TopicUsing High Energy Density Plasmas for Nuclear Experiments Relevant to Nuclear AstrophysicsView all 10 articles
Experiments performed on an inertial confinement fusion (ICF) platform offer a unique opportunity to study nuclear reactions, including reaction branches that are useful for diagnostic applications in ICF experiments as well as several that are relevant to nuclear astrophysics. In contrast to beam-accelerator experiments, experiments performed on an ICF platform occur over a short time scale and produce a plasma environment with physical parameters that are directly relevant to big bang and/or stellar nucleosynthesis. Several reactions of interest, such as D(T,γ)5He, H(D,γ)3He, H(T,γ)4He, and T(3He,γ)6Li produce high-energy gamma rays. S factors or branching ratios for these four reactions have recently been studied using various temporally-resolved Cherenkov detectors at the Omega laser facility. This work describes these detectors as well as the current standard technique for performing these measurements. Recent results for reactions D(T,γ)5He, H(D,γ)3He, H(T,γ)4He, and T(3He,γ)6Li are reviewed and compared to accelerator-based measurements. Limitations associated with implosion experiments and use of the current standard gamma detectors are discussed. A basic design for a gamma spectrometer for use at ICF facilities is briefly outlined.
Inertial confinement fusion (ICF) experiments typically involve laser-driven implosion of a spherical target which produces a high-energy-density (HED) plasma as temperatures and pressures increase to levels at which fusion of ions can occur. “High-performance” ICF experiments generally use cryogenic deuterium-tritium (DT) targets consisting of DT vapor surrounded by DT ice and seek to optimize target and laser parameters so as to promote self-heating of the target through redistribution of energy as 4He or α particles from the D(T,n)4He reaction slow down in the dense cryogenic DT ice layer. While these types of experiments are of interest from a fusion energy perspective, the ICF experimental platform can also be leveraged for the purpose of nuclear science experiments. This is especially interesting within the context of astrophysically-relevant nuclear reactions. In contrast to the previously mentioned “high performance” fusion energy-focused studies, nuclear experiments performed using an ICF experimental platform typically involve warm (i.e., room-temperature) targets consisting of thin glass or plastic shells filled with a gaseous mixture of reactants.
Nuclear measurements have traditionally been made via accelerator experiments. These accelerator experiments typically collect data using ions from a beam which collide with static target nuclei. In contrast, experiments performed on an ICF platform are able to more closely replicate conditions present in astrophysical environments, such as those relevant to big bang or stellar nucleosynthesis. For example, ICF experiments establish a population of moving ions in which reactions occur along with temperature, pressure, and electron screening effects that can come closer to those present when nucleosynthesis occurs in nature. There are, however, also potential disadvantages to use of the ICF platform for cross-section/S-factor measurements. For example, ICF experiments typically generate relatively large particle fluxes per unit time in comparison to accelerator experiments. This can be advantageous for the purpose of limiting backgrounds (e.g., backgrounds from cosmic rays), however, the production of particles in several distinct, pulse-like events instead of one continuous experiment means that particle statistics cannot be improved by a simple increase in the duration of the experiment. This means that certain very low cross-section reactions cannot currently be studied on an ICF platform, as particle statistics would be too poor to produce meaningful results. Furthermore, only certain types of detectors can be successfully used on an ICF platform. Traditional pulse height detectors, for example, cannot be used due to the short time scales of ICF experiments. Time-of-flight detectors are typically used instead, though calibration of these detectors can be challenging.
There are some further restrictions on which reactions can be studied via ICF experiments based on the reactants involved. ICF experiments can typically only accommodate nuclear experiments involving gaseous light ions (which are used as the target fill). Implosion of these targets produces primary fusion gammas and neutrons with the energies of the products depending on the reactants present in the gas fill. DT and DD gas fills are the most commonly used in ICF experiments. It is also possible to conduct experiments involving the collision of DT (14-MeV) or DD (2.45-MeV) neutrons on some material situated outside of the target [1]. It is generally not possible to further select the gamma or neutron energies produced by the implosion.
Production of additional reactions besides the reaction of interest to the experiment can also lead to backgrounds on the spectra of interest. For example, implosion of a DT target produces DD and TT neutrons as well as DT neutrons, and DD gammas as well as DT gammas. Considering these many differences from accelerator experiments as well as these unique advantages and disadvantages, it is clear that experiments performed on ICF platforms represent a valuable complement to specific types of accelerator experiments rather than a replacement for accelerator experiments. The properties and particle statistics involved in any given ICF-based experimental campaign that aims to make nuclear cross-section measurements must be closely evaluated before determining whether the ICF platform is suitable for a given study.
This work reviews the current standard procedure for studying gamma-producing nuclear fusion reactions in HED plasmas as produced by ICF experiments. The design and calibration of the standard gamma detectors present at ICF facilities are detailed. The standard procedure for calculating nuclear yields using these detectors is outlined and results of ICF-based studies focusing on the four reactions D(T,γ)5He, H(T,γ)4He, H(D,γ)3He, and T(3He,γ)6Li are then reviewed. Finally, potential directions for the development of a gamma spectrometer that is practical for use at ICF facilities are discussed.
To date, the fusion gammas from the reactions D(T,γ)5He, H(T,γ)4He, H(D,γ)3He, and T(3He,γ)6Li have been studied at the Omega laser facility. Due to its relatively large cross section, the reaction D(T,n)4He is considered to be among the most promising to focus upon for the purposes of fusion energy research. As such, DT implosions constitute the majority of experiments performed at ICF facilities, and neutrons from this reaction are studied intensively. Gamma rays from the branch D(T,γ)5He are produced simultaneously and are also used for complementary diagnostic purposes in fusion energy-focused implosion experiments. In particular, the DT gamma is currently used for measurements of burn width, which is considered a vital parameter in evaluating the performance of these implosions. Gammas from this reaction as well as H(T,γ)4He are additionally used in dedicated experiments that seek to study the mix of ablator material from the target’s shell into its hot spot, where most of the fusion occurs, as excessive mixing of ablator material into the hot spot is known to degrade overall implosion performance [2]. In addition to their importance to ICF itself, study of the gammas from these reactions serve as references for the design and execution of experiments that instead seek to perform nuclear measurements using implosions at facilities such as OMEGA or the National Ignition Facility (NIF). The DT gamma is also vital for the absolute calibration that is necessary to make such measurements, which will be further discussed in Section 2.
H(D,γ)3He and T(3He,γ)6Li are both important reactions within the context of big bang nucleosynthesis (BBN). These reactions are both relevant to the cosmological lithium problem, which describes 1) a factor of ∼ 3-4 discrepancy between the observed abundances of primordial 7Li and the primordial 7Li abundance that is expected based on the current standard model of BBN, and 2) a ∼3 order of magnitude discrepancy in the amount of 6Li observed in metal-poor stars and the 6Li abundance that is expected according to the standard model of BBN [3–6]. H(D,γ)3He is important to BBN (as well as to the evolution of protostars [7]) due to its consumption of deuterium and production of 3He. It is known to be the primary reaction which consumes deuterium and produces the 3He needed for the eventual production of heavier nuclei in BBN. It is therefore considered to be a limiting reaction in BBN, as uncertainties or perturbations in the cross section or S factor for this reaction would influence abundances of primordial D, 3He, and Li [6, 8]. T(3He,γ)6Li is clearly relevant to the lithium problem as a reaction that directly creates 6Li. Furthermore, there is limited experimental data available on the cross section for this reaction, especially at the low energies relevant to BBN [9]. Although there are several reactions that are relevant to BBN, these two reactions have been studied on an ICF platform due to their importance as well as due to the fact that their relatively high cross sections and the energies of their emitted gammas lend themselves towards successful measurements at conditions achievable via implosion experiments and with the gamma detectors that are currently available at ICF facilities.
Due to the relatively short (∼100-ps scale burn duration) time scales associated with ICF experiments, the standard gamma detectors available at ICF facilities are all current-mode (i.e., temporally-resolved) detectors. This means that the raw signal from these detectors is a voltage as a function of time. All of the standard gamma detectors currently available at ICF facilities (i.e., NIF and OMEGA) are Cherenkov detectors. These detectors typically involve a glass, plastic, or gas reservoir that serves as a radiator. The radiator is coupled to a photomultiplier tube (PMT). Because all gammas travel at the speed of light and generally are not scattered by materials present in ICF targets, these Cherenkov detectors typically detect all prompt fusion gammas within a relatively short spread of times. Secondary gammas such as neutron-induced inelastic gammas may also be observed at later times in the time-of-flight signal, the exact timing of which can be altered depending on the detector distance and the material’s distance from target chamber center (TCC). This configuration can be useful for calibration purposes.
Cherenkov detectors rely on the phenomenon of Cherenkov radiation. Incident gamma rays scatter electrons in the radiator, which produce electromagnetic radiation in the form of photons which are emitted in spherical wavefronts. If the speed of a given electron is greater than the local speed of light within the radiator, constructive interference between the spherical wavefronts produces a conical flux of photons (“Cherenkov radiation”) which can be detected by a photo-detector such as a PMT. The local speed of light in a medium is equal to c/n where c represents the speed of light in vacuum while n represents the index of refraction of a material. It is therefore clear that the minimum gamma energy that can be detected by a given Cherenkov detector depends on the index of refraction of its radiator.
The main detectors that are currently in use at ICF facilities and may be used for nuclear astrophysics experiments such as cross-section or S-factor measurements include the two Gas Cherenkov Detectors (GCD’s) GCD-1 [10, 11] and GCD-3 [12] as well as the Diagnostic for Areal Density (DAD) [13]. There are GCD’s available at both the NIF and OMEGA, however, the DAD is only available at OMEGA. The three detectors can be run simultaneously at OMEGA, and the two GCD’s can be run simultaneously at the NIF.
Both GCD-1 and GCD-3 use pressurized gases as a Cherenkov medium, though the two detectors have somewhat different designs (e.g., maximum operational pressure of GCD-1 is 100 psia while that of GCD-3 is 400 psia). Different gas fills may be used for various purposes. The type of gas and the gas pressure can be adjusted to change the threshold energy for detection via changes in the refractive index of the gas. GCD-1 can also use non-gaseous radiators such as fused silica or aerogel. Both GCD’s are re-entrant diagnostics. This means that they are fielded by placement in one of OMEGA’s ten inch manipulators (TIM’s) or one of the NIF’s diagnostic instrument manipulators (DIM’s). The TIM’s or DIM’s allow the detectors to enter the vacuum inside of the target chamber to reach close to the implosion for increased solid angle while also providing precise positioning capabilities for diagnostics. GCD-3 is an updated version of GCD-1 which includes additional shielding, improved seals, and a different snout design. Figure 1 shows a schematic for the two GCD’s and points out differences between their designs.
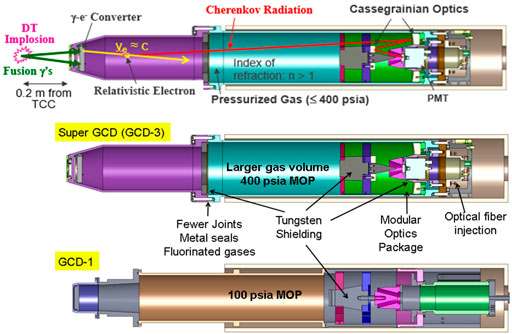
FIGURE 1. Schematic showing design of GCD-1 and GCD-3. The top diagram illustrates the general operation of these similar detectors while the lower two diagrams show the differences in design between GCD-1 and GCD-3. These detectors use Cherenkov radiation in high pressure gases to detect incident gamma rays. The threshold can be adjusted by changing the pressure of the gas. GCD-1 can also use other materials such as fused silica or aerogel radiators. These diagnostics are re-entrant diagnostics on OMEGA and the NIF. They are generally fielded close to TCC to maximize solid angle.
The DAD relies on Cherenkov radiation in fused silica. It is available at OMEGA only. It was originally deployed in 2014 to measure remaining shell areal densities via measurement of 4.4-MeV gammas from the first excited state of carbon [13], but is capable of measuring any gammas above ∼ 0.34 MeV (assuming the standard index of refraction n = 1.46 for fused silica). The DAD consists of 6 mm of tungsten shielding in front of a 6.39-cm diameter, 5-cm thick piece of fused silica, which is directly coupled to a PMT. Figure 2 shows a schematic illustrating the DAD detector design. This setup is situated directly on the wall of the OMEGA target chamber. The face of the detector is located ∼172.3 cm from TCC while the PMT and electronics are located outside the target chamber wall. In comparison to the GCD’s, the DAD has a smaller solid angle due to its location on the target chamber wall, so its particle statistics on a given experiment are generally poorer than those relevant to either GCD-1 or GCD-3. As a fixed diagnostic, however, it is much simpler to field at OMEGA, as it is always present on the target chamber and does not require any gas fill, leak testing, or precise positioning before a given shot. It is also capable of detecting low energy gammas that cannot be detected by GCD-3 (1.8 MeV minimum threshold with 400 psia C2F6) or GCD-1 (6.3 MeV minimum threshold with 100 psia CO2) with a gas fill. Its shielding as well as its location also serve to limit the presence of low level backgrounds that may be present in GCD signals. This is known to be a particular concern in the GCD-1 configuration that uses a fused silica radiator [14].
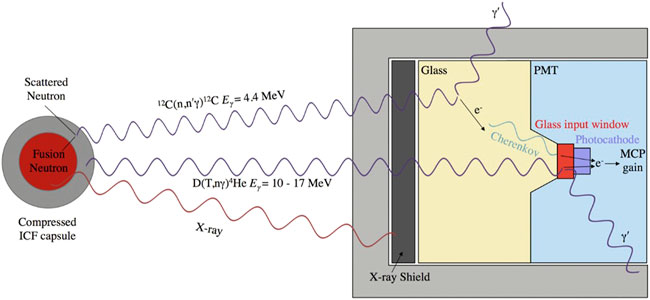
FIGURE 2. Schematic showing design of the DAD and illustrating its response to gamma rays of different energies. This detector uses Cherenkov radiation in fused silica to detect incident gamma rays. It can detect gamma rays above ∼ 0.34 MeV. It is a fixed diagnostic that is always located on the OMEGA target chamber wall, about 1.7 m from TCC. Its solid angle is therefore relatively low. Image originally published in Ref. 13 and reproduced with permission from the author and AIP Publishing.
Because they are temporally-resolved detectors and because implosion experiments occur on very short (∼ 100-ps scale burn duration) time scales, gamma detectors used at ICF facilities cannot be calibrated using the same methods as traditional pulse height gamma detectors. Temporally-resolved gamma detectors are instead calibrated in situ at OMEGA using the relatively well-known cross section for 4.4-MeV gammas produced when DT neutrons impinge upon 12C (i.e., C(n,n’)γ) [15, 16]. It is preferable to perform the calibration at OMEGA rather than the NIF due to the fact that warm DT implosions occur relatively frequently at OMEGA, so there is ample opportunity to ride along detectors for calibration without the need to secure dedicated shot days for this purpose. The faster shot cycle at OMEGA also allows for collection of much more data than would be possible at the NIF.
The general procedure for calibration involves attaching a carbon puck to the snout of a GCD during warm DT implosions, as shown in Figure 3. When the 14-MeV neutrons impinge upon the carbon puck, some of the carbon nuclei enter an excited state. Upon return to their ground state, 4.4-MeV gammas are emitted at various angles. Forward-directed gammas from the puck are then collected by the GCD holding the puck while the DAD collects backwards-directed gammas. It is also necessary to collect background data without the carbon puck in place but with the puck holder still present in order to obtain background measurements. After several shots, the data with the carbon puck present and the background data can each be averaged separately. Example signals from the DAD are shown in Figures 4, 5. The average signal without the puck present can be subtracted from the average signal with the puck present in order to isolate the signal from the 4.4-MeV carbon gamma. This signal can then be used with the differential (i.e., angularly-resolved) cross section for the C(n,n’)γ reaction as well as information about the PMT settings and the positions and solid angles of the puck and the detector to calculate a calibration constant (χ) as detailed in Refs. 15 and 16. The major source of uncertainty associated with this calibration procedure generally comes from uncertainties associated with the carbon cross section of interest.
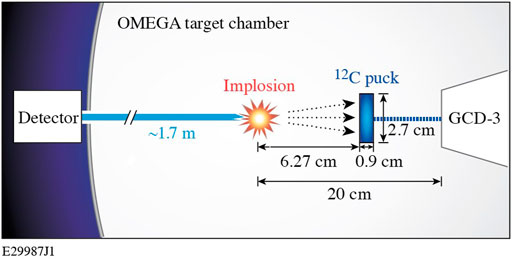
FIGURE 3. Diagram illustrating the setup for the carbon calibration. In this configuration, GCD-1 collects forward-directed gammas while the DAD collects backwards-directed gammas.
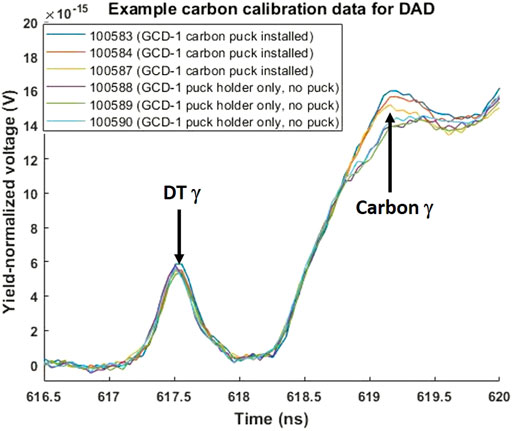
FIGURE 4. Sample of DAD data used for carbon calibration. The 9.92 g carbon puck was placed 6.6 cm away from TCC using the GCD-1 carbon puck holder. Carbon gammas from this puck were detected by DAD at an average scattering angle of 143°. Data was collected with and without the carbon puck in position. Background data without the carbon puck included the presence of the aluminum puck holder. All signals shown here are normalized to the relevant DT neutron yield.
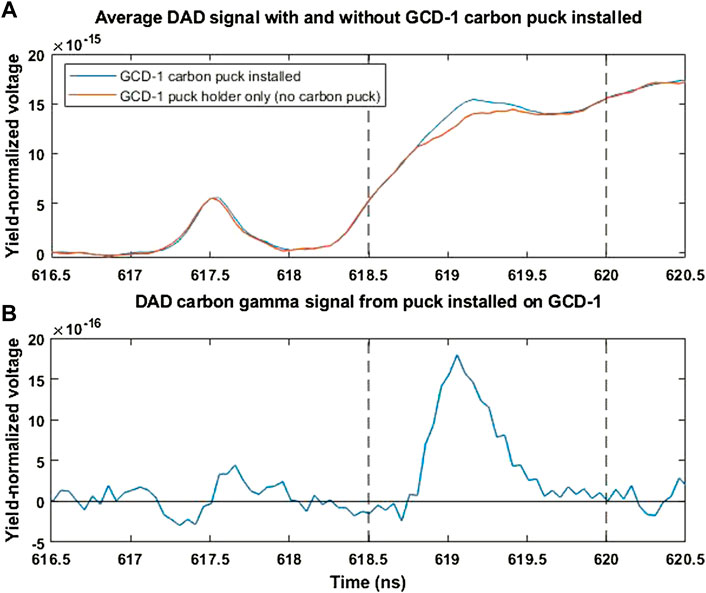
FIGURE 5. Average DAD calibration data with and without the carbon puck in place (A) and the carbon gamma data resulting from their subtraction (B). Background data without the carbon puck included the presence of the aluminum puck holder. The area of the subtracted signal is used to calculate the carbon calibration constant χ. The dashed vertical lines in the plot represent the times over which the area was calculated.
In addition to the GCD’s, the Quartz Cherenkov Detectors (QCD’s) and the Gamma Reaction History (GRH) diagnostic are also available at the NIF. The GRH is designed to use 4 GCD-like gas cells which are each coupled to a separate PMT. Each of these can be set to a different pressure (i.e., different low-energy threshold) and different PMT settings in order to measure different gamma rays of interest [17]. To date, GRH has only been absolutely calibrated to the D3He gamma, resulting in a calibration with over 30% uncertainty [18, 19]. Statistical uncertainties from the number of incident gammas as well as the number of Cherenkov photons generated in the detector only increase the total uncertainty on any given measurement using these detectors. Further calibration work would therefore be needed in order to make S-factor or cross-section measurements with reasonably low uncertainties. In addition, GRH is located 6 m from TCC, so it would be difficult to use this diagnostic for measurements related to reactions with low cross sections.
The QCD’s are similar to the DAD in that they use fused silica radiators, however, the QCD’s use a quartz rod paired to a PMT while the DAD at OMEGA uses a disc-shaped volume of quartz located directly in from of a PMT [20]. To date, the QCD’s lack absolute calibration and therefore cannot be used for nuclear astrophysics experiments such as cross-section or S-factor measurements. It could, in principle, be possible to build a duplicate QCD that can be calibrated at OMEGA in the same way that the GCD’s and DAD were calibrated. This would, however, be unlikely to enable use of the NIF QCD’s for cross-section/S-factor measurements of reactions relevant to nuclear astrophysics due to the fact that the NIF detectors are located very far from TCC, causing very low detection statistics for nucleosynthesis-relevant implosions which involve reactions with relatively low cross sections.
Once the calibration constant for a given detector is known, it can be used to calculate gamma yield based on a measured signal such that
where Aγ represents the signal area for the gamma of interest, Ω represents the detector solid angle, R represents digitizer impedance (i.e., 50 Ω), e represents electron charge, QE represents the PMT’s quantum efficiency, G represents the PMT’s gain, Cph(Eγ) represents the detector response to gammas of a given energy (i.e., Cherenkov photons produced per incident gamma), and χ represents the calibration constant. Note that the detector response Cph(Eγ) must be calculated at the relevant gamma energy and that the response as a function of energy is typically calculated using Monte Carlo simulations via a particle transport code such as Geant4 or ACCEPT. As Cherenkov detectors utilized at ICF facilities are temporally-resolved, energy-thresholded detectors and not true gamma spectrometers, the relevant gamma energy for a given implosion is generally assumed based on kinematic considerations rather than directly measured.
The gamma yield can then be used to calculate the S factor. As mentioned in the previous section, the S factor for a reaction of interest can be calculated in reference to the S factor for a reaction that is considered to be well-known such that
where the subscript r represents the reaction of interest, the subscript ref represents a reference reaction that produces particles simultaneously, fi represents fuel fractions for different species involved in a given implosion, and the factor
is used as shown in Ref. 21.
As previously mentioned, signals measured during implosion experiments may contain backgrounds by virtue of the fact that reactions other than the reaction of interest are occurring simultaneously. For example, in the case of implosion of targets filled with a mixture of H2 and D2 that aim to study the BBN-relevant reaction H(D,γ)3He, additional gammas are generated via the reaction D(D,γ)4He [14, 21]. Dedicated DD implosions must therefore be included in the experimental campaign in order to isolate the signal contribution from gammas associated with the reaction of interest. Potential backgrounds must therefore be carefully considered during the design phase of any experimental campaign that is to be performed on an ICF platform in order to properly incorporate any additional shots necessary to quantify backgrounds.
Note that any experiments involving tritium in the target fill will necessarily contain some deuterium which is present as an impurity in the tritium part of the fill. As the cross section for DT reactions is known to be relatively large, these reactions will also likely generate DT backgrounds in experiments that aim to study reactions involving tritium [14, 22].
The following is a review of gamma-branch fusion reactions that are relevant to nuclear astrophysics and have recently been studied at the Omega laser facility. Note that all of these experiments have so far been performed at the OMEGA. Although protons and neutrons from astrophysically-relevant reactions have been performed at the NIF [23], no studies of gamma-branch fusion reactions have yet occurred at this particular facility. It would be possible to perform such studies at the NIF, which has GCD’s available as outlined in the previous section, though the length of the NIF shot cycle would make it considerably more difficult to perform duplicate shots as well as to incorporate the shots that are necessary to examine backgrounds for these experiments. It may, however, be advantageous to design campaigns to study these reactions on the NIF at some point, as the NIF is able to reach laser energies (and therefore particle fluxes) that cannot be reached at OMEGA.
The DT gamma from the reaction D(T,γ)5He has primarily been studied within the context of the DT gamma-to-neutron branching ratio (i.e, the ratio between this gamma-producing reaction and the neutron-producing reaction D(T,n)4He). It is mainly of interest within the context of the endeavor to create a fusion-based source of sustainable energy, as the neutron branch DT reaction has a relatively high cross section and is therefore the focus of most NIF and OMEGA experiments that seek to reach ignition and/or determine improved approaches towards reaching ignition. While the gamma branch reaction is known to be several orders of magnitude lower in cross section than the neutron branch reaction, these gammas can be useful for diagnostic purposes because gammas generally do not scatter within remaining target material and do not experience Doppler broadening in transit (whereas neutrons do). As DT implosions are the most common type of experiments performed on ICF platforms, the DT reaction serves an important role in the calibration of gamma detectors that are to be used in subsequent experiments (as discussed in Section 2). The gamma and neutron branches of this reaction can also serve as important reference reactions for subsequent astrophysics- as well as fusion energy-relevant experiments that use these detectors.
The gamma branch DT reaction produces gammas into a distributed energy spectrum that is related to the nuclear structure of 5He. An example of the spectrum was recently reported in Ref. 24, which calculated a spectrum based on GCD-1 measurements collected with different gas pressures (i.e., different gamma energy thresholds) in combination with R-matrix values for the structure of 5He. The spectrum is reproduced in Figure 6.
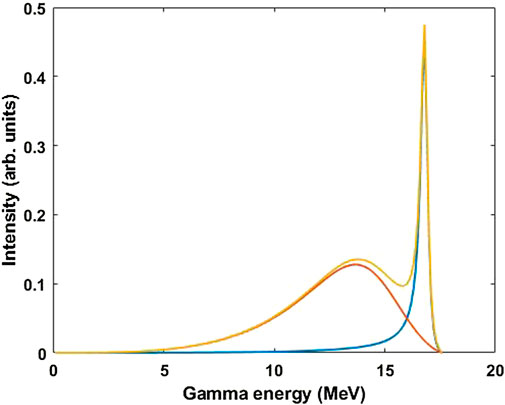
FIGURE 6. DT gamma spectrum used for weighting the DAD response function to determine a DT gamma-to-neutron branching ratio. Data from Ref. 24 has been reproduced with the permission of the corresponding author.
It should be noted that results reported from accelerator experiments span an entire order of magnitude for the DT gamma-to-neutron branching ratio. This is thought to be because accelerator targets generate a gamma background due to DT neutrons impinging upon target nuclei, as these target nuclei may then enter an excited state and emit gammas upon return to their ground states [18]. ICF facilities offer a unique opportunity to study this reaction without this gamma background and at low center-of-mass (CM) energies which are relevant to BBN and stellar nucleosynthesis but remain difficult to reach in accelerator experiments.
To date, two studies have attempted to determine the DT gamma-to-neutron branching ratio using the GCD’s at OMEGA while one study has made the same attempt using the DAD. All of these studies measured DT gammas and DT neutrons simultaneously. Each of the relevant experimental campaigns showed branching ratios that appeared to be constant over the range of ion temperatures (or CM energies) studied in the ICF experiments [16, 18, 19, 32]. No S factors were calculated for this reaction, as the shape of the D(T,γ)5He S factor would simply take on the shape of the well-known D(T,n)4He S factor with use of Eq. 2. The first ICF-based study of the DT gamma-to-neutron branching ratio used GCD-1 filled with 100 psia CO2, which corresponds to a threshold energy of 6.3 MeV. Two calibration approaches (absolute detector calibration and cross-calibration based on D3He implosions) were used to calculate a gamma-to-neutron branching ratio of (4.2 ± 2.0) × 10–5 [18, 19]. The 48% error bar on this measurement was largely due to the D3He calibration/cross section. The second study used GCD-3 filled with 400 psia CO2, which corresponds to a threshold energy of 2.6 MeV. The carbon calibration outlined in Section 2 and detailed in Ref. 15 was used to calculate a branching ratio of (4.56 ± 0.58) × 10–5 [32]. Note the reduced uncertainty due to the use of the carbon calibration, as the C(n,n’)γ cross section is more well-known than the D(3He,γ)5Li cross section.
A third study attempted to determine the DT gamma-to-neutron branching ratio using the DAD detector, which has a threshold energy of 0.34 MeV. Carbon calibration was performed for the DAD, resulting in a final branching ratio of (8.42 ± 2.84) × 10–5 [16, 33]. The relatively higher uncertainty on this measurement in comparison to the GCD-3 measurement from Ref. 32 comes mainly from the statistics involved in the carbon calibration as well as uncertainty in the DAD detector response (which was generated using Geant4 simulations).
These measurements are shown in comparison to some accelerator measurements in Figure 7. The DAD measurement from Ref. 16, 33 was a factor of ∼2 higher than the GCD measurements from Refs. 18, 19, and 32, but its error bars overlap with the error bars from the GCD-1 value from Refs. 18 or 19. Note that ICF-based measurements necessarily measure the gammas associated with the ground state of 5He (γ0) as well as the gamma associated with the first excited state of 5He (γ1). In contrast, some of the accelerator measurements aimed to measure the ground state gamma only. Considering the γ1: γ0 ratio of 2.1:1 reported in Ref. 24, the OMEGA measurements can be divided by 3.1 to get an approximate γ0 only branching ratio. All three Ω measurements [16, 18, 32] would give a γ0 measurement that appears to be consistent with the approximately linear trend in the accelerator data from Refs. 28 and 29. The DAD measurement, however, is the only of the three measurements with a total gamma measurement that seems consistent with the γ0 accelerator measurements from Refs. 28 and 29, as the DAD measurement gives a (γ0 + γ1) value that is larger than the accelerator γ0 quantities. In contrast, the total GCD-1 and GCD-3 (γ0 + γ1) measurements are lower than the γ0 only measurements from Refs. 28 and 29.
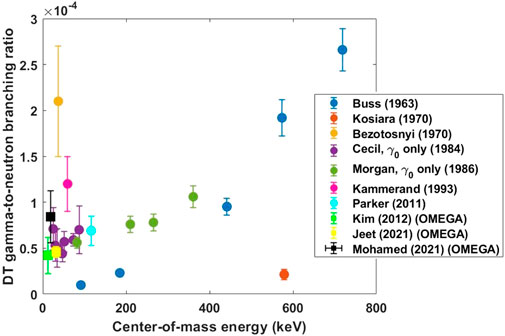
FIGURE 7. Branching ratio from the GCD-1, GCD-3, and DAD measurements on OMEGA shown along with those from accelerator experiments discussed in Refs. 25–32.
The reaction H(D,γ)3He is important within the context of BBN as a limiting reaction which consumes deuterium and produces the 3He needed to build heavier nuclei. As such, its cross section/S factor is considered to be an important bound on theoretical predictions of the primordial baryon density of the Universe [34–36]. Multiple accelerator experiments [7, 37–42] have produced S-factor measurements for this reaction, though it has been notoriously difficult to study on accelerators due to the low energy, low cross-section gammas it produces. The recent completion of the underground LUNA facility enabled high precision accelerator measurements for this reaction [42, 43]. This reaction is also considered important in the evolution of protostars [7].
Two ICF-based experimental campaigns have studied this reaction. Both campaigns included shots with targets filled with a mixture of H2 and D2 as well as targets filled with D2 only (to measure backgrounds from the reaction D(D,γ)4He, which produces a 23.9-MeV gamma) and targets filled with H2 only (to measure any contribution from non-nuclear sources such as laser-plasma interactions). Both campaigns used D(D,n)3He as the reference reaction for calculation of the H(D,γ)3He S factor using Eq. 2. DD neutrons were also used for ion temperature measurements.
The first study used GCD-3 at 400 psia CO2 (2.9 MeV energy threshold) and focused on implosions at ion temperatures of ∼ 5 keV (ECM = 16 keV) [21]. The second study [14, 33] used GCD-1 with a fused silica radiator (0.34 MeV energy threshold), GCD-3 with 400 psia CO2 (2.9 MeV energy threshold), and the DAD detector (0.34 MeV energy threshold) simultaneously. The goal of the second study was to span a range of ion temperatures (or CM energies) so as to determine an S factor as a function of CM energy for comparison to accelerator measurements. The implosions involved in this study spanned ion temperatures of 5.0–16.6 keV, corresponding to ECM = 17–37 keV. Of the three detectors used in the second study, only GCD-3 produced viable measurements, as GCD-1 showed considerable background during the H2 shots while the detection statistics on the DAD were too poor to produce a meaningful measurement for this low energy, low cross-section reaction [14, 33]. The GCD-3 measurements from both campaigns were in agreement at ∼ 5 keV ion temperature, though the value reported by Ref. 21 had a smaller uncertainty due to a larger number of shots at this ion temperature.
Both GCD-3 measurements used the carbon calibration outlined in Section 2 and detailed in Ref. 15. Both report values that appear to agree with accelerator measurements within their error bars. A comparison is shown in Figure 8. The OMEGA experiments both had larger uncertainties than those associated with accelerator measurements. This is due to a fundamental limitation associated with the implosion experiments involving low cross-section reactions: statistics on the number of particles incident on the detectors and the number of detector events resulting from these interactions are limited and cannot easily be increased at a given ion temperature/CM energy. To some extent, this issue can be addressed in accelerator experiments by increasing their run time, as accelerator experiments generally use time-integrated, energy-resolved measurements (i.e., pulse height detectors).
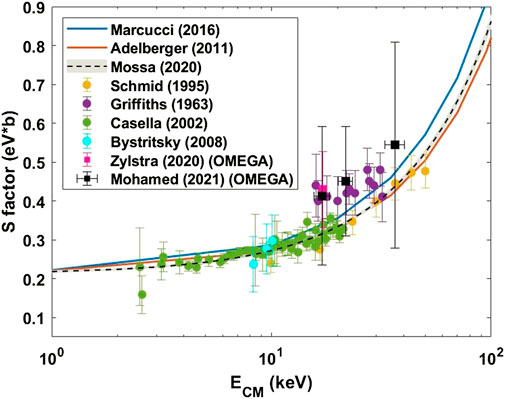
FIGURE 8. Comparison between OMEGA (GCD-3) S-factor measurements for H(D,γ)3He and accelerator measurements for this reaction. Accelerator results are from Refs. 7, 37–42. The OMEGA results inferred here appear to agree with the accelerator results within error bars, though the OMEGA error bars are generally larger due to detection statistics.
Approximate agreement between the ICF-based measurements and the accelerator measurements suggests that revision of the H(D,γ)3He cross section is not a viable solution to the cosmological lithium problem. It has been hypothesized that in situ stellar production of lithium or physics beyond the standard model may instead be responsible for the cosmological lithium problem, or that use of non-Maxwellian velocity distributions could resolve this issue from a theoretical standpoint [5, 44].
H(T,γ)4He is also a form of hydrogen burning. This reaction is directly relevant to high-performance ICF experiments that seek to achieve ignition and/or determine improved approaches towards reaching ignition, as it can be used in experiments that seek to examine burn histories of these implosions as well as to study mix of ablator material into the central hot spot [2]. The HT reaction only has a gamma branch. There is no corresponding neutron-producing branch, but small amounts of deuterium are present in the tritium part of the target fill, so DT gammas and DT neutrons are also generated in “HT” implosions. The D(T,n)4He reaction has a well-known S factor and can be used as a reference reaction for calculation of the H(T,γ)4He S factor using Eq. 2. DT neutrons can also be used to infer ion temperatures.
Despite its utility in mix experiments, studies such as those outlined in Ref. 2 typically use the HT γ for burn history measurements rather than cross-section, S-factor, or yield measurements. Only one recent OMEGA campaign has attempted to study the S factor for this reaction [14, 33]. The goal of this campaign was to span a range of ion temperatures (or CM energies) to determine an S factor as a function of CM energy for comparison with the accelerator data. The implosions involved spanned ion temperatures of 4.4–12.7 keV (ECM = 16–32 keV). Gamma detectors used in this campaign included GCD-1 with 100 psia CO2 (6.3 MeV energy threshold), GCD-3 with 30 psia CO2 (12 MeV energy threshold), and the DAD detector (0.34 MeV energy threshold). The GCD-3 signal included unexpected oscillations which were thought to be associated with the PMT while the DAD signal is believed to have been contaminated with secondary gammas from DT neutrons incident on the target’s shell, so only the GCD-1 data was considered to be reliable for the purpose of this measurement [14, 33].
The total gamma signal is known to include both the DT gamma and the HT gamma at similar levels, so a DT gamma background based on the GCD-1 measurements from Ref. 18 was subtracted from the total signal in order to isolate the HT gamma signal. The carbon calibration outlined in Section 2 and detailed in Ref. 15 was then used to calculate the HT gamma yield. Of the several accelerator measurements that have investigated this reaction [45–52], only one was conducted at energies comparable to the OMEGA measurement. The data from this experiment [52] appear to agree with the data from the OMEGA experiment within their error bars. A comparison is shown in Figure 9.
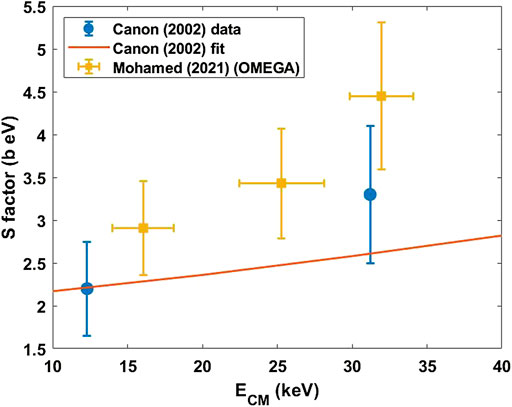
FIGURE 9. Comparison between OMEGA (GCD-1) S factor measurements for H(T,γ)4He and accelerator measurements for this reaction at similar energies. The accelerator data is from Ref. 52, which provides two data points at incident beam energies of 40 and 80 keV (or ECM = 12.3 and 31.2 keV) as well as a fit to these two data points along with data from Refs. 45 and 46. The OMEGA data points appear to agree with the data points from Ref. 52, though they are higher than the fit which included the data at higher CM energies.
The reaction T(3He,γ)6Li is astrophysically relevant within the context of BBN. This reaction is directly related to the 6Li component of the primordial lithium problem, which refers to the factor of ∼ 1000 discrepancy between predicted 6Li abundances based on the standard model of BBN and observations from low metallicity stars [3, 4]. The gamma spectrum for this reaction is known to span a range of energies with a spectrum like that shown in Figure 10. Some accelerator measurements for this reaction have been conducted, but not at CM energies relevant to BBN.
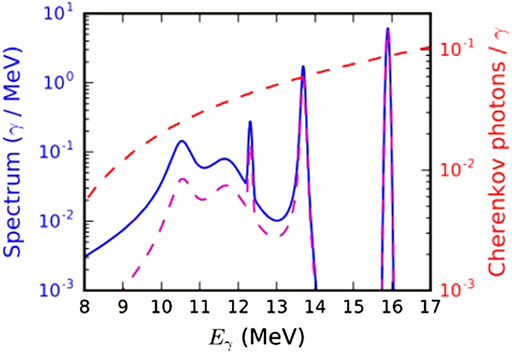
FIGURE 10. Gamma spectrum produced by the reaction T(3He,γ)6Li. The blue line shows the spectrum while the red dotted line shows the GCD response relevant to this experiment. The magenta dotted line shows the sensitivity-normalized spectrum. Plot originally published in Ref. 9 and reproduced with permission of the corresponding author. Copyright 2016 by The American Physical Society.
There was one OMEGA measurement for T(3He,γ)6Li which used GCD-3 with 100 psia CO2 (6.3 MeV energy threshold) [9]. Deuterium was also present in the implosion as an impurity in the tritium part of the target fill. Ion temperatures were determined from protons produced by the reaction D(3He,p)4He. The OMEGA measurement was performed at ECM = 81 keV, which is within the range relevant to BBN. Gamma backgrounds were produced by DT and D3He reactions, and dedicated shots were performed during the campaign to quantify these backgrounds. The reference reaction used to determine the T(3He,γ)6Li S factor in Eq. 2 was T(3He,D)4He. CR-39 tracks as well as dipole magnetic spectroscopy were used to detect deuterons from this reaction.
Ref. 9 notes that the ICF-based S factor for this reaction was determined over 4π (as is relevant to BBN) while the accelerator data from Ref. 53 was measured as a differential cross section at 90 degrees. Ref. 9 uses an R-matrix calculation based on the 90 degree data from Ref. 53 for comparison. The data point from the ICF experiment agrees with this R-matrix calculation [9]. The relevant comparison is shown is Figure 11. This agreement suggests that a nuclear solution to the lithium problem seems unlikely. It has been hypothesized that in situ stellar production of lithium or physics beyond the standard model may instead be responsible for the 6Li problem, or that use of non-Maxwellian velocity distributions could resolve the lithium problem from a theoretical standpoint [5, 44].
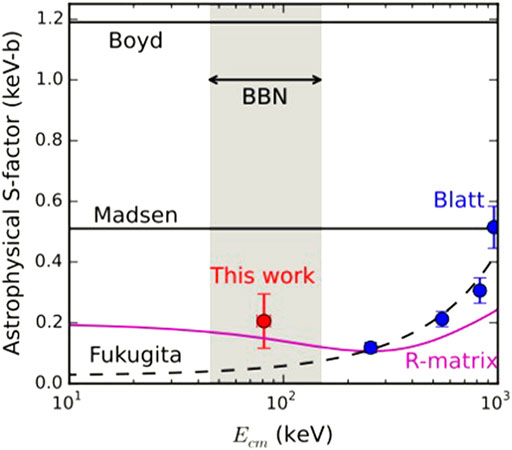
FIGURE 11. Comparison between OMEGA [9] and accelerator measurements [53–56] for the T(3He,γ)6Li S factor. The OMEGA measurement is the only of these experiments that was performed at an energy directly relevant to BBN. The “R-matrix” line is a fit performed to the data from Ref. 53 when corrected for angular effects [9]. The OMEGA measurement agrees with this fit. Plot originally published in Ref. 9 and reproduced with permission of the corresponding author. Copyright 2016 by The American Physical Society.
Based on the preceding review of the gamma detectors available for nuclear astrophysics measurements at OMEGA and the NIF as well as recent branching ratio and S-factor measurements performed at OMEGA, it is clear that it is possible to make such measurements for gamma branch fusion reactions on an ICF platform. Advantages associated with the use of the ICF platform include the presence of physical conditions such as ion populations, ion temperatures, and electron screening effects that are relevant to astrophysical situations as well as the relative ease of accessing low CM energies that are relevant to BBN and stellar nucleosynthesis. The fact that implosion experiments generate relatively large particle fluxes per unit time and therefore do not have the issue of background from cosmic rays that may arise in accelerator experiments is an additional advantage.
There are also clear complications that arise as a result of the use of ICF experimental platforms to study nuclear reactions via gamma detection. As previously mentioned, most implosion experiments will generate nuclear backgrounds in addition to the main reaction that is being examined. For example, an experiment that attempts to study the reaction H(D,γ)3He will produce gammas from this reaction as well as the reaction D(D,γ)4He. It is therefore necessary to allot shots with different target fills in order to properly quantify these backgrounds. This is one reason that HED experiments relevant to nuclear astrophysics are performed at OMEGA much more often than the NIF even though the NIF can produce reactions with higher yields: the NIF shot cycle is relatively long compared to the OMEGA shot cycle, so fewer shots are available per campaign and it is therefore difficult to complete a coherent campaign of this nature, which would require many shots to quantify backgrounds or to reach different ion temperatures.
The quality of ICF-based measurements for reactions relevant to nuclear astrophysics depends on the detectors used as well as the reaction in question. Reactions with low cross sections as well as reactions that produce gammas with low energies are generally more challenging to study on an ICF platform. ICF-based experimental campaigns that seek to study these reactions may yield results with larger error bars than equivalent accelerator experiments, as accelerator experiments may simply increase run time in order to improve particle statistics (assuming the facility and the relevant detectors are sufficiently shielded from backgrounds that may be generated by cosmic rays).
The availability of multiple Cherenkov detectors at OMEGA is advantageous, as different configurations of GCD-1 and GCD-3 radiators can be used together and in conjunction with the DAD detector, which has a lower energy threshold but receives less background signal due to its shielding and location. It is known that the DAD may collect data with poor counting statistics for low cross-section reactions, but it is simple to field and can therefore be employed in experimental campaigns without the special preparation that is required to field more complicated diagnostics like the GCD’s, which require highly pressurized gas, leak testing, and pointing within the target chamber.
All of these detectors are, however, somewhat complicated to calibrate in comparison to the pulse height detectors used at accelerator facilities. Uncertainties associated with the calibration of current-mode gamma detectors are a major source of uncertainty in S-factor measurements that come from these detectors. This issue could be addressed if another viable material for calibration could be identified. This material would need to produce secondary gammas when impinged upon by DT neutrons and would need to produce these gammas with a cross section that is more well-known than the C(n,n’)γ cross section in order to constitute improvement in the calibration of the OMEGA gamma detectors.
S factors for BBN-relevant reactions H(D,γ)3He and T(3He,γ)6Li have been studied at OMEGA [9, 14, 21, 33]. The inferred S factors were in agreement with those from accelerator-based measurements within their error bars, though the error bars from the ICF-based measurements were notably larger than those from the accelerator-based measurements. This agreement for both reactions suggests that a nuclear solution to the lithium problem is not likely. In situ stellar production of lithium or physics beyond the standard model may instead be responsible for the cosmological lithium problem [5]. It has also been shown that use of non-Maxwellian velocity distributions could resolve the issue from a theoretical standpoint [44].
As previously discussed, the gamma detectors available at ICF facilities are temporally-resolved, energy-thresholded current-mode detectors which do not collect direct spectral information. Experiments which seek to make yield, cross-section, or S-factor measurements using these detectors must therefore make some assumptions about the gamma spectrum of interest in order to proceed. With reactions such as H(T,γ)4He which are known to produce nearly monoenergetic gammas via a single reaction branch, it is simple to determine the energy of the incident gammas using kinematic calculations. It is, however, more complicated for reactions such as D(T,γ)5He or T(3He,γ)6Li, which produce gammas into a broad range of energies. Current best estimates of these gamma spectra are based on R-matrix calculations [9, 24], but at this time, there is no simple way to directly measure these gamma energy spectra.
Development of a true gamma spectrometer for use at ICF facilities would contribute an improved ability to determine cross sections/S factors for such experiments while expanding the ability to study nuclear reactions via implosion experiments in general. For example, though the reaction D(T,γ)5He is interesting due to its diagnostic utility in ICF experiments, the gamma spectrum from this reaction also contains information about the nuclear level structure of the 5He nucleus, which is not currently well understood despite the fact that it is expected to have a relatively simple shell structure. In addition to its utility for basic science experiments, the presence of a true gamma spectrometer at OMEGA and/or the NIF would provide expanded diagnostic capabilities for high-performance ICF experiments. Secondary gammas can, for example, be used in areal density and total yield measurements for ignition-relevant experiments.
There are two main difficulties in building a gamma spectrometer for use in ICF experiments: 1) Traditional pulse height gamma spectroscopy cannot be used for implosion experiments due to their short duration, and 2) ICF experiments generally produce neutron fluxes that are several orders of magnitude larger than the gamma flux. A concept for a gamma-to-electron magnetic spectrometer has been proposed for the NIF in the past [57, 58], however, this particular design was developed specifically for the NIF and has not been built due to the intensive resources that would be required. Brainstorming and some preliminary work towards the development of an alternative gamma spectrometer that could operate at OMEGA have been performed within the OMEGA nuclear group. Two potential technologies that could be used for this purpose include an electron-positron pair spectrometer and a single-hit detector [33].
The concept for an electron-positron pair spectrometer requires placement of a foil near the front face of the detector. When gamma rays are incident on the foil, electrons and positrons will be produced via pair production and Compton scattering. The energy spectra of these electrons and positrons can be measured using a permanent magnet that is located within the detector to deflect electrons/positrons onto image plates arranged along the sides of the detector. For most of the gamma reactions of astrophysical relevance that can be measured on an ICF platform, such a spectrometer would rely primarily on electrons and positrons from pair production rather than Compton electrons because photons with energies greater than 5 MeV have a pair-production cross section that is greater than the Compton scattering cross section. This design is a derivative of the existing Electron Positron Pair Spectrometer (EPPS) designed by Lawrence Livermore National Laboratory and fielded at the Omega laser facility and the NIF [59] in order to measure electrons and positrons coming directly from a plasma. Some basic design work for the electron-positron gamma spectrometer has already been carried out. Preliminary Monte Carlo simulations have shown that the optimal foil to use to detect the DT gamma is 100 μm of tungsten in an entrance slit of 2 mm × 4 mm. Assuming a DT gamma-to-neutron branching ratio of 4.2 × 10–5 [18, 19, 32] and a W foil located 10 cm from a DT-filled target that produces a neutron yield of 1014, this configuration would detect ∼1300 gamma rays with an energy resolution of ∼0.7 MeV. The issue with this method lies primarily in the use of image plates, which have proven to be susceptible to high levels of background from DT neutrons. It is, however, possible that microchannel plates (MCP’s) could be used instead of image plates. MCP’s offer spatial resolution (which is necessary to resolve an energy spectrum by this method) as well as the potential for temporal gating between the gamma and neutron signals.
An alternative to this design is a single-hit detector, which would be somewhat similar to the detector concept [57, 58] proposed for the NIF. Such a detector could easily use temporal discrimination between gamma rays and the neutrons to avoid the issue of the neutron background. Individual LaBr3(Ce) detectors (i.e., LaBr3(Ce) crystals paired with PMT’s) are readily available and are known to have decay times of ∼26 ns. They have been used in magnetic confinement experiments and are also used at the NIF in activation measurements, proving that they can withstand high neutron flux environments [60, 61]. The required distance from TCC and the necessary size of LaBr3(Ce) array required to make the desired spectral measurements would need to be further investigated in order to determine whether this would be a viable design.
Overall, much dedicated R&D work would be necessary to build and implement a true gamma spectrometer at OMEGA or the NIF. A gamma spectrometer has, however, been recognized by the OMEGA Laser Users Group as a potentially transformative diagnostic for several years, though little progress has yet been made towards this goal.
ZM wrote the article, some of which is based upon work that was conducted as part of her doctoral thesis. Review of the references/methods presented herein were vital to her ability to perform similar experiments as part of her thesis work. JK provided support as thesis advisor, assisting in experimental development and review/discussion of the methods and references discussed in the manuscript. YK provided additional editorial advice and suggestions as an expert on diagnostics relevant to this specific topic.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor MG declared a past co-authorship with the author YK, JK.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Forrest CJ, Knauer J, Schroeder W, Glebov V, Radha P, Regan S, et al. Nuclear science experiments with a bright neutron source from fusion reactions on the OMEGA laser system. Nucl Instr Methods Phys Res Section A: Acc Spectrometers Detectors Associated Equipment (2018) 888:169–76. doi:10.1016/j.nima.2018.01.072
2. Zylstra AB, Herrmann HW, Kim YH, McEvoy AM, Schmitt MJ, Hale G, et al. Simultaneous measurement of the HT and DT fusion burn histories in inertial fusion implosions. Rev Sci Instrum (2017) 88:053504. doi:10.1063/1.4983923
3. Anders M. First direct measurement of the 2H(α, γ)6Li cross section at big bang energies and the primordial lithium problem Phys Rev Lett (2014) 113:042501. doi:10.1103/PhysRevLett.113.042501
4. Asplund M, Lambert D, Nissen P, Primas F, Smith V. Lithium isotopic abundances in metal-poor halo stars. Astrophys J (2006) 644:229–59. doi:10.1086/503538
5. Fields BD. The primordial lithium problem. Annu Rev Nucl Part Sci (2011) 61:47–68. doi:10.1146/annurev-nucl-102010-130445
6. Cyburt RH, Fields BD, Olive KA, Yeh T. Big bang nucleosynthesis: Present status. Rev Mod Phys (2016) 88:015004. doi:10.1103/RevModPhys.88.015004
7. Adelberger EG, Garcia A, Robertson RGH, Snover KA, Balantekin AB, Heeger K, et al. Solar fusion cross sections. II. The pp chain and CNO cycles. Rev Mod Phys (2011) 83:195–245. doi:10.1103/revmodphys.83.195
8. Coc A, Petitjean P, Uzan JP, Vangioni E, Descouvemont P, Iliadis C, et al. New reaction rates for improved primordial D/H calculation and the cosmic evolution of deuterium. Phys Rev D (2015) 92:123526. doi:10.1103/physrevd.92.123526
9. Zylstra AB. Using inertial fusion implosions to measure the T + 3He fusion cross section at nucleosynthesis-relevant energies. Phys Rev Lett (2016) 117:035002. doi:10.1103/PhysRevLett.117.035002
10. Berggren RR, Caldwell SE, Lerche RA, Mack JM, Moy KJ, Oertel JA, et al. Gamma-ray-based fusion burn measurements. Rev Sci Instrum (2001) 72:873–6. doi:10.1063/1.1321003
11. Herrmann HW, Mack JM, Young CS, Malone RM, Stoeffl W, Horsfield CJ. Cherenkov radiation conversion and collection considerations for a gamma bang time/reaction history diagnostic for the NIF. Rev Sci Instrum (2008) 79:10E531. doi:10.1063/1.2979868
12. McEvoy AM, Herrmann HW, Kim Y, Zylstra AB, Young CS, Fatherley VE, et al. Gamma ray measurements at OMEGA with the newest gas Cherenkov detector ‘GCD-3’. J Phys: Conf Ser (2016) 717:012109. doi:10.1088/1742-6596/717/1/012109
13. Rubery MS, Horsfield CJ, Gales SG, Garbett WJ, LeAtherlAnd A, Young C, et al. First measurements of remaining shell areal density on the OMEGA laser using the Diagnostic for Areal Density (DAD). Rev Sci Instrum (2018) 89:083510. doi:10.1063/1.5023400
14. Mohamed ZL. S-factor measurements for H(D,γ)3He and H(T,γ)4He at low center-of-mass energies as measured in high-energy-density plasmas. submitted to Phys Rev C (2022).
15. Zylstra AB, Herrmann HW, Kim YH, McEvoy A, Meaney K, Glebov VY, et al. Improved calibration of the OMEGA gas Cherenkov detector. Rev Sci Instrum (2019) 90:123504. doi:10.1063/1.5128765
16. Mohamed ZL. DT gamma-to-neutron branching ratio determined using high-energy-density plasmas and a fused silica Cherenkov detector. submitted to Phys Rev C (2022).
17. Hermann HW. ICF gamma-ray reaction history diagnostics. J Phys Conf Ser (2010) 244:032047. doi:10.1088/1742-6596/244/3/032047
18. Kim Y, Mack JM, Herrmann HW, Young CS, Hale GM, Caldwell S, et al. Determination of the deuterium-tritium branching ratio based on inertial confinement fusion implosions. Phys Rev C (2012) 85:061601. doi:10.1103/physrevc.85.061601
19. Kim Y. D-T gamma-to-neutron branching ratio determined from inertial confinement fusion plasmas. Phys Plasmas (2012) 19:056313. doi:10.1063/1.4718291
20. Moore AS, Schlossberg DJ, Hartouni EP, Sayre D, Eckart MJ, Hatarik R, et al. A fused silica Cherenkov radiator for high precision time-of-flight measurement of DT γ and neutron spectra (invited). Rev Sci Instrum (2018) 89:10I120. doi:10.1063/1.5039322
21. Zylstra AB, Herrmann HW, Kim YH, McEvoy A, Frenje JA, Johnson MG, et al. 2H(p, γ)3He cross section measurement using high-energy-density plasmas. Phys Rev C (2020) 101:042802. doi:10.1103/physrevc.101.042802
22. Kim Y, Herrmann HW, Hoffman NM, Schmitt MJ, Kagan G, McEvoy AM, et al. First observation of increased DT yield over prediction due to addition of hydrogen. Phys Plasmas (2021) 28:012707. doi:10.1063/5.0030852
23. Gatu Johnson M. Development of an inertial confinement fusion platform to study charged-particle-producing nuclear reactions relevant to nuclear astrophysics. Phys Plasmas (2017) 24:041407. doi:10.1063/1.4979186
24. Horsfield CJ, Rubery MS, Mack JM, Herrmann HW, Kim Y, Young CS, et al. First spectral measurement of deuterium-tritium fusion γ rays in inertial fusion experiments. Phys Rev C (2021) 104:024610. doi:10.1103/physrevc.104.024610
25. Buss W, Wäffler H, Ziegler B. Radiative capture of deuterons by H3. Phys Lett (1963) 4:198–9. doi:10.1016/0031-9163(63)90362-7
26. Kosiara A, Willard H. Gamma ray-neutron branching ratio in the triton-deutron reaction. Phys Lett B (1970) 32:99–100. doi:10.1016/0370-2693(70)90596-4
27. Bezotosnyi VM, Zhmailo VA, Surov LM, Shvetsov MS. Cross section of the reaction T(d,γ)5He with emission of 16.7-MeV γ quanta at 25 – 100 keV deuteron energy. Sov J Nucl Phys (1970) 10:25–127.
28. Cecil FE, Wilkinson IFJ. Measurement of the ground-state gamma-ray branching ratio of the dt reaction at low energies. Phys Rev Lett (1984) 53:767–70. doi:10.1103/physrevlett.53.767
29. Morgan GL, Lisowski PW, Wender SA, Brown RE, Jarmie N, Wilkerson JF, et al. Measurement of the branching ratio 3H(d, γ)/3H(d, n) using thick tritium gas targets. Phys Rev C (1986) 33:1224–7. doi:10.1103/physrevc.33.1224
30. Kammeraad JE, Hall J, Sale KE, Barnes CA, Kellogg SE, Wang TR. Measurement of the cross-section ratio H(d,γ)5He/3H(d, α)n at 100 keV. Phys Rev C (1993) 47:29–35. doi:10.1103/physrevc.47.29
31. Parker CE. The 3H(d,γ) Reaction and the 3H(d,γ)/3H(d, n) Branching Ratio at ECM ≤ 300 keV. Ph.D. thesis. Ann Arbor, MI (Proquest): Ohio University (2016).
32. Jeet J, Zylstra AB, Rubery M, Kim Y, Meaney KD, Forrest C, et al. Inertial-confinement fusion-plasma-based cross-calibration of the deuterium-tritium γ-to-neutron branching ratio. Phys Rev C (2021) 104:054611. doi:10.1103/physrevc.104.054611
33. Mohamed ZL. Neutron and gamma time-of-flight measurements in inertial confinement fusion experiments. Ph.D. thesis. Rochester, NY University of Rochester (2021).
34. Iocco F, Mangano G, Miele G, Pisanti O, Serpico PD. Primordial nucleosynthesis: From precision cosmology to fundamental physics. Phys Rep (2009) 472:1–76. doi:10.1016/j.physrep.2009.02.002
35. Di Valentino E, Gustavino C, Lesgourgues J, Mangano G, Melchiorri A, Miele G, et al. Probing nuclear rates with Planck and BICEP2. Phys Rev D (2014) 90:023543. doi:10.1103/physrevd.90.023543
36. Fields BD, Olive KA, Yeh TH, Young C. Big bang nucleosynthesis after Planck. J Cosmol Astropart Phys (2020) 010. doi:10.1088/1475-7516/2020/03/0103
37. Griffiths GM, Lal M, Scarfe CD. The reaction D(p, γ)3He below 50 keV. Can J Phys (1963) 41:724–36. doi:10.1139/p63-077
38. Marcucci LE, Mangano G, Kievsky A, Viviani M. Implication of the proton-deuteron radiative capture for big bang nucleosynthesis. Phys Rev Lett (2016) 116:102501. doi:10.1103/physrevlett.116.102501
39. Schmid GJ. Effects of non-nucleonic degrees of freedom in the D(p,γ)3He and p(d,γ)3He reactions. Phys Rev Lett (1996) 76:3088. doi:10.1103/PhysRevLett.76.3088
40. Casella C, Costantini H, Lemut A, Limata B, Bonetti R, Broggini C, et al. First measurement of the d(p,γ)3He cross section down to the solar Gamow peak. Nucl Phys A (2002) 706:203–16. doi:10.1016/s0375-9474(02)00749-2
41. Bystritsky VM, Gerasimov V, Krylov A, Parzhitskii S, Dudkin G, Kaminskii V, et al. Study of the pd reaction in the astrophysical energy region using the Hall accelerator. Nucl Instr Methods Phys Res Section A: Acc Spectrometers Detectors Associated Equipment (2008) 595:543–8. doi:10.1016/j.nima.2008.07.152
42. Mossa V, Stockel K, Cavanna F, Ferraro F, Aliotta M, Barile F, et al. The baryon density of the Universe from an improved rate of deuterium burning,. Nature (2020) 587:210–3. doi:10.1038/s41586-020-2878-4
43. Mossa V, Stockel K, Cavanna F, Ferraro F, Aliotta M, Barile F, et al. Setup commissioning for an improved measurement of the D(p,γ)3He cross section at Big Bang Nucleosynthesis energies. Eur Phys J A (2020) 56:144. doi:10.1140/epja/s10050-020-00149-1
44. Hou SQ, He JJ, Parikh A, Kahl D, Bertulani CA, Kajino T, et al. Non-extensive statistics to the cosmological lithium problem. Astrophys J (2017) 834:165. doi:10.3847/1538-4357/834/2/165
45. Hahn KI, Brune CR, Kavanagh RW. 3H(p,γ)4He cross section. Phys Rev C (1994) 51:1624–32. doi:10.1103/physrevc.51.1624
47. Calarco JR. Absolute cross section for the reaction 3H(p, γ0)4He and a review of 4He(γ,p0)3H measurements. Phys Rev C (1983) 28:483. doi:10.1103/physrevc.28.483
48. Feldman G. 3H(p,γ)4He reaction and the (γ,p)/(γ,n) ratio in 4He. Phys Rev C (1990) 42:1167. doi:10.1103/physrevc.42.r1167
49. Bernabei R, Chisholm A, d’Angelo S, De Pascale MP, Picozza P, Schaerf C, et al. Measurement of the 4He(γ, p)3H total cross section and charge symmetry. Phys Rev C (1988) 38:1990–5. doi:10.1103/physrevc.38.1990
50. Gardner CC, Anderson JD. Gamma yield from the proton bombardment of tritium. Phys Rev (1962) 125:626–8. doi:10.1103/physrev.125.626
51. Gemmell DS, Jones GA. The T(p,γ)He4 reaction. Nucl Phys (1962) 33:102–9. doi:10.1016/0029-5582(62)90508-4
52. Canon RS. 3H(p,γ)4He reaction below Ep = 80 keV. Phys Rev C (2002) 65:044008. doi:10.1103/physrevc.65.044008
53. Blatt SL, Young AM, Ling SC, Moon KJ, Porterfield CD. Reaction T(3He,γ)6Li in the energy range 0.5-11 MeV. Phys Rev (1968) 176:1147–53. doi:10.1103/physrev.176.1147
54. Fukugita M, Kajino T. Contribution of the 3He(t,γ)6Li reaction to 6Li production in primordial nucleosynthesis. Phys Rev D (1990) 42:4251. doi:10.1103/PhysRevD.42.4251
55. Madsen J. CNO and 6Li from big-bang nucleosynthesis—Impact of unmeasured reaction rates. Phys Rev D (1990) 41:2472–8. doi:10.1103/physrevd.41.2472
56. Boyd RN, Brune CR, Fuller GM, Smith CJ. New nuclear physics for big bang nucleosynthesis. Phys Rev D (2010) 82:105005. doi:10.1103/physrevd.82.105005
57. Kim Y, Herrmann HW, Hilsabeck TJ, Moy K, Stoeffl W, Mack JM, et al. Gamma-to-electron magnetic spectrometer (GEMS): An energy-resolved γ-ray diagnostic for the National Ignition Facility. Rev Sci Instrum (2012) 83:10D311. doi:10.1063/1.4738650
58. Kim Y, Herrmann HW, Jorgenson HJ, Barlow DB, Young CS, Stoeffl W, et al. Conceptual design of the gamma-to-electron magnetic spectrometer for the National Ignition Facility. Rev Sci Instrum (2014) 85:11E122. doi:10.1063/1.4892900
59. Chen H, Link AJ, van Maren R, Patel PK, Shepherd R, Wilks SC, et al. High performance compact magnetic spectrometers for energetic ion and electron measurement in ultraintense short pulse laser solid interactions. Rev Sci Instrum (2008) 79:10E533. doi:10.1063/1.2953679
60. Giacomelli L, Rigamonti D, Nocente M, Rebai M, Tardocchi M, Cecconello M, et al. Conceptual studies of gamma ray diagnostics for DEMO control. Fusion Eng Des (2018) 136:1494–8. doi:10.1016/j.fusengdes.2018.05.041
Keywords: inertial confinement fusion, fusion gamma ray, laser-driven fusion, omega laser facility, nuclear astrophysics, big bang nucleosynthesis, gamma-ray emission spectra, S factor
Citation: Mohamed ZL, Kim Y and Knauer JP (2022) Gamma-based nuclear fusion measurements at inertial confinement fusion facilities. Front. Phys. 10:944339. doi: 10.3389/fphy.2022.944339
Received: 15 May 2022; Accepted: 26 September 2022;
Published: 18 October 2022.
Edited by:
Maria Gatu Johnson, Massachusetts Institute of Technology, United StatesReviewed by:
Massimo Nocente, University of Milano-Bicocca, ItalyCopyright © 2022 Mohamed, Kim and Knauer. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Z. L. Mohamed, emxtQGxhbmwuZ292, em1vaEBsbGUucm9jaGVzdGVyLmVkdQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.