Screening Effects in Stars and in the Laboratory

Nuclear reactions are the driver of the evolution of many astrophysical objects. In the astrophysical environment their respective reaction rates are, however, modified due to the presence of other charges. The effects depend on the relative importance of Coulomb energy versus thermal energy and are distinguished between weak and strong screening. In the extreme case of pycnonuclear reactions, fusion reactions can be induced by the zero-point motion of nuclei in a Coulomb crystal. This paper reviews the various screening situations and discusses important applications. We also briefly review laboratory approaches to study screening effects.

1 Introduction

Willy Fowler liked to tease his colleagues by calling astrophysics and astronomy applied nuclear physics. With this witty remark he pointed to the fact that the dynamics, and hence the evolution, of many astrophysical objects is driven by nuclear reactions of charged nuclei, in this way also producing the elements in the Universe. During their long lives in hydrostatic equilibrium stars generate the necessary energy by fusing nuclei in their interior. When the nuclear energy source finally ceases, massive stars collapse under their own gravity resulting in a supernova explosion which finally liberates the produced elements to make them available for the next generation of stars or as the building blocks of life on Earth-like planets. During the collapse, it is nuclear reactions mediated by the weak interaction which fight against gravity [1]. Nuclear reactions are also essential to trigger thermonuclear supernovae where carbon burning is ignited as a runaway in a White Dwarf in a binary system [2].

In astrophysical environments, nuclear reactions take place in the presence of other charges that impact the rates at which such reactions occur. The conditions of density and temperature defining the stellar environment are usually such that atoms are fully ionized and hence the surrounding exists as a plasma made of nuclei of different kinds and charges, and of electrons. However, there are also important situations where atoms are only partially ionized, as is the case for heavier nuclei in the solar interior.

The effect of the surrounding charges on the reactions depend on the competition between Coulomb and thermal energies, which for a one-component plasma is defined by the parameter

$\mathrm{\Gamma }=\frac{{\left(Ze\right)}^2}{akT}(1)$

where k is the Boltzmann constant, T the temperature, Ze the charge of the nucleus and a an appropriate distance between the interacting nuclei. If Γ ≪ 1, one speaks of a “weak screening regime” which is realized at high temperatures and/or low densities. In contrast, for high densities, i.e., Γ ≫ 1, one encounters the “strong screening regime”, if the most effective energy for nuclear reactions (Gamow peak energy) is sufficiently larger than the thermal energy, or the “pycnonuclear regime”, where, even at T = 0 K, fusion reactions are induced by density fluctuations. In between weak and strong regimes, one has a plasma with intermediate screening (Γ ≈ 1). The weak screening limit applies during stellar hydrostatic burning, while the ignition of the nuclear runaway in a type Ia supernova falls into the strong screening regime. Pyconuclear reactions, instead, are mainly important for the crust evolution of neutron stars [3]. While screening regimes are not strictly defined, Figure 1 sketches, as an example, the ranges of temperature and densities relevant to different screening in ¹²C matter.

FIGURE 1

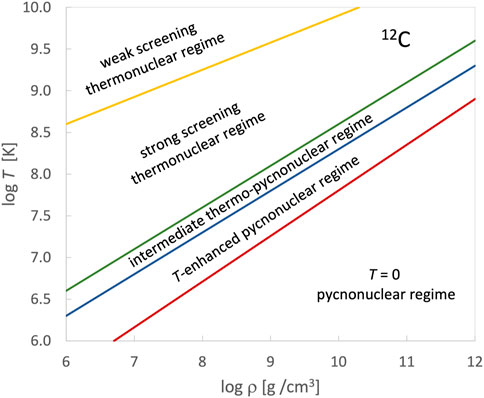
FIGURE 1. Temperature-density diagram covering the various screening regimes for ¹²C matter. The diagram follows the definition by Salpeter [4] and subsequent work by Gasques et al. [5] (for the definition and treatment of screening in the intermediate thermo-pycnonuclear and T-enhanced pycnonuclear regimes the reader is referred to [5]).

Here, we review screening effects of nuclear reactions in these interesting and important astrophysical scenarios, and briefly discuss the extreme case where reactions are initiated by density fluctuations rather than by the thermal motion of the reaction partners. While we mainly focus on nuclear fusion reactions, screening is also relevant for processes mediated by the weak interaction, such as beta decay and electron capture. Important examples are the electron captures on ⁷Be during solar hydrogen burning and generally on nuclei during core-collapse of massive stars leading to a type II supernova. While most of the work related to screening has been based on progress in modelling, recent years witnessed also advances in experimental approaches to study screening effects in laboratory plasmas made possible by laser facilities, and in measurements of low-energy nuclear reactions. In the latter case the experimentally observed effects are somewhat larger than theoretically predicted.

2 Stellar Fusion Reactions

Nuclear fusion reactions in stars occur at thermal energies E well below the Coulomb barrier between interacting nuclei. Thus the energy dependence of the fusion cross section σ(E) is dominated by the tunnel probability and is usually written as [6]:

$\sigma \left(E\right)=\frac{S\left(E\right)}{E}\exp \left[-2\pi \eta \left(E\right)\right](2)$

Here, η = Z₁Z₂e²/ℏv is the Sommerfeld parameter and v the relative velocity. The astrophysical S-factor S(E) accounts for nuclear effects and is a function usually mildly varying with energy. The astrophysical fusion rate is then given by folding the energy- (i.e. velocity-) dependent cross section with the stellar velocity distribution of the reaction partners, which is usually given by a Boltzmann distribution [6]. The product of the Boltzmann distribution and the tunnel probability has a pronounced peak at an energy (the Gamow peak energy) where the reaction occurs most effectively. The Gamow peak energy is noticeably larger than the thermal energy, but significantly smaller than the Coulomb barrier [6].

However, in the astrophysical environment the fusion reactions occur in the presence of other charges which modify the Coulomb barrier and hence have an impact on the astrophysical fusion rates. Starting with the pioneering work of Salpeter [4, 7], it has been customary and often possible to describe these screening effects by an enhancement factor F_sc which multiplies the bare nuclear reaction rate, yielding a screened rate:

$R_{\text{sc}}=F_{\text{sc}}{R}_{\text{bare}}(3)$

While R_bare depends on the temperature via the Boltzmann distribution, the enhancement factor is also a function of plasma properties such as density, temperature, degeneracy and composition. The factorization of Eq. (3) allows to treat the problem as two distinct parts and is a very efficient way to incorporate the screening effects into astrophysical simulations. The screening factor F_sc is customarily given in the form of an exponential function for weak and strong screening as discussed below.

In the weak screening case, in which the average interaction energy between the reaction partners is much smaller than their kinetic energy, the nuclei are surrounded by a screening cloud, such that they are attracted by the electrons and repelled by the nuclei in the partner’s cloud. Due to the effect of the screening clouds, the reaction partners with charges Z₁, Z₂ feel a screened Coulomb potential

$U_{\text{sc}}\left(r\right)=\frac{Z_1{Z}_2{e}^2}{r}\exp \left(-r/R_{\text{D}}\right)(4)$

rather than the Coulomb repulsion of bare nuclei, U_b(r) = Z₁Z₂e²/r, where the parameter R_D (Debye length) is given by $\zeta R_{\text{D}}={(\frac{kT}{4\pi \alpha \rho })}^{1/2}$ with the fine-structure constant α and the number density of nucleons ρ [8]. The parameter ζ depends on the composition of the plasma and its degree of degeneracy [4, 8]. Salpeter’s model of weak screening is equivalent to the Debye-Hückel theory of dilute solutions of electrolytes [9].

The tunnel process occurs at radii which are significantly smaller than the Debye radius. Thus, the exponential in the screened Coulomb potential (Eq. (4)) can be expanded to first order, exp (−r/R_D) ≈ 1 − r/R_D…. Hence, the effect of screening is a reduction of the Coulomb barrier by a constant screening energy U_sc = (Z₁Z₂e²)/R_D. Equivalently, the partners in the plasma fuse with a slightly increased energy (E + U_sc) and the enhancement factor in Eq. (3) reduces to F_sc = exp (−U_sc/kT).

The screening enhancement factors are incorporated in the stellar evolution codes. For the solar plasma, the Debye radius is of the order 10^–11 m and the screening enhancement of nuclear reactions at the relevant solar energies is relatively small, about 5% for the important proton-proton reaction [10]. Special care has to be taken for resonances as the modification of the Coulomb potential lowers the resonance energy compared to the reaction threshold. Hence, the resonance lifetime is increased due to screening. If screening is sufficiently strong, the resonance might get bound in the astrophysical environment; we will mention an example below. The theory for resonant screening has been discussed for example in Ref. [11].

The Debye-Hückel theory of screening, as adopted by Salpeter, is based on a mean-field approach. Hence, it depends on the distance between the reaction partners, but not on their velocity. It has been argued that such a static approach would not be appropriate for the solar plasma [12]. In fact, studies of dynamical screening performed within the molecular dynamics approach for a proton plasma [13–15] indicate that fast moving protons which might not be accompanied by their full screening cloud [15] experience less screening than slow moving ones. These studies suggest that the static screening overestimates the enhancement of nuclear reactions in stellar plasmas, as fast moving particles with energies around the Gamow peak dominate the reaction rates. This view has, however, been disputed by Bahcall and collaborators who argued that Salpeter’s screening approach is valid also at the Gamow peak energy due to the nearly perfect thermodynamic equilibrium present in the solar plasma [16].

At high densities, where Γ ≫ 1, the bulk of the nuclei form a lattice (or quantum fluid). If the Gamow peak energy is significantly larger than the thermal energy, the main contribution to the reaction rate will come from fusing nuclei with energies around the Gamow peak. Again, Salpeter laid out the basis for the treatment of this situation of “strong screening” [4]. He showed that electrons can be treated as a uniform background and derived an enhancement factor assuming that the fusing nuclei move while being surrounded by a uniform cloud of electrons that neutralise the nuclear charge. In this approximation, the enhancement factor can again be written as F_sc = exp (−U_sc/kT) and the screening energy U_sc is given by the difference of electrostatic energies between the fused system with combined (Z₁ + Z₂) charge and that of the two individual nuclei with charges Z₁ and Z₂.

An improved treatment of strong screening is obtained by determining the pair correlation function g(r) which is a measure for the probability for a given nucleus to find a reaction partner at distance r in the plasma. (In multicomponent plasmas g carries indices defining the partners.) The calculation of g(r) is identical to determining the mean potential of the plasma w(r), with g(r) = exp (−w(r)/kT).

Defining g and g₀ as the pair correlation functions with and without screening, the enhancement factor can be approximated as F_sc = g (0)/g₀ (0), where one considers that the ratio is quite insensitive to r at nuclear distances. The enhancement factor is usually split into a “classical” and a “quantum” part [17, 18], F_sc = exp (h₀ + h₁). The classical part is approximately related to the difference of free energies ΔF for the many-body system before and after the fusion reaction [19], leading to exp (h₀) = exp (ΔF/kT). The parameter h₀ can also be calculated using Monte Carlo techniques. A parametrized form of h₀ as a function of the Coulomb coupling parameter Γ and valid for 1 < Γ < 170 is given in [20]. The quantum contribution exp (h₁) considers that the potential is not constant during the tunnel process. It has been calculated in different approximate ways (by path integrals [21], within the WKB approach [22, 23], and directly by Monte Carlo techniques [24, 25]) and found to be small compared to the classical contribution.

An important astrophysical application of strong screening occurs for carbon fusion reactions which are believed to trigger type Ia supernovae in degenerate White Dwarfs in the so-called single-degenerate scenario [2]. Under these degenerate conditions carbon burning occurs as a thermonuclear runaway where the reaction rate is enhanced by many orders of magnitude due to screening effects. The different approximations to the quantum effects lead to noticeable differences in the enhancement factors, which, however, are small compared to the total enhancement. Hence the differences are not expected to be too relevant [5]. A convenient parametrization for the screening of the carbon fusion rate can be found in [5].

At high densities and sufficiently low temperatures the nuclei settle into a Coulombic lattice, for which usually a body-centred-cubic (bcc) structure is assumed [26]. At very high densities the lattice is destroyed due to the zero-point motion of the nuclei and the system rather becomes a quantum fluid. However, due to its strong dependence on charge, this transition occurs at such high densities that it is usually irrelevant for astrophysical purposes [27]. An exception is ⁴He, as we will see below. The energy scale of the zero-point motion can be estimated by the ion plasma frequency [7] and allows to tunnel the Coulomb barrier, which is significantly modified due to the interaction with other ions and the neutralising electron background. Such density-induced reactions are called pycnonuclear reactions [7] and they are the reason why no Coulomb crystal exists at arbitrarily large densities.

The pyconuclear reaction rate R_pyc for a one-component crystal can be expressed (in s⁻¹cm⁻³) as [5]:

$R_{\text{pyc}}=\rho X_{i}A{Z}^{4}S\left(E_{\text{pk}}\right)C_{\text{pyc}}10^{46}{\lambda }^{3-C_{\text{pl}}}\exp \left(-C_{\exp }/\sqrt{\lambda }\right)(5)$

where ρ is the density in g/cm³, X_i, A, Z are the mass fraction, mass number and charge of the fusing nuclei and the astrophysical S-factor S is evaluated at the energy E_pk of the plasma frequency (see [5] for details). Above (below) the neutron drip density at 4 × 10¹¹ g/cm³, X_i < 1 (X_i = 1) due to the presence of free neutrons. The parameter λ is defined as $\lambda =\frac{{\hslash }^2}{m{Z}^2{e}^2}{(n_i/2)}^{1/3}$ with nucleon mass m and number density n_i. The three parameters (C_pyc, C_pl, C_exp) in Eq. (5) have to be calculated using a model for the tunnel process. Various values are presented in [7, 24, 27].

Beyond the static approximation to the rate given in Eq. (5), effects related to the polarization of the surrounding Coulomb lattice were discussed by Schramm and Koonin [27]. They found that these dynamical effects, which are non-negligible per se, cancel each other. It is estimated that pycnonuclear reaction rates can be uncertain by a few orders of magnitude [26].

Pycnonuclear reactions play a role in the structure of isolated neutron stars which accrete matter from the interstellar medium [28]. Due to the accretion, the original matter of the neutron star crust is successively pushed to higher densities and hence undergoes a series of double electron captures which make the matter more neutron-rich. These captures produce free neutrons above the neutron drip density, until the system finally reaches densities at which nuclei become able to fuse by pycnonuclear reactions. In the pioneering work of [3, 29], where the original composition of the crust was assumed to consist purely of ⁵⁶Fe, pycnonuclear fusion is expected to occur for ³⁴Ne nuclei at densities slightly exceeding 10¹² g/cm³. Dynamical studies of the neutron star crust evolution encompassing a large reaction network are presented in [30]. These authors also find that the uncertainty in the pyconuclear reaction rates have only a modest effect on the crust evolution.

Special care has to be taken for ⁴He matter at high densities. Of particular interest is the triple-alpha rate, by which ⁴He is transformed into ¹²C. During helium burning in normal stars, temperatures are sufficiently high that the process occurs in two steps via the formation of an intermediate ⁸Be resonance (the ground state) at 92.2 keV above the α + α threshold [31]. In Wolf-Rayet stars, temperatures are lower and the triple-alpha reaction is enabled via the low-energy wing of the ⁸Be resonance [32, 33]. Finally, in accreting neutron stars, temperatures might be so low that the triple-alpha process occurs via pycnonuclear fusion [34]. At the relevant densities (ρ > 3 × 10⁸ g/cm³), zero-point motion transforms ⁴He matter into a quantum fluid. Under these conditions, the triple-alpha fusion rate was calculated in [35]. However, because of the low energy of the ⁸Be resonance, the nuclear α-α potential must also be included in addition to the Coulomb interaction. As it was pointed out in [36], screening in ⁴He matter becomes strong enough around 3 × 10⁹ g/cm³ to transform it to bound ⁸Be matter. This phase transition was confirmed in a study which described the ⁴He quantum fluid within the hypernetted chain approach taking higher-order correlations into account [37]. The study also showed that these correlations are strong enough to transform ⁴He matter into ¹²C at densities lower than the critical density for the phase transition to ⁸Be matter. The latter is then probably not realised in nature.

For screening effects of very strong magnetic fields on thermonuclear reactions the reader is referred to Refs. [38, 39] and references therein.

3 Reaction Mediated by the Weak Interaction

Although reactions mediated by the weak force are usually slower than competing time scales, they can be significantly altered by their astrophysical surroundings often with interesting consequences. For example, temperature can change the effective half lives of nuclei due to thermal population of excited nuclear states. In s-process nucleosynthesis this occurs at certain branching points making the rates for beta decays and neutron captures competitive. As a consequence, the matter flow branches at these nuclei allowing to determine the neutron density or the temperature of the astrophysical environment from the observed abundances [40, 41]. An extreme change in half life occurs for ¹⁸⁰Ta where a long-lived excited state with half live comparable to the age of the Universe is thermally mixed with the ground state which lives only a few hours [42, 43]. Other than by s-process nucleosynthesis [44, 45], ¹⁸⁰Ta can also be made by neutrino nucleosynthesis [46–48]. Finite-temperature effects also modify inelastic neutrino-nucleus cross sections, in particular at low and modest neutrino energies [49]. Inelastic neutrino scattering off nuclei had been discussed as a potential source for thermalization of neutrinos with matter during the collapse of massive stars [50, 51], but turns out to be rather unimportant [52].

The plasma density has important effects also on beta decays, as the presence of electrons blocks final states for the decay. This Pauli blocking effect at finite density reduces the rate and has to be accounted for in the derivation of stellar beta decay rates [53, 54]. As a consequence of this reduction, beta decays are basically prohibited during final collapse of a massive star, but play an interesting role during silicon burning where beta decay and electron capture rates are comparable and contribute significantly to the cooling of the stellar core without changing the electron-to-nucleon ratio [55]. The blocking of beta decays allows the collapsing core to get successively more neutron-rich by continuous electron captures on nuclei [1, 56, 57]. These electron captures accelerate the collapse as they reduce both the pressure of the relativistic electron gas and the entropy of the core matter. The latter effect is responsible for the fact that nuclei survive the collapse. Coulomb corrections are important for the thermodynamic properties of the high density plasma [58], but they also modify the weak interaction rates [59]. Screening contributes to these rates in two different ways. First, it changes the threshold energy between initial and final states. Second, the electron energy is reduced by the presence of the background compared to the unscreened case. Refs. [60, 61] present a formalism on how screening corrections can be incorporated into the stellar electron capture and beta decay rates. In general, electron capture rates are slightly reduced due to screening, while beta decay rates are enhanced [61], as shown in Figure 2.

FIGURE 2

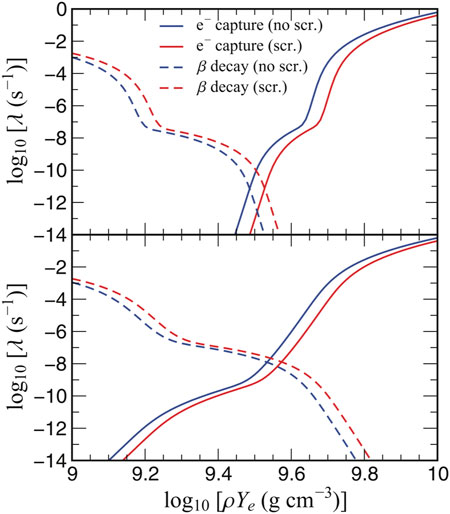
FIGURE 2. Rates for electron capture on ²⁰Ne (solid) and beta decay (dashed) of ²⁰F for densities typical for a collapsing NeMg core of an intermediate mass star and two relevant temperatures (T = 4 × 10⁸ K (top) and 10⁹ K (bottom)). The rates have been calculated with and without screening corrections (red and blue lines, respectively). Due to screening, the densities at which both rates become identical are shifted to higher values. Figure reprinted with permission from [61].

This result has important consequences for the URCA process which is essential for the cooling of NeMg cores in the final evolutionary stages of intermediate mass stars as it shifts the operation of the URCA process to higher densities [61–63]. Significant experimental and theoretical progress in determining stellar weak interaction rates has recently been reviewed in [64].

Electron captures on selected nuclei occur also during hydrostatic stellar burning. At such conditions screening cannot be treated as caused by a degenerate relativistic electron gas like during core collapse, but rather as due to an ideal electromagnetic plasma. A particularly interesting and important case is the electron capture on ⁷Be which, in competition with proton capture, determines the rate of high-energy neutrinos produced in the Sun. In the laboratory the half life of ⁷Be is about 53 days. As the electron density at the nucleus in the solar plasma is reduced compared to the atomic case, the half life is longer in the Sun. Under solar conditions, ⁷Be has a non-negligible probability, which also depends on screening effects, of having a bound K-shell electron. Therefore, a consistent treatment of ⁷Be ions embedded in the solar surroundings is required. Such studies have been performed on the basis of two quite distinct methods, a mean-field approach [65] and a density matrix formalism [66], yielding, however, nearly identical results for the solar ⁷Be half life (about 81 days).

4 Experimental Approaches to Study Screening Effects

The strategy to determine nuclear reaction rates for astrophysical applications is a two-step process: at first one derives the cross section (astrophysical S-factor) for bare nuclei, which is then modified to account for environmental effects. The measurement of the bare cross section is, however, an experimental challenge, as the astrophysically most important energy region (around the Gamow peak energy) lies far below the Coulomb barrier, where the cross sections are extremely small and their direct measurement in the laboratory is difficult with presently available techniques. Therefore, one measures the cross sections down to energies as low as possible and then extrapolates the data to the relevant energy region. It was generally believed that the uncertainty in the extrapolation procedure could be reduced by steadily lowering the energies at which data are taken in the laboratory. This approach, however, might be problematic as at very low energies the experimentally measured cross section does not represent the required case for bare nuclei: the cross section is enhanced due to screening effects connected with the electrons present in the target (and possibly in the projectile) [67].

The ³He (d,p)⁴He reaction is probably the best studied case for the experimental observation of laboratory screening, as the available low-energy data [68–71, 73] are the most definitive in this case.

In the laboratory the cross section was measured by shooting an ion beam of (bare) deuterons onto an atomic ³He gas (with two electrons per atom). At the lowest accessible energies, the separation of target and projectile during tunnelling is much smaller than the atomic radius; thus, the two electrons, originally bound to ³He, are now attracted by the joint charge of projectile and target, corresponding to ⁵Li. The gain in electronic binding energy (about ΔE ≃ 120 eV) between the fused ⁵Li and the well-separated (d+³He) systems should be transferred to the relative motion so that the fusion process occurs with a slightly enhanced energy compared to the case of bare nuclei. Analogue to Eq. (3) the measured cross section should be increased by an exponential factor which can be expresses as f_sc ≈ exp (πη(E)ΔE/E), considering that ΔE is much smaller than the relative energy E of the fusing nuclei [67]. Such an exponential enhancement is indeed experimentally observed [69, 70], as shown in Figure 3. However, the screening energy U_sc obtained by fitting the data to the exponential parametrization for f_sc is larger than the adiabatic limit ΔE, i.e. the difference in binding energies. Yet, the applicability of the adiabatic limit was confirmed within a Time Dependent Hartree-Fock (TDHF) calculation of the electron dynamics in the fusion reaction [74]. In addition, a noticeably smaller experimental screening energy was observed in an experiment performed in inverse kinematics using a molecular deuteron target [75]. A TDHF study of screening effects for proton scattering on a molecular hydrogen target shows a strong sensitivity of the enhancement factor to the orientation of the molecule [76]. It is smaller if the proton has to pass the spectator nucleus before the fusion process occurs. No isotopic dependence of the screening effect has been found, as expected [77, 78]. The use of possibly incorrect stopping powers, which the fusion energies have to be corrected for, has also been suggested in [79] as a possible solution of the difference between experimental results and adiabatic limit. Indeed, theoretical calculations [80, 81] of stopping power for the same systems mentioned above using dynamic calculations do not agree with extrapolations to lower energies, thus corroborating the findings in [79].

FIGURE 3

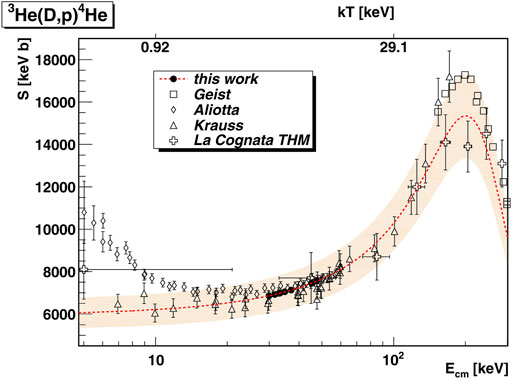
FIGURE 3. Low-energy S-factor for the d (³He,p)⁴He reaction, obtained by accelerator experiments [68, 70, 71] and high-power laser measurements (“this work” from [72]). The crosses represent results obtained with the Trojan-Horse Method (THM) [73]. The dashed curve shows the bare nuclear S-factor obtained from a fit to the data at higher energies. The exponential enhancement in the S-factor at low energies, observed in the data by Aliotta et al. [70], is attributed to screening effects. Figure reprinted with permission from [72].

Differences between experimental and adiabatic screening energies have been found also for other nuclear reactions [82]. In some cases, clustering configurations (e.g., d ⊕ α in ⁶Li) in the interacting nuclei could potentially explain the large screening potentials observed experimentally, as suggested in [83].

In general, an obvious source of uncertainty are the bare nuclear cross sections required to determine the experimental screening value. To eliminate this uncertainty experimental approaches like the Trojan Horse Method (THM) [84, 85] have been developed, which allow for an indirect determination of the bare nuclear cross sections also at very low energies. Figure 3 includes bare nuclear cross sections obtained via the THM [73] that are consistent with the extrapolation of the cross sections from higher energies. The S-factor has also been determined by an experiment where a molecular deuteron target was bombarded with intense and ultrafast laser pulses [72]. The discrepancy between observed and expected screening enhancement for gaseous targets is still not explained.

Large screening enhancements were also found for the low-energy d + d fusion reaction in deuterated metals [86–88]. Here the low-energy S-factor shows an exponential enhancement, but the deduced screening energy for metals can exceed the value obtained for a gas-target experiment by more than an order of magnitude [88, 89]. Importantly, if the deuterons are implanted into semiconductor or insulator materials, the screening energy is consistent with the gas-target result. This observation led to the proposal that the classical Debye theory might be applicable to describe the screening enhancement in metals [90]. The Debye model predicts a characteristic temperature dependence of the screening proportional to T^1/2 which was tentatively observed in [91]. Considering the ion-momentum distribution and inhomogeneous screening effects beyond the Debye model reduced the gap between prediction and observation [92, 93]. The Debye model was, however, questioned in [89]. These authors argued that the screening in deuterated metals requires a dynamical treatment of the deuteron density which indeed reproduced the dependence of the screening energy on the charge of the host material. But also this improved model predicts screening energies which are about a factor of 2 smaller than the observed values [89, 94]. A quantum-mechanical model for the screening effects was presented in [95], but has not yet been fully applied due to computer limitations.

The unresolved discrepancy between theoretical and experimental screening energies for atomic or molecular targets is an obstacle to reducing existing uncertainties for nuclear reactions with light ions. The problem would, of course, become obsolete if it was possible to measure the relevant cross sections directly for the appropriate astrophysical plasmas. At least for interactions between light ions in the Sun, in early stellar burning stages, or in Big Bang nucleosynthesis, this perspective becomes possible using high-intensity lasers. For example, a measurement of the low-energy d (³He,p)⁴He S-factor is included in Figure 3 [72]. Other laser-induced measurements of astrophysical S-factors dealt with the d(p,γ)³He [96] and the t+³He [97] reactions, both of interest for Big Bang nucleosynthesis. These pioneering works were, however, performed under plasma conditions at which screening is expected to be negligible. Such dedicated studies of plasma screening effects are envisioned for future laser facilities, including the Extreme Light Infrastructure ELI-NP under construction in Bucharest [98] making use of two laser-induced colliding plasmas [99]. An alternative approach, i.e. to measure directly the bare reaction cross section, exploits a unique combination of experimental devices at the CRYRING storage ring at GSI. Here, a stored beam of ions can be made to collide with a transverse beam and the reaction products be detected with a newly developed detection array [100]. If successful, such measurements have the potential for significant breakthroughs in our understanding of the electron screening effect.

5 Conclusion

In astrophysical environments nuclear reactions are affected by the presence of other charges in the stellar plasma. Starting with the pioneering work of Salpeter [4, 7] such effects have been included in astrophysical simulations taking also into account that the relative importance of Coulomb versus thermal energy, defined by the Coulomb plasma parameter Γ, requires different screening treatments under different physical conditions. The progress of these treatments is mainly theoretical. In the case of weak screening, as it applies for example to the solar plasma, the enhancement of the fusion reactions is quite small (typically, a few percent) and appears not to be a considerable source of uncertainty [8]. Similar conclusions also apply to the electron capture reaction on ⁷Be, which has drawn specific attention in [101]. The uncertainty in the enhancement factors for the strong screening case and in particular in the pyconuclear regime remains noticeably larger.

Experimental approaches to screening are so far restricted to studies of light-ion fusion reactions where (at the lowest energies reachable in accelerator experiments) the presence of electrons in the nuclear target (and possibly also in the projectile) screens the Coulomb barrier, effectively enhancing the relative energy of the collision partners during the tunnel process. The energy shift obtained from experimental data is often larger than the value expected if the collision proceeds adiabatically. This discrepancy is not yet fully understood and introduces some uncertainty into the determination of astrophysical cross sections for light ion reactions. For heavier nuclei the energies reachable in accelerator experiments are too high for screening effects to be relevant. In the future it might be possible to circumvent this uncertainty source by measuring the relevant cross sections directly in a laser-induced plasma.

Author Contributions

MA and KL have contributed, respectively, to some of the experimental and theoretical results presented in this review and have co-written the manuscript.

Funding

MA acknowledges funding from the UK Science and Technology Facilities Council (Grant ST/V001051/1).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors have benefited from the collaborations and discussions with many colleagues. In particular, they like to thank Claus Rolfs with whom they had the pleasure to collaborate and to learn from for many years. For the purpose of open access, the authors have applied a Creative Commons Attribution (CC BY) licence to any Author Accepted Manuscript version arising from this submission.

References

1. Bethe HA. Supernova Mechanisms. Rev Mod Phys (1990) 62:801–66. doi:10.1103/revmodphys.62.801

CrossRef Full Text | Google Scholar

2. Hillebrandt W, Kromer M, Röpke FK, Ruiter AJ. Towards an Understanding of Type Ia Supernovae from a Synthesis of Theory and Observations. Front Phys (2013) 8:116–43. doi:10.1007/s11467-013-0303-2

CrossRef Full Text | Google Scholar

3. Haensel P, Zdunik JL. Equation of State and Structure of the Crust of an Accreting Neutron star. Astron Astrophys (1990) 229:117.

Google Scholar

4. Salpeter E. Electron Screening and Thermonuclear Reactions. Aust J Phys (1954) 7:373. doi:10.1071/ph540373

CrossRef Full Text | Google Scholar

5. Gasques LR. Nuclear Fusion in Dense Matter: Reaction Rate and Carbon Burning. Phys Rev (2005) C72:025806.

CrossRef Full Text | Google Scholar

6. Burbidge EM, Burbidge GR, Fowler WA, Hoyle F. Synthesis of the Elements in Stars. Rev Mod Phys (1957) 29:547–650. doi:10.1103/revmodphys.29.547

CrossRef Full Text | Google Scholar

7. Salpeter EE, Van Horn HM. Nuclear Reaction Rates at High Densities. Astrophysical J (1969) 155:183. doi:10.1086/149858

CrossRef Full Text | Google Scholar

8. Adelberger EG, García A, Robertson RGH, Snover KA, Balantekin AB, Heeger K, et al. Solar fusion cross sections. II. The pp chain and CNO cycles. Rev Mod Phys (2011) 83:195. doi:10.1103/RevModPhys.83.195

CrossRef Full Text | Google Scholar

9. Debye P, Hückel E. Z Phys (1923) 24:305.

10. Ichimaru S. Nuclear fusion in dense plasmas. Rev Mod Phys (1993) 65:255. doi:10.1103/RevModPhys.65.255

CrossRef Full Text | Google Scholar

11. Zinner NT. Alpha decay rate enhancement in metals: An unlikely scenario. Nucl Phys A (2007) 781:81–7. doi:10.1016/j.nuclphysa.2006.10.071

CrossRef Full Text | Google Scholar

12. Carraro C, Schäfer A, Koonin SE. Dynamic screening of thermonuclear reactions. Astrophysical J (1988) 331:565. doi:10.1086/166582

CrossRef Full Text | Google Scholar

13. Shaviv NJ, Shaviv G. The Electrostatic Screening of Thermonuclear Reactions in Astrophysical Plasmas. I. Astrophysical J (1996) 468:433. doi:10.1086/177702

CrossRef Full Text | Google Scholar

14. Shaviv NJ, Shaviv G. The Electrostatic Screening of Nuclear Reactions in the Sun. Astrophysical J (2001) 558:925–42. doi:10.1086/322273

CrossRef Full Text | Google Scholar

15. Mao D, Mussack K, Däppen W. Dynamic Screening in Solar Plasma. Astrophysical J (2009) 701:1204–8. doi:10.1088/0004-637x/701/2/1204

CrossRef Full Text | Google Scholar

16. Bahcall JN, Brown LS, Gruzinov A, Sawyer RF. The Salpeter plasma corrections for solar fusion reactions. A&A (2002) 388:660. doi:10.1051/0004-6361:20020462

CrossRef Full Text | Google Scholar

17. Jancovici B. Pair correlation function in a dense plasma and pycnonuclear reactions in stars. J Stat Phys (1977) 17:357–70. doi:10.1007/bf01014403

CrossRef Full Text | Google Scholar

18. Schatzman E. On the Rate of Pycno-nuclear Reactions. Astron Astrophys (1978) 65:L17.

Google Scholar

19. DeWitt HE, Graboske HC, Cooper MS. Screening Factors for Nuclear Reactions. General Theory. Astrophysical J (1973) 181:439. doi:10.1086/152061

CrossRef Full Text | Google Scholar

20. DeWitt HE, Slattery W. Contrib Plasma Phys (1999) 43:279.

21. Alastuey A, Jancovici B. Nuclear reaction rate enhancement in dense stellar matter. Astrophysical J (1978) 226:1034. doi:10.1086/156681

CrossRef Full Text | Google Scholar

22. Itoh N, Totsuji H, Ichimaru S. Enhancement of thermonuclear reaction rate due to strong screening. Astrophysical J (1977) 218:477. doi:10.1086/155701

CrossRef Full Text | Google Scholar

23. Itoh N, Totsuji H, Ichimaru S, DeWitt HE. Enhancement of thermonuclear reaction rate due to strong screening. II - Ionic mixtures. Astrophysical J (1979) 234:1079. doi:10.1086/157590

CrossRef Full Text | Google Scholar

24. Ogata S, Iyetomi H, Ichimaru S. Nuclear reaction rates in dense carbon-oxygen mixtures. Astrophysical J (1991) 372:259. doi:10.1086/169971

CrossRef Full Text | Google Scholar

25. Ogata S. Enhancement of Nuclear Reaction Rates in Dense Stellar Matter: A Path‐Integral Monte Carlo Simulation Study. Astrophysical J (1997) 481:883–97. doi:10.1086/304086

CrossRef Full Text | Google Scholar

26. Yakovlev DG. Phys Rev (2006) C74:035803.

27. Schramm S, Koonin SE. Pycnonuclear fusion rates. Astrophysical J (1990) 365:296. doi:10.1086/169482

CrossRef Full Text | Google Scholar

28. Blaes O, Blandford R, Madau P, Koonin S. Slowly accreting neutron stars and the origin of gamma-ray bursts. Astrophysical J (1990) 363:612. doi:10.1086/169371

CrossRef Full Text | Google Scholar

29. Bisnovatyi-Kogan G, Chethetkin V. Soviet Phys Uspekhi (1979) 22:89.

30. Lau R, Beard M, Gupta SS, Schatz H, Afanasjev AV, Brown EF, et al. Nuclear Reactions in the Crusts of Accreting Neutron Stars. Astr J (2018) 859:62. doi:10.3847/1538-4357

CrossRef Full Text | Google Scholar

31. Salpeter EE. Nuclear Reactions in Stars Without Hydrogen. Astrophysical J (1952) 115:326. doi:10.1086/145546

CrossRef Full Text | Google Scholar

32. Nomoto K, Thielemann KK, Miyayi S. Astr Astrophys (1985) 149:239.

33. Langanke K, Wiescher M, Thielemann F-K. The triple-alpha-reaction at low temperatures. Z Physik A - At Nuclei (1986) 324:147–52. doi:10.1007/bf01325126

CrossRef Full Text | Google Scholar

34. Fushiki I, Lamb DQ. S-matrix calculation of the triple-alpha reaction. Astrophysical J (1987) 317:368. doi:10.1086/165284

CrossRef Full Text | Google Scholar

35. Schramm S, Koonin KSE, Langanke K. Pycnonuclear triple-alpha fusion rates. Astrophysical J (1992) 397:579. doi:10.1086/171815

CrossRef Full Text | Google Scholar

36. Langanke K, Lukas D, Müller HM, Schramm S, Koonin SE. Phase transition from a4He plasma to stable8Be matter. Z Physik A - Hadrons Nuclei (1991) 339:419–20. doi:10.1007/bf01560646

CrossRef Full Text | Google Scholar

37. Müller H-M, Langanke K. Study of dense helium plasma in the optimal hypernetted chain approximation. Phys Rev C (1994) 49:524–32. doi:10.1103/physrevc.49.524

CrossRef Full Text | Google Scholar

38. Luo ZQ, Peng QH. Chin Astron Astrophys (1997) 21:28.

39. Famiano M, Balantekin AB, Kajino T, Kusakabe M, Mori K, Luo Y. Nuclear Reaction Screening, Weak Interactions, and r-process Nucleosynthesis in High Magnetic Fields. Astrophysical J (2020) 898:163. doi:10.3847/1538-4357/aba04d

CrossRef Full Text | Google Scholar

40. Käppeler F, Gallino R, Bisterzo S, Aoki W. Thesprocess: Nuclear physics, stellar models, and observations. Rev Mod Phys (2011) 83:157–93. doi:10.1103/revmodphys.83.157

CrossRef Full Text | Google Scholar

41. Wiescher M, Käppeler F, Langanke K. Critical Reactions in Contemporary Nuclear Astrophysics. Annu Rev Astron Astrophys (2012) 50:165–210. doi:10.1146/annurev-astro-081811-125543

CrossRef Full Text | Google Scholar

42. Mohr P, Käppeler F, Gallino R. Survival of nature's rarest isotope ¹⁸⁰Ta under stellar conditions. Phys Rev (2007) C75:012802. doi:10.1103/PhysRevC.75.012802

CrossRef Full Text | Google Scholar

43. Hayakawa T, Mohr P, Kajino T, Chiba S, Mathews GJ. Reanalysis of the (J=5) state at 592 keV in ¹⁸⁰Ta and its role in the ν-process nucleosynthesis of ¹⁸⁰Ta in supernovae. Phys Rev (2010) C82:058801. doi:10.1103/PhysRevC.82.058801

CrossRef Full Text | Google Scholar

44. Belic D, Arlandini C, Besserer J, de Boer J, Carroll JJ, Enders J, et al. Photo-induced depopulation of the ¹⁸⁰Ta^m isomer via low-lying intermediate states: Structure and astrophysical implications. Phys Rev (2002) C65:035801. doi:10.1103/PhysRevC.65.035801

CrossRef Full Text | Google Scholar

45. Käppeler F, Arlandini C, Heil M, Voss F, Wisshak K, Reifarth R, et al. Stellar neutron capture on ¹⁸⁰Ta^m. II. Defining the s-process contribution to nature’s rarest isotope. Phys Rev (2004) C69:055802. doi:10.1103/PhysRevC.69.055802

CrossRef Full Text | Google Scholar

46. Woosley SE, Hartmann DH, Hoffman RD, Haxton WC. The nu-process. Astrophysical J (1990) 356:272. doi:10.1086/168839

CrossRef Full Text | Google Scholar

47. Heger A, Kolbe E, Haxton WC, Langanke K, Martínez-Pinedo G, Woosley SE. Neutrino nucleosynthesis. Phys Lett B (2005) 606:258–64. doi:10.1016/j.physletb.2004.12.017

CrossRef Full Text | Google Scholar

48. Sieverding A, Langanke K, Martínez-Pinedo G, Bollig R, Janka H-T, Heger A. The ν-process with Fully Time-dependent Supernova Neutrino Emission Spectra. Astrophysical J (2019) 876:151. doi:10.3847/1538-4357/ab17e2

CrossRef Full Text | Google Scholar

49. Langanke K, Martínez-Pinedo G, Richter PA, von Neumann-Cosel P. Supernova Inelastic Neutrino-Nucleus Cross Sections from High-Resolution Electron Scattering Experiments and Shell-Model Calculations. Phys Rev Lett (2004) 93:202501. doi:10.1103/physrevlett.93.202501

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Haxton WC. Neutrino Heating in Supernovae. Phys Rev Lett (1988) 60:1999–2002. doi:10.1103/physrevlett.60.1999

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Bruenn SW, Haxton WC. Neutrino-nucleus interactions in core-collapse supernovae. Astrophysical J (1991) 376:678. doi:10.1086/170316

CrossRef Full Text | Google Scholar

52. Langanke K, Martínez-Pinedo G, Müller B, Janka HT, Marek A, Hix WR, et al. Effects of Inelastic Neutrino-Nucleus Scattering on Supernova Dynamics and Radiated Neutrino Spectra. Phys Rev Lett (2008) 100:011101. doi:10.1103/physrevlett.100.011101

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Fuller GM, Fowler WA, Newman MJ. Astr J (1982) 42:447.

54. Langanke K, Martı́nez-Pinedo G. Shell-model calculations of stellar weak interaction rates: II. Weak rates for nuclei in the mass range in supernovae environments. Nucl Phys A (2000) 673:481–508. doi:10.1016/s0375-9474(00)00131-7

CrossRef Full Text | Google Scholar

55. Heger A, Woosley SE, Martinez‐Pinedo G, Langanke K. Presupernova Evolution with Improved Rates for Weak Interactions. Astrophysical J (2001) 560:307–25. doi:10.1086/324092

CrossRef Full Text | Google Scholar

56. Langanke K, Martínez-Pinedo G. Nuclear weak-interaction processes in stars. Rev Mod Phys (2003) 75:819–62. doi:10.1103/revmodphys.75.819

CrossRef Full Text | Google Scholar

57. Janka H, Langanke K, Marek A, Martinezpinedo G, Muller B. Theory of core-collapse supernovae. Phys Rep (2007) 442:38–74. doi:10.1016/j.physrep.2007.02.002

CrossRef Full Text | Google Scholar

58. Yakovlev DG, Shalybkov DA. Sov Sci Rev E Astrophys Space Phys (1989) 7:311.

59. Bravo E, García-Senz D. Coulomb corrections to the equation of state of nuclear statistical equilibrium matter: implications for SNIa nucleosynthesis and the accretion-induced collapse of white dwarfs. Mon Not R Astron Soc (1999) 307:984–92. doi:10.1046/j.1365-8711.1999.02694.x

CrossRef Full Text | Google Scholar

60. Juodagalvis A, Langanke K, Hix WR, Martínez-Pinedo G, Sampaio JM. Improved estimate of electron capture rates on nuclei during stellar core collapse. Nucl Phys A (2010) 848:454–78. doi:10.1016/j.nuclphysa.2010.09.012

CrossRef Full Text | Google Scholar

61. Martinez-Pinedo G. Phys Rev (2014) C89:045806.

62. Kirsebom OS, Hukkanen M, Kankainen A. Measurement of the 2⁺→0⁺ ground-state transition in the β decay of ²⁰F. Phys Rev (2019) C100:065805. doi:10.1103/PhysRevC.100.065805

CrossRef Full Text | Google Scholar

63. Zha S, Leung S-C, Suzuki T, Nomoto Ki.. Evolution of ONeMg Core in Super-AGB Stars toward Electron-capture Supernovae: Effects of Updated Electron-capture Rate. Astrophysical J (2019) 886:22. doi:10.3847/1538-4357/ab4b4b

CrossRef Full Text | Google Scholar

64. Langanke K, Martínez-Pinedo G, Zegers RGT. Electron capture in stars. Rep Prog Phys (2021) 84:066301. doi:10.1088/1361-6633/abf207

CrossRef Full Text | Google Scholar

65. Johnson CW, Kolbe E, Koonin SE, Langanke K. The fate of Be-7 in the sun. Astrophysical J (1992) 392:320. doi:10.1086/171431

CrossRef Full Text | Google Scholar

66. Gruzinov AV, Bahcall JN. The7Be Electron Capture Rate in the Sun. Astrophysical J (1997) 490:437–41. doi:10.1086/304854

CrossRef Full Text | Google Scholar

67. Assenbaum HJ, Langanke K, Rolfs C. Effects of electron screening on low-energy fusion cross sections. Z Physik A - At Nuclei (1987) 327:461–8. doi:10.1007/bf01289572

CrossRef Full Text | Google Scholar

68. Krauss A, Becker HW, Trautvetter HP, Rolfs C, Brand K. Low-energy fusion cross sections of D + D and D + 3He reactions. Nucl Phys A (1987) 465:150–72. doi:10.1016/0375-9474(87)90302-2

CrossRef Full Text | Google Scholar

69. Engstler S, Krauss A, Neldner K, Rolfs C, Schröder U, Langanke K. Effects of electron screening on the 3He(d, p)4He low-energy cross sections. Phys Lett B (1988) 202:179–84. doi:10.1016/0370-2693(88)90003-2

CrossRef Full Text | Google Scholar

70. Aliotta M, Raiola F, Gyurky G, Formicola A, Bonetti R, Broggini C, et al. Electron screening effect in the reactions ³He(d, p)⁴He and d(³He, p)⁴He. Nucl Phys (2001) A690:790. doi:10.1016/S0375-9474(01)00366-9

CrossRef Full Text | Google Scholar

71. Geist WH, Brune CR, Karwowski HJ, Ludwig EJ, Veal KD, Hale GM. Phys Rev (2003) C60:054003. doi:10.1103/PhysRevC.60.054003

CrossRef Full Text

72. Barbui M, Bang W, Bonasera A, Hagel K, Schmidt K, Natowitz JB, et al. Measurement of the Plasma Astrophysical S Factor for the ³He(d,p)⁴He Reaction in Exploding Molecular Clusters. Phys Rev Lett (2013) 111:082502. doi:10.1103/PhysRevLett.111.082502

PubMed Abstract | CrossRef Full Text | Google Scholar

73. La Cognata M. Phys Rev (2005) C72:065802.

74. Shoppa TD, Koonin SE, Langanke K, Seki R. One- and two-electron atomic screening in fusion reactions. Phys Rev C (1993) 48:837–40. doi:10.1103/physrevc.48.837

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Schröder U, Engstler S, Krauss A, Neldner K, Rolfs C, Somorjai E, et al. Search for electron screening of nuclear reactions at sub-coulomb energies. Nucl Instr Meth (1989) 40/41:466. doi:10.1016/0168-583X(89)91022-7

CrossRef Full Text | Google Scholar

76. Shoppa TD, Jeng M, Koonin SE, Langanke K, Seki R. Electron screening in molecular fusion reactions. Nucl Phys A (1996) 605:387–402. doi:10.1016/0375-9474(96)00183-2

CrossRef Full Text | Google Scholar

77. Engstler S, Raimann G, Angulo C, Greife U, Rolfs C, Schröder U, et al. Test for isotopic dependence of electron screening in fusion reactions. Phys Lett (1992) B279:20. doi:10.1016/0370-2693(92)91833-U

CrossRef Full Text | Google Scholar

78. Engstler S, Raimann G, Angulo C, Greife U, Rolfs C, Schröder U, et al. Isotopic dependence of electron screening in fusion reactions. Z Physik A - Hadrons Nuclei (1992) 342:471–82. doi:10.1007/bf01294958

CrossRef Full Text | Google Scholar

79. Langanke K, Shoppa TD, Barnes CA, Rolfs C. Energy loss, electron screening and the astrophysical 3He(d, p)4He cross section. Phys Lett B (1996) 369:211–4. doi:10.1016/0370-2693(96)00066-4

CrossRef Full Text | Google Scholar

80. Bertulani CA. Electronic stopping in astrophysical fusion reactions. Phys Lett B (2004) 585:35–41. doi:10.1016/j.physletb.2004.01.082

CrossRef Full Text | Google Scholar

81. Bertulani CA, de Paula DT. Stopping of swift protons in matter and its implication for astrophysical fusion reactions. Phys Rev C (2000) 62:045802. doi:10.1103/physrevc.62.045802

CrossRef Full Text | Google Scholar

82. Strieder F, Rolfs C, Spitaleri C, Corvisiero P. Electron-screening effects on fusion reactions. Naturwissenschaften (2001) 88:461–7. doi:10.1007/s001140100267

CrossRef Full Text | Google Scholar

83. Spitaleri C, Bertulani CA, Fortunato L, Vitturi A. The electron screening puzzle and nuclear clustering. Phys Lett B (2016) 755:275–8. doi:10.1016/j.physletb.2016.02.019

CrossRef Full Text | Google Scholar

84. Baur G, Bertulani CA, Rebel H. Coulomb dissociation as a source of information on radiative capture processes of astrophysical interest. Nucl Phys A (1986) 458:188–204. doi:10.1016/0375-9474(86)90290-3

CrossRef Full Text | Google Scholar

85. Typel S, Baur G. Theory of the Trojan-Horse method. Ann Phys (2003) 305:228–65. doi:10.1016/s0003-4916(03)00060-5

CrossRef Full Text | Google Scholar

86. Czerski K, Huke A, Biller A, Heide P, Hoeft M, Ruprecht G. Enhancement of the electron screening effect for d + d fusion reactions in metallic environments. Europhys Lett (2001) 54:449–55. doi:10.1209/epl/i2001-00265-7

CrossRef Full Text | Google Scholar

87. Kasagi J, Yuki H, Baba T, Noda T, Ohtsuki T, G. Lipson A. Strongly Enhanced DD Fusion Reaction in Metals Observed for keV D+Bombardment. J Phys Soc Jpn (2002) 71:2881–5. doi:10.1143/jpsj.71.2881

CrossRef Full Text | Google Scholar

88. Raiola F, Migliardi P, Gangak L, Bonomo C, Gyürky G, Bonetti R, et al. Electron screening in d(d, p)t for deuterated metals and the periodic table. Phys Lett (2002) B547:193. doi:10.1016/S0370-2693(02)02774-0

CrossRef Full Text | Google Scholar

89. Huke A, Czerski K, Heide P, Ruprecht G, Targosz N, Żebrowski W. Enhancement of deuteron-fusion reactions in metals and experimental implications. Phys Rev (2008) C78:015803. doi:10.1103/PhysRevC.78.015803

CrossRef Full Text | Google Scholar

90. Bonomo C, Fiorentini G, Fulop Z, Gang L, Gyurky G, Langanke K, et al. Enhanced electron screening in d(d, p)t for deuterated metals: a possible classical explanation. Nucl Phys (2003) A719:37c. doi:10.1016/S0375-9474(03)00955-2

CrossRef Full Text | Google Scholar

91. Raiola F. Eur Phys Journ (2006) A27:79.

92. Coraddu M, Lissia M, Quarati P. Anomalous enhancements of low-energy fusion rates in plasmas: the role of ion momentum distributions and inhomogeneous screening. Cent Eur J Phys (2009) 7:527. doi:10.2478/s11534-009-0068-y

CrossRef Full Text | Google Scholar

93. Coraddu M, Lissia M, Quarati P, Scarfone AM. Nuclear problems in astrophysical q-plasmas and environments. Braz J Phys (2009) 39:380. doi:10.1590/s0103-97332009000400006

CrossRef Full Text | Google Scholar

94. Targosz-Sleczka N, Czerski K, Huke A, Ruprecht G, Weissbach D, Martin L, et al. Experiments on screening effect in deuteron fusion reactions at extremely low energies. Eur Phys Journ Spec Top (2013) 222:2353. doi:10.1140/epjst/e2013-02016-9

CrossRef Full Text | Google Scholar

95. Huke A, Czerski K, Chun SM, Biller A, Heide P. Quantum mechanical Ab Initio simulation of the electron screening effect in metal deuteride crystals. Eur Phys J A (2008) 35:243–52. doi:10.1140/epja/i2007-10532-1

CrossRef Full Text | Google Scholar

96. Zylstra AB, Herrmann HW, Kim YH, McEvoy A, Frenje JA, Gatu Johnson M, et al. ²H(p,γ)³He cross section measurement using high-energy-density plasmas. Phys Rev (2020) C101:042802(R). doi:10.1103/PhysRevC.101.042802

CrossRef Full Text | Google Scholar

97. Zylstra AB, Herrmann HW, Gatu Johnson M, Kim YH, Frenje JA, Hale G, et al. Using Inertial Fusion Implosions to Measure the T+3He Fusion Cross Section at Nucleosynthesis-Relevant Energies. Phys Rev Lett (2016) 117:035002. doi:10.1103/PhysRevLett.117.035002

PubMed Abstract | CrossRef Full Text | Google Scholar

98. Wu Y, Pálffy A. Determination of Plasma Screening Effects for Thermonuclear Reactions in Laser-generated Plasmas. Astrophysical J (2017) 838:55. doi:10.3847/1538-4357/aa6252

CrossRef Full Text | Google Scholar

99.M Roth, and P Thirolf, editors. Laser Driven Nuclear Physics at ELI-NP (2016). Technical Design Report (ELI-NP RA3-TDR, version 5.1).

Google Scholar

100. Bruno CG. Letter of Intent (E155) Submitted at the 2020 GSI G-PAC (2022). Private Communication.

Google Scholar

101. Adelberger EG. Solar fusion cross sections. Rev Mod Phys (1998) 70:1265. doi:10.1103/RevModPhys.70.1265

CrossRef Full Text | Google Scholar