- 1Space Research Institute, Austrian Academy of Sciences, Graz, Austria
- 2Victoria University of Wellington, Wellington, New Zealand
- 3Department of Astronautical Engineering, University of Southern California, Los Angeles, CA, United States
Collisionless plasmas in space often evolve into turbulence by exciting an ensemble of broadband electromagnetic and plasma fluctuations. Such dynamics are observed to operate in various space plasmas such as in the solar corona, the solar wind, as well as in the Earth and planetary magnetospheres. Though nonlinear in nature, turbulent fluctuations in the kinetic range (small wavelengths of the order of the ion inertial length or smaller) are believed to retain some properties reminiscent of linear-mode waves. In this paper we discuss what we understand, to the best of our ability, was Peter Gary’s view of kinetic-range turbulence. We call it the Gary picture for brevity. The Gary picture postulates that kinetic-range turbulence exhibits two different channels of energy cascade: one developing from Alfvén waves at longer wavelengths into kinetic Alfvén turbulence at shorter wavelengths, and the other developing from magnetosonic waves into whistler turbulence. Particle-in-cell simulations confirm that the Gary picture is a useful guide to reveal various properties of kinetic-range turbulence such as the wavevector anisotropy, various heating mechanisms, and control parameters that influence the evolution of turbulence in the kinetic range.
1 Introduction
Understanding solar wind dynamics requires the ability to model not only the plasma flows and the evolution of turbulent electromagnetic field fluctuations, but also the exchange of energy between the plasma and the turbulent fluctuations. This exchange between fields and plasma can be thought of as operating in two regimes: the relatively long wavelengths of the inertial range (where the fluid description of plasma is valid) and the relatively shorter wavelengths of the kinetic range (where the kinetic behavior of plasma plays an important role).
The kinetic-range turbulence makes a marked difference from fluid turbulence. Due to the collisionless nature of space plasma, the velocity distribution can take any non-Maxwellian form allowed by the Vlasov equation. The non-Maxwellian features could include, for example, a beam component or temperature anisotropy as internal degree of freedom [1,2]. The non-Maxwellian features necessitate a kinetic treatment where the particle motions play an important role. Many collective effects such as wave-particle resonances (e.g. Landau and cyclotron resonances) [3,4] and kinetic instabilities [5,6] come into play, enriching the kinetic range dynamics significantly.
In both the fluid and kinetic regimes the fluctuation energy undergoes a forward energy cascade from longer to shorter wavelengths. In incompressible MHD (magnetohydrodynamics) the energy supplied by the largest scales is distributed across scales in the inertial range by a conservative cascade down to the dissipative scales [7–9]. The MHD cascade also develops strong anisotropy in the wavenumber space, with excess energy in perpendicular wavevector components k⊥ > k∥ [8,10], where k⊥ and k∥ denote the wavevector components perpendicular and parallel to the mean magnetic field B0, respectively. This picture modifies when compressive effects are included. At some scale in the inertial range, the compressive and incompressible cascades decouple and progress independently [11,12]. The nature of the cascade changes even more drastically near the kinetic scales. Accurate modeling of short-wavelength turbulence requires using the fully kinetic framework of Vlasov-Maxwell equations (1), (2), (13)–(16). The equations are typically studied under various limits: linear, quasi-linear, and nonlinear. The tools used vary from linear dispersion solvers to fully nonlinear kinetic simulations or a combination thereof [17–21].
In the spirit of celebrating the achievements and legacy of Stephen Peter Gary (1939–2021) and of extending his review [22], here we discuss the detailed profile of short-wavelength turbulence such as the energy cascade and wavevector anisotropy, heating rates, potential controlling parameters, competition between linear instabilities and nonlinearities. This is not going to be a comprehensive description of kinetic-range turbulence, but a summary of what we believe Peter Gary’s view of kinetic-range turbulence was, which we call the Gary picture of kinetic-range turbulence.
Peter Gary was a pioneer of using the kinetic theory and numerical simulations, and tackled many different problems in space plasma physics. He discovered, for example, in his seminal work in Gary [23] the reversal of field rotation sense as the ion cyclotron wave (left-hand polarized wave) turns into the kinetic Alfvén wave (right-hand polarized) at highly oblique propagation. The mechanism remained a mystery for a long time, and was finally understood as the transition from the Hall current into the diamagnetic current in the wave dynamics [24]. Peter Gary used analytic and numerical methods to understand the properties of linear-mode waves and microinstabilities in the kinetic plasma theory with applications to the wave activity in space plasmas such as the solar corona, the solar wind, the shock-upstream and shock-downstream regions, the magnetosphere, and the planetary and cometary environments [5]. Peter Gary also developed and ran simulations to reveal the nonlinear processes in turbulent plasmas beyond the limit of linear kinetic theory.
A huge amount of literature has been devoted to the nature of kinetic-range turbulence (see e.g., [22,25–29], and many references therein). There is an ongoing discussion in the solar wind turbulence community as to the character of the constituent fluctuations of the kinetic range; the majority of observations indicate that kinetic Alfvén modes are dominant at proton scales, while a minority of measurements implies that significant amplitudes of magnetosonic/whistler (MSW) mode are present as well [30–32]. The Gary picture is based on the notion that both types of fluctuations are present with an emphasis that the relative importance of these modes is given as functions of the plasma and turbulence parameters. The Gary picture has widely been tested against both two- and three-dimensional PIC (particle-in-cell) simulations (see, e.g. [33], about the concept and algorithm). The interpretation of the simulation results by Gary and his collaborators was accompanied by linear Vlasov theory and spacecraft observations in the solar wind.
2 Two Competing Channels of Energy Cascade
One may define plasma turbulence as an ensemble of broadband, relatively large amplitude, stochastic incoherent fluctuations in an ionized gas. Plasma turbulence is observed in many astrophysical systems [34,35], in the solar corona [36], in the solar wind [37,38], as well as in terrestrial and planetary magnetospheres [28]. The energy in turbulent magnetic fields is a likely source of accelerating or thermalizing electrons and ions in many space and astrophysical plasmas, although the scientific understanding of these energy transfer processes is yet incomplete and is the subject of substantial current research [39–41].
Given the highly nonlinear nature of turbulent processes, a common strategy is to perform simulations that run on massively parallel computers. Depending on the regime of interest single/multi fluid MHD simulations or kinetic simulations with varied levels of physics are used to study plasma turbulence [20,21,42–49]. In the kinetic range fully kinetic simulations that treat both ions and electrons as kinetic species are desirable. Of these, the most common simulation method is particle-in-cell [20,21]. Nonlinear computations usually lead to complex results which are not subject to simple interpretations such as scalings predicted by linear theory. Yet, the quasi-linear theory offers a hope that, perhaps under some conditions, some aspects of plasma turbulence can be represented in terms of relatively simple scaling relations.
The adjectives whistler and kinetic Alfvén are widely used to describe components of short-wavelength turbulence in space. The Gary picture describes whistler turbulence and kinetic Alfvén turbulence as co-existing, competing channels of energy cascade as follows:
1. Wavevectors develop nearly perpendicular to the local mean magnetic field (as a consequence of magnetohydrodynamic turbulence).
2. Whistler and kinetic Alfvén waves (or whistler and kinetic Alfvén turbulence, respectively1) are dominant at shorter wavelengths (in the sense that the energy exceeds that of other components such as sideband waves, pumped waves by wave-wave couplings, and short-living coherent or solitary waves).
3. Both of whistler and kinetic Alfvén channels forms an inertial-range spectrum with a power law.
4. Ions (protons) are primarily heated by the interaction with the kinetic Alfvén waves; Electrons are primarily heated by the interaction with the whistler waves.
The evidence is far from conclusive that only one kind of fluctuation mode is dominant in energetics throughout the inertial as well as the kinetic ranges. Figure 1 illustrates how both kinetic Alfvén and magnetosonic/whistler fluctuations contribute to kinetic-range turbulence. Although the overall energy density of magnetosonic/whistler turbulence may be small compared to that of Alfvén turbulence, it is possible that the former type may dominate fluctuation amplitudes and electron dissipation at sufficiently short wavelengths.
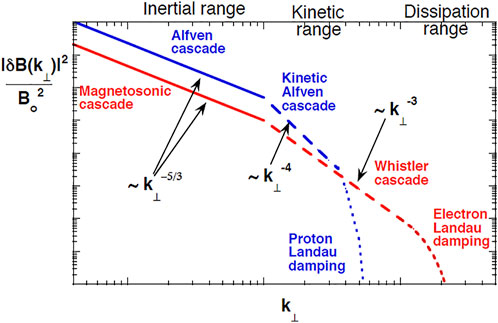
FIGURE 1. Schematic energy spectra suggesting the co-existence and competition between kinetic Alfvén turbulence (Alfvén channel) and whistler turbulence (magnetosonic channel) in the short-wavelength range. Each type of turbulence may have a non-trivial domain over which it dominates the magnetic fluctuation spectra. Picture drawn by Peter Gary.
From a theoretical perspective, Howes et al. [50] argued using gyrokinetic linear theory that the solar wind like parameters are a sweet spot for kinetic Alfvén waves to have very low damping rates and hence argued that kinetic Alfvén waves can cascade down to electron scales. Podesta et al. [51] however argued that the damping rates of kinetic Alfvén waves become significant before electron scales are approached. Howes et al. [52] used data from WIND spacecraft to argue that the fast mode fluctuations in the inertial range have much less power compared to the Alfvén fluctuations. They further argued that this implied negligible power in the fast magnetosonic/whistler branch in the kinetic scales. However theoretical considerations from compressible MHD turbulence suggest that Alfvén-Alfvén-fast triadic interactions, that are missing in incompressible MHD turbulence such as that by Goldreich and Sridhar [53], can pump power into higher wavenumber fast mode fluctuations [54]. There is evidence that in compressible MHD, there is a parallel cascade of the compressive fluctuations [55]. The compressive cascade decouples from the incompressible cascade at some scale in the inertial range and proceeds independently in a conservative fashion [12]. Such a decoupling could provide conditions for the cascade of compressive fluctuations to potentially transfer energy down to electron scales.
Another important fluctuation type is the left-hand polarized ion-cyclotron waves (or Alfvén-cyclotron waves) at relatively high frequencies in space plasmas. Parallel propagating cyclotron waves are likely to be local sources of turbulent energy in the solar wind. Indeed, the ion-cyclotron waves are observed by the Wind spacecraft in the solar wind, and the wave events are reported and analyzed by Peter Gary himself [56], indicating the excitation of ion-cyclotron waves (ICWs) by proton temperature anisotropy (with an excess of perpendicular temperature) and the excitation of whistler-type right-hand polarized magnetosonic waves by the ion component relative flows. The spacecraft observations of magnetic helicity by Podesta and Gary. [57], He et al. [58] support the presence of both kinetic Alfvén waves and parallel propagating ion-cyclotron waves or whistler waves in the turbulent solar wind. It was hypothesized by Klein et al. [59] that the ICWs and whistler waves are produced by kinetic instabilities and are not part of the turbulent cascade. Recent hybrid kinetic simulations of imbalanced turbulence, relevant to inner heliospheric conditions, also show evidence for possible localized generation of ICWs [60]. These ICWs were suggested to not have a significant energy budget but have enough energy perpendicularly heat of ions.
3 Lessons From Theoretical and Numerical Studies
Peter Gary and his collaborators have done extensive PIC simulations and other theoretical analyses to test the Gary picture. The PIC simulations are typically initialized with a narrow-band spectrum of relatively gyrotropic, relatively long wavelength normal modes which satisfy the properties of kinetic Alfvén waves and/or whistler waves derived from the linear Vlasov theory. It is possible to visualize the turbulence energy in the four-dimensional spectral domain (spanning the frequencies and the three components of wavevectors), and the spectra from the PIC simulations can nowadays be compared to that from the multi-spacecraft data [61]. The nonlinear temporal evolution of the system leads to a forward energy cascade that develops a broadband, anisotropic spectrum of turbulence. Both electrons and ions gain energy as well as show increased species entropies. The simulations were performed using two different codes: 1) the P3D code with MHD-like initial conditions under both 2.5D and 3D configurations [62], [63] and 2) the 3D-EMPIC code [64] in which initial spectra of relatively long-wavelength fluctuations were imposed. Both P3D and 3D-EMPIC are fully three-dimensional (3D) codes. The simulations represent magnetized collisionless plasmas and a broad range of kinetic waves (such as kinetic Alfvén and whistler waves) are set.
3.1 Energy Cascade and Wavevector Anisotropy
Cascade Mechanism
The fundamental processes of energy cascade are formulated by nonlinear interactions that transfer energy across scales. The most likely process (in terms of probability or cross section) is the triadic interaction which models two waves interacting with each other to generate a different wave. These triadic interactions are constrained to the conservation of frequencies and wavenumbers in the form of.
These couplings hold regardless of whether the fluctuations are linear wave like or nonlinear. Peter Gary liked to think of these interactions in the sense of two waves interacting to produce a third wave [7,53]. Any combination of the frequencies between ω1 and ω2 is possible although the most efficient couplings in hydrodynamics are k1 ∼ k2 and ω1 ∼ ω2. If the generated wave ω3 falls onto the solution of linear Vlasov dispersion equation, the wave ω3 may have a longer lifetime as the fluctuation is supported by the background plasma condition. In general, the generated wave ω3 does not fall onto the linear-mode dispersion relation and appears as a pumped or forced wave. The frequency and wavevector matching conditions (Eqs. 1 and 2) are a useful tool to test for the hypothesis that the forward cascade leads to wavevector anisotropies in a homogeneous, collisionless, magnetized plasma.
Gary [65] revisited the linear Vlasov theory and evaluated the matching conditions for three linear-mode modes: 1) Alfvén-cyclotron waves (at longer wavelengths), 2) magnetosonic waves (at longer wavelengths), and 3) whistler waves (at intermediate wavelengths). The test successfully explains that Alfvén waves and magnetosonic-whistler waves develop into forward cascade and wavevector anisotropy in favor of generating higher wavenumbers perpendicular to the mean magnetic field (energy spectrum extending perpendicular to the mean field). An exceptional case is that when the ion beta is close to unity, the cascade of long wavelength magnetosonic waves is favored by k⊥∼ k‖. The forward cascade of whistler turbulence shows a consistent development to wavevector directions predominantly quasi-perpendicular to the mean magnetic field in the PIC simulations [66–68] and in the Cluster and MMS observations in the solar wind [32,69–71].
Kinetic extension is needed to account for the energy transfer from the waves into the particles in the quasi-linear fashion. The wave-particle interactions occur efficiently when either the Landau resonance condition
or the cyclotron resonance condition
is satisfied. Here, v‖ is the parallel velocity of particle of jth species, and Ωj is the cyclotron frequency of jth species. The wave-particle interactions involving wave-wave couplings are, for example, represented by the condition
for the Landau resonance [22].
The dispersion relation was used by Narita and Gary [72] and Saito et al. [73] to derive scaling laws for self-interacting whistler waves at highly oblique propagation with respect to the mean magnetic field. In the fashion of a phenomenological model, the inertial-range spectrum was constructed for homogeneous, highly-oblique whistler turbulence as a generalization of the Iroshnikov-Kraichnan model for magnetohydrodynamic turbulence [7,74]. The modeled whistler turbulence is characterized by an energy spectrum with a spectral index of −5/2 as a function of the perpendicular components of the wavevectors.
Wavevector Anisotropy
The simulations by Chang et al. [45,66,67,75], Gary et al. [68], and Hughes et al. [46,76] used a realistic ion-to-electron mass ratio of 1836, and focused on understanding the relationships between field fluctuations and both the electron and ion dynamics. These computations followed the time evolution of whistler fluctuations as they decay via forward cascade into a broadband, anisotropic, turbulent spectrum at shorter wavelengths (Figure 2). This cascade leads to a spectrum of fluctuations that are consistent with the linear dispersion solution for whistler modes especially in the low electron-beta case βe ≪ 1 (Figure 3).

FIGURE 2. 3D PIC simulations of whistler turbulence cascade. Simulation domain: 20483 cells. Macro-particles: 2.75 × 1011/species. The plot shows magnetic energy wavevector spectra at two times: t = 0 (top) and t Ωe = 78.3 (bottom). Left column: kx − ky spectra cut at k∥ = 0. Right column: k∥ − k⊥ spectra reduced over the azimuthal angle of the perpendicular wavevectors [45].
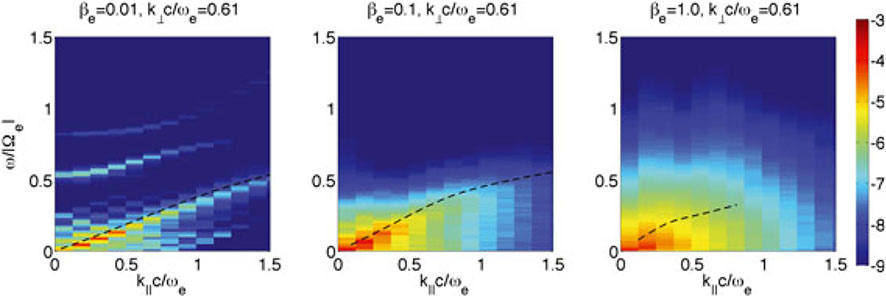
FIGURE 3. Energy spectrum in the domain of frequency and parallel wavenumber to the mean magnetic field computed over the full time evolution of PIC simulation using three different values electron beta: 0.01 (left), 0.1 (middle), and 1 (right). From Chang et al. [67].
The consequent reduced magnetic fluctuation spectra show clear breaks as functions of k⊥ corresponding to transitions from relatively steep slopes at long wavelengths to even steeper slopes at shorter wavelengths, similar to electron-scale spectral break measured near 50 Hz in Cluster spacecraft measurements of solar wind turbulence [30,77,78].
Defining the wavevector anisotropy factor A as the spectral moment (see, e.g. [79])
the forward cascade of whistler turbulence in the 3D PIC simulations consistently leads to wavevector anisotropy extending perpendicular to the mean magnetic field characterized by A ≫ 1, consistent with analytic and numerical calculations for electron magnetohydrodynamic (EMHD) [80,81] as well as two-dimensional PIC simulations [82]. As the plasma beta increases, whistler turbulence becomes less anisotropic and evolves towards nearly isotropic spectra. This has been shown to be true in both PIC simulations [67] as well as the solar wind observations [83].
3.2 Heating Profile
Using 3D PIC simulations, a number of papers by Peter Gary and collaborators also elaborated on the issue of electron and ion heating rates by whistler turbulence [46,47,56,76]. The heating rate of jth species is evaluated by
where Tj is the temperature of jth species (in units of energy, including the Boltzmann constant), Tj,ini is the initial temperature, and t the elapsed time normalized to the electron plasma frequency. The temperature is estimated from the pressure pj (the trace of pressure tensor) and the number density nj as
Considering the maximum values of the heating rates Qi (for ions) and Qe (for electrons) across each simulation, an approximately linear relationship was found between the heating rate ratio Qi/Qe and the mass ratio mi/me, suggesting that an artificially reduced mass ratio may not change the fundamental physics of whistler turbulence dissipation. Hughes et al. [76] showed that, although whistler turbulence heats electrons more rapidly than ions, ion heating does play a role in whistler turbulence dissipation. In particular, the ions experience the majority of their energy gain in directions perpendicular to the mean magnetic field, consistent with the temperature anisotropy observed in the solar wind [1,2,84,85]. Moreover, successively larger simulation domains corresponding to successively longer wavelengths of whistler turbulence yield weaker electron heating and stronger ion heating. This is consistent with the findings of Saito and Nariyuki [86] who used 2.5D PIC simulations of whistler turbulence leading to perpendicular proton heating. This is also qualitatively consistent with the findings of Wu et al. [87] and Matthaeus et al. [88]. In particular, Matthaeus et al. [88] suggested that the ratio of ion cyclotron time to nonlinear time computed at the proton scales is an important factor in determining the relative heating of ions and electrons. The ratio is directly proportional to a positive power of the system size (λ2/3). See Eq. 3 in Matthaeus et al. [88].
Gary et al. [56] used 3D PIC simulations to study ion and electron heating due to whistler turbulence as functions of the fluctuation energy
They found that the maximum rate of electron heating scales approximately linearly with the fluctuation energy, suggesting a quasi-linear type heating due to electron Landau damping. The maximum ion heating on the other hand scales with the fluctuation energy roughly by a power of 3/2,
suggesting a nonlinear mechanism acting to heat the relatively unmagnetized ions (Figure 4). The scalings (Eq. 9) are consistent with the non-resonant “stochastic heating” discussed by Chandran et al. [89], and is also close to the scaling
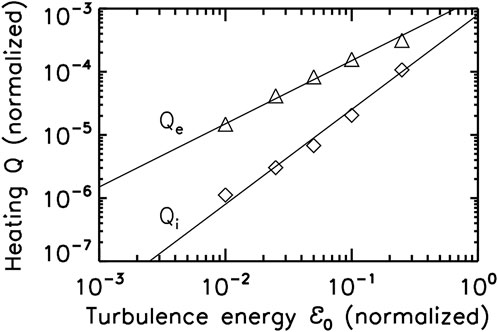
FIGURE 4. Heating rate Q for electrons and ions as a function of the magnetic fluctuation energy
Hughes et al. [46] used 3D PIC simulations to study electron and ion heating due to kinetic Alfvén turbulence. Similar to the 3D PIC simulations of whistler turbulence, the computations represent the forward cascade of freely-decaying turbulence carried out as an initial-value problem on a collisionless, homogeneous, magnetized plasma. In common with the whistler turbulence simulations, electron heating by kinetic Alfvén turbulence is preferentially in directions parallel/anti-parallel to the mean magnetic field (Landau damping) and the maximum electron heating rate linearly scales with the initial fluctuation energy,
Based on the considerations above, a desirable set of simulations would cover not only a large inertial range above ion scales, but also have a realistic mass ratio. This is still computationally challenging by the present standards.
3.3 Search for Control Parameters and Scaling Relations
In the physical sense, dynamics and dissipation mechanism of kinetic-range turbulence are expected to depend on control parameters such as the fluctuation energy
These parameters are varied over a broad range of values. For example, in the linear theory calculations, Verscharen et al. [91] studied 1 < mi/me < 1836 and 10–4 < vA/c < 1/3. In nonlinear PIC simulations Gary et al. [56] studied 25 < mi/me < 1836 and Hughes et al. [93] studied 0.025 < vth, e/c < 0.10. Verscharen et al. [91] showed that mass ratio had a drastic effect on quasi-parallel magnetosonic/whistler branch, and quasi-perpendicular kinetic Alfvén branch. The kinetic Aflvén waves get critically damped for realistic mass ratio but can reach electron scales for artificially large electron mass. vA/c was not shown to have significant effect on the wave properties in the non-relativistic case. The simulations give us a sense of how the unphysical values affect the simulation results so that, even if we do not have the resources to run simulations with fully physical values, we can expect that whistler turbulence dissipation is likely to scale as the mass ratio me/mi. In another study Parashar and Gary [63] studied the effect of variations in relative ion/electron temperatures. They found that
There is ample evidence that the dissipation of kinetic-range turbulence happens in an intermittent way similar to magnetohydrodynamic turbulence [4,97–99]. Statistical tools such as probability density functions of increments, or scale dependent kurtosis are useful tools to quantify this intermittency. Using PIC simulations Chang et al. [75] showed that intermittency level increases with the fluctuation energy
Within the theme of identifying scaling relations, Peter Gary also studied how the species entropies change with turbulence amplitude. For instance, Gary et al. [92] showed that the electron and ion heating rate (Figure 5A) and electron and ion entropies (Figure 5B) can be summarized as simple power law relations as a function of the dimensionless fluctuating magnetic field energy
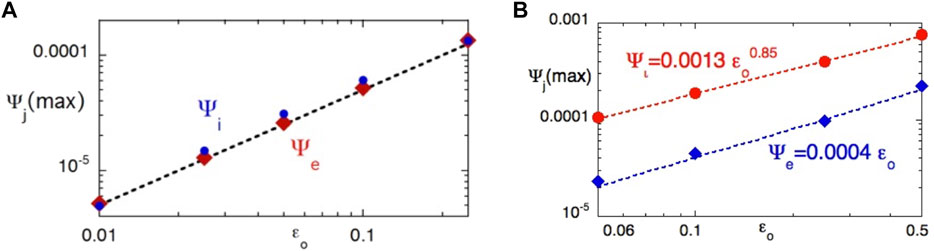
FIGURE 5. Simple scaling relations derived from PIC simulations [92]. (A) The maximum values of the dimensionless time rates of change of the electron (blue dots) and ion (red diamonds) entropies derived from the whistler turbulence PIC simulations of [56]. The scaling relations derived for whistler turbulence are: the maximum entropy increase for electron:
3.4 Linear Instabilities Versus Nonlinear Effects
An important dichotomy that arises in kinetic theory is the interplay of linear waves and instabilities with nonlinear turbulence. Solar wind and magnetosheath data organize themselves in the β‖—Rp plane, where β‖ is the parallel proton beta and Rp is the anisotropy of protons, in such a way that linear instability thresholds appear to constrain the data [6,100]. Based on these observations, it has been suggested that the microinstabilities play an important role in regulating the solar wind evolution. It has also been suggested that “majority of solar wind intervals support ion-driven instabilities” [101]. This raises a natural question: What is the relative importance of linear time scales (wave frequencies and instability growth rates) compared to nonlinear time scales? Peter Gary and collborators have addressed this question in many papers [102–105].
Matthaeus et al. [102] showed that the kinetic scale nonlinear times in the solar wind are comparable to or smaller than the linear timescales of waves and instabilities. Qudsi et al. [103] analyzed data from the MMS spacecraft as well as fully kinetic 2.5D simulations of turbulence with mean magnetic field out of the plane of simulation. The instability growth rates were computed based on the local β‖ and proton anisotropies Rp. They showed that the instabilities thresholds are large in intermittent locations near intense current sheets. It has been shown that a lot of kinetic activity happens near strong current sheets [106–108]. Intense distortions of the distribution function can happen near such current sheets and can render the distribution function unstable. Qudsi et al. [103] showed this proximity of instability growth rates and intermittent structures in both PIC simulations and MMS data.
As discussed earlier, the computational expense of fully kinetic simulations forces one to run them with artificial parameters and in reduced dimensionality. A good understanding of dissipative processes in kinetic plasmas requires comparative studies of various models and geometries. In the spirit of Turbulent Dissipation Challenge [98], Gary et al. [104] compared simulations in three different geometries to study the relative importance of instability time scales and nonlinear times. Figure 6 shows two dimensional probability distribution functions (PDFs) of kinetic instability rates and nonlinear rates computed at the scale of maximum instability growth rate at each point for 1) 2.5D perpendicular turbulence with mean magnetic field out of the plane of simulation, 2) 2.5D parallel turbulence with mean magnetic field in the plane of the simulation, and 3) a fully 3D turbulence simulation. It is evident from all three panels that the nonlinear rates are almost always larger than the instability growth rates. Only a small fraction of population lies in the regime where the instability growth rate is larger than the nonlinear rate. 2.5D perpendicular-plane simulation shows a complete dominance of nonlinear rates. Although the 2.5D parallel simulation shows a dominance of nonlinear rates, the ratio of the two rates is closer to unity compared to the perpendicular simulation. 3D simulation shows a wide spread in the rates while retaining the dominance of nonlinear rates. The PDFs in the 3D simulation show many qualitative and quantitative similarities to the magnetosheath dara from the MMS spacecraft and the solar wind data from the Wind spacecraft [105].

FIGURE 6. Probability distribution functions (PDFs) of tnl vs tinst. for three fully kinetic simulations [104]. (A) 2.5D perpendicular PIC with mean field out of the plane of simulation, (B) 2.5D parallel PIC with mean field in the plane of simulation, and (C) 3D PIC. The 2.5D perp PIC simulation shows a dominance of nonlinear time scales. The 2.5D parallel PIC simulation shows a distribution where nonlinear timescale dominates still. However, the distribution lies close to unity. 3D PIC shows a distribution that is similar to observations in the magnetosheath [105].
Peter Gary studied instabilities extensively starting in the 1990s, e.g. Gary et al. [109]. While the linear instabilities were often studied under the simplified assumption of a single anisotropic distribution, the presence of secondary populations, either as proton beams or alpha particles, can significantly impact the stability and thus the predicted growth rates.
The streaming speed of alpha particles relative to the protons (which is about the local Alfvén speed in the solar wind) can cause alpha/proton magnetosonic and Alfvén instabilities [110]. The relative flow difference between the alpha particles and the protons changes the occurrence of maximum growth rate for the temperature anisotropy instability of protons (exciting the ion cyclotron waves) into the direction of flow difference [111].
Linear instability analysis using the Helios data shows that the alpha particles in the solar wind play a more important role at larger distances from the Sun [112]. The growth rate under the presence of alph particles becomes non-negligible when compared with the turbulent cascade rate. Hence, the alpha particles can potentially impact the turbulent cascade through this channel.
4 Conclusions and Outlook
Observations of solar wind turbulence near proton scales, the beginning of kinetic range, show that kinetic Alfvén turbulence dominates magnetosonic-whistler turbulence at those scales. However, at shorter wavelengths of the order of the electron inertial lengths neither observations nor fully kinetic simulations have yielded definitive results. The studies carried out by Peter Gary and collaborators addressed several specific questions across the kinetic range to construct a more complete picture of plasma turbulence:
1. How do the spectra for kinetic Alfvén and whistler turbulence compare and scale with the plasma parameters beta and the fluctuation amplitudes?
2. What are the dissipation mechanisms for kinetic Alfvén and whistler turbulence, and if there is a cross-over from the former to the latter, what are its scaling properties?
3. Sample computations show that electrons are preferentially heated in directions parallel/anti-parallel to the large-scale magnetic field in both kinetic Alfvén and whistler turbulence, while the solar wind observations indicate that both an excess of parallel temperature and that of perpendicular temperare are possible. How can we systematically understand the electron temperature evolution in the frame of kinetic-range turbulence?
4. What are the parametric dependencies for electron and ion heating by kinetic Alfvén and whistler turbulence scenarios?
5. Can kinetic-range fluctuations be represented by dispersion relations derived from linear Vlasov theory while at the same time the fluctuations participate in the strongly nonlinear interactions characteristic of intermittent turbulence?
The central thesis of the Gary picture is that the kinetic Alfvén cascade dominates at the proton scales but critically damps before reaching electron scales. Near the electron scales, whistler turbulence starts dominating and plays an important role in electron dynamics. The kinetic-range turbulence depends on many variables, physical as well as numerical. Physical variables include the temperatures of ions and electrons (Te, Ti), their anisotropy (Tj,⊥/Tj‖), their plasma betas (βe, βi), the amplitude of turbulent fluctuations at the largest scales
Peter Gary through his numerous collaborations addressed various aspects of kinetic-range turbulence that support the Gary picture. Many papers have studied these parameter variations in the kinetic range using linear Vlasov theory, fully kinetic simulations in varied geometries, as well as spacecraft data from the solar wind and magnetosheath. Their results show that whistler and kinetic Alfvén turbulence can generate or sustain anisotropic power spectra, predict heating rates from whistler and kinetic Alfvén turbulence under varied conditions, explore effects of parameter variations on such heating profiles, and identify potential channels for the interplay between linear instabilities and intermittent structures. The work done by Peter Gary and collaborators contributing to the Gary picture of turbulence raises further questions that should be addressed by future studies.
6. What are the important parameters that determine the nature of kinetic range cascade and dissipation?
The large parameter space that needs to be explored implies that many linear theory studies and nonlinear kinetic studies are needed to identify how the variations of temperatures, betas, fluctuation amplitudes, and system size affect the kinetic-range turbulence. For example, careful and detailed maps of damping rates as a function of various physical and numerical parameters are still lacking. A catalogue of such maps can prove valuable to guide parameter searches for much more expensive nonlinear numerical simulations. Another interesting direction to explore within this theme is a comprehensive study to identify the nature of fluctuations near electron scales from large fully kinetic simulations. These simulations will need to span a large range of scales from the inertial range down to sub-electron scales. Parameter variations such as large-scale turbulence amplitude, plasma beta, and anisotropies etc. will need to be varied to get more details.
7. How do kinetic instabilities interplay with turbulence driven by large scales into the kinetic range?
Many papers have started to appear under this theme recently but much needs to be explored. How much power can such instabilities pump into the kinetic range? How frequent are such instabilities? Do they happen only near intermittent structures or can they be pumped by large scale conditions as well?
8. How critical are the approximations of the model used to describe kinetic-range turbulence?
Many models such as gyrokinetic, ten-moment two fluid, hybrid kinetic, Vlasov-Maxwell etc. are used to study kinetic-range turbulence. The gyrokinetic model, for example, does not include whistler physics and hence cannot address the issues regarding the competition between kinetic Alfvén and whistler cascades. The hybrid kinetic model does not include electron kinetic physics and hence is also unable to describe the electron scale kinetic physics. Ten-moment models, successfully applied to the global simulations of Earth’s magnetosphere and the plasma environment around Ganymede and Mercury, do not contain a time-evolution equation for the heat flux although the models include the evaluation of third-order moments in the anisotropy and non-gyrotropy of the pressure tensor [114]. Fully kinetic models are extremely expensive. Hence, comparative studies of these models are critical to identify the right tools and physics. On the numerical front, PIC has traditionally been the popular model for its relatively less computational expense. However, the noise stemming from finite number of particles can affect the electron scale dynamics significantly. On the other hand, the Eulerian Vlasov models have been computationally much more expensive. Newer finite element [48] and Hermite spectral methods [115] are being developed as well. With increasing computing power and improved numerical schemes, such models may become more desirable than PIC.
9. What are desirable analyses to identify and differentiate between whistler and kinetic Alfvén fluctuations and their role in plasma heating?
Commonly employed analyses include power spectra, heating rates, and intermittency analyses. Other potential analysis to perform could be to theoretically identify and analyse various dissipation measures such as Pi-D [99], stochastic heating [89], and field particle correlator [116]. Can four-dimensional Fourier spectra of kinetic-range turbulence simulations yield some interesting differentiating conclusions?
This is just a sampling of questions that directly follow up on Peter Gary’s contributions. The Gary picture addresses a relatively less explored part of the kinetic range, i.e., between proton and electron scales. Hence, the Gary picture has the potential, when properly validated and revised, to not only strengthen our understanding of turbulence in the near-Earth solar wind but will also lay the groundwork for interpretation of data collected by the on-going missions in the inner heliosphere by Parker Solar Probe, Solar Orbiter, and BepiColombo, and the upcoming HelioSwarm mission.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledement and Dedication
The authors are highly indebted to S. Peter Gary for his mentorship over the years and have written this paper as their tribute to him. Through his exceptional career spanning many decades, he not only made major contributions to the field of space plasma physics but also served as a mentor to countless number of young scientists. That includes the authors of this paper. A curious, passionate, and humble man, he treated beginning students as his peers and supported many young PhDs in finding their own place in field. Many like us, who were fortunate enough to interact with Peter for a long time, will keep getting inspired over the coming decades, fondly remembering our interactions with him. Though Peter is no longer with us, his legacy will continue to inspire young minds for the decades to come.
Dedication by TNP: I have very clear and inspirational memories of my first encounter with Peter. I was a first year graduate student when I met him on my poster in the 2007 AGU Fall Meeting. I was scared to get one of the great scientists of my field on my first ever poster. When Peter started discussing, I didn't feel like a student for a moment. He treated me as a peer, asked me questions as if he would ask a seasoned scientist. His curiosity, passion, and humility left a lifelong impression on me. Peter guided me to get my first ever proposal funded. He was actively mentoring a lot of my peers in a way similar to how he mentored me. The animated, highly educational, and all the time inspiring arguments with Peter on various topics have shaped my thought process significantly.
Dedication by JW: I first met Peter in 1992 via emails on research questions and discussions at the AGU Fall meeting. That encounter quickly turned into a mentorship and friendship from Peter lasting for almost 30 years. I am indebted to Peter not only for his guidance in our research collaboration but also for sharing his advice and wisdom on life. I would also like to thank Peter on behalf of my students, O. Chang, S. Hughes, and C. Cui, for helping to guide their Ph.D dissertations. A true scientist to the end, Peter was as passionate and sharp as ever debating the possible sources of kinetic-range turbulence at our last research zoom meeting just a few days before his passing.
Dedication by YN: I first met Peter at the IAGA conference in Toulouse, France, in July 2005. We chatted about some physics, and I confessed to him that I was a fan of Peter's paper series. Peter answered, “Thank you, but don't trust all of my papers. You are working in the observations. You should visit Los Alamos!” Peter really invited me to Los Alamos in December 2006. Peter showed me the laboratory, introduced me to his friends and colleagues, and took me to hiking and swimming (he was my swimming teacher, too). I really enjoyed working with Peter on the observational data and theoretical modeling of turbulence, and also thank him for hosting not only my visit but also the visit of my student (C. Perschke) to Los Alamos.
References
1. Marsch E. Kinetic Physics of the Solar corona and Solar Wind. Living Rev Solar Phys (2006) 3. doi:10.12942/lrsp-2006-1
2. Marsch E. Solar Wind and Kinetic Heliophysics. Ann Geophys (2018) 36:1607–30. doi:10.5194/angeo-36-1607-2018
3. Hollweg JV, Isenberg PA. Generation of the Fast Solar Wind: A Review with Emphasis on the Resonant Cyclotron Interaction. J Geophys Res (2002) 107:SSH-12. doi:10.1029/2001JA000270
4. TenBarge JM, Howes GG, Dorland W. Collisionless Damping at Electron Scales in Solar Wind Turbulence. Astrophysical J (2013) 774:139. doi:10.1088/0004-637X/774/2/139
5. Gary SP. Theory of Space Plasma Microinstabilities. Cambridge: Cambridge University Press (1993). doi:10.1017/CBO9780511551512
6. Bale SD, Kasper JC, Howes GG, Quataert E, Salem C, Sundkvist D. Magnetic Fluctuation Power Near Proton Temperature Anisotropy Instability Thresholds in the Solar Wind. Phys Rev Lett (2009) 103:211101. doi:10.1103/PhysRevLett.103.211101
7. Kraichnan RH. Inertial-range Spectrum of Hydromagnetic Turbulence. Phys Fluids (1965) 8:1385–7. doi:10.1063/1.1761412
8. Goldreich P, Sridhar S. Magnetohydrodynamic Turbulence Revisited. Astrophysical J (1997) 485:680–8. doi:10.1086/304442
10. Shebalin JV, Matthaeus WH, Montgomery D. Anisotropy in MHD Turbulence Due to a Mean Magnetic Field. J Plasma Phys (1983) 29:525–47. doi:10.1017/S0022377800000933
11. Aluie H. Compressible Turbulence: the cascade and its Locality. Phys Rev Lett (2011) 106:174502. doi:10.1103/PhysRevLett.106.174502
12. Bian X, Aluie H. Decoupled Cascades of Kinetic and Magnetic Energy in Magnetohydrodynamic Turbulence. Phys Rev Lett (2019) 122:135101. doi:10.1103/PhysRevLett.122.135101
13. Schekochihin AA, Cowley SC, Dorland W, Hammett GW, Howes GG, Quataert E, et al. Astrophysical Gyrokinetics: Kinetic and Fluid Turbulent Cascades in Magnetized Weakly Collisional Plasmas. The Astrophysical JournalS (2009) 182:310–77. doi:10.1088/0067-0049/182/1/310
14. Boldyrev S, Horaites K, Xia Q, Perez JC. Toward a Theory of Astrophysical Plasma Turbulence at Subproton Scales. Astrophysical J (2013) 777:41. doi:10.1088/0004-637X/777/1/41
15. Eyink GL. Cascades and Dissipative Anomalies in Nearly Collisionless Plasma Turbulence. Phys Rev X (2018) 8:041020. doi:10.1103/PhysRevX.8.041020
16. Matthaeus WH, Yang Y, Wan M, Parashar TN, Bandyopadhyay R, Chasapis A, et al. Pathways to Dissipation in Weakly Collisional Plasmas. Astrophysical J (2020) 891:101. doi:10.3847/1538-4357/ab6d6a
17. Bowers KJ, Albright BJ, Yin L, Bergen B, Kwan TJT. Ultrahigh Performance Three-Dimensional Electromagnetic Relativistic Kinetic Plasma Simulation. Phys Plasmas (2008) 15:055703. doi:10.1063/1.2840133
18. Klein KG, Howes GG, TenBarge JM, Bale SD, Chen CHK, Salem CS. Using Synthetic Spacecraft Data to Interpret Compressible Fluctuations in Solar Wind Turbulence. Astrophysical J (2012) 755:159. doi:10.1088/0004-637X/755/2/159
19. Verscharen D, Chandran BDG. NHDS: the new hampshire Dispersion Relation Solver. Res Notes AAS (2018) 2:13. doi:10.3847/2515-5172/aabfe3
20. Derouillat J, Beck A, P,érez F, Vinci T, Chiaramello M, Grassi A, et al. Smilei : A Collaborative, Open-Source, Multi-Purpose Particle-In-Cell Code for Plasma Simulation. Comput Phys Commun (2018) 222:351–73. doi:10.1016/j.cpc.2017.09.024
21. Bird R, Tan N, Luedtke SV, Harrell SL, Taufer M, Albright B. VPIC 2.0: Next Generation Particle-In-Cell Simulations. IEEE Trans Parallel Distrib Syst (2022) 33:952–63. doi:10.1109/TPDS.2021.3084795
22. Gary SP. Short-wavelength Plasma Turbulence and Temperature Anisotropy Instabilities: Recent Computational Progress. Phil Trans R Soc A (2015) 373:20140149. doi:10.1098/rsta.2014.0149
23. Gary SP. Low-frequency Waves in a High-Beta Collisionless Plasma: Polarization, Compressibility and Helicity. J Plasma Phys (1986) 35:431–47. doi:10.1017/S0022377800011442
24. Narita Y, Roberts OW, Vörös Z, Hoshino M. Transport Ratios of the Kinetic Alfvén Mode in Space Plasmas. Front Phys (2020) 8:166. doi:10.3389/fphy.2020.00166
25. Servidio S, Valentini F, Perrone D, Greco A, Califano F, Matthaeus WH, et al. A Kinetic Model of Plasma Turbulence. J Plasma Phys (2015) 81:325810107. doi:10.1017/S0022377814000841
26. Chen CHK. Recent Progress in Astrophysical Plasma Turbulence from Solar Wind Observations. J Plasma Phys (2016) 82:535820602. doi:10.1017/S0022377816001124
27. Verscharen D, Klein KG, Maruca BA. The Multi-Scale Nature of the Solar Wind. Living Rev Sol Phys (2019) 16:5. doi:10.1007/s41116-019-0021-0
28. Sahraoui F, Hadid L, Huang S. Magnetohydrodynamic and Kinetic Scale Turbulence in the Near-Earth Space Plasmas: A (Short) Biased Review. Rev Mod Plasma Phys (2020) 4:1–33. doi:10.1007/s41614-020-0040-2
29. Matthaeus WH. Turbulence in Space Plasmas: Who Needs it? Phys Plasmas (2021) 28:032306. doi:10.1063/5.0041540
30. Sahraoui F, Goldstein ML, Belmont G, Canu P, Rezeau L. Three Dimensional AnisotropickSpectra of Turbulence at Subproton Scales in the Solar Wind. Phys Rev Lett (2010) 105:131101. doi:10.1103/PhysRevLett.105.131101
31. Salem CS, Howes GG, Sundkvist D, Bale SD, Chaston CC, Chen CHK, et al. Identification of Kinetic Alfvén Wave Turbulence in the Solar Wind. Astrophysical J (2012) 745:L9. doi:10.1088/2041-8205/745/1/L9
32. Narita Y, Gary SP, Saito S, Glassmeier K-H, Motschmann U. Dispersion Relation Analysis of Solar Wind Turbulence. Geophys Res Lett (2011) 38:a–n. doi:10.1029/2010GL046588
33. Birdsall CK, Langdon AB. Plasma Physics via Computer Simulation. New York: McGraw-Hill Book Company (1985).
34. Schuecker P, Finoguenov A, Miniati F, Böhringer H, Briel UG. Probing Turbulence in the Coma Galaxy Cluster. A&A (2004) 426:387–97. doi:10.1051/0004-6361:20041039
35. Churazov E, Vikhlinin A, Zhuravleva I, Schekochihin A, Parrish I, Sunyaev R, et al. X-ray Surface Brightness and Gas Density Fluctuations in the Coma Cluster. Mon Not R Astron. Soc. (2012) 421:1123–35. doi:10.1111/j.1365-2966.2011.20372.x
36. Kasper JC, Klein KG, Lichko E, Huang J, Chen CHK, Badman ST, et al. Parker Solar Probe Enters the Magnetically Dominated Solar corona. Phys Rev Lett (2021) 127:255101. doi:10.1103/PhysRevLett.127.255101
37. Tu C-Y, Marsch E. MHD Structures, Waves and Turbulence in the Solar Wind: Observations and Theories. Space Sci Rev (1995) 73:1–210. doi:10.1007/BF00748891
38. Bruno R, Carbone V. The Solar Wind as a Turbulence Laboratory. Living Rev Solar Phys (2013) 10:2. doi:10.12942/lrsp-2013-2
39. Caprioli D, Brunetti G, Jones TW, Kang H, Kunz M, Oh SP, et al. Plasma 2020 – Intracluster Medium Plasmas. arXiv:1903.08751 (2019). doi:10.48550/arXiv.1903.08751
40. Shalchi A. Perpendicular Transport of Energetic Particles in Magnetic Turbulence. Space Sci Rev (2020) 216:1–134. doi:10.1007/s11214-020-0644-4
41. Oughton S, Engelbrecht NE. Solar Wind Turbulence: Connections with Energetic Particles. New Astron (2021) 83:101507. doi:10.1016/j.newast.2020.101507
43. Lipatov AS. The Hybrid Multiscale Simulation Technology: An Introduction with Application to Astrophysical and Laboratory Plasmas. Berlin, Germany: Springer-Verlag (2002).
44. Valentini F, Trávníček P, Califano F, Hellinger P, Mangeney A. A Hybrid-Vlasov Model Based on the Current advance Method for the Simulation of Collisionless Magnetized Plasma. J Comput Phys (2007) 225:753–70. doi:10.1016/j.jcp.2007.01.001
45. Chang O, Gary SP, Wang J. Whistler Turbulence Forward cascade versus Inverse cascade: Three-Dimensional Particle-In-Cell Simulations. Astrophysical J (2015) 800:87. doi:10.1088/0004-637X/800/2/87
46. Hughes RS, Gary SP, Wang J. Particle-in-cell Simulations of Electron and Ion Dissipation by Whistler Turbulence: Variations with Electron β. Astrophysical J (2017) 835:L15. doi:10.3847/2041-8213/835/1/L15
47. Hughes RS, Gary SP, Wang J, Parashar TN. Kinetic Alfvén Turbulence: Electron and Ion Heating by Particle-In-Cell Simulations. Astrophysical J (2017) 847:L14. doi:10.3847/2041-8213/aa8b13
48. Juno J, Hakim A, TenBarge J, Shi E, Dorland W. Discontinuous Galerkin Algorithms for Fully Kinetic Plasmas. J Comput Phys (2018) 353:110–47. doi:10.1016/j.jcp.2017.10.009
49. Koshkarov O, Manzini G, Delzanno GL, Pagliantini C, Roytershteyn V. The Multi-Dimensional Hermite-Discontinuous Galerkin Method for the Vlasov-Maxwell Equations. Comput Phys Commun (2021) 264:107866. doi:10.1016/j.cpc.2021.107866
50. Howes GG, Cowley SC, Dorland W, Hammett GW, Quataert E, Schekochihin AA. A Model of Turbulence in Magnetized Plasmas: Implications for the Dissipation Range in the Solar Wind. J Geophys Res (2008) 113:a–n. doi:10.1029/2007JA012665
51. Podesta JJ, Borovsky JE, Gary SP. A Kinetic Alfvén Wave Cascade Subject to Collisionless Damping Cannot Reach Electron Scales in the Solar Wind at 1 Au. Astrophysical J (2010) 712:685–91. doi:10.1088/0004-637X/712/1/685
52. Howes GG, Bale SD, Klein KG, Chen CHK, Salem CS, TenBarge JM. The Slow-Mode Nature of Compressible Wave Power in Solar Wind Turbulence. Astrophysical J (2012) 753:L19. doi:10.1088/2041-8205/753/1/L19
53. Goldreich P, Sridhar S. Toward a Theory of Interstellar Turbulence. 2: Strong Alfvenic Turbulence. Astrophysical J (1995) 438:763–75. doi:10.1086/175121
54. Chandran BDG. Weak Compressible Magnetohydrodynamic Turbulence in the Solar Corona. Phys Rev Lett (2005) 95(26):265004. doi:10.1103/physrevlett.95.265004
55. Yang Y, Shi Y, Wan M, Matthaeus WH, Chen S. Energy cascade and its Locality in Compressible Magnetohydrodynamic Turbulence. Phys Rev E (2016) 93:061102. doi:10.1103/PhysRevE.93.061102
56. Gary SP, Hughes RS, Wang J. Whistler Turbulence Heating of Electrons and Ions: Three-Dimensional Particle-In-Cell Simulations. Astrophysical J (2016) 816:102. doi:10.3847/0004-637X/816/2/102
57. Podesta JJ, Gary SP. Magnetic Helicity Spectrum of Solar Wind Fluctuations as a Function of the Angle with Respect to the Local Mean Magnetic Field. Astrophysical J (2011) 734:15. doi:10.1088/0004-637X/734/1/15
58. He J, Marsch E, Tu C, Yao S, Tian H. Possible Evidence of Alfvén-Cyclotron Waves in the Angle Distribution of Magnetic Helicity of Solar Wind Turbulence. Astrophysical J (2011) 731(2):85. doi:10.1088/0004-637x/731/2/85
59. Klein KG, HowesTen Barge GG, Ten Barge JM, Podesta JJ. Physical Interpretation of the Angle-dependent Magnetic Helicity Spectrum in the Solar Wind: the Nature of Turbulent Fluctuations Near the Proton Gyroradius Scale. Astrophysical J (2014) 785(2):138. doi:10.1088/0004-637x/785/2/138
60. Squire J, Meyrand R, Kunz MW, Lev A, Schekochihin AA, Quataert E. High-frequency Heating of the Solar Wind Triggered by Low-Frequency Turbulence. Nat Astron (2022) 2022:1–9. doi:10.1038/s41550-022-01624-z
61. Narita Y. Space-time Structure and Wavevector Anisotropy in Space Plasma Turbulence. Living Rev Sol Phys (2018) 15:2. doi:10.1007/s41116-017-0010-0
62. Zeiler A, Biskamp D, Drake JF, Rogers BN, Shay MA, Scholer M. Three-dimensional Particle Simulations of Collisionless Magnetic Reconnection. J Geophys Res (2002) 107:1230. doi:10.1029/2001JA000287
63. Parashar TN, Gary SP. Dissipation of Kinetic Alfvénic Turbulence as a Function of Ion and Electron Temperature Ratios. Astrophysical J (2019) 882:29. doi:10.3847/1538-4357/ab2fc8
64. Wang J, Liewer P, Decyk V. 3D Electromagnetic Plasma Particle Simulations on a MIMD Parallel Computer. Comput Phys Commun (1995) 87:35–53. doi:10.1016/0010-4655(94)00167-Z
65. Gary SP. Test for Wavevector Anisotropies in Plasma Turbulence Cascades. Astrophysical J (2013) 769:36. doi:10.1088/0004-637X/769/1/36
66. Chang O, Peter Gary S, Wang J. Whistler Turbulence Forward cascade: Three-Dimensional Particle-In-Cell Simulations. Geophys Res Lett (2011) 38:a–n. doi:10.1029/2011GL049827
67. Chang O, Gary SP, Wang J. Whistler Turbulence at Variable Electron Beta: Three‐dimensional Particle‐in‐cell Simulations. J Geophys Res Space Phys (2013) 118:2824–33. doi:10.1002/jgra.50365
68. Gary SP, Chang O, Wang J. Forward cascade of Whistler Turbulence: Three-Dimensional Particle-In-Cell Simulations. Astrophysical J (2012) 755:142. doi:10.1088/0004-637X/755/2/142
69. Narita Y, Nakamura R, Baumjohann W, Glassmeier K-H, Motschmann U, Giles B, et al. On Electron-Scale Whistler Turbulence in the Solar Wind. Astrophysical J (2016) 827:L8. doi:10.3847/2041-8205/827/1/L8
70. Perschke C, Narita Y, Gary SP, Motschmann U, Glassmeier K-H. Dispersion Relation Analysis of Turbulent Magnetic Field Fluctuations in Fast Solar Wind. Ann Geophys (2013) 31:1949–55. doi:10.5194/angeo-31-1949-2013
71. Roberts OW, Alexandrova O, Kajdič P, Turc L, Perrone D, Escoubet CP, et al. Variability of the Magnetic Field Power Spectrum in the Solar Wind at Electron Scales. Astrophysical J (2017) 850:120. doi:10.3847/1538-4357/aa93e5
72. Narita Y, Gary SP. Inertial-range Spectrum of Whistler Turbulence. Ann Geophys (2010) 28:597–601. doi:10.5194/angeo-28-597-2010
73. Saito S, Gary SP, Narita Y. Wavenumber Spectrum of Whistler Turbulence: Particle-In-Cell Simulation. Phys Plasmas (2010) 17:122316. doi:10.1063/1.3526602
74. Iroshnikov PS. Turbulence of a Conducting Fluid in a strong Magnetic Field. Sov Astron (1964) 7:566–71. Available at: https://ui.adsabs.harvard.edu/abs/1964SvA.....7..566I/ (Accessed June 30, 2022).
75. Chang O, Peter Gary S, Wang J. Energy Dissipation by Whistler Turbulence: Three-Dimensional Particle-In-Cell Simulations. Phys Plasmas (2014) 21:052305. doi:10.1063/1.4875728
76. Hughes RS, Gary SP, Wang J. Electron and Ion Heating by Whistler Turbulence: Three-Dimensional Particle-In-Cell Simulations. Geophys Res Lett (2014) 41:8681–7. doi:10.1002/2014GL062070
77. Alexandrova O, Saur J, Lacombe C, Mangeney A, Mitchell J, Schwartz SJ, et al. Universality of Solar-Wind Turbulent Spectrum from MHD to Electron Scales. Phys Rev Lett (2009) 103:165003. doi:10.1103/PhysRevLett.103.165003
78. Sahraoui F, Goldstein ML, Robert P, Khotyaintsev YV. Evidence of a cascade and Dissipation of Solar-Wind Turbulence at the Electron Gyroscale. Phys Rev Lett (2009) 102:231102. doi:10.1103/PhysRevLett.102.231102
79. Narita Y. Spectral Moments for the Analysis of Frequency Shift, Broadening, and Wavevector Anisotropy in a Turbulent Flow. Earth Planets Space (2017) 69:73. doi:10.1186/s40623-017-0658-7
80. Galtier S, Bhattacharjee A. Anisotropic Weak Whistler Wave Turbulence in Electron Magnetohydrodynamics. Phys Plasmas (2003) 10:3065–76. doi:10.1063/1.1584433
81. Cho J, Lazarian A. The Anisotropy of Electron Magnetohydrodynamic Turbulence. Astrophysical J (2004) 615:L41–L44. doi:10.1086/425215
82. Saito S, Gary SP, Li H, Narita Y. Whistler Turbulence: Particle-In-Cell Simulations. Phys Plasmas (2008) 15:102305. doi:10.1063/1.2997339
83. Narita Y, ComiÅŸel H, Motschmann U. Spatial Structure of Ion-Scale Plasma Turbulence. Front Phys (2014) 2:13. doi:10.3389/fphy.2014.001310.3389/fphy.2014.00013
84. Hellinger P, Matteini L, Štverák Š, Trávníček PM, Marsch E. Heating and Cooling of Protons in the Fast Solar Wind between 0.3 and 1 AU: Helios Revisited. J Geophys Res (2011) 116:a–n. doi:10.1029/2011JA016674
85. Hellinger P, Trávníček PM, Štverák Š, Matteini L, Velli M. Proton thermal Energetics in the Solar Wind: Helios Reloaded. J Geophys Res Space Phys (2013) 118:1351–65. doi:10.1002/jgra.50107
86. Saito S, Nariyuki Y. Perpendicular Ion Acceleration in Whistler Turbulence. Phys Plasmas (2014) 21:042303. doi:10.1063/1.4870757
87. Wu P, Wan M, Matthaeus WH, Shay MA, Swisdak M. von Kármán Energy Decay and Heating of Protons and Electrons in a Kinetic Turbulent Plasma. Phys Rev Lett (2013) 111:121105. doi:10.1103/PhysRevLett.111.121105
88. Matthaeus WH, Parashar TN, Wan M, Wu P. Turbulence and Proton-Electron Heating in Kinetic Plasma. Astrophysical J (2016) 827:L7. doi:10.3847/2041-8205/827/1/L7
89. Chandran BDG, Li B, Rogers BN, Quataert E, Germaschewski K. Perpendicular Ion Heating by Low-Frequency Alfvén-Wave Turbulence in the Solar Wind. Astrophysical J (2010) 720:503–15. doi:10.1088/0004-637X/720/1/503
90. Vasquez BJ, Markovskii SA, Chandran BDG. Three-dimensional Hybrid Simulation Study of Anisotropic Turbulence in the Proton Kinetic Regime. Astrophysical J (2014) 788:178. doi:10.1088/0004-637X/788/2/178
91. Verscharen D, Parashar TN, Gary SP, Klein KG. Dependence of Kinetic Plasma Waves on Ion-To-Electron Mass Ratio and Light-To-Alfvén Speed Ratio. Mon Not R Astron. Soc. (2020) 494:2905–11. doi:10.1093/mnras/staa977
92. Gary SP, Zhao Y, Hughes RS, Wang J, Parashar TN. Species Entropies in the Kinetic Range of Collisionless Plasma Turbulence: Particle-In-Cell Simulations. Astrophysical J (2018) 859:110. doi:10.3847/1538-4357/aac022
93. Hughes RS, Wang J, Decyk VK, Gary SP. Effects of Variations in Electron thermal Velocity on the Whistler Anisotropy Instability: Particle-In-Cell Simulations. Phys Plasmas (2016) 23:042106. doi:10.1063/1.4945748
94. Kawazura Y, Barnes M, Schekochihin AA. Thermal Disequilibration of Ions and Electrons by Collisionless Plasma Turbulence. Proc Natl Acad Sci U.S.A (2019) 116:771–6. doi:10.1073/pnas.1812491116
95. Schekochihin AA, Kawazura Y, Barnes MA. Constraints on Ion versus Electron Heating by Plasma Turbulence at Low Beta. J Plasma Phys (2019) 85:905850303. doi:10.1017/S0022377819000345
96. Zhdankin V, Uzdensky DA, Werner GR, Begelman MC. Electron and Ion Energization in Relativistic Plasma Turbulence. Phys Rev Lett (2019) 122:055101. doi:10.1103/PhysRevLett.122.055101
97. Parashar TN, Servidio S, Shay MA, Breech B, Matthaeus WH. Effect of Driving Frequency on Excitation of Turbulence in a Kinetic Plasma. Phys Plasmas (2011) 18:092302. doi:10.1063/1.3630926
98. Parashar TN, Salem C, Wicks RT, Karimabadi H, Gary SP, Matthaeus WH. Turbulent Dissipation challenge: A Community-Driven Effort. J Plasma Phys (2015) 81:10. doi:10.1017/S0022377815000860
99. Yang Y, Matthaeus WH, Parashar TN, Wu P, Wan M, Shi Y, et al. Energy Transfer Channels and Turbulence cascade in Vlasov-Maxwell Turbulence. Phys Rev E (2017) 95:061201. doi:10.1103/PhysRevE.95.061201
100. Maruca BA, Chasapis A, Gary SP, Bandyopadhyay R, Chhiber R, Parashar TN, et al. MMS Observations of Beta-dependent Constraints on Ion Temperature Anisotropy in Earth's Magnetosheath. Astrophysical J (2018) 866:25. doi:10.3847/1538-4357/aaddfb
101. Klein KG, Alterman BL, Stevens ML, Vech D, Kasper JC. Majority of Solar Wind Intervals Support Ion-Driven Instabilities. Phys Rev Lett (2018) 120:205102. doi:10.1103/PhysRevLett.120.205102
102. Matthaeus WH, Oughton S, Osman KT, Servidio S, Wan M, Gary SP, et al. Nonlinear and Linear Timescales Near Kinetic Scales in Solar Wind Turbulence. Astrophysical J (2014) 790:155. doi:10.1088/0004-637X/790/2/155
103. Qudsi RA, Bandyopadhyay R, Maruca BA, Parashar TN, Matthaeus WH, Chasapis A, et al. Intermittency and Ion Temperature-Anisotropy Instabilities: Simulation and Magnetosheath Observation. Astrophysical J (2020) 895:83. doi:10.3847/1538-4357/ab89ad
104. Gary SP, Bandyopadhyay R, Qudsi RA, Matthaeus WH, Maruca BA, Parashar TN, et al. Particle-in-cell Simulations of Decaying Plasma Turbulence: Linear Instabilities versus Nonlinear Processes in 3D and 2.5D Approximations. Astrophysical J (2020) 901:160. doi:10.3847/1538-4357/abb2ac
105. Bandyopadhyay R, Ramiz AQ, Matthaeus WH, Parashar TN, Maruca BA, Gary SP, et al. Interplay of Turbulence and Proton-Microinstability Growth in Space Plasmas. arXiv:2006.10316 (2020). doi:10.48550/arXiv.2006.10316
106. Servidio S, Valentini F, Califano F, Veltri P. Local Kinetic Effects in Two-Dimensional Plasma Turbulence. Phys Rev Lett (2012) 108:045001. doi:10.1103/PhysRevLett.108.045001
107. Greco A, Valentini F, Servidio S, Matthaeus WH. Inhomogeneous Kinetic Effects Related to Intermittent Magnetic Discontinuities. Phys Rev E (2012) 86:066405. doi:10.1103/PhysRevE.86.066405
108. Parashar TN, Matthaeus WH. Propinquity of Current and Vortex Structures: Effects on Collisionless Plasma Heating. Astrophysical J (2016) 832:57. doi:10.3847/0004-637X/832/1/57
109. Gary SP, Yin L, Winske D. Electromagnetic Proton Cyclotron Anisotropy Instability: Wave-Particle Scattering Rate. Geophys Res Lett (2000) 27:2457–9. doi:10.1029/2000GL000055
110. Gary SP, Yin L, Winske D, Reisenfeld DB. Electromagnetic Alpha/proton Instabilities in the Solar Wind. Geophys Res Lett (2000) 27:1355–8. doi:10.1029/2000GL000019
111. Podesta JJ, Gary SP. Effect of Differential Flow of Alpha Particles on Proton Pressure Anisotropy Instabilities in the Solar Wind. Astrophysical J (2011) 742:41. doi:10.1088/0004-637X/742/1/41
112. Klein KG, Martinović M, Stansby D, Horbury TS. Linear Stability in the Inner Heliosphere: Helios Re-evaluated. Astrophysical J (2019) 887:234. doi:10.3847/1538-4357/ab5802
113. Pierrard V, Lazar M, Poedts S, Štverák Š, Maksimovic M, Trávníček PM. The Electron Temperature and Anisotropy in the Solar Wind. Comparison of the Core and Halo Populations. Sol Phys (2016) 291:2165–79. doi:10.1007/s11207-016-0961-7
114. Ng J, Hakim A, Wang L, Bhattacharjee A. An Improved Ten-Moment Closure for Reconnection and Instabilities. Phys Plasmas (2020) 27:082106. doi:10.1063/5.0012067
115. Roytershteyn V, Delzanno GL. Spectral Approach to Plasma Kinetic Simulations Based on Hermite Decomposition in the Velocity Space. Front Astron Space Sci (2018) 5:27. doi:10.3389/fspas.2018.00027
116. Howes GG, Klein KG, Li TC. Diagnosing Collisionless Energy Transfer Using Field-Particle Correlations: Vlasov-Poisson Plasmas. J Plasma Phys (2017) 83:705830102. doi:10.1017/S0022377816001197
117. Cerri SS, Arzamasskiy L, Kunz MW. On Stochastic Heating and its Phase-Space Signatures in Low-Beta Kinetic Turbulence. Astrophysical J (2021) 916(2):120. doi:10.3847/1538-4357/abfbde
118. Gary SP, Jian LK, Broiles TW, Stevens ML, Podesta JJ, Kasper JC. Ion‐driven Instabilities in the Solar Wind: Wind Observations of 19 March 2005. J Geophys Res Space Phys (2016) 121:30–41. doi:10.1002/2015JA021935
119. Gary SP, Cui C, Wang J. Plasma Turbulence from the Alfvén-Cyclotron Instability: Particle-In-Cell Simulations, SH016-0002. In: American Geophysical Union Fall Meeting (Virtual); December 1–17, 2020 (2020).
120. Howes GG. The Inherently Three-Dimensional Nature of Magnetized Plasma Turbulence. J Plasma Phys (2015) 81:325810203. doi:10.1017/S0022377814001056
121. Karimabadi H, Roytershteyn V, Wan M, Matthaeus WH, Daughton W, Wu P, et al. Coherent Structures, Intermittent Turbulence, and Dissipation in High-Temperature Plasmas. Phys Plasmas (2013) 20:012303. doi:10.1063/1.4773205
122. Parashar TN, Matthaeus WH, Shay MA, Wan M. Transition from Kinetic to MHD Behavior in a Collisionless Plasma. Astrophysical J (2015) 811:112. doi:10.1088/0004-637X/811/2/112
123. Parashar TN, Matthaeus WH, Shay MA. Dependence of Kinetic Plasma Turbulence on Plasma β. Astrophysical J (2018) 864:L21. doi:10.3847/2041-8213/aadb8b
Keywords: plasma turbulence, kinetic range, particle-in-cell simulations, whistler waves, Kinetic Alfvén waves
Citation: Narita Y, Parashar TN and Wang J (2022) The Gary Picture of Short-Wavelength Plasma Turbulence—The Legacy of Peter Gary. Front. Phys. 10:942167. doi: 10.3389/fphy.2022.942167
Received: 12 May 2022; Accepted: 20 June 2022;
Published: 04 August 2022.
Edited by:
Joseph E Borovsky, Space Science Institute, United StatesReviewed by:
Kristopher G Klein, University of Arizona, United StatesCopyright © 2022 Narita, Parashar and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Y. Narita, eWFzdWhpdG8ubmFyaXRhQG9lYXcuYWMuYXQ=
 Y. Narita
Y. Narita T.N. Parashar2
T.N. Parashar2 J. Wang
J. Wang