Rotational Doppler Effect With Vortex Beams: Fundamental Mechanism and Technical Progress

Structured light beams such as optical vortices can carry the orbital angular momentum (OAM) with an unbounded quantum number. Recent years have witnessed a growing interest in the rotational Doppler effect with vortex light. Here we present an overview on the technical progress in measuring the rotational Doppler effect associated with OAM. This includes how a high-order OAM light beam is crucial for realizing high-sensitivity remote sensing of rotating objects. The basic physical mechanism of rotational Doppler effect is manifested from both perspectives of the wave property and the conservation law of energy. Besides, we summarize the extension of the rotational Doppler effect from linear optics to nonlinear optics, and to quantum realms. Also, we discuss the main challenges and opportunities of angular remote sensing in a realistic scenario for future applications.

Introduction

What would happen when placing a watch at the center of a rotating turntable, and viewed from above? Obviously, the watch hands will speed up or slow down depending on the rotation direction of the turntable [1]. If one applies this effect to all rotating vectors, for example to the spatial pattern of the electric field of any light beam carrying angular momentum [2–4], the additional rotation of the beam will result in a frequency shift proportional to the rate of rotation of the beam [5, 6]. This is the direct understanding of the rotational Doppler effect (RDE).

At first, this effect was found related to the circular polarization (CP) of the photon and was called the angular Doppler effect [7]. When the CP photon interacts with the rotating matter, the interchanges of rotational kinetic energy will bring a rotational frequency shift of $\sigma \omega$ to the photon, where $\omega$ is the rotating frequency and $\sigma =\pm 1$ for the right and left CP state of the photon. This phenomenon can be observed with manifestations ranging from the quantum world to satellite-based global positioning systems [8], and also can be observed when the CP light wave propagates through a gas of synchronously spinning molecules [9]. In 1992, Allen et al. established that light beams with helical phase-fronts, described by a transverse phase structure of $\exp \left(i\ell \phi \right)$, can carry the orbital angular momentum (OAM) many times greater than the spin angular momentum of the photon [10], where $\phi$ is the azimuthal angle and $\ell$ is the topological charge. The most typical beam carrying OAM is the Laguerre–Gaussian (LG) beam [11–13]. Subsequently, people realized that this kind of helical beam may also introduce an azimuthal Doppler shift which is many times larger than the angular Doppler effect induced by the CP of the photon [14]. This azimuthal Doppler effect differs significantly from the conventional linear Doppler frequency shift when it is born [7, 15]. The azimuthal Doppler shift in frequency arises not from linear motion, but rotation [16]. This effect should also not be confused with the Doppler effect observed for rotating objects due to the object having a linear velocity with respect to the observer. Unlike the linear Doppler effect (LDE) which is maximal in the plane of the rotation, the RDE is maximal in the direction of the angular velocity vector where the linear Doppler shift is zero [17].

After a simple coaxial superposition between the LG beam and the Gaussian beam, the RDE frequency shift can be observed directly due to the beat frequency phenomenon [5]. The technique of the superposition beam is soon widely used in RDE observation and OAM recognition [6, 18–20]. Especially, people can generate any superposition mode and high-order OAM beam with the development of spatial light modulators [21]. If the two components of the superposition beam have the same OAM number but opposite signs, this superposition beam can be called the phase-conjugated beam which has the self-interference property and is immune to the influence of the linear motion [22, 23]. These concepts were soon extended from linear optics to nonlinear optics and even quantum physics and many new applications have been derived [24–27].

In the 40 years of development since the concept of angular Doppler effect was first proposed, the RDE associated with structured light has established itself as one of the most interesting topics in structured light sensing applications, with relevance from spin to orbital angular momentum, from linear optics to nonlinear optics, even in the quantum optics and elsewhere. The method of rotational speed measurement based on the rotational Doppler effect applies to both microscopic particles and macroscopic objects. In the ongoing research, it is believed that this effect will bring more surprise to people.

The Basic Mechanism of Rotational Doppler Effect

The Interpretation From the Wave Properties

In 1842, the Austrian physicist Christian Doppler proposed that the wavelength of the radiation of an object will change due to the relative motion of the wave source and the observer, that is, the Doppler effect. When the object moves in a certain direction at a constant speed $v$ , the electromagnetic wave will have a path difference during the propagation process, so the frequency shift of the beam received by the observer on the surface of the object is,

$\mathrm{\Delta }f=\frac{f_{0}v\cos \theta }{c}(1)$

where $f_0$ is the frequency of the wave source, $\theta$ is the angle between the velocity vector and the wave vector, $c$ is the light speed.

For a beam with helical phase, its Poynting vector, and hence the optical momentum, has an azimuthal component at every position within the beam. The angle $\alpha$ between the Poynting vector and the beam axis can be deduced theoretically and measured experimentally [11, 28, 29], as shown in Figure 1A [30]. The magnitude of angle $\alpha$ can be written as $\alpha =\ell \lambda /2\pi r$, where $r$ is the radius from the beam axis to the position of the photon in the light field and $\ell$ denotes the topological charge of the beam, $\lambda$ represents the wavelength. Light scattered from a moving surface is Doppler-shifted in frequency that can be observed both in translation and rotation [31], as is shown in Figures 1B,C, respectively. When a vortex beam illuminates the rotating disk on its axis, the angle between the velocity vector of each scatter and the Poynting vector is $\alpha$, whose relationship with $\theta$ is $\alpha +\theta =\pi /2$. Combined with Eq. 1, the rotational Doppler shift can be can be expressed by $\mathrm{\Delta }f=\ell \mathrm{\Omega }/2\pi$. This is the basic expression of the RDE frequency shift. A typical form of using vortex light to obtain the RDE frequency shift is by interfering the scattered light with a reference light, as shown in Figure 1D. The RDE frequency shift also can be directly observed by a superposition state light with two components of opposite values of $\ell$, as illustrated in Figure 1E.

FIGURE 1

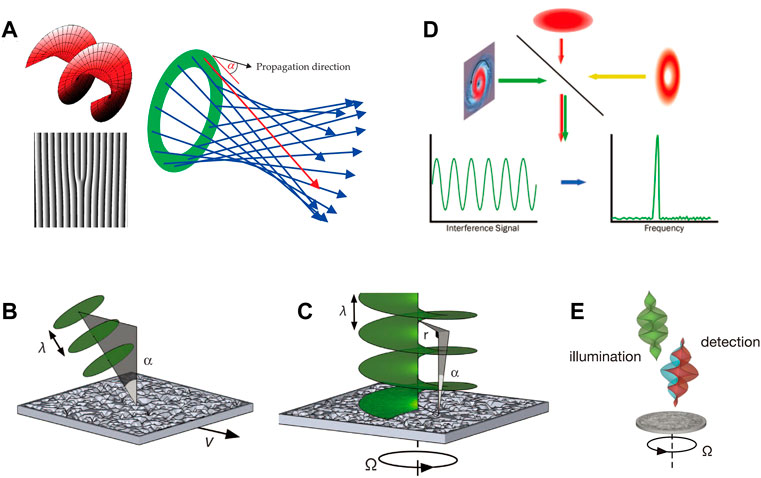
FIGURE 1. The wave properties of optical vortex and the measurement of RDE frequency [30] (A) The Poynting vector of the vortex light (B) Translational Doppler frequency shift and (C) rotational Doppler frequency shift [31] (D) The detection scheme of the rotational Doppler shift with structured light [36] (E) A superposition of helically phased beams with opposite signs of $\ell$ incident on a surface rotating at a speed $\mathrm{\Omega }$, results in a Doppler shift of the coaxial light.

On one hand, the RDE can be seen to have the same origin as the traditional LDE [32]. On the other hand, there is a significant difference between the LDE and RDE, namely, RDE frequency shift is independent of the wave frequency of the detected beam, such that the RDE can be observed using a white-light source [33]. Actually, the same RDE frequency shift also can be observed in the OAM-based radar [34, 35].

Since the light frequency is too high to be detected, like the conventional laser Doppler velocimetry, the RDE frequency shift can be observed by the interference phenomenon. As shown in Figure 1D, through the interference between the scattered beam and the reference beam, this frequency shift can be observed by extracting the beat frequency. Besides, when the illuminating light comprises two helically phased beams with topological charge $\pm \ell$, their scattering into a common detection mode gives opposite frequency shifts, and thus yielding an intensity modulation of doubled frequency of the basic RDE frequency shift [31].

The above interpretation only considers the rotation of the object. When the scatter has a compound motion of linear motion and rotation, the particles in the vortex field would experience both linear and rotational Doppler frequency shift. This can be understood from the phase change of the vortex field. The incident radiation wave can be simply written as,

$E\left(\overrightarrow{r},t\right)=E_0\exp \left\{-i\left[2\pi ft-kz-\mathrm{\Phi }\left({\overrightarrow{r}}_{\perp }\right)\right]\right\}(2)$

where the longitude phase is determined by propagation distance $z$ and the phase in the cross section is defined by $\mathrm{\Phi }\left({\overrightarrow{r}}_{\perp }\right)$. For the vortex beam, the transverse phase is given by $\mathrm{\Phi }\left({\overrightarrow{r}}_{\perp }\right)=\ell \phi$, where $\phi$ is the angular coordinates. As shown in Figure 2A, when a particle with both linear motion and rotational in the vortex field, it generates a burst of optical echoes which can be expressed by [37],

$i\left(t\right)=i_0\exp \left\{i\left[2kz\left(t\right)+\ell \phi \left(t\right)\right]\right\}(3)$

where $z\left(t\right)=v_{z}t$ and $\phi \left(t\right)=\mathrm{\Omega }t$. As a result, the total frequency shift can be expressed by $\mathrm{\Delta }f=\frac{1}{2\pi }\left(2k{v}_z+\ell \mathrm{\Omega }\right)$, appearing as a combination of the linear and the rotational frequency shift. Such a characteristics of the vortex light can then be used to detect the compound motion of the target as shown in Figure 2B.

FIGURE 2

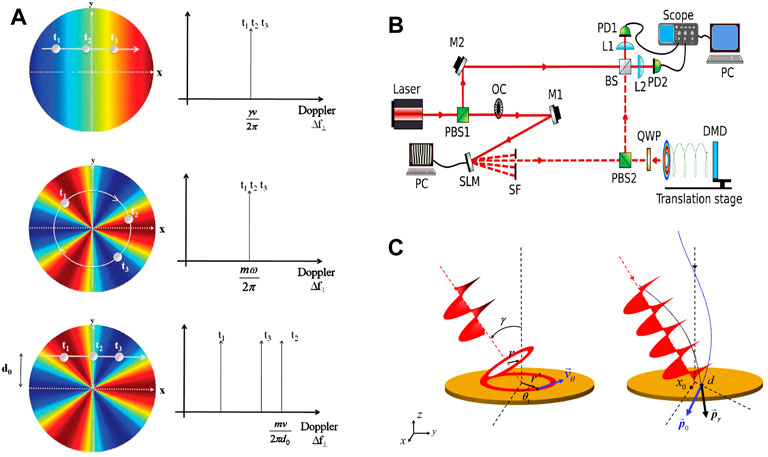
FIGURE 2. (A) The production of Doppler effect with structured light [37]. (B) Compound motion detection scheme [38]. (C) Rotational Doppler effect at vortex light oblique incidence [23].

Furthermore, the above deduction is effective only on the condition that the beam illuminates on the axis of the rotating object. When the vortex illuminates the rotating body non-coaxially as shown in Figure 2C, the RDE behaves differently. The radius of the vortex light and the radius of each small scatter on the rotating body under the light field are always the same when the vortex light illuminate the rotating object on its axis, while these two radii are unequal when the light illuminates non-coaxially. Based on the small scatterer model, Qiu et al. deduced the rotational Doppler shift when there is a small lateral misalignment or oblique angle between the vortex axis and rotating axis, respectively [23, 39]. The corresponding RDE frequency shift is given by,

$\mathrm{\Delta }{f}_d=\frac{\ell \mathrm{\Omega }}{2\pi }\left(1+\frac{d\cos \theta }{r_1}\right)(4)$

$\mathrm{\Delta }{f}_{\theta }=\frac{\ell \mathrm{\Omega }\left({\sin }^2{\theta }_z+\cos \gamma {\cos }^2{\theta }_z\right)}{2\pi \sqrt{1-{\left(\sin \gamma \sin {\theta }_z\right)}^2}}(5)$

where $d$ and $\gamma$ denote the lateral misalignment distance and the oblique angle, respectively. When the illuminating light is not coaxial with the rotational axis, the RDE frequency spectrum would be broadened.

The Energy Transfer in RDE

It is also instructive to understand the RDE from the conservation laws of energy and angular momentum when photons interact with the medium. For a rotating particle, the rotational kinetic energy due to the rotational motion can be expressed as,

$E=\frac{L^2}{2I}(6)$

where $L$ is the angular momentum of the particle and its magnitude is given by $L=I\mathrm{\Omega }$ ($\mathrm{\Omega }=v/r$), $I$ is the momentum of inertia whose value can be expressed by $I=m{r}^2$.

In the case of rotation, a system composed of rotating particles and the photons obeys the kinetic energy conversion, namely [7, 40],

$\frac{L_1^2}{2I}+E_1=\frac{L_2^2}{2I}+E_2+h\left(\nu +\mathrm{\Delta }\nu \right)(7)$

where $L_1$ and $L_2$ represent the angular momentum that the rotating particle has before and after interacting with the beam, respectively. $E_1$ and $E_2$ represent the intermediate electric energy of atoms or molecules that the particle receives and emits before and after the action of the detection light; $\nu$ represents the frequency of the scattered light at different times when the particle is stationary, and $\mathrm{\Delta }\nu$ represents the angular Doppler frequency shift of the scattered photons due to the rotation of the particle.

During the emission or absorption of photons by atoms, the energy transfer can be expressed by $E_1-E_2=h\nu$. Combined with Eq. 7 we have,

$h\mathrm{\Delta }\nu =\frac{L_1^2-L_2^2}{2I}=\frac{\left(L_1-L_2\right)\left(L_1+L_2\right)}{2I}=\frac{\mathrm{\Delta }L}{I}\left(\frac{L_1+L_2}{2}\right)(8)$

For the systems interacted by beams and rotating particles, there is also a momentum conservation relationship,

$L_a+{\mathrm{ℒ}}_a^{\prime }=L_b+{\mathrm{ℒ}}_b^{\prime }(9)$

where ${\mathrm{ℒ}}_a^{\prime }$ and ${\mathrm{ℒ}}_b^{\prime }$ represent the angular momentum carried by the photons before and after the beam interacts with the rotating particle, respectively. $L_a$ and $L_b$ denote the angular momentum carried by the rotating particle. For the linearly polarized vortex beam, the magnitude of the angular momentum is $\ell \hslash$. Therefore, the momentum transformation of the photons can be expressed as,

${\mathrm{ℒ}}_b^{\prime }-{\mathrm{ℒ}}_a^{\prime }=\left({\ell }_b-{\ell }_a\right)\hslash (10)$

where ${\ell }_a$ and ${\ell }_b$ are the topological charge of the incident vortex light and the scatter light to be detected, respectively.

By combining Eqs 8–10, we can obtain the RDE frequency shift as,

$\mathrm{\Delta }\nu =\left({\ell }_b-{\ell }_a\right)\mathrm{\Omega }/2\pi (11)$

If the scattered light to be detected is in the fundamental Gaussian mode, i.e., ${\ell }_b=0$, the above formula becomes exactly the same as that of the RDE frequency shift, namely, $\mathrm{\Delta }\nu =\ell \mathrm{\Omega }/2\pi$. Note that the LG modes form a complete and orthogonal basis for paraxial light beams. Therefore, the RDE frequency shift can also be observed by detecting the high-order OAM mode of the scattered light. When the scattered light is not in the fundamental mode, the RDE frequency shift can be calculated according to Eq. 11. The magnitude of the frequency shift is determined by the rotational speed and the OAM mode difference between the incident and the scattered light [41].

In the nonlinear regime, the perspective of energy and momentum conservation also can be used to interpret the origin of RDE. When the circularly polarized beam passes through a spinning nonlinear optical crystal with three-fold rotational symmetry, the beam would experience a Doppler shift of three times that of the optical crystal [24]. Furthermore, based on the mirror symmetry for electromagnetic interactions, the RDE frequency shift can be doubled through cascading two rotational Doppler processes [25]. This cascaded RDE can also be understood according to the law of conservation of momentum.

The magnitude of the frequency shift is proportional to both the topological charge and the rotational speed, as can be directly seen from the RDE formula. In order to ensure the frequency shift can be measured, this scheme is more available for measuring objects rotating at high speed rather than low speed [42]. On the other hand, the RDE frequency is also proportional to the topological charge of the illuminating beam; therefore, the detection sensitivity can be increased by using higher-order OAM beams. Up to now, a myriad of approaches have been developed for the generation of higher-order OAM beams, demonstrating up to $\ell =100$ by using a metasurface OAM laser [43], up to $\ell =600$ by using a spatial light modulator [44], and as high as $\ell \approx 10000$ with a spiral phase mirror [45].

Application of Rotational Doppler Effect

RDE in the Rotational Motion Detection

Since Allen et al. proposed their inspiring scheme of the detection of a spinning object by using light’s orbital angular momentum, there have been massive relevant research literatures in this area. In addition to the rotational speed, other rotation parameters such as rotating direction and acceleration rate have been measured as well. Since the beat frequency effect can only provide the magnitude of the frequency shift without the direction information [46], the acquisition of the rotation direction becomes a tricky problem. Rosales-Guzman et al. devised a scheme to impart an additional rotation on the illuminating vortex beam, which can give a reference to identify the rotation direction [47]. By employing dual-frequency vortex light, as shown in Figure 3A, Li et al. transform the Doppler signals from the low-frequency domain to the medium-frequency domain, and thus distinguishing the rotational direction by comparing the modulated signal and the reference signal [48].

FIGURE 3

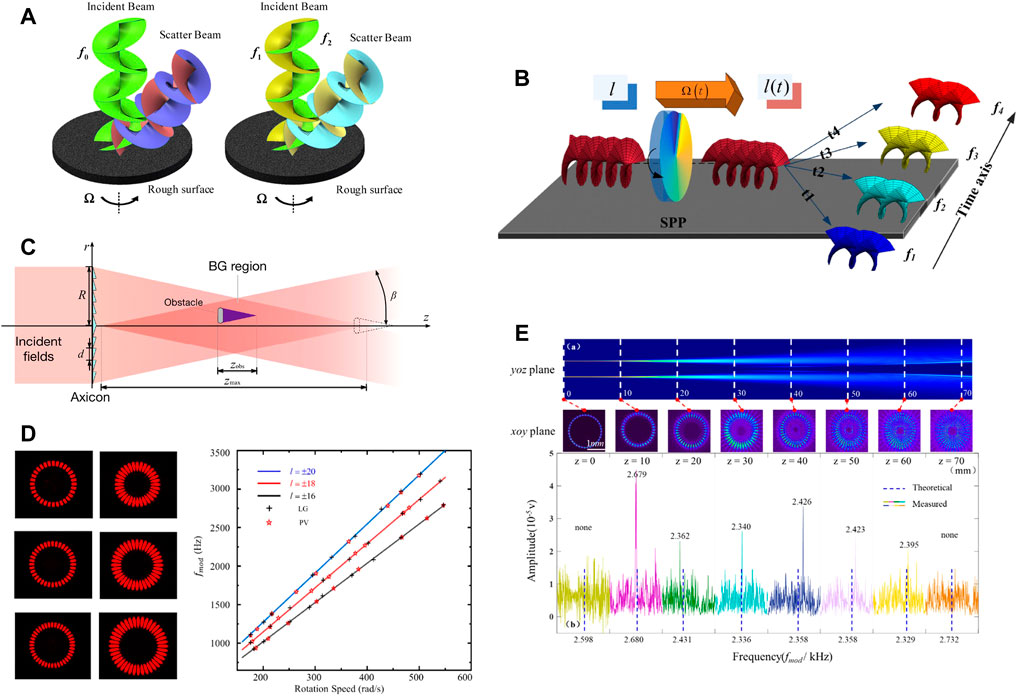
FIGURE 3. RDE in rotational speed detection. (A) Direction-sensitive detection by dual-frequency optical vortex [48]. (B) Detection of angular acceleration based on optical RDE [51]. (C) Non-diffractive Bessel-Gaussian beams for the detection of rotational speed [57]. (D) RDE detection results by using perfect optical vortex [58]. (E) The measured results of RDE frequency shift along the propagation path of ring Airy Gaussian vortex [59].

Recently, the vectorial counterpart of RDE was revealed, which uses vectorial polarization fields and shows the potential to retrieve the full vectorial motion information of the moving object [49, 50]. The above measurements are based on the constant rotation velocity. While for variable rotation, Zhai et al. succeeded in measuring the angular acceleration through a time-frequency analysis of the RDE frequency shift [51]. The transformation of OAM beams when passing through a non-uniform spinning SPP is shown in Figure 3B.

At present, the accuracy of RDE-based speed measurement is relatively high, generally reaching over 95% [31, 33, 47]. Even under the light noncoaxial incidence condition, the rotational speed still can be measured in a high accuracy through the extraction the frequency difference in the discrete frequency shift signals [52]. However, the accuracy of the speed measurement also fluctuates in response to changes in measurement conditions [53]. Moreover, since the frequency shift caused by the RDE is proportional to the object’s angular velocity, in order to ensure the frequency shift can be measured, this scheme is more available for measuring objects rotating at high speed rather than low speed [54]. The rotational speed can be measured in most laboratory conditions is larger than $2\pi$ rad/s, and only a handful of measurement experiments those use the spatial light modulators to mimic real rotating objects can reach a lower speed [55, 56].

RDE Introduced by Different Types of Vortex Beams

Researchers have tried using different types of structured vortex beams to investigate RDE, including Laguerre–Gaussian (LG) beam [31], Bessel-Gaussian (BG) beam [57], Perfect Optical Vortex (POV) beam [58, 60, 61], and Ring Airy Gaussian Vortex (RAiGV) [59]. The LG beam is the most popular structured light used in the RDE detection which can stably propagates over a long distance. The transverse beam profile is a single intensity ring with zero radial index $p=0$. For the LG beams with non-zero radial index, multiple rings would appear in the radial direction. Experiments have shown that the LG beams of nonzero radial indices can enhance the light intensity and the amplitude of the RDE frequency signal, in comparison with those of zero radial index [62]. The BG beam has been proved to have non-diffractive and self-recovery characteristics which can be immune to the influence of the small obstacles in the optical path [57], as shown in Figure 3C.

Also, POV have recently attracted a lot of research attention, owing to its characteristic feature that they have the same intensity profile regardless of carrying different topological charges, as is shown in Figure 3D [58]. Therefore, the POV beam is more flexible when detecting the objects of different sizes. In particular, when the topological charges of the two components of a superposition beam are not the same magnitude, the POV performs better than the LG beam [58]. It was reported that, as is shown in Figure 3E, the RAiGV has the same well performance in spinning speed detection as other vortex beams [59]. Besides, the RAiGV beam has self-focusing property, which enables the best detection results on its focal length. These researches fully considered the RDE detection effect of the different types of vortex beams, which offers useful instructions in choosing suitable vortex beams for realistic applications.

RDE in Compound Motion Measurement

In the actual applications, we usually encounter the compound motion, e.g., translation, rotation, and other kinds of micro-motion. Accordingly, the scattered light would experience LDE, radial Doppler effect [63], RDE, and micro-Doppler effect [64, 65]. These frequency shifts are generally coupled to each other. Thus, a question arises naturally as to how we can measure them individually. It was reported that the translational and rotational velocities of the particles can both be determined by switching between two modes. They were able to isolate the longitudinal frequency shift by illuminating a Gaussian beam while measure the rotational frequency shift by using LG modes. In 2019, Carmelo et al. put forward a novel three-dimensional technique that enables the direct and simultaneous measurement of both the longitudinal and angular speed of cooperative targets [66], as was shown in Figure 4A.

FIGURE 4

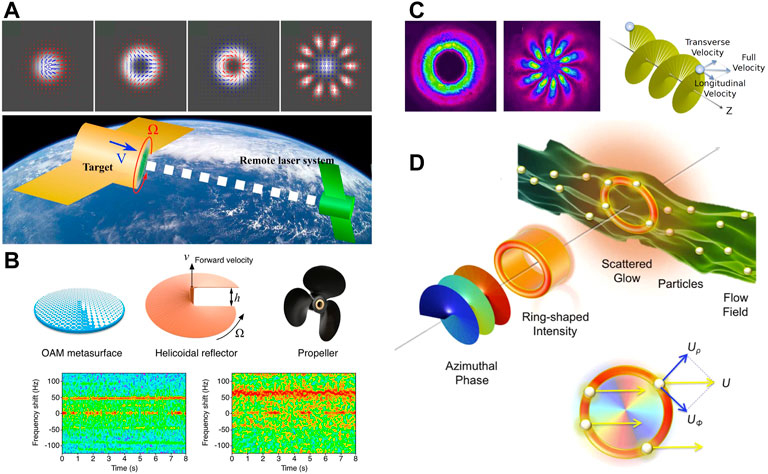
FIGURE 4. Compound motion detection by RDE of structured light. (A) In-suit detection of a cooperative target’s longitudinal and angular speed using structured light [66]. (B) Experimental observation of linear and rotational Doppler shift from several designer surface [67]. (C) Measuring the translational and rotational velocities of particles [38]. (D) Measurement of flow velocity with helical beams of light [69].

The rotational Doppler shift could be separated from the micro-Doppler shift by using two microwave beams of opposite OAM [67]. Figure 4B shows the spectrogram of a normal 5.8 GHz incident wave reflected from a spinning helicoidal reflector, and the scattered waves produce both linear and rotational Doppler shifts. Figure 4C reveals the reason why a particle moving along a spiral trajectory will produce both linear and rotational frequency shifts. By employing the OAM interferometry of the multi-mode beam, decoupled measurement of linear velocity and rotational speed can be achieved [55, 68]. These methods can partially resolve the decoupled measurements of the compound motion with OAM beam. It is expected that the use of multidimensional information about light beams may provide new solutions to this engineering challenge in the future.

It was found that not only the rotational speed, but also the flow velocity could be accurately estimated by making use of the transversal Doppler effect of the returned signals that depend only on the azimuthal indices of the vortex beams [69], as was shown in Figure 4D. Also, the fluid flow vorticity could also be measured in a straightforward way by taking advantage of the RDE [70], which allowed for a localized real-time determination of vorticity in a fluid flow with three-dimensional resolution.

RDE in Nonlinear and Quantum Optics Field

When the circularly polarized beam passes through a spinning nonlinear optical crystal with three-fold rotational symmetry, it was found that the second harmonic generation signals may experience a Doppler effect of three times the spinning speed [24]. Figures 5A,B illustrate the RDE in the linear and nonlinear optical regime. This demonstration of RDE provided us with an insight into the interaction of light with moving nonlinear media. By using the post-selection and beating frequency techniques, researchers further simplified the conventional nonlinear RDE measurement setup and successfully observed the RDE of second harmonic generation waves [71]. As shown in Figure 5C, when the forward propagating fundamental wave with left- and right-circular polarization pass through the spinning nonlinear material with three-fold rotational symmetry, the RDE frequency shift is three times of the spinning speed [71]. Besides, the RDE also can be detected by using the near-infrared light to illuminate the rotating object, in which the rotational frequency shifts can be transferred to the visible regime after parametric up-conversion [72]. The corresponding up-conversion detection scheme is shown in Figure 5D.

FIGURE 5

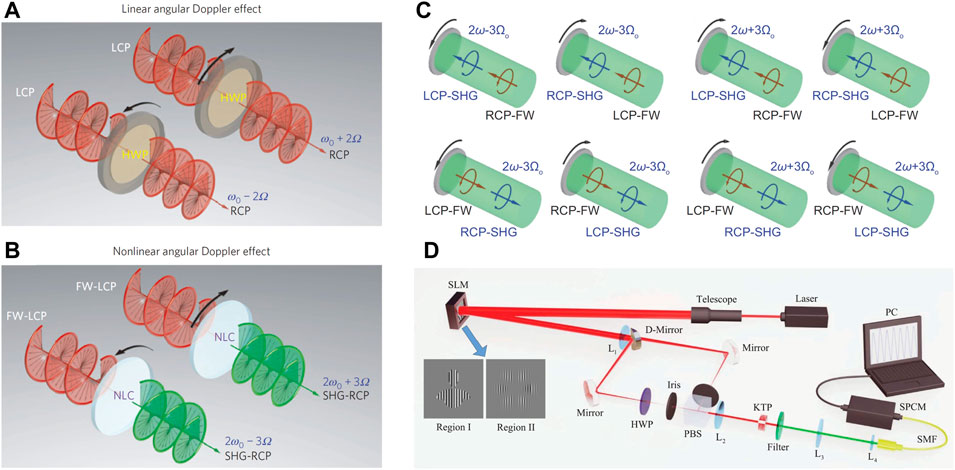
FIGURE 5. RDE in nonlinear optics. RDE in (A) linear and (B) nonlinear optics. The second harmonic generation signal experiences a Doppler shift of three times [24]. (C) The evolution of RDE of second harmonic generation from a quartz coated with silver mirror [71]. (D) RDE detection by frequency up-conversion [72].

In addition to those classical methods, quantum remote sensing with OAM-entangled photon pairs enabled an improved angular resolution that can be amplified by large OAM values [73]. By using photonic entanglement of high orbital angular momenta, Flicker et al. demonstrated a method of increasing the angular resolution in remote sensing [26]. As shown in Figure 6A, the polarization entanglement is created in a parametric down-conversion process and afterward transferred to modes with high quanta of OAM. Also, Zhang et al. showed that the object’s angular rotational speed can be measured nonlocally, the corresponding experimental scheme is shown in Figure 6B. They revealed that the angular sensitivity of the object in the path of idler photons is proportional to the OAM values of signal photons, which can be considered as a quantum version of RDE [74].

FIGURE 6

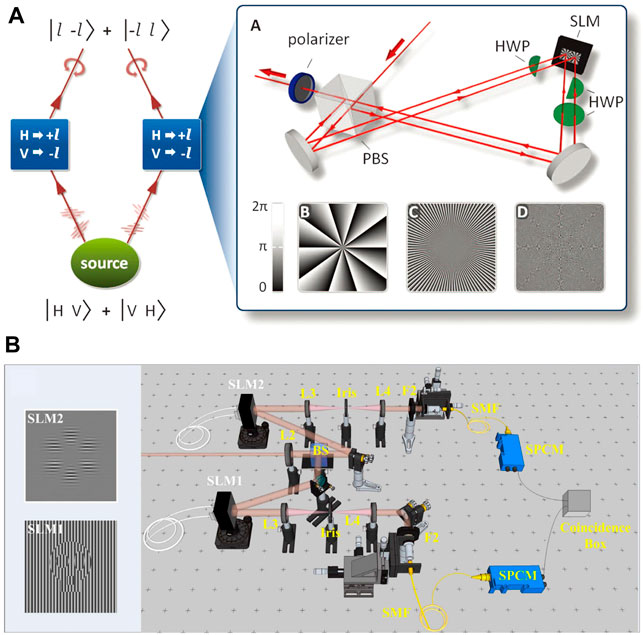
FIGURE 6. RDE in quantum optics. (A) Quantum entanglement of high order angular momenta [26]. (B) Quantum remote sensing of the angular rotation of structured objects [74]. It suggests potential applications in developing a noncontact way for angular remote sensing of object.

RDE in Various Bands

Since the RDE has nothing to do with the wavelength of the detection beam [33]. In recent years, the RDE in the radio domain is investigated widely [65]. Zhao et al. used the phase accumulation method to experimentally verify the RDE in the microwave band [35]. Although the measurement accuracy of the rotational speed is high, phase accumulation takes relatively long time and has certain limitations in practical applications. Similar to the detection technique of the light wave, Brousseau et al. realized the RDE detection of the microwave at 2.47 GHz by the spectrum analyzer [75]. Both the rotational speed and the direction can be measured through this model. The RDE of uniformly accelerated targets has also been studied in the radio frequency band by means of time-frequency analysis [76].

For the microwave band, the signal extraction process when detecting the target is more convenient. However, vortex electromagnetic waves in the microwave band are difficult to propagate over long distances. Structured laser can be transmitted over long distances, but the probe beam is easy to be disturbed by the atmospheric turbulence [77]. Further, the extraction of weak light signals under long-distance detection is more troublesome.

Conclusion and Perspectives

In summary, with the technological advancements in the structured light generation, propagation, manipulation, and detection, we have offered a systematic understanding on the physical origin and behaviors of the RDE, from both fundamental and applied points of view. We have analyzed the basic mechanism of the RDE from the perspective of the wave property of light and the conservation of energy. Moreover, we have summarized the recent developments in rotational speed measurement based on RDE, ranging from the molecular motion to the rotation of macro-objects, and from linear optics to nonlinear optics, and to quantum optical realms.

It is noted that, although a lot of studies have been conducted on the fundamental and applied aspects of RDE, there is still a long way to go in terms of developing a viable system and putting this technique into practical applications. There are various hurdles to solve in order to implement detection from the lab to the outside scale. Firstly, atmospheric turbulence has a significant impact on the mode purity of an OV beam as it propagates across free space [77–81]. This is a challenge that must be solved, both for OAM-based communication and detection applications. Secondarily, the relative pose between the detection OV beam and the rotating object has a significant influence on the detection signal [68, 82–84], therefore the distribution of the RDE signals under different conditions of motion and positions needs to be further investigated. Thirdly, the receiving and processing of signals is an important aspect for the detection system, especially for weak signals at the photon-counting level [54]. Also, as the RDE is independent of the wavelength of the beam [75, 76], we can anticipate that an extension of the RDE into the radar band might lead to some new discoveries. In future studies, we can imagine that the RDE with structured light will provide us with more and more surprises.

Author Contributions

LC and YR conceived the idea. YR and LC supervised the project. SQ combed through the entire relevant literature. All authors discussed the results. SQ and TL drafted the papers with the input from all authors.

Funding

Key Research Projects of Foundation Strengthening Program of China (2019-JCJQ-ZD); National Natural Science Foundation of China (61805283 and 62173342).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Padgett M. Electromagnetism: Like a Speeding Watch. Nature (2006) 443:924–5. doi:10.1038/443924a

PubMed Abstract | CrossRef Full Text | Google Scholar

2. O'Neil AT, MacVicar I, Allen L, Padgett MJ. Intrinsic and Extrinsic Nature of the Orbital Angular Momentum of a Light Beam. Phys Rev Lett (2002) 88:053601. doi:10.1103/PhysRevLett.88.053601

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Mohammadi SM, Daldorff LKS, Forozesh K, Thidé B, Bergman JES, Isham B, et al. Orbital Angular Momentum in Radio: Measurement Methods. Radio Sci (2010) 45. doi:10.1029/2009rs004299

CrossRef Full Text | Google Scholar

4. Bialynicki-Birula I, Bialynicka-Birula Z. Rotational Frequency Shift. Phys Rev Lett (1997) 78:2539–42. doi:10.1103/PhysRevLett.78.2539

CrossRef Full Text | Google Scholar

5. Basistiy IV, Slyusar VV, Soskin MS, Vasnetsov MV, Bekshaev AY. Manifestation of the Rotational Doppler Effect by Use of an off-Axis Optical Vortex Beam. Opt Lett (2003) 28:1185–7. doi:10.1364/ol.28.001185

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Vasnetsov MV, Torres JP, Petrov DV, Torner L. Observation of the Orbital Angular Momentum Spectrum of a Light Beam. Opt Lett (2003) 28:2285–7. doi:10.1364/ol.28.002285

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Garetz BA. Angular Doppler Effect. J Opt Soc Am (1981) 71:609–11. doi:10.1364/josa.71.000609

CrossRef Full Text | Google Scholar

8. Ashby N. Relativity in the Global Positioning System. Living Rev Relativ (2003) 6:1. doi:10.12942/lrr-2003-1

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Korech O, Steinitz U, Gordon RJ, Averbukh IS, Prior Y. Observing Molecular Spinning via the Rotational Doppler Effect. Nat Photon (2013) 7:711–4. doi:10.1038/nphoton.2013.189

CrossRef Full Text | Google Scholar

10. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital Angular Momentum of Light and the Transformation of Laguerre-Gaussian Laser Modes. Phys Rev A (1992) 45:8185–9. doi:10.1103/PhysRevA.45.8185

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Allen L, Padgett MJ. The Poynting Vector in Laguerre-Gaussian Beams and the Interpretation of Their Angular Momentum Density. Opt Commun (2000) 184:67–71. doi:10.1016/s0030-4018(00)00960-3

CrossRef Full Text | Google Scholar

12. Molina-Terriza G, Torres JP, Torner L. Management of the Angular Momentum of Light: Preparation of Photons in Multidimensional Vector States of Angular Momentum. Phys Rev Lett (2002) 88:013601. doi:10.1103/PhysRevLett.88.013601

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Padgett MJ, Allen L. Orbital Angular Momentum Exchange in Cylindrical-Lens Mode Converters. J Opt B Quan Semiclass. Opt. (2002) 4:S17–S19. doi:10.1088/1464-4266/4/2/362

CrossRef Full Text | Google Scholar

14. Allen L, Babiker M, Power WL. Azimuthal Doppler Shift in Light Beams with Orbital Angular Momentum. Opt Commun (1994) 112:141–4. doi:10.1016/0030-4018(94)00484-6

CrossRef Full Text | Google Scholar

15. Censor D. Theory of the Doppler Effect: Fact, Fiction and Approximation. Radio Sci (1984) 19:1027–40. doi:10.1029/RS019i004p01027

CrossRef Full Text | Google Scholar

16. Marrucci L. Spinning the Doppler Effect. Science (2013) 341:464–5. doi:10.1126/science.1242097

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Yao AM, Padgett MJ. Orbital Angular Momentum: Origins, Behavior and Applications. Adv Opt Photon (2011) 3:161–204. doi:10.1364/aop.3.000161

CrossRef Full Text | Google Scholar

18. Zhou H-L, Fu D-Z, Dong J-J, Zhang P, Chen D-X, Cai X-L, et al. Orbital Angular Momentum Complex Spectrum Analyzer for Vortex Light Based on the Rotational Doppler Effect. Light Sci Appl (2016) 6:e16251. doi:10.1038/lsa.2016.251

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Berkhout GCG, Lavery MPJ, Padgett MJ, Beijersbergen MW. Measuring Orbital Angular Momentum Superpositions of Light by Mode Transformation. Opt Lett (2011) 36:1863–5. doi:10.1364/OL.36.001863

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Lavery MPJ, Berkhout GCG, Courtial J, Padgett MJ. Measurement of the Light Orbital Angular Momentum Spectrum Using an Optical Geometric Transformation. J Opt (2011) 13:064006. doi:10.1088/2040-8978/13/6/064006

CrossRef Full Text | Google Scholar

21. Wang X, Nie Z, Liang Y, Wang J, Li T, Jia B. Recent Advances on Optical Vortex Generation. Nanophotonics (2018) 7:1533–56. doi:10.1515/nanoph-2018-0072

CrossRef Full Text | Google Scholar

22. Okulov AY. Rotational Doppler Shift of a Phase-Conjugated Photon. J Opt Soc Am B (2012) 29:714–8. doi:10.1364/josab.29.000714

CrossRef Full Text | Google Scholar

23. Qiu S, Liu T, Ren Y, Li Z, Wang C, Shao Q. Detection of Spinning Objects at Oblique Light Incidence Using the Optical Rotational Doppler Effect. Opt Express (2019) 27:24781–92. doi:10.1364/OE.27.024781

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Li G, Zentgraf T, Zhang S. Rotational Doppler Effect in Nonlinear Optics. Nat Phys (2016) 12:736–40. doi:10.1038/nphys3699

CrossRef Full Text | Google Scholar

25. Deng J, Li KF, Liu W, Li G. Cascaded Rotational Doppler Effect. Opt Lett (2019) 44:2346–9. doi:10.1364/OL.44.002346

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Fickler R, Lapkiewicz R, Plick WN, Krenn M, Schaeff C, Ramelow S, et al. Quantum Entanglement of High Angular Momenta. Science (2012) 338:640–3. doi:10.1126/science.1227193

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Guo Z, Meng J, An M, Cheng P, Jia J, Chang Z, et al. Remote Angular Velocity Measurement by the Cascaded Rotational Doppler Effect. Appl Opt (2021) 60:9892–5. doi:10.1364/AO.438997

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Leach J, Keen S, Padgett MJ, Saunter C, Love GD. Direct Measurement of the Skew Angle of the Poynting Vector in a Helically Phased Beam. Opt Express (2006) 14:11919–24. doi:10.1364/oe.14.011919

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Qiu S, Ren Y, Liu T, Liu Z, Wang C, Ding Y, et al. Directly Observing the Skew Angle of a Poynting Vector in an Oam Carrying Beam via Angular Diffraction. Opt Lett (2021) 46:3484–7. doi:10.1364/OL.432771

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Padgett M. A New Twist on the Doppler Shift. Phys Today (2014) 67:58–9. doi:10.1063/pt.3.2286

CrossRef Full Text | Google Scholar

31. Lavery MPJ, Speirits FC, Barnett SM, Padgett MJ. Detection of a Spinning Object Using Light's Orbital Angular Momentum. Science (2013) 341:537–40. doi:10.1126/science.1239936

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Fang L, Padgett MJ, Wang J. Sharing a Common Origin between the Rotational and Linear Doppler Effects. Laser Photon Rev (2017) 11:1700183. doi:10.1002/lpor.201700183

CrossRef Full Text | Google Scholar

33. Lavery MPJ, Barnett SM, Speirits FC, Padgett MJ. Observation of the Rotational Doppler Shift of a White-Light, Orbital-Angular-Momentum-Carrying Beam Backscattered from a Rotating Body. Optica (2014) 1:1–4. doi:10.1364/optica.1.000001

CrossRef Full Text | Google Scholar

34. Kang L, Cheng Y, Xiang L, Wang H, Qin Y, Yue G. Spinning Target Detection Using Oam-Based Radar. In: International Workshop on Electromagnetics: Applications & Student Innovation Competition; 2017 May 30–Jun 1; London, United Kingdom. London, UK: IEEE (2017). p. 29–30.

Google Scholar

35. Zhao M, Gao X, Xie M, Zhai W, Xu W, Huang S, et al. Measurement of the Rotational Doppler Frequency Shift of a Spinning Object Using a Radio Frequency Orbital Angular Momentum Beam. Opt Lett (2016) 41:2549–52. doi:10.1364/OL.41.002549

PubMed Abstract | CrossRef Full Text | Google Scholar

36.A Forbes, TE Lizotte, C Rosales-Guzmán, A Belmonte, and JP Torres, editors. Optical Metrology with Structured Light. Laser Beam Shaping XVII. San Diego, CA: SPIE (2016). p. 995007.

Google Scholar

37. Belmonte A, Torres JP. Optical Doppler Shift with Structured Light. Opt Lett (2011) 36:4437–9. doi:10.1364/OL.36.004437

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Rosales-Guzmán C, Hermosa N, Belmonte A, Torres JP. Measuring the Translational and Rotational Velocities of Particles in Helical Motion Using Structured Light. Opt Express (2014) 22:16504–9. doi:10.1364/OE.22.016504

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Qiu S, Liu T, Li Z, Wang C, Ren Y, Shao Q, et al. Influence of Lateral Misalignment on the Optical Rotational Doppler Effect. Appl Opt (2019) 58:2650–5. doi:10.1364/AO.58.002650

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Garetz BA, Arnold S. Variable Frequency Shifting of Circularly Polarized Laser Radiation via a Rotating Half-Wave Retardation Plate. Opt Commun (1979) 31:1–3. doi:10.1016/0030-4018(79)90230-X

CrossRef Full Text | Google Scholar

41. Zhou H, Fu D, Dong J, Zhang P, Zhang X. Theoretical Analysis and Experimental Verification on Optical Rotational Doppler Effect. Opt Express (2016) 24:10050–6. doi:10.1364/OE.24.010050

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Deng D, Zhao H, Ni J, Li Y, Qiu C-W. A Phase-To-Intensity Strategy of Angular Velocity Measurement Based on Photonic Orbital Angular Momentum. Nanophotonics (2022) 11:865–72. doi:10.1515/nanoph-2021-0461

CrossRef Full Text | Google Scholar

43. Sroor H, Huang Y-W, Sephton B, Naidoo D, Vallés A, Ginis V, et al. High-Purity Orbital Angular Momentum States from a Visible Metasurface Laser. Nat Photon (2020) 14:498–503. doi:10.1038/s41566-020-0623-z

CrossRef Full Text | Google Scholar

44. Pinnell J, Rodríguez-Fajardo V, Forbes A. Probing the Limits of Orbital Angular Momentum Generation and Detection with Spatial Light Modulators. J Opt (2021) 23:015602. doi:10.1088/2040-8986/abcd02

CrossRef Full Text | Google Scholar

45. Fickler R, Campbell G, Buchler B, Lam PK, Zeilinger A. Quantum Entanglement of Angular Momentum States with Quantum Numbers up to 10,010. Proc Natl Acad Sci U.S.A (2016) 113:13642–7. doi:10.1073/pnas.1616889113

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Varghese B, Rajan V, van Leeuwen TG, Steenbergen W. Discrimination between Doppler-Shifted and Non-shifted Light in Coherence Domain Path Length Resolved Measurements of Multiply Scattered Light. Opt Express (2007) 15:13340–50. doi:10.1364/oe.15.013340

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Rosales-Guzmán C, Hermosa N, Belmonte A, Torres JP. Direction-Sensitive Transverse Velocity Measurement by Phase-Modulated Structured Light Beams. Opt Lett (2014) 39:5415–8. doi:10.1364/OL.39.005415

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Li Z, Liu T, Ren Y, Qiu S, Wang C, Wang H. Direction-Sensitive Detection of a Spinning Object Using Dual-Frequency Vortex Light. Opt Express (2021) 29:7453–63. doi:10.1364/OE.418192

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Wan Z, Fang L, Wang J. Direction-discriminated Rotational Doppler Velocimetry with Circularly Polarized Vortex Beams. Opt Lett (2022) 47:1021–4. doi:10.1364/ol.443022

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Fang L, Wan Z, Forbes A, Wang J. Vectorial Doppler Metrology. Nat Commun (2021) 12:4186. doi:10.1038/s41467-021-24406-z

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Zhai Y, Fu S, Yin C, Zhou H, Gao C. Detection of Angular Acceleration Based on Optical Rotational Doppler Effect. Opt Express (2019) 27:15518–27. doi:10.1364/OE.27.015518

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Qiu S, Ding Y, Liu T, Liu Z, Ren Y. Rotational Object Detection at Noncoaxial Light Incidence Based on the Rotational Doppler Effect. Opt Express (2022) 30:20441–50. doi:10.1364/oe.461179

CrossRef Full Text | Google Scholar

53. Ding Y, Liu T, Liu Z, Qiu S, Xu L, Ren Y. Detection of a Spinning Object with Circular Procession Using an Optical Vortex Beam. Opt Lett (2022) 47:2398–401. doi:10.1364/ol.458270

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Seghilani M, Myara M, Sagnes I, Chomet B, Bendoula R, Garnache A. Self-Mixing in Low-Noise Semiconductor Vortex Laser: Detection of a Rotational Doppler Shift in Backscattered Light. Opt Lett (2015) 40:5778–81. doi:10.1364/OL.40.005778

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Ren Y, Qiu S, Liu T, Liu Z, Cai W. Non-Contact Ultralow Rotational Speed Measurement of Real Objects Based on Rotational Doppler Velocimetry. IEEE Trans Instrum Meas (2022) 71:1–8. doi:10.1109/tim.2022.3141155

CrossRef Full Text | Google Scholar

56. Zhang W, Gao J, Zhang D, He Y, Xu T, Fickler R, et al. Free-Space Remote Sensing of Rotation at the Photon-Counting Level. Phys Rev Appl (2018) 10:044014. doi:10.1103/PhysRevApplied.10.044014

CrossRef Full Text | Google Scholar

57. Fu S, Wang T, Zhang Z, Zhai Y, Gao C. Non-Diffractive Bessel-Gauss Beams for the Detection of Rotating Object Free of Obstructions. Opt Express (2017) 25:20098–108. doi:10.1364/OE.25.020098

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Qiu S, Ren Y, Liu T, Chen L, Wang C, Li Z, et al. Spinning Object Detection Based on Perfect Optical Vortex. Opt Lasers Eng (2020) 124:105842. doi:10.1016/j.optlaseng.2019.105842

CrossRef Full Text | Google Scholar

59. Qiu S, Ren Y, Sha Q, Ding Y, Wang C, Li Z, et al. Observation of the Rotational Doppler Shift of the Ring Airy Gaussian Vortex Beam. Opt Commun (2021) 490:126900. doi:10.1016/j.optcom.2021.126900

CrossRef Full Text | Google Scholar

60. Pinnell J, Rodríguez-Fajardo V, Forbes A. How Perfect Are Perfect Vortex Beams? Opt Lett (2019) 44:5614–7. doi:10.1364/OL.44.005614

PubMed Abstract | CrossRef Full Text | Google Scholar

61. García-García J, Rickenstorff-Parrao C, Ramos-García R, Arrizón V, Ostrovsky AS. Simple Technique for Generating the Perfect Optical Vortex. Opt Lett (2014) 39:5305–8. doi:10.1364/OL.39.005305

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Qiu S, Ren Y, Liu T, Li Z, Liu Z, Wang C, et al. Rotational Doppler Effect Detection by Lg Beams with a Nonzero Radial Index. Opt Express (2021) 29:10275–84. doi:10.1364/OE.421705

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Zhai Y, Fu S, Zhang R, Yin C, Zhou H, Zhang J, et al. The Radial Doppler Effect of Optical Vortex Beams Induced by a Surface with Radially Moving Periodic Structure. J Opt (2019) 21:054002. doi:10.1088/2040-8986/ab146f

CrossRef Full Text | Google Scholar

64. Chen VC, Fayin Li L, Shen-Shyang Ho H, Wechsler H. Micro-Doppler Effect in Radar: Phenomenon, Model, and Simulation Study. IEEE Trans Aerosp Electron Syst (2006) 42:2–21. doi:10.1109/taes.2006.1603402

CrossRef Full Text | Google Scholar

65. Luo Y, Chen YJ, Zhu YZ, Li WY, Zhang Q. Doppler Effect and micro‐Doppler Effect of Vortex‐electromagnetic‐wave‐based Radar. IET Radar Sonar Navigation (2020) 14:2–9. doi:10.1049/iet-rsn.2019.0124

CrossRef Full Text | Google Scholar

66. Hu X-B, Zhao B, Zhu Z-H, Gao W, Rosales-Guzmán C. In Situ Detection of a Cooperative Target's Longitudinal and Angular Speed Using Structured Light. Opt Lett (2019) 44:3070–3. doi:10.1364/OL.44.003070

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Liu B, Chu H, Giddens H, Li R, Hao Y. Experimental Observation of Linear and Rotational Doppler Shifts from Several Designer Surfaces. Sci Rep (2019) 9:8971. doi:10.1038/s41598-019-45516-1

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Ren Y, Qiu S, Liu T, Liu Z. Compound Motion Detection Based on Oam Interferometry. Nanophotonics (2022) 11:1127–35. doi:10.1515/nanoph-2021-0622

CrossRef Full Text | Google Scholar

69. Belmonte A, Rosales-Guzmán C, Torres JP. Measurement of Flow Vorticity with Helical Beams of Light. Optica (2015) 2:1002–5. doi:10.1364/optica.2.001002

CrossRef Full Text | Google Scholar

70. Ryabtsev A, Pouya S, Safaripour A, Koochesfahani M, Dantus M. Fluid Flow Vorticity Measurement Using Laser Beams with Orbital Angular Momentum. Opt Express (2016) 24:11762–7. doi:10.1364/OE.24.011762

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Li KF, Deng JH, Liu X, Li G. Observation of Rotational Doppler Effect in Second Harmonic Generation in Reflection Mode. Laser Photon Rev (2018) 12:1700204. doi:10.1002/lpor.201700204

CrossRef Full Text | Google Scholar

72. Guo H, Qiu X, Qiu S, Hong L, Lin F, Ren Y, et al. Frequency Upconversion Detection of Rotational Doppler Effect. Photon Res (2021) 10:183–8. doi:10.1364/prj.441785

CrossRef Full Text | Google Scholar

73. Jha AK, Agarwal GS, Boyd RW. Supersensitive Measurement of Angular Displacements Using Entangled Photons. Phys Rev A (2011) 83:053829. doi:10.1103/PhysRevA.83.053829

CrossRef Full Text | Google Scholar

74. Zhang W, Zhang D, Qiu X, Chen L. Quantum Remote Sensing of the Angular Rotation of Structured Objects. Phys Rev A (2019) 100:043832. doi:10.1103/PhysRevA.100.043832

CrossRef Full Text | Google Scholar

75. Brousseau C, Mahdjoubi K, Emile O. Measurement of the Rotational Sense and Velocity of an Object Using OAM Wave in the Radio‐frequency Band. Electron Lett (2019) 55:709–11. doi:10.1049/el.2019.0942

CrossRef Full Text | Google Scholar

76. Zheng J, Zheng S, Shao Z, Zhang X. Analysis of Rotational Doppler Effect Based on Radio Waves Carrying Orbital Angular Momentum. J Appl Phys (2018) 124:164907. doi:10.1063/1.5050448

CrossRef Full Text | Google Scholar

77. Rodenburg B, Lavery MPJ, Malik M, O’Sullivan MN, Mirhosseini M, Robertson DJ, et al. Influence of Atmospheric Turbulence on States of Light Carrying Orbital Angular Momentum. Opt Lett (2012) 37:3735–7. doi:10.1364/OL.37.003735

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Ren Y, Xie G, Huang H, Bao C, Yan Y, Ahmed N, et al. Adaptive Optics Compensation of Multiple Orbital Angular Momentum Beams Propagating through Emulated Atmospheric Turbulence. Opt Lett (2014) 39:2845–8. doi:10.1364/OL.39.002845

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Xie G, Ren Y, Huang H, Lavery MPJ, Ahmed N, Yan Y, et al. Phase Correction for a Distorted Orbital Angular Momentum Beam Using a Zernike Polynomials-Based Stochastic-Parallel-Gradient-Descent Algorithm. Opt Lett (2015) 40:1197–200. doi:10.1364/OL.40.001197

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Fu S, Zhang S, Wang T, Gao C. Pre-turbulence Compensation of Orbital Angular Momentum Beams Based on a Probe and the Gerchberg-Saxton Algorithm. Opt Lett (2016) 41:3185–8. doi:10.1364/OL.41.003185

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Krenn M, Handsteiner J, Fink M, Fickler R, Ursin R, Malik M, et al. Twisted Light Transmission over 143 Km. Proc Natl Acad Sci U.S.A (2016) 113:13648–53. doi:10.1073/pnas.1612023113

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Angelsky OV, Bekshaev AY, Popov AY. Noncollinear Rotational Doppler Effect. In: Sixth International Conference on Correlation Optics; 2004 Jun 4; Chernivsti, Ukraine. Chernivsti, Ukraine: Proc. SPIE (2004). p. 55–66.

Google Scholar

83. Zhang Z, Cen L, Zhang J, Hu J, Wang F, Zhao Y. Rotation Velocity Detection with Orbital Angular Momentum Light Spot Completely Deviated Out of the Rotation Center. Opt Express (2020) 28:6859–67. doi:10.1364/OE.380324

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Ding Y, Ren Y, Liu T, Qiu S, Wang C, Li Z, et al. Analysis of Misaligned Optical Rotational Doppler Effect by Modal Decomposition. Opt Express (2021) 29:15288–99. doi:10.1364/oe.424943

PubMed Abstract | CrossRef Full Text | Google Scholar