Tunable diamond raman lasers for resonance photo-ionization and ion beam production

Lasers with wide tunability and tailored linewidth are key assets for spectroscopy research and applications. We show that diamond, when configured as a Raman laser, provides agile access to a broad range of wavelengths while being capable of efficient and selective photo-excitation of atomic species and suitable spectroscopic applications thanks to its narrow linewidth. We demonstrate the use of a compact diamond Raman laser capable of efficient ion beam production by resonance ionization of Sm isotopes in a hot metal cavity. The ionization efficiency was compared with a conventional Ti:sapphire laser operating at the same wavelength. Our results show that the overall ion current produced by the diamond Raman laser was comparable -or even superior in some cases-to that of the commonly used Ti:sapphire lasers. This demonstrates the photo-ionization capability of Raman lasers in the Doppler broadening-dominated regime, even with the considerable differences in their spectral properties. In order to theoretically corroborate the obtained data and with an eye on studying the most convenient spectral properties for photo-ionization experiments, we propose a simple excitation model that analyzes and compares the spectral overlap of the Raman and Ti:Sapphire lasers with the Doppler-broadened atomic spectral line. We demonstrate that Raman lasers are a suitable source for resonance photo-ionization applications in this regime.

1 Introduction

Over the years, the capability of light to interact with matter has been widely exploited. In the field of nuclear research, photo-ionization of atoms is one of the key processes for selective and efficient delivery of ion beams. Tunable lasers play a crucial role providing photons that resonantly match the electronic transitions of the atoms. By using multiple resonant steps, sometimes in conjunction with a last, non-resonant excitation step, the ionization potential (IP) can be surpassed and the atom thus ionized. Moreover, for efficient resonance laser ionization, the effective linewidth of the atomic transitions in the experimental environment requires a spectrally matched light source. Thus, lasers are a suitable tool for the research of molecular and atomic structures [1].

At CERN, experiments involving isotope production with the ISOL (Isotope Separation On-Line) method of extraction directly from a high energy proton beam-impacted production target, typically rely on several approaches for ionization, with resonance laser photo-ionization being one of the most convenient and widely applied techniques. This method is applied in what is called the resonance ionization laser ion source (RILIS) [2]. The laser sources are employed to selectively ionize the desired (radiogenic) elements in a hot cavity, after which the ions are extracted and guided through a mass separation system to select the particular isotope of interest. The main purpose of this infrastructure is to provide the Isotope Separator On-Line Device (ISOLDE) facility with pure ion beams for the subsequent study of radioactive isotopes and exotic particles at dedicated experimental setups [3]. Alternatively, atomic and nuclear structure effects can be directly investigated on very low production rates by performing laser spectroscopy directly in the ion source [4].

In general, lasers capable of fulfilling the demanding requirements for high precision atomic studies are hard or expensive to come by. For high efficiency in the ionization process and in non-linear frequency conversion techniques to enlarge the available wavelength range, lasers with a high repetition rate and a high peak power, are required. At the same time, the spectral laser linewidth should match the effective transition linewidth in the experimental environment to address the complete atomic ensemble. For applications at ISOLDE, nanosecond pulse lasers at tens of kHz repetition rate range exhibiting linewidths between 1–15 GHz (for Doppler broadened transitions in hot cavity ion sources at around 2000°C are suitable. Additionally, wide-range tunability is a key attribute, since it allows to access a large variety of transitions of most chemical elements [5]. In the RILIS laser setup, light covering the UV to blue and near-IR spectral regions is provided by solid-state Ti:sapphire (Ti:Sa) lasers, while the visible range and part of the UV range is covered by dye lasers [6]. In contrast to solid-state lasers, dye lasers maintenance is an operationally more challenging task and continuous operation is constrained by regularly required dye changes [7]. Overall, the laser system used at RILIS covers the UV to mid-IR spectrum well, except for the range around 532 nm, which is the wavelength used for pumping of the tunable lasers. Thus, the development of efficient and broadly tunable solid-state laser sources for the visible spectral range entails an interesting challenge since it would on the one hand offer the possibility to replace the spectral range provided by the dye lasers and on the other hand increase the total coverage of accessible wavelengths. The possibility to finally meet these requirements has recently enlivened the exploration of alternative solid-state light sources for ionization experiments.

A proposed solution consists of a continuously tunable diamond Raman laser capable of generating a frequency shift from a Ti:Sa pumping laser, gaining access to the visible spectral range [8]. Furthermore, a compact version of the resonator is able to diversify the spectral coverage by producing multiple Stokes orders while preserving the linewidth of the pump. This laser source was characterized and tested for resonant ionization spectroscopy experiments, by exciting the atomic transition $4s^{21}{S}_0\to 4s4p^1{P}_1^0$ of calcium at 422.79 nm. The Ca⁺ isotopes were produced inside an atomic beam unit in cross-beam geometry, where a time-of-flight spectrometer was used to measure the ion signal [9]. The results showed that the technology has great potential to cope with the demanding requirements of resonantly exciting atomic transitions of different elements. A pivotal feature here is that the laser operates in what is called the “coherent Raman scattering regime”, where the achievable Stokes linewidth is approximately the same as for the pumping light [9].

More detailed evaluation shows that—even if the Raman resonator replicates the average linewidth of the Ti:Sa laser—the spectral lineshape and distribution of the axial longitudinal modes within the lasing bandwidth is substantially different. Thus, the performance of the Raman laser system to efficiently ionize atoms in the typical application environment required further investigation. Moreover, the arrangement of the cavity produces a specific spectral content, for instance a simple hemi-spherical setup compared to a z-fold design with a longer length, will generate substantially lower number of spectral modes but with an increased axial mode linewidth due to noise. Hence, studying the spectral performance of laser pulses with varied spectra would allow the construction of more efficient ionization sources.

In order to understand the interplay between the laser spectral features and the atomic transition of interest we have developed a computational model that simulates the excitation process of lasers with arbitrary spectral content. This enables us to compare the different laser technologies for producing the most convenient pulses. We complete the study by experimentally demonstrating the performance of Raman lasers for efficient ionization applications, showing a comparable performance in the ion current produced compared to the Ti:Sa laser when operating in the ionization saturation regime.

We also study the behaviour of Raman lasers considering their dependency on operating wavelength. The computational model also calculates the effect of the polarization angle in terms of accessibility to the maximum Raman gain [10]. In combination with the aforementioned spectral model, the behaviour of a Raman resonator can be predicted and optimized, being able to calculate key designing parameters for Raman laser construction, such as the lasing threshold or the slope efficiency.

Needless to say, the diamond Raman laser applicability is not reduced to spectroscopy experiments. The combination of outstanding optical and thermal properties makes them particularly interesting for a variety of applications; such as construction of high power lasers [11, 12], or integrated photonic devices [13, 14] at extended wavelength ranges [15, 16] providing wide tunability [17], and quantum applications [18, 19]. In fact, selective and efficient ionization is interesting in quantum technologies as it provides means for producing atomic quantum states with high fidelity [20, 21].

In this work, we present the different tools developed for Raman laser design and characterization, along with the latest improvements towards wavelength diversification thanks to efficient cascading, narrow linewidth preservation, and ionization efficiency depending on the spectral properties of the laser pulses. We compare the results from our mathematical model with results from photo-ionization experiments, where samarium (Sm) atoms were resonantly ionized in a two-step ionization scheme, consisting of a resonant first step at 433.9 nm and a second step for non-resonant ionization above the IP at 355 nm. With this setup saturated ion beam efficiency measurements were performed, to compare the performance of the Raman and Ti:Sa lasers for the excitation of ¹⁵²Sm⁺ isotopes, willing to verify the suitability of the new technology.

2 Widely tunable diamond Raman laser design

For constructing Raman lasers functional across a broad spectral range, it is important to consider the dependency of the Raman gain with the wavelength as well as the spectral response of the optical elements used in the resonator. We present a multi-Stokes Raman scattering simulator that takes this wavelength dependency into account, by appropriately modifying the standard coupled differential equations for steady-state Raman processes proposed in the literature [22]. For nanosecond pulses, this theory reproduces with enough accuracy the dynamic nonlinear Raman process. Mathematically we have that

$\begin{array}{ll}\hfill & \frac{d{I}_P}{dz}=-\frac{{\omega }_P}{{\omega }_{s1}}{g}_{R1}{I}_P{I}_{s1}-{\alpha }_P{I}_L,\hfill \\ \hfill & \frac{d{I}_{s1}}{dz}=g_{R1}{I}_P{I}_{s1}-g_R\frac{{\omega }_{s1}}{{\omega }_{s2}}{I}_{s1}{I}_{s2}-{\alpha }_{s1}{I}_{s1},\hfill \\ \hfill & \frac{d{I}_{s2}}{dz}=g_{R2}{I}_{s1}{I}_{s2}-g_R\frac{{\omega }_{s2}}{{\omega }_{s3}}{I}_{s2}{I}_{s3}-{\alpha }_{s2}{I}_{s2},\hfill \end{array}(1)$

where I_P refers to the pump intensity, while I_sx defines the Stokes intensity with x donating the order of the Stokes. In the same way, ω is the angular frequency and g_R the Raman gain at the pumping frequency. Finally, g_Rx refers to the Raman gain associated to each Stokes order and α_x to the corresponding loss coefficients. Assuming that cavity losses predominate over the system, it is reasonable to consider the loss coefficients α_x from Eq. 1 to be negligible, especially since their effect is often not perceivable for diamond in the visible spectral range [22]. The Raman gain for higher Stokes orders g_Ri is calculated as follows [23],

$g_{Ri}=g_R\left({\omega }_P\right)\frac{{\omega }_{si}}{{\omega }_P},(2)$

where ω_si corresponds to the angular frequency of the higher Stokes orders and ω_P the angular frequency of the pump. To determine g_R for each of the simulated wavelengths a fit across a broad spectral range was computed based on the experimental data obtained from the literature [15, 24]. It is important to remark that the expected theoretical value for g_R in the UV was considerably higher than the measured one [15]. The resulting fit is depicted in Figure 1 and it is based on the wavelength dependant Raman gain formula found in [25]:

$g_R\left({\omega }_P\right)=\frac{A\left({\omega }_P-B\right)}{{\left(C-{\omega }_P^2\right)}^2},(3)$

where in our case for diamond, the value for each constant was A = 976 ⋅ 10⁴⁸, B = 251 ⋅ 10¹² and C = 169 ⋅ 10¹⁴.

FIGURE 1

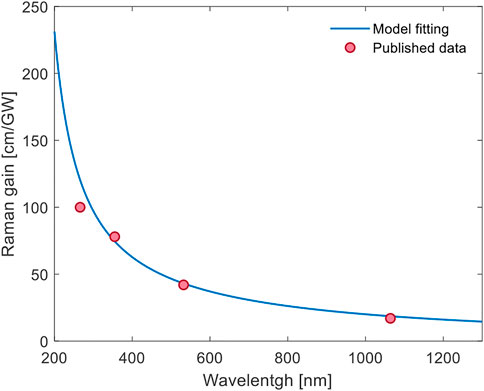
FIGURE 1. Wide-range fit of a diamond Raman gain model according to [25] (blue) on experimental data (red) from the literature [15, 24].

The obtained Raman gain parameters were adjusted depending on the pump polarization state of both the pump and Stokes, by using the adequate Müller matrix for each particular case. Here, the light propagation occurs through the <110> crystallographic axis as explained in [10]. Under these conditions, the polarization angle that maximizes the cascading process is ±54.7° with respect to the [001] direction, since it produces Stokes orders with polarization states parallel to the <111> crystallographic axis, maximizing the gain. We refer to cascading as the process in which not only the photons from the pumping light are Raman shifted to produce a first Stokes, but when this process is replicated in order to produce a second Stokes and higher Stokes orders consecutively.

In order to design a Raman converter that is wavelength agile and provides a useful output at a broad spectral range, we have opted for a minimalist hemi-spherical cavity design composed uniquely of a Raman medium and a curved retro-reflector as depicted in Figure 2. In this arrangement, the output coupler is the uncoated surface of the diamond, while the coatings of both the second diamond surface (anti-reflection) and the curved mirror (high reflector) are broadband and operating in the 450–850 nm range. The pump was focused into the diamond by means of a focusing lens, producing a spot size of approximately 50 μm diameter (1/e²). The separation between pump and Stokes beams is provided by a dichroic mirror that can be chosen according to the pumping wavelength and is not part of the resonator. The spectral output produced (in terms of number of longitudinal modes) by such a resonator depends on the cavity length and the pumping conditions, which will be discussed in section 3 in more detail.

FIGURE 2

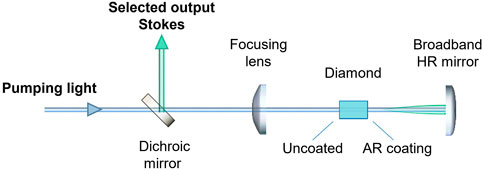
FIGURE 2. Schematic of the hemi-spherical diamond Raman cavity simulated in the Stokes generation mathematical tool, where all the elements depicted and the spacing between them are variable and considered in the simulator.

Specifically, the previously presented differential equations Eq. 1 are resolved for the cavity illustrated in Figure 2 by dividing the diamond bulk into differential slabs and neglecting dispersion and diffractive effects through the diamond thanks to its relatively small size compared to the Rayleigh length of the cavity modes. The pump light travels through the crystal twice, while the Stokes orders resonate in the cavity. We only considered here cascading up to the second Stokes order. Computationally, the equations were solved by employing a fixed-step finite differences method, with a grid fine enough to accurately reproduce the temporal dynamics of the Raman process. Regarding the boundary conditions of the diamond, in the anti-reflection coating we assumed non-perfect behaviour so the transmission was set to a value of 0.95. While for the uncoated side reflected light into the resonator was calculated by the Snell law in combination of the Sellmeier equation for diamond. Additionally, a loss factor was applied to the re-injected light since not all the reflected light in the uncoated surfaces necessarily resonates back. In particular the value for the re-injected pump light was negligible and this is why we considered that it just propagates twice through the crystal.

The simulated pumping pulse resembles the one used in the experiments produced by a gain-switched Ti:Sa laser described in section 4. For the simulated cavity parameters the length of the crystal is selected to be 5 mm, the output coupler corresponds to the uncoated side of the crystal and the high reflector concave mirror is assumed to be ideal (100% of reflectivity). A 50 ns pulse is focused into the Raman medium with an intensity exceeding 0.1 GW/cm², the corresponding temporal envelope is represented as a solid red line in Figure 3. Here it can also be appreciated the depleted pump (discontinuous red line), along with the produced first and second Stokes pulses. As the pump pulse increases in intensity, it reaches the lasing threshold and the first Stokes is produced. The growth rate of the Stokes pulse is fast thanks to the small resonator dimensions, quickly depleting the available pump. A similar dynamic is observed when the lasing threshold for the second Stokes is reached, represented by the pronounced depletion in the first Stokes lineshape. The fast dynamics observed in the temporal pulse shapes are a consequence of the relatively high losses and compactness of our laser resonator. The resulting Stokes pulses have non-Gaussian envelopes and a duration that is considerably shorter than the pump pulse. Such effect was experimentally observed also in [9].

FIGURE 3

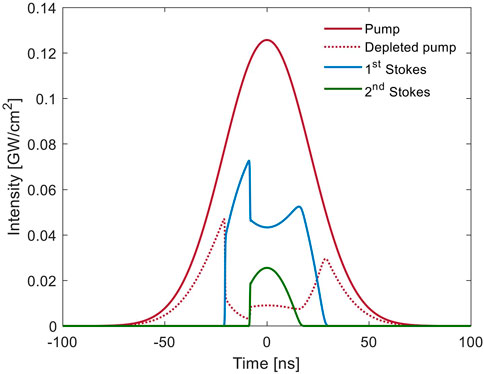
FIGURE 3. Example of the simulated depleted signal (dotted red) of a nanosecond laser pulse (solid red), along with the calculated first (blue) and second (green) Stokes generation.

The laser dynamics depend on the pump pulse intensity. In order to study the energy transfer dynamics, we simulated a scan scanned the pump power producing different cascading conditions, as shown in Figure 4, where we compare the produced Stokes output powers for three different pumping wavelengths (450, 650, and 850 nm) at the same pump intensity and maintaining the spot size. It is obvious that thanks to the wavelength dependency of the Raman gain, Raman lasers will be more efficient at shorter wavelengths, and they should require a lower power for reaching the lasing threshold. Particularly, Figure 4A shows the different output powers for the first and second Stokes orders depending on the pumping power at different wavelengths. The first Stokes output power is capped whenever the second Stokes lasing threshold is reached, which is also observed in Figure 3. Figure 4B illustrates the calculated lasing threshold of the Stokes as a function of the wavelength. The cascading process can be optimized in terms of necessary cavity reflectivity and pump intensity with the relatively simple model presented here.

FIGURE 4

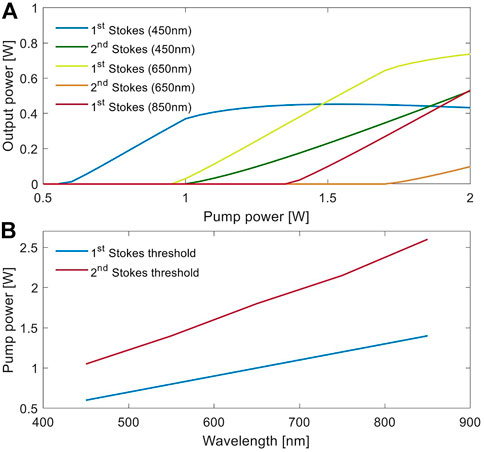
FIGURE 4. (A) Simulation results of Stokes output power for different pump laser wavelengths (450 nm, 650 and 850 nm) under same conditions and alongside a range of different pump powers. (B) Required pump power to produce first and second Stokes (lasing threshold) at a broad spectral range in the visible.

The spectral content of the laser pulses plays a crucial role in the efficiency of the atomic photo-ionization process. In our laser, the spectral properties of each pulse strongly depend on the resonator length, round-trip reflectivity, and Raman gain. In particular, the number of longitudinal modes and the linewidth of each of them must be considered to assess the ultimate performance of Raman lasers for photo-ionization efficiency and spectroscopy applications.

3 Spectrum dependant excitation model

The interaction of light with atomic orbitals, and subsequent photo-ionization processes, has been widely studied in the literature, including the description of multi-step laser ionization processes [1]. The most simple and general case is to study the two-level atom interaction. Here we will refer to the two states as |1⟩ and |2⟩ with resonance frequency ν₂₁ = (E₂ − E₁)/h and pumping frequency ν_P with detuning δ = ν_P − ν₂₁. Under steady state conditions and following [26] the excited state population ρ is given by

$\rho =\frac{S_0/2}{1+S_0+4{\delta }^2/{\xi }^2},(4)$

where ξ is the spontaneous decay rate of state |2⟩ and S₀ is the resonant saturation parameter defined as S₀ = I/I_S with the saturation intensity I_S given by

$I_S=\frac{\pi hc}{3{\lambda }_P^3\tau }.(5)$

Here λ_P is the center wavelength of the ionizing laser and τ the lifetime of the excited state. However, the calculation of ρ is not taking into account the effect of the spectral content in the ionization process. In this work, we aim at quantifying this effect by proposing a laser spectrum-dependant excitation model.

Our simulation tool calculates the spectral overlap of defined laser-like spectra with the spectrum produced by a heated cloud of Sm atoms (although the same formalism applies to any atomic species). This spectrum would have a Gaussian envelope stretched by the Doppler broadening of the atoms ruled by the oven temperature and given by [27].

$\mathrm{\Delta }{\omega }_{\mathit{Doppler}}=\frac{2{\omega }_0}{c}\sqrt{2\ln 2\frac{kT}{m_0}},(6)$

where ω₀ is the central frequency of the Sm atom transition, k is the Boltzmann constant, T is the temperature of the oven, c is the speed of light and m₀ is the atomic mass of Sm. The Gaussian lineshape is given by the fact that each of the atoms presents a Lorentzian natural linewidth at a random frequency normally distributed across the whole spectrum defined by the Doppler effect. As determined by the central limit theorem, the summation of a high enough number of Lorentzian lineshapes results in a Gaussian one [28]. The computed Gaussian lineshape for Sm at the experiment temperature of 2000°C presented a full width half maximum (FWHM) linewidth of 1.81 GHz. Which lineshape would be defined as

$A_{Sm}\left(\nu \right)=e^{-\frac{{\left(\nu -{\nu }_0\right)}^2}{\mathrm{\Delta }{\nu }_{\mathit{Doppler}}}},(7)$

where ν₀ is the central frequency of the transition and the lineshape is normalized in amplitude. Note that in general, in the excitation process, the atoms are individually ionized, and therefore during the saturation process the spectral shape of the absorption will vary accordingly. This is similar to what is known in laser systems as “spectral hole burning”.

Along with the atoms spectral distribution, we also define the spectral modes of two ideal laser sources similar to the ones employed in the experiment, based on theoretical models [29] and selecting envelope linewidths better matching the Doppler broadening than the real ones. The calculated spectrum to resemble the Raman laser behaviour was defined as a Gaussian envelope of 6.4 GHz FWHM linewidth with 300 MHz linewidth longitudinal modes separated by a free spectral range (FSR) of 2 GHz. For the laser modes modeled here, we generated the spectrum by summing truncated Lorentzian lineshapes, where the offset is determined by the lasing threshold as was proposed in [30]. For comparison purposes we generated a similar spectrum but with Gaussian axial mode lineshapes, in order to quantify the effect of the modes spectral distribution. Regarding the Ti:Sa laser representation, the generated envelope had a FWHM linewidth of 3.1 GHz with 20 MHz linewidth modes separated by a FSR of 300 MHz, as we assumed Fourier-limited modes. The resulting spectra can be observed in Figure 5, where we present together the Gaussian envelope for the Doppler broadened transition of the Sm atoms, and the spectra for the Raman and Ti:Sa laser with truncated Lorentzian modes.

FIGURE 5

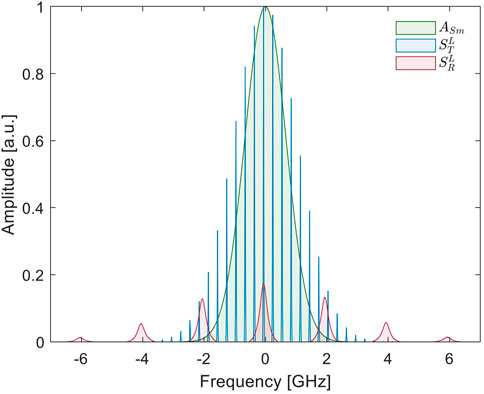
FIGURE 5. The different generated spectra for simulations, including the Sm Doppler broadened Gaussian and the Ti:Sa and Raman laser spectra, both presenting Lorentzian truncated modes.

To mathematically construct the laser spectrum S(ν) we first need to compute the product of the laser emission spectral bandwidth A(ν) with the cavity longitudinal modes. Since we evaluate the spectra for two different modal lineshapes, for the Gaussian lineshape axial modes $m_j^G(\nu )$ we will have a resulting laser spectral shape S^G(ν) of

$\begin{array}{ccc}\hfill S^G\left(\nu \right)& =\hfill & A\left(\nu \right)\cdot \sum _j{m}_j^G\left(\nu \right)\hfill \\ \hfill & =\hfill & A_0^G{e}^{-\frac{{\left(\nu -{\nu }_0^e\right)}^2}{2{\gamma }_e^2}}\cdot \sum _j{e}^{-\frac{{\left(\nu -{\nu }_{0_j}^m\right)}^2}{2{\gamma }_m^2}},\hfill \end{array}(8)$

and for the Lorentzian lineshape axial modes $m_j^L(\nu )$ a resulting laser spectral shape S^L(ν) of

$\begin{array}{ccc}\hfill & S^L\left(\nu \right)=A\left(\nu \right)\cdot \sum _j{m}_j^L\left(\nu \right)\hfill & \hfill \\ \hfill & =A_0^L{e}^{-\frac{{\left(\nu -{\nu }_0^e\right)}^2}{2{\gamma }_e^2}}{\left(\sum _j\frac{{\gamma }_m/\pi }{{\left(\nu -{\nu }_{0_j}^m\right)}^2+{\gamma }_m^2}-T_L\right)}^{+}\hfill & \hfill \end{array}(9)$

where γ_e is the half width half maximum (HWHM) linewidth of the envelope and ${\nu }_0^e$ the central frequency. γ_m is the HWHM linewidth of the mode, and the central frequency of the modes is defined as ${\nu }_{0_j}^m={\nu }_0^m\pm j\mathrm{\Delta }{\nu }_m$ with j = 0, 1, 2 … with Δν_m equal to the corresponding free spectral range (FSR). T_L accounts for the lasing threshold of the longitudinal modes which we take as 0.1 in our simulations.

The super-index defines the distribution employed for the modes (G for Gaussian, L for Lorentzian), and the sub-index will define the specific laser (T for Ti:Sa, R for Raman). Thus, $S_R^L(\nu )$ will refer to the Raman laser spectrum with Lorentzian lineshape axial modes, whereas $S_R^G(\nu )$ will refer to Gaussian lineshape axial modes; correspondingly, $S_T^L(\nu )$ will refer to the Ti:Sa laser spectrum with Lorentzian and $S_T^G(\nu )$ will refer to the Ti:Sa laser spectrum with Gaussian lineshape axial modes.

In order to compare laser pulses with the same energy, we set ∫_νS_T(ν) = ∫_νS_L(ν). The relative scaling of the Raman and Ti:Sa laser spectra is taken such max (A_T(ν)) = 1, meaning that the amplitude of the spectral envelope of the Ti:Sa laser is at the threshold for the saturation of the ionization process.

The resulting ion current is then proportional to the integral of the overlap of the Raman and Ti:Sa lasers spectra with the Sm absorption distribution. To calculate the excitation ratio ${\mathrm{\Theta }}_{R,T}^{G,L}$ approximated by the overlap we have

${\mathrm{\Theta }}_{R,T}^{G,L}=\frac{{\int }_{\nu }{A}_{Sm}\left(\nu \right)\cdot S_{R,T}^{G,L}\left(\nu \right)d\nu }{{\int }_{\nu }{A}_{Sm}\left(\nu \right)d\nu }.(10)$

To obtain a relative performance of the excitation process and the theoretical saturation curves of each laser spectrum, a power scan of the overlap between their spectra ($S_R^L$, $S_R^G$, $S_T^L$ and $S_T^G$) and the Sm Doppler broadened Gaussian envelope (A_Sm) was simulated. For this computation, the amplitude of all the simulated spectra were multiplied by a scaling factor k ranging from 0.1 to 100, which is a broad enough range to determine the saturation point and the behaviour of the lasers in experimental conditions, as will be seen in section 5. All the calculations were performed over 20,000 laser pulses with uniformly distributed ${\nu }_0^m$ values and therefore the average results for all of the simulated pulses were calculated at all the different powers. Note that for k values of less than 1, the result resembles non-saturated ionization conditions, whereas for k > 1, the saturation process starts for the Ti:Sa laser, although not necessarily for the Raman laser.

The model agrees well with the obtained experimental data in terms of the slope behaviour and saturation point for both lasers, as will be shown in section 5. For our particular case, we consider the saturation effect by capping the increment of the signal power to a fixed spectral amplitude. After computing the ionization signal for a wide laser power range by applying a scaling factor to the laser spectra, the laser spectral function is capped to one to reproduce the effect of ionization saturation. We consider that this approximation is good enough to verify the points of interest in this work, although the effect of spectral hole burning is not considered in this model [30]. Thus, by introducing the aforementioned function capping ${\left[S_{R,T}^{G,L}(\nu )\cdot k\right]}_0^1$ (which limits the function between 0 and 1), the rate of ionized atoms defined in Eq. (10) will result in

${\mathrm{\Theta }}_{R,T}^{G,L}=\frac{{\int }_{\nu }{A}_{Sm}\left(\nu \right)\cdot {\left[S_{R,T}^{G,L}\left(\nu \right)\cdot k\right]}_0^{1}d\nu }{{\int }_{\nu }{A}_{Sm}\left(\nu \right)d\nu }.(11)$

Employing Eq. 11, we can then calculate the relative ionization efficiency for both lasers assuming Lorentzian and Gaussian axial modes. The results using the spectra shown in Figure 5 are depicted in Figure 6. Here, it can be seen that wider spectral modes, as the ones generated for the Raman spectrum, enhance by nearly a factor of two the excitation capability comparing equivalent laser powers, regardless of the assumption of axial mode spectral shape. Meaning that non-ideal, thus noisy, laser sources with broadened spectral modes are more suitable for excitation or ionization processes based on the spectral overlap approach presented in this work.

FIGURE 6

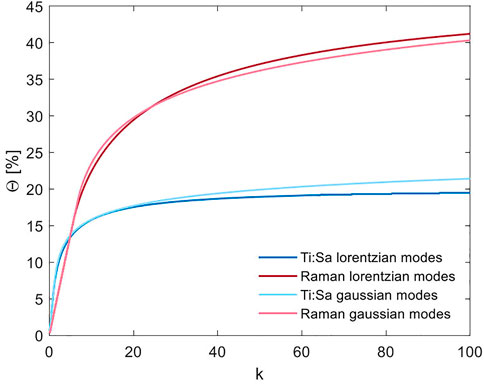
FIGURE 6. Saturation curves simulated by the model based on the overlap of the laser spectra with the Doppler Gaussian spectrum of the Sm atoms A_Sm (rate of ionized atoms) depending on the scaling factor k that emulates the laser power.

4 Experimental setup

In order to determine the ionization efficiency of the diamond Raman laser, its performance was compared with the ionization capabilities of a Ti:Sa laser, which is commonly used at RILIS. This comparison was carried out in a laser ionization setup similar to the one used at ISOLDE. After ionization of the Sm atoms with the ionization scheme and setup depicted in Figure 7 the Sm was mass separated and the ions detected by a Faraday-cup (FC).

FIGURE 7

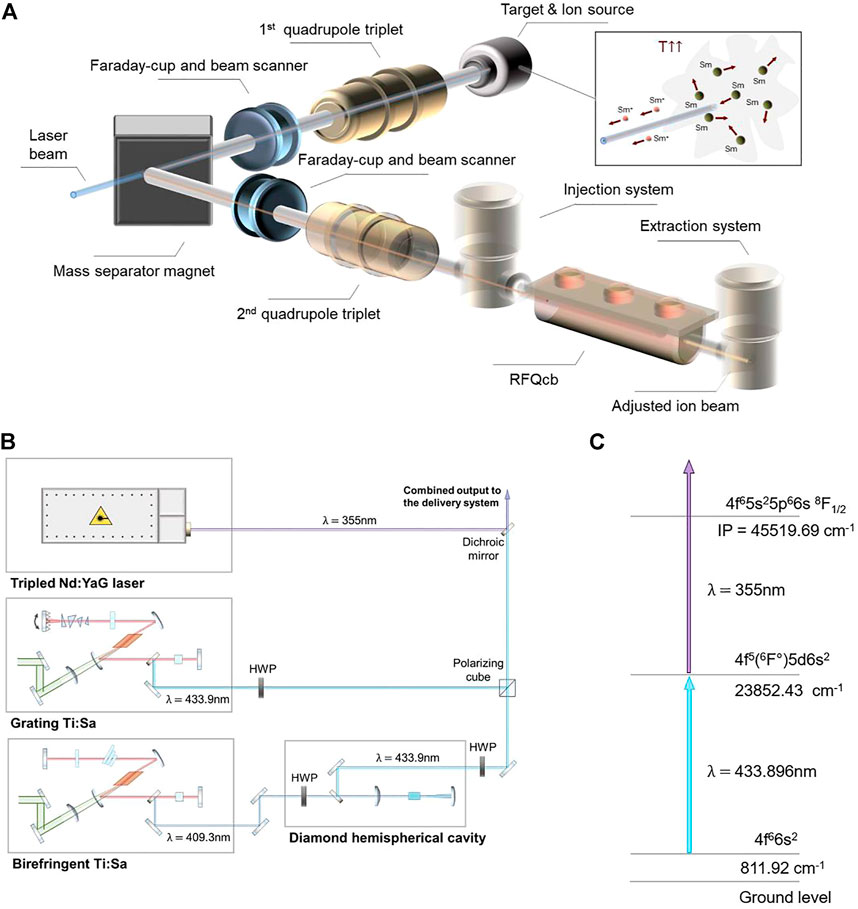
FIGURE 7. (A) Sketch of the Offline-2 beam line with Sm atoms heated in the hot cavity, which are consequently ionized by a laser beam, producing a pure ion beam after the mass separator. In the experiment the final measurements of the ions were performed in the second FC, meaning that the elements shown in transparent depiction were not used. (B) Laser setup presenting the Nd:YAG laser for non-resonant ionization into the continuum, the grating Ti:Sa used for generating the first step and the diamond Raman laser, pumped by the birefringent Ti:Sa, also used for the first step. Additionally, the power control system for adjustment of the pump laser power composed by half-wave-plates and a polarizing cube is shown. The first and second step laser beams were combined with a dichroic mirror. (C) The two steps color scheme employed for the experiment including the resonant first step and the non-resonant second step surpassing the ionization potential.

The Offline-2 facility at CERN provides a testbed for the technology to be subsequently used in the ISOLDE facility and here our experiments took place. The frontend is equivalent to the one in the ISOLDE facility, details about this facility can be found in [3]. The process by which atoms are resonantly ionized can be followed by observing Figure 7A. The laser beams are focused into the ion source, where a cloud of atoms is formed in a hot cavity, which consists of a refractory metal tube, with an internal diameter of 3 mm and a length of 34 mm, for further details see [4]. The atoms are ionized by the photons. The produced ions are then extracted as a beam by an extraction electrode at a potential difference of 30 kV, and the beam is transported through a system of ion beam optics. This beam can be characterized by an instrumentation setup composed by a Faraday-cup and a beam scanner. Afterwards, an isotopically pure ion beam is obtained by selecting only the isotopes of interest (¹⁵²Sm⁺) with a mass separator dipole magnet. Again, the ion beam intensity can be obtained from measurements with a Faraday-cup and the beam shape can be investigated with a beam scanner set.

The laser light in charge of the ionization process is delivered from an adjacent laser lab. The setup employed for this experiment is depicted in Figure 7B, while the two color ionization scheme followed to ionize the Sm atoms is illustrated in Figure 7C. The first step transition 4f ⁶6s² → 4f ⁵(6F °)5 d6s² is provided by the two different laser sources for comparison. On the one hand, we have a frequency-doubled grating tunable Ti:Sa laser presenting an output maximum power of 900 mW at 433.9 nm wavelength and 10 kHz repetition rate. It is arranged in a Z-fold geometry and the intra-cavity doubling was obtained with a Beta Barium Borate (BBO) crystal, cavity mirrors were conveniently coated for the operation range, for further information see [31]. On the other hand, we have the hemi-spherical diamond Raman cavity composed by a 6 mm diamond crystal acting as the Raman medium and a 50 mm ROC concave mirror. A half-wave-plate (HWP) was used to control the polarization of the pump, a 150 mm focusing lens to pump the diamond, and a dichroic crystal to separate the pump from the output first Stokes. The resonator was encompassed this way by the uncoated side of the crystal (approximate reflectivity of 17%) and the broad high reflectivity (∼99%) concave mirror, presenting a consequent FSR of around 2 GHz. The laser presented a maximum output power of 400 mW at 433.9 nm and 10 kHz repetition rate. The Raman laser was pumped by a tunable Ti:Sa cavity frequency-doubled by a BiB₃O₆ (BiBO) crystal and producing a 1 W maximum pump power at 409.3 nm. Frequency stability was equal and below 0.005 cm⁻¹ for both Ti:Sa lasers, and consequently identical for the Raman laser. For further details regarding the Raman resonator see [9]. Both lasers performed separately the first resonant excitation step of the Sm atoms. In order to be able to measure the ion production saturation curves for these lasers, a second non-resonant step was required. For this purpose, a high power frequency-tripled Q-switched InnoSlab Nd:YAG laser from Edgewave ^ⓒ was utilized, with a maximum power of 10 W at 355 nm wavelength. The output was synchronized in time and optimized for each of the two lasers to be able to suitably perform the ionization scheme presented in Figure 7C.

The beam characterization was performed by measuring on-line the center wavelength and linewidth (of the spectral envelope of the modes) of the lasers using a HighFinesse/Ångstrom WS/6 wavemeter with a resolution better than $<$0.066  cm⁻¹. The obtained data was checked by measuring the generated ion current while performing a frequency sweep, obtaining the resulting linewidth of the convolution between the lasers’ and the transitions linewidth, since the measurement was taken below the saturation point. In addition, the spot size of each laser was measured by utilizing a Basler acA1920-40 gm CMOS camera and post-analysis of the image.

5 Results

As mentioned before, in this experiment ion beams were produced by using the presented two lasers in combination with a frequency-tripled Nd:YAG laser. The generated ion current of ¹⁵²Sm ions in the Faraday-cup was measured for different output powers of the Raman and Ti:Sa resonators within a range of ∼0.15–100 mW. The obtained results are depicted in Figure 8, along with their corresponding fits.

FIGURE 8

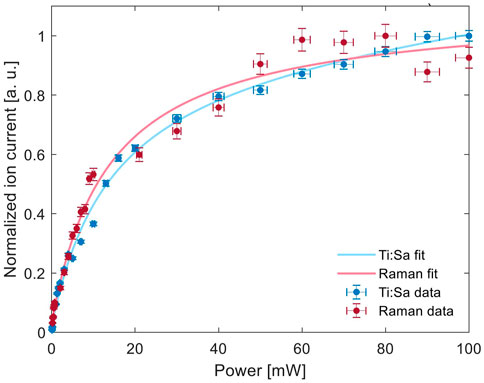
FIGURE 8. Normalized values of the measured ion current for the Raman and the Ti:Sa lasers depending on the output power of each laser along with their corresponding fits and the obtained saturation point.

For comparison purposes and to corroborated the mathematical model presented here, it is known from the literature [32] that the measured ion current F(p) in an ionization process can be approximated as

$F\left(P\right)\propto I_0+C_1\frac{1}{1+\left(P/P_S\right)}+C_{2}P,(12)$

where p is the absorbed laser power, P_S the saturation power, I₀ the background ion current, C₁ is a constant and C₂P the linear term for the non-resonant photo-ionization contribution. Which for our measurements I₀ = 339.4 for the Raman fit, I₀ = 158.1 for the Ti:Sa fit, C₁ = −329.7 for the Raman fit, C₁ = −154.7 for the Ti:Sa fit, P_S = 13.54 mW for the Raman fit, P_S = 13.97 mW for the Ti:Sa fit, C₂ = 0.0286 for the Raman fit and C₂ = 0.2566 for the Ti:Sa fit. The obtained curves follow the predicted behaviour in the simulation as can be observed in Figures 8A,B. However, the measurements were performed under unstable conditions, meaning that the obtained values for each laser can not be compared in terms of absolute ion current. Charging and discharging effects of the ion optics could be observed through instabilities in the delivered ion beam, leading to the total ion current changing over time. This problem has been possible to solve only after the experiment, meaning that the total observed ion current in each of the data sets is different. The dataset depicted here was selected among multiple different measurements, as it presented the smallest deviations between the first and last point measured at the same power of the laser for which the saturation was measured. Thus, for comparison purposes we normalized the obtained data by the maximum ion current measured ofr each laser as can be seen in Figure 8. The values obtained here and in the fits parameters provide then comparable information, as the saturation power P_S is independent of the absolute measured ion current. The presented results not only demonstrate that the diamond Raman laser is a suitable tool for efficient photo-ionization, but the performance is at least comparable to the current technology. To provide further evidences about the spectral advantage that the model suggests, additional research is required under more stable conditions with constant ion beam intensities.

Regarding the spectroscopic measurements of the Sm transition line using both lasers, Figure 9 shows a comparison resulting from frequency sweep scans, representing the convolution between the lasers’ spectral envelopes and the Sm transition’s linewidth. For Gaussian linewidths the total measured linewidth is approximately ${\gamma }_T=\sqrt{\mathrm{\Delta }{\omega }_{\mathit{Doppler}}^2+{\gamma }_e^2}$. Which is 8.3 GHz for the Raman convolution, this is around 8.1 GHz for the Raman linewidth and 5.9 GHz for the Ti:Sa convolution, meaning that the laser linewidth itself is around 5.6 GHz.

FIGURE 9

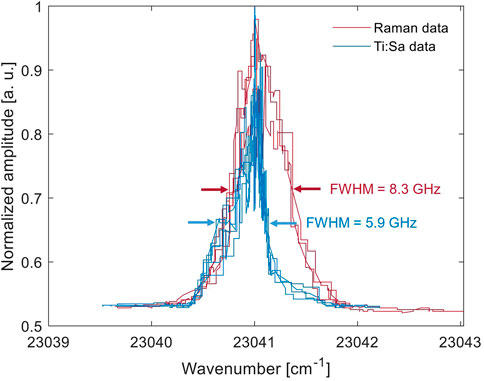
FIGURE 9. Measured spectra for the excitation of the transition while performing a frequency sweep with the Raman and Ti:Sa lasers wavelength and the resulting linewidths for both convolutions.

Moreover, the model assumes that the beam spot size is identical for both laser sources. The ion current was optimized for each of the laser beams by optimization of the focal position inside the ion source. The spot size measurements showed that when removing the ion source after the experiment and placing the camera in the same position, the spot size of the Raman laser was around 50% bigger than the Ti:Sa in the horizontal axis. Nevertheless, the area of interaction is smaller than both beams spot size (3 mm of interaction against over 5 mm of beam size), meaning that performing a fair comparison of the ionization efficiency for both lasers, within the experiment and with respect to the theoretical results, is more complex. In spite of these difficulties, the results appear to be promising and suggest that the presented simple model is a convenient tool for laser source-selection and optimization of their spectral characteristics.

6 Conclusion

In this work we consider the aspects that affect diamond Raman laser performance as resonance ionization sources for ion beam production. We presented two mathematical tools that try to bring some detailed explanation into what was observable during not only this experiment, but also previous studies. The main results are the demonstration of the wide and continuous tunability of these kind of lasers, which at the same time preserve the pump’s spectral linewidth and exhibit a theoretically more convenient modal distribution for atomic photo-ionization than some other conventional sources. These findings could in consequence lead to a consideration of alternative photonic sources for nuclear and quantum applications which are better matched to the requirements of excitation of the electronic transitions.

The herein presented models show that laser cavities with broader spectral modes, which have specific spectral features that have an impact in the efficiency of resonance ionization processes. This is due to the fact that the better the spectral overlap with the transition is, the better the excitation capability becomes, suggesting that a rather noisy pulse will better match the Doppler-broadened transition than a source with a cleaner spectral profile. Since the modal lineshape is broadened and the effective overlap area is increased. This is particularly appreciable when ionizing in the saturation regime, where the spectral overlap integral is two times higher for the proposed noisy spectrum than the cleaner one. The Stokes generation simulator provides useful designing approaches for Stokes generation and cascading efficiency maximization, such as the optimal pump polarization angle or the most suitable parameters to reduce the lasing threshold.

In fact, the presented results provide useful information for the design of optimal Raman resonators, as key parameters to be considered when efficient Stokes generation and cascading are desired have been proposed. Moreover, parametric simulations such as the ones depicted in section 2, suggest that it is overall more efficient to perform frequency alterations, like frequency doubling, to the pumping light rather than to the Raman shifted output, which is an important aspect to consider when developing a Raman laser system.

The experiment showed that the presented hemi-spherical diamond Raman cavity followed the models predictions, being able to efficiently ionize Sm atoms. Since the Raman laser can extend the Ti:Sa laser spectral coverage while preserving the linewidth and its continuous tunability, the technology serves as an all-solid-state solution to less convenient laser sources for nuclear and atomic experiments. Moreover, the results suggest that the overall ionization performance of the current light sources can be improved by selecting light sources with particular spectral properties, meaning that other fields such as quantum technologies, could benefit from this enhancement. Particularly, its spectral properties could improve the fidelity of the quantum states of ions as it can perform atomic excitation with higher probability. The technology can also bridge in a simple manner the gap between 450 and 650 nm, which is otherwise hard to reach by using other available solid-state light sources based on nonlinear frequency conversion. Allowing atomic manipulation of desired isotopes like ¹³³Ba⁺ [21] in a simplified way. In conclusion, this work provides evidence of the capabilities of diamond Raman lasers in the field of efficient resonance photo-ionization.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

The manuscript was written and prepared by DE and EG. The mathematical model conception and development was performed by DE and EG. All the authors contributed to the preparation and installation of the laser setup, while the design and installation of the Raman resonator was performed by DE and EG. The beamline and hot cavity preparation was performed by KC and RH. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 861198–LISA–H2020-MSCA-ITN-2019 and it was also partially funded by CERN (Knowledge Transfer Fund—Singular Light project).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Letokhov VS. Lasers in atomic, molecular, and nuclear physics. Singapore: World Scientific Publishing Co. Pte. Ltd. (1987). p. 422.

Google Scholar

2. Marsh B Resonance ionization laser ion sources. In: Bailey R. editor. CAS - CERN accelerator school : Ion sources (2013) 61. doi:10.5170/CERN-2013-007.203.61

CrossRef Full Text | Google Scholar

3. Catherall R, Andreazza W, Breitenfeldt M, Dorsival A, Focker GJ, Gharsa TP, et al. The ISOLDE facility. J Phys G: Nucl Part Phys (2017) 44:094002. doi:10.1088/1361-6471/aa7eba

CrossRef Full Text | Google Scholar

4. Fedosseev V, Chrysalidis K, Goodacre TD, Marsh B, Rothe S, Seiffert C, et al. Ion beam production and study of radioactive isotopes with the laser ion source at ISOLDE. J Phys G: Nucl Part Phys (2017) 44:084006. doi:10.1088/1361-6471/aa78e0

CrossRef Full Text | Google Scholar

5. Demtröder W. Laser spectroscopy. Germany: Springer Science & Business Media (2002). 986.

Google Scholar

6. Rothe S, Marsh BA, Mattolat C, Fedosseev VN, Wendt K. A complementary laser system for ISOLDE RILIS. J Phys : Conf Ser (2011) 312:052020. doi:10.1088/1742-6596/312/5/052020

CrossRef Full Text | Google Scholar

7. Sinha S, Sasikumar S, Ray AK, Dasgupta K. The effect of dye photodegradation on the performance of dye lasers. Appl Phys B (2004) 78:401–8. doi:10.1007/s00340-003-1383-4

CrossRef Full Text | Google Scholar

8. Chrysalidis K, Fedosseev VN, Marsh BA, Mildren RP, Spence DJ, Wendt KDA, et al. Continuously tunable diamond Raman laser for resonance laser ionization. Opt Lett (2019) 44:3924. doi:10.1364/OL.44.003924

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Echarri DT, Chrysalidis K, Fedosseev VN, Marsh BA, Mildren RP, Olaizola SM, et al. Broadly tunable linewidth-invariant Raman Stokes comb for selective resonance photoionization. Opt Express (2020) 28:8589. doi:10.1364/OE.384630

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Echarri DT, Mildren RP, Olaizola SM, Granados E. Cascaded Stokes polarization conversion in cubic Raman crystals. Opt Express (2021) 29:291. doi:10.1364/OE.413098

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Williams RJ, Kitzler O, Bai Z, Sarang S, Jasbeer H, McKay A, et al. High power diamond Raman lasers. IEEE J Sel Top Quan Electron (2018) 24:1–14. doi:10.1109/JSTQE.2018.2827658

CrossRef Full Text | Google Scholar

12. Yang X, Kitzler O, Spence DJ, Bai Z, Feng Y, Mildren RP, et al. Diamond sodium guide star laser. Opt Lett (2020) 45:1898. doi:10.1364/OL.387879

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Hausmann BJM, Bulu I, Venkataraman V, Deotare P, Lončar M. Diamond nonlinear photonics. Nat Photon (2014) 8:369–74. doi:10.1038/nphoton.2014.72

CrossRef Full Text | Google Scholar

14. Latawiec P, Venkataraman V, Burek MJ, Hausmann BJM, Bulu I, Lončar M, et al. On-chip diamond Raman laser. Optica (2015) 2:924. doi:10.1364/OPTICA.2.000924

CrossRef Full Text | Google Scholar

15. Granados E, Spence DJ, Mildren RP. Deep ultraviolet diamond Raman laser. Opt Express (2011) 19:10857. doi:10.1364/OE.19.010857

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Sabella A, Piper JA, Mildren RP. Diamond Raman laser with continuously tunable output from 3.38 to 3.80 μm. Opt Lett (2014) 39:4037. doi:10.1364/OL.39.004037

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Yang X, Bai Z, Chen D, Chen W, Feng Y, Mildren RP, et al. Widely-tunable single-frequency diamond Raman laser. Opt Express (2021) 29:29449. doi:10.1364/OE.435023

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Granados E, Granados C, Ahmed R, Chrysalidis K, Fedosseev VN, Marsh BA, et al. Spectral synthesis of multimode lasers to the Fourier limit in integrated fabry–perot diamond resonators. Optica (2022) 9:317. doi:10.1364/OPTICA.447380

CrossRef Full Text | Google Scholar

19. Granados E, Stoikos G, Echarri DT, Chrysalidis K, Fedosseev VN, Granados C, et al. Tunable spectral squeezers based on monolithically integrated diamond Raman resonators. Appl Phys Lett (2022) 120:151101. doi:10.1063/5.0088592

CrossRef Full Text | Google Scholar

20. Noek R, Vrijsen G, Gaultney D, Mount E, Kim T, Maunz P, et al. High speed, high fidelity detection of an atomic hyperfine qubit. Opt Lett (2013) 38:4735. doi:10.1364/OL.38.004735

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Christensen JE, Hucul D, Campbell WC, Hudson ER. High-fidelity manipulation of a qubit enabled by a manufactured nucleus. Npj Quan Inf (2020) 6:35. doi:10.1038/s41534-020-0265-5

CrossRef Full Text | Google Scholar

22. Pask H. The design and operation of solid-state Raman lasers. Prog Quan Electronics (2003) 27:3–56. doi:10.1016/S0079-6727(02)00017-4

CrossRef Full Text | Google Scholar

23. von der Linde D, Maier M, Kaiser W. Quantitative investigations of the stimulated Raman effect using subnanosecond light pulses. Phys Rev (1969) 178:11–7. doi:10.1103/PhysRev.178.11

CrossRef Full Text | Google Scholar

24. Savitski VG, Reilly S, Kemp AJ. Steady-state Raman gain in diamond as a function of pump wavelength. IEEE J Quan Electron (2013) 49:218–23. doi:10.1109/JQE.2012.2237505

CrossRef Full Text | Google Scholar

25. Lisinetskii VA, Rozhok SV, Bus’ko DN, Chulkov RV, Grabtchikov AS, Orlovich VA, et al. Measurements of Raman gain coefficient for barium tungstate crystal. Laser Phys Lett (2005) 2:396–400. doi:10.1002/lapl.200510007

CrossRef Full Text | Google Scholar

26. Citron ML, Gray HR, Gabel CW, Stroud CR. Experimental study of power broadening in a two-level atom. Phys Rev A (Coll Park) (1977) 16:1507–12. doi:10.1103/PhysRevA.16.1507

CrossRef Full Text | Google Scholar

27. Haken H, Wolf HC, Brewer WD. The physics of atoms and quanta. Germany: Springer (2005). doi:10.1007/3-540-29281-0

CrossRef Full Text | Google Scholar

28. Laplace P. Théorie analytique des probabilités. Paris: Courcier (1812).

Google Scholar

29. Duarte F. Tunable lasers handbook. In: Duarte F, editor. Tunable lasers handbook. San Diego: Academic Press (1995). Optics and Photonics. doi:10.1016/B978-0-12-222695-3.50013-1

CrossRef Full Text | Google Scholar

30. Svelto O, Hanna DC. Principles of lasers. New York: Plenum Press (2010). doi:10.1007/978-1-4419-1302-9

CrossRef Full Text | Google Scholar

31. Teigelhöfer A, Bricault P, Chachkova O, Gillner M, Lassen J, Lavoie JP, et al. Grating tuned ti:sa laser for in-source spectroscopy of rydberg and autoionizing states. Hyperfine Interact (2010) 196:161–8. doi:10.1007/s10751-010-0171-x

CrossRef Full Text | Google Scholar

32. Mostamand M. Laser developments and study of Rydberg and autoionizing Rydberg states in Tm, La and at using resonant ionization laser spectroscopy. Ph.D. thesis. University of Manitoba Winnipeg (2020).

Google Scholar