Ultraprecise Off-Axis Atom Localization With Hybrid Fields

Atom localization enables a high-precision imaging of the atomic position, which has provided vast applications in fundamental and applied science. In the present work, we propose a scheme for realizing two-dimensional off-axis atom localization in a three-level Λ system. Benefiting from the use of a hybrid coupling field, which consists of one Gaussian beam and one Laguerre–Gaussian beam, our scheme shows that the atoms can be localized at arbitrary position with high spatial resolution. Considering realistic experimental parameters, our numerical simulation predicts that the atoms can be precisely localized with a spatial resolution of $\sim 200$ nm in the range of a radial distance of a few micrometers to the beam core. Our results provide a more flexible way to localize atoms in a two-dimensional system, possibly paving one-step closer to the nanometer scale atom lithography and ultraprecise microscopy.

1 Introduction

Nowadays, the Laguerre–Gaussian (LG) beam [1] has engendered tremendous advanced applications [2–7]. For example, it is widely used in the superresolution fluorescence microscopy such as the stimulated emission depletion [8, 9] and minimal photon fluxes [10, 11] in order to overcome the diffraction limit. Another approach to this target is utilizing the spatially dependent coherent light–matter interaction in atom-light coupling systems [12–14], which essentially depends on a spatially modulated atom-light coupling. By the detection of spontaneously emitted photons [15–18], level population [19–25], absorption [26–28], and gain [29, 30], subwavelength-scale atom localization can be obtained.

As far as we know, atom localization with LG beams can exhibit a large number of advantages [31, 32]. For example, the LG beam has a donut intensity spot naturally, which may avoid the need of two orthogonal standing wave (SW) fields for generating spatially modulated atom-light coupling in a two-dimensional (2D) atom localization system. That fact largely reduces the complexity of experimental implementation. Moreover, it is easier to create a single excitation spot in its core by a LG beam. In traditional SW-based localization schemes, due to the periodicity of the SW field intensity there may exist more than one localization spots within single optical wavelength. Therefore after one-time measurement, the probability of finding atoms at a certain position can be deeply reduced. So far, some approaches have been proposed to break this periodicity of SW fields, via utilizing the sensitivity of light–matter interactions to the light phase in a closed-loop atomic system [33, 34] and the interference of multiple SW fields with different wavelengths and phases [35, 36]. These methods, however, will increase the complexity of experimental setup. Although the LG beam has the aforementioned advantages in localization, it can only localize atoms in the vicinity of its beam core where the laser intensity is close to zero. Off-axis atom localization must be accompanied by the movement of the LG beam itself, which undoubtedly adds to extra complexity.

In traditional SW localization schemes, the superposition of multiple SW lasers with different wavelengths and phases is commonly adopted for reaching a single excitation point [35, 36]. In addition this effect between two LG beams can show interesting patterns such as optical Ferris wheels where the light intensity can be modulated to be zero in certain positions [37]. Inspired by these contributions, in the present work, we study a 2D off-axis atom localization in a three-level Λ system, in which a Gaussian beam serves as the probe field and a LG beam together with a Gaussian beam as the hybrid coupling field. The quantum interference effect between these two beams (LG and Gaussian) can achieve a unique zero-intensity spot at arbitrary position. We show that by appropriately tuning the ratio of peak amplitudes between the LG and any Gaussian beams, atoms can be localized at arbitrary position, with a certain distance to the beam core. Both the spatial resolution and radial distance of localization can be flexibly manipulated via tuning laser Rabi frequencies. Depending on the numerical simulation with experimental parameters our scheme enables the realization of an efficient off-axis 2D atom localization, accompanied by a best spatial resolution $\sim 200$ nm and a radial distance of a few micrometers. Our scheme provides a more convenient route to the target of ultraprecise off-axis 2D atom localization.

2 Theoretical Strategy

To describe the scheme mechanism we consider a simple three-level Λ system as displayed in Figure 1, where states $\left|1\right.⟩$ and $\left|3\right.⟩$ are resonantly coupled by a weak probe field Ω_p and states $\left|3\right.⟩$ and $\left|2\right.⟩$ are connected by another coupling field Ω_c2, with zero detuning. In order to realize an off-axis atom excitation, we have assumed that the probe and coupling beams as Gaussian beams, which are

${\mathrm{\Omega }}_i\left(r\right)={\mathrm{\Omega }}_{i0}{e}^{-\frac{r^2}{W_i^2}},(1)$

where i = p, c2 and Ω_i0 represent the peak amplitude and W_i the Gaussian spot size. Remarkably, states $\left|3\right.⟩$ and $\left|2\right.⟩$ are also coupled by a second LG field Ω_c1 at the same time, as [38].

${\mathrm{\Omega }}_{c1}\left(r,\theta \right)={\mathrm{\Omega }}_{\mathit{c10}}{\left(\frac{r}{W_{c1}}\right)}^{|l|}{e}^{-\frac{r^2}{W_{c1}^2}}{e}^{il\left(\theta +{\theta }_{c1}\right)},(2)$

where Ω_c10, W_c1, θ_c1, and l are the peak amplitude, the beam waist, the initial phase, and the winding number, respectively. r and θ are the cylindrical radius and the azimuthal angle, respectively. Here, we take the winding number l = 1, which enables a single-spot excitation. Other higher-order modes with l > 1 would lower the localization precision by redistributing the atomic population among multiple azimuthal nodes. To our knowledge, this three-level model can be experimentally realized by the D1 line of ultracold ⁸⁷Rb atoms with energy levels $|1\rangle =\left|5S_{1/2},F=1\right.⟩$, $|2\rangle =\left|5S_{1/2},F=2\right.⟩$, and $|3\rangle =\left|5P_{1/2},F=2\right.⟩$. Based on Ref. [14], we assume the decay rates from |3⟩ → |1⟩ and |3⟩ → |2⟩ are equal, typically calculated by Γ₃₁ = Γ₃₂ = 2π × 5.75 MHz. The decay rate between two hyperfine ground states |1⟩ and |2⟩ is Γ₂₁ = 5 kHz, satisfying Γ₂₁ ≪Γ₃₁, Γ₃₂ [39] so the lifetime of $\left|2\right.⟩$ is about 200μs. The beam width is W_i = W_c1 = W estimated to be same for simplicity. Under the frozen-gas limit where the atomic center of mass is unvaried we can take a measurement for the population on state |2⟩ by collecting its fluorescence signals with a CCD camera and a well-localized position distribution of atoms could facilitate this measurement [14].

FIGURE 1

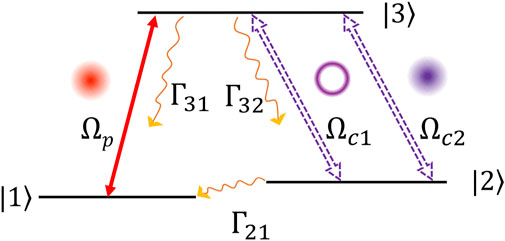
FIGURE 1. Schematic of a Λ-type three-level system where the probe field Ω_p for the transition of states |1⟩ and |3⟩ is a Gaussian beam. The coupling field between |3⟩ and |2⟩ is composed by one LG beam Ω_c1 and one Gaussian beam Ω_c2. Γ_nm denotes the spontaneous decay rates from |n⟩ to |m⟩.

Considering a frozen atomic gas the time evolution of the systematic density-matrix elements can be described by (ℏ = 1) [40].

$\begin{array}{cc}\hfill {\dot{\rho }}_{11}& ={\mathrm{\Gamma }}_{31}{\rho }_{33}+{\mathrm{\Gamma }}_{21}{\rho }_{22}-i{\mathrm{\Omega }}_p\left({\rho }_{31}-{\rho }_{13}\right),\hfill \\ \hfill {\dot{\rho }}_{33}& =-\left({\mathrm{\Gamma }}_{31}+{\mathrm{\Gamma }}_{32}\right){\rho }_{33}-i{\mathrm{\Omega }}_p\left({\rho }_{13}-{\rho }_{31}\right)-i{\mathrm{\Omega }}_c\left({\rho }_{23}-{\rho }_{32}\right),\hfill \\ \hfill {\dot{\rho }}_{12}& =-{\gamma }_{12}{\rho }_{12}-i{\mathrm{\Omega }}_p{\rho }_{32}+i{\mathrm{\Omega }}_c{\rho }_{13},\hfill \\ \hfill {\dot{\rho }}_{13}& =-{\gamma }_{13}{\rho }_{13}-i{\mathrm{\Omega }}_p\left({\rho }_{33}-{\rho }_{11}\right)+i{\mathrm{\Omega }}_c{\rho }_{12},\hfill \\ \hfill {\dot{\rho }}_{23}& =-{\gamma }_{23}{\rho }_{23}+i{\mathrm{\Omega }}_p{\rho }_{21}-i{\mathrm{\Omega }}_c\left({\rho }_{33}-{\rho }_{22}\right),\hfill \end{array}(3)$

where ${\rho }_{nm}={\rho }_{mn}^{*}$ and ${\sum }_{n=1}^3{\rho }_{nn}=1$ mean the conservation. The population on state |2⟩ is solved by ρ₂₂ = 1 − ρ₁₁ − ρ₃₃. In deriving Eq. 3 we have defined

${\mathrm{\Omega }}_c={\mathrm{\Omega }}_{c1}+{\mathrm{\Omega }}_{c2},(4)$

representing the superposition of two coupling fields. Γ_nm denotes the spontaneous decay from $\left|n\right.⟩$ to $\left|m\right.⟩$ and γ_nm is defined as

${\gamma }_{12}={\mathrm{\Gamma }}_{21}/2,{\gamma }_{13}=\left({\mathrm{\Gamma }}_{31}+{\mathrm{\Gamma }}_{32}\right)/2,{\gamma }_{23}=\left({\mathrm{\Gamma }}_{32}+{\mathrm{\Gamma }}_{31}+{\mathrm{\Gamma }}_{21}\right)/2.(5)$

The steady solutions of Eq. 3 can be obtained by assuming ${\dot{\rho }}_{nm}={\dot{\rho }}_{nn}=0$. Due to the presence of decay Γ₂₁, it is intuitive that ρ₂₂ decreases with Γ₂₁. Luckily, accounting for the condition of Γ₂₁ ≪ Γ₃₁₍₃₂₎ that makes the effect of Γ₂₁ negligible [23, 39], then ρ₂₂ takes a simple form of

${\rho }_{22}\left(r,\theta \right)=\frac{1}{1+I_c\left(r,\theta \right)/I_p\left(r\right)},(6)$

where Γ₃₁ = Γ₃₂, Γ₂₁ = 0 are used. $I_c={\left|{\mathrm{\Omega }}_{c1}+{\mathrm{\Omega }}_{c2}\right|}^2$ and $I_p={\left|{\mathrm{\Omega }}_p\right|}^2$ stand for the laser intensities. Note that ρ₂₂ (r, θ) reveals a position-dependent feature due to the use of several structured fields. From Eq. 6, it is apparent that the condition I_c(r_loc, θ) ≪ I_p(r_loc) will cause ρ₂₂ → 1, which means a perfect atomic confinement can be achieved at arbitrary position r_loc in our scheme.

3 Off-Axis Localization

According to Eq. 4 together with the definitions in Eqs 1, 2, the intensity of the hybrid coupling field can be written as

$I_c\left(r,\theta \right)=|{\mathrm{\Omega }}_{c1}+{\mathrm{\Omega }}_{c2}{|}^2=\frac{{\mathrm{\Omega }}_{\mathit{c10}}}{W^2}{e}^{-\frac{2r^2}{W^2}}{\left|r+{\kappa }_{c}W{e}^{-i\left(\theta +{\theta }_{c1}\right)}\right|}^2,(7)$

where the peak ratio is κ_c = Ω_c20/Ω_c10, which can be tuned by Ω_c20 if Ω_c10 is fixed. Note that this hybrid coupling field is composed by one LG beam and one Gaussian beam, which resonantly couple states |2⟩ and |3⟩ at the same time. Finally we can arrive at an analytical solution to the equation I_c(r, θ) = 0, that is, the perfect condition of localization can be reached at

$\left(r_{\mathit{loc}},{\theta }_{\mathit{loc}}\right)=\left({\kappa }_{c}W,\pi -{\theta }_{c1}\right),(8)$

where the population ρ₂₂ attains 1.0 in principle. That means atoms can be precisely placed at any desired position (r_loc, θ_loc) with a very high probability. While in fact, owing to the influence from intrinsic noises in the experimental setup, the observed localization resolution is quite limited. In Section 5 we will discuss the fluctuation of laser intensities, the steady time as well as the noise from atomic thermal motion, in order to present a practical estimation for the experimental observation. Moreover, we have to point out that benefiting from the interference between two hybrid coupling fields Ω_c1 and Ω_c2 [41], the localization position (r_loc, θ_loc) can be widely adjusted by the beam parameters, which is not restricted merely at the beam core as in most previous works [31, 32].

As illustrated in Figure 2A, we show that atoms denoted as the steady population ρ₂₂ on state |2⟩, can be confined in any spatial position (r_loc, θ_loc) by changing the parameters (κ_c, θ_c1). For example when (κ_c, θ_c1) = (0.1, π), (0.5, π), (0.5, π/4), (0.5, − π/4), Figure 2A explicitly shows the off-axis atom localization at different positions as labeled by A ∼D. Figures 2B1–B4 amplify the distribution of atoms at different localized places. It is apparent that the spatial resolution of atom localization remains unchanged for different κ_c and θ_c1. Therefore, thanks to the zero-intensity point (I_c(r, θ) = 0) created by the interference between two light beams Ω_c10 and Ω_c20, our scheme can realize an effective off-axis localization at arbitrary position in a 2D space.

FIGURE 2

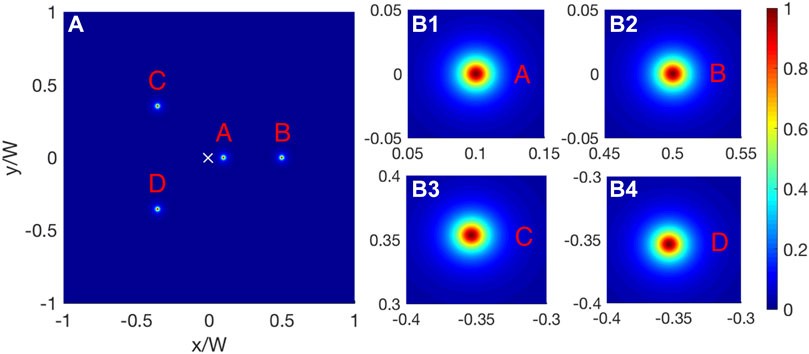
FIGURE 2. Off-axis atom localization. (A) Off-axis localized positions A, B, C, and D with respect to (κ_c, θ_c1) = (0.1, π), (0.5, π), (0.5, π/4), (0.5, − π/4). The white cross denotes the center of light beams. (B1–B4) show the amplified images for the localized atomic positions, which have an off-axis feature. Here, Ω_p0/Ω_c10 = 0.01.

4 Ultraprecise Localization

The quality of localization also depends on a high spatial resolution, which is characterized by the full width at half maximum (FWHM) of the steady distribution ρ₂₂ (r, θ). A narrower linewidth indicates that the position of atoms can be well-resolved within a smaller range. By replacing the profiles of light fields (Eqs 1, 2) the expression of ρ₂₂(r) takes an explicitly Lorentz form

${\rho }_{22}\left(r\right)=\frac{1}{1+\frac{{\left(r-{\kappa }_{c}W\right)}^2}{{\kappa }_p^2{W}^2}},(9)$

where we have omitted the azimuth angle by letting θ = π − θ_c1 and paid attention to the variation of ρ₂₂(r) along the radial direction. We treat the FWHM of function ρ₂₂(r) as a measurement to localization, which can also be analytically solved,

$a_r=2{\kappa }_{p}W.(10)$

In Figure 3, we plot the steady distribution ρ₂₂(r) vs. r for different peak ratios κ_p. Clearly a weaker probe field leads to the atomic population more confined in the vicinity of the localization point r = r_loc = 0.5W, promising for a higher resolution localization. For example, we find that a_r = 0.02W when κ_p = 0.01, but this value is decreased by one order of magnitude, which is a_r = 0.004W as κ_p reduces to 0.002. From Eq. 10, it is intuitive that a_r → 0 if κ_p ≪ 1, enabling an ultraprecise localization under a sufficiently weak probe field. However in a realistic system, the fact that the time for a steady state becomes much longer in the weak probe limit, results in the atomic motion non-negligible. We will discuss this point in Section 5.2.

FIGURE 3

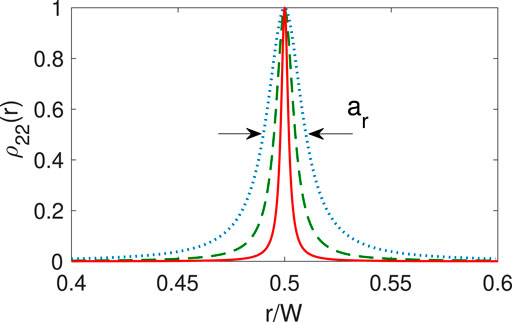
FIGURE 3. Steady population distribution ρ₂₂(r) along the radial direction r for κ_p = Ω_p0/Ω_c10 = 0.01 (blue-dotted), 0.005 (green-dashed), and 0.002 (red-solid). a_r is the FWHM, which characterizes the spatial resolution of localization. Here, we use κ_c = 0.5.

5 Feasibility Discussion

The numbers presented in this work are considered from ⁸⁷Rb where the lifetime of state |3⟩( = |5P_1/2, F = 2⟩) is 27.7 ns [42], leading to the decay rates Γ₃₁ = Γ₃₂ = 2π × 5.75 MHz, and the lifetime of |2⟩( = |5S_1/2, F = 2⟩) is 200 μs, leading to Γ₂₁ = 5 kHz. We assume that the co-propagating probe and coupling lasers are overlapping in space and have a same beam width W = 5 μm. As explicitly presented in section 3 and section 4, our scheme can achieve an ultraprecise off-axis atom localization due to the flexible manipulation of peak ratios κ_c and κ_p, together with the azimuth angle θ_c1. Due to the rotational invariance we ignore θ_c1 by focusing on the radial distance r. However, as for an experimental implementation these parameters are also restrained. In this section, we numerically solve the spatial resolution a_r and the peak value of ρ₂₂(r) by evolving the motional Eq. 3 under more realistic conditions coming from measurement.

5.1 Laser Intensity Noise

To obtain realistic results evaluating experimental conditions, we introduce a perturbed laser intensity by adding a random intensity noise δΩ_i (i = p, c1, c2) to the peak value Ω_i0 [43, 44]. The resulting fluctuated Rabi frequencies ${\mathrm{\Omega }}_{i0}^{\prime }$ can be written as

${\mathrm{\Omega }}_{i0}^{\prime }={\mathrm{\Omega }}_{i0}+\delta {\mathrm{\Omega }}_i.(11)$

In the calculation, we assume δΩ_i/Ω_i0 ∈ [− ξ, ξ] and pay attention to the radial population distribution ρ₂₂(r). During each measurement, the perturbation term δΩ_i can be a random number obtained from the range of [− ξ, ξ]Ω_i0. By taking account of sufficient measurements, the average result can show the realistic observation in the experimental setup. Note that a larger Rabi frequency leads to stronger laser noise since δΩ_i ∝Ω_i0.

Figure 4 illustrates the distribution of steady population ρ₂₂(r) under the influence of laser intensity noise, which is characterized by the factor ξ. By comparing Figures 4A–D it is apparent that a bigger ξ will give rise to a broadened population distribution with smaller peak values, which lowers the precision of localization. Furthermore, as for atoms localized closer to the beam core (r = 0) the intensity noise δΩ_c2 [∝Ω_c20] is smaller due to r_loc = κ_cW. Therefore by positioning atoms far from the beam core the observation will suffer from a stronger laser intensity noise, in turn yielding a lower-quality localization, see Figures 4A–D. This fact gives a limitation to our protocol that the atoms cannot be placed very far from the beam core. A rough estimation (not shown) shows that the average peak value of ρ₂₂(r) will be smaller than 0.2 if the radial localization distance r_loc is larger than 10 μm. In the experiment, a better control for the laser intensity noise can improve the scheme performance.

FIGURE 4

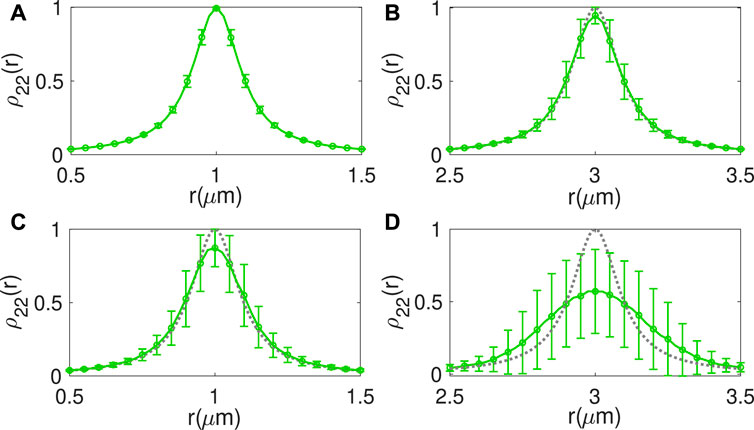
FIGURE 4. Radial population distribution ρ₂₂(r) under different intensity noises, which are given by (A,B) ξ = 1.0% and (C,D) ξ = 5.0% at different positions. We take 500 measurements for each point denoted by the error bar and the average result is shown by the green solid line. For comparison the black-dotted line indicates the result without any intensity noise, that is, ξ = 0. Here, Ω_c20/2π = (30, 90) MHz, respectively for (A,C) and (B,D), corresponding to the localization positions r_loc = (1.0, 3.0) μm. Other parameters are Ω_p0/2π = 3 MHz, Ω_c10/2π = 150 MHz, and W = 5 μm.

5.2 Time Needed for a Steady State

From section 4, we have known that ultraprecise localization with a_r → 0 in principle relies on a sufficiently small κ_p, that is, Ω_p0 ≪Ω_c10. This condition leads to the time T_s for reaching steady localization much longer. Because T_s is inversely proportional to the exact laser Rabi frequencies. For a longer T_s, the atomic thermal motion does play roles and the frozen-gas approximation fails. A discussion for the effect of atomic thermal motion can be seen in section 5.3. An efficient localization reports that T_s is so short to make the atomic movement during the steady time negligible. In the calculation, we consider atoms under the temperature T = 1 μK [14], with a most probable velocity $v_p=\sqrt{2k_{B}T/M}\approx 1.4$ cm/s, where k_B is the Boltzmann constant and M is the atomic mass. We introduce a new constraint to the resolution factor a_r

$v_p{T}_s^{\mathit{max}}\le a_r/10,(12)$

where the real time T_s for a steady state should be smaller than $T_s^{\max }$ so as to make the atomic motion negligible during the measurement.

Figure 5 exhibits the steady time T_s as a function of the localization distance r_loc for different peak probe Rabi frequencies Ω_p0. Here, T_s is obtained by numerically evolving the master Eq. 3, considering all spontaneous decays. From Figures 5A–D, as decreasing Ω_p0 we find that the steady time T_s (blue-solid) increases significantly; although the position of atoms can be well-resolved with a better spatial resolution (a_r becomes smaller) at the same time. According to the constraint (12), the maximal steady time $T_s^{\max }$ permitted for localization is labeled by the red-dashed line in the figure. When $T_s<T_s^{\max }$ atoms can obtain a robust localization. Obviously, in Figures 5A,B where the spatial resolution a_r is relatively large, atoms can be well localized within a wider radial range r_loc < 5.3 μm and r_loc < 3.7 μm. Insets explicitly show the area of off-axis localization, which is denoted as a gray disk. In fact via an appropriate adjustment of κ_c and θ_c1, atoms can be confined at arbitrary position inside the gray disk.

FIGURE 5

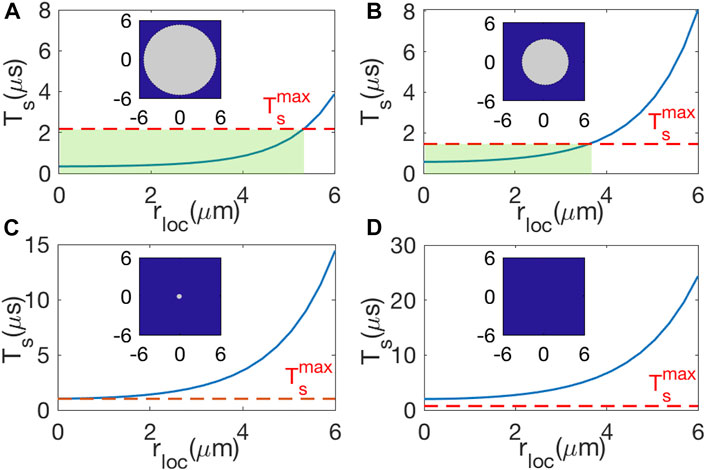
FIGURE 5. Steady time T_s vs. the radius distance r_loc under (A) Ω_p0/2π = 4.5 MHz and a_r = 300 nm, (B) Ω_p0/2π = 3.0 MHz and a_r = 200 nm, (C) Ω_p0/2π = 2.1 MHz and a_r = 141 nm, and (D) Ω_p0/2π = 1.5 MHz and a_r = 100 nm. The red-dashed line denotes the maximal T_s permitted for an efficient localization. The shaded-green region stands for the radial range where atoms can be localized. Insets: effective off-axis localization is enabled within the gray disk. Here, Ω_c10/2π = 150 MHz, W = 5 μm, Ω_c20 = r_locΩ_c10/W, T = 1 μK, and Γ₂₁ = 5 kHz.

Whereas, when Ω_p0 is reduced to 2π × 2.1 MHz (Figure 5C), the reduction of a_r causes $T_s^{\max }\le T_s$ persistently. In this case only atom positioned at the beam core can be accurately confined so the protocol of off-axis localization fails. Furthermore, if a_r < 141 nm, for example, a_r = 100 nm as in Figure 5D, the steady time T_s is maintained larger than the required $T_s^{\max }$, calculated by Eq. 12 so no atoms could be localized. Because during such a longer steady time T_s most atoms have been moved away from the localization spot caused by their thermal motions, leading to a poor resolution (also see the discussion in section 5.3). Therefore, based on our analysis, we treat a_r = 141 nm as the best spatial resolution yet atoms can only be localized at the beam core. Effective off-axis localization needs to be at the expense of the spatial resolution. For example, a resolution of a_r = 200 nm (300 nm) can be obtained within a localized radius of r_loc < 3.7 μm (5.3 μm), see the insets of Figures 5A,B for a more visible representation. In addition, since the steady time is inversely proportional to the exact Rabi frequencies the limitation for a best off-axis localization can further be overcome by a stronger coupling laser. For example, when Ω_c10/2π = 300 MHz and Ω_p0/2π = 2.7 MHz the best spatial resolution of our protocol can be reduced to 91 nm if atoms are localized in the beam core (not shown).

5.3 Noise From Atomic Thermal Motion

In a real experimental setup due to atomic thermal motion, the laser intensity ‘seen’ by atoms would have a strong perturbation, which intuitively brings a noise on detecting the steady atomic population. Here, we consider atoms move randomly in space whose velocities satisfy a two-dimensional Maxwell–Boltzmann distribution [45].

$f\left(v_x,v_y\right)=\frac{1}{\pi v_p^2}{e}^{-\left(v_x^2+v_y^2\right)/v_p^2}.(13)$

Here, v_p is the most probable velocity defined by $v_p=\sqrt{2k_{B}T/M}$. Other interatomic collisions are ignored. During the jth measurement we assume a simple uniform motion of atoms by letting

$\left(x_j,y_j\right)\to \left(x_j+v_x{T}_{\mathit{meas}},y_j+v_y{T}_{\mathit{meas}}\right),(14)$

where (v_x, v_y) are obtained stochastically from the velocity function f (v_x, v_y) and T_meas is the time for single measurement. By inserting Eq. 14 into Eqs 1, 2 atoms can feel a fluctuated Rabi frequency Ω_i(t) (i = p, c1, c2) for each measurement. The final results are based on an average of 500 times random samplings of the velocity (v_x, v_y).

In Figure 6, we show the calculated population distribution ρ₂₂(r) under sufficient measurements in the x–y frame. Clearly, from Figures 6A1–A4 due to a larger probable velocity of atoms caused by the growing temperature, the peak value ${\rho }_{22}^{\mathit{peak}}$ has an explicit decrease together with a lower spatial resolution a_r. For example, when T = 1 μK, a_r = 206 nm which is close to the value at T = 0. Because the average distance of atoms during each measurement (T_meas = 1 μs) is only v_pT_meas ≈ 14 nm, which is much smaller than a_r. However, as for a higher temperature the movement of atoms during each measurement can cause a bigger effect making the precision of atom localization worse. See the case of T = 10 μK in Figure 6A4, we observe that ${\rho }_{22}^{\mathit{peak}}=0.8$ and a_r = 247 nm. For comparison in Figures 6B1–B4 we also study the case of a longer measurement time (T_meas = 5 μs) where atoms can move farther, leading to a very poor spatial resolution at a finite temperature. We numerically show that at T = 10 μK the distribution of atomic population ρ₂₂(r) has become slightly deformed with its peak value (spatial resolution) as low as ${\rho }_{22}^{\mathit{peak}}=0.22$(a_r = 687 nm). That fact means such a long-time measurement has made most atoms away from the localization spot via their thermal movements. Therefore a faster measurement accompanied by a lower environment temperature can facilitate high-quality atom localization.

FIGURE 6

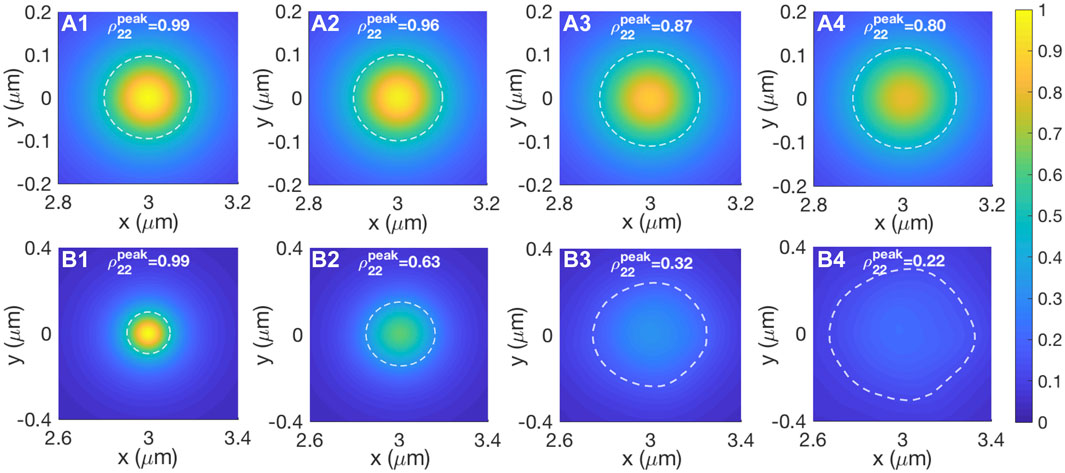
FIGURE 6. (A1–A4) 2D population distribution of ρ₂₂(r) under different temperatures T = (0, 1, 5, 10)μK. The peak value of ρ₂₂(r) is given in the picture and the diameter of white-dashed rings stands for the spatial resolution a_r, which is a_r = (200, 206, 222, 247) nm, respectively. Here, we assume the measurement time is T_meas = 1 μs. Analogous to (A1–A4), (B1–B4) show the case of T_meas = 5 μs and the calculated resolution is a_r = (200, 308, 530, 687) nm. Every point is obtained by averaging over 500 measurements.

6 Conclusion

To conclude, our scheme presents a novel 2D atom localization, having both ultraprecise and off-axis features. Differing from the previous works using a single LG field we adopt a LG beam together with a Gaussian beam as the hybrid coupling field. The previous contributions can only localize atom in the beam core where the intensity of coupling field is zero. While our protocol shows that atoms can be localized at arbitrary position due to the effect of quantum interference between these two coupling beams that leads to a zero-intensity spot in space. Our numerical simulation confirms that with an appropriate adjustment for the peak ratios of laser Rabi frequencies a wider off-axis localization range and higher quality spatial resolution can be achieved at the same time. Under experimentally feasible parameters an estimation for the implementation of realistic off-axis atom localization is predicted, promising for a resolution of $\sim 200$ nm and a localized radius of a few μm. In addition, we also discuss the weakness of our scheme when some intrinsic quantum noises from imperfect measurement, including laser intensity noise, limited steady time, and atomic thermal motion, are considered. Our approach may provide unique application to atomic lithography with more flexibility and better resolution [46]. An extension to the 3D off-axis atom localization is possible by implementing a spatial modulation to the probe detuning which is our next-step work [32].

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

The idea was first conceived by NJ. NJ was responsible for the physical modeling, the numerical calculations, and writing the original draft under the supervision of JQ. JQ contributed to review and editing. JQ verified results of the theoretical calculation. X-DZ contributed to editing the draft. X-DZ and W-RQ contributed to the discussion of the results.

Funding

This work was supported by the National Natural Science Foundation of China under Grant Nos 12104308, 12174106, 11474094, 11104076, 12104135, and 11604086; by the Science and Technology Commission of Shanghai Municipality under Grant No. 18ZR1412800.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Babiker M, Andrews DL, Lembessis VE. Atoms in Complex Twisted Light. J Opt (2018) 21:013001. doi:10.1088/2040-8986/aaed14

CrossRef Full Text | Google Scholar

2. Grier DG. A Revolution in Optical Manipulation. Nature (2003) 424:810–6. doi:10.1038/nature01935

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Padgett M, Bowman R. Tweezers with a Twist. Nat Photon (2011) 5:343–8. doi:10.1038/nphoton.2011.81

CrossRef Full Text | Google Scholar

4. Ran L-L, Guo Z-Y, Qu S-L. Rotational Motions of Optically Trapped Microscopic Particles by a Vortex Femtosecond Laser. Chin Phys. B (2012) 21:104206. doi:10.1088/1674-1056/21/10/104206

CrossRef Full Text | Google Scholar

5. Dholakia K, Simpson NB, Padgett MJ, Allen L. Second-Harmonic Generation and the Orbital Angular Momentum of Light. Phys Rev A (1996) 54:R3742–R3745. doi:10.1103/PhysRevA.54.R3742

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Kong F, Zhang C, Bouchard F, Li Z, Brown GG, Ko DH, et al. Controlling the Orbital Angular Momentum of High Harmonic Vortices. Nat Commun (2017) 8:14970. doi:10.1038/ncomms14970

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Gauthier D, Ribič PR, Adhikary G, Camper A, Chappuis C, Cucini R, et al. Tunable Orbital Angular Momentum in High-Harmonic Generation. Nat Commun (2017) 8:14971. doi:10.1038/ncomms14971

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Vicidomini G, Bianchini P, Diaspro A. Sted Super-Resolved Microscopy. Nat Methods (2018) 15:173–82. doi:10.1038/nmeth.4593

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Schermelleh L, Ferrand A, Huser T, Eggeling C, Sauer M, Biehlmaier O, et al. Super-Resolution Microscopy Demystified. Nat Cell Biol (2019) 21:72–84. doi:10.1038/s41556-018-0251-8

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Masullo LA, Steiner F, Zähringer J, Lopez LF, Bohlen J, Richter L, et al. Pulsed Interleaved Minflux. Nano Lett (2021) 21:840–6. doi:10.1021/acs.nanolett.0c04600

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Balzarotti F, Eilers Y, Gwosch KC, Gynnå AH, Westphal V, Stefani FD, et al. Nanometer Resolution Imaging and Tracking of Fluorescent Molecules with Minimal Photon Fluxes. Science (2017) 355:606–12. doi:10.1126/science.aak9913

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Proite NA, Simmons ZJ, Yavuz DD. Observation of Atomic Localization Using Electromagnetically Induced Transparency. Phys Rev A (2011) 83:041803. doi:10.1103/PhysRevA.83.041803

CrossRef Full Text | Google Scholar

13. Miles JA, Simmons ZJ, Yavuz DD. Subwavelength Localization of Atomic Excitation Using Electromagnetically Induced Transparency. Phys Rev X (2013) 3:031014. doi:10.1103/PhysRevX.3.031014

CrossRef Full Text | Google Scholar

14. Miles JA, Das D, Simmons ZJ, Yavuz DD. Localization of Atomic Excitation Beyond the Diffraction Limit Using Electromagnetically Induced Transparency. Phys Rev A (2015) 92:033838. doi:10.1103/PhysRevA.92.033838

CrossRef Full Text | Google Scholar

15. Qamar S, Zhu S-Y, Zubairy MS. Precision Localization of Single Atom Using Autler-Townes Microscopy. Opt Commun (2000) 176:409–16. doi:10.1016/S0030-4018(00)00535-6

CrossRef Full Text | Google Scholar

16. Ghafoor F, Qamar S, Zubairy MS. Atom Localization via Phase and Amplitude Control of the Driving Field. Phys Rev A (2002) 65:043819. doi:10.1103/PhysRevA.65.043819

CrossRef Full Text | Google Scholar

17. Ghafoor F. Subwavelength Atom Localization via Quantum Coherence in a Three-Level Atomic System. Phys Rev A (2011) 84:063849. doi:10.1103/PhysRevA.84.063849

CrossRef Full Text | Google Scholar

18. Wan R-G, Zhang T-Y. Two-Dimensional Sub-Half-Wavelength Atom Localization via Controlled Spontaneous Emission. Opt Express (2011) 19:25823–32. doi:10.1364/OE.19.025823

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Yavuz DD, Proite NA. Nanoscale Resolution Fluorescence Microscopy Using Electromagnetically Induced Transparency. Phys Rev A (2007) 76:041802. doi:10.1103/PhysRevA.76.041802

CrossRef Full Text | Google Scholar

20. Paspalakis E, Knight PL. Localizing an Atom via Quantum Interference. Phys Rev A (2001) 63:065802. doi:10.1103/physreva.63.065802

CrossRef Full Text | Google Scholar

21. Kapale KT, Agarwal GS. Subwavelength Atom Localization via Coherent Population Trapping. In: Frontiers in Optics (Optica Publishing Group) (2006). p. FThO5. doi:10.1364/FIO.2006.FThO5

CrossRef Full Text | Google Scholar

22. Ivanov V, Rozhdestvensky Y. Two-Dimensional Atom Localization in a Four-Level Tripod System in Laser Fields. Phys Rev A (2010) 81:033809. doi:10.1103/PhysRevA.81.033809

CrossRef Full Text | Google Scholar

23. Ivanov VS, Rozhdestvensky YV, Suominen K-A. Three-Dimensional Atom Localization by Laser Fields in a Four-Level Tripod System. Phys Rev A (2014) 90:063802. doi:10.1103/PhysRevA.90.063802

CrossRef Full Text | Google Scholar

24. Wang Z, Yu B. High-Precision Two-Dimensional Atom Localization via Quantum Interference in a Tripod-Type System. Laser Phys Lett (2014) 11:035201. doi:10.1088/1612-2011/11/3/035201

CrossRef Full Text | Google Scholar

25. Zhu Z, Yang W-X, Chen A-X, Liu S, Lee R-K. Dressed-State Analysis of Efficient Three-Dimensional Atom Localization in a Ladder-Type Three-Level Atomic System. Laser Phys (2016) 26:075203. doi:10.1088/1054-660x/26/7/075203

CrossRef Full Text | Google Scholar

26. Sahrai M, Tajalli H, Kapale KT, Zubairy MS. Subwavelength Atom Localization via Amplitude and Phase Control of the Absorption Spectrum. Phys Rev A (2005) 72:013820. doi:10.1103/PhysRevA.72.013820

CrossRef Full Text | Google Scholar

27. Sahrai M, Mahmoudi M, Kheradmand R. Atom Localization of a Two-Level Pump-Probe System via the Absorption Spectrum. Laser Phys (2007) 17:40–4. doi:10.1134/S1054660X07010082

CrossRef Full Text | Google Scholar

28. Zhang D, Yu R, Sun Z, Ding C, Zubairy MS. Efficient Three-Dimensional Atom Localization Using Probe Absorption in a Diamond-Configuration Atomic System. J Phys B: Mol Opt Phys (2019) 52:035502. doi:10.1088/1361-6455/aaf5ec

CrossRef Full Text | Google Scholar

29. Qamar S, Mehmood A, Qamar S. Subwavelength Atom Localization via Coherent Manipulation of the Raman Gain Process. Phys Rev A (2009) 79:033848. doi:10.1103/PhysRevA.79.033848

CrossRef Full Text | Google Scholar

30. Wan R-G, Zhang T-Y, Kou J. Two-Dimensional Sub-Half-Wavelength Atom Localization via Phase Control of Absorption and Gain. Phys Rev A (2013) 87:043816. doi:10.1103/PhysRevA.87.043816

CrossRef Full Text | Google Scholar

31. Kazemi SH, Veisi M, Mahmoudi M. Atom Localization Using Laguerre-Gaussian Beams. J Opt (2019) 21:025401. doi:10.1088/2040-8986/aafe61

CrossRef Full Text | Google Scholar

32. Jia N, Qian J, Kirova T, Juzeliūnas G, Reza Hamedi H. Ultraprecise Rydberg Atomic Localization Using Optical Vortices. Opt Express (2020) 28:36936–52. doi:10.1364/OE.411130

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Ding C, Li J, Yang X, Zhang D, Xiong H. Proposal for Efficient Two-Dimensional Atom Localization Using Probe Absorption in a Microwave-Driven Four-Level Atomic System. Phys Rev A (2011) 84:043840. doi:10.1103/PhysRevA.84.043840

CrossRef Full Text | Google Scholar

34. Hamedi HR, Juzeliūnas G. Phase-Sensitive Atom Localization for Closed-Loop Quantum Systems. Phys Rev A (2016) 94:013842. doi:10.1103/PhysRevA.94.013842

CrossRef Full Text | Google Scholar

35. Rahmatullah U, Qamar S. Two-Dimensional Atom Localization via Probe-Absorption Spectrum. Phys Rev A (2013) 88:013846. doi:10.1103/PhysRevA.88.013846

CrossRef Full Text | Google Scholar

36. Hong Y, Wang Z, Yu B. High-Precision Three-Dimensional Atom Localization via Kerr Nonlinearity. J Opt Soc Am B (2019) 36:746–51. doi:10.1364/JOSAB.36.000746

CrossRef Full Text | Google Scholar

37. Franke-Arnold S, Leach J, Padgett MJ, Lembessis VE, Ellinas D, Wright AJ, et al. Optical Ferris Wheel for Ultracold Atoms. Opt Express (2007) 15:8619–25. doi:10.1364/OE.15.008619

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Hamedi HR, Paspalakis E, Žlabys G, Juzeliūnas G, Ruseckas J. Complete Energy Conversion Between Light Beams Carrying Orbital Angular Momentum Using Coherent Population Trapping for a Coherently Driven Double- Λ Atom-Light-Coupling Scheme. Phys Rev A (2019) 100:023811. doi:10.1103/PhysRevA.100.023811

CrossRef Full Text | Google Scholar

39. Wang Z, Yu B. Efficient Three-Dimensional Atom Localization via Probe Absorption. J Opt Soc Am B (2015) 32:1281–6. doi:10.1364/JOSAB.32.001281

CrossRef Full Text | Google Scholar

40. Paspalakis E, Terzis AF, Knight PL. Quantum Interference Induced Sub-Wavelength Atomic Localization. J Mod Opt (2005) 52:1685–94. doi:10.1080/09500340500072489

CrossRef Full Text | Google Scholar

41. Qiu J, Wang Z, Yu B. Generation of New Structured Beams via Spatially Dependent Transparency. Quan Inf Process (2019) 18:160. doi:10.1007/s11128-019-2278-6

CrossRef Full Text | Google Scholar

42. Volz U, Schmoranzer H. Precision Lifetime Measurements on Alkali Atoms and on Helium by Beam-Gas-Laser Spectroscopy. Phys Scr (1996) T65:48–56. doi:10.1088/0031-8949/1996/t65/007

CrossRef Full Text | Google Scholar

43. Dridi G, Guérin S, Hakobyan V, Jauslin HR, Eleuch H. Ultrafast Stimulated Raman Parallel Adiabatic Passage by Shaped Pulses. Phys Rev A (2009) 80:043408. doi:10.1103/PhysRevA.80.043408

CrossRef Full Text | Google Scholar

44. Kang Y-H, Chen Y-H, Shi Z-C, Huang B-H, Song J, Xia Y. Nonadiabatic Holonomic Quantum Computation Using Rydberg Blockade. Phys Rev A (2018) 97:042336. doi:10.1103/PhysRevA.97.042336

CrossRef Full Text | Google Scholar

45. Huo X, Chen JF, Qian J, Zhang W. Interaction-Enhanced Transmission Imaging with Rydberg Atoms. Phys Rev A (2022) 105:012817. doi:10.1103/PhysRevA.105.012817

CrossRef Full Text | Google Scholar

46. Johnson KS, Thywissen JH, Dekker NH, Berggren KK, Chu AP, Younkin R, et al. Localization of Metastable Atom Beams with Optical Standing Waves: Nanolithography at the Heisenberg Limit. Science (1998) 280:1583–6. doi:10.1126/science.280.5369.1583

PubMed Abstract | CrossRef Full Text | Google Scholar