Stochastic Methods and Complexity Science in Climate Research and Modeling

Franzke, Christian L. E.; Blender, Richard; O’Kane, Terence J.; Lembo, Valerio

doi:10.3389/fphy.2022.931596

REVIEW article

Front. Phys., 06 June 2022

Sec. Interdisciplinary Physics

Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.931596

Stochastic Methods and Complexity Science in Climate Research and Modeling

Christian L. E. Franzke^1,2*

Richard Blender³

Terence J. O’Kane⁴

Valerio Lembo⁵

¹Center for Climate Physics, Institute for Basic Science, Busan, South Korea
²Pusan National University, Busan, South Korea
³Meteorological Institute, University of Hamburg, Hamburg, Germany
⁴CSIRO Oceans and Atmosphere, Hobart, TAS, Australia
⁵Consiglio Nazionale delle Ricerche, Istituto di Scienze dell’Atmosfera e del Clima (CNR-ISAC), Bologna, Italy

The 2021 Nobel prize for physics was awarded to two climate scientists, Syukuro Manabe and Klaus Hasselmann, and the physicist Giorgio Parisi. While at first sight the work of Parisi seems not to be related to climate science, this is not the case. Giorgio Parisi developed and contributed to many complexity science methods which are nowadays widely used in climate science. Giorgi Parisi also was involved in the development of the “stochastic resonance” idea to explain paleoclimate variability, while Klaus Hasselmann developed stochastic climate models. Here we review and discuss their work from a complex and stochastic systems perspective in order to highlight those aspects of their work. For instance, fractal and multi-fractal analysis of climate data is now widely used and many weather prediction and climate models contain stochastic parameterizations, topics Parisi and Hasselmann have pioneered. Furthermore, Manabe’s work was key to understanding the effects of anthropogenic climate change by the development of key advances in the parameterization of convection and radiative forcing in climate models. We discuss also how their inventive research has shaped current climate research and is still influencing climate modeling and future research directions.

1 Introduction

In 2021 the Nobel prize for physics was awarded to Klaus Hasselmann, Syukuro Manabe and Giorgio Parisi for major contributions to complexity science and the understanding and modelling of the climate system [1]. Syukuro Manabe and Klaus Hasselmann have pioneered “the physical modelling of Earth’s climate, quantifying variability and reliably predicting global warming”, while Giorgio Parisi made breakthrough advances in the “discovery of the interplay of disorder and fluctuations in physical systems from atomic to planetary scales” [1]. This was the first Nobel prize for physics awarded to climate scientists. In 1995, Paul Crutzen, Mario Molina, and Sherwood Rowland got awarded the Nobel Prize in Chemistry “for their work in atmospheric chemistry, particularly concerning the formation and decomposition of ozone” [2]; and in 2007 the Intergovernmental Panel on Climate Change was awarded the Nobel Peace prize “for their efforts to build up and disseminate greater knowledge about man-made climate change, and to lay the foundations for the measures that are needed to counteract such change” [3].

The continuing relevance of Syukuro Manabe’s and Klaus Hasselmann’s work can be seen in the latest IPCC reports [4,5], which rely heavily on coupled climate model simulations. Their work was essential in our ability to simulate potential and plausible future evolutions of the coupled Earth system and to unequivocally demonstrate humanities responsibility for global climate change.

The medalists made groundbreaking contributions to climate science, stochastic methods and complexity science for a better understanding of the complex climate system. [6] performed a systematic publication review of the three Nobel laureates; discussing their publication behavior. She also lists their ten most cited papers, which is an indication for their most important work, and they will be discussed in more detail below.

The 2021 Nobel prize is a testimony of the power and wide applicability of physical principles for better understanding and predicting our precious world. We will discuss and review their scientific work from this perspective. We will show how their work has contributed to modern stochastic and complexity science methods and climate modelling, now enabling us to better understand the Earth system and make skillful predictions. They performed this work decades ago, but their work still shapes current research and we believe that it will still be relevant for future research. For this reason a synthesis of these aspects of their work is necessary and useful.

2 The Development of Stochastic Climate Models and Random Wave Field Methods

Klaus Hasselmann pioneered multiple areas of climate science; among others he developed optimal finger-printing [7,8] which enables the optimal identification of climate change signals, nonlinear ocean wave dynamics [9,10], Integrated Assessment Models [11], and stochastic climate models [12].

An important topic in climate modelling is the use of stochastic models to represent model error and model uncertainty [13,14]. Klaus Hasselmann’s paper on stochastic climate models [12] is a modern classic and started a new field of climate science and improved our understanding of the origin of climate variability. Hasselmann was motivated to provide an explanation for the observed spectra of climate variability on long time scales, from decadal-scale variability to ice ages and beyond. He observed that these spectra reveal “a continuous variance distribution encompassing all resolvable frequencies, with higher levels at lower frequencies” [12]. This is already a link to fractal methods [15], and the work by Giorgio Parisi, since it has been shown that many climate time series are scaling, which is an imprint of fractals [15,16]. Fractal methods is an area to which Giorgio Parisi also made contributions (e.g., [17]), and which is nowadays widely applied in climate research (e.g., [15,16]).

Stochastic models of climate variability are based on the idea that climate can be decomposed into fast fluctuations, i.e., weather disturbances, and slow variations, i.e., sea-ice or oceanic variations. The fast weather disturbances then produce an integral response of the slow climate variables. Here the fast weather disturbances are represented by a stochastic process. The usefulness of a stochastic process for numerically representing a physically deterministic process can be intuitively understood as follows: from a numerical point of view, the slow variables can be modeled with a much larger time step than the fast variables; the fastest process in a numerical model determines the time step size. While both, slow and fast, processes are deterministic, the fast process decorrelates quickly on the time scale of the slow process. Due to this decorrelation, the fast process can effectively be represented by a stochastic process. On the long time scale the exact physical process representation of the fast process becomes unnecessary. A schematic of this idea is given in Figure 1.

FIGURE 1

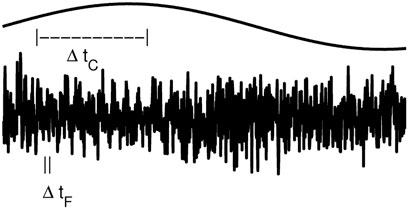
FIGURE 1. Schematic illustration of the underlying idea of stochastic climate modeling. The slow climate model can numerically be modelled with a time step Δt_C (top line), while the fast fluctuation needs a much smaller time step Δt_F (bottom line). While both processes are deterministic, the fast process decorrelates on the slow time scale Δt_C and, thus, can be represented by a stochastic process in an effective climate model which only simulates the slow climate mode.

Hasselmann [12] also argued that the evolution of the corresponding probability density distribution is described by a Fokker-Planck equation [14,18,19]. In the Fokker-Planck equation the stochastic terms appear as diffusion terms. The stochastic term, which has the form of a Wiener process or Brownian motion [14,19–21] would lead to unlimited growth without negative feedbacks or damping. Such stabilising feedbacks lead to a bounded climate probability distribution and consistency with conservation laws, such as energy conservation [22–24]. Thus, it is important that stochastic climate models contain all important physical feedback processes of the climate system. Hasselmann’s stochastic climate model was the first model which reproduced and explained the observed continuous climate variability “without invoking internal instabilities or variable external boundary conditions” [12].

Mathematically, the basic assumption of the Hasselmann stochastic climate model is that the complete state vector z can be decomposed into a fast y and a slow x component: z = (x, y). The equations of motion can now be written as follows:

\frac{d x}{d t} = F (x, y) (1)

\frac{d y}{d t} = G (x, y), (2)

where F and G are nonlinear functions. Under the assumption of a time scale separation between x and y the following effective stochastic climate model can be written:

d x = H (x) d t + Σ (x) d W (3)

where H and Σ are nonlinear functions and W is the Wiener process [20]. Later, Andrew J. Majda (1949–2021) and collaborators developed a systematic approach of deriving stochastic climate models with good predictive skill [14,19,21,22,25–30] which is based on the mathematical theory of adiabatic elimination [20,31–38] which was developed at the same time as Hasselmann’s paper was published.

Hasselmann’s stochastic climate model then pioneered the explanation of climate variability [39–41] and sea ice variability [42]. The importance of Hasselmann’s work lies in the fact, that the stochasic climate model shows that climate as an integrated response to fast weather fluctuation is transforming the white weather noise spectrum into a red spectrum which is widely observed in nature [12].

While the original Hasselmann model is with additive noise, the more general derivation of stochastic climate models showed that the nonlinear interactions between slow and fast fluctuations create multiplicative or state-dependent noise [19,21]. Using the heat budget equation, [43] showed that the Hasselmann model can be extended to include multiplicative noise when considering higher order terms in a Taylor expansion.

Hasselmann’s seminal papers inspired a large body of work leading to stochastic processes nowadays being routinely implemented into operational models [44–48,48–59]. Also empirical approaches are common in fitting stochastic models [22,60–68]. Hence, the Hasselmann’s pioneering work on stochastic climate models is still relevant today.

Klaus Hasselmann also made important contributions to model reduction which is to this day widely used in the development of reduced order stochastic models and data analysis. In a seminal paper [69], he developed a systematic approach to identify the most dynamically important modes of dynamical systems, Principal Interaction Patterns (PIP). PIPs are able to capture the nonlinear dynamics of the full dimensional system in a reduced order subspace [70–75]. While PIPs are a very powerful method, they are computationally expensive to estimate and require the dynamical equations for their estimation. A linearization of PIPs are the Principal Oscillation Patterns (POP) developed by Hasselmann in the same paper [69]. POPs are based on the lagged covariance matrix, where the nonlinearities are represented as a Gaussian white noise forcing [69,76]. Hence, POPs can be straightforwardly estimated directly from data; no knowledge of the underlying dynamical equations are needed. POPs have subsequently been used for a better understanding of climate variability [77–81], and have been further developed into Linear Inverse Models (LIM), which are linear stochastic models where the covariance matrix of the stochastic noise is derived via the Lyapounov equation [82–88]. It has also been shown that PIP, POPs and LIMs can be related to the Koopman operator [89–91]. The Koopman operator is a infinite-dimensional linear operator whose spectral decomposition describes the behavior of nonlinear dynamical systems [91,92]. The approximation of the Koopman operator by Dynamic Mode Decomposition (DMD) [91–94] can be related to the PIP and POP decompositions [91]. This shows the deep connection of PIPs and POPs to the underlying nonlinear dynamics of the system. DMDs are now also getting more popular in climate research [92,95–97].

In earlier work, Hasselmann was one of the first to apply diagrammatic methods to examine energy transfers due to weak nonlinear interactions in random wave fields in order to quantify the surface ocean wave spectra. Hasselmann [10] considered the special case of conservative wave-wave interactions using normal mode coordinates, where the scattering theory is first presented in a Hamiltonian form and the analogy is made to quantum field theory via the interpretation of the transfer expressions in terms of collision processes between hypothetical “particles,” “antiparticles,” and “virtual particles.” A formal perturbation expansion is then applied to the physical energy and momentum transfer rates facilitating expressions for all scattering processes to only a few general interaction rules.

Moving beyond the particle interpretation, this approach was subsequently generalized to include non-conservative interactions between waves and external fields. In this framework, the transfer expressions, summarized in terms of “transfer” diagrams, may still be regarded as corresponding to collision diagrams in the particle picture [98]. Considering interactions between gravity waves and the turbulent atmospheric boundary layer, and applying a closure hypothesis in terms of assumptions of Gaussianity with respect to the cumulants and the linear wave field, Hasselmann was able to derive a complete set of more general lowest order transfer diagrams. At lowest order, these interactions (diagrams) were shown to contain both the Phillips mechanism for the scattering of surface gravity waves by turbulent currents [99–101] and the Miles mechanism of wave generation [101,102]. The combined theory was checked against experimental data by Gilchrist [104]. Hasselmann’s theory extended the Miles-Phillips theory for the directional spectrum of wind-driven surface waves by including additional wave-turbulence interactions associated with energy exchange and production.

These investigations formed the basis of the so-called resonant interaction formalism [10,105] which has proven to provide a key framework for understanding the oceanic internal gravity wave field. The assumption that the timescale for interactions is much longer than the component wave periods, i.e., weak interaction, was challenged in situations where nonlinear effects dominate, such as for interactions between internal gravity waves and turbulence [106,107]. In order to develop a statistical dynamical theory in which all scales and strengths of interactions between waves and turbulence were handled self consistently, Carnevale and Frederiksen [108] employed the prior-time fluctuation dissipation theorem (FDT)

C_{k} (t, t^{'}) \equiv R_{k} (t, t^{'}) C_{k} (t^{'}, t^{'}) (4)

to relate the two-time spectral covariance C_k(t, t′) at wavenumber k to the response function R_k (t, t′) and the prior single-time covariance C_k(t′, t′). In this way the general nonlinear field treats the larger scales as wavelike with turbulence dominating the small scales. Formally, the theory makes no distinction between waves and turbulence. The choice of FDT distinguishes the various statistical closures [109], be they for two- [110] or three-dimensional [111] turbulence or for the two-dimensional internal gravity wave turbulence problem [106,108]. An important class of closures, the Eddy Damped Quasi-Normal Markovian (EDQNM) approximation, has been used to study turbulence interacting with Rossby waves [108,112,113]. The EDQNM reduces to the resonant wave interaction limit of [10] as the damping vanishes (i.e. steady state form of the triad relaxation time μ → 0) [114,115].

The work of Hasselmann occurred at a time when applications of field theoretic methods to problems in geophysical flows were leading to major advances in understanding turbulent flows including the seminal closure works of Kraichnan [110,116], the use of Feynman diagrams for homogeneous isotropic turbulence (HIT) [117] and application to magneto-hydrodynamic turbulence [118]. This work has laid the foundations for subsequent advances in field theoretic approaches to HIT [10,111,119] including functional operator [121,122] and functional (path) integral [123] formalisms. More recent efforts have developed explicit turbulence closures for inhomogeneous turbulence [124,125], including computationally efficient Markovian variants [109] as well as subgrid scale parameterizations directly based on closures [126,127] or data driven approaches inspired by field theoretic approaches for geophysical flows [128–130]. For a comprehensive review of turbulence theories and statistical closures see [131].

Finally it remains to be noted that, in order to be realizable, that is to guarantee non-negative energies in the kinetic energy spectrum, the above mentioned statistical-dynamical approaches must be underpinned by an exact stochastic model representation, i.e., an Ornstein-Uhlenbeck process, or generalised Langevin equation. In this way, statistical and stochastic dynamical systems have a shared underpinning framework.

3 Complexity Science and Stochastic Resonance

Giorgio Parisi was awarded the Nobel Prize in Physics in 2021 for his work on disordered systems, and in particular random Ising models and the replica method for the understanding of spin glasses. Nevertheless, Parisi’s connection to climate sciences is manifold, and it descends from his interests on some very fundamental aspects of dynamical systems, especially non-equilibrium and “slightly” non-equilibrium systems. Here, we will focus on disordered systems, as per the scope of the present work, and stochastic resonance, given its close connection to the stochastic models introduced by Hasselmann in the late 70s.

Before we move to these topics, we want to mention, although we will not touch it for sake of brevity, Parisi’s contribution to the modern development of the theory of turbulence. In fact, he was the first, together with Uriel Frisch, to introduce the multifractal formalism [132] to explain the intermittency of velocity fluctuations, overcoming the traditional Kolmogorov’s spectral framework. The rigorous mathematical derivation, though, can be traced back to the works of Frisch [133] and successive studies of Parisi and colleagues (e.g. [17]). This approach has been applied in several studies of turbulence in the atmosphere [134,135], and has been particularly successful in its applications to precipitation (e.g. Venugopal et al. [136]) and clouds (e.g. Lovejoy [137]).

3.1 Spin Glasses: Disorder and Fluctuations

A major part of Giorgio Parisi’s scientific work is devoted to statistical physics of spin glasses, which are disordered magnetic systems formulated within the Ising model with random spin-spin interactions (see the thorough and pedagogical introduction by Castellani and Cavagna [138]). Spin glasses can be modelled by an Ising model with frozen random interactions. The Ising model is a mathematical model for spins σ(i) = ±1, arranged typically on a lattice with grid points i, and with nearest neighbour interactions J_ij contributing to the total energy. The complete state of N spins is given by the configuration σ = {σ(i), i = 1 … , N}. The response to an external magnetic field h is probed with the interaction energy contribution − hσ(i) in the Hamiltonian

H [σ] = - \sum_{< i j >} J_{i j} σ (i) σ (j) - h \sum_{i} σ (i) (5)

where J_ij are the coupling coefficients in the sum for adjacent spins ⟨ij⟩. In two dimensions, the Ising model shows a phase transition between aligned and disordered spins.

In spin glasses the coupling coefficients J_ij are random numbers which remain constant in a quenched spin-glass. In this state of matter a system can be in one of many local minima N_min separated by large barriers [139] (growing with N), coined as pure states. Complexity Σ (or configurational entropy) is defined by the dependency N_min ∼ exp (NΣ). Thus, ergodicity is broken and spin glasses are not in a definite pure thermodynamic state, but in a mixture of pure states [140].

Replicas are physically equivalent configurations σ_a of the system subjected to the same random interactions. The Hamiltonian for a set with n replicas is the sum $H = \sum_{a = 1}^{n} H [σ_{a}]$ [141]. Due to the disorder, the average magnetization $\bar{m} = (1 / N) \sum_{i} \bar{⟨ σ (i) ⟩}$ vanishes (the bar denotes averaging of interaction coefficients J_ij), since all directions are equally probable at low temperatures and cannot be used as order parameter. Therefore, Parisi defined order parameters as the overlap between replicas by a n × n matrix as

Q_{a b} = \frac{1}{N} \sum_{i = 1}^{N} ⟨ σ_{a} (i) σ_{b} (i) ⟩, a \neq b, Q_{a a} = 0 (6)

for the replicas a, b and where ⟨… ⟩ denotes thermal averages [140]. In the thermodynamic limit the free energy is a function of Q.

The existence of infinitely many pure states can be associated with a spontaneous replica symmetry break. A symmetry break can be detected by a discontinuity in the correlations between two replicas 1 and 2 when the Hamiltonian is perturbed by a small symmetric term, $H = H [σ_{1}] + H [σ_{2}] + ϵ \sum_{i = 1}^{N} σ_{1} (i) σ_{2} (i)$ . This Hamiltonian remains invariant for changes of 1 and 2. The states in a spin glass are described as a branching process, where branching points are phase transitions [140,142].

The calculation of thermodynamic properties of spin glasses is achieved with the so-called replica trick. For a model in contact with a heat bath at temperature T, the partition function Z describes the statistical properties of a system in thermodynamic equilibrium, Z = ∑_σ exp (−H [σ]/k_bT) and observables can be derived through the free energy F = −k_BT ln Z. A main difficulty is the calculation of the mean $\bar{\ln Z}$ averaging the interaction coefficients. This is solved by the replica trick which uses the limit ln Z = lim_n→0 (Zⁿ − 1)/n, and the calculation of the means $\bar{Z^{n}}$ for the number n of replicas by Gaussian integrals [142].

The Ising model has been applied to various problems in geosciences with unresolved small scale processes.

• Pleimling et al. [143] consider convection cells in an Ising lattice gas in contact with two thermal reservoirs. In the non-equilibrium stationary state, convection cells emerge which are driven by spontaneous symmetry breaking below the critical temperature.

• Ma et al. [144] describe the formation of ponds in Arctic sea ice during melting in late spring which determine the albedo through their geometric structure. The authors use a binary Ising model which predicts observed power law scaling of the pond size distribution, correlation lengths and fractal dimensions of the clustered ponds. Such results may be useful for the parameterization in global climate models.

• Khouider [145] applies the Ising model as a stochastic multicloud model for organized tropical convection introduced recently to improve the variability in climate models. Each lattice is either clear sky or occupied by one of three cloud types. The coarse-graining could be extended to multi-type particle systems with nearest neighbour interactions and a multi-dimensional birth-death process. Local interactions induce a shift in the climatology and intermittency through coherent cloud clusters and long time excursions.

The idea of long-lived metastable states found in spin glasses has been applied in climate science to explain the recovery from a snow ball Earth, a climatic state with an Earth covered by ice or snow which ended 700 Mio years ago [146]. This state is stable on long time scales due to the ice albedo effect and transitions can be excited by stochastic solar forcing Lucarini and Bódai [147] with a hysteresis effect [148].

Atmospheric circulation regimes [149–151], are metastable states [152] of the atmosphere having a significant impact on surface conditions and predictability, particularly as the formation and decay of such structures on synoptic scales, commonly referred to as “blockings”, are often associated with significant reductions in operational forecast skill. The concept of metastability, i.e., states that are coherent and locally stationary in time, has also been applied to enable the construction of reduced order stochastic models directly from data thereby enabling an understanding of the predictability of atmospheric circulation regimes [22,152–154,156–158] including error growth in weather prediction [159,160] and for the detection and attribution of the external drivers of trends in the frequency of occurrence, persistence and structure of said regimes over time [14].

3.2 Stochastic Resonance

The idea for what would have been later referred to as “stochastic resonance”, arose when an important aspect of the Milankovitch explanation of glacial-interglacial periods succession, was left unanswered, given that the periodicities in orbital parameters were unable to capture the 10⁵ year periodicity in the Milankovitch spectrum [161]. When Parisi, together with his colleagues Roberto Benzi, Alfonso Sutera and Angelo Vulpiani at Rome La Sapienza University, started to work on a possible solution to this problem, the seminal work by Hasselmann [12] (see section 2) had already stressed that the long-term variability of the climate system could be treated as long-term forced variations with a stochastic fast-scale perturbation superimposed on it. Sutera [162] had already demonstrated that such fast-scale stochastic perturbations would be able to induce random transitions in a Budyko-Sellers type Energy Balance Model (EBM) [163,164], for which multiple stable states, namely a glacial and an inter-glacial state, were identified. Similar arguments were also brought up by Nicolis and Nicolis [165] in the very same year. Despite being able to exhibit random transitions induced by stochastic noise, this model was not capable of transitioning between glacial and interglacial states, no matter what the variance attributed to the noise was. Indeed, Parisi and his colleagues demonstrated that no transition would occur in this stochastically perturbed EBM, unless a periodic forcing (the Milankovitch forcing, in their probe at the 10⁵ year frequency) would be introduced. In other words, the concept of “stochastic resonance” relies on the fact that the stochastic noise introduced in the model introduces the possibility of a transition between observable states of the system, when the variance of the noise “couples” with the amplitude of a periodic forcing. For a rigorous derivation of the concept, one might refer to Benzi et al. [166]. In the following, we will discuss some of the fundamental passages of the application in the context of paleoclimate, as described in Benzi et al. [167].

As a starting point, they consider a Battacharya-Ghil model [168,169], that relies on a parametrization of the albedo allowing for two stable states separated by a 10 K global mean temperature difference. The model can be written as:

\frac{d T}{d t} = F (T, t) = \frac{ϵ T}{C} \{\frac{μ (t)}{1 + β [(1 - T / T_{1}) (1 - T / T_{2}) (1 - T / T_{3})]} - 1\} + σ η (t) (7)

where:

• F (T, t) is a function of temperature and time, whose integral is the pseudo-potential Φ(T, t). Maxima and minima of Φ represent the stable and unstable solutions of the budget Equation (7);

• C is the thermal capacity of the Earth;

• ϵ is the global mean emissivity of the Earth;

• μ(t) is the Milankovitch periodic forcing, in our case written as μ(t) = 1 + 0.0005 cos (ωt) with ω = 2π/10⁵ year, thus representing the 50,000 years periodicity;

• T₁, T₂ and T₃ are the global mean equilibrium temperatures for two stable regimes (T₁, T₃) and one unstable state (T₂). Here, it is assumed that ΔT = (T₃ − T₁)/2 is equal to 5 K;

• β is a dimensionless parameter, a function of the decaying time τ, so that $τ^{- 1} = {\frac{d F}{d T}|}_{T = T_{3}}$ ;

• σ is the variance associated with a Wiener process represented by η(t). This member of the equation represents the stochastic part of the model.

It is worth noticing that similar results were achieved through the usage of a Fokker-Planck equation, and that the Equation 7 can be non-dimensionalized, noticing that we can define a new variable $ϕ = \frac{T - T_{0}}{Δ T}$ , where T₀ is the median temperature between T₁ and T₃ and a time t′ = tτ_s, with τ_s an observational-based relaxation time. We eventually obtain:

\frac{d T}{d t} = ϕ (1 - ϕ^{2}) + σ η (t) + A (t) (8)

where A(t) is again the Milankovitch forcing, that we assume for the sake of simplicity to oscillate between A₀ and − A₀.

From the theory of stochastic differential equations, it is known that the average random transition time between one stable state and another (in the absence of forcing), is given by (e.g. [170]):

⟨ τ ⟩ \sim τ_{s} \exp (Δ T^{2} / σ τ_{s}) (9)

When the Milankovitch forcing is also included, and in the two cases ± A₀, we have:

〈 τ 〉 \sim τ_{s} \exp [τ_{s} (Δ T^{2} + A_{0}) / σ] = 〈 {τ 〉}_{A = 0} \exp (τ_{s} A_{0} / σ) (10)

〈 τ 〉 \sim τ_{s} \exp [τ_{s} (Δ T^{2} - A_{0}) / σ] = 〈 {τ 〉}_{A = 0} \exp (- τ_{s} A_{0} / σ) (11)

In other words, it is found that when the amplitude of the stochastic noise is sufficiently large, and the noise gets in phase with the Milankovitch periodic forcing, its effect can be exponentially amplified or dampened, depending on the sign. This was the main result of the Benzi et al. [167] paper.

A question that was left unanswered, at that time, was whether a specific physical mechanism had to be invoked, triggering the transition, or the noise, somehow reaching the phase and amplitude for the stochastic resonance, was randomly pushing the system towards a transition. From the theory of stochastic differential equations, it was shown that the probability for a random transition with characteristic timescale τ is given by:

P (τ) = {〈 τ 〉}^{- 1} \exp (τ / 〈 τ 〉) (12)

meaning that the transition could be understood as a “rare event” and large deviation theory would be sufficient to investigate the effect of the noise. It was not immediately clear, though, how the noise generated by turbulence, where the turbulent cascade does not allow for a clear scale separation between noise and the large-scale behavior, would ever be useful to obtain this kind of transitions in the system. This problem was later addressed in Benzi [171], by showing that a Sabra shell model of turbulence would exhibit stochastic resonant behavior.

As argued at the beginning of the section, the concept of stochastic resonance has its roots in paleoclimate studies, and found a wide range of applications going well beyond this initial field of research. A few of them are reviewed in Gammaitoni et al. [172]. Here, we briefly describe a selected number of related works that have proved their relevance for climate sciences:

• Ganopolski and Rahmstorf [173] propose the stochastic resonance mechanism to explain the shifts in Northern Atlantic freshwater formation regions as a trigger of millennial climate variability during glacial times;

• As reviewed in Crucifix [174], there have been several studies attempting to investigate the onset of Dansgaard-Oeschger (DO) events in terms of stochastic resonance, either relying on the 1,500 occurrence time of these events [175], or in terms of the synchronisation between noise and different periodicities of the solar cycle [176,177];

• The large deviation algorithm by Ragone et al. [178] relies on the probability of rare events to help the detection of extreme events in modelling studies;

A historical perspective on the achievements by Parisi and his team on the topic of stochastic resonance, in the context of the 2021 Nobel Prize, is also found in a recent contribution on the Nature Italy blog [179].

4 Starting the March Towards a Digital Twin of Earth

Syukuro Manabe has, in contrast to Klaus Hasselmann and Giorgio Parisi, not made any direct contributions to complexity science. However, he was instrumental in the development of three dimensional numerical coupled Atmosphere-Ocean models [180,181], which are some of the most complex numerical models in science which are running on the fastest and biggest super computers in the world nowadays. Due to limited computing power in the 1960s these numerical models of the complex Earth system had to be simplified in such a way that they were computationally feasible but still contained the most important aspects of the climate system. With the model in whose development he was instrumental, he showed the impact of increasing greenhouse gases concentrations on Earth climate, evidencing how they lead to increasing surface temperatures. In order to accomplish the development of three dimensional models, Syukuro Manabe had to develop a one-dimensional model of the atmosphere [182] with which they estimated the climate sensitivity, i.e. the amount of warming a doubling of CO₂ would produce. The climate sensitivity is nowadays an important aspect of climate change science [183–186] and is an important parameter of Integrated Assessment Models [187–192]. To investigate the climate sensitivity Syukuro Manabe developed a radiative-convective model. With this model he explored the role played by atmospheric gases such as water vapor, carbon dioxide and ozone in setting the thermal structure of the atmosphere. This model was a major step towards the development of the three dimensional model with which he made poineering contributions to understanding of the anthropogenic greenhouse effect [193–195].

Like Giorgio Parisi, Syukuro Manabe worked on paleoclimate [196–198]. He was one of the first to simulate abrupt climate change. Traditionally, it was thought that climate evolved in a slow and smooth way and abrupt climate changes were considered unlikely. However, paleoclimate records showed evidence for abrupt climate changes during glacial periods [199]. In order to examine such abrupt climate changes, he simulated the influx of freshwater from melting ice sheets. This freshwater flux into the North Atlantic caused a shutdown of the Atlantic Meridional Overturning Circulation (AMOC). This shutdown of the ocean circulation has a strong impact on the heat transport, leading to rapid changes in temperature and, hence abrupt climate change. A shutdown of the AMOC is considered a potential tipping element in a warmer world [200] and there is evidence that the AMOC is slowing down in recent years [201].

His work started numerical modeling of the complex Earth system. In 2021 European Union scientists started the project “Destination Earth”, aimed at building a digital twin of the Earth system by 2030, which will enable the mapping of the evolution of the climate system and simulation of extreme events in time and space [202]. In about 50 years the climate science community made the journey from what we nowadays consider to be very simplified, if not crude, climate models to aiming to develop a twin of our Earth in unprecedented high resolution and process representation and which can resolve and simulate “the regional impacts of climate change, natural hazards, marine ecosystems or urban spaces” [202].

5 Discussion

The 2021 Nobel prize for physics was awarded to work mainly done in the 1970s and 1980s. However, the pioneering work done by Klaus Hasselmann, Syukuro Manabe and Giorgio Parisi is still relevant and influential today. For instance, while stochastic parameterizations are incorporated in more and more operational weather and climate prediction models [13], there is still a lot of research going on in this area, involving energy consistent stochastic schemes [30,59,97,203–209,211] or the systematic inclusion of memory terms [127,128,130,212]. Combined with complexity science, scaling and fractional noise ideas are becoming more widespreadly used [15,213,214,214–216].

Still an important issue, not only of fundamental interest but also of practical importance, is climate sensitivity. The current generation of Earth system models has a higher climate sensitivity than previous generations [217]. This high climate sensitivity is, however, inconsistent with paleoclimate data [218]. Suggesting, a problem pioneered using numerical models by Syukuro Manabe, still is unsolved and implies large uncertainty about the future evolution of the climate system. Further research is needed, to reveal whether this uncertainty is intrinsic to the complex Earth system with its many interlinked components or whether new generations of models with improved process representation and stochastic parameterizations will reduce this uncertainty. Stochastic and complexity science methods will surely prove essential in this task.

Author Contributions

CF conceived the idea of this manuscript. All authors contributed equally to the writing of the manuscript.

Funding

CF was supported by the Institute for Basic Science (IBS), Republic of Korea, under IBS-R028-D1, and Pusan National University Research Grant 2021.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank two reviewers for their comments.

References

1.NobelPrize.org. The Nobel Prize in Physics 2021. In: Tech. Rep. Cambridge, MA, USA: Nobel Price (2021) (Accessed February 12, 2022).

Google Scholar

2.NobelPrize.org. The Nobel Prize in Chemistry 1995. In: Tech. Rep. Cambridge, MA, USA: Nobel Price (1995) (Accessed April 25, 2022).

Google Scholar

3.NobelPrize.org. The Nobel Peace Prize 2007. In: Tech. Rep. Cambridge, MA, USA: Nobel Price (2007) (Accessed April 25, 2022).

Google Scholar

4. Masson-Delmotte V, Zhai P, Pirani A, Connors S, Péan C, Berger S, et al. Climate Change 2021: The Physical Science Basis: Working Group I Contribution to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge: Cambridge University Press (2021).

Google Scholar

5. Pörtner H, Roberts D, Tignor M, Poloczanska E, Mintenbeck K, Alegría A, et al. Climate Change 2022: Impacts, Adaptation, and Vulnerability. Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, Vol. In Press. Cambridge: Cambridge University Press (2022).

Google Scholar

6. Bohémier KA. Analysis for Science Librarians of the 2021 Nobel Prize in Physics: Climate, Spin Glass, and Complex Systems. Sci Technol Libraries (2022) 41:1–23.

Google Scholar

7. Hasselmann K. On the Signal-To-Noise Problem in Atmospheric Response Studies. In: D Shaw, editor. Meteorology of Tropical Oceans. London: Royal Meteorological Society (1979). p. 251–9.

Google Scholar

8. Hasselmann K. Optimal Fingerprints for the Detection of Time-dependent Climate Change. J Clim (1993) 6:1957–71. doi:10.1175/1520-0442(1993)006<1957:offtdo>2.0.co;2