Calculation of the Coupling Coefficient in Step-Index Multimode Polymer Optical Fibers Based on the Far-Field Measurements

Savović, Svetislav; Djordjevich, Alexandar; Drljača, Branko; Simović, Ana; Min, Rui

doi:10.3389/fphy.2022.927907

ORIGINAL RESEARCH article

Front. Phys., 25 May 2022

Sec. Optics and Photonics

Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.927907

This article is part of the Research Topic Applications of Photonic Sensors in Smart Cities View all 9 articles

Calculation of the Coupling Coefficient in Step-Index Multimode Polymer Optical Fibers Based on the Far-Field Measurements

Svetislav Savović^1,2

Alexandar Djordjevich³

Branko Drljača⁴

Ana Simović²

Rui Min¹*

¹Center for Cognition and Neuroergonomics, State Key Laboratory of Cognitive Neuroscience and Learning, Beijing Normal University, Zhuhai, China
²Faculty of Science, University of Kragujevac, Kragujevac, Serbia
³Department of Mechanical Engineering, City University of Hong Kong, Kowloon, China
⁴Faculty of Sciences, University of Priština in Kosovska Mitrovica, Kosovska Mitrovica, Serbia

Using the power flow equation (PFE), this article investigates mode coupling in step-index (SI) multimode (MM) polymer optical fiber (POF). This equation’s coupling coefficient was initially fine-tuned so that it could appropriately reconstruct previously recorded far-field (FF) power distributions. The equilibrium mode distribution (EMD) and steady-state distribution (SSD) in the SI MM POF were found to be obtained at lengths L_c = 15 m and z_s = 41 m, respectively. These lengths are substantially shorter than their glass optical fiber counterparts. Such characterization of the investigated POF can be used in its employment as a part of the communication or sensory system. Namely, the POF’s bandwidth is inverse linear function of fiber length (z⁻¹) below the coupling length L_c. However, it has a z^−1/2 dependence beyond this equilibrium length. Thus, the shorter the coupling length L_c, the sooner transition to the regime of slower bandwidth decrease occurs. It is also important to be able to determine a modal distribution at a certain length of the POF employed as a part of optical fiber sensory system.

Introduction

Silica optical fiber has a lot of advantages such as a low loss, lightweight, and high bandwidth [1–4]. Although silica optical fiber has a lot of advantages, is not appropriate for short-distance applications such as automotive [5], local area networks [6], and visible light communication (VLC) applications [7]. On the other hand, POFs are made of poly (methylmethacrylate) (PMMA) [8, 9], polycarbonate (PC) [10, 11], ZEONEX ® [12, 13], TOPAS ® [14, 15], poly dimethyl siloxane (PDMS) [16, 17] or hydrogel [18, 19].

Apart from optical fiber material, optical fibers usually have step-index or graded-index refractive index distribution, and can operate in a single-mode or multimode regime. There are several typical commercial POFs, such as Mitsubishi Rayon’s Eska Extra EH 4001 SI MM POF [20] and CYTOP^® graded index (GI) POF [21], both of them could transmit a large number of modes, and have been used for short-range communications and sensing area in fiber optic sensory systems [22]. Additionally, micro-structured polymer optical fiber which was first produced by Argyros’ group, is one very specific type of POF [23]. However, due to the transmission loss and but-coupling with commercial silica optical fiber, only one Start-up Company supplied the commercial product [24]. PMMA SI MM POF is still the most common one with lots of commercial products on the market.

Mode coupling has a significant impact on the transmission performance of PMMA SI MM POF. The transfer of power between nearby modes is represented by such coupling. It causes the launched light’s angular power distribution to be disrupted [25, 26]. It is caused by the optical fiber’s intrinsic perturbation effects (for example, variations of the refractive index distribution and microscopic bends). The angular power distribution is predicted to be influenced by the launch conditions and mode coupling characteristics. Thus, a Gaussian beam launched at an angle θ₀ in respect to the optical fiber axis, at the output end of a short piece of optical fiber, is seen as a sharp ring pattern (the ring diameter depends on θ₀). Mode coupling, on the other hand, causes such a ring pattern to be distorted in longer fibers and finally transformed into disk. The coupling length L_c marks the fiber length at which the ring pattern of the highest order guiding mode evolved into disk, indicating that an EMD is established. Coupling can fully complete at optical fiber length z_s (z_s > L_c), which is referred to as an SSD.

The light transmission performance of PMMA SI MM POF is investigated in this work. The modal power diffusion model is used to obtain the coupling coefficient D. In this way, we computed the L_c required to accomplish the EMD and the length z_s to achieve the SSD. By such a characterization of mode coupling process in an optical fiber one can predict at which length z = L_c one can expect that bandwidth decrease with length would start to decelerate, as explained in more details in Results and Discussion. It is also important to know the state of mode coupling in an optical fiber employed as a part of optical fiber sensory system, especially in terms of the modal distribution at certain fiber length.

Power Flow Equation

The Gloge’s PFE has the following form [27]:

\frac{\partial P (θ, z)}{\partial z} = - α (θ) P (θ, z) + \frac{D}{θ} \frac{\partial}{\partial θ} (θ \frac{\partial P (θ, z)}{\partial θ}) (1)

where P(θ, z) is the angular power distribution, θ is the angle of propagation, z is the distance of the propagation, D is the coupling coefficient (assumed constant [27, 28]) and $α (θ)$ is the modal attenuation. Eq. 1 can be reduced to [29]:

\frac{\partial P (θ, z)}{\partial z} = \frac{D}{θ} \frac{\partial P (θ, z)}{\partial θ} + D \frac{\partial^{2} P (θ, z)}{\partial θ^{2}} (2)

Steady-state solution of Eq. 2 is given as [28]:

P (θ,z) = J_{0} (2.405 \frac{θ}{θ_{c}}) \exp (- γ_{0} z) (3)

where J₀ is the Bessel function of the first and zero-order, γ₀ [m⁻¹] = 2.405²D/θc² is the attenuation coefficient. In this work, solved Eq. 2 using the explicit finite difference method [29].

In our earlier published work, we proposed a method which enables that the coupling coefficient D can be obtained from just two output angular power distributions P(θ, z) in the case of centrally launched beam [30]. As an alternative, in this work we propose a method for calculating the coupling coefficient D on the basis of the measured FFPs p(x, z), illustrated in Figure 1.

FIGURE 1

FIGURE 1. Schematics of measuring FF power distributions.

Results and Discussion

We used the PFE (2) to calculate the lengths L_c and z_s for the POF that Ribeiro et al. [31] studied experimentally. This POF (Mitsubishi Rayon’s Eska Extra EH 4001) had NA = 0.47, the inner critical angle $θ_{c}$ = 18^o ( $θ_{c}$ = 27.4^o measured in air), core refractive index n_core = 1.4897, numerical aperture NA = 0.46 and fiber diameter d = 1 mm. Ribeiro et al. focused a He-Ne laser beam at 633 nm onto the input end of the fiber in their experiment (Figure 1). They used a CCD to detect the FF patterns of the fiber output.

The coupling coefficient D is obtained by its fine-tuning in the PFE, thus recreating the Ribeiro et al.’s measured FF patterns in this fiber for lengths of z = 1 m and z = 19 m (Figure 2). This necessitated numerically calculating the PFE for various values of D. The value of D = 9.2 × 10⁻⁴ rad²/m enabled the best fit between the calculated and measured output power distributions.

FIGURE 2

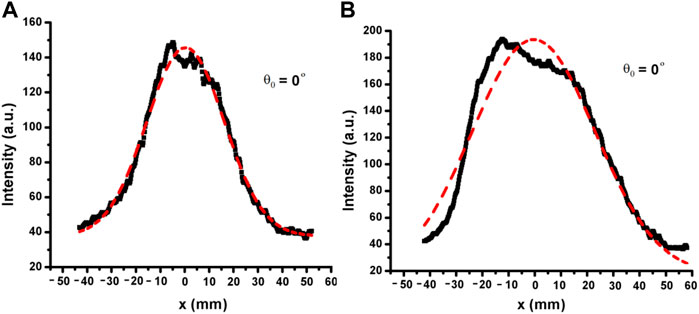
FIGURE 2. The measured FF pattern from (A) ∼1 m and (B) ∼19 m PMMA SI MM POF lengths. The light was launched at θ₀ = 0^o [31].

A Gaussian launch beam with (FWHM)_z=0 = 7^o is used in the computations. Figure 3 shows the output power distribution for a z = 1 and 19 m length POF with an input angle of θ₀ = 0^o obtained as numerical solution of Eq. 2. The distributions P (x, z = 1 and 19 m, L = 110 mm) are generated from the distributions P (θ, z = 1 and 19 m, L = 110 mm), where x = L⋅tgθ and L is the receiving distance.

FIGURE 3

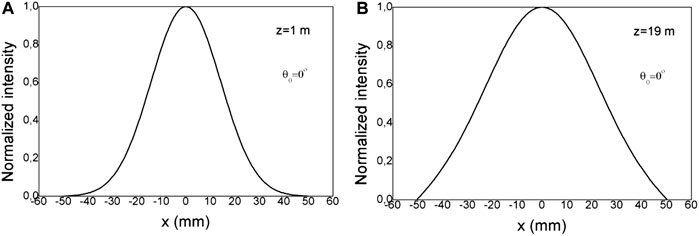
FIGURE 3. Normalized output power distribution P (x, z = 1 and 19 m, L = 110 mm) at the end of (A) 1 m and (B) 19 m long PMMA SI MM POF, obtained by solving the PFE for Gaussian launch distribution with input angle θ₀ = 0°, obtained from the P (x, z = 1 and 19 m, L = 110 mm), for x = L⋅tgθ, where L is the receiving distance.

In Figure 4, our numerical results for the normalized output angular power distribution for input angles θ₀ = 0, 5, 10, and 15^o are shown. At short fiber lengths, a significant mode coupling is observed for low order modes, as can be seen in Figure 4A. The EMD is achieved at length z = L_c = 15 m (Figure 4C), while the SSD is established at z_s = 41 m in Figure 4D.

FIGURE 4

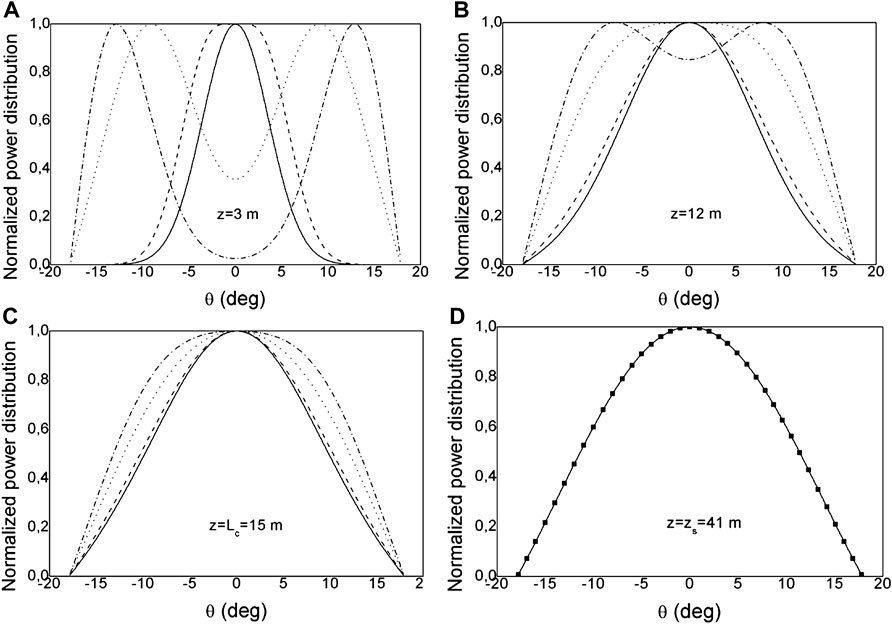
FIGURE 4. The normalized angular power distribution at the end of PMMA SI MM POF, obtained by solving the PFE for four Gaussian launch distributions with input angles θ₀ = 0^o (—), θ₀ = 5^o (− −), θ₀ = 10^o (•••) and θ₀ = 15^o (−•−), with (FWHM)_z=0 = 7^o (g represent the analytical SSD).

The coupling coefficient D for the PMMA SI MM POF evaluated in this work is similar to those which we obtained for other investigated POFs (∼10⁻⁴ rad²/m), so the characteristic lengths for coupling, L_c and z_s, are similar (L_c is between ≃15–35 m and z_s is between ≃40 and 100 m [25, 29, 30]). We have previously reported that glass optical fibers show the weakest strength of mode coupling (D ∼ 10⁻⁷ to 10⁻⁶ rad²/m), so their SSD lengths z_s are between ≃ 1–10 km [32].

It is worth noting that the length dependence of the bandwidth of POF is determined by mode coupling behavior. The bandwidth is inverse linear function of fiber length (z⁻¹) below the coupling length L_c. However, it has a z^−1/2 dependence beyond this equilibrium length. Thus, the shorter the coupling length L_c, the sooner transition to the regime of slower bandwidth decrease occurs [26]. It is obvious that mode coupling has a beneficial influence on bandwidth. Therefore, it is of great interest to characterize mode coupling in an optical fiber in order to predict its transmission characteristics, especially to determine at which coupling length L_c one can expect that bandwidth would start to improve. It is also important to know the state of mode coupling in an optical fiber employed as a part of optical fiber sensory system, especially in terms of the modal distribution at certain fiber length.

Conclusion

We investigate a mode coupling along a PMMA SI MM POF previously investigated experimentally by Ribeiro et al. [31]. To appropriately recreate the measured FF patterns reported before, the coupling coefficient D in the PFE is tweaked. As a result, the lengths L_c and z_s that characterize the coupling process are obtained. Such characterization of the investigated PMMA SI MM POF can be used in its employment as a part of communication or sensory system. In practice, by characterization of mode coupling in an optical fiber one can predict its transmission characteristics, especially to determine length-dependent bandwidth behavior. Since POF’s bandwidth is inverse linear function of fiber length (z⁻¹) below the coupling length L_c, while it has a z^−1/2 dependence beyond this equilibrium length, it is obvious that the shorter the coupling length L_c leads to the sooner transition to the regime of slower bandwidth decrease. It is also important to be able to determine a modal distribution at a certain length of the fiber employed as a part of optical fiber sensory system.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

SS: methodology, conceptualization, formal analysis, validation, writing—original draft. RM: conceptualization, formal analysis, funding acquisition, writing—review and editing. AD: formal analysis, validation, writing—review and editing. BD: validation, writing—review and editing. AS: validation, writing—review and editing.

Funding

This research was funded by the National Natural Science Foundation of China (62003046, 6211101138); the Strategic Research Grant of City University of Hong Kong (Project No. CityU 7004600); Serbian Ministry of Education, Science and Technological Development (Agreement No. 451-03-68/2020-14/200122); Science Fund of the Republic Serbia (Agreement No. CTPCF-6379382); Guangdong Basic and Applied Basic Research Foundation (2021A1515011997); The Innovation Team Project of Guangdong Provincial Department of Education (2021KCXTD014); Special project in the key field of Guangdong Provincial Department of Education (2021ZDZX1050).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Min R, Liu Z, Pereira L, Yang C, Sui Q, Marques C. Optical Fiber Sensing for marine Environment and marine Structural Health Monitoring: A Review. Opt Laser Techn (2021) 140:107082. doi:10.1016/j.optlastec.2021.107082