Transient Turing patterns in a morphogenetic model

One of the most surprising mechanisms to explain the symmetry breaking phenomenon linked to pattern formation is known as Turing instabilities. These patterns are self-organising spatial structures resulting from the interaction of at least two diffusive species in specific conditions. The ideas of Turing have been used extensively in the specialised literature both to explain developmental patterns, as well as synthetic biology design. In the present work we study a previously proposed morphogenetic synthetic circuit consisting of two genes controlled by the same regulatory system. The spatial homogeneous version of this simple model presents a rich phase diagram, since it has a saddle-node bifurcation, spirals and limit cycle. Linear stability analysis and numerical simulations of the complete model allow us to determine the conditions for the development of Turing patterns, as well as transient patterns. We found that the parameter region where Turing patterns are found is much smaller than the region where transient patterns occur. We observed that the temporal evolution towards Turing patterns can present one or two different length scales, depending on the initial conditions. Further, we found a parameter region where the persistence time of the transient patterns depends on the distance between the parameters values on which the system is operating and the boundary of Turing patterns. This persistence time has a singularity at a critical distance that gives place to metastable patterns. To the best of our knowledge, transient and metastable patterns associated with Turing instabilities have not been previously reported in morphogenetic models.

1 Introduction

Pattern formation in morphogenetic system is one of the central problems in developmental biology. One of the best-known mechanism of autonomous pattern formation is the Turing instability. This symmetry breaking mechanism was introduced in 1952 by Alan Turing in the context of models for morphogenesis [1]. The basic idea is that Turing instability arises from the coupling between diffusion and reaction which can destabilize spatially homogenous equilibrium and lead to the formation of patterns. The minimum biological system able to present Turing instabilities consists in only two interacting diffusible components: an activator with a slow diffusion rate and an inhibitor with a fast diffusion rate [2].

There is a large body of literature focused on the mechanism proposed by Turing to explain the patterns of self-organization during the animal development [3–11]. However, the identification of the molecular agents driving Turing patterns remains an unsolved issue in most cases.

Thanks to recent progress in synthetic genetic circuit engineering, several researchers have embarked on the implementation of Turing ideas on cell culture [12–17]. To engineer such biological systems, one needs to know the mandatory properties and genetic circuit that support the biological patterning process. It is well known that two key factors underlying the Turing model are the differential diffusion between activator and inhibitor, and also the non-linearity in the reactive terms. In addition, it has been shown that the latter can be as important as the differential diffusion [18, 19]. In this sense, a Turing model has been proposed where the activator and inhibitor are under the control of the same promoter, a simplification that can be exploited in the design of synthetic morphogenetic circuits. This biological simplification allows a mathematical analysis which has highlighted the role of cooperative regulation as source of non-linearity [18]. However, beyond this contribution, the single-promoter model has not been explored to its full potential in either theoretical or experimental studies. In this paper we present a deep theoretical analysis of this simple model and report that it has a rich phase diagram that include: saddle-node, limit cycles and Turing patterns. We also observe transient patterns, driven by Turing instability, which hereafter will be referred to as transient Turing patterns. Previous reports about transient Turing patterns have been done in the context of closed systems, when chemical species are being consumed [20–22] and for noise-driven stochastic patterns in a multicellular cyanobacterial organism [23]. Moreover, out of the reaction-diffusion context, transient Turing patterns have been reported in a neural field model of working memory [24]. Except for the last case, the reaction-diffusion systems associated with transient Turing patterns are composed by several species, which posses the additional challenge to derive analytical predictions or to associate a phase diagram to study them. On the other hand, the present model can be associated with biological systems [25, 26] and the analysis of the associated reaction-diffusion equations are feasible for some values of the Hill exponent of regulatory function. The present results show that in this model the transient patterns are due to the presence of a saddle node which have associated spatial modes with no-null amplification rate. Patterns initiated around this steady state can experiment a transition to Turing pattern associated with a stable steady state, or disappear. The existence of transient patterns brings with it the question of their persistence. This question is especially important given that in the biological context Turing patterns are associated with spatial distributions of molecules that induce morphogenetic processes whose time scales must be finely orchestrated. Interestingly, we observe that the persistence time of the transient patterns suffers a critical transition when parameters values approaches at a critical distance of the boundary that separate Turing stable patterns. This critical distance defines a region for metastable patterns, where the spatial pattern remains stable over large time scales while no disturbances operate. Metastable transient patterns have been previously reported in the context of 1D reaction-diffusion systems [27, 28]. To the best of our knowledge, metastable Turing patterns are a novel feature as far as morphogenetic models are concerned, because are related to unstable nodes, which have not been considered in previous studies on Turing instability.

2 The morphogenetic model

The minimum biological system able to present Turing instabilities consists of two interacting diffusible proteins, named morphogens. In the case of the model considered here, the self-activating morphogen A also activates the morphogen H, which in turn inhibits both morphogens (see the sketch in Figure 1A). The activator and the inhibitor morphogens are coupled through the regulatory functions associated with the genes that encode them. The regulatory functions describe mathematically how the protein synthesis rate depends on the concentration of activators and inhibitors. A morphogenetic model was recently introduced which considers that both morphogens are regulated by the same promoter [18]. That means that regulatory functions that control the synthesis rate of both morphogens will be the same. Thus, in this case, the temporal evolution of the system is described by a couple of reaction-diffusion equations of the form.

$\frac{\partial a}{\partial t}=D_a{\nabla }^{2}a+{\rho }_{a}f\left(a,h\right)-{\mu }_{a}a(1)$

$\frac{\partial h}{\partial t}=D_h{\nabla }^{2}h+{\rho }_{h}f\left(a,h\right)-{\mu }_{h}h,(2)$

Where a (x, t) and h (x, t) denote the concentration of the activator A and the inhibitor H, respectively, as a function of spatial position and time. The last term on the right hand side of each equation describes the degradation process and was assumed to be linear. The function f corresponds to the regulatory function that controls the expression of both activator and inhibitor. As in the previous study [18], we consider a sigmoidal regulatory function where activator and inhibitor compete for the same regulatory site in the form:

$f\left(a,h\right)=\frac{a^{n_H}}{1+{\left(h/k_h\right)}^{n_H}+{\left(a/k_a\right)}^{n_H}},(3)$

where n_H is the Hill exponent that describes the steepness of the sigmoidal function (considered equal for both activator and inhibitor), while k_a and k_h are related to the effective dissociation constant for the activator and inhibitor, respectively. However, non-competitive regulatory function can also be used [29, 30]. At this point it is convenient to introduce dimensionless variables for time $\widehat{t}$, position $\widehat{x}$, and the concentrations $\widehat{a}$ and $\widehat{h}$ as follow:

$\widehat{x}=x\sqrt{{\mu }_a/D_h},\widehat{t}=t{\mu }_a,\widehat{a}=a/k_a,\widehat{h}=h/k_h.$

To simplify the notation we introduced the abbreviations d = D_a/D_h, μ = μ_h/μ_a, $r_a={\rho }_a{k}_a^{n-1}/{\mu }_a$ and $r_h={\rho }_h{k}_a^n/({\mu }_a{k}_h)$. Thus, Eqs. 1, 2 can be rewritten as:

$\frac{\partial \widehat{a}}{\partial t}=d{\nabla }^2\widehat{a}+F\left(\widehat{a},\widehat{h}\right),(4)$

$\frac{\partial \widehat{h}}{\partial t}={\nabla }^2\widehat{h}+G\left(\widehat{a},\widehat{h}\right).(5)$

Where.

$F\left(\widehat{a},\widehat{h}\right)=r_{a}f\left(\widehat{a},\widehat{h}\right)-\widehat{a},(6)$

$G\left(\widehat{a},\widehat{h}\right)=r_{h}f\left(\widehat{a},\widehat{h}\right)-\mu \widehat{h}.(7)$

Next, we carried out a detailed mathematical analysis of local stability of this dimensionless model for the case without diffusion. After that, we presented the Turing-instability conditions. From now on we will write new variables without the hat in order to simplify the notation. The Hill exponent on the regulatory function f is usually associated with the number of regulatory sites in the promoter, but as a consequence of the finite free energy involved in the interaction between regulators molecules [31, 32], the exponent is not an integer number. Despite that, hereafter we set n_H = 2 for mathematical convenience since it allows the derivation of analytical expressions which will help to obtain the results on the next Section.

FIGURE 1

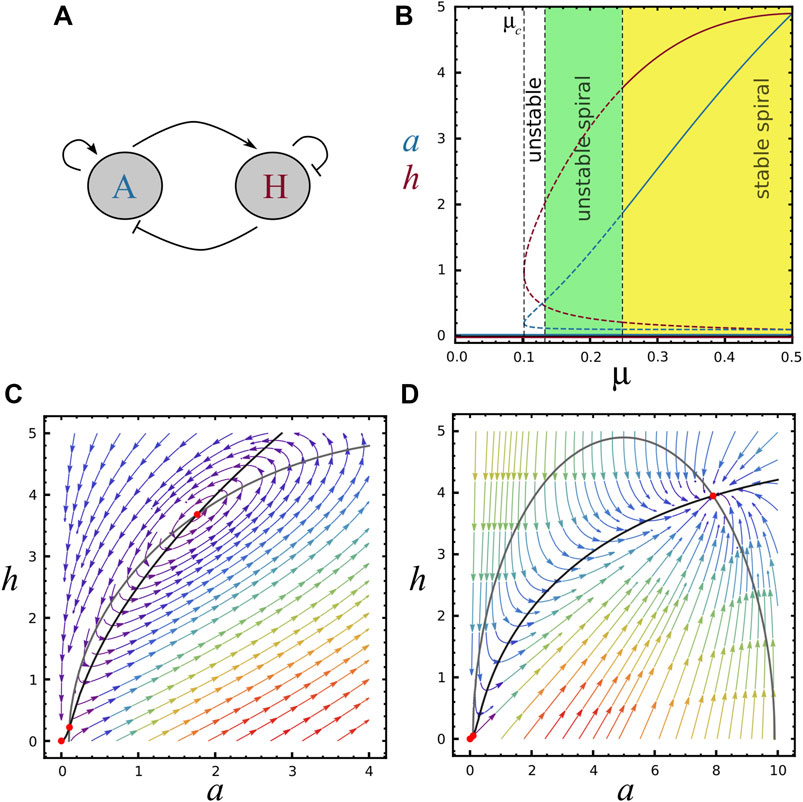
FIGURE 1. Bifurcation diagram and nullclines, (A) Schematic representation of the two-component system, A is the activator morphogene (activates both reactants), H is the inhibitor morphogene (inhibits both reactants). (B) Bifurcation diagram showing the behavior of concentrations a (blue) and h (red) as a function of μ, with r_a =10 and r_h =5. The trivial fixed point S₀=(0,0) is present for all μ values. The saddle-node bifurcation at μ = μ_c ≈0.10 marks the emergence of two new fixed points (S₁ and S₂). Continuous and dashed curves represent respectively regions of stable and unstable steady state solutions. Black vertical dashed lines refer to μ_c and the stability of steady-state S₂, indicating regions of unstable node (white area, where TrA <0, det A >0 and Δ >0), unstable spiral (green area, where TrA <0, det A >0 and Δ <0) and stable spiral (yellow area, where TrA >0, det A >0 and Δ <0). For μ = μ₂ the system displays a limit cycle (TrA =0 and det A >0). For visualisation in the phase diagram, see horizontal line in Supplementary Figure S1B. (C) Black and grey curves represent F and G functions (nullclines) for the parameters value (μ, r_a, r_h)=(0.24,10,5) (S₂ is an unstable spiral). (D) Nullclines for the parameters value (μ, r_a, r_h)=(1,10,5) (S₂ is a stable node). Red points represent fixed points.

3 Results

3.1 Stability analysis for the non-spatial model

In order to determine the general conditions for diffusion-driven instabilities, it is necessary to study the temporal evolution of the diffusion-less system:

$\frac{\partial a}{\partial t}=F\left(a,h\right),(8)$

$\frac{\partial h}{\partial t}=G\left(a,h\right).(9)$

The homogeneous steady states S = (a_ss, h_ss) system of (Eqs. 8, 9) are the positive solutions of equations F (a_ss, h_ss) = 0 and G (a_ss, h_ss) = 0. The system can present up to three fixed points: the trivial solution S₀ = (0, 0), and two non-trivial solutions, identified as S₁ = (a₁, h₁) and S₂ = (a₂, h₂) with.

$a_1=\frac{{\mu }^2{r}_a^3-\mu r_a\sqrt{{\mu }^2{r}_a^4-4\left({\mu }^2{r}_a^2+r_h^2\right)}}{2\left({\mu }^2{r}_a^2+r_h^2\right)},h_1=a_1\frac{r_h}{\mu r_a},(10)$

$a_2=\frac{{\mu }^2{r}_a^3+\mu r_a\sqrt{{\mu }^2{r}_a^4-4\left({\mu }^2{r}_a^2+r_h^2\right)}}{2\left({\mu }^2{r}_a^2+r_h^2\right)},h_2=a_2\frac{r_h}{\mu r_a}.(11)$

The non-trivial steady-states, S₁ and S₂, are real in a parameter region defined by

${\mu }^2{r}_a^4-4\left({\mu }^2{r}_a^2+r_h^2\right)>0.(12)$

Hence, ${\mu }_c^2{r}_a^4-4\left({\mu }_c^2{r}_a^2+r_h^2\right)=0$ defines a surface in the parameter space where a saddle-node bifurcation is found. In that way, for fixed values of r_a and r_h, it is possible to define a critical value for μ

${\mu }_c=\frac{2r_h}{r_a}\sqrt{\frac{1}{r_a^2-4}}\text{with}{r}_a>2.(13)$

For μ > μ_c the three steady-states are real, while for μ < μ_c only the trivial one is found. For μ = μ_c the two non-trivial solutions merge together (see Figure 1B). Similarly, we can obtain analytical expressions for critical values of r_a and r_h as a function of the remaining parameters.

In Figure 1B it is possible to appreciate the activator and inhibitor concentrations as a function of μ for the three steady states, when r_a and r_h are kept as constants. Note that μ = μ_c is a saddle-node bifurcation and the non-trivial stead-states S₁ and S₂ are present only for μ > μ_c. Similarly, Supplementary Figure S1A shows a and h as a function of r_h keeping constants μ and r_a. Supplementary Figure S1B depicts a stability phase diagram for S₂ in the plane μ-r_h with r_a = 10, where the different regions of stability are indicated by colors. Horizontal dashed line shows the section of the parameter region explored in Figure 1B (r_a = 10 and r_h = 5), with dots indicating the dashed lines of Figure 1B. Vertical dashed line shows the section of the parameter region explored in Supplementary Figure S1A.

Typical phase planes can be seen in Figures 1C,D, for different values of μ. Note that increasing μ brings S₀ and S₁ closer together, as it can also be seen in Figure 1B.

Linearising the system about the steady-states S = (a_ss, h_ss) it is possible to determine the stability of each state S. Therefore, we define

$\mathbf{v}=\left(\begin{array}{c}\hfill a-a_{ss}\hfill \\ \hfill h-h_{ss}\hfill \end{array}\right).(14)$

For the case of |v| small, it is possible to approximate Eqs. 8 and 9 as

$\frac{\partial \mathbf{v}}{\partial t}=\mathbf{A}\mathbf{v},\mathbf{A}={\left(\begin{array}{cc}\hfill F_a\hfill & \hfill F_h\hfill \\ \hfill G_a\hfill & \hfill G_h\hfill \end{array}\right)}_{a_{ss},h_{ss}}(15)$

where A is the Jacobian matrix, with $F_a=\frac{\partial F}{\partial a}$, $F_h=\frac{\partial F}{\partial h}$, $G_a=\frac{\partial G}{\partial a}$ and $G_h=\frac{\partial G}{\partial h}$. Where the partial derivatives of F and G are evaluated at the steady-state S = (a_ss, h_ss) under consideration. For each steady state, the eigenvalues are given by

${\lambda }_{\mathrm{1,2}}=\frac{1}{2}\left[\mathrm{T}\mathrm{r}\mathbf{A}\pm \sqrt{\mathrm{\Delta }}\right],(16)$

with $\mathrm{\Delta }={\left(\mathrm{T}\mathrm{r}\mathbf{A}\right)}^2-4\det \mathbf{A}$. Following Routh–Hurwitz criterion, a fixed point is linearly stable if the real part of the eigenvalues of the associated Jacobian matrix A are negative. According to Eq. 16 this is guaranteed if

$\mathrm{T}\mathrm{r}\mathbf{A}<0\mathrm{a}\mathrm{n}\mathrm{d}\det \mathbf{A}>0.(17)$

The trivial steady-state S₀ is always a stable node, whereas S₁ is an unstable saddle-point for the parameter region delimited by the inequality (Eq. 12). S₂ has a more intricate behaviour, as it is discussed below.

The stability of S₂ depends on the values of r_a, r_h and μ, as shown in Figure 2A. As it can be seen, the region where S₂ is stable becomes smaller as the inhibitor production rate r_h increases. On the other hand, this region rises with the activator production rate r_a and the relative degradation rate μ. We observe that a and h concentrations in S₂ can present oscillations, which can be stable or unstable (see Figure 2B). Interestingly, in the region of unstable spirals (where TrA > 0 and Δ < 0), oscillations drive the system to the trivial steady-state S₀ (see Figure 2C and the phase-plane of Figure 1C). Otherwise, when TrA < 0 (with Δ < 0) the stable spirals around S₂ are damped until the system reaches the stable steady-state (see Supplementary Figure S1C). On the boundary of unstable and stable spirals, when Reλ = 0 and Imλ ≠ 0 (TrA = 0 and det A > 0), a stable limit circle is found, as shown in Supplementary Figure S1D. The rich behaviour of the system around S₂ can also be seen in the μ-r_h phase diagram of Supplementary Figure S1B: four regions indicate when S₂ is an unstable node, unstable spiral, stable spiral or stable node. Besides, the saddle-node bifurcation line and the limit-circle line are shown.

FIGURE 2

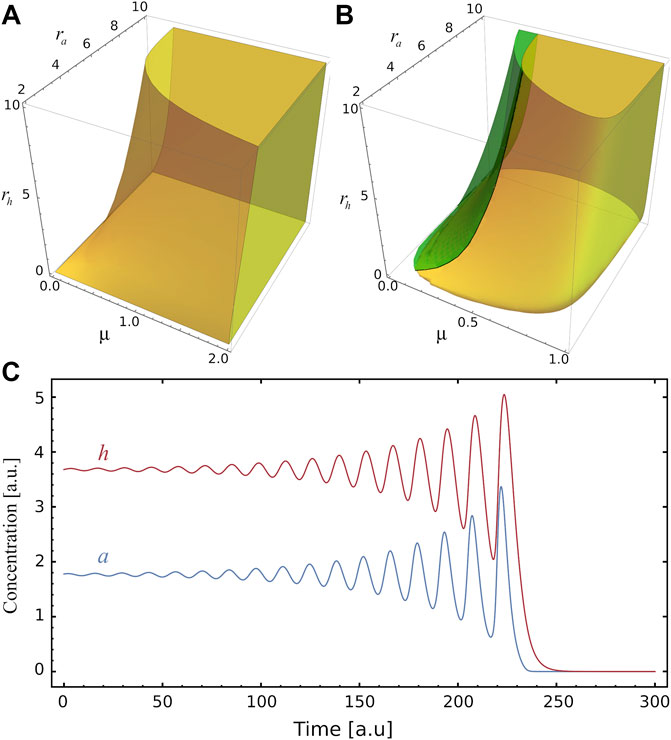
FIGURE 2. Stability and instability of the fixed point S₂. (A) Yellow volume delimits, in the parameters space (μ, r_a, r_h), the region where the steady state S₂ is stable. (B) The green region corresponds to the values of the parameters where the system develops a spiral source behaviour in the steady state S₂ (see panel C), while in the yellow region there is a spiral sink behaviour at S₂. Only at the interface of these two regions does the system exhibit a limit cycle. (C) Example illustrating of unstable oscillatory behaviour for a and h, as function of time, for (μ, r_a, r_h)=(0.24,10,5), the amplitudes increase until they reach the stable trivial fixed point S₀.

In Figure 1B the stability of S₂ for increasing μ is presented: it changes from an unstable node to unstable and stable oscillations. In the phase-plane of Figure 1C, S₂ is an unstable spiral while for Figure 1D it is a stable node. The stability of S₂ as a function of r_h is shown in Supplementary Figure S1A. In this case, greater values of r_h lead the system towards instability. The points μ = μ_c and r_h = r_hc shown respectively in Figure 1B and Supplementary Figure S1A, where S₁ = S₂, are saddle points.

3.2 Conditions for Turing patterns

As it was mentioned in the previous section, the fixed point S₂ is stable in a region of the parameter space. The addition of diffusive terms to the system of (Eqs. 8, 9) can destabilise the spatially homogeneous equilibrium and lead to the formation of patterns, known as Turing patterns. To obtain the mathematical conditions for Turing instability let us consider a one-dimensional version of Eq. 15, that includes the diffusive process,

$\frac{\partial \mathbf{v}}{\partial t}=\mathbf{\text{A v}}+\mathbf{D}\frac{{\partial }^2\mathbf{v}}{\partial x^2},\mathbf{D}=\left(\begin{array}{cc}\hfill d\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right),(18)$

and the boundary conditions. We are interested in the zero-flux boundary condition, i.e., that morphogens cannot diffuse beyond the boundaries [0,L]. This implies that the wave number k of solutions of Eq. 18 takes discrete values k_n = nπ/L, with n = 0, 1, 2, …. As usual, the steady solution S is perturbed with ${\mathit{\delta }}_n\left(x,t\right)=({\delta }_a,{\delta }_h)e^{(\omega t-i{k}_{n}x)}$. Substituting $\mathbf{v}={\mathit{\delta }}_n\left(x,t\right)$ in Eq. 18 we obtain

$\omega {\mathit{\delta }}_n=\mathbf{A}{\mathit{\delta }}_n-\mathbf{D}{k}_n^2{\mathit{\delta }}_n.(19)$

The perturbation ${\mathit{\delta }}_n\left(x,t\right)$ can be different from zero (non-trivial solution), if and only if

$\det \left(\omega I-\mathbf{A}+\mathbf{D}{k}_n^2\right)=0.(20)$

Therefore, for the stable homogeneous state to become unstable upon perturbation δ_n it is required that Re(ω) > 0. This is fulfilled if any of the conditions below are satisfied

$\mathrm{T}\mathrm{r}\left(\mathbf{A}-k_n^2\mathbf{D}\right)>0(21)$

$\det \left(\mathbf{A}-k_n^2\mathbf{D}\right)<0(22)$

As (Eq. 21) is never true for a stable fixed point, the only necessary condition is (Eq. 22). Taking into account that det A > 0 on stable fixed point, condition (Eq. 22) implies in

$F_a+d{G}_h>0.(23)$

The condition for a non-trivial solution Eq. 20 leads to the relation of the eigenvalues as function of the wave number k, knows as dispersion relation

${\omega }^{\pm }\left(k\right)=\frac{-\alpha \left(k\right)\pm \sqrt{\alpha {\left(k\right)}^2-4\beta \left(k\right)}}{2},(24)$

where α(k) and β(k) are functions of k² and given by

$\alpha \left(k\right)=\left(d+1\right)k^2-\mathrm{T}\mathrm{r}\mathbf{A},(25)$

$\beta \left(k\right)=d{k}^4-\left(F_a+d{G}_h\right)k^2+\det \mathbf{A},(26)$

where the partial derivatives of F and G are evaluated at the steady-state S under consideration. In the following we will consider only the dispersion relation ω⁺ because ω⁻ is negative in the parameter region of interest.

Furthermore, we are looking for positive k² such that β(k) < 0 for some nonzero k. Thus it is necessary that the minimum of β be negative. By differentiating with respect to k² we obtain that the minimum of β is at $k_{\min }^2=(F_a+d{G}_h)/2d$, and the condition for β negative can be written as:

${\left(F_a+d{G}_h\right)}^2>4d\det \mathbf{A}.(27)$

Thus, the necessary and sufficient conditions for Turing instability can be summarised by the conditions for the existence of a stable homogeneous state in the absence of diffusion (Eq. 17), and conditions (Eq. 23) and (Eq. 27). These four conditions determine that the system will develop Turing patterns when a stable fixed point is disturbed by a perturbation with a certain wave number.

Figure 3A depicts the region of the parameter space spanned by parameters μ, r_a and r_h where the reaction-diffusion system of (Eqs. 8, 9) satisfies the conditions for Turing instabilities for d = 0.01. However, we observe that some perturbations can also propagate even when the fixed point in question is unstable, given rise in this case to transient patterns, or transitions between spatial patterns with different wave numbers. To analyse this aspect lets us remark that the temporal evolution of a spatial perturbation is dominated by the value of the wave number associated with the largest amplification rate, i.e., k value which maximises ${\omega }^{+}\left(k\right)$. This wave number, denoted here by k_max, is related to the size of the emergent pattern, and the characteristic pattern size is given by π/k_max. Note that spatial patterns will be developed when $k_{\max }^2$ and ${\omega }^{+}\left(k_{\max }\right)$ are positive. In fact, these conditions are implicit in the derivation of Turing conditions (Eq. 23) and (Eq. 27). Therefore, referring to the stable fixed point S₂, the parameter region where $k_{\max }^2$ and ${\omega }^{+}\left(k_{\max }\right)$ are positive is the same that the region where the four Turing conditions are verified, and will be denoted by R₂ (Figure 3A). On the other hand, the parameter region where $k_{\max }^2$ and ${\omega }^{+}\left(k_{\max }\right)$ are positive for the unstable saddle-point S₁, gives a finite region showed in Figure 3B, and will be called R₁. In region of overlap between R₁ and R₂, there are two characteristic pattern sizes related to the unstable and stable fixed points S₁ and S₂, respectively. Depending on the initial conditions, unidirectional transitions between spatial patterns with different wave numbers are expected. Furthermore, in the region of R₁ that extends beyond of R₂, we expect to observe transient patterns related to the unstable fixed point S₁. In the next subsection we will exemplify these possibilities by numerical simulations considering a diffusion rate value of d = 0.01 in all cases. For the sake of simplifying the notation, hereafter, the expression ${\omega }^{+}\left(k_{\max }\right)$ computed over steady state S_i will be denoted by ω(S_i).

FIGURE 3

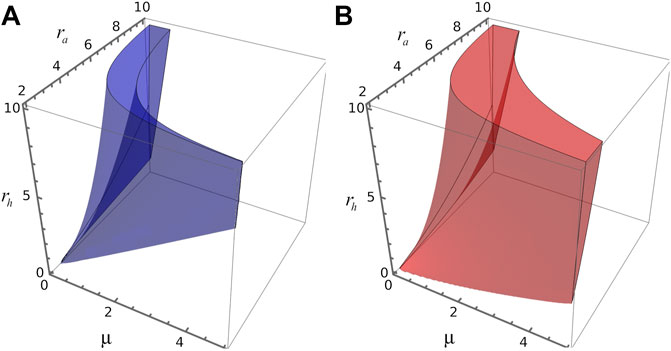
FIGURE 3. 3D parameters space. (A) Blue volume delimits, in the space spanned by parameters (μ, r_a, r_h), the region where the four Turing conditions are verified for steady state S₂. (B) Red volume delimits, in the space spanned by parameters (μ, r_a, r_h), the region where k²>0 and ω >0 for the steady state S₁.

3.3 Stable and transient Turing patterns

To illustrate some features of stable and transient Turing patterns, we perform 1D simulations of the reaction-diffusion equations at different values of the parameters μ, r_a and r_h. In Figure 4A we superpose Figures 3A,B on the plane spanned by parameters μ and r_h for r_a = 6. In this way, we identify the region where stable Turing patterns are found (overlap between R₁ and R₂, light blue); and the region where only transient patterns are observed (R₂, red). Black points in the plane correspond to parameter values used in different numerical simulations. Figure 4B depicts the Turing patterns developed by the activator, for parameters (μ, r_a, r_h) = (1, 6, 10). In both simulations the spatial perturbation is the same, ∝ exp [ − (x − 40)²/0.25], however the simulations differ in the initial spatial distribution to be perturbed. The top panel of Figure 4B corresponds to a perturbation of homogeneous distribution associated with the fixed point S₁ (saddle node), while the bottom panel corresponds to a perturbation of homogeneous distribution associated with the stable fixed point S₂. In the first case the system develops quickly a central pattern, with small wave number. Over time, the ridges split in two, increasing the wave number of the pattern. These splits evidence the transition to a stable Turing pattern with the same wave number as that observed in the bottom panel. We also see in Figure 4B that the amplification rate of the perturbation of S₂ is lower than in the case where S₁ is perturbed.

FIGURE 4

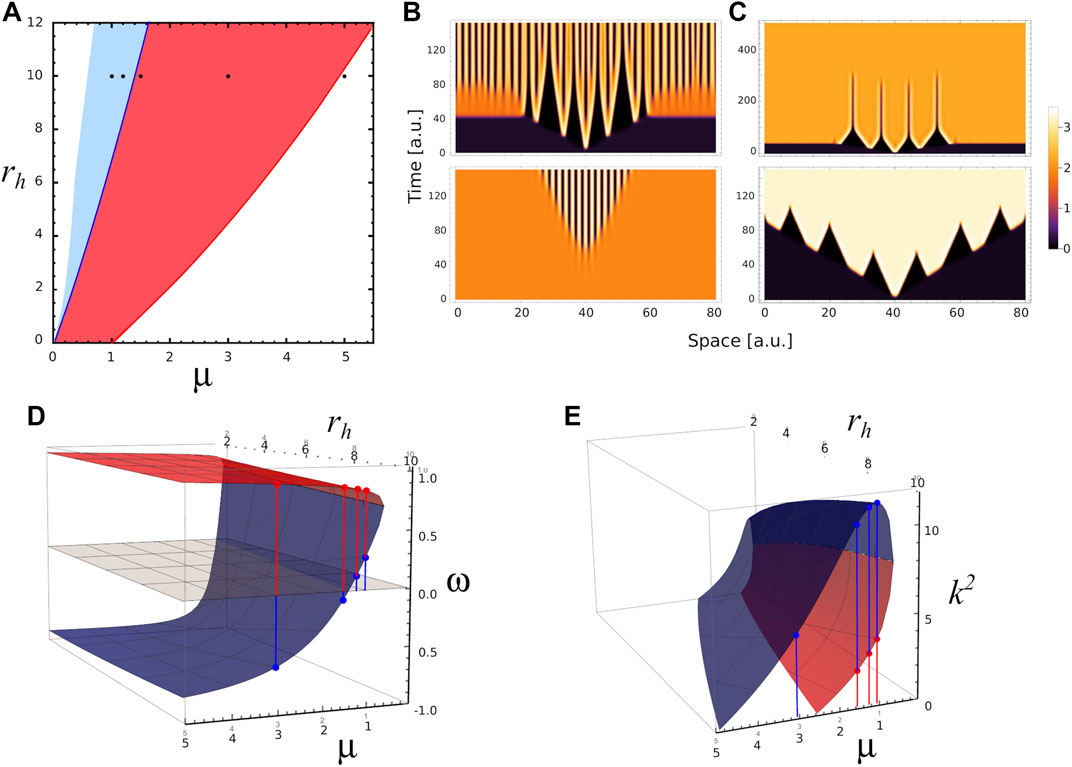
FIGURE 4. Different spatial scales. (A) 2D phase diagram shows the parameters region where the system presents stable Turing patterns (blue area) and unstable or transient Turing patterns (red area) for r_a=6.0. Black dots correspond to different triplet of parameters values (μ, r_a, r_h) where numerical simulation were performed: P₁=(1.0,6,10), P₂=(1.2,6,10) in the Turing pattern region, P₃=(1.5,6,10), P₄=(3.0,6,10) in the transient Turing pattern region, and P₅=(5.0,6,10) in the region for uniform distributions. (B) 1-D numerical simulations showing the temporal evolution of activator concentration distribution a for parameters value P₂ with two different initial conditions. Top (bottom) panel corresponds to the temporal evolution when fixed point S₁ (S₂) is perturbed by a small perturbation at x =40, note the different spatial scales of patterns on the panels. The temporal evolution of a for parameters values P₁, P₃ and P₅ are shown in Supplementary Figure S2. (C) 1-D numerical simulations showing the temporal evolution of a for parameters values P₃ (top panel) and P₄ (bottom panel) when the same fixed point S₁ is perturbed at x = 40. (D) Red and blue surfaces correspond to ω-value as function of μ and r_h associated with fixed points S₁ and S₂, respectively. (E) k²-values as function of μ and r_h associated with S₁ (red surface) and S₂ (blue surface). In both panels D and E, r_a =6.0, and the red and blue dots indicate ω and k² values for P₁, P₂, P₃ and P₄ in each case.

We also perform numerical simulations in the region of transient patterns for μ = 1.5 and 3.0 (top and bottom panels of Figure 4C), when a small perturbation is applied on fixed point S₁. In these cases the system makes a transition to a stable homogeneous distribution associated with state S₂. These transitions occur in a spatially heterogeneous manner, as long as ω(S₁) and $k_{\max }^2$ computed over S₁ are positive. One can also note in Figure 4C that the decay times to homogeneous state S₂ in top panel is lower than in bottom panel. This aspect will be discussed in the next section. Illustrative simulations, corresponding to the points μ = 1.2 and 5.0, showed in the parameter space Figure 4A, can be appreciated in Supplementary Figure S2. Figure 4D shows ω as function of μ and r_h with r_a = 6.0, computed for steady states S₁ (red sheet) and S₂ (blue sheet). Similarly, Figure 4E depicts $k_{\max }^2$ for these steady states, for the same parameters. The points/bars at μ = 1.0, 1.2, 1.5 and 3.0 indicate the values at which numerical simulations were performed. For all cases, we can see that $\omega \left(S_1\right)\ge \omega \left(S_2\right)$. Further, ω(S₂) can present positive and negative values, while ω(S₁) is always positive. Thus, only simulations for μ = 1.0 and 1.2 fall in the region of stable Turing patterns, since ω(S₂) > 0 is required. Transient Turing patterns are observed for μ = 1.5 and 3.0, i.e., when $\omega \left(S_1\right)>0$ and $\omega \left(S_2\right)<0$ (red region of Figure 4A). In addition, we can also note in Figure 4E that $k_{\max }^2(S_1)\le k_{\max }^2(S_2)$, indicating that the characteristic size of the initial pattern is greater than that one related to the stable Turing pattern, which agrees with the simulations shown in panels of Figure 4B.

3.4 Metastable spatial patterns

In an effort to further understand the transient patterns exhibited by our model, Figure 5 depicts analyses and simulations for r_a = 2.5 where there is a narrow region for Turing instabilities (light blue region) and a large region for transient Turing patterns (red region). In this case, the $k_{\max }^2$ is highly folded and the predicted wave number values associated with S₁ and S₂ are very close. However, the rate ω(S₁) has a higher dynamic range than in the case shown in Figure 4. Figure 5B depicts numerical simulations in the region of stable Turing patterns, near the stable-transient patterns interface (P₁ = (3.9, 2.5, 7)). Patterning is reached quickly when the unstable fixed point S₁ is perturbed (top panel of Figure 5B), while a very long transient is observed when the same perturbation is applied to the stable steady state S₂ (bottom panel). Figure 5C depicts numerical simulations for P₂ = (4.1, 2.5, 7) (top panel) and P₃ = (5, 2.5, 7) (bottom panel), both in the region of transient Turing patterns, when a small perturbation is applied on homogeneous distribution at S₁. In the first case, the system develops a spatial pattern that does not end on the course of simulation, while the bottom panel shows a short-lived pattern that finishes in the homogeneous distribution associated with the steady state S₂. The time to reach the patterns showed in Figures 5B,C, and also their sizes, are in agreement with the functions ω and k² (see Figures 5D,E). However, they do not provide information on what determines the duration of the transient patterns.

FIGURE 5

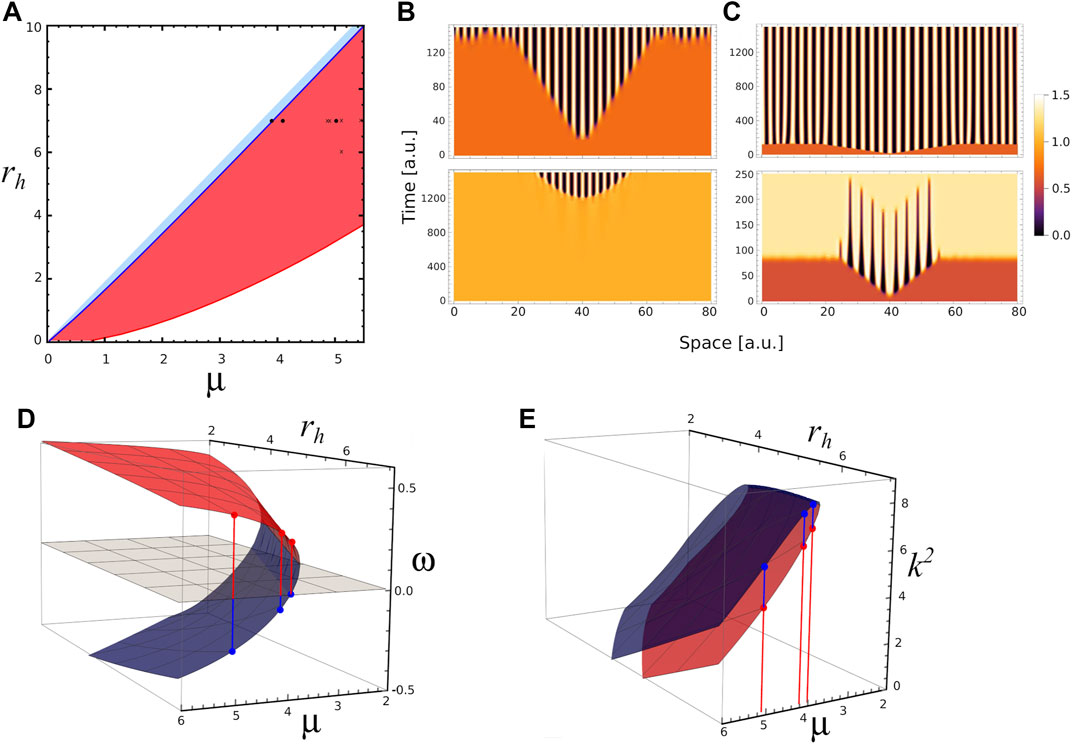
FIGURE 5. Different time scales. (A) 2D phase diagram shows the parameters region where the system presents stable Turing patterns (narrow blue area) and unstable or transient Turing patterns (blue area) for r_a =2.5. Black dots correspond to different triplet of parameters values (μ, r_a, r_h) where numerical simulation were performed: P₁=(3.9,2.5,7), in the Turing pattern region, P₂=(4.1,2.5,7) and P₃=(5.0,2.5,7) in the transient Turing pattern region. The crosses indicate parameters values used on Figure 6. (B) 1-D numerical simulations showing the temporal evolution of activator concentration distribution a for parameters value P₁ with two different initial conditions. Top (bottom) panel corresponds to the temporal evolution when fixed point S₁ (S₂) is perturbed by a small perturbation at x =40, note the different timescales on the panels. (C) 1-D numerical simulations showing the temporal evolution of a for parameters values P₂ (top panel) and P₃ (bottom panel) when the same fixed point S₁ is perturbed at x =40, note the different timescales on the panels. (D) Red and blue surfaces correspond to ω-value as function of μ and r_h (r_a =2.5) associated with fixed points S₁ and S₂, respectively. (E) k²-values as function of μ and r_h associated with S₁ (red surface) and S₂ (blue surface). Red and blue dots indicate k² values for P₁, P₂ and P₃ in each case.

Regarding the pattern on Figure 5C, we hypothesise that when the parameter values approach to the boundary between regions of stable and transient Turing patterns (blue line in Figure 5A), the resulting transient patterns would be associated with larger half-lives. Let us define the persistence time of a transient pattern, τ, as the duration of the central ridge, that is before it merges with the neighbours ones; and b as the Euclidean distance from actual parameters value to the boundary between regions of stable and transient Turing patterns. Following our ansatz, we compute the persistence time τ on several transient patterns, depicted on panels A–E of Figure 6, obtained for r_a = 2.5, and different values of r_h and μ. Also, Figure 6F depicts the persistence time as function of the distance b. Interestingly, the plot suggests that near Turing-patterns boundary the persistence time exhibits a singularity at b_c. This means that, in this region of the parameters space (r_a = 2.5 and r_h ≈ 7.0), a system operating with parameters value corresponding to b smaller than b_c will present patterns with infinite persistence time, i.e. metastable patterns. This is the case of the top panel of Figure 5C. This could be a particular characteristic of this region, since no metastable patterns were observed in the parameter region studied in Figure 4 (r_a = 6), where transient patterns were also observed.

FIGURE 6

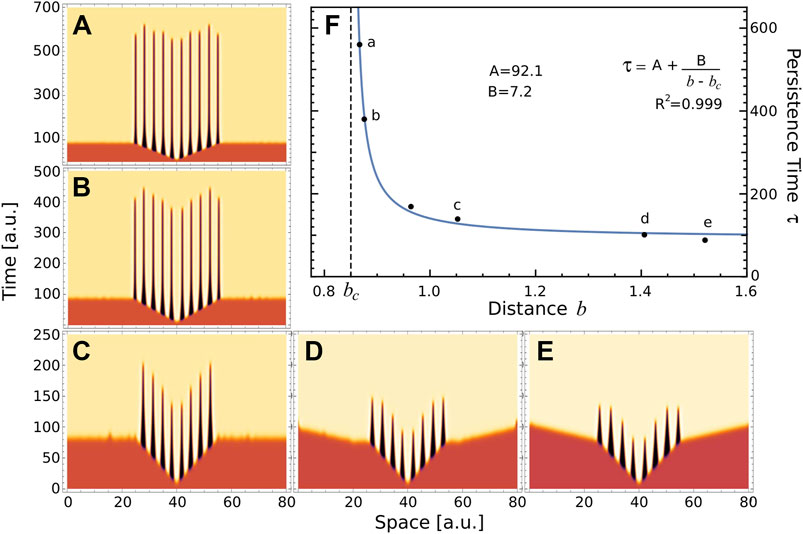
FIGURE 6. Persistence time. (A–E) These panels depict the temporal evolution of a, when the uniform distribution associated with fixed point S₁ is perturbed at x =40, for different values of the parameters (μ, r_a, r_h)=(4.89,2.5,7) (A) (4.9, 2.5,7) (B) (5.1,2.5,7) (C) (5.5,2.5,7) (D) and (5.1,2.5,6) (E). These parameters values were indicated by crosses on 5A. (F) Raster-plot of persistence time τ and distance b for the numerical simulations (A–E) and also P₃=(5.0,2.5,7) depicted in bottom panel of 5C. Blue line corresponds to the rational function A+ B/(b − b_c), where the value of parameters were obtained by nonlinear fitting (A =92.1, B =7.2 and b_c =0.85). Letters a-e indicated the corresponding panel.

These results suggest the existence of a new interface separating two types of transients Turing patterns associated to S₁: those with finite τ and the metastable patterns. Although establishing the mechanisms that determine this interface is beyond the scope of this work, we believe that the morphogenetic model proposed by Diambra et al. could be suitable for such study. To the best of our knowledge, transient and metastable patterns arising from Turing instability mechanism have not been previously reported.

3.5 Turing patterns in 2D

As noticed in the previous subsections, the trajectory of the system upon perturbation depends on whether the system is initially on state S₁ or S₂, however the final states after a transient are the same (as shown in Figure 4B, Figure 5B). We wonder if this also happens in two dimensions. And to answer this question we performed numerical simulations of Eqs. 4 and 5 in a 2D region Ω = [0, 40] × [0, 40] with periodic boundary conditions. In order to solve the equations, we discretized space and time using NDSolve routine in Mathematica 12.1, in which we take Δx = Δy = 0.01. The temporal step size used is adaptative so that the estimated error in the numerical solution is lower than 10^–6. We consider the same perturbation $\exp [-\left.({(x-20)}^6+{(y-20)}^6)\right)/1.5]$ at the centre of Ω applied to two different initial conditions: 1) uniform distributions of a and h, at concentrations fixed by steady point S₂; and 2) in a similar fashion but considering the steady point S₁. The parameters value used in this numerical experiment are (μ, r_a, r_h) = (0.25, 10, 5) which fall in the region of stable Turing patterns (blue region in Figure 7A). Figure 7B depicts the density plots of a at different times when the stable steady point S₂ is perturbed. In this case the perturbation propagates from the centre, forming radial stripes (Supplementary Movie S1B). On the other hand, when the initial condition corresponds to the steady point S₁, the system develops a pattern based on spots with splitting dynamics. In this case, the initial perturbation first divides in four spots, each of which in turn splits tangentially into two other spots. Each of the resulting eight spots split again, but now in radial manner. The spots are distributed in a circular shape with the same radius as the circular bands of the previous case (Supplementary Movie S2). The stripes (spots) stabilise after formation (splitting) and the activity concentrate at expanding Frontier. Although the characteristic sizes are preserved, the resulting 2D patterns are different depending on whether the initial condition is close to S₁ or S₂.

FIGURE 7

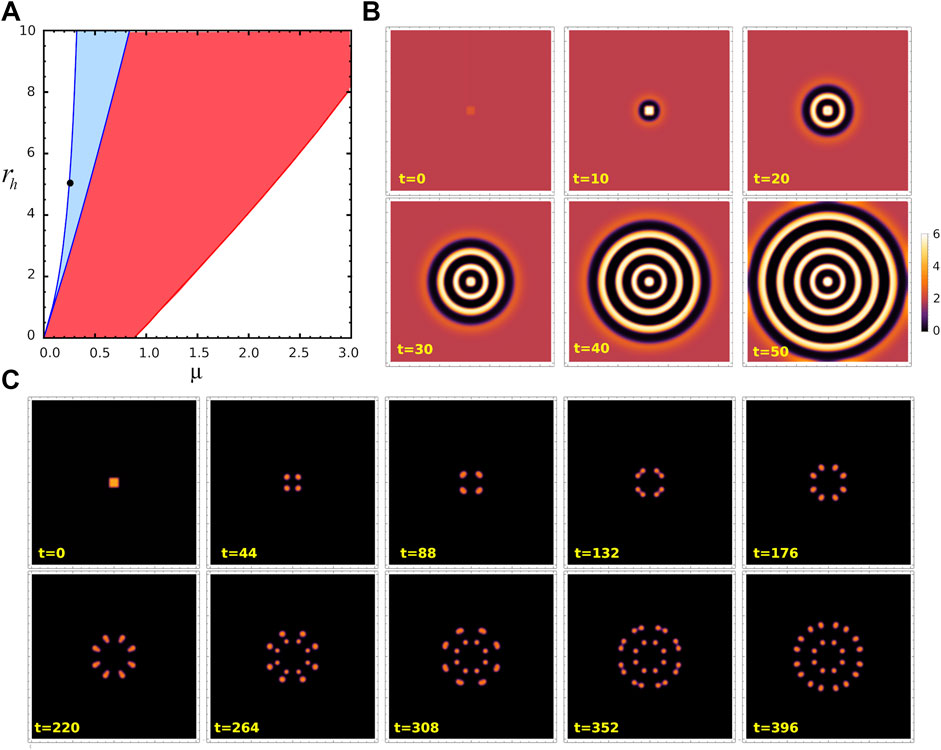
FIGURE 7. Turing patterns in 2D. (A) Parameter region where stable Turing patterns (blue) and unstable Turing patterns (red) can be found, for r_a =10. Black dot corresponds to (μ, r_a, r_h)=(0.25,10,5)= P₁, in the stable Turing pattern region. (B) Snapshots from space-temporal 2D simulations showing activator concentration pattern for parameters value P₁ at different time t. These panels corresponds to the case when fixed point S₂ is perturbed by a small perturbation at the centre of the field. (C) Snapshots from space-temporal 2D simulations showing a for the same parameters value, when uniform distribution associated to fixed point S₁ is perturbed by the same perturbation. The region considered is 40×40 with periodic conditions. Animated Movies associated to these simulations are available as Supplementary Movies S1 and S2.

4 Discussion and conclusion

In this paper we have analysed a two-gen reaction–diffusion system that operates under only one regulatory function, as previously proposed by [18]. The non-diffusive model presents three fixed points. One of them corresponds to the trivial solution and is referred to as S₀, while the other two non-trivial solutions, identified as S₁ and S₂, are originated in a saddle-node bifurcation. We obtain analytically that the saddle-node bifurcation defines a surface in the 3D parameter space. The trivial solution S₀ is a stable node and S₁ is an unstable saddle-point for all the parameter region studied. On the other hand, S₂ is stable for a certain region of the parameter space and when perturbed can also present oscillations and a stable limit circle. In the region of unstable spirals of S₂, oscillations drive the system to the trivial steady-state S₀, while stable spirals are damped until the perturbed system reaches S₂.

To derive the Turing-instability conditions, one requires an stable homogeneous steady state, like S₂, to guarantee that instabilities will be solely spatially dependent. However, diffusion-driven patterns can also raise up from an unstable steady state, like S₁. In fact, by linearizing the spatial version of the model around these steady states we found that both points have associated a dispersion relation where ω > 0 and k > 0, indicating the presence of a spatial patterns. We denote the parameter region where S₁ has ω > 0 and k > 0 as R₁. Similarly, in R₂ the steady state S₂ has ω > 0 and k > 0. We observe that R₁ is greater than R₂ and R₂ is included in R₁.

The final state of the system, when a small spatial perturbation is applied to S₁ or S₂ fixed points, depends on where the parameters value falls relative to R₁ or R₂. As expected, we observe that a spatial perturbation of the S₂ state, for parameters values belong to R₂, leads to stable Turing patterns. On the other hand, if S₂ is perturbed for parameters values outside R₂, no pattern will be developed. When S₁ is perturbed for parameter values that are in the intersection region of R₁ and R₂, then a spatially heterogeneous transition to stable Turing patterns with sizes typical of the S₂ state develops. In this sense we have seen examples where the initial peaks with typical size of the state S₁ split. But if the values of the parameters fall outside R₂ and inside R₁, the system develops in the face of disturbance a transient spatial pattern whose typical size is predicted by the dispersion relation in S₁. In the region of the parameter space with low r_a-value, the system can present transitory patterns, as well as metastable patterns. In the former case, we observed that the persistence time of these transitory patterns is related to the distance between the value of the system parameters and the boundary between regions of stable and transient Turing patterns. We found that this dependence has a singularity which delimits a new boundary between metastable patterns and transient patterns with finite time life. However, the present analysis did not allow to determines the boundary, in the parameters space, separating metastable patterns and short transients.

Furthermore, in the synthetic patterning endeavour is critical the range of kinetic parameters, Hill coefficient and diffusion ratio between activator and inhibitor, that support Turing patterns development [18]. Consequently, alternatives to reduce the requirement for differential diffusion are always welcomed. The present results show that transient patterns can expand the parameter space for an initial breaking-symmetry. These initial patterns, although transient, could induce other gene regulatory circuits able to stabilise patterning but without breaking-symmetry ability. In this manner, transient patterns could play a role in developmental biology as breaking-symmetry triggers rather than to be responsible for the whole patterning process. We believe that the current findings open the door to further theoretical studies which can offer new insights into the nature of patterning mechanisms in developmental biology.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

LD conceived the paper. NG and LD developed the structure and design of the manuscript. NG and LD developed the analysis, and algorithms and wrote the manuscript. Both NG and LD revised the manuscript and approved the final version.

Funding

This research was supported by CONICET, Argentine (PIP N° 0597 and PIP N° 1748).

Acknowledgments

NG and LD are reasearchers at the CONICET (Argentine). We are thankful for Karina Mazzitello’s judicious comments on the manuscript, and Celina Guisoni’s help in preparing graphics.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.927152/full#supplementary-material

References

1. Turing AM. The chemical basis of morphogenesis. Philos Trans R Soc B (1952) 237:37. doi:10.1098/rstb.1952.0012

CrossRef Full Text | Google Scholar

2. Meinhardt H, Gierer A. Applications of a theory of biological pattern formation based on lateral inhibition. J Cel Sci (1974) 15:321. doi:10.1242/jcs.15.2.321

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Asai R, Taguchi E, Kume Y, Saito M, Kondo S. Zebrafish leopard gene as a component of the putative reaction-diffusion system. Mech Dev (1999) 89:87–92. doi:10.1016/s0925-4773(99)00211-7

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Painter KJ, Maini PK, Othmer HG. Stripe formation in juvenile pomacanthus explained by a generalized Turing mechanism with chemotaxis. Proc Natl Acad Sci U S A (1999) 96:5549–54. doi:10.1073/pnas.96.10.5549

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Diambra L, Costa LDF. Pattern formation in a gene network model with boundary shape dependence. Phys Rev E (2006) 73:031917. doi:10.1103/PhysRevE.73.031917

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Yamaguchi M, Yoshimoto E, Kondo S. Pattern regulation in the stripe of zebrafish suggests an underlying dynamic and autonomous mechanism. Proc Natl Acad Sci U S A (2007) 104:4790–3. doi:10.1073/pnas.0607790104

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Kondo S, Miura T. Reaction-diffusion model as a framework for understanding biological pattern formation. Science (2010) 329:1616–20. doi:10.1126/science.1179047

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Salazar-Ciudad I, Jernvall J. A computational model of teeth and the developmental origins of morphological variation. Nature (2010) 464:583–6. doi:10.1038/nature08838

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Sheth R, Marcon L, Bastida MF, Junco M, Quintana L, Dahn R, et al. Hox genes regulate digit patterning by controlling the wavelength of a Turing-type mechanism. Science (2012) 338:1476–80. doi:10.1126/science.1226804

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Economou AD, Ohazama A, Porntaveetus T, Sharpe PT, Kondo S, Basson MA, et al. Periodic stripe formation by a Turing mechanism operating at growth zones in the mammalian palate. Nat Genet (2012) 44:348–51. doi:10.1038/ng.1090

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Inaba M, Chuong CM. Avian pigment pattern formation: developmental control of macro-(across the body) and micro-(within a feather) level of pigment patterns. Front Cel Dev Biol (2020) 8:620. doi:10.3389/fcell.2020.00620

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Basu S, Gerchman Y, Collins CH, Arnold FH, Weiss R. A synthetic multicellular system for programmed pattern formation. Nature (2005) 434:1130–4. doi:10.1038/nature03461

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Kämpf MM, Engesser R, Busacker M, Hörner M, Karlsson M, Zurbriggen MD, et al. Rewiring and dosing of systems modules as a design approach for synthetic mammalian signaling networks. Mol Biosyst (2012) 8:1824. doi:10.1039/c2mb05509k

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Karig D, Martini KM, Lu T, DeLateur NA, Goldenfeld N, Weiss R, et al. Stochastic Turing patterns in a synthetic bacterial population. Proc Natl Acad Sci U S A (2018) 115:6572–7. doi:10.1073/pnas.1720770115

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Konow C, Somberg NH, Chavez J, Epstein IR, Dolnik M. Turing patterns on radially growing domains: experiments and simulations. Phys Chem Chem Phys (2019) 21:6718–24. doi:10.1039/c8cp07797e

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Santos-Moreno J, Schaerli Y. Using synthetic biology to engineer spatial patterns. Adv Biosyst (2019) 3:1800280. doi:10.1002/adbi.201800280

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Luo N, Wang S, You L. Synthetic pattern formation. Biochemistry (2019) 58:1478–83. doi:10.1021/acs.biochem.8b01242

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Diambra L, Senthivel VR, Menendez DB, Isalan M. Cooperativity to increase Turing pattern space for synthetic biology. ACS Synth Biol (2015) 4:177–86. doi:10.1021/sb500233u

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Marcon L, Diego X, Sharpe J, Müller P. High-throughput mathematical analysis identifies Turing networks for patterning with equally diffusing signals. Elife (2016) 5:e14022. doi:10.7554/elife.14022

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Lengyel I, Kádár S, Epstein IR. Transient Turing structures in a gradient-free closed system. Science (1993) 259:493–5. doi:10.1126/science.259.5094.493

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Kadar S, Lengyel I, Epstein IR. Modeling of transient Turing-type patterns in the closed chlorine dioxide-iodine-malonic acid-starch reaction system. J Phys Chem (1995) 99:4054–8. doi:10.1021/j100012a028

CrossRef Full Text | Google Scholar

22. Szalai I, De Kepper P. Turing patterns, spatial bistability, and front instabilities in a reaction-diffusion system. J Phys Chem A (2004) 108:5315–21. doi:10.1021/jp049168n

CrossRef Full Text | Google Scholar

23. Di Patti F, Lavacchi L, Arbel-Goren R, Schein-Lubomirsky L, Fanelli D, Stavans J, et al. Robust stochastic Turing patterns in the development of a one-dimensional cyanobacterial organism. Plos Biol (2018) 16:e2004877. doi:10.1371/journal.pbio.2004877

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Elvin AJ, Laing CR, Roberts MG. Transient Turing patterns in a neural field model. Phys Rev E (2009) 79:011911. doi:10.1103/PhysRevE.79.011911

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Carvalho A, Menendez DB, Senthivel VR, Zimmermann T, Diambra L, Isalan M, et al. Genetically encoded sender-receiver system in 3D mammalian cell culture. ACS Synth Biol (2014) 3:264–72. doi:10.1021/sb400053b

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Senthivel VR, Sturrock M, Piedrafita G, Isalan M. Identifying ultrasensitive hgf dose-response functions in a 3d mammalian system for synthetic morphogenesis. Sci Rep (2016) 6:39178. doi:10.1038/srep39178

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Carr J, Pego RL. Metastable patterns in solutions of u_t = ε²u_xx −f(u). Commun Pure Appl Math (1989) 42:523–76. doi:10.1002/cpa.3160420502

CrossRef Full Text | Google Scholar

28. Folino R, Plaza RG, Strani M. Metastable patterns for a reaction-diffusion model with mean curvature-type diffusion. J Math Anal Appl (2021) 493:124455. doi:10.1016/j.jmaa.2020.124455

CrossRef Full Text | Google Scholar

29. Sick S, Reinker S, Timmer J, Schlake T. WNT and DKK determine hair follicle spacing through a reaction-diffusion mechanism. Science (2006) 314:1447–50. doi:10.1126/science.1130088

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Scholes NS, Schnoerr D, Isalan M, Stumpf MP. A comprehensive network atlas reveals that Turing patterns are common but not robust. Cel Syst (2019) 9:243–2574. doi:10.1016/j.cels.2019.07.007

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Gutierrez PS, Monteoliva D, Diambra L. Role of cooperative binding on noise expression. Phys Rev E (2009) 80:011914. doi:10.1103/physreve.80.011914

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Gutierrez PS, Monteoliva D, Diambra L. Cooperative binding of transcription factors promotes bimodal gene expression response. PLoS ONE (2012) 7:44812. doi:10.1371/journal.pone.0044812

PubMed Abstract | CrossRef Full Text | Google Scholar