Significance of Ramped Temperature in the Dynamics of Unsteady Viscoelastic Fluid Subjected to Lorentz Force

Viscoelastic fluids, such as polymers, paints, and DNA suspensions, are almost everywhere and very useful in the industry. This article aims to study the significance of ramped temperature in the dynamics of viscoelastic fluid. Magnetohydrodynamic (MHD) effect is considered in the presence of Lorentz force. The flow is considered in a porous medium using generalized Darcy’s law. Heat transfers through convection, and the fluid near the plate takes heat in a ramped nature. Instead of the classical fluid model which has certain limitations, a generalized model is considered with fractional derivatives of the Atangana–Baleanu type. The well-known technique of Laplace transform was adopted to obtain the solutions which are displayed in various plots with detailed discussion analysis. From the graphical analysis, it is worth noting that the Atangana–Baleanu fractional model shows a good memory effect on the dynamics of the viscoelastic fluid as compared to its classical form.

1 Introduction

Viscoelastic fluids (VFs) form a subclass of non-Newtonian fluids such as the blend of a solvent and some polymer. Other examples include paints, DNA suspensions, some biological fluids, and other products from the chemical industry. One of the well-known examples from the list of VFs is an Oldroyd-B fluid (OBF). Due to the non-linear relationship between stress and rate of strain, OBF has the same nature as that of a non-Newtonian fluid. The idea of OBF was introduced in 1950, in the pioneering work [1]. The OBF has many applications in fluid dynamics. This model is the generalization of the Maxwell model. Many researchers analyzed OBFs based on their real-world applications: the authors in Ref. [2] studied unsteady OBF over a vertical plate in a porous medium. The authors in Ref. [3] analyzed the influence of generalized OBFs using numerical simulations. The authors in Ref. [4] developed analytical and numerical solutions of a two-dimensional multi-term time‐fractional OBF model. The authors in Ref. [5] considered generalized OBF flow between two infinite parallel rigid plates and numerically simulated the results. In the literature, the flow of Oldroyd-B is less investigated using ramped wall velocity and temperature. These fluids have many applications in different practical situations and real-world problems [6]. Some researchers tried to investigate ramped wall velocity and temperature in their studies. The authors in Ref. [7] examined natural convection in polyethylene glycol-based molybdenum disulfide nanofluid under ramped wall condition and other additional effects. The authors in Ref. [8] discussed ramped wall temperature and ramped wall concentration with the Hall effect in an unsteady MHD flow of a second-grade fluid through a porous medium. The authors in Ref. [9] developed a general solution of MHD free convection flows over a vertical plate with ramped wall temperature. The authors in Ref. [10] examined entropy generation in MHD flow over a vertical plate embedded in a porous medium. The authors in Ref. [11] considered ramped wall temperature conditions and studied irreversibility analysis in time-dependent flow past a plate (vertical) with arbitrary wall shear stress. The authors in Ref. [12] studied MHD flow over an inclined plate under a conjugate effect and ramped wall temperature condition in a porous medium.

Recently, many fractional derivative operators have been used for different scientific reasons in the field of fluid dynamics and in many other dynamical systems. Some of these applications are found in fractional-order neurons for parameter estimation, fractional viscoelasticity models, fractional single-phase-lag models of heat conduction, and the eigenproblem of molecular alignment, as discussed in Ref. [13] and in many other references. Sene [14, 15] used fractional derivatives and developed two different fluid models. He obtained exact analytical solutions and plotted results graphically with a detailed discussion analysis. In Ref. [16], the authors studied fractional derivatives together with their various applications in reservoir engineering problems. In Ref. [17], the authors investigated radial basis functions using a fractional derivative approach. In Ref. [18],the authors applied fractional derivatives in the field of physics and modern sciences. In Ref. [19],the authors discussed the theory of fractional derivatives and its application in mathematics, physics, chemistry, and engineering. In Ref. [20],the authors introduced new fractional derivatives (AB fractional derivatives) with non-local and no-singular kernel. They presented some useful and important properties of the new derivative with application in a fractional heat transfer model. After that, this new idea was applied to several other problems. In Ref. [21], the authors applied the Atangana–Baleanu fractional derivative in the Caputo sense to the convective flow of CMC-based CNT nanofluid in a vertical microchannel. In Ref. [22],the authors studied the magnetic field effect on the convection flow of Newtonian viscous fluid past a moving plate such that its temperature is constant at the boundary and its concentration depends on time. The problem is modeled using the Caputo–Fabrizio time fractional derivative. In Ref. [23], the authors used the Caputo time-fractional derivative and examined the natural convection flow through a vertical cylinder. In Ref. [24], Sheikh et al. provided a comparative analysis of Caputo–Fibrizio and Atangana–Baleanu derivatives for a generalized Casson fluid model with heat generation and chemical reaction.

In this work, the idea of fractional derivatives (Atangana–Baleanu fractional derivative in the Caputo sense) is applied to develop a fractional model of OBF. The OBF is considered as electrically conducting and passing through a porous medium. The flow is considered over a vertical plate with ramped heating, which sufficiently influences thermal analysis and the flow itself due to the involvement of convection term in momentum equation (25). This article is arranged in the following sections. Section 2 includes the mathematical modeling of the problem. The governing equations are derived from the constitutive equations of OBF. Initial and boundary conditions are defined. The next section (Section 3) includes solution methodology with a basic definition of the AB fractional derivatives. The solution of energy equation is given in sub-Section 3.1, and the solution of momentum equation is given in sub-Section 3.2. The results are computed and plotted in Section 4 with a detailed discussion analysis. At the end, conclusion remarks are added in Section 5.

2 Mathematical Modeling

This report focuses on the dynamics of incompressible unsteady OBF over a vertical plate. The flow is considered in a porous medium with the magnetic field applied in a perpendicular direction. The equations of continuity and momentum are given as follows:

$\nabla \cdot \overrightarrow{\text{V}}=0,(1)$

$\rho \left[\frac{\partial \overrightarrow{V}}{\partial t}+\left(\overrightarrow{V}\cdot \nabla \right)\overrightarrow{V}\right]=\text{div}\mathbf{T}+\mathbf{J}\times \mathbf{B}+g\rho {\beta }_T(T-T_{\infty })+\Re .(2)$

Here, $\overrightarrow{\text{V}}$ is the velocity vector and $\mathbf{T}$ is the Cauchy stress tensor T.

The velocity field (for one-dimensional and uni-directional flow) is given as follows:

$\overrightarrow{V}=\left[u\left(y,t\right),\mathrm{0,0}\right].(3)$

The corresponding Cauchy stress tensor is given as follows:

$\mathbf{T}=-p\mathbf{I}\mathbf{+S}\text{.}(4)$

Here, $-p\mathbf{I}\text{and}\mathbf{S}$ represent the indeterminate stress tensor and extra stress tensor, respectively. In addition, extra stress tensor $\mathbf{S}$ is given by the following relation:

$\mu \left(1+\frac{{\lambda }_{\Re }.\mathbf{D}}{\mathbf{D}\mathrm{t}\mathbf{ }}\right)\mathbf{=S}\left(1+\frac{\lambda .\mathbf{D}}{\mathbf{D}\mathrm{t}\mathbf{ }}\right),(5)$

where $\mu ,{\lambda }_r,\text{and}\lambda$ show dynamic viscosity, retardation time, and relaxation time, respectively. Furthermore, material time derivative $\frac{\mathbf{D}}{\mathbf{D}\mathrm{t}\mathbf{ }}$ and Rivlin–Ericksen tensor ${\mathbf{A}}_1$ can be written as follows:

$\frac{\mathbf{DS}}{\mathbf{D}\mathrm{t}\mathbf{ }}=\frac{\partial \mathbf{S}}{\partial t}+u\left(\frac{\partial \mathbf{S}}{\partial x}\right)+v\left(\frac{\partial \mathbf{S}}{\partial y}\right)+w\left(\frac{\partial \mathbf{S}}{\partial z}\right),(6)$

${\mathbf{A}}_1=\nabla .\overrightarrow{V}+{\left(\nabla .\overrightarrow{V}\right)}^T=\left[\begin{array}{l}0u_y\\ u_{y}0\end{array}\right].(7)$

In the given study, we have considered Oldroyd-B fluid; therefore, modified Darcy’s law can be written in the following form:

$-\frac{\mu \varphi }{k_0}\left(1+{\lambda }_{\Re }\frac{\partial }{\partial t}\right).\overrightarrow{V}=\left(1+\lambda \frac{\partial }{\partial t}\right)\Re ,(8)$

where $\varphi$ represents the porous medium and $k$ represents permeability of the porous medium.

From Maxwell equations,

$\overrightarrow{\nabla }\cdot \mathit{B}=0,(9)$

$\overrightarrow{\nabla }\times \overrightarrow{E}=-\frac{\partial \mathit{B}}{\partial E}=0,\mathrm{where}E=0.(10)$

Here, $E$ is the total electric field. By Ohm’s law (generalized form),

$\mathit{J}=\sigma \left(\overrightarrow{E}+\overrightarrow{V}\times \mathit{B}\right)=\sigma \left(\overrightarrow{V}\times \mathit{B}\right).(11)$

The cross product with the magnetic field gives

$\mathit{J}\times \mathit{B}=\sigma \left(\overrightarrow{V}\times \mathit{B}\right)\times \mathit{B}\mathit{B}=B_0+b,(12)$

Here, $B_0$ is the applied magnetic field and $b$ is the induced magnetic field by polarization (perturbation produced by fluid motion).

Eq. 12 further reduces to

$\mathit{J }\times \mathit{B}=-\sigma \left\{\mathit{B}\times \left(\overrightarrow{V}\times \mathit{B}\right)\right\}=-\sigma \left\{\left(\mathit{B}\cdot \mathit{B}\right)\overrightarrow{V}-\left(\mathit{B}\cdot \overrightarrow{V}\right)\mathit{B}\right\}(13)$

$\mathit{J}\times \mathit{B}=-\sigma \left\{\left(\mathit{B}\cdot \mathit{B}\right)\overrightarrow{V}-0\right\}=-\sigma {\mathit{B}}_0^{2}u.(14)$

In view of Eqs 3–14, equations take the following form:

$\rho \left(1+\lambda \frac{\partial }{\partial t}\right)\frac{\partial u}{\partial t}=\mu \left(1+{\lambda }_{\Re }\frac{\partial }{\partial t}\right)\frac{{\partial }^{2}u}{\partial y^2}-\sigma {\mathit{B}}_0^2\left(1+\lambda \frac{\partial }{\partial t}\right)u-\frac{\mu \varphi }{k_0}\left(1+{\lambda }_{\Re }\frac{\partial }{\partial t}\right)u+g\rho {\beta }_T\left(1+\lambda \frac{\partial }{\partial t}\right)\left(T-T_{\infty }\right).(15)$

Similarly, the temperature equation in the presence of thermal radiation and heat generation is given as follows:

$\rho C_p\frac{\partial T}{\partial t}=k\frac{{\partial }^{2}T}{\partial y^2}-\frac{\partial q_r}{\partial y}+H_0\left(T-T_{\infty }\right).(16)$

Here, $\rho C_p,q_r,k,\text{and}{H}_0$ are heat capacitance, radiation, thermal conductivity, and heat generation constant, respectively. Eq. 16 is the same as Eq. 8 in Ref. [24].

The radiative heat flux $q_r^{\prime }$ is given as follows:

$q_r=\frac{-4{\sigma }_1}{3k_1}\frac{\partial T^4}{\partial y},(17)$

Using the Taylor series expansion to linearized $T^4$ given in Eq. 17, we get

$T^4=4T{T}_{\infty }^3-3T{T}_{\infty }^4(18)$

Substituting the result obtained in Eq. 18 into Eq. 17 yields

$\frac{\partial q_r}{\partial y}=-\frac{16{\sigma }_1}{3k_1}{T}_{\infty }^3\frac{{\partial }^{2}T}{\partial y^2}.(19)$

Substituting Eq. 19 in Eq. 16 gives

$\rho C_p\frac{\partial T}{\partial t}=k\left(1+\frac{16{\sigma }_1}{3k{k}_1}{T}_{\infty }^3\right)\frac{{\partial }^{2}T}{\partial y^2}+H_0\left(T-T_{\infty }\right).(20)$

The following constraints on the physical model are imposed. Initially, when time $t=0$, the fluid and plate were at rest at initial temperature $T_w$. At time $t>0$, both the temperature and velocity are higher or lower than $T_{\infty }+\left(T_w-T_{\infty }\right)\frac{t}{t_0}$ and $u_0\frac{t}{t_0}$ when $t<t_0$, respectively. This condition is also known as ramped condition for temperature and velocity. But when $t\ge t_0$, the temperature and velocity remain unchanged. In other words, for small values of time, the temperature and velocity are referred to as ramped velocity and temperature, while for greater values of time, the velocity and temperature are known as isothermal velocity and temperature.

Under the aforementioned assumption, the following initial and boundary conditions are defined:

$\begin{array}{l}u\left(y,t\right)=0,T\left(y,t\right)=T_{\infty },\text{for}y\mathit{>0}\text{and}t\mathit{=0,}\\ u\left(y,t\right)=\{\begin{array}{l}{u}_0\frac{t}{t_0}\text{if}0<t<t_0\\ u_{0}i\text{f}t>t_0\end{array},\text{for}y\mathit{=0}\text{and}t\mathit{>0,}\\ T\left(y,t\right)=\{\begin{array}{l}{T}_{\infty }+\left(T_w-T_{\infty }\right)\frac{t}{t_0}\text{if}0<t<t_0\\ T_{w}i\text{f}t>t_0\end{array},\text{for}y=0\text{and}t>0,\\ u\left(y,t\right)=0,T\left(y,t\right)=T_{\infty },\text{for}y\to \infty \text{and}t>0.\end{array}\}(21)$

The following dimensionless variables are used for dimensional analysis:

$\eta =\frac{u}{u_0},\xi =\frac{u_{0}y}{\nu },\tau =\frac{t{u}_0^2}{\upsilon },{\tau }_0=\frac{\upsilon }{u_0^2},\mathrm{\Theta }=\frac{T-T_{\infty }}{T_w-T_{\infty }},(22)$

Introducing the aforementioned equation in Eq. 15, 20, the following non-dimensional system is obtained:

$\left(m_0+{\lambda }_0\frac{\partial }{\partial \tau }\right)\frac{\partial \eta }{\partial \tau }=\left(1+{\lambda }_1\frac{\partial }{\partial \tau }\right)\frac{{\partial }^2\eta }{\partial {\xi }^2}-m_1\eta +Gr\left(1+{\lambda }_0\frac{\partial }{\partial \tau }\right)\mathrm{\Theta }(23)$

$\frac{\partial \mathrm{\Theta }}{\partial \tau }=\left(\frac{1+Nr}{\mathrm{Pr}}\right)\frac{\partial \mathrm{\Theta }}{\partial {\xi }^2}+H_1\mathrm{\Theta },(24)$

with transformed initial and boundary conditions

$\begin{array}{l}\eta \left(\xi ,\tau \right)=0,\mathrm{\Theta }\left(\xi ,\tau \right)=0\text{for}\xi >\text{0}\text{and}\tau =\text{0}\\ {\eta }_{\tau }\left(\xi ,\tau \right)=0,{\eta }_{\xi }\left(\xi ,\tau \right)=0\text{for}\xi >0\text{and}\tau =\text{0}\end{array}(25)$

$\begin{array}{l}\eta \left(\xi ,\tau \right)=\{\begin{array}{l}\tau 0<\tau \le 1\\ 1\tau >1\end{array}\text{for}\xi =\text{0}\text{and}\tau \text{>}0\\ \mathrm{\Theta }\left(\xi ,\tau \right)=\{\begin{array}{l}\tau 0<\tau \le 1\\ 1\tau >1\end{array}\text{for}\xi =\text{0}\text{and}\tau \text{>}0\end{array}\}(26)$

and the non-dimensional parameters and constants are as follows:

$M=\frac{\sigma {\mathit{B}}_0^2\nu }{u_0^2\rho },\mathrm{Pr}=\frac{\mu C_p}{k},Gr=\frac{g{\beta }_T\nu \left(T_w-T_{\infty }\right)}{u_0^3},$

$\frac{1}{K}=\frac{{\upsilon }^2\varphi }{k_0{u}_0^2},Nr=\frac{16{\sigma }_1}{3k{k}_1}{T}_{\infty }^3,{\lambda }_0=\frac{\lambda u_0^2}{\upsilon },{\lambda }_1=\frac{{\lambda }_{\Re }{u}_0^2}{\upsilon }$

$H_1=\frac{H_0{\upsilon }^2}{k{u}_0^2},m_0=1+{\lambda }_{0}M+\frac{{\lambda }_1}{K},m_1=M+\frac{1}{K}.$

3 Research Methodology: Atangana–Baleanu Fractional Derivative

To transform the OBF classical model into the Atangana–Baleanu (AB) fractional model of order $\beta$, it is required to first define the Atangana–Baleanu fractional derivative as follows:

Definition: The Atangana–Baleanu (AB) time fractional derivative in the Caputo sense, with fractional order $\beta$, is defined as [20, 21]

${}^{AB}{{\displaystyle \mathbf{D}}}_{\tau }^{\beta }F\left(\tau \right)=\frac{B\left(\beta \right)}{\left(1-\beta \right)}{\displaystyle \underset{0}{\overset{\tau }{\int }}{F}^{\prime }\left(\chi \right)E_{\beta }\left(\frac{-\beta {\left(\tau -\chi \right)}^{\beta }}{1-\beta }\right)}d\chi ,(27)$

where $B\left(\beta \right)$ is the normalization function, $B\left(1\right)=B\left(0\right)=1$ and $\beta \in \left[\mathrm{0,1}\right].$

Here, $E_{\beta }$ is the generalized form of the Mittag–Leffler function, which is defined as follows:

$E_{\beta }\left(-t^{\beta }\right)={\displaystyle \sum _{n=0}^{\infty }\frac{{\left(-t\right)}^{\beta n}}{\mathrm{\Gamma }\left(\beta n+1\right)}.}(28)$

The Laplace transform (LT) of the AB fractional derivative in the Caputo sense is given as follows:

$L({}^{AB}{{\displaystyle \mathbf{D}}}_{\tau }^{\beta }F\left(\tau \right))=\frac{s^{\beta }L(F\left(\tau \right))-s^{\beta -1}F\left(0\right)}{\left(1-\beta \right)s^{\beta }+\beta }.(29)$

3.1 Solution of Energy Equation

The non-dimensional classical heat Eq. 24 is transformed into the fractional form by incorporating the AB fractional derivative of order $\beta$ as given in the following:

${}^{AB}{{\displaystyle \mathbf{D}}}_{\tau }^{\beta }\Theta \left(\xi ,\tau \right)=\left(\frac{1+Nr}{\mathrm{Pr}}\right)\frac{{\partial }^2\Theta }{\partial {\xi }^2}+H_1\Theta .(30)$

Note that Eq. 30 is similar to Eq. 12 in Ref. [24]. The Laplace transform is applied to Eq. 30, taking into account the initial condition from Eq. 25, the following transformed equation is obtained:

$\left[\frac{s^{\beta }}{\left(1-\beta \right)s^{\beta }+\beta }\right]\overline{\Theta }\left(\xi ,s\right)=\left(\frac{1+Nr}{\mathrm{Pr}}\right)\frac{{\partial }^2\overline{\Theta }}{\partial {\xi }^2}+H_1\overline{\Theta }.(31)$

Eq. 31 can be written in a more suitable form as follows:

$\frac{s^{\beta }{N}_1}{s^{\beta }+N_2}\overline{\Theta }\left(\xi ,s\right)=\left(\frac{1+Nr}{\mathrm{Pr}}\right)\frac{{\partial }^2\overline{\Theta }}{\partial {\xi }^2}+H_1\overline{\Theta }.(32)$

The solution of Eq. 32 gives

$\overline{\Theta }\left(\xi ,s\right)=c_1{e}^{-\xi \sqrt{\mathrm{Pr}{D}_1\left(s\right)}}+c_2{e}^{\xi \sqrt{\mathrm{Pr}{D}_1\left(s\right)}},(33)$

where $N_1=\frac{1}{1-\beta },N_2=\frac{\beta }{1-\beta },$ and $D_1\left(s\right)=\frac{\left[N_1{s}^{\beta }-H_1\left(s^{\beta }+N_2\right)\right]}{\left(s^{\beta }+N_2\right)\left(1+Nr\right)}.$

Now using the boundary conditions from Eq. 26, Eq. 33 gives the following solution:

$\overline{\Theta }\left(\xi ,s\right)=\left[\frac{1-e^{-s}}{s^2}\right]e^{-\xi \sqrt{\mathrm{Pr}{D}_1\left(s\right)}}.(34)$

After the Laplace inversion, Eq. 34 gives

$\Theta \left(\xi ,\tau \right)={\Theta }_1\left(\tau \right)\otimes {\Theta }_2\left(\xi ,\tau \right),(35)$

where

${\Theta }_1\left(\tau \right)=L^{-1}\left[{\Theta }_1\left(s\right)=\left[\frac{1-e^{-s}}{s^2}\right]\right];{\Theta }_2\left(\xi ,\tau \right)=L^{-1}\left[{\Theta }_2\left(\xi ,s\right)=\left[e^{-\xi \sqrt{\mathrm{Pr}{D}_1\left(s\right)}}\right]\right].$

The $\otimes$ symbol shows the convolution product.

3.2 Solution of Momentum Equation

The fractional form of Eq. 23, after using the Laplace transform method, reduces to the following form:

$\left(m_0+\frac{{\lambda }_0{s}^{\beta }}{\left(1-\beta \right)s^{\beta }+\beta }\right)s\overline{\eta }\left(\xi ,s\right)=\left(1+\frac{{\lambda }_1{s}^{\beta }}{\left(1-\beta \right)s^{\beta }+\beta }\right)\frac{{\partial }^2\overline{\eta }\left(\xi ,s\right)}{\partial {\xi }^2}-m_1\overline{\eta }\left(\xi ,s\right)+Gr\left(1+\frac{{\lambda }_0{s}^{\beta }}{\left(1-\beta \right)s^{\beta }+\beta }\right)\overline{\Theta }\left(\xi ,s\right),(36)$

equivalently

$\left(m_0+\frac{s^{\beta }{\lambda }_0{N}_1}{s^{\beta }+N_2}\right)s\overline{\eta }\left(\xi ,s\right)=\left(1+\frac{s^{\beta }{\lambda }_1{N}_1}{s^{\beta }+N_2}\right)\frac{{\partial }^2\overline{\eta }\left(\xi ,s\right)}{\partial {\xi }^2}-m_1\overline{\eta }\left(\xi ,s\right)+Gr\left(1+\frac{s^{\beta }{\lambda }_0{N}_1}{s^{\beta }+N_2}\right)\overline{\Theta }\left(\xi ,s\right).(37)$

The aforementioned equation can be written in more appropriate forms as follows:

$\left(1+\frac{s^{\beta }{\lambda }_1{N}_1}{s^{\beta }+N_2}\right)\frac{{\partial }^2\overline{\eta }\left(\xi ,s\right)}{\partial {\xi }^2}-\left(m_0+\frac{s^{\beta }{\lambda }_0{N}_1}{s^{\beta }+N_2}\right)s\overline{\eta }\left(\xi ,s\right)-m_1\overline{\eta }\left(\xi ,s\right)=-Gr\left(1+\frac{s^{\beta }{\lambda }_0{N}_1}{s^{\beta }+N_2}\right)\overline{\mathrm{\Theta }}\left(\xi ,s\right),$

$\frac{{\partial }^2\overline{\eta }\left(\xi ,s\right)}{\partial {\xi }^2}-\frac{\left(m_0+\frac{s^{\beta }{\lambda }_0{N}_1}{s^{\beta }+N_2}\right)}{\left(1+\frac{s^{\beta }{\lambda }_1{N}_1}{s^{\beta }+N_2}\right)}s\overline{\eta }\left(\xi ,s\right)-\frac{m_1}{\left(1+\frac{s^{\beta }{\lambda }_1{N}_1}{s^{\beta }+N_2}\right)}\overline{\eta }\left(\xi ,s\right)=-Gr\frac{\left(1+\frac{s^{\beta }{\lambda }_0{N}_1}{s^{\beta }+N_2}\right)}{\left(1+\frac{s^{\beta }{\lambda }_1{N}_1}{s^{\beta }+N_2}\right)}\overline{\mathrm{\Theta }}\left(\xi ,s\right),$

$\frac{{\partial }^2\overline{\eta }\left(\xi ,s\right)}{\partial {\xi }^2}-\frac{\left[\left(m_0\left(s^{\beta }+N_2\right)+s^{\beta }{\lambda }_0{N}_1\right)\right]s}{\left(s^{\beta }+N_2+s^{\beta }{\lambda }_1{N}_1\right)}\overline{\eta }\left(\xi ,s\right)-\frac{m_1\left(s^{\beta }+N_2\right)}{\left(s^{\beta }+N_2+s^{\beta }{\lambda }_1{N}_1\right)}\overline{\eta }\left(\xi ,s\right)=-Gr\frac{\left(s^{\beta }+N_2+s^{\beta }{\lambda }_0{N}_1\right)}{\left(s^{\beta }+N_2+s^{\beta }{\lambda }_1{N}_1\right)}\overline{\mathrm{\Theta }}\left(\xi ,s\right),$

$\frac{{\partial }^2\overline{\eta }\left(\xi ,s\right)}{\partial {\xi }^2}-D_2\left(s\right)\overline{\eta }\left(\xi ,s\right)-D_3\left(s\right)\overline{\eta }\left(\xi ,s\right)=-Gr{D}_4\left(s\right)\overline{\mathrm{\Theta }}\left(\xi ,s\right)\text{,}(38)$

where $D_2\left(s\right)=\frac{\left[m_0\left(s^{\beta }+N_2\right)+s^{\beta }{\lambda }_0{N}_1\right]s}{s^{\beta }+N_2+s^{\beta }{\lambda }_1{N}_1}$; $D_3\left(s\right)=\frac{m_1\left(s^{\beta }+N_2\right)}{\left(s^{\beta }+N_2+s^{\beta }{\lambda }_1{N}_1\right)}$; and $D_4\left(s\right)=\frac{\left(s^{\beta }+N_2+s^{\beta }{\lambda }_0{N}_1\right)}{\left(s^{\beta }+N_2+s^{\beta }{\lambda }_1{N}_1\right)}$.

The solution of the homogeneous part of Eq. 38 is

${\overline{\eta }}_c\left(\xi ,s\right)=c_3{e}^{-\xi \sqrt{D_5\left(s\right)}}+c_4{e}^{\xi \sqrt{D_5\left(s\right)}},(39)$

and the corresponding non-homogeneous part is

${\overline{\eta }}_p\left(\xi ,s\right)=D_6{\left(s\right)}^{-\xi \sqrt{\mathrm{Pr}{D}_1\left(s\right)}};D_5\left(s\right)=D_2\left(s\right)+D_3\left(s\right);D_6=\frac{1-e^{-s}}{s^2\left[\mathrm{Pr}{D}_1\left(s\right)-D_5\left(s\right)\right]}.(40)$

Eqs 39, 40 give the total solution as

${\overline{\eta }}_c\left(\xi ,s\right)=c_3{e}^{-\xi \sqrt{D_5\left(s\right)}}+c_4{e}^{\xi \sqrt{D_5\left(s\right)}}-D_6{\left(s\right)}^{-\xi \sqrt{\mathrm{Pr}{D}_1\left(s\right)}}.(41)$

With the help of the boundary condition given in Eq. 26, and after finding constants, the final solution is

$\overline{\eta }\left(\xi ,s\right)=D_7\left(s\right)e^{-\xi \sqrt{D_5\left(s\right)}}+D_6\left(s\right)e^{-\xi \sqrt{\mathrm{Pr}{D}_1\left(s\right)}};D_7\left(s\right)=\frac{1-e^{-s}}{s^2}-D_6\left(s\right).(42)$

The inverse Laplace transform of Eq. 42 is

$\eta \left(\xi ,\tau \right)=D_7\left(\tau \right)\otimes D_8\left(\xi ,\tau \right)+D_6\left(\tau \right)\otimes D_9\left(\xi ,\tau \right)(43)$

with

$D_6\left(\tau \right)=L^{-1}\left[D_6\left(s\right)\right];D_7\left(\tau \right)=L^{-1}\left[D_7\left(s\right)\right];D_8\left(\xi ,\tau \right)=L^{-1}\left[e^{-\xi \sqrt{D_5\left(s\right)}}\right];D_9\left(\xi ,\tau \right)=L^{-1}\left[e^{-\xi \sqrt{\mathrm{Pr}{D}_1\left(\tau \right)}}\right].$

4 Results and Discussion

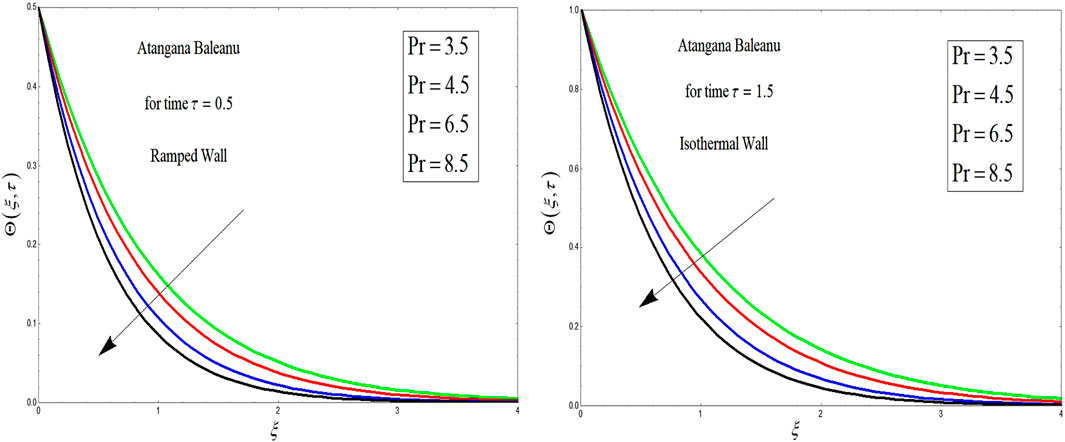
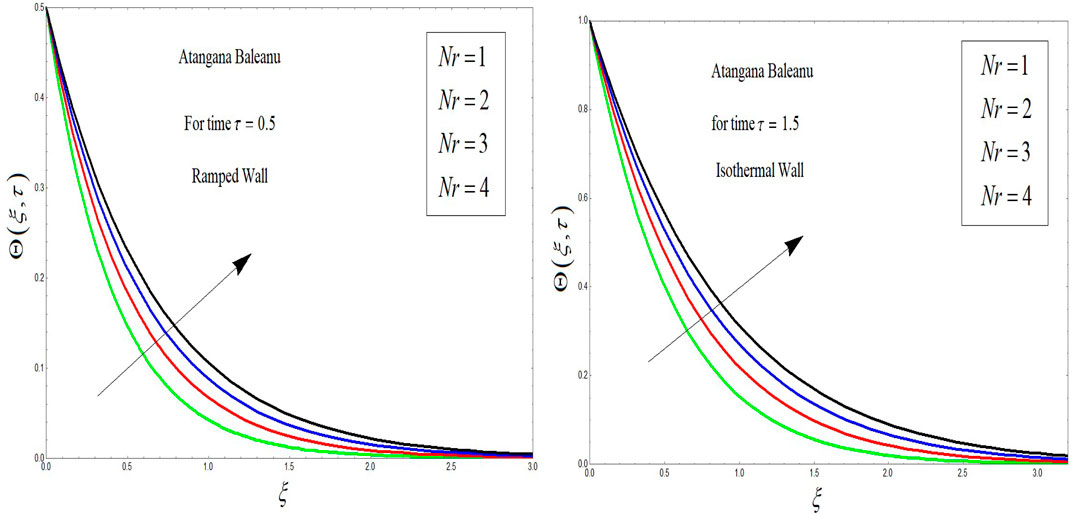
This section provides the graphical analysis of OBF with MHD and porous medium effects with ramped wall velocity and temperature. The problem is formulated in terms of Atangana–Baleanu fractional derivatives. To find the analytical solutions, the Laplace transform technique is applied. All the flow parameters are discussed by graphical analysis. The solutions obtained for the Atangana–Baleanu fractional OBF model have been discussed, and the influence of all parameters is shown. The influence of Grashof number Gr, magnetic number M, Prandtl number Pr, radiation number Nr, and Atangana–Baleanu β is studied in various plots.

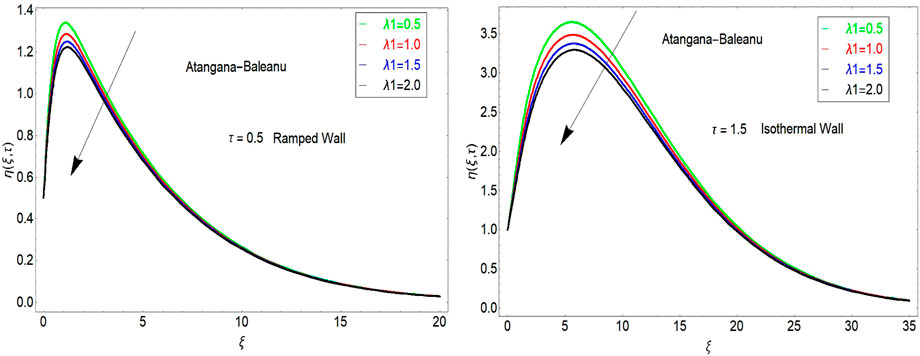
The influence of fractional parameters $\beta$ on velocity profile is highlighted in Figure 1. It is found that an increase in fractional parameters results in a decrease in velocity for both cases of ramped and isothermal temperature. This figure clearly shows that as $\beta \to 1$, the fractional model reduces to the classical OBF model.

FIGURE 1

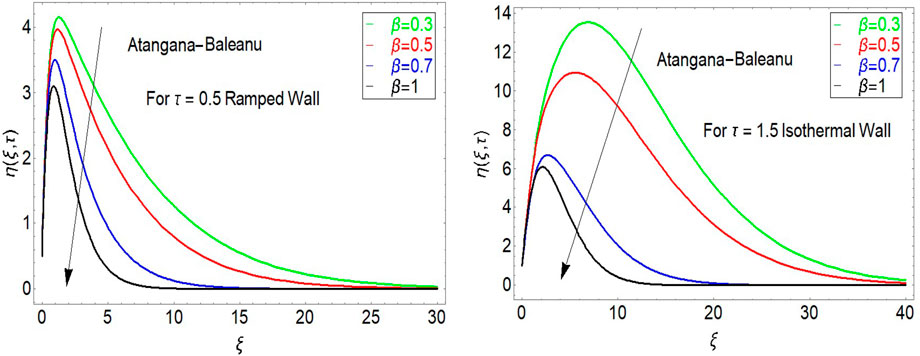
FIGURE 1. Influence of the AB fractional operator on velocity for ramped and isothermal wall temeprature.

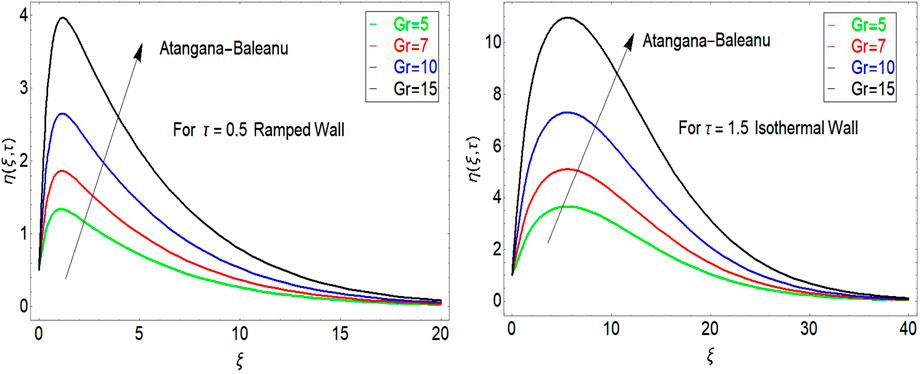
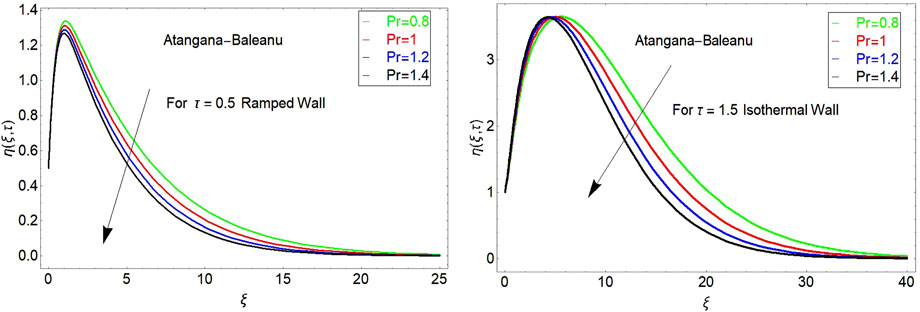
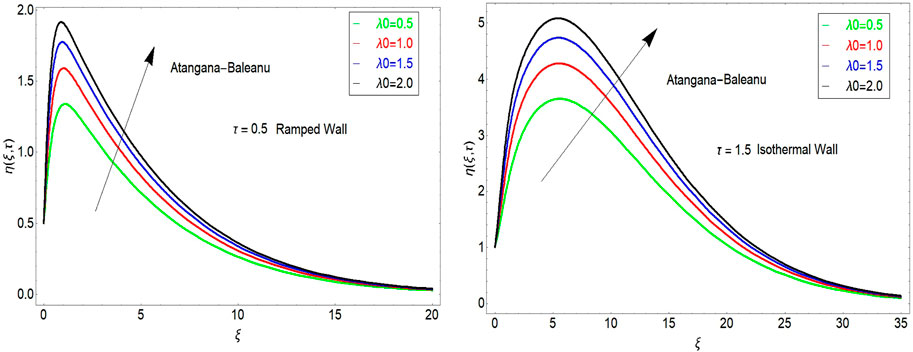
The impact of $Gr$ on velocity profiles is shown in Figure 2. From this figure, it is clear that increasing $Gr$ results in an increase in the buoyancy force, which enables to speed up the fluid motion, thus resulting in an increase in the velocity of OBF. Figure 3 shows the influence of $\mathrm{Pr}$ on AB fractional velocity profiles. From this figure, it can be seen that increasing $\mathrm{Pr}$ results in a decrease in the OBF velocity. Note that the Prandtl number variation is shown only to see its effect on velocity, and its chosen values do not correspond to a specific non-Newtonian liquid. The effect of magnetic parameter on OBF fractional velocity is highlighted in Figure 4. The influence of $M$ on velocity in both cases of ramped and constant temperature increases, resulting in a decrease in the velocity. However, the variation in velocity profiles in case of constant temperature is more visible. It is true physically as increasing $M$ leads to an increase in the Lorentz forces, and as a result, the retardation force increases and hence the fluid velocity decreases.

FIGURE 2

FIGURE 2. Influence of Gr on velocity for constant and ramped temperature.

FIGURE 3

FIGURE 3. Influence of Pr on velocity for constant and ramped temperature.

FIGURE 4

FIGURE 4. Influence of M on velocity for constant and ramped temperature.

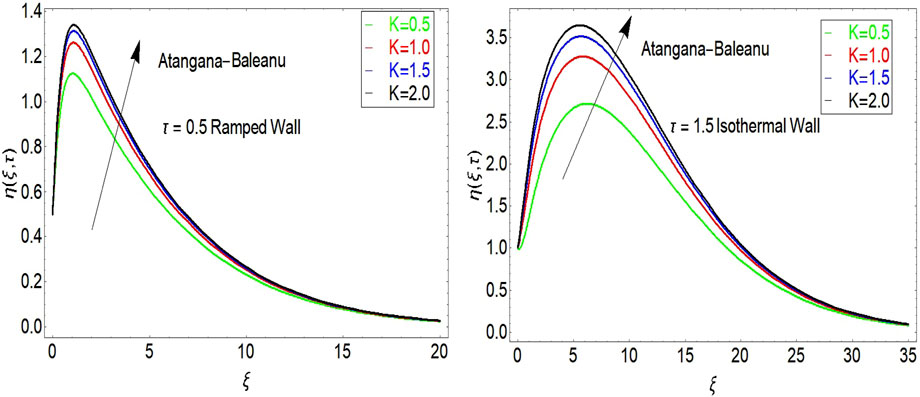
The impact of porosity parameter is shown in Figure 5. It is found that velocity increases with larger values of porosity parameter. The impact of $K$ on the fluid velocity is same as expected. With increasing porosity, the retardation impact decreases to a more permeable surface, and hence the velocity increases. Figure 6 shows the influence of relaxation time ${\lambda }_0$ on the velocity profile for OBF AB fractional velocity. It is found that by increasing ${\lambda }_0$, the magnitude of velocity profile increases. The influence of retardation time ${\lambda }_1$ is highlighted in Figure 7. From this figure, it is found that by increasing ${\lambda }_1$, the magnitude of the velocity profile decreases.

FIGURE 5

FIGURE 5. Influence of K on velocity for constant and ramped temperature.

FIGURE 6

FIGURE 6. Influence of on velocity for constant and ramped temperature.

FIGURE 7

FIGURE 7. Influence of λ₁ on velocity for constant and ramped temperature.

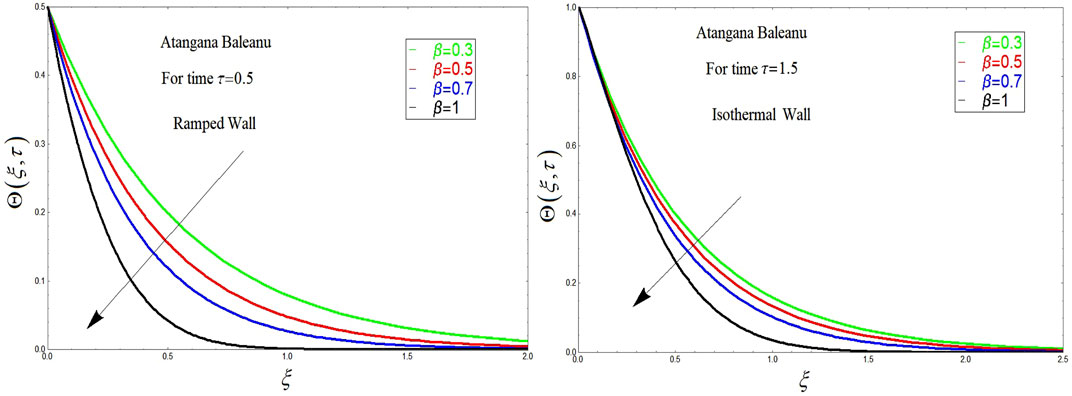
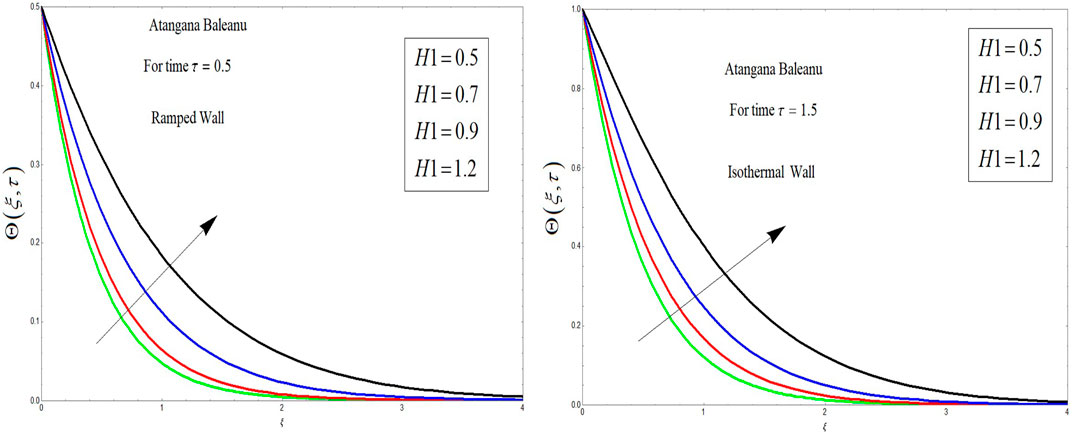
The influence of the AB fractional operator on temperature distributions is highlighted in Figure 8. From this figure, it is clear that with the increase in the fractional parameter in the case of the AB derivative, the temperature of the OBF decreases. It is worth noting that for $\beta \to 1$, the temperature goes to the classical form, which provides a comparison between the classical and fractional forms. Figure 9 shows the influence of Pr on temperature distribution. From this graph, it is clear that with increasing Pr, the temperature of the fluid decreases. The influence of Nr on temperature is highlighted in Figure 10. From this figure, it is found that with the increase in the values of Nr, the temperature of the fluid increases. Figure 11 shows the influence of H1 on the temperature profile. It is found that an increase in H1 results in an increase in OBF temperature.

FIGURE 8

FIGURE 8. Impact of the AB fractional operator on temperature.

FIGURE 9

FIGURE 9. Impact of Pr on temperature (AB fractional model).

FIGURE 10

FIGURE 10. Impact of Nr on temperature (AB fractional model).

FIGURE 11

FIGURE 11. Impact of H1 on temperature (AB fractional model).

5 Conclusion

This study aimed to investigate the dynamics of OBF flowing over a vertical plate with ramped heating and time-dependent velocity. The effect of MHD is considered under the Lorentz force. Additional effects of porosity, thermal radiation, and heat generation are also considered. The fractional model of OBF was first developed using Atangana–Baleanu fractional derivatives and then the well-known technique of Laplace transform was adopted to obtain the solutions, which are displayed in various plots with detailed discussion analysis. The significance of rising ramped temperature on the dynamics of the unsteady viscoelastic fluid subject to Lorentz force is concluded with the following main points.

• Atangana–Baleanu fractional parameter $\beta$ reduces OBF velocity in both isothermal wall temperature and ramped heating; however, in ramped heating, the velocity profiles are closer than in the isothermal heating case.

• Increasing $Gr,K,\text{and}{\lambda }_0$, the OBF velocity increases in both isothermal wall temperature and ramped heating.

• Increasing $M,\mathrm{Pr},\text{and}{\lambda }_1$, the OBF velocity decreases in both isothermal wall temperature and ramped heating.

• The greater values of $H_1\text{and}\text{Nr}$ increase the OBF temperature in both isothermal wall temperature and ramped heating.

• The greater values of $\beta \text{and}\mathrm{Pr}$ decrease the temperature of the fluid in both isothermal wall temperature and ramped heating.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

IK formulated, solved the problem, and wrote the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Oldroyd JG. On the Formulation of Rheological Equations of State. In: Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences (1950) 200(1063):523–41.

Google Scholar

2. Zhao J, Zheng L, Zhang X, Liu F, Chen X. Unsteady Natural Convection Heat Transfer Past a Vertical Flat Plate Embedded in a Porous Medium Saturated with Fractional Oldroyd-B Fluid. J Heat Transfer (2017) 139(1). doi:10.1115/1.4034546

CrossRef Full Text | Google Scholar

3. Liu Y, Liu F, Feng L, Xin B. Novel Numerical Analysis for Simulating the Generalized 2D Multi-Term Time Fractional Oldroyd-B Fluid Model. arXiv preprint arXiv:1903.07816 (2019). doi:10.48550/arXiv.1903.07816

CrossRef Full Text | Google Scholar

4. Zhang J, Liu F, Anh VV. Analytical and Numerical Solutions of a Two‐Dimensional Multi‐Term Time‐Fractional Oldroyd‐B Model. Numer Methods Partial Differential Eq (2019) 35(3):875–93. doi:10.1002/num.22327

CrossRef Full Text | Google Scholar

5. Feng L, Liu F, Turner I, Zhuang P. Numerical Methods and Analysis for Simulating the Flow of a Generalized Oldroyd-B Fluid between Two Infinite Parallel Rigid Plates. Int J Heat Mass Transfer (2017) 115:1309–20. doi:10.1016/j.ijheatmasstransfer.2017.08.105

CrossRef Full Text | Google Scholar

6. Feng L, Liu F, Turner I, Zheng L. Novel Numerical Analysis of Multi-Term Time Fractional Viscoelastic Non-Newtonian Fluid Models for Simulating Unsteady MHD Couette Flow of a Generalized Oldroyd-B Fluid. Fractional Calculus Appl Anal (2018) 21(4):1073–103. doi:10.1515/fca-2018-0058

CrossRef Full Text | Google Scholar

7. Ali F, Arif M, Khan I, Sheikh N, Saqib M. Natural Convection in Polyethylene Glycol Based Molybdenum Disulfide Nanofluid With Thermal Radiation, Chemical Reaction and Ramped Wall Temperature. Int J Heat Technology (2018):619–631. doi:10.18280/ijht.360227

CrossRef Full Text | Google Scholar

8. VeeraKrishna M, Chamkha AJ. Hall Effects on Unsteady MHD Flow of Second Grade Fluid Through Porous Medium with Ramped wall Temperature and Ramped Surface Concentration. Phys Fluids (2018) 30(5):053101. doi:10.1063/1.5025542

CrossRef Full Text | Google Scholar

9. Shah NA, Zafar AA, Akhtar S. General Solution for MHD-Free Convection Flow Over a Vertical Plate with Ramped Wall Temperature and Chemical Reaction. Arab J Math (2018) 7(1):49–60. doi:10.1007/s40065-017-0187-z

CrossRef Full Text | Google Scholar

10. Khan A, Khan I, Ali F, Shafie S. A Note on Entropy Generation in MHD Flow Over a Vertical Plate Embedded in a Porous Medium with Arbitrary Shear Stress and Ramped Temperature. J Porous Media (2016) 19(2):175. doi:10.1615/jpormedia.v19.i2.50

CrossRef Full Text | Google Scholar

11. Khan A, ul Karim F, Khan I, Ali F, Khan D. Irreversibility Analysis in Unsteady Flow Over a Vertical Plate with Arbitrary Wall Shear Stress and Ramped Wall Temperature. Results Phys (2018) 8:1283–90. doi:10.1016/j.rinp.2017.12.032

CrossRef Full Text | Google Scholar

12. Khan A, Khan I, Ali F, Shafie S. Effects of wall Shear Stress on MHD Conjugate Flow over an Inclined Plate in a Porous Medium with Ramped wall Temperature. Math Probl Eng (2014) 2014:15. doi:10.1155/2014/861708

CrossRef Full Text | Google Scholar

13. Yavuz M, Sene N, Yıldız M. Analysis of the Influences of Parameters in the Fractional Second-Grade Fluid Dynamics. Mathematics (2022) 10:1125. doi:10.3390/math10071125

CrossRef Full Text | Google Scholar

14. Sene N. Fractional Model and Exact Solutions of Convection Flow of an Incompressible Viscous Fluid under the Newtonian Heating and Mass Diffusion. J Mathematics (2022) 2022:8785197. doi:10.1155/2022/8785197

CrossRef Full Text | Google Scholar

15. Sene N. Analytical Solutions of a Class of Fluids Models with the Caputo Fractional Derivative. Fractal Fract (2022) 6:35. doi:10.3390/fractalfract6010035

CrossRef Full Text | Google Scholar

16. Obembe AD, Al-Yousef HY, Hossain ME, Abu-Khamsin SA. Fractional Derivatives and Their Applications in Reservoir Engineering Problems: a Review. J Pet Sci Eng (2017) 157:312–27. doi:10.1016/j.petrol.2017.07.035

CrossRef Full Text | Google Scholar

17. Liu Q, Zhuang P, Liu F, Lai J, Anh V, Chen S. An Investigation of Radial Basis Functions for Fractional Derivatives and Their Applications. Comput Mech (2020) 65(2):475–86. doi:10.1007/s00466-019-01779-z

CrossRef Full Text | Google Scholar

18. Hilfer R. Applications of Fractional Calculus in Physics. Singapore: World Scientific (2000).

Google Scholar

19. Yang XJ. General Fractional Derivatives: Theory, Methods and Applications. Chapman and Hall: CRC Press (2019): 380.

Google Scholar

20. Atangana A, Baleanu D. New Fractional Derivatives with Nonlocal and Non-singular Kernel: Theory and Application to Heat Transfer Model. Therm Sci (2016) 20(2):763–9. doi:10.2298/tsci160111018a

CrossRef Full Text | Google Scholar

21. Saqib M, Khan I, Shafie S. Application of Atangana-Baleanu Fractional Derivative to MHD Channel Flow of CMC-Based-CNT's Nanofluid through a Porous Medium. Chaos, Solitons and Fractals (2018) 116:79–85. doi:10.1016/j.chaos.2018.09.007

CrossRef Full Text | Google Scholar

22. Shah NA, Elnaqeeb T, Animasaun IL. Insight into the Natural Convection Flow through a Vertical Cylinder Using Caputo Time-Fractional Derivatives. Int J Appl Comput Math (2018) 4:80. doi:10.1007/s40819-018-0512-z

CrossRef Full Text | Google Scholar

23. Shah NA, Ahmad H, Hajizadeh A, Zeb M, Ahmad S, Mahsud Y, et al. Effect of Magnetic Field on Double Convection Flow of Viscous Fluid over a Moving Vertical Plate with Constant Temperature and General Concentration by Using New Trend of Fractional Derivative. Open J Math Sci (2018) 2018:253–65. doi:10.30538/oms2018.0033

CrossRef Full Text | Google Scholar

24. Sheikh NA, Ali F, Saqib M, Khan I, Jan SAA, Alshomrani AS, et al. Comparison and Analysis of the Atangana-Baleanu and Caputo-Fabrizio Fractional Derivatives for Generalized Casson Fluid Model with Heat Generation and Chemical Reaction. Results Phys (2017) 7:789–800. doi:10.1016/j.rinp.2017.01.025

CrossRef Full Text | Google Scholar

25. Animasaun IL, Shah NA, Wakif A, Mahanthesh B, Sivaraj R, Koriko OK. Ratio of Momentum Diffusivity to Thermal Diffusivity: Introduction, Meta-Analysis, and Scrutinization. New York: Chapman and Hall/CRC.

Nomenclature

$\mathbf{S}$ Extra stress tensor $\left(Kg{m}^{-3}\right)$

$C_p$ Specific heat (pressure constant) $\left(JKg{K}^{-1}\right)$

$C_f$ Skin friction coefficient $(-)$

$\mathbf{T}$ Cauchy stress tensor $(-)$

$\frac{\mathbf{D}}{\mathbf{D}\mathrm{t}\mathbf{ }}$ Material time derivative $(-)$

${\mathbf{A}}_1$ Rivlin–Ericksen tensor $(-)$

$k_1$ Mean spectral absorption coefficient $(-)$

$K$ Permeability $\left(m^2\right)$

$N_r$ $\left(=\frac{16{\sigma }_1}{3k_1}\frac{T^3}{\kappa }\right)$ Radiation number $(-)$

$\mathrm{Pr}$ $\left(=\frac{\mu C_p}{\kappa }\right)$ Prandtl number $(-)$

$q_r$ $\left(=\frac{4{\sigma }_1}{3k_1}\frac{\partial T^4}{\partial y}\right)$ Radiative energy flux $(-)$

$s$ Transform parameter $(-)$

$T$ Temperature $\left(K\right)$

$T_{\infty }$ Temperature away from the boundary $\left(K\right)$

$T_w$ Temperature at the boundary ($K$)

$u$ Velocities along the x-axis $\left(m{s}^{-1}\right)$

$u_0$ Uniform velocity $(-)$

$\left(y,t\right)$ Co-ordinates (space and time) $\left(m,s\right)$

$g$ Acceleration due to gravity $\left(m{s}^{-2}\right)$

H₀ Heat generation coefficient in the dimensional form $(-)$

H₁ Heat generation coefficient in the non-dimensional form $(-)$

$Gr$ Grashof number ($-)$

Greek letters

$\beta$ Fractional parameter ($-)$

${\beta }_T$ Volumetric coefficient of thermal expansion $\left(K^{-1}\right)$

${\lambda }_r$ Retardation time $\left(m{s}^{-2}\right)$

$\lambda$ Relaxation time ($s$)

$\kappa$ Thermal conductivity $W/\left(mK\right)$

$\mu$ Dynamic viscosity $\left(kg/ms\right)$

$\nu$ $\left(=\frac{\mu }{\rho }\right)$ Kinematic viscosity $\left(m^2{s}^{-1}\right)$

$\rho$ Density of the fluid $\left(Kg/m^3\right)$

${\sigma }_1$ Stefan–Boltzmann constant $\left(W{m}^{-2}{K}^{-4}\right)$

$\eta$ Non-dimensional velocity $(-)$

$\Theta$ Non-dimensional temperature $\left(K\right)$

$\xi$ Non-dimensional space variable (-)