Configuration-Induced Directional Nonlinearity Enhancement in Composite Thermal Media

Nonlinear thermal response enables flexible heat manipulation and management with artificial structures. In particular, intrinsic temperature-dependent parameters of constitutive materials guide the design of self-adaptive thermal metamaterials. However, the geometrical effect in nonlinear composites has not been adequately studied, which may limit the potential multiple functionalities and versatile control. Here, under the effective medium approximation framework, we develop a unified theory for predicting anisotropic nonlinear equivalent thermal conductivities of elliptical inclusions in homogeneous media. By means of the derived results, enhancement of value in nonlinear coefficient can be achieved in a specified direction, based on geometrically anisotropic configurations and temperature-dependent properties. Quantitative relations between directional enhancement and inclusive shape factors are given by analytical theory and verified by numerical simulation. The proposed theoretical methods can be further extended to arbitrary non-circular configurations of complex structures, and the directional nonlinearity enhancement effect will facilitate refined heat control, combined with other nonlinear mechanisms such as spatiotemporal modulation or harmonic generation.

1 Introduction

Nonlinearity is one of the fundamental phenomena in nature and human society [1, 2]. By means of nonlinear mechanisms applied in artificial complex systems, various devices or concepts such as transistors, lasers, and artificial intelligence were created, leading to the dramatic revolution in modern science and technology [3–6]. On the other hand, nonlinearity in macro-scale heat transport systems is lacking study in both theory and applications [7, 8], although its counterpart at micro or nano scale has been a significant topic of phononics in the last two decades [9–11]. Comparable to the coupling-induced inharmonic interaction in phonon transfer [12], nonlinearity in macro-scale heat diffusion is mainly reflected in the intrinsic response to external fields, for example, thermal conductivity or capacity is varying with temperature [13, 14]. The absence of macroscopic phenomenological theory (under the Fourier’s law) makes it difficult to handle nonlinear parts in heat conduction and limits the regulation or management of heat in industrial engineering and daily life.

Thermal metamaterials have flourished as a promising scheme for manipulating heat since the proposal of transformation thermotics [15–19]. The range and sensitivity of accessible thermal conductivities are thus extended to the level far beyond natural materials [20–23]. More recently, various design methods have been generalized from linear to nonlinear systems, in which thermal parameters are temperature dependent [24–27], and lead to a broad category of smart or self-adapting thermal metadevices [28, 29]. In particular, composites of artificial architectures can result in a larger value on the coefficient of an effective nonlinear term than building-unit materials, which is usually called nonlinearity enhancement [8]. This effect in random [30], periodic [31], and core-shell [32] structures have been proposed. However, besides the enhanced parameter ranges, anisotropy in functionality is also a crucial benefit of utilizing artificial architectures [33–35], allowing several regulating abilities integrated into a single installation. But the effective thermal conductivities considered in the above works [30–32] are all in scalar form, i.e., isotropic. When composites have relatively strong anisotropy in configuration, such as ellipses inclusions, effective thermal conductivities will be anisotropic. Then the nonlinearity enhancement effect may be directional, depending on the intensity of anisotropy in composite media.

In this work, we aim at designing directional nonlinearity enhancement in composite thermal media. Directionality can be induced by elliptical particles embedded in homogeneous media with identical orientations. We build a two-dimensional theoretical model for deducing an analytical relation between directional enhancement and corresponding influencing factors, including the inclusive area fraction, shape factor, and ratio of linear part in intrinsic thermal conductivities, and demonstrate total-factor analyses with numerical methods. Finite-element simulations verify the designed model and give a visualized range and level of directional nonlinearity enhancement. Considering the universality of ellipses for mimicking a number of geometrical configurations such as clavae or circles by tuning shape factors, the proposed basic model may be extended to other anisotropic systems and inspire a broad category of multifunctional or Janus nonlinear thermal metadevices.

2 Theory

Let us consider a two-dimensional composite model in which a large number of ellipse inclusions are randomly distributed in a host matrix with identical orientation, see Figure 1. We use subscripts i, m, and e to indicate the parameters of inclusion, matrix, and effective medium, respectively. Then κ_i(T) and κ_m(T) are denoted to the intrinsic temperature-dependent thermal conductivities of two constituents, and κ_e(T) is the effective thermal conductivity of the composite. For simplification without loss of generality, intrinsic thermal conductivities are set to be composed of two parts, namely the linear and nonlinear components. They can be written in as

${\kappa }_i\left(T\right)={\kappa }_{i0}+{\chi }_i{T}^{\alpha }(1)$

and

${\kappa }_m\left(T\right)={\kappa }_{m0}+{\chi }_m{T}^{\beta }.(2)$

The first terms on the right hand of the above two equations are linear parts (constants), while the second terms are nonlinear parts. χ is the nonlinear coefficient and T represents the local temperature. α and β can be assigned as arbitrary real numbers. It is noted that we consider the weak nonlinearity effect here, which is common for most solid crystals within the room temperature range. So κ_i0 ≫ χ_iT^α and κ_m0 ≫ χ_mT^β should be satisfied. Naturally, the Taylor expansion technique is adapted for deriving the analytical form of κ_e(T) from κ_i(T) and κ_m(T). Executing Taylor expansion on κ_e(T) by regarding χ_iT^α and χ_mT^β as small quantities, it can be expected to retain

${\kappa }_e\left(T\right)={\kappa }_{e0}+{\eta }_1{\chi }_i{T}^{\alpha }+{\eta }_2{\chi }_m{T}^{\beta }+O\left({\chi }_i{T}^{\alpha }\right)+O\left({\chi }_m{T}^{\beta }\right),(3)$

where η₁χ_iT^α and η₂χ_mT^β are first-order expansion terms, and O(χ_iT^α) and O(χ_mT^β) are their higher-order expansion terms. By comparing first-order nonlinear terms of the effective medium and its components, we can obtain nonlinear gain coefficients. In our following analyses, we focus on the first-order nonlinear term, higher-order nonlinear terms are ignored. Eq. 3 implies that η₁ and η₂ are dimensionless nonlinear gain coefficients resulted from composite effects. It can be employed to evaluate the level of nonlinearity enhancement.

FIGURE 1

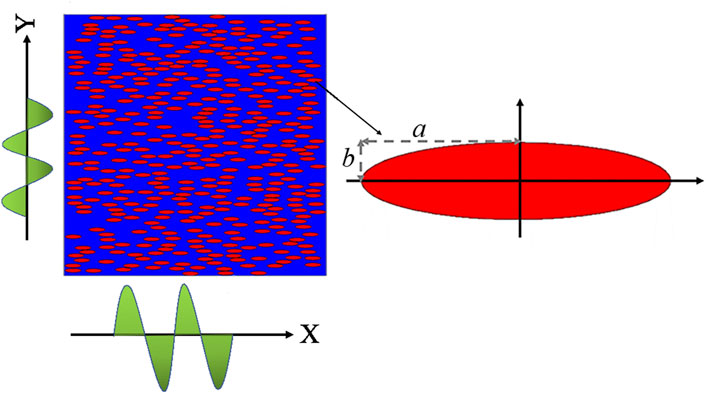
FIGURE 1. Schematic of a nonlinear thermal composite. All the ellipse inclusions have the same shapes and orientations (main axes are along the x axis). Nonlinearity is intensified in the x direction, while it is weakened in the y direction, coming into directional nonlinearity enhancement. Ellipse inclusions are amplified at the right hand. a and b are the semi-axis length in the x and y direction, respectively.

To proceed, we refer to the analytical form describing the effective thermal conductivity of the composite in the linear case, which is also known as the generalized Maxwell-Garnett (M&G) equation [36]. Under the case that the long axes of ellipse inclusions are along x axis, the nonlinear thermal conductivity in the x direction is expressed as

${\kappa }_{ex}\left(T\right)={\kappa }_m\left(T\right)+\frac{f\left({\kappa }_i\left(T\right)-{\kappa }_m\left(T\right)\right){\kappa }_m\left(T\right)}{\left(g_x\left({\kappa }_i\left(T\right)-{\kappa }_m\left(T\right)\right)+{\kappa }_m\left(T\right)\right)\left(1-\frac{f{g}_x\left({\kappa }_i\left(T\right)-{\kappa }_m\left(T\right)\right)}{g_x\left({\kappa }_i\left(T\right)-{\kappa }_m\left(T\right)\right)+{\kappa }_m\left(T\right)}\right)},(4)$

where f is the area ratio of inclusions to the whole media and g_x is the major-axis shape factor of ellipse inclusions, which is defined exactly in Ref. [36]. Similarly, the thermal conductivity in the y direction can be obtained by replacing x with y in Eq. 4. We can see the shape factor g is the key for constructing anisotropic effective thermal conductivities because g_x and g_y are different for κ_ex(T) and κ_ey(T), respectively. So we can naturally consider that g will induce divergent nonlinearity enhancement effects in different directions. Next, we will deduce the detailed form of effective nonlinear modulation coefficients. For defining them explicitly, we consider two simplified cases. One is that nonlinear inclusions embedded in linear matrix, the other is that linear inclusions embedded in nonlinear matrix.

2.1 Nonlinear Inclusion

When we only consider nonlinearity in inclusions, the thermal conductivity of matrix will be reduced to its linear part κ_m0, and the nonlinear gain coefficient of composite is simply embodied in η₁ in Eq. 3. Now the analytical form of effective thermal conductivity in Eq. 4 can be written as

${\kappa }_{eA}\left(T\right)={\kappa }_{m0}+\frac{f\left({\kappa }_{i0}+{\chi }_i{T}^{\alpha }-{\kappa }_{m0}\right){\kappa }_{m0}}{\left(g\left({\kappa }_{i0}+{\chi }_i{T}^{\alpha }-{\kappa }_{m0}\right)+{\kappa }_{m0}\right)\left(1-\frac{fg\left({\kappa }_{i0}+{\chi }_i{T}^{\alpha }-{\kappa }_{m0}\right)}{g\left({\kappa }_{i0}+{\chi }_i{T}^{\alpha }-{\kappa }_{m0}\right)+{\kappa }_{m0}}\right)}.(5)$

Executing Taylor expansion at κ_i0 to the first order of χ_iT^α, we obtain

$\begin{array}{c}\hfill {\kappa }_{eA}\left(T\right)={\kappa }_{m0}+\frac{f\left({\kappa }_{i0}-{\kappa }_{m0}\right){\kappa }_{m0}}{\left(g\left({\kappa }_{i0}-{\kappa }_{m0}\right)+{\kappa }_{m0}\right)\left(1-\frac{fg\left({\kappa }_{i0}-{\kappa }_{m0}\right)}{g\left({\kappa }_{i0}-{\kappa }_{m0}\right)+{\kappa }_{m0}}\right)}\\ \hfill +\frac{f}{{\left(\left(1-f\right)g\left(\frac{{\kappa }_{i0}}{{\kappa }_{m0}}-1\right)+1\right)}^2}{\chi }_i{T}^{\alpha }+O\left({\chi }_i{T}^{\alpha }\right).\end{array}(6)$

Comparing Eq. 6 with Eq. 3, we can see that the zero-order expansion term is exactly the linear effective thermal conductivity of composite, and the gain coefficient of first-order term is derived in a concise form as

${\eta }_A=\frac{f}{{\left(\left(1-f\right)g\left(\frac{{\kappa }_{i0}}{{\kappa }_{m0}}-1\right)+1\right)}^2}.(7)$

η_A is related to area fraction f, elliptical shape factor g, and linear-part conductivity ratio of inclusions and matrix κ_i0/κ_m0. In particular, g has anisotropic nature because of the oriented arrangement of ellipse inclusions, inducing the expected directional nonlinearity enhancement.

For quantitatively depicting physical pictures of directional nonlinearity enhancement, we show the variation of dependent variable η_A with its several independent variables in Figure 2. η_A is along the vertical axis, while κ_i0/κ_m0 and f are in the horizontal plane. A to I in Figure 2 demonstrate their relations under different g. We use five different colors to distinguish value regions of η_A, see the bottom color bar. The red region represents nonlinearity enhancement (η_A > 1). It is noted that for two-dimensional elliptical-inclusion composite, the sum of g in x and y directions is 1. So A and I, B and H, C and G, D and F in Figure 2 are four pairs of counterparts for the anisotropic nonlinear response, with four varieties of aspect ratio in inclusions. Here, nonlinearity enhancement is achieved when g > 0.5 (corresponding to Figures 2F–I), while there is no enhancement in another direction (corresponding to Figures 2A–D) simultaneously. If g goes to 0.5, the inclusions become circular, and the gain coefficient is then non-directional or isotropic, echoing with the results in Ref. [30].

FIGURE 2

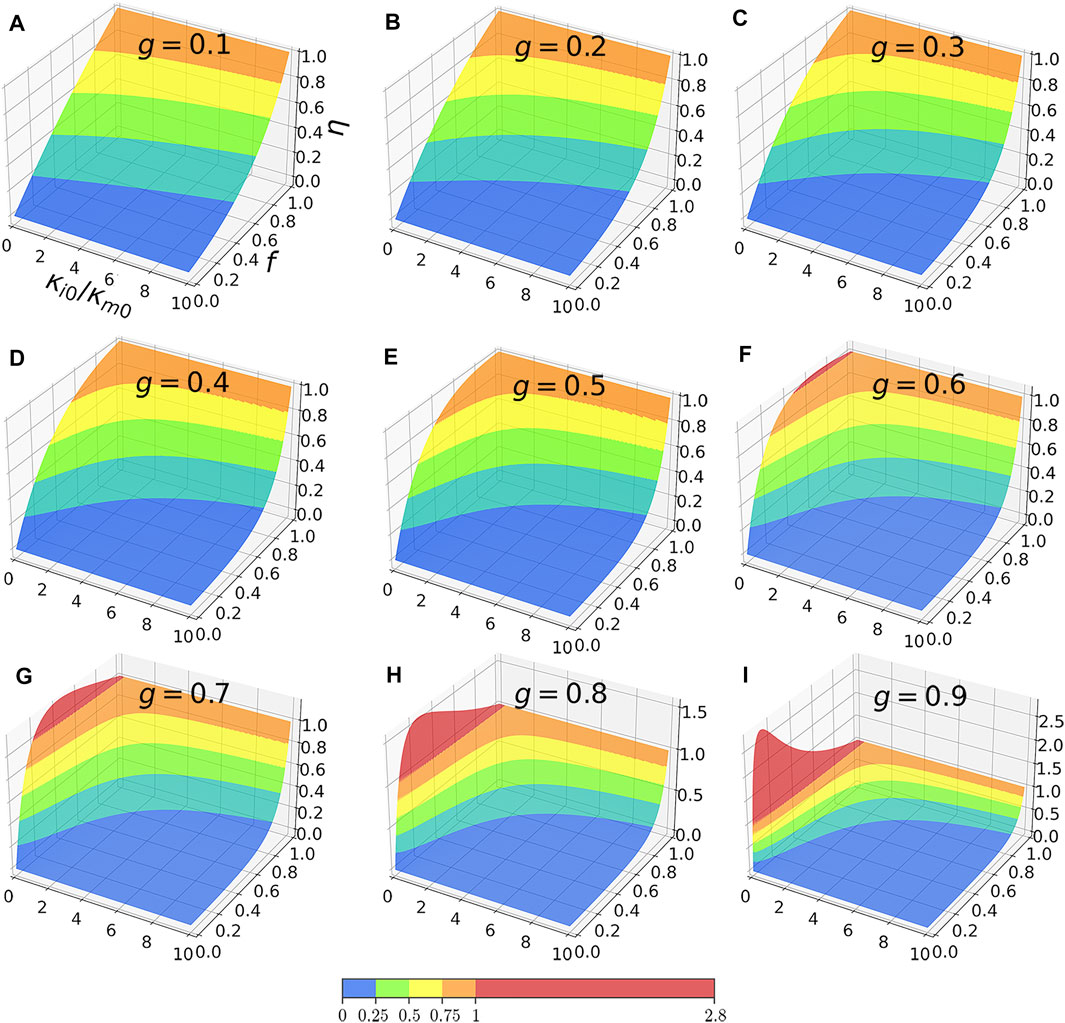
FIGURE 2. Values of η for nonlinear inclusions and linear matrix. Each subplot shows how η varies with f and κ_i0/κ_m0 given a different value of g from 0.1 to 0.9. In particular, the surface when η > 1 is plotted in red.

2.2 Nonlinear Matrix

Then we consider that linear inclusions are embedded in a nonlinear matrix. In this case, effective thermal conductivity is

$\begin{array}{cc}\hfill & {\kappa }_{eB}\left(T\right)={\kappa }_{m0}+{\chi }_m{T}^{\beta }\hfill \\ \hfill & +\frac{f\left({\kappa }_{i0}-{\kappa }_{m0}-{\chi }_m{T}^{\beta }\right)\left({\kappa }_{m0}+{\chi }_m{T}^{\beta }\right)}{\left(g\left({\kappa }_{i0}-{\kappa }_{m0}-{\chi }_m{T}^{\beta }\right)+{\kappa }_{m0}+{\chi }_m{T}^{\beta }\right)\left(1-\frac{fg\left({\kappa }_{i0}-{\kappa }_{m0}-{\chi }_m{T}^{\beta }\right)}{g\left({\kappa }_{i0}-{\kappa }_{m0}-{\chi }_m{T}^{\beta }\right)+{\kappa }_{m0}+{\chi }_m{T}^{\beta }}\right)}.\hfill \end{array}(8)$

Similar to the method in above subsection, after executing Taylor expansion at κ_m0, Eq. 8 can be transformed to

$\begin{array}{c}\hfill {\kappa }_{eB}\left(T\right)={\kappa }_{m0}+\frac{f\left({\kappa }_{i0}-{\kappa }_{m0}\right){\kappa }_{m0}}{\left(g\left({\kappa }_{i0}-{\kappa }_{m0}\right)+{\kappa }_{m0}\right)\left(1-\frac{fg\left({\kappa }_{i0}-{\kappa }_{m0}\right)}{g\left({\kappa }_{i0}-{\kappa }_{m0}\right)+{\kappa }_{m0}}\right)}\\ \hfill +1+\frac{f\left(\left(1-f\right)g{\left(\frac{{\kappa }_{i0}}{{\kappa }_{m0}}-1\right)}^2+1\right)}{{\left(\left(1-f\right)g\left(\frac{{\kappa }_{i0}}{{\kappa }_{m0}}-1\right)+1\right)}^2}{\chi }_m{T}^{\beta }+O\left({\chi }_m{T}^{\beta }\right).\end{array}(9)$

Then, we obtain the gain coefficient of the first expansion term as

${\eta }_B=1+\frac{f\left(\left(1-f\right)g{\left(\frac{{\kappa }_{i0}}{{\kappa }_{m0}}-1\right)}^2+1\right)}{{\left(\left(1-f\right)g\left(\frac{{\kappa }_{i0}}{{\kappa }_{m0}}-1\right)+1\right)}^2}.(10)$

We can see that η_B are related regarding area fraction f, shape factor g, and thermal conductivity ratio κ_i0/κ_m0, similar to η_A.

We also demonstrate the variation of η_B with its three independent variables in Figure 3. We can see nonlinearity enhancement is achieved regardless of shape factor g. But their values are different. In detail, η_B in orthometric directions show distinct enhancement, which can be read from A and I, B and H, C and G, D and F in Figure 3. This result is distinguished from the isotropic composite as Figure 3E shows.

FIGURE 3

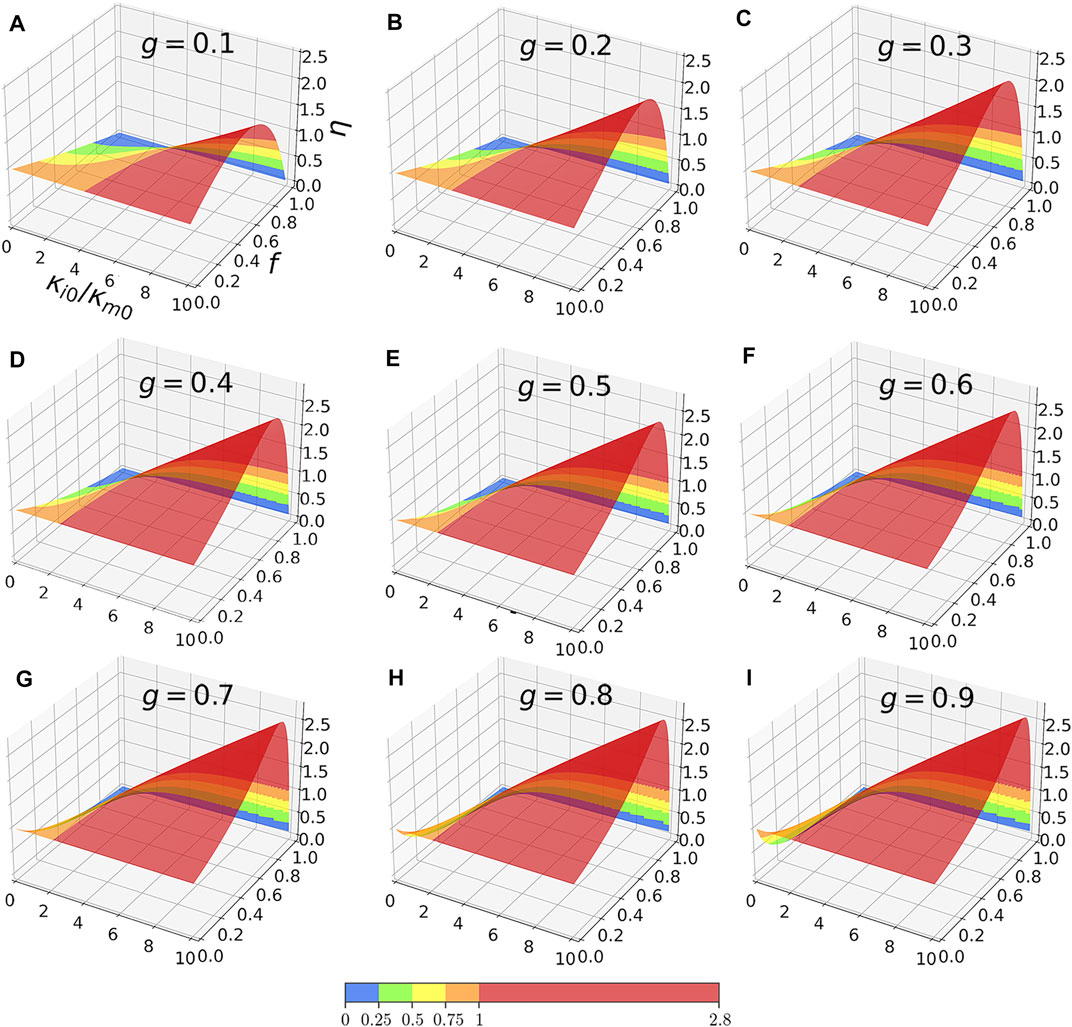
FIGURE 3. Same as Figure 2, but for linear inclusions and nonlinear matrix.

3 Numerical Simulation Verification

To check our theory, we perform finite-element simulations solving the heat conduction equation with the commercial software COMSOL Multiphysics (www.comsol.com). The whole composite media is constructed as a square with a side length of 10 cm. A total of 400 ellipse particles are randomly embedded in the matrix. Each particle has a semi-axis length a in the x direction (see Figure 1), and the thermal bias ΔT = 1 K is also applied in this direction with the hot (cold) source at 301 K (300 K). For different cases, we take κ_i0 = 4 W m⁻¹ K⁻¹ and change the ratio κ_i0/κ_m0. To generate a weak nonlinearity, the nonlinear coefficient for the nonlinear material is set as 10^–4 W m⁻¹ K⁻². The effective nonlinear coefficient is calculated by comparing the effective conductivities when the thermal bias exists or is absent. In addition, the temperature in the effective nonlinear thermal conductivity is set as the average temperature over the inclusions, which is approximately equal to 300.5 K.

First, to show the (directional) nonlinearity enhancement by nonlinear inclusions and linear matrix, we give the simulated η with the theoretical results in Figure 4. According to Figure 2, we take g = 0.8 here to see the effect of nonlinearity enhancement in Figure 4A. For plots in different colors, we take κ_i0/κ_m0 = 0.1, 1/3, 1, 3, and 10, respectively. The data for the scatter plot are the average value of simulations using three different random position sets for the inclusions. The trend of the scatter plots basically agrees with the theoretical value. When κ_i0/κ_m0 = 0.1, we can see obvious nonlinearity enhancement when f ≥ 0.2. In addition, η is greater than the theoretical value when f is not small. This deviation comes from the overly simplistic assumption that the M&G theory only considers the dipole effect. In Figure 4B, we compare η with different g values while κ_i0/κ_m0 is fixed. The plots of g = 0.9 and g = 0.1 (or g = 0.7 and g = 0.3) tell that the directional nonlinearity enhancement do exists. Then, we give similar results for linear inclusions and nonlinear matrix in Figure 5. We can see the condition of κ_i0/κ_m0 for nonlinearity enhancement is different from the case in Figure 4. Anyway, we can observe (directional) nonlinearity enhancement as well.

FIGURE 4

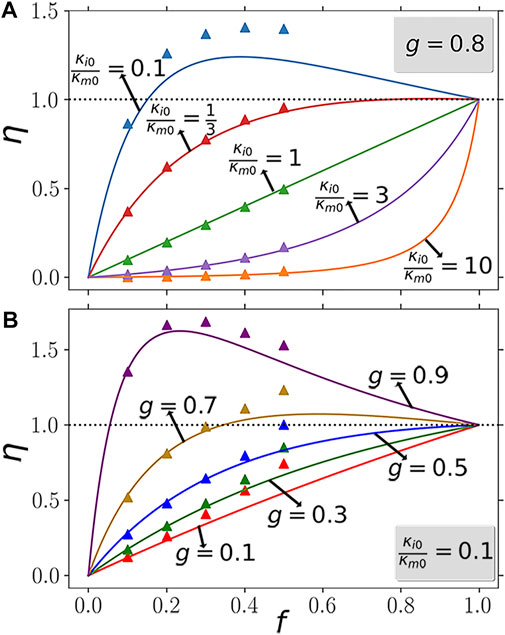
FIGURE 4. How η varies with f for nonlinear inclusions and linear matrix. The scatter plots represent the numerical results for f = 0.1, 0.2, 0.3, 0.4, and 0.5, while the solid lines show the theoretical values. (A) g is 0.8 while κ_i0/κ_m0 takes different values. (B) κ_i0/κ_m0 is 0.1 while g takes different values.

FIGURE 5

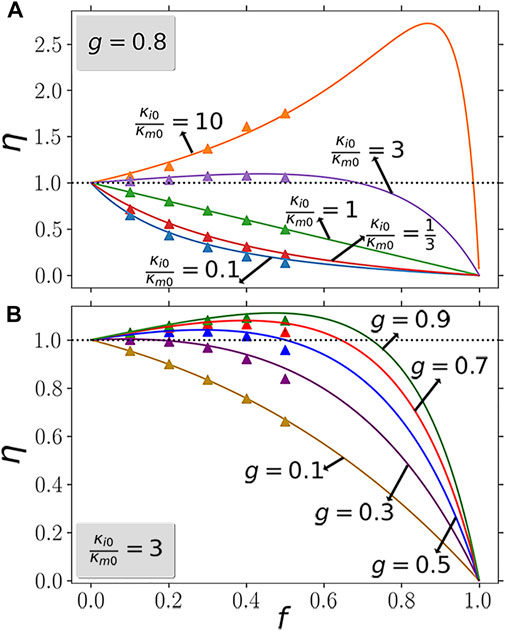
FIGURE 5. Same as Figure 4, but for linear inclusions and nonlinear matrix. In addition, to show directional nonlinearity enhancement, κ_i0/κ_m0 takes 3 in (B).

4 Discussion and Conclusion

Hereto, we have demonstrated the directional nonlinearity enhancement in anisotropic thermal media. Different from the previously-studied isotropic structures, non-circular configurations introduce directionality into effective nonlinear thermal conductivity, inducing different effective nonlinear coefficients in orthometric directions. In particular, the case that nonlinear inclusions embedded in linear matrix leads to a one-way nonlinearity enhancement. This is inaccessible in isotropic media which results in omnidirectional nonlinearity reduction. Thanks to the shape factor g, we can achieve both nonlinearity enhancement and directionality in this case. Another condition we study above is those linear inclusions embedded in a nonlinear matrix. It also benefited from the shape factor g that the degrees of enhancement are distinguished in different directions. When g = 0.5, our results accord with the circular particle dispersing in isotropic media. The proposed theoretical models and simulation methods can also be extended to higher-order nonlinearity, which may be expected to design flexible thermal multistability or higher heat harmonic wave generation. Taking advantage of anisotropy in configuration, directional nonlinearity enhancement can be utilized for constructing multifunctional nonlinear metadevices.

We should point out that we discuss weak nonlinearity cases in this work so that Taylor expansion can be employed, which is common in naturally-occuring solid crystals. We take first-order nonlinear terms and ignore high-order terms to clearly demonstrate the proposed methods and effects. The Taylor expansion method is universal for arbitrary order nonlinear terms, and high-order terms may be taken into consideration in some wave-like heat transfer cases. It is noted that the gain coefficient we discussed in this work has an upper limit. It depends on the intrinsic composite structures. Elliptical particles diffusing in a matrix naturally introduce this confinement of about 2.8. However, if we consider other models (for example, core-shell or diamond-shaped structure) [33, 37], the upper limits will be different. Another limitation that should be pointed out is that we employ M&G theory for deriving nonlinear effective thermal conductivities, It fits well with actual situations at the dilution limit. However, if the area fraction is large enough, simulation results will deviate from theoretical predictions. We suggest that the Rayleigh method applies to correcting the deviation between practical issues and physical models [31].

In summary, we propose an anisotropic thermal composite model for realizing directional nonlinearity enhancement. On basis of the regulation with geometrical configuration, coefficients of nonlinear terms in thermal conductivities can be enhanced in the expected directions, compared with isotropic constituent materials. By directly executing Taylor expansion on effective nonlinear thermal conductivities, we give analytical forms of nonlinearity enhancement, which is related to shape factors, linear conductivities, and area ratio of constituents. Numerical results echo the theoretical prediction and indicate the conditions for achieving directional enhancement. Moreover, we point out some limitations of our models and suggest several measures for promoting the level of directionality and enhancement. Our results may not only provide a theoretical framework for constructing directional thermal nonlinearity enhancement but also enlighten multifunctional or Janus thermal metadevice design.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author Contributions

JW designed the research and deduced the model. GD programmed the codes and executed numerical calculations. JW and GD discussed the results and wrote the manuscript.

Funding

The authors acknowledge financial support from the National Natural Science Foundation of China under Grants No. 12147169.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors are grateful to Dr. Boyan Tian for beneficial discussions.

References

1. Strogatz SH. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. Boca Raton: CRC Press (2018).

Google Scholar

2. Urbakh M, Klafter J, Gourdon D, Israelachvili J. The Nonlinear Nature of Friction. Nature (2004) 430:525–8. doi:10.1038/nature02750

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Smith SD. Lasers, Nonlinear Optics and Optical Computers. Nature (1985) 316:319–24. doi:10.1038/316319a0

CrossRef Full Text | Google Scholar

4. Carleo G, Cirac I, Cranmer K, Daudet L, Schuld M, Tishby N, et al. Machine Learning and the Physical Sciences. Rev Mod Phys (2019) 91:045002. doi:10.1103/RevModPhys.91.045002

CrossRef Full Text | Google Scholar

5. Bloembergen N. Nonlinear Optics. New York: Benjamin (1964).

Google Scholar

6. Pulfrey DL. Understanding Modern Transistors and Diodes. Cambridge: Cambridge University Press (2010).

Google Scholar

7. Lapine M, Shadrivov IV, Kivshar YS. Colloquium: Nonlinear Metamaterials. Rev Mod Phys (2014) 86:1093–123. doi:10.1103/RevModPhys.86.1093

CrossRef Full Text | Google Scholar

8. Dai G-L. Designing Nonlinear thermal Devices and Metamaterials under the Fourier Law: A Route to Nonlinear Thermotics. Front Phys (2021) 16:53301. doi:10.1007/s11467-021-1048-y

CrossRef Full Text | Google Scholar

9. Li B, Wang L, Casati G. Thermal Diode: Rectification of Heat Flux. Phys Rev Lett (2004) 93:184301. doi:10.1103/PhysRevLett.93.184301

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Wang L, Li B. Thermal Logic gates: Computation with Phonons. Phys Rev Lett (2007) 99:177208. doi:10.1103/PhysRevLett.99.177208

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Wang L, Li B. Thermal Memory: a Storage of Phononic Information. Phys Rev Lett (2008) 101:267203. doi:10.1103/PhysRevLett.101.267203

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Li N, Ren J, Wang L, Zhang G, Hänggi P, Li B. Colloquium: Phononics: Manipulating Heat Flow with Electronic Analogs and beyond. Rev Mod Phys (2012) 84:1045–66. doi:10.1103/RevModPhys.84.1045

CrossRef Full Text | Google Scholar

13. Glassbrenner CJ, Slack GA. Thermal Conductivity of Silicon and Germanium from 3°K to the Melting Point. Phys Rev (1964) 134:A1058–A1069. doi:10.1103/PhysRev.134.A1058

CrossRef Full Text | Google Scholar

14. Zeller RC, Pohl RO. Thermal Conductivity and Specific Heat of Noncrystalline Solids. Phys Rev B (1971) 4:2029–41. doi:10.1103/PhysRevB.4.2029

CrossRef Full Text | Google Scholar

15. Fan CZ, Gao Y, Huang JP. Shaped Graded Materials with an Apparent Negative thermal Conductivity. Appl Phys Lett (2008) 92:251907. doi:10.1063/1.2951600

CrossRef Full Text | Google Scholar

16. Narayana S, Sato Y. Heat Flux Manipulation with Engineered thermal Materials. Phys Rev Lett (2012) 108:214303. doi:10.1103/physrevlett.108.214303

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Wang J, Dai G, Huang J. Thermal Metamaterial: Fundamental, Application, and Outlook. iScience (2020) 23:101637. doi:10.1016/j.isci.2020.101637

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Yang S, Wang J, Dai G, Yang F, Huang J. Controlling Macroscopic Heat Transfer with thermal Metamaterials: Theory, experiment and Application. Phys Rep (2021) 908:1–65. doi:10.1016/j.physrep.2020.12.006

CrossRef Full Text | Google Scholar

19. Li Y, Li W, Han T, Zheng X, Li J, Li B, et al. Transforming Heat Transfer with thermal Metamaterials and Devices. Nat Rev Mater (2021) 6:488–507. doi:10.1038/s41578-021-00283-2

CrossRef Full Text | Google Scholar

20. Xu G, Dong K, Li Y, Li H, Liu K, Li L, et al. Tunable Analog thermal Material. Nat Commun (2020) 11:6028. doi:10.1038/s41467-020-19909-0

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Li J, Li Y, Cao PC, Yang T, Zhu XF, Wang W, et al. A Continuously Tunable Solid‐Like Convective Thermal Metadevice on the Reciprocal Line. Adv Mater (2020) 32:2003823. doi:10.1002/adma.202003823

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Hua C, Lindsay L. Space-time Dependent thermal Conductivity in Nonlocal thermal Transport. Phys Rev B (2020) 102:104310. doi:10.1103/PhysRevB.102.104310

CrossRef Full Text | Google Scholar

23. Xi Q, Zhong J, He J, Xu X, Nakayama T, Wang Y, et al. A Ubiquitous Thermal Conductivity Formula for Liquids, Polymer Glass, and Amorphous Solids*. Chin Phys. Lett. (2020) 37:104401. doi:10.1088/0256-307x/37/10/104401

CrossRef Full Text | Google Scholar

24. Li Y, Shen X, Wu Z, Huang J, Chen Y, Ni Y, et al. Temperature-Dependent Transformation Thermotics: From Switchable Thermal Cloaks to Macroscopic Thermal Diodes. Phys Rev Lett (2015) 115:195503. doi:10.1103/PhysRevLett.115.195503

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Shen X, Li Y, Jiang C, Huang J. Temperature Trapping: Energy-free Maintenance of Constant Temperatures as Ambient Temperature Gradients Change. Phys Rev Lett (2016) 117:055501. doi:10.1103/PhysRevLett.117.055501

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Li J, Li Y, Wang W, Li L, Qiu C-W. Effective Medium Theory for thermal Scattering off Rotating Structures. Opt Express (2020) 28:25894–907. doi:10.1364/OE.399799

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Lei M, Wang J, Dai GL, Tan P, Huang JP. Temperature-dependent Transformation Multiphysics and Ambient-Adaptive Multiphysical Metamaterials. EPL (2021) 135:54003. doi:10.1209/0295-5075/ac159d

CrossRef Full Text | Google Scholar

28. Xu L, Huang J. Metamaterials for Manipulating thermal Radiation: Transparency, Cloak, and Expander. Phys Rev Appl (2019) 12:044048. doi:10.1103/PhysRevApplied.12.044048

CrossRef Full Text | Google Scholar

29. Guo J, Xu G, Tian D, Qu Z, Qiu CW. A Real‐Time Self‐Adaptive Thermal Metasurface. Adv Mater (2022) 34:2201093. doi:10.1002/adma.202201093

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Dai G, Shang J, Wang R, Huang J. Nonlinear Thermotics: Nonlinearity Enhancement and Harmonic Generation in thermal Metasurfaces. Eur Phys J B (2018) 91:59. doi:10.1140/epjb/e2018-80596-8

CrossRef Full Text | Google Scholar

31. Dai G, Huang J. Nonlinear thermal Conductivity of Periodic Composites. Int J Heat Mass Transfer (2020) 147:118917. doi:10.1016/j.ijheatmasstransfer.2019.118917

CrossRef Full Text | Google Scholar

32. Yang S, Xu L, Huang J. Metathermotics: Nonlinear thermal Responses of Core-Shell Metamaterials. Phys Rev E (2019) 99:042144. doi:10.1103/PhysRevE.99.042144

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Han T, Yang P, Li Y, Lei D, Li B, Hippalgaonkar K, et al. Full-parameter Omnidirectional thermal Metadevices of Anisotropic Geometry. Adv Mater (2018) 30:1804019. doi:10.1002/adma.201804019

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Su Y, Li Y, Yang T, Han T, Sun Y, Xiong J, et al. Path‐Dependent Thermal Metadevice beyond Janus Functionalities. Adv Mater (2021) 33:2003084. doi:10.1002/adma.202003084

CrossRef Full Text | Google Scholar

35. Su Y, Zhang X, Sun Y, Xiong J. Janus Functional thermal Metadevice with Predictable thermal Rotation. Appl Phys Lett (2022) 120:141901. doi:10.1063/5.0078014

CrossRef Full Text | Google Scholar

36. Tian B, Wang J, Dai G, Ouyang X, Huang J. Thermal Metadevices with Geometrically Anisotropic Heterogeneous Composites. Int J Heat Mass Transfer (2021) 174:121312. doi:10.1016/j.ijheatmasstransfer.2021.121312

CrossRef Full Text | Google Scholar

37. Feng H, Ni Y. Temperature-dependent Switchable thermal Bifunctions in Different diamond-shaped Devices. Appl Math Comput (2022) 423:127006. doi:10.1016/j.amc.2022.127006

CrossRef Full Text | Google Scholar