Prospects for Neutron Reactions on Excited States in High-Density Plasmas

With the reactions of high flux neutrons, such as in a DT plasma, there is a prospect of seeing new kinds of neutron-nucleus reactions for the first time. If neutrons excite a heavy nucleus, for example, there is possibility of a second neutron reacting on excited states of the residual nucleus before that nucleus has de-excited to its ground state. The possibility of such reactions on excited states has rarely been considered. The cross section for neutron induced fission on the isomeric state of ²³⁵U has been measured (D’Eer et al., Phys. Rev. C, 1988, 38: 1270–1276) and calculated (Younes et al., 2003, Maslov, 2007), and reactions on rotationally excited nuclear states has been calculated (Kawano et al., Phys. Rev. C, 2009, 80: 024611). In high flux plasmas, however, a much wider range of reactions is possible. We therefore need to consider excited states at much higher-energies than previously modeled, and then estimate whether second neutrons are likely to rescatter on those excited states. To determine the likelihood of such rescattering events, we first need to know the probable time series of nuclear decays of those excited states. The lifetimes of many low-lying states have been measured experimentally, but now we need to know the lifetimes of the many higher excited states that could be produced from incident 14 MeV neutrons. These are too numerous to be measured and also too numerous to be calculated individually, so statistical Hauser-Feshbach decay models are used. I show some lifetime calculations for ⁸⁹Y, ¹⁶⁹Tm, and ¹⁹⁷Au targets, and predictions for the number of rescattering events in plausible plasma scenarios.

Introduction

Traditionally nuclear reactions are measured and modeled with both the projectile and the target starting in their ground states. At high temperatures in the interior of stars, the thermal energy will keep a statistical fraction of the nuclides in excited states, but that is difficult to reproduce in the laboratory. The closest we come to this so far is inside the imploding capsules during inertial confinement experiments such as those in the National Ignition Facility NIF [1]. In such locations with a high flux of neutrons, a nuclide may receive enough energy from incident neutrons that a second incident neutron could react with it before it stops emitting particles or gamma rays. There can then be two successive energy transfers, and the increased amount of excitation energy may enable reactions not possible before. To date the cross sections for neutron induced fission on the isomeric state of ²³⁵U has been measured [2] and calculated [3, 4], and reactions on rotationally excited nuclear states has been calculated [5]. If incident 14 MeV neutrons are used that result from DT fusion, then a great many more inelastic states will have been excited and maybe subject to a second neutron reaction.

The first step in seeing whether this could occur is to calculate the lifetimes of the excited states that could arise in reactions induced by 14 MeV neutrons. The low-lying levels in nuclei will have had their lifetimes measured in experiments, but now we will need to calculate the lifetimes of the higher-lying states that are predicted to be produced by statistical decay models following the Hauser-Feshbach (HF) method. The HF methods work by calculating the decay rate of excited states by summing the rates of possible decay paths for different kinds of decays such as by neutron, proton, alpha or gamma emissions. This is a statistical method that ignores the quantum interferences possible when multiple decay paths end at the same final state, and assumes that collections of states are well characterized by their average properties and so may be gathered into energy groups of similar spins and parities. It needs an optical potential for each incoming and exiting particle, as well as an equivalent ‘strength function’, as defined below, for gamma transitions. The HF methods include higher-lying compound-nucleus states which will have longer lifetimes than collective rotational levels, though still with shorter lifetimes than many known isomeric levels.

Nuclear Lifetimes

The average decay rate of an excited state λ is related to the width Γ of that state by Γ = ℏλ, and to its lifetime by τ = 1/λ. These determine the survival probabilities P(t) = exp (−t/τ), so the half life (the time for an initial population to decay by a half) is T_1/2 = τ ln (2) = 0.693τ. We denote the averages of these properties over similar states by ⟨λ⟩ and ⟨Γ⟩. If there are multiple exit channels c from a given state then each route will have its own partial width Γ_c, and the total width will be Γ_T = ∑_cΓ_c. The decay rates λ will add similarly, and the result will be shorter lifetime for that state. The decays of excited states thus depend on the branching ratios B_c = Γ_c/Γ_T which, summing up to unity, give the probability of a decay proceeding via channel c.

The Hauser-Feshbach method requires knowledge of the level density ρ(E) of levels per unit energy. These are connected to the average partial widths by physical principles that depend on the type of channel c. If these are particle decay channels, then information from the scattering optical potential is used to give a transmission coefficient T_c, which is the probability that such an incoming particle will be absorbed by typical compound-nucleus resonances and so leave the elastic channel. By time reversal, the same transmission coefficients apply to the emission probabilities of those particles. From R-matrix scattering theory [6, ch. 11], the transmission coefficients are related to the average partial widths of levels by T_c = 2π⟨Γ_c⟩ρ(E). The decay branching ratios calculated in the Hauser-Feshbach method are B_c = T_c/∑_cT_c. If a level decays by gamma (photon) emission, then the partial gamma widths are typically described as ${\mathrm{\Gamma }}_{\gamma }=E_{\gamma }^{2L+1}{f}_L(E_{\gamma })/\rho (E)$ in terms of a gamma strength function f_L (E_γ). The E_γ is the energy of the gamma-ray emitted, and L is its multipolarity (sentence removed).

The other parameters of Hauser-Feshbach calculations have been estimated by nuclear evaluators as they use these reaction and decay models to fit the known reaction data for a 14 MeV neutron incident on the targets ⁸⁹Y, ¹⁶⁹Tm, and ¹⁹⁷Au we are considering. These three materials are chosen because they have only one stable isotope each, and so any products of neutron capture or removal will produce experimentally distinctive decay products. Hauser-Feshbach codes Talys [7], Empire [8] and Yahfc [9] are all widely available to use, and include good collections of default parameter sets. Yahfc takes discrete levels from [10], gamma strength parameters from [7] using the functional form of [11], and neutron optical potentials from [12]. I am thus able to use the default parameter sets that give a reasonably good description of how these targets are excited and subsequently decay.

I use an instrumented version of Yahfc, wherein the Hauser-Feshbach denominators D = ∑_cT_c are saved separately for each level, as well as specifications of the chain of intermediate states appearing in each Monte Carlo instance of a decay path. These denominators D = ∑_c2π⟨Γ_c⟩ρ(E) may be used to calculate the average total width of each state by Γ_T = ∑_cT_c/2πρ(E) = D/2πρ(E), and they give us its average lifetime τ = 2πℏ ρ(E)/D. Figure 1 shows the lifetimes of some positive-parity levels in ¹⁹⁷Au. Above the neutron emission threshold at 6.3 MeV the lifetimes become much shorter because neutrons are emitted more quickly than gamma rays. The lifetimes are longer for higher spin states because the wave functions for both gammas and neutrons behave as (kr)^L+1 at short distances r with wave number k well within the range kr ≪ 1, so larger multipolarities L will give weaker transitions and hence longer lifetimes.

FIGURE 1

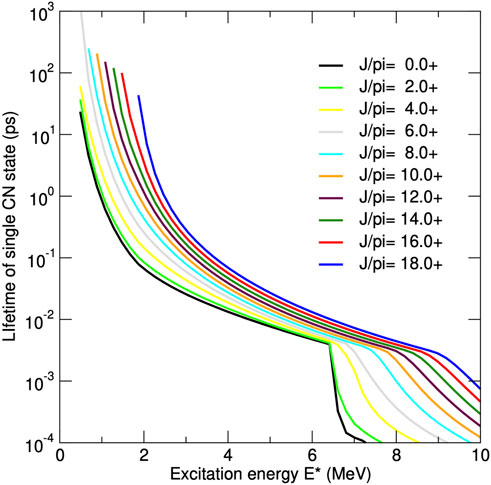
FIGURE 1. Calculated level lifetimes in pico-seconds (10^–12 s) from a Hauser-Feshbach model of ¹⁹⁷Au decay mechanisms for positive parity compound-nucleus levels with a selection of spins. The lines end on the left at known discrete levels, or when the level density drops below 1 level per MeV.

For each saved instance of a decay path, we can determine how long on average each decay process took. Each step in a Monte Carlo instance of a decay chain generates a random time interval of a level before it decays by sampling an exponential decay time probability distribution P(t) = τ⁻¹ exp (−t/τ). The cumulative persistence time t_p for a level is the sum of all the previous individual level durations t in that path. Using this information, we can determine the persistence cross sections σ₀₁ (t_p, E*) for the population of excited states at E* for a range of times after the initial neutron reaction.

Figure 2 show the persistence cross sections σ₀₁ (t_p, E*) on the left 1) for levels in ¹⁹⁷Au* after (n,n′) reactions, and on the right 2) for levels in after (n, 2n) reactions for times up to 500 ps. The legend of plot 1) shows at least four isomeric states in ¹⁹⁷Au but in the plot these do not give long-lived levels: they must have been rarely produced in this reaction. Some energy groups at low energies increase with time rather than decaying since they are fed by the incoming decays from states at higher excitation energies.

FIGURE 2

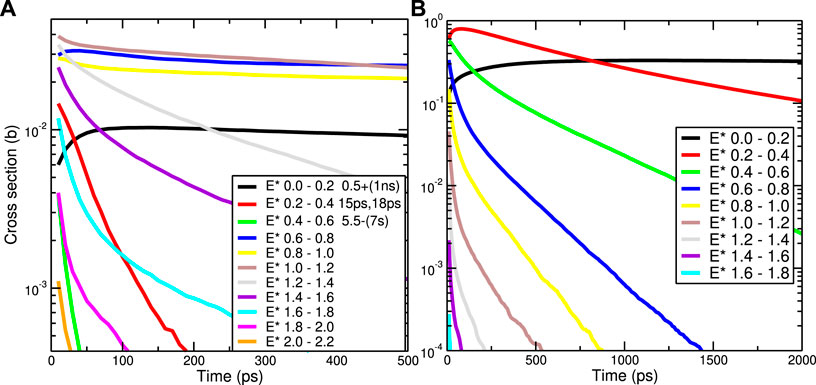
FIGURE 2. Persistence cross sections σ₀₁ (t, E*) for the population of excited states for a range of times t in pico-seconds from Hauser-Feshbach models of 14 MeV incident neutrons on ¹⁹⁷Au nuclei. Levels are shown after (n,n′) in (A), and after (n, 2n) in (B). The decay levels at excitation energies E* are grouped in bins 0.2 MeV wide.

Calculating Reactions on Excited States

During neutron pulses, the produced excited states may undergo second reactions if there are enough neutrons incident on them during the persistence times shown in Figure 2. High fluxes of neutrons (many neutrons per second per unit area) will make this more likely to occur. The number of such reactions per second is the product of the incident flux, the above production cross section, and the number of targets.

Let n₀ be the number of incident neutrons of energy E₀ in a pulse of duration T passing through an area A at a constant rate, giving an incident neutron flux of j₀ = n₀/AT. Suppose there are n₁ heavy target nuclei in the area A such as the surface of a sphere inside which the neutrons are generated. The excited states (called particle 2) are then produced at a rate dn₂(t)/dt = j₀n₁σ₀₁, which when integrated gives n₂(t) as their produced population. After being produced, they persist or decay according to curves shown in Figure 2. The needed effective persistence cross section is the average of σ₀₁ (t₂ − t₀, E*) for both first-scattering time t₀ and second-scattering time t₂ within the pulse duration. If the flow of neutrons is constant during the pulse duration, then the second scattering rate depends on the direct average cross section

${\sigma }_{\text{eff}}\left(T,E^{\ast }\right)=\frac{2}{T^2}{\int }_0^{T}d{t}_2{\int }_0^{t_2}d{t}_0{\sigma }_{01}\left(t_2-t_0,E^{\ast }\right).(1)$

Figure 3 shows these effective averaged cross sections for producing excited states for a range of pulse durations from 14 MeV incident neutrons on ¹⁹⁷Au nuclei after (n,n′) reactions (a), and on ¹⁶⁹Tm nuclei after (n, 2n) reactions (b). Figure 3A takes for its input the data in Figure 2A, and is similar only in general terms because of the averaging. If the flow rate of neutrons varies significantly over the pulse duration then an experimentally-specific calculation will be needed.

FIGURE 3

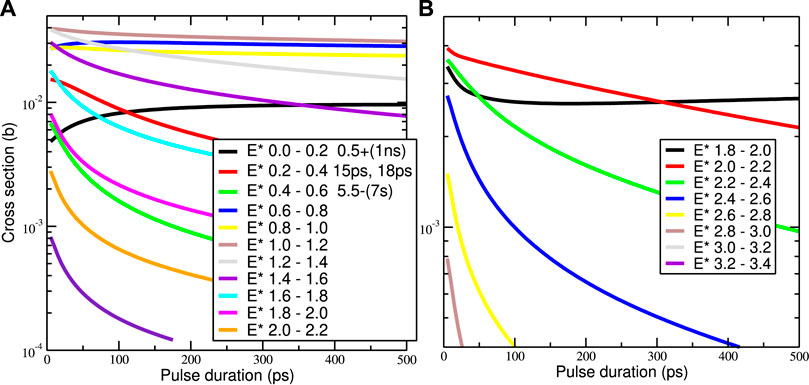
FIGURE 3. Effective production cross sections σ_eff (T, E*) for the population of excited states for a range of pulse durations T in pico-seconds from 14 MeV incident neutrons on ¹⁹⁷Au nuclei after (n,n′) reactions (A), and on ¹⁶⁹Tm nuclei after (n, 2n) reactions (B).

When a second neutron rescatters on the n₂(t) excited-state targets, the products of that reaction (called particle 3) in the pulse of duration T will be counted by

$n_3\left(T,E^{\ast }\right)=\frac{1}{2}{\sigma }_{02}\left(E_0+E^{\ast }\right)\frac{n_0^2}{A^2}{n}_1{\sigma }_{\text{eff}}\left(T,E^{\ast }\right).(2)$

This depends quadratically in the incident neutron areal density n₀/A because the first and second scatterings are both linear in that density. The factor of 1/2 is because of the averaging the linear time production of excited states during the neutron pulse. The cross section to produce particle three from particle two is written as σ₀₂ (E₀ + E*) because the incident neutron energy and the excitation energy are added together to give that combined energy of the compound system after the second reaction. That would be the incident energy of a single neutron to produce the same intermediate state.

Responses in Short Neutron Pulses

For a numerical example, consider from the experiment [13] the number n₀ = 1.73 × 10¹⁶ of neutrons passing at 14 MeV energy through the surface of a sphere of radius 25 μm taken from the measured radius of implosion hotspot [13, Figure 5C]. We now consider a trial calculation for these neutrons incident on 10¹⁶ heavy target nuclei implanted in that surface. If the effective production σ_eff and rescattering cross sections σ₀₂ are given in barns, then

$n_3=\frac{1}{2}{\sigma }_{02}\frac{n_0^2}{A^2}{n}_1{\sigma }_{\text{eff}}=4.44\times 10^8{\sigma }_{02}{\sigma }_{\text{eff}}.(3)$

FIGURE 5

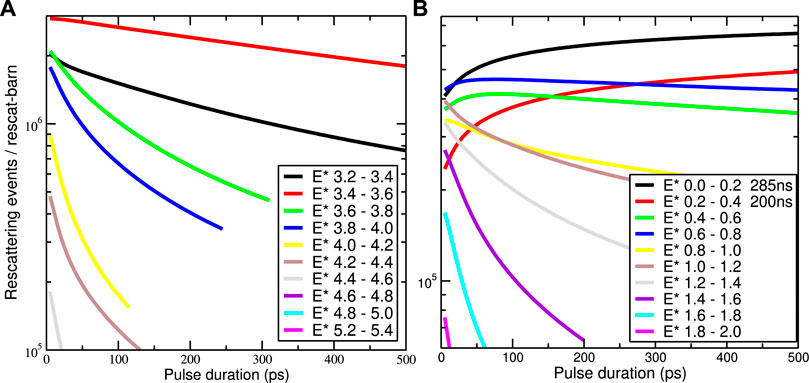
FIGURE 5. Numbers of neutron rescattering events per barn of rescattering cross section for a range of pulse durations T in pico-seconds from 14 MeV incident neutrons after (n,n′) reactions on ⁸⁹Y nuclei (A), and after (n,p) reactions on ¹⁶⁹Tm nuclei (B).

Since we know σ_eff from above, but not σ₀₂, I will in Figures 4, 5 show plots of n₃/σ₀₂ as the number of neutron rescattering events per barn of rescattering cross section for targets of ⁸⁹Y, ¹⁶⁹Tm, and ¹⁹⁷Au. Because I am assuming constant neutron flux during the incident pulse, Figure 4A is simply a scaled Figure 3A. Figures 4B, 5 show further reaction varieties with shapes different from ¹⁹⁷Au. Figures 4B, 5B are dominated by known isomer states at low energies. Apart from such isomer states, the most likely excited states to be subject to rescattering events are between 1 and 3 MeV: much larger the 50–150 keV considered in any of the earlier models [2–4]. Furthermore, it is encouraging that the 2020 NIF experiment [13] has high enough flux that rescattering cross sections even in the millibarn range ought to produce 100 or 1,000 rescattering events.

FIGURE 4

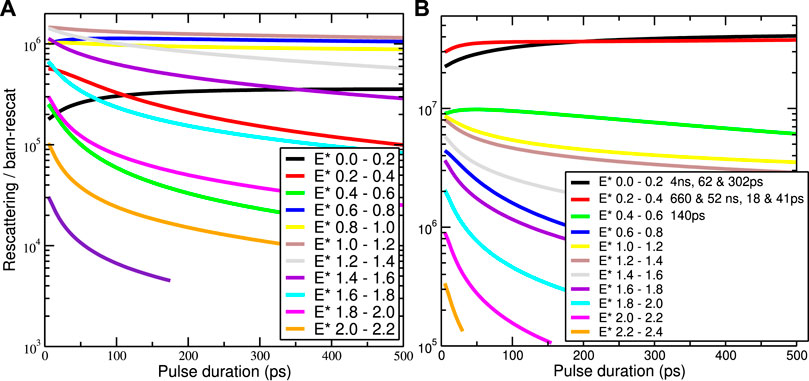
FIGURE 4. Numbers of neutron rescattering events per barn of rescattering cross section for a range of pulse durations T in pico-seconds from 14 MeV incident neutrons on ¹⁹⁷Au nuclei (A) and ¹⁶⁹Tm nuclei (B) after (n,n′) reactions.

Detecting Rescattering Events

To detect these rescattering events on excited states in a distinctive manner, we would ideally want their cross sections σ₀₂ (E₀ + E*) to be rather sensitive to the additional compound-state energy E*. Then there might be new reactions such as (n, 3n) that would likely not occur with only an energy of E₀ from a single incident neutron. The threshold for the ¹⁹⁷Au (n, 3n)¹⁹⁵Au reaction is just above 14 MeV, as shown in Figure 6. In principle, the detection of specific gamma decay peaks in the decay spectrum of ¹⁹⁵Au would be indicative of higher-order reactions of the kinds described in this paper. We note, however, that the (n, 3n) cross sections are themselves small near threshold, and these small values are those needed to convert the quantities in Figures 4, 5 in scattering events. It will also be necessary to allow for an energy spread in the initial neutrons around 14 MeV. A more detailed transport calculation, however, is beyond the scope of this paper.

FIGURE 6

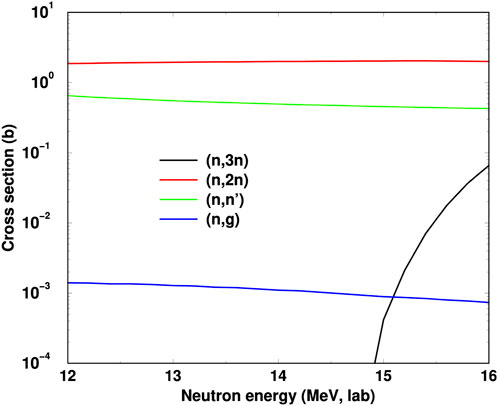
FIGURE 6. Cross sections for neutrons incident on ¹⁹⁷Au in the range 12–16 MeV, from default Talys Hauser-Feshbach calculations [7].

Conclusion

New experimental facilities with high-fluence neutron pulses may allow new measurements of neutron reactions on excited states. We have the theory and modeling methods needed to calculate the lifetimes of excited states during decay cascades. This is possible not only for the known discrete levels at low excitation energies, but also at the higher energies where particle emission can compete with gamma production mechanisms. At the higher energies it is necessary to use statistical Hauser-Feshbach models of the decay processes, since the denominators of the branching ratios in those models may be directly converted to average decay widths and hence also average lifetimes. With that lifetime information we can model the time progress of excitation energies, and in this preliminary study calculate the rescattering rates on excited states during the neutron pulses. These rescattering events would show themselves in experiments by the decays of residual nuclei that would not otherwise be produced.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

IT is the sole contributor.

Funding

This work was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. D’Eer A, Wagemans C, Nève de Mévergnies M, Gönnenwein F, Geltenbort P, Moore MS, et al. Neutron-induced Fission of the 26 minU235isomer. Phys Rev C (1988) 38:1270–6. doi:10.1103/PhysRevC.38.1270

CrossRef Full Text | Google Scholar

2. Younes W, Britt HC, Becker JA. Simulated (N,f) Cross Section of Isomeric ^235mU. Tech. Rep. UCRL-CONF-201697. Lawrence Livermore National Laboratory (2003).

Google Scholar

3. Maslov VM. ^235mU and ²³⁵U Neutron-Induced Fission. Les Ulis Cedex, France: EDP Sciences: ND2007 proceedings (2007). doi:10.1051/ndata:07242

CrossRef Full Text | Google Scholar

4. Kawano T, Talou P, Lynn JE, Chadwick MB, Madland DG. Calculation of Nuclear Reaction Cross Sections on Excited Nuclei with the Coupled-Channels Method. Phys Rev C (2009) 80:024611. doi:10.1103/PhysRevC.80.024611

CrossRef Full Text | Google Scholar

5. Moses EI, Atherton J, Lagin L, Larson D, Keane C, MacGowan B, et al. The National Ignition Facility: Transition to a User Facility. J Phys Conf Ser (2016) 688:012073. doi:10.1088/1742-6596/688/1/012073

CrossRef Full Text | Google Scholar

6. Thompson I, Nunes F. Nuclear Reactions for Astrophysics: Principles, Calculation and Applications of Low-Energy Reactions. Cambridge, UK: Cambridge University Press (2009).

Google Scholar

7. Koning AJ, Rochman D. Modern Nuclear Data Evaluation with the Talys Code System. Nucl Data Sheets (2012) 113:2841–934. doi:10.1016/j.nds.2012.11.002

CrossRef Full Text | Google Scholar

8. Herman M, Capote R, Carlson BV, Obložinský P, Sin M, Trkov A, et al. Empire: Nuclear Reaction Model Code System for Data Evaluation. Nucl Data SheetsSpecial Issue Evaluations Neutron Cross Sections (2007) 108:2655–715. doi:10.1016/j.nds.2007.11.003

CrossRef Full Text | Google Scholar

9. Ormand WE. Monte Carlo Hauser-Feshbach Computer Code System to Model Nuclear Reactions: YAHFC. Tech. Rep. LLNL-TR-824700. Lawrence Livermore National Laboratory (2021). doi:10.2172/1808762

CrossRef Full Text | Google Scholar

10.[Dataset] Capote R, Herman M, Young P, Goriely S, Belgya T. Reference Input Parameter Library (RIPL-3) (2009). Available at: https://www-nds.iaea.org/RIPL-3/(accessed 10 25, 2020).

Google Scholar

11. Kopecky J, Uhl M. Test of Gamma-ray Strength Functions in Nuclear Reaction Model Calculations. Phys Rev C (1990) 41:1941–55. doi:10.1103/PhysRevC.41.1941

CrossRef Full Text | Google Scholar

12. Koning AJ, Delaroche JP. Local and Global Nucleon Optical Models from 1 keV to 200 MeV. Nucl Phys A (2003) 713:310. doi:10.1016/s0375-9474(02)01321-0

CrossRef Full Text | Google Scholar

13. Baker KL, Thomas CA, Casey DT, Hohenberger M, Khan S, Spears BK, et al. Hotspot Parameter Scaling with Velocity and Yield for High-Adiabat Layered Implosions at the National Ignition Facility. Phys Rev E (2020) 102:023210. doi:10.1103/PhysRevE.102.023210

PubMed Abstract | CrossRef Full Text | Google Scholar