Stick-Slip Dynamics in a Granular Material With Varying Grain Angularity

Experiments, simulations, and theoretical treatments of granular materials typically feature circular or elliptical grains. However, grains found in natural systems often have flat faces that introduce local rotational constraints; these rotational constraints have been shown to affect, for example, the jamming transition, discontinuous shear thickening, and ordered states in colloids and thermalized grains. In this work, we experimentally investigate the effects of grain angularity on stick-slip dynamics. A weighted slider is pulled by a spring over a gravity-packed granular bed composed of polygonal grains with varying angularity. We find that packings of triangular or square grains have higher shear strengths than packings of pentagons, hexagons, heptagons, or disks. Additionally, as the number of sides increases, sticking periods, during which the slider remains motionless while the spring force on it increases, become shorter on average, with the material yielding at smaller applied stresses. Lastly, we find that dilation of the medium during sticking periods tends to be larger for grains with higher angularity, in part because of the presence of stilt-like columnar structures that prop the slider up. We report on measurements of the pulling force on the slider, particle dynamics during slip events, and properties of force-bearing contact networks identified via photoelasticity. Our findings indicate that high angularity of grains (pentagons, squares, triangles) leads to differences in grain-scale flow and macroscopic stick-slip dynamics of bulk granular materials. Our experiments also indicate a continuous change in dynamics with decreasing angularity as the circular grain limit is approached.

1 Introduction

Stick-slip dynamics occurs in a variety of systems and materials spanning many size scales, from bulk metallic glasses [1, 2] and AFM microscope tips [3] to the motion of macroscopic frictional or sticky surfaces such as rocks [4, 5], Bristol board [6, 7], and rosin-coated bowstrings [8], to large-scale geophysical systems such as the fault gouge between tectonic plates [9–13]. These dynamics are characterized by a cycle of loading phases (sticking periods), in which macroscopic shear stress builds under slowly increasing shear, and intermittent, relatively rapid releases of shear stress accompanied by deformations (slip events). Stick-slip dynamics have also been modeled via purely empirical, yet effective, nonlinear rate-and-state laws [14–17]. Despite advances in understanding the universality of stick-slip dynamics [2, 18, 19] and modeling stick-slip with empirical models [14–17], the microscopic origins of this behavior are not well understood, particularly in the case of granular materials.

In slowly driven dense granular materials, stick-slip dynamics manifests as transitions between stable, jammed states and yielding, unjammed states featuring plastic deformation and flow [12, 13, 20–26]; understanding granular stick-slip thus additionally provides insights into the physics of granular materials driven near the jamming transition (see, e.g. [27, 28]). A multitude of experiments and simulations have characterized critical scaling laws of granular avalanches [22, 29, 30] and the transitions with varying driving parameters among steady sliding, periodic stick-slip, and irregular stick-slip regimes [12, 13, 20, 23, 31, 32]. Most studies of stick-slip in granular materials, however, have been restricted to idealized spheres (disks in two dimensions) or naturally occurring granular materials like soils and sands whose shape and size are not systematically controlled [33–35]. Grain shape (as well as other micro-scale features like friction and cohesion) has been shown to affect the macroscopic stability [30, 33, 36–46] and flow [47–51] of granular materials in numerous contexts, so it is likely to influence stick-slip dynamics in granular materials as well.

In this work, we perform experiments in which a slider is pulled by a spring across a bed of grains with varying angularity, as shown in Figure 1A, to quantify differences in the stick-slip dynamics of the slider. We find that increasing angularity increases the average duration of sticking periods and energy released in slip events, both resulting from the increased shear strength of packings of more angular grains. Through particle tracking and photoelastimetry [52, 53], we then examine grain-scale dynamics and stresses in the granular material. We find that in disk packings, grains tend to form a pile in front of the slider, whereas angular grains do not. We also observe that angular grains, unlike disks, can form columnar stilts composed of a few grains at the surface that prop up the slider during sticking periods. Lastly, we show that the depths of grain motion (i.e., the depth of the shear band [54]) and changes in stress fields between slip events are approximately the same, with similar decay lengths of about 10 particle diameters for all grain angularities that we consider.

FIGURE 1

FIGURE 1. (A) Schematic of system under study. The slider of weight Mg rests on top of a gravity-packed granular material and is pulled by a spring of stiffness k at speed c. The location (x, y) of the front hole is used to represent the position of the slider, and the angle β from the horizontal to the segment joining the two holes represents the orientation of the slider, with β > 0 corresponding to counterclockwise rotation. (B) Subtraction images (bottom) are obtained by subtracting white light images (top) and photoelastic images (middle).

2 Materials and Methods

A slider of mass M = 0.191 ± 0.001 kg and length $\sim 20d_s$ (where d_s is the small grain diameter) is pulled with a spring across a quasi-two-dimensional (2D) bed of gravity-packed photoelastic grains in a channel that is about 200d_s long and 19d_s deep between two vertical glass plates, as shown in Figure 1A. The bottom of the slider is composed of a sequence of teeth that range in shape from triangle to disk (all shapes that we use in our experiments) periodically. We fix the depth of the teeth and use the size corresponding to the smaller of each type of grain in each bidisperse packing (see below). This design is used so that the slider is effectively rough for all grain shapes in this work. The front of the slider is angled at 20° above the horizontal to allow the slider to move along the surface of the packing rather than burrowing into it. Several slider shapes were tested to ensure that the slider exhibited stick-slip dynamics without significant burrowing for all of the grain shapes studied in this work, though some pile formation occurred for the disk packing, as discussed below in Section 3.1. Detailed studies of the influence of the slider’s shape are beyond the scope of this work.

The granular materials studied are bidisperse (to prevent crystallization [55]) packings of disks and regular polygons ranging from triangles (N = 3 sides) to heptagons (N = 7). We examine behaviors as a function of the angularity α ≡ 2π/N of each packing’s constituent grains using $\alpha =2\pi \left[0,\frac{1}{7},\frac{1}{6},\frac{1}{5},\frac{1}{4},\frac{1}{3}\right]$ and packings with equal-area mixtures of pentagons, hexagons, and heptagons that serve as a simple model of a more realistic granular material in nature with variations of size and shape [35, 56].

The small disks have diameter d_s = 1.280 ± 0.003 cm and the large disks have diameters d_l = 1.602 ± 0.003 cm. The other shapes have circumscribing radii corresponding approximately to the disk radii, as shown in Table 1. All grains have the same thickness (width) of 0.6 cm. For each packing of a given angularity, the number ratio of large to small grains is 10:11. For the mixture of grains, the number ratio for small pentagons, small hexagons, and small heptagons is 18:17:15, and 17:15:15 for all corresponding large shapes. This choice of ratios keeps the area contributed by grains of each shape approximately the same while maintaining a large to small ratio of approximately 10:11 for each individual shape.

TABLE 1

TABLE 1. Sizes of photoelastic grains of varying angularity.

The interparticle friction coefficient, a property of the material composing individual grains, for all grain shapes is μ = 0.7 ± 0.1. We measure the interparticle friction for each shape by tilting a surface until a layer of grains (of a single shape and with the same orientation), initially resting edge-to-edge on an identical layer that is the fixed to the surface, begins to slide. For angular grains, we set the top and bottom layers to have flat contacts between them. The angle of repose is then used to calculate a coefficient of static friction; we perform ten trials per shape to obtain averages and standard errors for each shape, which are all in agreement. Friction between grains and the glass walls is negligible because forces in the system are primarily vertical.

The slider is pulled by a spring of spring constant k = 16 N/m at a fixed pulling rate c = 5 mm/s. k and c have been chosen such that the system is in the stick-slip dynamical regime for all grain shapes [12, 20, 24]. For each shape, at least 25 runs are performed in which the slider is pulled across the entire length of the channel. Approximately 30 stick-slip cycles occur per run. In between runs, the granular material is stirred to prevent compaction after many runs. After stirring, the surface of the granular material is leveled so that the initial height of the material is $\sim 19d_{\text{s}}$.

A force sensor measures the pulling force F that the spring exerts on the slider. During a sticking period, this also corresponds to the shearing force that the slider exerts on the surface of the granular material. In this work, we normalize F by Mg, the weight of the slider. The ratio F/Mg at which the granular material yields (a slip event is initiated) approximates the shear strength of the granular material, which is rigorously defined as the ratio of shear to normal stress in a packing that is slowly sheared between parallel walls [38]. In our system, the spring force is parallel to the surface of the granular material, and the stress exerted by the slider is primarily a shear stress, though a small pressure force (≪ Mg) arises due to the front slope.

Two cameras visualize the granular material and slider, with one recording a white light image to track the slider and grains and another recording a polarized light image to visualize grain-scale stresses with a dark-field polariscope [52, 53]. The cameras record videos at 120 frames per second, or 8.33 ms between frames. Subtraction images obtained from white light and polarized light images, as explained in Figure 1B and shown for different packings in Figure 2, are used to qualitatively visualize both motion of grains and stresses within the material simultaneously.

FIGURE 2

FIGURE 2. Images obtained by subtracting polarized light from white light images, displaying both grains and grain stresses. Dark grains are experiencing significant forces from other grains and the slider.

3 Results

3.1 Slider Dynamics

Figure 3 shows sample time series of F/Mg and the horizontal velocity v_x of the slider for experimental runs over an interval of 180 s. Time is rescaled by c to give a cumulative drive distance in cm. v_x, given in units of small grain size d_s per second, is computed by taking the difference in the slider’s horizontal position in two consecutive frames and dividing by the time step of 8.33 ms between frames. Sticking periods correspond to times in which the velocity of the slider is low (v_x ≈ 0) and the pulling force increases linearly with time. The sticking periods that we detect are indicated by the gray regions of the plots. Slip events are the rapid decreases in force that occur as the granular material yields and the slider slides across the granular surface. We detect slip events from the force time series using a wavelet transformation that distinguishes rapid decreases in force from noisy fluctuations more successfully than a derivative threshold [57]. The average slip event duration is 0.4 s. Note that there is some creep of the slider and packing during sticking periods, partly due to the slight compression of the grains at their contacts and partly due to the rotational and vertical degrees of freedom of the slider (see Section 3.1.3).

FIGURE 3

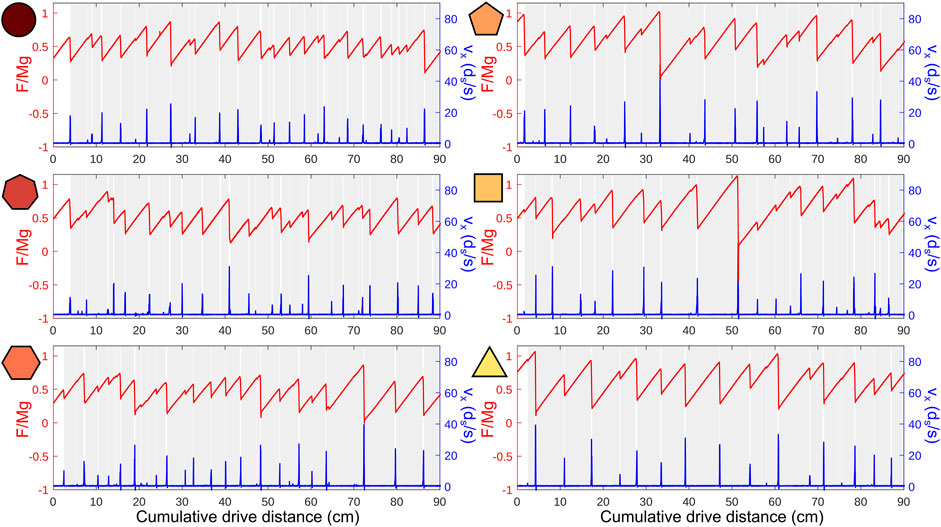
FIGURE 3. Sample time series for all shapes from disks, heptagons, and hexagons (left column) to pentagons, squares, and triangles (right column). The normalized pulling force is plotted in red on the left axis and the horizontal velocity of the slider is plotted in blue on the right axis. Detected sticking periods (with v_x ∼ 0) are indicated by gray regions.

For disks, heptagons, and hexagons, the sample time series appear to show similar patterns of sticking periods and force drops. For pentagons, squares, and triangles, however, events are visibly less frequent and, correspondingly, the forces developed during sticking periods are larger. As one might expect, the velocities of the slider during slip events are larger as well. We next present quantitative statistics to better compare the slider dynamics for all packings.

3.1.1 Statistics of Slider Motion

Figure 4 shows a variety of probability density functions (PDFs) describing the motion and position of the slider for each packing. Panels (a) and (b) show the PDFs of pulling forces and horizontal slider velocities, respectively, for all runs with each packing. As suggested by the time series in Figure 3, the most angular grains indeed have larger average force and a greater variance of forces than the less angular grains (disks, hexagons, and heptagons). For these and all other quantities we measure, the mixture packing (with pentagons, hexagons, and heptagons) exhibits similar statistics to the packing of hexagons.

FIGURE 4

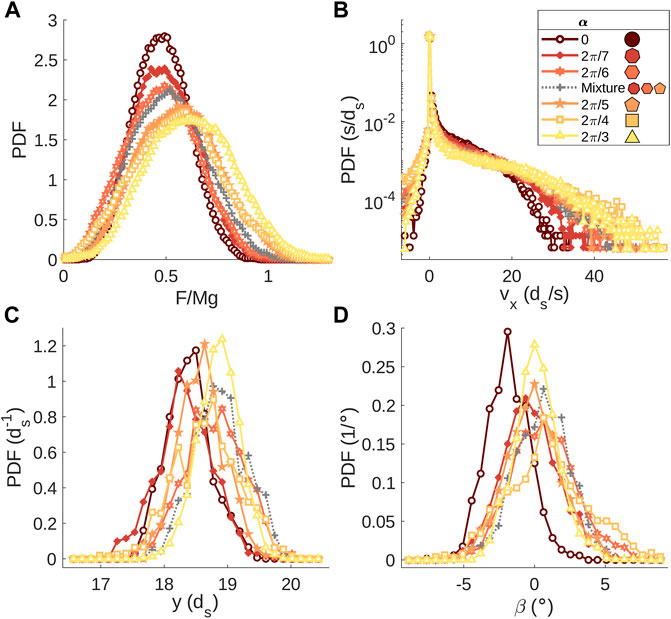
FIGURE 4. PDFs of various quantities describing motion and position of the slider. All distributions are produced from the combined time series of all experimental runs for each packing. (A) PDF of the normalized pulling force on the slider. (B) PDF of the horizontal component of the slider’s velocity. (C) PDF of the vertical position of the slider. (D) PDF of the angle of the slider.

Figures 4C,D display PDFs of the slider’s vertical position h above the bottom boundary and angle β, respectively. Though each packing is prepared with an initial height around 19d_s, the vertical position of the slider fluctuates and is slightly higher, on average, for more angular grains. For most packings, the slider’s angle fluctuates around 0°. With the disk packing, though, the slider orientation is biased slightly below the horizontal due to the accumulation of grains in a pile in front of the slider as the slider moves along the channel, as shown in Figure 5. The formation of a pile is less common for other shapes, though it can occur depending on how the initial surface of the packing along the channel is prepared. We have confirmed that the stick-slip statistics of the slider, presented below, are not influenced by the growth of this pile (or fluctuations in the pile size with all grains) as the slider moves along the channel.

FIGURE 5

FIGURE 5. Images of the disk packing early in an experimental run and later in the experimental run; the disks have formed a pile in front of the slider.

3.1.2 Stick-Slip Statistics

We next present statistics of the stick-slip dynamics of the slider. Figures 6A,B shows PDFs of the duration of sticking periods ΔT and the energy released by the spring in slip events ΔE, defined as

$\mathrm{\Delta }E=\frac{1}{2k}\left(F_{\text{Y}}^2-F_{\text{S}}^2\right)(1)$

FIGURE 6

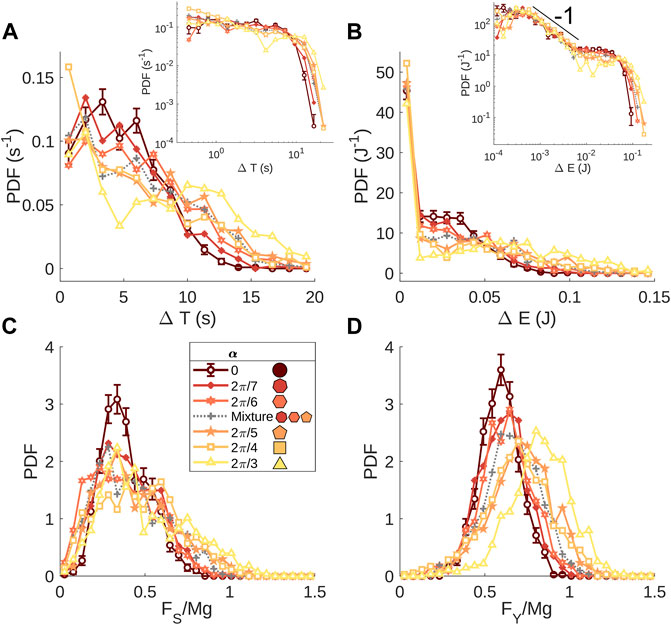
FIGURE 6. PDFs of (A) the duration of sticking periods ΔT, (B) the energy released in slip events ΔE, (C) the force F_S on the slider at the start of a sticking period, and (D) the force F_Y at the end of a sticking period, when the materials starts to yield. Insets in (A,B): Probability density functions of ΔT and ΔE, respectively, on a log-log scale; the black line has a slope of −1. Error bars for disk (α = 0) data are representative of the scale of error bars on other data sets (not shown).

where F_Y and F_S are the forces exerted by the spring at the beginning and end, respectively, of a slip event. ΔT peaks at small durations for all packings, but with increasing angularity, events of longer duration occur and the PDF broadens. Similarly, for ΔE there is a relatively large number of low energy events. We show the PDF of ΔE on a log-log scale in the inset of Figure 6B to display the statistics of these events; the PDF of low energy events does not depend on the angularity of the grains. The structures of the energy PDFs do differ, however, at larger ΔE, with greater energy releases for larger grain angularity.

According to the inset of Figure 6B, the PDFs of ΔE are cut off at large values. While the slip size PDF in many stick-slip and crackling systems exhibits power law statistics [17, 29, 30, 32], our system has an excess of large energy events near a cutoff. The excess of higher energies is primarily due to the inertia of the slider [17], and the cutoff is set by the maximum pulling force (see below) that the granular material can sustain on average (i.e., the maximum F_Y in Eq. 1).

Finally, Figures 6C,D shows the PDFs of the pulling force on the slider at the beginning F_Y and end F_S of slip events. ⟨F_Y/Mg⟩ is an estimate of the shear strength of a granular material, as F_Y corresponds to a shear force that causes the packing to yield under the weight Mg (applied normal to the surface of the packing). With increasing α, the PDF of F_S/Mg broadens: we observe both smaller and larger forces than the disk packing on average. For F_Y, with increasing α the peak of the PDF shifts to higher forces and the PDFs broaden slightly. In other words, with increasing α the granular material yields at higher shear forces and the shear force supported at the end of slip events is more broadly distributed.

Figure 7 summarizes the average and standard deviations of the PDFs in Figures 6C,D. The average pulling forces ⟨F_S⟩ and ⟨F_Y⟩ depend weakly on α between 0 and 2π/7. The averages and spreads of forces increase with α more quickly beyond 2π/6. These results are qualitatively similar to macroscopic friction coefficients (the ratio of shear stress to pressure) measured in simulations of packings of frictional polygons under biaxial shear [38]. We have tested the distributions of F_S and F_Y with a one-way ANOVA test to confirm that the means presented in Figure 7 are statistically distinguishable for almost all angularities, with the one exception being ⟨F_S/Mg⟩ for disks and heptagons.

FIGURE 7

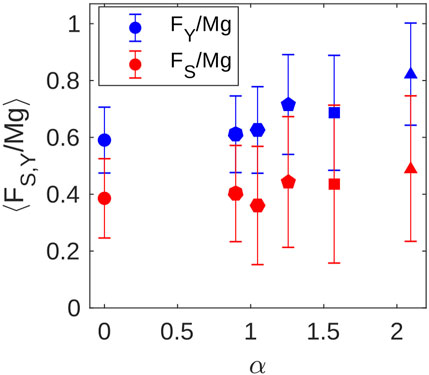
FIGURE 7. Average force at yielding ⟨F_Y/Mg⟩ (blue) and at the end of slip events ⟨F_S/Mg⟩ (red). Error bars represent the standard deviation. The standard error of the average is smaller than the marker size.

3.1.3 Vertical and Rotational Degrees of Freedom of the Slider

The spring pulls the slider at only one corner, and the slider is thus free to rotate in-plane and to translate vertically. Figures 4C,D show that the slider’s vertical position y fluctuates within a range of width d_s, and the angle β fluctuates between ±5° as the slider is pulled across the granular material. Although the slider’s mass is uniformly distributed and the front end is sloped and smooth, the front usually bears the most significant load (as seen in Figure 2, with the slider contacting the most stressed grains on its front end). During sticking periods, the pulling force thus tends to rotate the slider about a pivot point that is located near the sloped front end; y and β increase as a result. Figures 8A,B displays PDFs of Δy and Δβ, the changes in the vertical position (as defined in Figure 1) and angle of the slider from the beginning to end of sticking periods. With increasing angularity, both PDFs broaden towards larger values.

FIGURE 8

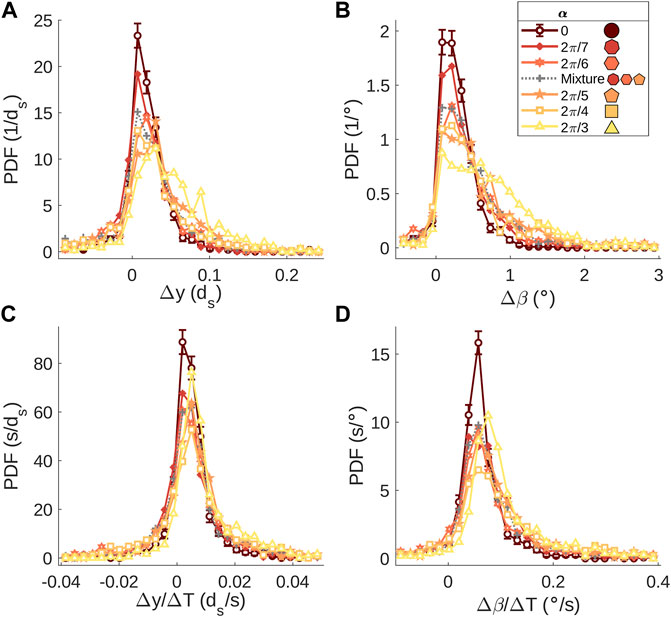
FIGURE 8. (A) PDF of the total change of the slider’s vertical position y (defined in Figure 1) during a sticking period. (B) PDF of the total change of the slider’s angle β during a sticking period. (C) PDF of change in vertical position normalized by sticking period duration. (D) PDF of change in angle normalized by sticking period duration. Error bars for disk (α =0) data are representative of the scale of error bars on other data sets (not shown).

If y and β primarily increase because the spring rotates the slider around a pivot point near the front end of the slider, then Δy and Δβ should roughly scale with the duration of a sticking period. In Figures 8C,D we show the PDFs of Δy/ΔT and Δβ/ΔT, normalizing Δy and Δβ for a given sticking period to the duration of that sticking period. Though the PDFs become more similar with this normalization, there are still differences–the PDFs for angular grains are slightly larger for larger values of Δy and Δβ than disks. Differences in the PDFs of Figures 8C,D suggest that interactions between the slider and grains, in some sticking periods, may cause the slider to slowly rise and tilt in addition to (or instead of) rotation about the front-end pivot point.

One possible mechanism contributing to the broader PDF tails for angular grains that we have observed is the formation of columnar stilts on the surface of the packing. Figure 9 shows a clear example of a stilt made of three square grains with edge-edge contacts that rotates slowly as the spring force on the slider increases, increasing the angle and vertical position of the slider by several grain diameters in a single sticking period. We observe that stilting does not occur in every stick-slip cycle, that the amount the slider lifts due to stilting varies, and that stilts seem to be composed exclusively of grains with edge-edge contacts. This phenomenon, we note, is not likely to lead to measureable creep in angle or vertical position for a much larger slider that would have many more contacts with the surface of the granular material than our slider does. The system we use is sensitive to the dynamics of stilts, though, and further quantitative analysis may yield insight into the formation and destruction of mesoscale structures that depend on grain shape.

FIGURE 9

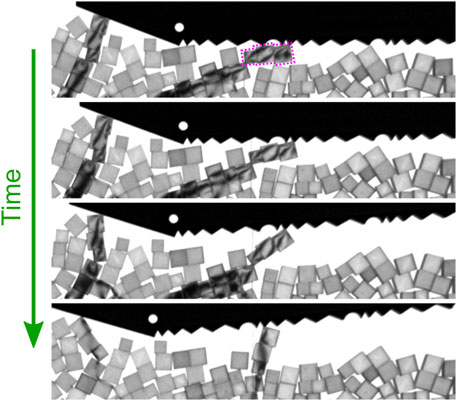
FIGURE 9. A sample sticking period in which the slider contacts a column of square grains (purple dotted outline in top segment) that rotates as the horizontal force from the slider increases. The angle and vertical position of the slider increase because of the rotation of this columnar stilt.

3.2 Dynamics and Stresses of the Granular Material

In this section, we present observations of dynamics of grains and the stresses in the granular material. The motion of grains–translational and rotational–during slip events is captured from video tracking using the correlation template matching method described in [58, 59] with white light images of the system. Detected disks and pentagons are shown in Figure 10. Stresses in the packing are visualized using photoelastimetry [52, 53].

FIGURE 10

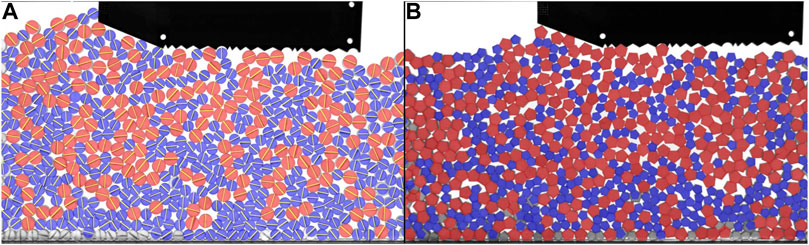
FIGURE 10. Tracked grains drawn over white light image from experiments for (A) the disk packing and (B) the packing of pentagons. The large grain in the bidisperse packing is drawn as red and the small grain as blue. For disks, orientations are marked with yellow bars.

The motion of grains is measured at each frame via the finite difference of positions and orientations of each grain at the current frame with their positions and orientations in the following frame (1 time step). The position, velocity, and angular velocity of each grain are then used to produce spatial maps–flow fields–of the grain speeds and angular speeds, with values at each point in space determined by interpolation of values at nearby grain positions. Figure 11 shows average flow fields of grain speed and angular speed during slip events for pentagons and disks. The average is taken over representative flow fields from each detected slip event. We choose the representative flow field of each slip to be the flow at the time in which the slider is moving fastest in each particular slip event. We have also considered other choices of a representative flow field for each slip, for example, averaging over all frames for each slip event, and found the qualitative results in Figure 11 to be robust.

FIGURE 11

FIGURE 11. Average speed and rotational speed flow fields during slip events for disks (left) and pentagons (right). The baseline noise for rotational speed of pentagons is significantly greater than that of disks due to differences in the methods used to track orientations of disks and angular grains. A schematic of the slider has been drawn near each flow field for reference.

For both grain shapes, motion of grains occurs near the free surface, and rotations of grains are maximal beneath the toothed bottom of the slider–grains most often roll along the surface during slips. Unlike with pentagons, with disks the slider needs to plough through the pile of grains that develops as the slider moves along the channel. Hence, the flow fields exhibit motion in a larger region in front of the slider. We have confirmed that the average flow field for pentagons is essentially identical to the average flow fields for hexagons and heptagons, which have no qualitative (nor quantitative) features distinct from those shown in Figure 11. (Flow fields for triangles and squares were not possible to obtain since the these particles cluster densely and are significantly more difficult to track than pentagons, hexagons, heptagons, and disks.)

We note that while positions of disks and pentagons are detected with a comparable resolution, the orientations of disks are measured with greater precision than the polygons. Disk orientations are found via the orientations of bars drawn on them, while the orientations of pentagons and other angular grains are determined by the orientation of the mask that best matches each particular pentagon in the image, which only gives a resolution of 1°. The rotational speed flow field (the absolute value of angular velocity of grains rotating about their centers of mass) for pentagons thus has a higher baseline noise than disks; pentagons are not physically rotating except near the surface.

3.3 Estimation of Shear Band Depth

Deformation of sheared dense granular materials is often localized in narrow regions near the driving boundaries called shear bands [54, 60, 61]. The flow fields in Figure 11 demonstrate that the packings in our system also deform in a narrow shear band near the surface; we next ask whether the depth of this shear band is influenced by grain shape. For disks, pentagons, hexagons, and heptagons, tracking grains is feasible with the correlation template matching approach used throughout this dissertation. The grain tracking method is significantly less successful for triangles and squares. To compare all grain shapes, then, we use a semi-quantitative estimate for the shear band depth rather than using grain tracking.

Figures 12A–C shows the method used to estimate the shear band depth via image subtraction. White light images before I_W1 and after I_W2 a slip event are subtracted, and the absolute value of the subtraction is obtained: |ΔI_W|. The average intensity change image, ⟨|ΔI_W|⟩, is computed by averaging |ΔI_W| for all slip events with a given grain shape. Prior to averaging, all images are translated so that the vertical position of the slider at the end of slip events is fixed. (Figure 12C shows, for visualization purposes, the difference image (I_W1 − I_W2 + 255)/2, where gray pixels (255/2) indicate no change between the two images.) Lastly, the average intensity with depth across the width of ⟨|ΔI_W|⟩, as indicated schematically by the green arrow in Figure 12C, is computed to estimate the depth of intensity changes and therefore grain motion. Figure 13A plots this average intensity with depth for all grain angularities. Changes in intensity decay over a depth of $\sim 10d_{\text{s}}$, a value consistent with the typical size of shear bands in granular materials [54]. This semi-quantitative measure does not distinguish grains of varying grain angularity, suggesting that the shear band depth is unaffected by grain angularity.

FIGURE 12

FIGURE 12. (A–C) White light images (A) before and (B) after a slip event are subtracted to estimate the depth of grain motion across many slip events. (C) The difference image between (A,B) (D–F) Polarized light images (A) before and (B) after a slip event are subtracted to estimate the depth of influence of force chains across many slip events. (C) The difference image between (A,B). Before averages are computed across slip events, the absolute value of the before-after difference image must be taken. The green arrows and boxes demonstrate the measurement of intensity change with depth that is performed on (C) ⟨|ΔI_W|⟩ and (D) ⟨|ΔI_P|⟩ to produce the data in Figure 13.

FIGURE 13

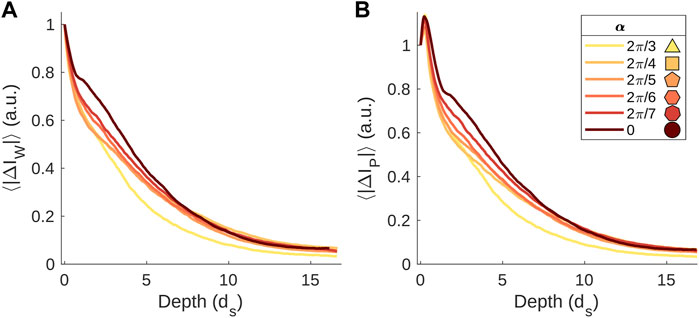
FIGURE 13. (A) Average intensity of ⟨|ΔI_W|⟩ with depth, rescaled by the intensity at a depth of 0d_s, for each grain angularity. (B) Average intensity of ⟨|ΔI_P|⟩ with depth, rescaled by the intensity at a depth of 0d_s, for each grain angularity.

Though the length scale of plastic deformation in a shear band is approximately the same for all grain angularities we study, the length scale associated with force chains that stabilize against the applied shear from the slider may differ with angularity. We quantify the extent of stress changes in the same manner as described above, now with photoelastic rather than white light images; by subtracting images before and after slips, we are able to eliminate the effects of stresses in the packing that result from gravity alone. The image |ΔI_P| is obtained from polarized light images just before I_P1 and after I_P2 each detected slip event, as demonstrated in Figures 12D–F, and the average ⟨|ΔI_P|⟩ is found across all slip events for each packing. Figure 13B shows the average intensity of ⟨|ΔI_P|⟩ with depth for all grain angularities. As with the white light images, the depth of decay in photoelastic response is roughly 10d_s and does not change significantly with grain angularity. The force chains that break and form during slip events seem to be spatially correlated with grain motion–near the bottom of the system where grains are stationary, changes in stresses are minimal from one sticking period to the next, suggesting a fixed bed of grains and contact forces that support the shear band.

4 Discussion

In this work, we have explored the effects of grain angularity on stick-slip dynamics in novel experiments with systematically-controlled grain angularity. We have demonstrated that the yield force increases with grain angularity, in agreement with results from simulations of quasi-statically sheared angular packings [36–38, 42] and experiments with 3D granular materials composed of faceted or irregularly shaped grains [30, 33]. We further find that, as a result of the enhanced shear strength with angularity, the stick-slip dynamics of the slider are also modified with angularity. Sticking periods have longer durations and slip events release more energy on average for more angular grains. These statistical changes are most prominent for highly angular grains (pentagons, squares, and triangles); the hexagons and heptagons yield statistics that are closer to the statistical measures from disks. We also show that the creep motion of the slider (observed primarily in the vertical and rotational degrees of freedom of the slider) is influenced by increasing angularity, with the slider lifting and rotating more during sticking periods. Finally, we observe that a mixture of pentagons, hexagons, and heptagons yields similar stick-slip statistics to a packing of hexagons.

Using particle tracking and photoelastimetry, we also explore the dynamics of grains and stresses in each packing. We observe that in packings of angular grains the slider can be propped up by columnar stilts composed of a few grains with edge-edge contacts; these stilts are analogous to columnar structures within sheared angular packings that have been shown in simulations to bear strong forces without supporting weak forces [42, 62]. We also find that disks tend to form a pile in front of the slider, similar to wedges formed in front of plates that plow through granular materials [63], while the angular grains do not under the same driving conditions in this experiment. For all grain angularities, though, motion of the yielding granular material mostly occurs close to the free surface and the shear band depth is approximately the same. Lastly, we find that the average depth of changes in stresses between slip events–the depth of fluctuations of force chains that support the shearing force of the slider as opposed to just gravity–does not depend on grain angularity.

Many of our observations, such as the accumulation of disks in a pile that does not occur with angular grains, or the columnar stilts that prop the slider above the surface in angular but not disk packings, motivate the need for further studies designed to understand how grain-scale interactions modify collective dynamics of grains. Future works might explore the relative importance of rolling or sliding of angular and disk grains near the surface of the bed, as well as changes in force chains deeper in the packing than the shear band to characterize how grain angularity influences the changes in stresses (if any) induced by grain rearrangements near the surface of the bed. Moreover, it would be interesting to quantify the statistics of stilts–how often they form given different grain angularities, the typical length scale of stilts, and how much shear force or rotation they tend to sustain. Properties of these stilts may yield insight into shear jamming of angular grains. The formation of a shear jammed state in frictional disk packings has been shown recently [64] to be the result of trimer buckling; the dynamics of trimers (or higher-order structures) of angular grains with edge-edge contacts will likely differ and may have important consequences for the shear jamming transition.

Overall, our findings demonstrate that grain shape is indeed important in modifying macroscopic stick-slip of sheared granular materials. Some features of the grain-scale dynamics, such as the size of shear-bands, do not strongly depend on grain angularity, while other features do, such as collective motion of grains at the surface of the packing and the PDF of energy released in slip events.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

RK contributed to experiment design, data acquisition, analysis of data, figure production, literature review, and writing of the manuscript. HZ contributed to experiment design and the writing of the manuscript. KD and JS contributed to experiment design, analysis of data, figure production, and writing of the manuscript. JS contributed, in addition, through acquisition and budgeting of funds.

Funding

This work was supported by the US Army Research Office through grant W911NF1810184.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Klaumünzer D, Maaß R, Löffler JF. Stick-slip Dynamics and Recent Insights into Shear Banding in Metallic Glasses. J Mater Res (2011) 26:1453–63. doi:10.1557/jmr.2011.178

CrossRef Full Text | Google Scholar

2. Denisov DV, Lőrincz KA, Wright WJ, Hufnagel TC, Nawano A, Gu X, et al. Universal Slip Dynamics in Metallic Glasses and Granular Matter - Linking Frictional Weakening with Inertial Effects. Scientific Rep (2017) 7:43376. doi:10.1038/srep43376

CrossRef Full Text | Google Scholar

3. Mate CM, McClelland GM, Erlandsson R, Chiang S. Atomic-scale Friction of a Tungsten Tip on a Graphite Surface. Phys Rev Lett (19871945) 59:1942. doi:10.1103/PhysRevLett.59.1942

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Brace WF, Byerlee JD. Stick-slip as a Mechanism for Earthquakes. Science (1966) 153:990. doi:10.1126/science.153.3739.990

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Scholz CH. Earthquakes and Friction Laws. Nature (1998) 391:37. doi:10.1038/34097

CrossRef Full Text | Google Scholar

6. Baumberger T, Heslot F, Perrin B. Crossover from Creep to Inertial Motion in Friction Dynamics. Nature (1994) 367:544–6. doi:10.1038/367544a0

CrossRef Full Text | Google Scholar

7. Heslot F, Baumberger T, Perrin B, Caroli B, Caroli C. Creep, Stick-Slip, and Dry-Friction Dynamics: Experiments and a Heuristic Model. Phys Rev E (1994) 49:4973–88. doi:10.1103/PhysRevE.49.4973

CrossRef Full Text | Google Scholar

8. Schelleng JC. The Physics of the Bowed String. Scientific Am (1974) 230:87–95. doi:10.1038/scientificamerican0174-87

CrossRef Full Text | Google Scholar

9. Scholz CH. The Mechanics of Earthquakes and Faulting. 2nd ed. Cambridge: Cambridge University Press (2002). p. 53–81.

Google Scholar

10. Brace W. Laboratory Studies of Stick-Slip and Their Application to Earthquakes. Tectonophysics (1972) 14:189–200. doi:10.1016/0040-1951(72)90068-6

CrossRef Full Text | Google Scholar

11. Byerlee J. The Mechanics of Stick-Slip. Tectonophysics (1970) 9:475–86. doi:10.1016/0040-1951(70)90059-4

CrossRef Full Text | Google Scholar

12. Abed Zadeh A, Barés J, Behringer RP. Crackling to Periodic Dynamics in Sheared Granular media. Phys Rev E (2019) 99(R):040901. doi:10.1103/PhysRevE.99.040901

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Hayman NW, Ducloué L, Foco KL, Daniels KE. Granular Controls on Periodicity of Stick-Slip Events: Kinematics and Force-Chains in an Experimental Fault. Pure Appl Geophys (2011) 168:2239–57. doi:10.1007/s00024-011-0269-3

CrossRef Full Text | Google Scholar

14. Ruina A. Slip Instability and State Variable Friction Laws. J Geophys Res Solid Earth (1983) 88:10359–70. doi:10.1029/JB088iB12p10359

CrossRef Full Text | Google Scholar

15. Lacombe F, Zapperi S, Herrmann HJ. Dilatancy and Friction in Sheared Granular media. The Eur Phys J E (2000) 2:181. doi:10.1007/s101890050052

CrossRef Full Text | Google Scholar

16. Hayakawa H. Simple Model for Granular Friction. Phys Rev E (1999) 60:4500–4. doi:10.1103/PhysRevE.60.4500

CrossRef Full Text | Google Scholar

17. Baldassarri A, Dalton F, Petri A, Zapperi S, Pontuale G, Pietronero L. Brownian Forces in Sheared Granular Matter. Phys Rev Lett (2006) 96:118002. doi:10.1103/PhysRevLett.96.118002

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Sethna JP, Dahmen KA, Myers CR. Crackling Noise. Nature (2001) 410:242–50. doi:10.1038/35065675

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Fisher DS. Collective Transport in Random media: from Superconductors to Earthquakes. Phys Rep (1998) 301:113–50. doi:10.1016/S0370-1573(98)00008-8

CrossRef Full Text | Google Scholar

20. Albert I, Tegzes P, Albert R, Sample JG, Barabási AL, Vicsek T, et al. Stick-slip Fluctuations in Granular Drag. Phys Rev E (2001) 64:031307. doi:10.1103/PhysRevE.64.031307

CrossRef Full Text | Google Scholar

21. Tordesillas A, Hilton JE, Tobin ST. Stick-slip and Force Chain Evolution in a Granular Bed in Response to a Grain Intruder. Phys Rev E (2014) 89:042207. doi:10.1103/PhysRevE.89.042207

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Dalton F, Corcoran D. Self-organized Criticality in a Sheared Granular Stick-Slip System. Phys Rev E (2001) 63:061312. doi:10.1103/PhysRevE.63.061312

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Métayer JF, Suntrup DJ, Radin C, Swinney HL, Schröter M. Shearing of Frictional Sphere Packings. Europhysics Lett (2011) 93:64003. doi:10.1209/0295-5075/93/64003

CrossRef Full Text | Google Scholar

24. Nasuno S, Kudrolli A, Bak A, Gollub JP. Time-resolved Studies of Stick-Slip Friction in Sheared Granular Layers. Phys Rev E (1998) 58:2161–71. doi:10.1103/PhysRevE.58.2161

CrossRef Full Text | Google Scholar

25. Barés J, Wang D, Wang D, Bertrand T, O’Hern CS, Behringer RP. Local and Global Avalanches in a Two-Dimensional Sheared Granular Medium. Phys Rev E (2017) 96:052902. doi:10.1103/PhysRevE.96.052902

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Clark AH, Behringer RP, Krim J. Vibration Can Enhance Stick-Slip Behavior for Granular Friction. Granular Matter (2019) 21:55. doi:10.1007/s10035-019-0895-5

CrossRef Full Text | Google Scholar

27. Dahmen KA, Behringer RP. Avalanches in Slowly Sheared Disordered Materials. In: SV Franklin, and MD Shattuck, editors. Handbook of Granular Materials. Boca Raton: CRC Press (2016). p. 307–35. chap. 9.

Google Scholar

28. Behringer RP, Chakraborty B. The Physics of Jamming for Granular Materials: a Review. Rep Prog Phys (2018) 82:012601. doi:10.1088/1361-6633/aadc3c

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Abed Zadeh A, Barés J, Socolar JES, Behringer RP. Seismicity in Sheared Granular Matter. Phys Rev E (2019) 99:052902. doi:10.1103/PhysRevE.99.052902

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Murphy KA, Dahmen KA, Jaeger HM. Transforming Mesoscale Granular Plasticity through Particle Shape. Phys Rev X (2019) 9:011014. doi:10.1103/PhysRevX.9.011014

CrossRef Full Text | Google Scholar

31. Nasuno S, Kudrolli A, Gollub JP. Friction in Granular Layers: Hysteresis and Precursors. Phys Rev Lett (1997) 79:949–52. doi:10.1103/PhysRevLett.79.949

CrossRef Full Text | Google Scholar

32. Dahmen KA, Ben-Zion Y, Uhl JT. A Simple Analytic Theory for the Statistics of Avalanches in Sheared Granular Materials. Nat Phys (2011) 7:554–7. doi:10.1038/nphys1957

CrossRef Full Text | Google Scholar

33. Mair K, Frye KM, Marone C. Influence of Grain Characteristics on the Friction of Granular Shear Zones. J Geophys Res Solid Earth (2002) 107. ECV 4–1–ECV 4–9. doi:10.1029/2001jb000516

CrossRef Full Text | Google Scholar

34. Anthony JL, Marone C. Influence of Particle Characteristics on Granular Friction. J Geophys Res Solid Earth (2005) 110:1–14. doi:10.1029/2004JB003399

CrossRef Full Text | Google Scholar

35. Cho GC, Dodds J, Santamarina JC. Particle Shape Effects on Packing Density, Stiffness, and Strength: Natural and Crushed Sands. J Geotechnical Geoenvironmental Eng (2006) 132:5915–602. doi:10.1061/(ASCE)1090-024110.1061/(asce)1090-0241(2006)132:5(591)

CrossRef Full Text | Google Scholar

36. Azéma E, Estrada N, Radjaï F. Nonlinear Effects of Particle Shape Angularity in Sheared Granular media. Phys Rev E (2012) 86:041301. doi:10.1103/PhysRevE.86.041301

CrossRef Full Text | Google Scholar

37. Azéma E, Radjaï F, Dubois F. Packings of Irregular Polyhedral Particles: Strength, Structure, and Effects of Angularity. Phys Rev E (2013) 87:062203. doi:10.1103/PhysRevE.87.062203

CrossRef Full Text | Google Scholar

38. Binaree T, Azéma E, Estrada N, Renouf M, Preechawuttipong I. Combined Effects of Contact Friction and Particle Shape on Strength Properties and Microstructure of Sheared Granular media. Phys Rev E (2020) 102:022901. doi:10.1103/PhysRevE.102.022901

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Zhao Y, Barés J, Socolar JES. Yielding, Rigidity, and Tensile Stress in Sheared Columns of Hexapod Granules. Phys Rev E (2020) 101:062903. doi:10.1103/PhysRevE.101.062903

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Zhao Y, Barés J, Zheng H, Bester CS, Xu Y, Socolar JES, et al. Jamming Transition in Non-spherical Particle Systems: Pentagons versus Disks. Granular Matter (2019) 21. doi:10.1007/s10035-019-0940-4

CrossRef Full Text | Google Scholar

41. Zeravcic Z, Xu N, Liu AJ, Nagel SR, van Saarloos W. Excitations of Ellipsoid Packings Near Jamming. Europhysics Lett (2009) 87:26001. doi:10.1209/0295-5075/87/26001

CrossRef Full Text | Google Scholar

42. Azéma E, Radjaï F, Peyroux R, Saussine G. Force Transmission in a Packing of Pentagonal Particles. Phys Rev E (2007) 76:011301. doi:10.1103/PhysRevE.76.011301

CrossRef Full Text | Google Scholar

43. Donev A, Cisse I, Sachs D, Variano EA, Stillinger FH, Connelly R, et al. Improving the Density of Jammed Disordered Packings Using Ellipsoids. Science (2004) 303:990–3. doi:10.1126/science.1093010

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Pugnaloni LA, Carlevaro CM, Kramár M, Mischaikow K, Kondic L. Structure of Force Networks in Tapped Particulate Systems of Disks and Pentagons. I. Clusters and Loops. Phys Rev E (2016) 93:062902. doi:10.1103/PhysRevE.93.062902

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Zuriguel I, Mullin T, Rotter JM. Effect of Particle Shape on the Stress Dip under a Sandpile. Phys Rev Lett (2007) 98:028001. doi:10.1103/PhysRevLett.98.028001

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Wang C, Dong K, Yu A. Structural Characterization of the Packings of Granular Regular Polygons. Phys Rev E (2015) 92:062203. doi:10.1103/PhysRevE.92.062203

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Tang J, Behringer RP. Orientation, Flow, and Clogging in a Two-Dimensional Hopper: Ellipses vs. Disks. Europhysics Lett (2016) 114:34002. doi:10.1209/0295-5075/114/34002

CrossRef Full Text | Google Scholar

48. Goldberg E, Carlevaro CM, Pugnaloni LA. Flow Rate of Polygonal Grains through a Bottleneck: Interplay between Shape and Size. Pap Phys (2015) 7:070016. doi:10.4279/pip.070016

CrossRef Full Text | Google Scholar

49. Goldberg E, Carlevaro CM, Pugnaloni LA. Clogging in Two-Dimensions: Effect of Particle Shape. J Stat Mech Theor Exp (2018) 2018:113201. doi:10.1088/1742-5468/aae84b

CrossRef Full Text | Google Scholar

50. Hafez A, Liu Q, Finkbeiner T, Alouhali RA, Moellendick TE, Santamarina JC. The Effect of Particle Shape on Discharge and Clogging. Scientific Rep (2021) 11:3309. doi:10.1038/s41598-021-82744-w

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Tang Z. Fluid Dynamics of the Evolution of Supernova Remnants and Granular Materials. Raleigh, NC: North Carolina State University (2018). Ph.D. thesis.

Google Scholar

52. Daniels KE, Kollmer JE, Puckett JG. Photoelastic Force Measurements in Granular Materials. Rev Scientific Instr (2017) 88:051808. doi:10.1063/1.4983049

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Abed Zadeh A, Barés J, Brzinski TA, Daniels KE, Dijksman J, Docquier N, et al. Enlightening Force Chains: a Review of Photoelasticimetry in Granular Matter. Granular Matter (2019) 21:83. doi:10.1007/s10035-019-0942-2

CrossRef Full Text | Google Scholar

54. Schall P, van Hecke M. Shear Bands in Matter with Granularity. Annu Rev Fluid Mech (2010) 42:67–88. doi:10.1146/annurev-fluid-121108-145544

CrossRef Full Text | Google Scholar

55. O’Hern CS, Silbert LE, Liu AJ, Nagel SR. Jamming at Zero Temperature and Zero Applied Stress: The Epitome of Disorder. Phys Rev E (2003) 68:011306. doi:10.1103/PhysRevE.68.011306

CrossRef Full Text | Google Scholar

56. Nguyen DH, Azéma E, Sornay P, Radjaï F. Effects of Shape and Size Polydispersity on Strength Properties of Granular Materials. Phys Rev E (2015) 91:032203. doi:10.1103/PhysRevE.91.032203

CrossRef Full Text | Google Scholar

57. Abed Zadeh A, Barés J, Behringer RP. Avalanches in a Granular Stick-Slip experiment: Detection Using Wavelets. EPJ Web of Conferences (2017) 140:03038. doi:10.1051/epjconf/201714003038

CrossRef Full Text | Google Scholar

58. Kozlowski R, Zheng H, Daniels KE, Socolar JES. Particle Dynamics in Two-Dimensional point-loaded Granular media Composed of Circular or Pentagonal Grains. EPJ Web Conf (2021) 249:06010. doi:10.1051/epjconf/202124906010

CrossRef Full Text | Google Scholar

59. Kozlowski R. Polygongraintrack (2021). Available at: https://github.com/rykozlo1633/PolygonGrainTrack.git.

Google Scholar

60. Veje CT, Howell DW, Behringer RP. Kinematics of a Two-Dimensional Granular Couette experiment at the Transition to Shearing. Phys Rev E (1999) 59:739–45. doi:10.1103/PhysRevE.59.739

CrossRef Full Text | Google Scholar

61. Utter B, Behringer RP. Experimental Measures of Affine and Nonaffine Deformation in Granular Shear. Phys Rev Lett (2008) 100:208302. doi:10.1103/PhysRevLett.100.208302

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Radjaï F, Wolf DE, Jean M, Moreau JJ. Bimodal Character of Stress Transmission in Granular Packings. Phys Rev Lett (1998) 80:61–4. doi:10.1103/PhysRevLett.80.61

CrossRef Full Text | Google Scholar

63. Gravish N, Umbanhowar PB, Goldman DI. Force and Flow Transition in Plowed Granular media. Phys Rev Lett (2010) 105:128301. doi:10.1103/PhysRevLett.105.128301

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Wang D, Ren J, Dijksman JA, Zheng H, Behringer RP. Microscopic Origins of Shear Jamming for 2d Frictional Grains. Phys Rev Lett (2018) 120:208004. doi:10.1103/PhysRevLett.120.208004

PubMed Abstract | CrossRef Full Text | Google Scholar