Takagi Topological Insulator on the Honeycomb Lattice

Recently, real topological phases protected by PT symmetry have been actively investigated. In two dimensions, the corresponding topological invariant is the Stiefel-Whitney number. A recent theoretical advance is that in the presence of the sublattice symmetry, the Stiefel-Whitney number can be equivalently formulated in terms of Takagi’s factorization. The topological invariant gives rise to a novel second-order topological insulator with odd PT-related pairs of corner zero modes. In this article, we review the elements of this novel second-order topological insulator, and demonstrate the essential physics by a simple model on the honeycomb lattice. Novelly, the higher-order topological boundary modes can not only be tuned by the parameters but also the geometric shape of the sample.

Introduction

The symmetry-protected topological phases, such as topological (crystalline) insulators (TIs) and superconductors (TSCs), have been one of the most active fields of physics during the last 15 years [1–9]. Based on the topological K theory, the topological band theory has been established to classify and characterize various topological states [10–12]. Symmetry plays an fundamental role in the classification of topological phases. Considering three discrete symmetries, namely time reversal $\mathcal{T}$, charge conjugation $\mathcal{C}$ and chiral symmetry $\mathcal{S}$, physical systems can be classified into ten symmetry classes, termed Altland-Zirnbauer (AZ) classes [10–15], among which the eight ones with at least $\mathcal{T}$ or $\mathcal{C}$ are called real AZ classes. The topological classifications in the framework of the eight real AZ classes correspond to the real K theory. Using the real K theory, gapped systems including topological insulators and topological superconductors were first classified [11, 12, 16], and then gapless systems were classified as well [17–20]. All the classification tables exhibit an elegant eightfold periodicity along the dimensions for the eight real AZ classes. After internal symmetries like $\mathcal{T}$ and $\mathcal{C}$, more and more spatial symmetries were involved to enrich symmetry-protected topological matter. It was noticed that combined symmetries $\mathcal{P}\mathcal{T}$ and $\mathcal{C}\mathcal{P}$ correspond to the orthogonal K theory with $\mathcal{P}$ the spatial inversion, since they leave every k point fixed in the reciprocal space. Hence, the topological classification table was worked out [21]. A remarkable feature is that groups $\mathbb{Z}$, ${\mathbb{Z}}_2$ and 0 in the table appear in the reversed order in dimensionality, compared with previous tables for the real AZ classes. $\mathcal{P}\mathcal{T}$ and $\mathcal{C}\mathcal{P}$ are fundamental in nature, and therefore the classification table has been applied to explore topological phases in various physical systems, such as quantum materials [6, 22, 23], topological superconductors [24–27], and photonic/phononic crystals and electric-circuit arrays [27–35], and can generate unique topological structures with many novel consequences, such as non-Abelian topological charges, cross-order boundary transitions, and nodal-loop linking structures [22, 23, 36–40].

Remarkably, from the classification table, the symmetry class with ${(\mathcal{P}\mathcal{T})}^2=1$ corresponds to the ${\mathbb{Z}}_2$ classification for d = 1 and d = 2. As revealed in Ref. [22], ${(\mathcal{P}\mathcal{T})}^2=1$ leads to real band structures in contrast to conventional complex band structures. Then, the ${\mathbb{Z}}_2$ topological invariant w₁ for d = 1 can be formulated as the quantized Berry phase in units of π modulo 2π. The case of d = 2 is much fascinating. The topological invariant is the Euler number, a real version of the Chern number, for two valence bands. The Euler number is valued in $\mathbb{Z}$, but only its parity is stable if more trivial valence bands are added into consideration. The parity, namely the Euler number modulo 2, is just the Stiefel-Whitney number w₂ in two dimensions, which determines whether the real vector bundle can be lifted into a spinor bundle.

The topological invariant w₂ gives rise to novel topological phases with extraordinary properties. In 3D, it characterizes a real Dirac semimetal, which can be transformed into a nodal ring with symmetry-preserving perturbations. Then, the nodal ring is characterized by two topological charges (w₁, w₂). In 2D, it describes a topological insulator. The common topological wisdom is that the bulk topological invariant determines a unique form of the boundary modes, namely the well-known one-to-one bulk-boundary correspondence. However, a remarkable discovery in Ref. [41] is that w₂ corresponds to multiple forms of boundary modes, extending the one-to-one correspondence to one-to-many. The 2D topological insulator can host various second-order phases with odd $\mathcal{P}\mathcal{T}$-related pairs of corner zero-modes, which are mediated by first-order phases with helical edge states. Similarly, the 3D semimetal can host second-order hinge Fermi arcs and first-order surface Dirac states as well. Recently, graphynes have been proposed as the material candidates which can realize both the 2D topological insulator and the 3D topological semimetal [37, 42, 43].

As aforementioned, the second-order phases of the 2D topological insulator feature odd $\mathcal{P}\mathcal{T}$-related pairs of corner zero modes. It is interesting to look for its 3D analog, which has been presented in Ref. [44]. Referring to the topological classification table for $\mathcal{P}\mathcal{T}$ and $\mathcal{C}\mathcal{P}$ symmetries, we notice that although the classification for ${(\mathcal{P}\mathcal{T})}^2=1$ is trivial, with an additional chiral symmetry $\mathcal{S}$ with $\{\mathcal{P}\mathcal{T},\mathcal{S}\}=0$ the classification is preserved as ${\mathbb{Z}}_2$ in 2D and, more importantly, becomes non-trivial as ${\mathbb{Z}}_2$ in 3D. It is found that the corresponding topological invariants can be formulated in terms of Takagi’s factorization. The topological invariant in 2D is equivalent to w₂, while that in 3D is a new topological invariant. Either in 2D or in 3D the bulk topological invariant can be manifested as odd $\mathcal{P}\mathcal{T}$-related pairs of corner zero-modes. Now, with the chiral symmetry, the two zero-modes in each pair are eigenstates with opposite eigenvalues of the chiral symmetry.

In this article, we review the elements of 2D $\mathcal{P}\mathcal{T}$-protected topological insulators with or without chiral symmetry. The essential physics is demonstrated by the Honeycomb-lattice model, with only the nearest-neighbor hopping amplitudes. We show that under certain dimerization patterns the model is a topological insulator with non-trivial Stiefel-Whitney number or the Takagi topological invariant, and therefore presents all the non-trivial topological phenomena. Particularly, under various $\mathcal{P}\mathcal{T}$-invariant geometries, there are always odd $\mathcal{P}\mathcal{T}$-related pairs of corner zero-modes for the second-order topological phase. Before diving into the details, it is noteworthy that the dimerized honeycomb model can be regarded as an abstraction from the graphynes [37, 42, 43].

The Honeycomb-Lattice Model

Let us start with presenting the honeycomb-lattice model, the lattice structure is shown in Figure 1A. The Hamiltonian in momentum space is given by

$\mathcal{H}\left(\mathit{k}\right)=\left[\begin{array}{cccccc}\hfill 0\hfill & \hfill t_3\hfill & \hfill 0\hfill & \hfill {\chi }_{\mathit{k}}^{\left(2\right)}\hfill & \hfill 0\hfill & \hfill t_1\hfill \\ \hfill t_3\hfill & \hfill 0\hfill & \hfill t_2\hfill & \hfill 0\hfill & \hfill {\bar{\chi }}_{\mathit{k}}^{\left(1\right)}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill t_2\hfill & \hfill 0\hfill & \hfill t_1\hfill & \hfill 0\hfill & \hfill {\chi }_{\mathit{k}}^{\left(3\right)}\hfill \\ \hfill {\bar{\chi }}_{\mathit{k}}^{\left(2\right)}\hfill & \hfill 0\hfill & \hfill t_1\hfill & \hfill 0\hfill & \hfill t_3\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\chi }_{\mathit{k}}^{\left(1\right)}\hfill & \hfill 0\hfill & \hfill t_3\hfill & \hfill 0\hfill & \hfill t_2\hfill \\ \hfill t_1\hfill & \hfill 0\hfill & \hfill {\bar{\chi }}_{\mathit{k}}^{\left(3\right)}\hfill & \hfill 0\hfill & \hfill t_2\hfill & \hfill 0\hfill \end{array}\right],(1)$

where ${\chi }_{\mathit{k}}^{(i)}=t_i^{\prime }{e}^{-i\mathit{k}\cdot {\mathit{a}}_i}$ with i = 1, 2, 3. Here, a_i are the bond vectors connecting the centers of nearest-neighbor unit cells, as indicated in Figure 1A with ∑_ia_i = 0. The Hamiltonian has inversion symmetry with $\widehat{\mathcal{P}}={\sigma }_1\otimes I_3\widehat{I}$, spinless time-reversal symmetry with $\widehat{\mathcal{T}}=\widehat{\mathcal{K}}\widehat{I}$, and therefore spacetime-inversion symmetry with $\widehat{\mathcal{P}}\widehat{\mathcal{T}}={\sigma }_1\otimes I_3\widehat{\mathcal{K}}$, where $\widehat{\mathcal{K}}$ is the complex conjugation and $\widehat{I}$ is the inversion of momenta. Note that σ’s are the Pauli matrices acting on the sublattice space (see Figure 1A), and I₃ is the 3 × 3 identity matrix. Each inversion center is taken as the center of a hexagon in real space. The sublattice symmetry operator is $\widehat{\mathcal{S}}=I_3\otimes {\sigma }_3$. Since the inversion exchanges sublattices, both $\mathcal{P}$ and $\mathcal{P}\mathcal{T}$ anti-commute with $\mathcal{S}$, namely, $\{\widehat{\mathcal{P}},\widehat{\mathcal{S}}\}=\{\widehat{\mathcal{P}}\widehat{\mathcal{T}},\widehat{\mathcal{S}}\}=0$.

FIGURE 1

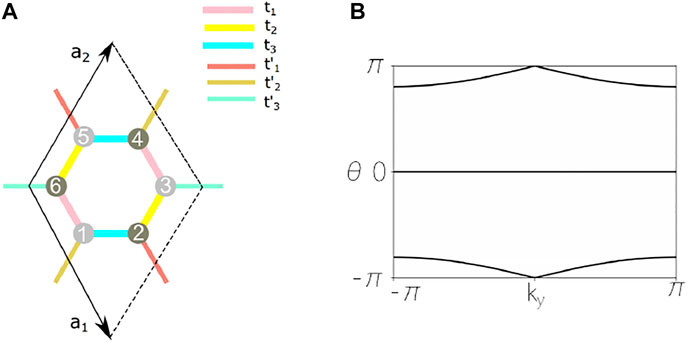
FIGURE 1. (A) Schematic of the honeycomb-lattice model. t_i represents intracell hoppings and $t_i^{\prime }$ represents intercell hoppings with i = 1, 2, 3. The six atomic sites in a unit cell can be divided into two sublattice, as marked by the gray and brown circles, so that a site in one sublattice has all its nearest neighbors from the other sublattice. (B) The winding of Wilson loop around k_y for topological nontrivial case. The Wilson loop is computed along a large circle parametrized by k_x for fixed k_y (where k_x,y represents periodic direction along a₁, a₂ or a₃). The loop exhibits a cross at θ = π and k_y = 0, which means the ${\mathbb{Z}}_2$ topological invariant ν = 1. The parameters are set as $t_1=t_2=t_3=1,t_1^{\prime }=t_2^{\prime }=t_3^{\prime }=3$.

To obtain the non-trivial topological phases, we calculate the determinant of the Hamiltonian (Eq. 1) at Γ point¹ in the Brillouin zone as

$\det \left[\mathcal{H}\left(\mathrm{\Gamma }\right)\right]=-{\left(t_1^2{t}_1^{\prime }+t_2^2{t}_2^{\prime }+t_3^2{t}_3^{\prime }-2t_1{t}_2{t}_3-t_1^{\prime }{t}_2^{\prime }{t}_3^{\prime }\right)}^2.(2)$

Since the bulk topological criticality generally corresponds gap-closing point, we can obtain the topological phase-transition points by letting $\det [\mathcal{H}(\mathrm{\Gamma })]=0$, which gives

$t_1^2{t}_1^{\prime }+t_2^2{t}_2^{\prime }+t_3^2{t}_3^{\prime }=2t_1{t}_2{t}_3+t_1^{\prime }{t}_2^{\prime }{t}_3^{\prime }.(3)$

Interestingly, if (Eq. 3) holds, the system is generally reduced to a topologically equivalent graphene model with two Dirac points in the first Brillouin zone [45]. When $t_1^2{t}_1^{\prime }+t_2^2{t}_2^{\prime }+t_3^2{t}_3^{\prime }<2t_1{t}_2{t}_3+t_1^{\prime }{t}_2^{\prime }{t}_3^{\prime }$, the system steps into a topological phase, while conversely the system becomes a trivial phase, which can be checked by computing Stiefel-Whitney number or Takagi’s factorization.

Topological Invariants

The topology can be determined by various formulas of the topological invariant. We now briefly review them. First, as given in Ref. [22], the topological invariant can be determined by the Wilson loop

$\mathcal{W}\left(k_y\right)=P\exp \left(-i{\int }_{C_{k_y}}d{k}_x\mathcal{A}\left(k_x,k_y\right)\right)(4)$

(with P indicating the path order) along large circles parametrized by k_x. $C_{k_y}$ is the contour at a fixed k_y and $\mathcal{A}(k_x,k_y)$ is the non-Abelian Berry connection for the valence bands. The topological information is encoded in the phase factors $\theta (k_y)\in \left(-\pi ,\pi \right]$ of the N eigenvalues λ_m(k_y) of $\mathcal{W}(k_y)$ for valence bands:

${\theta }_m\left(k_y\right)=\mathrm{Im}\left[\log {\lambda }_m\left(k_y\right)\right].(5)$

Different from the conventional TIs and Chern insulators, the Wilson loop spectral flow for real phases are mirror symmetric with respect to the θ = 0 axis see Figure 1B. This is because $\mathcal{W}(k_y)$ is equivalent to a mapping from k_y ∈ S¹ to O(N) up to a unitary transformation [22]. The topological information can be pictorially derived from counting how many times ζ the trajectories cross θ = π as

$w_2=\zeta \mathrm{mod}2.(6)$

For honeycomb lattice with $t_1^2{t}_1^{\prime }+t_2^2{t}_2^{\prime }+t_3^2{t}_3^{\prime }<2t_1{t}_2{t}_3+t_1^{\prime }{t}_2^{\prime }{t}_3^{\prime }$, a single crossing exsit as shown in Figure 1B, namely, w₂ = 1, which indicates the model is in a topological non-trivial phase.

As aforementioned, our system is protected by spacetime inversion symmetry $\mathcal{P}\mathcal{T}$ and sublattice (chiral) symmetry $\mathcal{S}$. These symmetries constraint the classifying space of $\mathcal{H}(\mathit{k})$ to be symmeric unitary matrices. Thus the ${\mathbb{Z}}_2$ invariant from the Takagi’s factorization can be defined [44], which leads to an alternative formulation for w₂. We now prove the equivalence of the two formulas. For technical simplicity, we assume the momentum space as a sphere S², which is sufficient to present the essential ideas.

In general, $\mathcal{S}$ requires the Hamiltonian $\mathcal{H}(\mathit{k})$ to be block anti-diagonal and $\mathcal{P}\mathcal{T}$ requires the upper-right block to be symmetric. Thus the flattened Hamiltonian $\tilde{\mathcal{H}}(\mathit{k})$ is given by

$\tilde{\mathcal{H}}\left(\mathit{k}\right)=\left[\begin{array}{cc}\hfill 0\hfill & \hfill \mathcal{Q}\left(\mathit{k}\right)\hfill \\ \hfill {\mathcal{Q}}^{†}\left(\mathit{k}\right)\hfill & \hfill 0\hfill \end{array}\right],\mathcal{Q}={\mathcal{Q}}^T,\mathcal{Q}{\mathcal{Q}}^{†}=I_M,(7)$

where $\mathcal{Q}(\mathit{k})=\mathcal{U}(\mathit{k}){\mathcal{U}}^T(\mathit{k})$ is a unitary symmetric matrix for each k and M denotes the number of valence (conduction) bands. $\mathcal{U}(\mathit{k})\in U(M)$ is the Takagi factor. The classifying space for this symmetric class is US(M) = U(M)/O(M) [44]. Here, ${\pi }_2[US(M)]={\mathbb{Z}}_2$ corresponds to the topological invariant of our system. Consider a 2D sphere S², which is divided into north and south hemispheres $D_{N,S}^2$, overlapping along the equator S¹. The Takagi factors ${\mathcal{U}}_{N/S}$ over $D_{N/S}^2$, respectively, can be transformed to each other by a gauge transformation ${\mathcal{O}}_{S^1}$ over the equator S¹, as shown in Figure 2. ${\mathcal{O}}_{S^1}$ is given by

${\mathcal{O}}_{S^1}={\mathcal{U}}_N^{†}{|}_{S^1}{\mathcal{U}}_S{|}_{S^1},{\mathcal{O}}_{S^1}\in O\left(M\right).$

${\pi }_1[O(M)]={\mathbb{Z}}_2$ for M > 2 leads to obstructions for a global Takagi’s factorization over S².

FIGURE 2

FIGURE 2. The Takagi factors in 2D. $D_S^2$ and $D_N^2$ represent the south hemisphere and north hemisphere respectively, the overlapping region is equator S¹. ${\mathcal{U}}_{N/S}$ is the Takagi factors over $D_{N/S}^2$.

The conduction and valence wavefunctions of $\tilde{\mathcal{H}}(\mathit{k})$ can be given by

$|+,n\rangle =\frac{1}{\sqrt{2}}\left[\begin{array}{c}\hfill \mathcal{U}{\phi }_n\hfill \\ \hfill {\mathcal{U}}^{\ast }{\phi }_n\hfill \end{array}\right],|-,n\rangle =\frac{i}{\sqrt{2}}\left[\begin{array}{c}\hfill \mathcal{U}{\phi }_n\hfill \\ \hfill -{\mathcal{U}}^{\ast }{\phi }_n\hfill \end{array}\right],(8)$

where n ∈ {1, 2, … , M}. φ_n = (0 0 ⋯ 0 1 0 0 ⋯ 0)^T is a unit vector with “1” locating at the n-th position.

Performing a unitary transformation ${\mathcal{U}}_R=e^{-i\pi /4}{e}^{i\pi {\sigma }_1/4}$ on this system, the Hamiltonian and valence wavefunctions both become real. Meanwhile, $\mathcal{P}\mathcal{T}$ and $\mathcal{S}$ are transformed to $\widehat{\mathcal{K}}$ and σ₂, respectively. Over the intersection S¹, transition function $t_{S^1}$ of real valence wavefunctions can be given by

${\left[t_{S^1}\right]}_{mn}={\left.\langle -,m{|}_N\right|}_{S^1}{\mathcal{U}}_R^{†}{\mathcal{U}}_R{\left.|-,{n\rangle }_S\right|}_{S^1}={\left[{\mathcal{O}}_{S^1}\right]}_{mn}.(9)$

Thus, we know the transition function $t_{S^1}$ of real valence wavefunctions is equal to the gauge transformation ${\mathcal{O}}_{S^1}$. As noted in Ref. [22], w₂ is just the parity of the winding number of the transition function for valence bands. Thus, we see the equivalence of two 2D topological invariants.

Physical Consequence

The high-order topological phase in the honeycomb model features novel bulk-boundary correspondence that is different from the traditional one, namely, it has one-to-many bulk-boundary correspondence. Furthermore, the boundary modes can be tuned by the boundary selection. According to analytical and numerical methods, we reveal that three pairs of hopping parameters t_i and $t_i^{\prime }$ (with i = 1, 2, 3) jointly determine the configuration of topological boundary modes. To facilitate understanding the relation between distinct boundary modes and parameters, we define a boundary effective mass term m_i for each edge:

$m_i=t_i{t}_i^{\prime }-t_j{t}_k\text{with}i\ne j\ne k,(10)$

where the subscript i denotes the hopping along the primitive vector a_i direction (a₃ = −a₁ − a₂). The above Eq. 10 can be derived from the boundary effective Hamiltonian². Hence, if m_i = 0, the corresponding edges are gapless, which is also the boundary critical condition to separate two second-order topological phases.

To demonstate the boundary modes, we consider a rhombic-shaped 2D sample with armchair termination, i.e., by opening boundary along a₁ and a₂ direction, as shown in Figure 3. If m₁ = 0 and m₂ ≠ 0, the helical edge modes along periodic a₁ can be obtained, as shown in Figure 3B. However, once m_1,2 ≠ 0, the helical edge modes will be gapped and the localized corner modes will emerge. More specifically, for the case with sgn(m₁) = sgn(m₂) (sgn(m₁) = − sgn(m₂)), the corner modes will locate at 120° (60°) corners, as shown in Figures 3A,C respectively. The $\mathcal{P}\mathcal{T}$ symmetry requires that the corner zero-modes always come in pairs and the chiral symmetry sets the midgap modes exactly at zero energy ³.

FIGURE 3

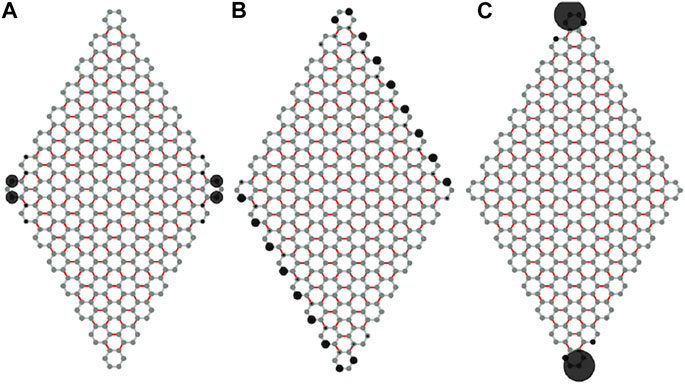
FIGURE 3. (A–C) Possible topological boundary modes for the rhombic-shaped sample with 10, ×, 10 unit cells. Black circles indicate the distribution of density of zero-mode (A,C) Second-order TI phases with a single pair of zero-modes corners in diagonal and off-diagonal (or horizontal and vertical) directions, respectively. (B) Helical edge modes with the boundary effective mass m_i = 0, which is a critical state separating two second-order TI phases. Parameters are set as (A) $t_{\mathrm{1,2,3}}=1,t_{\mathrm{1,2,3}}^{\prime }=3$, (B) $t_1=1,t_2=2,t_3=1.5,t_{\mathrm{1,2,3}}^{\prime }=3$, (C) $t_1=1.8,t_2=0.2,t_3=0.8,t_{\mathrm{1,2,3}}^{\prime }=3$.

To keep the completeness of honeycomb unit cell in a rhomboid sample, one only has three kinds of armchair edges, namely the edge parallel to a_i direction with i = 1, 2, 3. If the edge connected by the same corner has the same mass term m_i sign, the corner zero-modes will be localized at the obtuse angle of the rhomboid, otherwise at acute corners. We shall theoretically explain these numerical results in the next section. It is emphasized that in the whole process of the edge-phase transitions, the bulk gap is always open and the symmetries are preserved, therefore, the bulk invariant ν is unchanged. Thus the conventional bulk-boundary correspondence is not appliable for TTI, namely, the bulk invariant can not uniquely determine the boundary modes, but dictates an edge criticality, as the concept mentioned in previous work [41].

As promised in introduction, we now proceed to tune the boundary modes with fixed parameters. In the rhombic case, all samples terminate with armchair edges and exhibit parameter-depended boundary modes. As long as $\mathcal{P}\mathcal{T}$ and $\mathcal{S}$ are not violated, the finite samples can be cut with not only rhomb as shown in Figure 3, but also hexagon(see Figure 5). Beside armchair edges, zigzag edges can serve as termination too. Creatively, with fixed parameters but different boundary selections, one can also find various distinguishable boundary modes. For instance, helical edge states emerge on the zigzag edges in a rectangle sample as shown in Figure 4B, with the same hopping parameters as Figure 4A. This result further proves that the bulk topological invariant can not uniquely determine the topological boundary modes. We also study lots of other patterns with the same parameters, and abundant topological boundary modes consisting of corner zero modes and gapless edge modes can be obtained (see Supplementary Appendix SAD). They are all boundary-selection-depended. Hence, we propose that one can obtain needed topological boundary modes by choosing particular boundary geometry, without tuning parameters, which is usually difficult to perform in real systems.

FIGURE 4

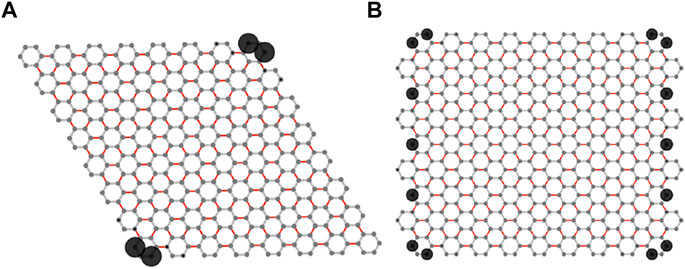
FIGURE 4. (A) Topological corner modes in rhombic sample with $t_i=1,t_i^{\prime }=3$. (B) Topological edge modes in rectangle sample with same parameters as rhombic$(t_{\mathrm{1,2,3}}=1,t_{\mathrm{1,2,3}}^{\prime }=3)$.

Novelly, in both situations discussed above, for second-order topological phases, the number of the zero-energy corners must be odd pairs. For example, for a hexagonal sample, we can only find one or three pairs of zero-mode corners, as shown in Figures 5A,B. Similarly, the Octagonal sample also has one or three pairs of zero-mode corners as shown in Figures 5C,D.

FIGURE 5

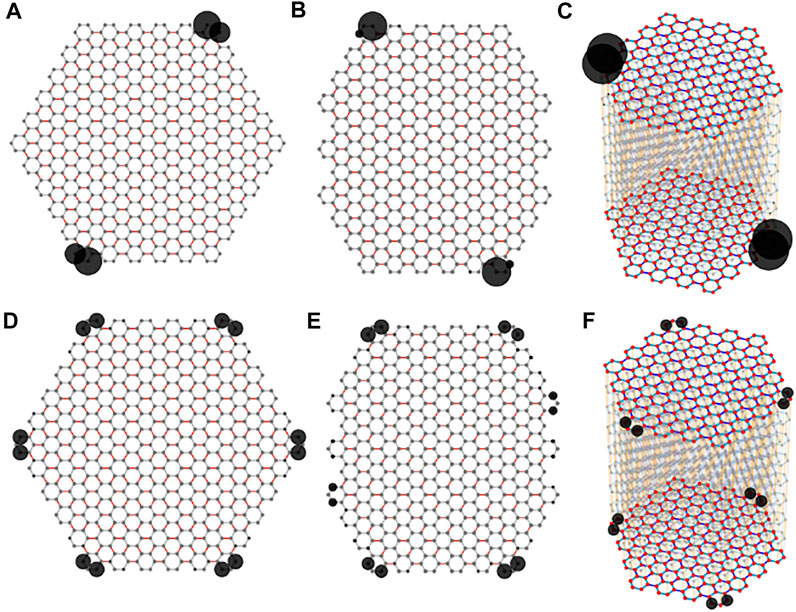
FIGURE 5. (A,D) Orthohexagonal sample with one and three pairs of zero-mode corners respectively. The parameters are set as $t_1=1.3,t_2=1.5,t_3=0.5,t_{\mathrm{1,2,3}}^{\prime }=3$ for (A) and $t_{\mathrm{1,2,3}}=1,t_{\mathrm{1,2,3}}^{\prime }=3$ for (D). (B,E) Octagonal sample with one and three pairs of zero-mode corners respectively. The parameters are set as $t_{\mathrm{1,2}}=1,t_3=0.3,t_{\mathrm{1,3}}^{\prime }=3,t_2^{\prime }=2$. for (B) and $t_{\mathrm{1,2,3}}=1,t_{\mathrm{1,3}}^{\prime }=3,t_2^{\prime }=2$ for (E). (C,F) Hexagonal prisms sample with one and three pairs of corner zero-modes respectively. The parameters can be seen in Supplementary Appendix SAC.

We find that the peculiarity of odd-pair-zero-modes is universal and it can be generalized to a higher-dimensional situation, such as 3D [44]. The 3D model is constructed by stacking the 2D honeycomb TTI discussed above in a staggered manner to preserve the sublattice symmetry $\mathcal{S}$. The details of the construction of the model can be found in Supplementary Appendix SAC. The inversion center is chosen as the center of hexagonal in one layer. Thus the anti-commuting relation of $\mathcal{P}\mathcal{T}$ and $\mathcal{S}$ are preserved. We cut a finite hexagonal prisms sample that keeps the symmetries. One can find only odd pairs (one or three) of corner states related by $\mathcal{P}\mathcal{T}$ appear. Note that the corner zero-modes can be driven to other corners by tunning the hopping parameters like in a 2D situation.

Analytic Method

We first proceed to solve the boundary criticality along the periodic a₁ direction and openning boundary with a₂. Replace $e^{-i\mathit{k}\cdot {\mathbf{a}}_{\mathbf{2}}}$ by S in Hamiltonian Eq. 1, with S ladder operator and S|i⟩ = |i + 1⟩, S^†|i⟩ = |i − 1⟩. Then $e^{-i\mathit{k}\cdot {\mathbf{a}}_3}$ can be represented by $e^{i\mathit{k}\cdot {\mathbf{a}}_1}{S}^{†}$ since a₃ = −(a₁ + a₂). After a series of tedious derivation (see Supplementary Appendix SAA), we obtian the effective Hamiltonian of the bottom boundary:

$\begin{array}{c}\hfill {\mathcal{H}}_B\left(\mathit{k}\cdot {\mathbf{a}}_1\right)=\left[\begin{array}{cccc}\hfill 0\hfill & \hfill t_3\hfill & \hfill 0\hfill & \hfill t_1\hfill \\ \hfill t_3\hfill & \hfill 0\hfill & \hfill t_1^{\prime }{e}^{i\mathit{k}\cdot {\mathbf{a}}_1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill t_1^{\prime }{e}^{-i\mathit{k}\cdot {\mathbf{a}}_1}\hfill & \hfill 0\hfill & \hfill t_2\hfill \\ \hfill t_1\hfill & \hfill 0\hfill & \hfill t_2\hfill & \hfill 0\hfill \end{array}\right].\end{array}(11)$

Following the same argument with aforementioned bulk criticality, we can obtain the boundary criticality by letting $\det [{\mathcal{H}}_B(\mathit{k}\cdot {\mathbf{a}}_1)]=0$, which leads to

$t_1{t}_1^{\prime }-t_2{t}_3=0.(12)$

The above Eq. 12 holds only at k ⋅a₁ = 0. Thus, when the system is in a topological non-trivial case, Eq. 12 related edge criticality separates two different second-order topological phases with corner zero modes. Likely, we can obtain similar results for periodic a₂ and a₃ directions. For convenience, we can define boundary effective mass by the left of Eq. 12 for edges parallel to a₁. Or, generally Eq. 10 for edges parallel to a_i. Different from the armchair edges, the zigzag terminations has an additional boundary criticality, namely, the effective masses can be defined by

$M_i=\frac{1}{2}\sum _{j,k}{ϵ}_{ijk}\left(t_j^2{t}_j^{\prime }-t_k^2{t}_k^{\prime }\right).(13)$

The derived details can be found in the Supplementary Appendix SAB.

With the effective mass orderly distributing on each edge (²), the existence of corner zero-modes is reduced to a Jackiw-Rebbi problem [46]. The corners with opposite effective masses on both sides can have zero-modes.

Discussion

In this article, we present a simple 2D realizable honeycomb-lattice model to demonstrate the essential physics of the Takagi topological insulator. It is found that with unchanged topological invariant, one can tune topological boundary modes by not only parameters, but also boundary selections. It goes beyond the common wisdom about bulk-boundary correspondence, and gives rise to much richer boundary physics.

Our model with novel physics is closely related to real systems. It is easier to realize our model by photonic/phononic crystals, electric-circuit arrays and mechanics systems, since only have nearest-neighbor hopping amplitudes are included into the model. Several special cases of our model have been recently realized in photonic/phononic crystals [47, 48], where hopefully the general form of our model can be further experimentally examined.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

The authors acknowledge the support from the National Natural Science Foundation of China under Grants (Nos 11874201, 12174181, and 12161160315).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.915764/full#supplementary-material

Footnotes

¹By the numerical calculation of Wilson loop, one can easily check that only the algebra of parameters obtained at Γ point is the real bulk criticality, while the others are not.

²Note that a pair of opposite edges parallel to ai have opposite mass terms since $\mathcal{P}\mathcal{T}$ symmetry inverses the effective mass.

³Finite-size effects can split the degenerate zero modes and deviate them from zero to form a ingap corner modes, but the deviation is exponentially suppressed with the sample size.

References

1. Volovik GE. Universe in a Helium Droplet. Oxford UK: Oxford University Press (2003).

Google Scholar

2. Hasan MZ, Kane CL. Colloquium: Topological Insulators. Rev. Mod. Phys. (2010) 82:3045–67. doi:10.1103/revmodphys.82.3045

CrossRef Full Text | Google Scholar

3. Qi X-L, Zhang S-C. Topological Insulators and Superconductors. Rev. Mod. Phys. (2011) 83:1057–110. doi:10.1103/revmodphys.83.1057

CrossRef Full Text | Google Scholar

4. Fu L. Topological Crystalline Insulators. Phys. Rev. Lett. (2011) 106:106802. doi:10.1103/physrevlett.106.106802

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Chiu C-K, Teo JCY, Ascnyder AP, Ryu S. Rev. Mod. Phys. (2016) 88:035005. doi:10.1103/revmodphys.88.035005

CrossRef Full Text

6. Kruthoff J, de Boer J, van Wezel J, Kane CL, Slager R-J. Phys. Rev. X (2017) 7:041069. doi:10.1103/physrevx.7.041069

CrossRef Full Text

7. Benalcazar WA, Bernevig BA, Hughes TL. Electric Multipole Moments, Topological Multipole Moment Pumping, and Chiral Hinge States in Crystalline Insulators. Phys. Rev. B (2017) 96:245115. doi:10.1103/physrevb.96.245115

CrossRef Full Text | Google Scholar

8. Liu F, Deng H-Y, Wakabayashi K. Phys. Rev. Lett. (2019) 122:086804. doi:10.1103/physrevlett.122.086804

PubMed Abstract | CrossRef Full Text

9. Xie B, Wang H-X, Zhang X, Zhan P, Jiang J-H, Lu M, et al. Higher-order Band Topology. Nat. Rev. Phys. (2021) 3:520–32. doi:10.1038/s42254-021-00323-4

CrossRef Full Text | Google Scholar

10. Atiyah MF. K-theory and Reality. Q J Math (1966) 17:367–86. doi:10.1093/qmath/17.1.367

CrossRef Full Text | Google Scholar

11. Kitaev A. Periodic Table for Topological Insulators and Superconductors. AIP Conf Proc (2010) 1134:22.

Google Scholar

12. Schnyder AP, Ryu S, Furusaki A, Ludwig AWW. Classification of Topological Insulators and Superconductors in Three Spatial Dimensions. Phys. Rev. B (2008) 78:195125. doi:10.1103/physrevb.78.195125

CrossRef Full Text | Google Scholar

13. Altland A, Zirnbauer MR. Nonstandard Symmetry Classes in Mesoscopic Normal-Superconducting Hybrid Structures. Phys. Rev. B (1997) 55:1142–61. doi:10.1103/physrevb.55.1142

CrossRef Full Text | Google Scholar

14. Hořava P. Stability of Fermi Surfaces and K Theory. Phys. Rev. Lett. (2005) 95:016405. doi:10.1103/PhysRevLett.95.016405

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Zhao YX, Wang ZD. Topological Connection between the Stability of Fermi Surfaces and Topological Insulators and Superconductors. Phys. Rev. B (2014) 89:075111. doi:10.1103/physrevb.89.075111

CrossRef Full Text | Google Scholar

16. Ryu S, Schnyder AP, Furusaki A, Ludwig AWW. Topological Insulators and Superconductors: Tenfold Way and Dimensional Hierarchy. New J. Phys. (2010) 12:065010. doi:10.1088/1367-2630/12/6/065010

CrossRef Full Text | Google Scholar

17. Matsuura S, Chang P-Y, Schnyder AP, Ryu S. Protected Boundary States in Gapless Topological Phases. New J. Phys. (2013) 15:065001. doi:10.1088/1367-2630/15/6/065001

CrossRef Full Text | Google Scholar

18. Zhao YX, Wang ZD. Topological Classification and Stability of Fermi Surfaces. Phys. Rev. Lett. (2013) 110:240404. doi:10.1103/physrevlett.110.240404

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Chiu C-K, Schnyder AP. Classification of Reflection-Symmetry-Protected Topological Semimetals and Nodal Superconductors. Phys. Rev. B (2014) 90:205136. doi:10.1103/physrevb.90.205136

CrossRef Full Text | Google Scholar

20. Shiozaki K, Sato M. Topology of Crystalline Insulators and Superconductors. Phys. Rev. B (2014) 90:165114. doi:10.1103/physrevb.90.165114

CrossRef Full Text | Google Scholar

21. Zhao YX, Schnyder AP, Wang ZD. Unified Theory ofPTandCPInvariant Topological Metals and Nodal Superconductors. Phys. Rev. Lett. (2016) 116:156402. doi:10.1103/physrevlett.116.156402

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Zhao YX, Lu Y. Phys. Rev. Lett. (2017) 118:056401. doi:10.1103/physrevlett.118.056401

PubMed Abstract | CrossRef Full Text

23. Ahn J, Park S, Yang B-J. Failure of Nielsen-Ninomiya Theorem and Fragile Topology in Two-Dimensional Systems with Space-Time Inversion Symmetry: Application to Twisted Bilayer Graphene at Magic Angle. Phys. Rev. X (2019) 9. doi:10.1103/PhysRevX.9.021013

CrossRef Full Text | Google Scholar

24. Timm C, Schnyder AP, Agterberg DF, Brydon PMR. Inflated Nodes and Surface States in Superconducting Half-Heusler Compounds. Phys. Rev. B (2017) 96:094526. doi:10.1103/physrevb.96.094526

CrossRef Full Text | Google Scholar

25. Yu T, Kennes DM, Rubio A, Sentef MA. Nematicity Arising from a Chiral Superconducting Ground State in Magic-Angle Twisted Bilayer Graphene under In-Plane Magnetic Fields. Phys. Rev. Lett. (2021) 127:127001. doi:10.1103/physrevlett.127.127001

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Tomonaga A, Mukai H, Yoshihara F, Tsai JS. Quasiparticle Tunneling and 1/f Charge Noise in Ultrastrongly Coupled Superconducting Qubit and Resonator. Phys. Rev. B (2021) 104:224509. doi:10.1103/physrevb.104.224509

CrossRef Full Text | Google Scholar

27. Lapp CJ, Börner G, Timm C. Experimental Consequences of Bogoliubov Fermi Surfaces. Phys. Rev. B (2020) 101:024505. doi:10.1103/physrevb.101.024505

CrossRef Full Text | Google Scholar

28. Zhang F, Kane CL, Mele EJ. Surface State Magnetization and Chiral Edge States on Topological Insulators. Phys. Rev. Lett. (2013) 110:046404. doi:10.1103/physrevlett.110.046404

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Yang Z, Gao F, Shi X, Lin X, Gao Z, Chong Y, et al. Topological Acoustics. Phys. Rev. Lett. (2015) 114:114301. doi:10.1103/physrevlett.114.114301

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Imhof S, Berger C, Bayer F, Brehm J, Molenkamp LW, Kiessling T, et al. Topolectrical-circuit Realization of Topological Corner Modes. Nat Phys (2018) 14:925–9. doi:10.1038/s41567-018-0246-1

CrossRef Full Text | Google Scholar

31. Ozawa T, Price HM, Amo A, Goldman N, Hafezi M, Lu L, et al. Topological Photonics. Rev. Mod. Phys. (2019) 91:015006. doi:10.1103/revmodphys.91.015006

CrossRef Full Text | Google Scholar

32. Ma G, Xiao M, Chan CT. Topological Phases in Acoustic and Mechanical Systems. Nat Rev Phys (2019) 1:281–94. doi:10.1038/s42254-019-0030-x

CrossRef Full Text | Google Scholar

33. Serra-Garcia M, Peri V, Süsstrunk R, Bilal OR, Larsen T, Villanueva LG, et al. Observation of a Phononic Quadrupole Topological Insulator. Nature (2018) 555:342–5. doi:10.1038/nature25156

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Yu R, Zhao YX, Schnyder AP. 4D Spinless Topological Insulator in a Periodic Electric Circuit. Natl Sci Rev (2020) 7:1288–95. doi:10.1093/nsr/nwaa065

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Peterson CW, Benalcazar WA, Hughes TL, Bahl G. A Quantized Microwave Quadrupole Insulator with Topologically Protected Corner States. Nature (2018) 555:346–50. doi:10.1038/nature25777

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Yu R, Weng H, Fang Z, Dai X, Hu X. Topological Node-Line Semimetal and Dirac Semimetal State in Antiperovskite Cu₃PdN. Phys. Rev. Lett. (2015) 115:036807. doi:10.1103/physrevlett.115.036807

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Sheng X-L, Chen C, Liu H, Chen Z, Yu Z-M, Zhao YX, et al. Two-Dimensional Second-Order Topological Insulator in Graphdiyne. Phys. Rev. Lett. (2019) 123:256402. doi:10.1103/physrevlett.123.256402

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Wu Q, Soluyanov AA, Bzdušek T. Non-Abelian Band Topology in Noninteracting Metals. Science (2019) 365:1273–7. doi:10.1126/science.aau8740

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Wang Z, Wieder BJ, Li J, Yun B, Bernevig BA. Higher-Order Topology, Monopole Nodal Lines, and the Origin of Large Fermi Arcs in Transition Metal Dichalcogenides XTe₂ (X = Mo;W). Phys. Rev. Lett. (2019) 123:186401.

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Li H, Mekawy A, Krasnok A, Alù A. Virtual Parity-Time Symmetry. Phys. Rev. Lett. (2020) 124:193901. doi:10.1103/physrevlett.124.193901

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Wang K, Dai J-X, Shao LB, Yang SA, Zhao YX. Boundary Criticality of PT -Invariant Topology and Second-Order Nodal-Line Semimetals. Phys. Rev. Lett. (2020) 125:126403. doi:10.1103/physrevlett.125.126403

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Chen C, Wu W, Yu Z-M, Chen Z, Zhao YX, Sheng X-L, et al. Graphyne as a Second-Order and Real Chern Topological Insulator in Two Dimensions. Phys. Rev. B (2021) 104:085205. doi:10.1103/physrevb.104.085205

CrossRef Full Text | Google Scholar

43. Chen C, Zeng X-T, Chen Z, Zhao YX, Sheng X-L, Yang SA. Second-Order Real Nodal-Line Semimetal in Three-Dimensional Graphdiyne. Phys. Rev. Lett. (2022) 128:026405. doi:10.1103/physrevlett.128.026405

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Dai J-X, Wang K, Yang SA, Zhao YX. Takagi Topological Insulator with Odd PT Pairs of Corner States. Phys. Rev. B (2021) 104:165142. doi:10.1103/physrevb.104.165142

CrossRef Full Text | Google Scholar

45. Haldane FDM. Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the “Parity Anomaly”. Phys. Rev. Lett. (1988) 61:2015–8. doi:10.1103/physrevlett.61.2015

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Jackiw R, Rebbi C. Solitons with Fermion Number ½. Phys. Rev. D (1976) 13:3398–409. doi:10.1103/physrevd.13.3398

CrossRef Full Text | Google Scholar

47. Yang Z-Z, Li X, Peng Y-Y, Zou X-Y, Cheng J-C. Helical Higher-Order Topological States in an Acoustic Crystalline Insulator. Phys. Rev. Lett. (2020) 125:255502. doi:10.1103/physrevlett.125.255502

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Noh J, Benalcazar WA, Huang S, Collins MJ, Chen KP, Hughes TL, et al. Topological Protection of Photonic Mid-gap Defect Modes. Nat Phot (2018) 12:408–15. doi:10.1038/s41566-018-0179-3

CrossRef Full Text | Google Scholar