
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 19 July 2022
Sec. Condensed Matter Physics
Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.915619
This article is part of the Research TopicNematicity in Iron-Based SuperconductorsView all 10 articles
A rich variety of nematic/smectic orders in Fe-based superconductors is an important unsolved problem in strongly correlated electron systems. A unified understanding of these orders has been investigated for the last decade. In this study, we explain the B1g symmetry nematic transition in FeSe1−xTex, the B2g symmetry nematicity in AFe2As2 (A = Cs, Rb), and the smectic state in BaFe2As2 based on the same framework. We investigate the quantum interference mechanism between spin fluctuations by developing the density wave equation. The observed rich variety of nematic/smectic orders is naturally understood in this mechanism. The nematic/smectic orders depend on the characteristic shape and topology of the Fermi surface (FS) of each compound. 1) In FeSe1−xTex (nd = 6.0), each FS is very small and the dxy-orbital hole pocket is below the Fermi level. In this case, the small spin fluctuations on three dxz, dyz, and dxy orbitals cooperatively lead to the B1g nematic (q = 0) order without magnetization. The experimental Lifshitz transition below the nematic transition temperature (TS) is naturally reproduced. 2) In BaFe2As2 (nd = 6.0), the dxy-orbital hole pocket emerges around the M point, and each FS is relatively large. The strong spin fluctuations due to the dxy-orbital nesting give rise to the B1g nematic (q = 0) order and the smectic [q = (0, π)] order, and the latter transition temperature (T* ∼ 170K) exceeds the former one (TS ∼ 140K). 3) In heavily hole-doped AFe2As2 (nd = 5.5), the large dxy-orbital hole pocket and the four tiny Dirac pockets appear due to the hole-doping. The B2g nematic bond order emerges on the dxy-orbital hole pocket because of the same interference mechanism. The present paramagnon interference mechanism provides a unified explanation of why the variety of nematic/smectic orders in Fe-based superconductors is so rich, based on the well-established fermiology of Fe-based superconductors.
The emergence of an electron nematic (q = 0) state is one of the most important unsolved problems in Fe-based superconductors [1]. In LaFeAsO and Ba122 compounds, the antiferro (AF) magnetic state appears at the Néel temperature TN, which is lower than the nematic transition temperature TS. Since the superconducting phase with a high transition temperature (Tc) appears near the nematic phase and the AF magnetic phase, it is expected that the nematic fluctuations and the spin fluctuations are related to the mechanism of the high-Tc superconductivity. However, the questions appear before discussing the superconductivity: 1) what is the order parameter of the nematic state? 2) What is the driving force of the nematic state? 3) Why do the diverse nematic states emerge in various compounds?
It is known that the nematic order cannot be derived from the mean-field theory since the spin-channel order always dominates over the nematic order unless unphysical parameters (such as negative Hund’s coupling) are assumed. Previously, to explain the nematic state [2], the vestigial order (spin nematic) scenario [3–9] and the orbital order scenario [10–22] have been proposed.
To investigate the nematic state, the FeSe family is an ideal platform since the AF magnetic state is absent [23–26]. This family is also ideal from the aspect of superconductivity since the highest Tc ≳ 65K in Fe-based superconductors has been reported in electron-doped FeSe [27–31]. In FeSe, the orbital polarization between dxz and dyz orbitals in the nematic state has been observed by angle-resolved-photoemission spectroscopy (ARPES) [32–36]. To be more precise, the orbital polarization energy Exz − Eyz has k dependence and changes the sign between the Γ point and the X (Y) point. This sign reversal orbital polarization has been explained by the orbital order scenario [16, 17, 19, 20] based on the paramagnon interference mechanism and by the renormalization group (RG) theory [37, 38]. In both theories, the vertex correction (VC) of the Coulomb interaction, which corresponds to the higher-order many-body effect, plays an essential role. Since the AF magnetic correlation is weak in FeSe, it is difficult to explain the nematic state by the vestigial order (spin nematic) scenario. Based on the paramagnon interference mechanism, the B1g nematic orders in LaFeAsO and FeSe [14–18] and the nematic orders in cuprate superconductors [39–41] and magic-angle twisted bilayer graphene [42] have been explained as the orbital/bond orders. CDW orders in the transition metal dichalcogenide [43] and kagome metal [44] have also been explained by the paramagnon interference mechanism.
The rich variety of nematicity in the FeSe family remains a significant open problem. In FeSe1−xSx, TS disappears at x ∼ 0.17, where the emergence of the nematic quantum critical point (QCP) has been suggested by experiments [45–48]. Recently, the whole x dependent phase diagram for FeSe1−xTex (x ≲ 0.6) has been reported [49–51]. In the phase diagram shown in Figure 1A, TS decreases with Te doping x, and TS disappears at x ∼ 0.5. Tc becomes maximum
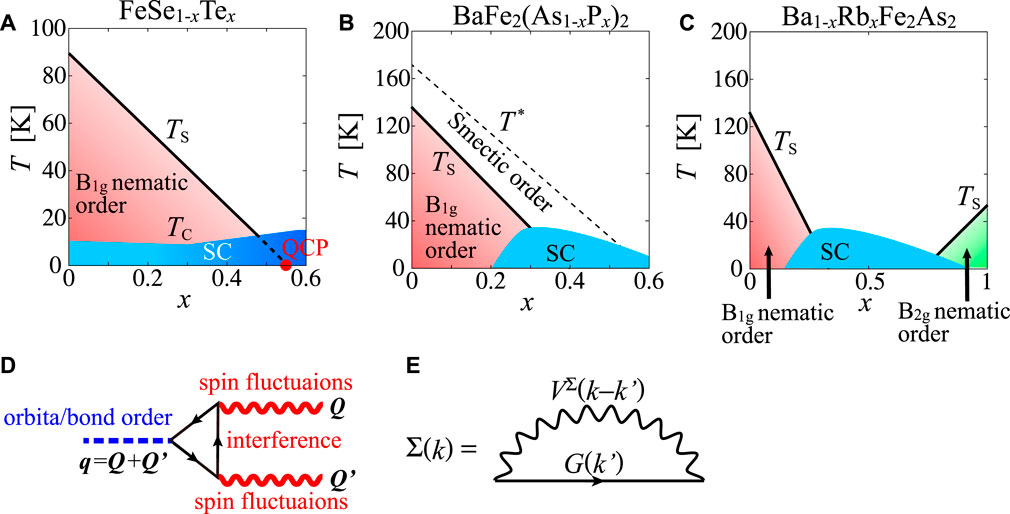
FIGURE 1. (A) Schematic x-T phase diagram of FeSe1−xTex, where TS decreases with x, and Tc becomes maximum near the nematic QCP. (B) Schematic x-T phase diagram of
In addition, a significant open issue in nematicity is the emergence of another type of nematicity in various Ba122 compounds below T = T*, which is higher than TS by tens of Kelvin, as shown in Figure 1B. An actual bulk nematic transition at T = T* has been reported in many experimental studies, such as a magnetic torque study [52], an X-ray study [53], an optical measurement study [54], and a laser photoemission electron microscope (PEEM) study [55]. Since the orthorhombicity (a − b)/(a + b) ≪ 0.1% below T* is tiny, an extrinsic origin such as inhomogeneity of the nematic transition temperature TS due to local uniaxial pressure and randomness was proposed [4, 56–60]. On the other hand, T* seems not to be sensitive to the sample quality and the local strain, and the domain structure of nematicity observed above TS is homogeneous [54, 55]. It is noteworthy that bulk orbital polarization starts to emerge at T = T*(>TS) in Ba122 compounds, according to the recent PEEM study [55]. In this study, we will explain the multistage smectic/nematic transitions: the smectic order (q ≠ 0) at T = T* and the nematic order (q = 0) at TS. In this scenario, T* is given by the intrinsic smectic order free from randomness.
In contrast to B1g nematicity in typical Fe-based superconductors, the emergence of 45°-rotated B2g nematicity in heavily hole-doped AFe2As2 (A = Cs, Rb) has been reported in Refs. [61–64], while Refs. [65, 66] have reported the absence of the nematic order. As shown in Figure 1C, the dominant B1g nematicity changes to B2g nematicity with doping x in Ba1−xRbxFe2As2. As for the mechanism of B2g nematicity, vestigial nematic order by using the double-stripe magnetic configuration was suggested [67]. However, no SDW transition has been observed [64, 68] in AFe2As2, and the spin fluctuations are weak around TS in RbFe2As2 [69]. In this study, we reveal the emergence of B2g-symmetry bond order in AFe2As2.
As described previously, the variety of nematicity in Fe-based superconductors is very rich. To understand the mechanism of nematic/smectic states and superconductivity, it is important to explain these nematic/smectic states in the same theoretical framework.
In this study, we study B1g nematicity in FeSe1−xTex (nd = 6.0), the tiny nematicity below T* in BaFe2As2 (nd = 6.0), and B2g nematicity in AFe2As2 (A = Cs, Rb) (nd = 5.5) by developing the density wave (DW) equation theory. In this theory, the paramagnon interference mechanism due to the Aslamazov–Larkin (AL) type VCs shown in Figure 1D is taken into account. We also take into account of the self-energy effect shown in Figure 1E. In this mechanism, the rich variety of nematicity is naturally understood. The obtained nematicity depends on the shape and topology of FSs, as shown in Figures 2A–C. 1) In FeSe1−xTex, all FSs are very small, and dxy-orbital hole pocket is absent. The small spin fluctuations on the three dxz, dyz, and dxy orbitals cooperatively lead to the B1g nematic order, where the orbital order for dxz and dyz orbitals coexists with the bond order for the dxy orbital. The experimental Lifshitz transition below TS is naturally explained by the nematic order. 2) In BaFe2As2, the dxy hole pocket emerges, and each FS is relatively large. The smectic order at T = T*(>TS) and the nematic order at T = TS emerge due to the strong dxy-orbital nesting. The smectic order explains the tiny nematicity below T*, and the multistage transitions are explained by the smectic and nematic orders. 3) In heavily hole-doped AFe2As2, the large dxy-orbital hole pocket and the four tiny Dirac pockets appear. The B2g nematic bond order emerges due to the dxy-orbital paramagnon interference mechanism, where the nesting between the Dirac pockets and the large dxy-orbital hole pocket plays an important role. By considering the fermiology of each compound, these various nematic/smectic states are explained by the same theoretical framework based on the paramagnon interference mechanism.
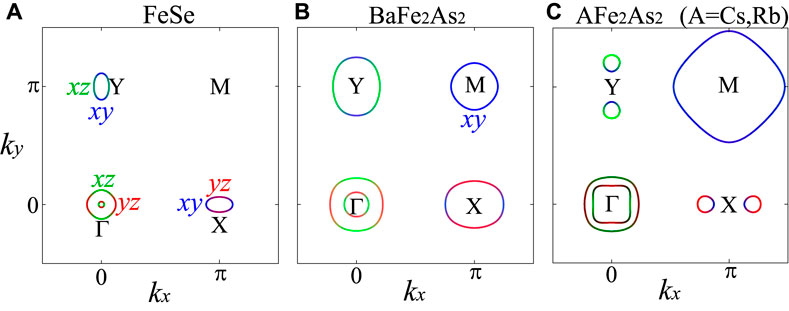
FIGURE 2. FSs of (A) FeSe (nd = 6.0), (B) BaFe2As2 (nd = 6.0), and (C) AFe2As2 (A = Cs, Rb) (nd = 5.5). The colors green, red, and blue correspond to orbitals 2, 3, and 4, respectively. A variety of nematic/smectic states originates from the characteristic structure of FSs.
In the present study, we intensively study the effect of self-energy on the nematic/smectic orders. It has been dropped in many previous studies, despite the fact that self-energy is necessary to satisfy the criteria of Baym–Kadanoff’s conserving approximation [70, 71]. We revealed that 1) the nematic/smectic order is stabilized by the AL-type VCs, while 2) TS is reduced to become realistic (
Here, we introduce multiorbital models based on the first principle’s calculations. We analyze the following two-dimensional d-p Hubbard model with a unique parameter r, which controls the strength of the Coulomb interaction [16]:
where
We use the d-orbital Coulomb interaction introduced by the constraint random phase approximation (RPA) method in Ref. [74]. The Coulomb interactions for the spin and charge channels are generally given as
The Hamiltonian of the Coulomb interaction is given as
where σ, σ′ = ±1 denote spin.
By using the multiorbital Coulomb interaction, the spin (charge) susceptibility
where irreducible susceptibility is
Here, we introduce the multiorbital fluctuation exchange (FLEX) approximation [15, 75]. The FLEX approximation satisfies the conserving approximation formalism of Baym and Kadanoff [70, 71]. In the FLEX approximation, self-energy is given as
which is shown by the Feynman diagram in Figure 1E. The effective interaction
where
We derive the strongest charge-channel density-wave (DW) instability without assuming the order parameter and wave vector. For this purpose, we use the DW equation method developed in Refs. [16, 19, 76]. We obtain the optimized non-local form factor
where λq is the eigenvalue of the form factor
where as = 3, ac = 1, p = (p, ωl), and
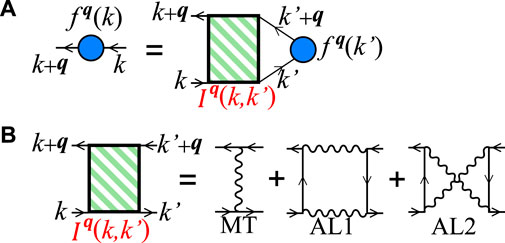
FIGURE 3. Feynman diagrams of (A) DW equation and (B) charge-channel irreducible four-point vertex. Each wavy line represents a spin-fluctuation-mediated interaction.
In Eq. 11, the first line corresponds to the Maki-Thompson (MT) term, and the second and third lines give the AL terms, respectively. Feynman diagrams of the MT terms and AL terms are shown in Figure 3B.
The AL terms are enhanced by the paramagnon interference
In this section, we show that 1) the B1g nematic orbital + bond order originates from the paramagnon interference, and 2) the effect of self-energy is essential to reproduce the x dependence of TS as shown in Figure 1A in FeSe1−xTex. The effect of self-energy on the nematic/smectic order caused by the VCs is systematically studied in the present work. Because of self-energy, TS is reduced to become realistic (
Hereafter, we fix r = 0.35, T = 15 meV in calculations with self-energy and r = 0.15, T = 15 meV in calculations without the self-energy, unless otherwise noted.
Figures 4A,B show x dependent FSs and band structures, respectively. The FSs are small compared to other Fe-based superconductors. The dxy orbital level
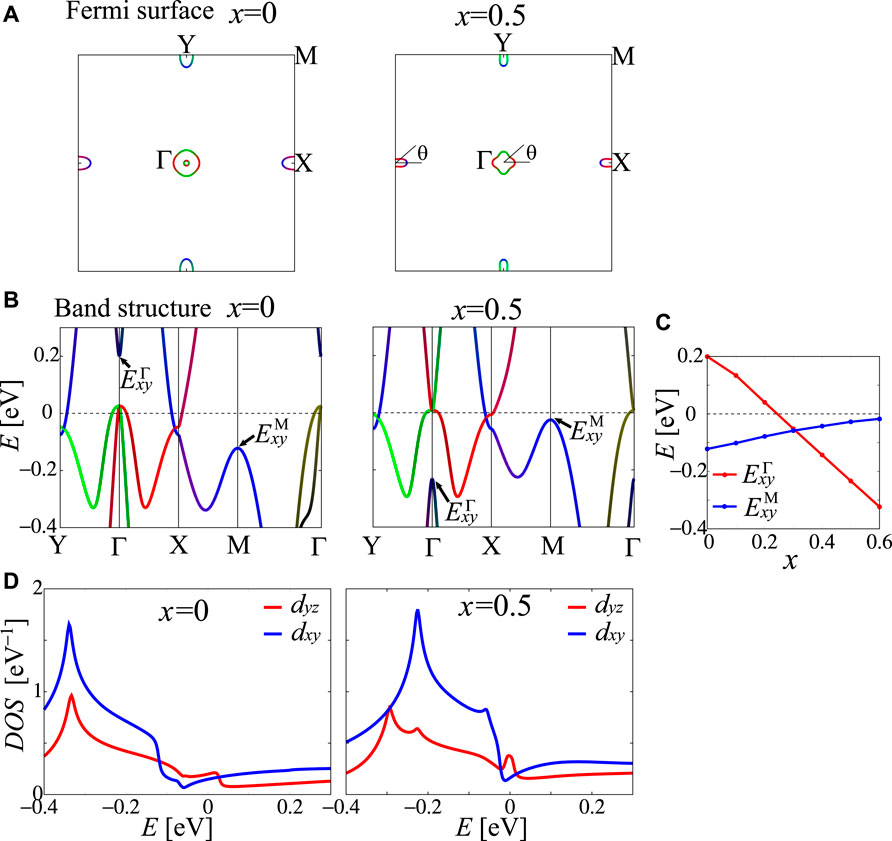
FIGURE 4. (A) FSs and (B) band structures of FeSe1−xTex for x = 0 and 0.5. (C) x dependences of
To discuss the self-energy effect, we calculate the mass enhancement factors. Figure 5 shows the obtained x dependence of the mass enhancement factors
Figure 6 shows x dependences of
Hereafter, we discuss the DW instability given by the DW Eq. 9. Figure 7A shows x dependences of λ0 for the B1g nematic state with and without the self-energy. λ0 without the self-energy rapidly increases with doping x due to the paramagnon interference shown in Figure 1D. λ0 is enlarged by the interference between
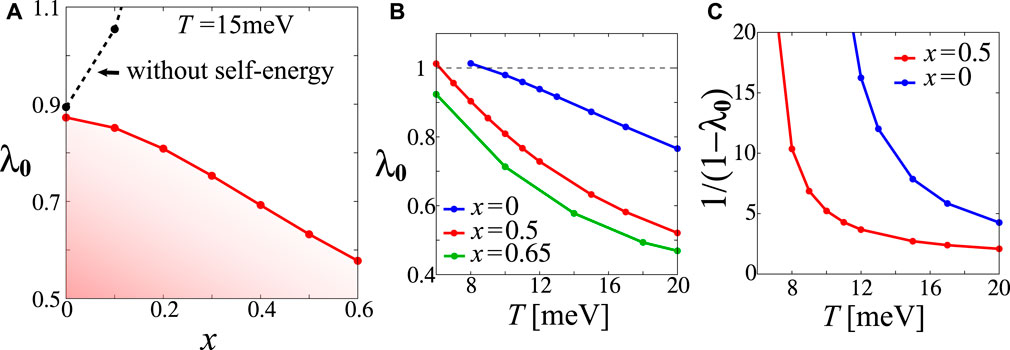
FIGURE 7. (A) x dependences of λ0 in the DW equation with and without self-energy at T = 15 meV. (B) T dependences of λ0 with self-energy for x = 0, 0.5, 0.65. (C) T dependences of 1/(1 − λ0) with self-energy for x = 0, 0.5.
Here, we analytically explain that TS is reduced by self-energy by focusing on the mass renormalization factor z. As discussed in Ref. [17], αs(c) is independent of z under the scaling T → zT and r → r/z. Under this scaling, the eigenvalue of the DW equation is unchanged [17]. Thus, TS obtained by the DW equation without the self-energy is reduced to zTS because of the self-energy. As a result, realistic TS is obtained by taking self-energy into account.
Figure 8A shows q dependences of λq with the self-energy at x = 0, 0.5. λq has peak at q = 0, which means that the ferro nematic order is favored. Figure 8B shows k dependences of the static form factors
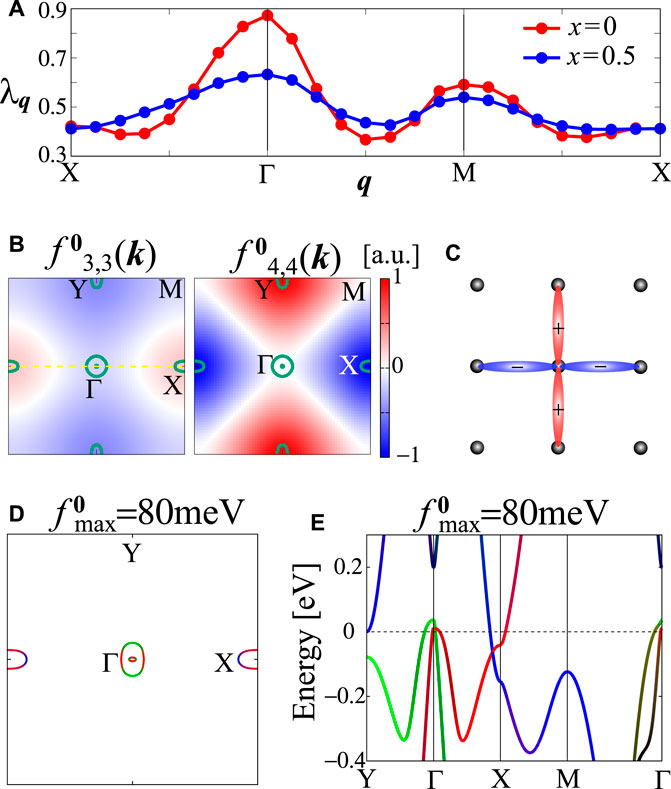
FIGURE 8. (A) q dependences of λq with self-energy for x = 0, 0.5. (B) k dependences of
Here, we confirm that the dxy orbital levels at Γ and M points are important for the x dependence of λ0. We use the simple model, where only the shift of
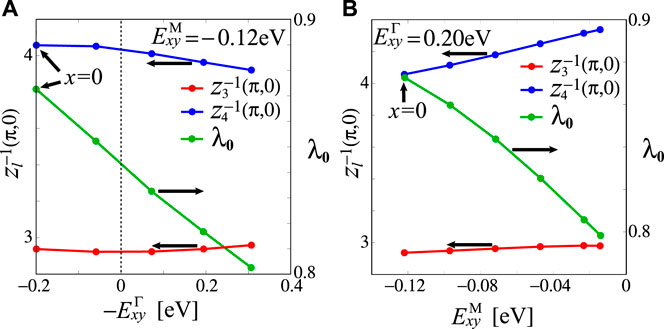
FIGURE 9. (A)
In this section, we discuss the multi-nematicity in BaFe2As2 [20].
The effect of self-energy on the nematic/smectic orders caused by the VCs is studied in the present work. Transition temperatures are reduced to become realistic because of the self-energy, while the symmetries of the nematic/smectic orders are unchanged. We reveal the origin of the tiny nematicity below T = T* and explain the multistage transitions at T = T* and TS in the phase diagram shown in Figure 1B. As shown in Figure 2B, the size of the hole FS around the M point comprising the dxy orbital is similar to that of electron FSs around the X and Y points, which causes good intra- and inter-orbital nestings. As explained later, inter-orbital nesting is important to realize the smectic state at T = T*.
Figure 10A shows the q-dependence of λq with and without self-energy. The q = (0, π) smectic bond order is dominant over the q = 0 nematic orbital + bond order because of the relation λ(0,π) > λ0, which is robust in the presence of moderate spin fluctuations αs ≳ 0.85. Thus, the nematic orbital + bond transition temperature TS is lower than T*, where the smectic bond order appears. Figure 10B shows the dominant component of the static form factor,
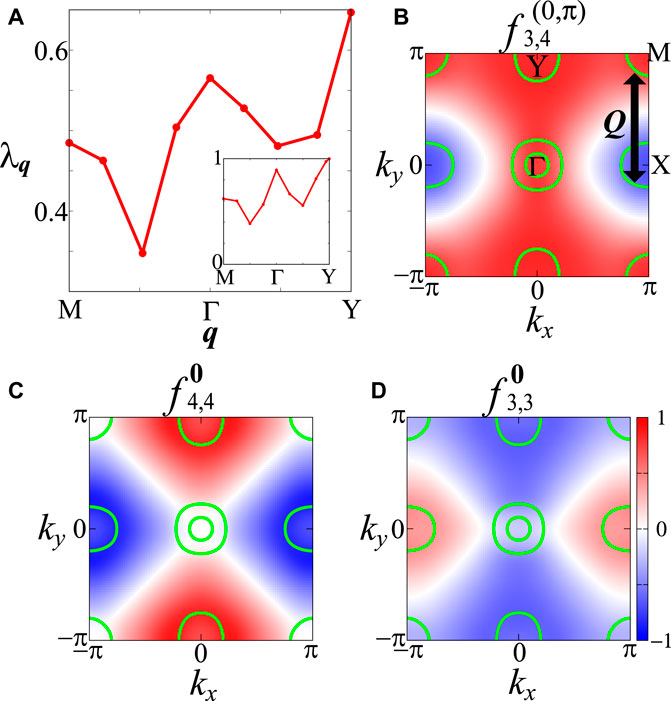
FIGURE 10. (A) q dependence of λq with self-energy for r = 0.68 at T = 5 meV in BaFe2As2, and that without self-energy for r = 0.30 at T = 32.4 meV in the inset. (B) k dependence of the dominant form factor at q = (0, π),
As shown in Figure 1D, the origin of the smectic bond order
Here, we examine the DOS under the smectic bond order to verify the present theory. For T < T* = 32.4 meV without self-energy, we introduce the mean-field-like T-dependent form factor
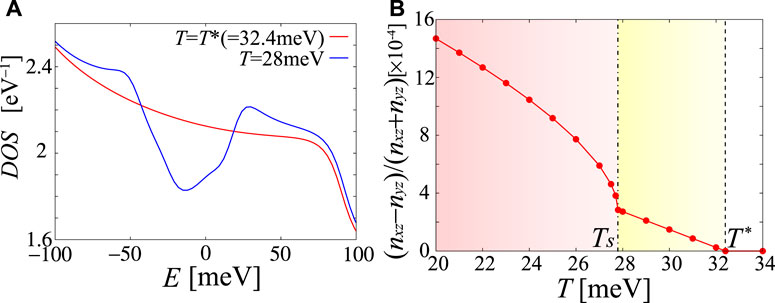
FIGURE 11. (A) DOS at T = T* = 32.4 meV and that at T = 28 meV(<T*), including the smectic bond order. (B) T dependence of nematicity ψ = (n2 − n3)/(n2 + n3) including both the smectic-bond order for T < T* and the ferro-orbital/bond order for T < TS.
Next, we focus on another mystery, the T-linear behavior of tiny nematicity ψ in Ba122 [52] below T*. To solve this mystery, we calculate the T dependence of uniform nematicity ψ = (n2 − n3)/(n2 + n3) in Figure 11B, where both
We stress that the present mechanism of the bulk nematicity for TS < T < T* is intrinsic and free from the strength of the disorder and local strain in the system. The present smectic order originates from the AL–VC and the FS nesting between the dxy-orbital hole pocket and the electron pockets [20]. We stress that the present theory explains the absence of the smectic order in bulk FeSe [55] because the dxy-orbital hole pocket, which is necessary for smectic order formation, is below the Fermi level in FeSe.
Here, we explain the details of the recent microscopic measurements in P-doped Ba122 [54, 55] that support the present intrinsic scenario. These are bulk and real-space measurements. In the PEEM measurement [55], very uniform bulk nematic domains have been observed for TS < T < T*. The width of each nematic domain is about 500 nm. The structure of the nematic domains is unchanged for T < TS. In addition, once the nematic domain completely disappears by increasing T, it never appears at the same location if the temperature is lowered again. These results are consistent with the present intrinsic smectic order scenario for TS < T < T* in P-doped Ba122. In the photo-modulation measurement [54], uniform nematic domains have also been observed. The observed nematicity becomes small near the nematic domain boundary, irrespective of the fact that large local strain anisotropy is observed at the domain boundary. The observed anticorrelation between the nematicity and the local strain anisotropy may conflict with the assumption of the extrinsic scenario of the nematicity above TS.
In contrast, the extrinsic scenario has been proposed by other groups [4, 56–60]. In the extrinsic mechanism, nematicity for T > TS in Co-doped Ba122, which exhibits large residual resistivity (>100 μΩcm), has been explained by the inhomogeneity of TS induced by the disorder and local strain. However, it is not easy to explain the nematicity above TS in clean P-doped (non-doped) Ba122 on the same footing in the extrinsic scenario.
We note that the multistage smectic/nematic transitions observed in NaFeAs [92] are also explained by the present intrinsic mechanism [20].
In this section, we discuss B2g nematicity in heavily hole-doped compound AFe2As2 (A = Cs, Rb) [19]. The effect of self-energy on the nematic order caused by the VCs is studied in the present work. Because of self-energy, TS is reduced to become realistic, whereas the symmetry of the nematic order is unchanged. The direction of B2g nematicity is rotated by 45° from that of the conventional B1g nematicity. Figure 2C shows FSs of CsFe2As2: the hole FS around the M point comprising the dxy-orbital is large, whereas the Dirac pockets near the X and Y points are small. In this system, the dxy-orbital spin fluctuations are dominant.
Figure 12A shows the q dependence of the largest eigenvalue λq with self-energy for r = 0.96 at T = 5 meV and that without self-energy for r = 0.30 at T = 20 meV λq becomes maximum at q = 0 and the dominant form factor
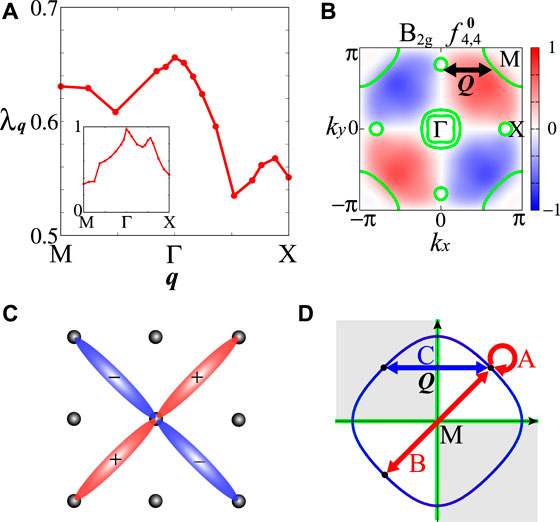
FIGURE 12. (A) q dependence of λq with self-energy in CsFe2As2, and that without self-energy in the inset. (B) k dependence of the B2g form factor
We comment on the recent experiments on RbFe2As2. The specific heat jump at TS = 40K (ΔC/TS) is very small [64]. However, it is naturally understood based on the recent theoretical scaling relation
Finally, we discuss the x dependence of nematicity in Ba1−xAxFe2As2 (A = Cs, Rb). The schematic phase diagram of Ba1−xRbxFe2As2 given by the experiment [64] is shown in Figure 1C. We introduce the model Hamiltonian for Ba1−xCsxFe2As2, by interpolating between the BaFe2As2 model and the CsFe2As2 model with the ratio 1 − x: x. Figure 13A shows x dependences of λq=0 without self-energy for the B2g and the B1g symmetries by fixing T = 30 meV and r = 0.30. Below x = xc ∼ 0.5, the B1g nematic orbital order is dominant as discussed in the previous section, while the B2g nematic bond order dominates over the B1g nematic orbital order for x > xc. As shown in Figure 13B, the Lifshitz transition occurs at x ∼ xc, where the electron pockets split into the four tiny Dirac pockets. Thus, the B2g nematic bond order appears when the nesting vector Q between the electron pockets and hole pocket around the M point becomes short Q ∼ (0.5π, 0). By taking account of the Lifshitz transition at x ∼ xc, the schematic phase diagram in Figure 1C is also well reproduced by the orbital/bond order because of the paramagnon interference mechanism. We note that the q = (0, π) smectic order is dominant over the q = 0 B1g nematic order at x = 0, as shown in the previous section.
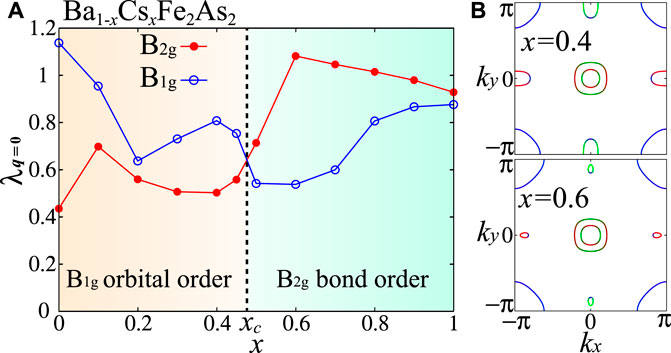
FIGURE 13. (A) x dependences of λq=0 without self-energy for B1g and B2g symmetries in Ba1−xCsxFe2As2. (B) FSs for x = 0.4 and x = 0.6. The dominant nematic order changes at x = xc ∼ 0.5 near the Lifshitz transition, where the electron FSs split into the four tiny Dirac pockets.
We discussed the rich variety of nematic/smectic states in Fe-based superconductors in the same theoretical framework based on the paramagnon interference mechanism. In this mechanism, the charge-channel order is induced by the quantum interference between the spin fluctuations, as shown in Figure 1D. The form factor and wave vector of the DW instability are derived from the DW equation based on the paramagnon interference mechanism. Recently, a rigorous formalism of the DW equation has been constructed based on the Luttinger–Ward (LW) theory in Ref. [87]. According to Ref. [87], the solution of the DW equation gives the minimum of the grand potential in the LW theory. Thus, the nematic/smectic order discussed in the present study is thermodynamically stable in the framework of the conserving approximation.
By considering the characteristic fermiology of each compound, the paramagnon interference mechanism explains the rich variety of the nematic/smectic states. In Figures 14A–C, we summarized the nematic/smectic orders revealed by the mechanism in the present study. 1) In FeSe1−xTex, each FS is very small and the dxy-orbital hole pocket is absent. In this case, the small spin fluctuations on the three orbitals cooperatively lead to the B1g orbital order for the dxz and dyz orbitals coexisting with the dxy-orbital bond order, as shown in Figure 14A. The nematic orbital + bond order causes the Lifshitz transition, where the FS around the Y point disappears, which is consistent with the recent experiments. The x dependence of TS in the phase diagram is reproduced by introducing self-energy. 2) In BaFe2As2, the dxy-orbital hole pocket emerges. Since each electron and hole pocket is relatively large and similar in size, the strong dxy-orbital spin fluctuations due to good nesting give rise to the smectic order shown in Figure 14B and the B1g nematic order. The smectic order explains the tiny T-linear nematicity below T = T*(>TS). We predict the multistage transitions with the smectic order at T = T* and the nematic order at TS. 3) In heavily hole-doped AFe2As2 (A = Cs, Rb), the tiny Dirac pockets around the X(Y) point and the large dxy-orbital hole pocket appear due to hole-doping. The B2g bond order for the dxy orbital shown in Figure 14C emerges due to the dxy-orbital paramagnon interference mechanism. The B2g bond order is triggered by the Lifshitz transition of the electron FSs by hole-doping.
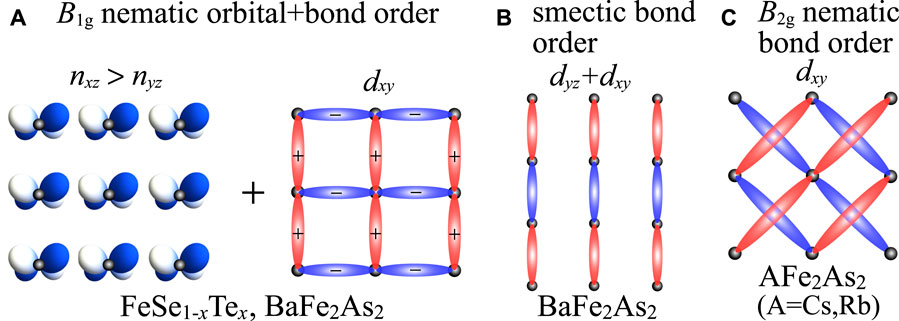
FIGURE 14. (A) Schematic picture of the B1g nematic orbital + bond order in FeSe1−xTex and BaFe2As2, where the orbital order for the dxz and dyz orbitals coexists with the bond order for the dxy orbital. (B) Schematic picture of the smectic bond order for dyz and dxy orbitals in BaFe2As2. (C) Schematic picture of the B2g nematic bond order for the dxy orbital in AFe2As2 (A = Cs, Rb).
The limitation of this theory is that the calculated VCs are reduced to an infinite series of the MT and AL terms. To verify the validity of the present theory, we performed the functional renormalization group (fRG) analysis for the single-orbital Hubbard model for cuprates [41] and the two-orbital Hubbard model for ruthenates [94], and obtained the bond-order (orbital order) in the former (latter) model. These results are consistent with previous experiments, and they are also obtained by the DW equation analysis. In the fRG theory, a huge number of higher-order VCs are generated in an unbiased manner by solving the RG equation. Thus, the significance of the MT and AL terms in the present theory has been confirmed by the different and excellent theoretical frameworks.
In future, it is to clarify the mechanism of superconductivity and non-Fermi-liquid behaviors of transport phenomena in the FeSe family by considering the nematic fluctuations enlarged near the nematic QCP. This issue will be discussed in future studies [95].
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
SO performed all calculations with contributions from HK. SO and HK wrote the manuscript.
This work was supported by Grants-in-Aid for Scientific Research from MEXT, Japan (No.s JP19H05825, JP18H01175, and JP17K05543), and Nagoya University Research Fund.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
We acknowledge Y. Yamakawa, R. Tazai, and S. Matsubara for their collaboration in the theoretical studies. We are grateful to Y. Matsuda, T. Hanaguri, T. Shibauchi, S. Kasahara, T. Shimojima, and Y. Mizukami for useful discussions about experiments.
1. Hosono H, Kuroki K. Iron-based Superconductors: Current Status of Materials and Pairing Mechanism. Physica C: Superconductivity its Appl (2015) 514:399–422. doi:10.1016/j.physc.2015.02.020
2. Hirschfeld PJ, Korshunov MM, Mazin II. Gap Symmetry and Structure of Fe-Based Superconductors. Rep Prog Phys (2011) 74:124508. doi:10.1088/0034-4885/74/12/124508
3. Fernandes RM, VanBebber LH, Bhattacharya S, Chandra P, Keppens V, Mandrus D, et al. Effects of Nematic Fluctuations on the Elastic Properties of Iron Arsenide Superconductors. Phys Rev Lett (2010) 105:157003. doi:10.1103/PhysRevLett.105.157003
4. Fernandes RM, Abrahams E, Schmalian J. Anisotropic In-Plane Resistivity in the Nematic Phase of the Iron Pnictides. Phys Rev Lett (2011) 107:217002. doi:10.1103/PhysRevLett.107.217002
5. Wang F, Kivelson SA, Lee D-H. Nematicity and Quantum Paramagnetism in FeSe. Nat Phys (2015) 11:959–63. doi:10.1038/nphys3456
6. Yu R, Si Q. Antiferroquadrupolar and Ising-Nematic Orders of a Frustrated Bilinear-Biquadratic Heisenberg Model and Implications for the Magnetism of FeSe. Phys Rev Lett (2015) 115:116401. doi:10.1103/PhysRevLett.115.116401
7. Glasbrenner JK, Mazin II, Jeschke HO, Hirschfeld PJ, Fernandes RM, Valentí R. Effect of Magnetic Frustration on Nematicity and Superconductivity in Iron Chalcogenides. Nat Phys (2015) 11:953–8. doi:10.1038/nphys3434
8. Fang C, Yao H, Tsai WF, Hu J, Kivelson SA. Theory of Electron Nematic Order in LaFeAsO. Phys Rev B (2008) 77:224509. doi:10.1103/PhysRevB.77.224509
9. Fernandes RM, Chubukov AV. Low-energy Microscopic Models for Iron-Based Superconductors: a Review. Rep Prog Phys (2017) 80:014503. doi:10.1088/1361-6633/80/1/014503
10. Krüger F, Kumar S, Zaanen J, van den Brink J. Spin-orbital Frustrations and Anomalous Metallic State in Iron-Pnictide Superconductors. Phys Rev B (2009) 79:054504. doi:10.1103/PhysRevB.79.054504
11. Lv W, Wu J, Phillips P. Orbital Ordering Induces Structural Phase Transition and the Resistivity Anomaly in Iron Pnictides. Phys Rev B (2009) 80:224506. doi:10.1103/physrevb.80.224506
12. Lee CC, Yin WG, Ku W. Ferro-Orbital Order and Strong Magnetic Anisotropy in the Parent Compounds of Iron-Pnictide Superconductors. Phys Rev Lett (2009) 103:267001. doi:10.1103/PhysRevLett.103.267001
13. Kontani H, Onari S. Orbital-Fluctuation-Mediated Superconductivity in Iron Pnictides: Analysis of the Five-Orbital Hubbard-Holstein Model. Phys Rev Lett (2010) 104:157001. doi:10.1103/PhysRevLett.104.157001
14. Onari S, Kontani H. Self-consistent Vertex Correction Analysis for Iron-Based Superconductors: Mechanism of Coulomb Interaction-Driven Orbital Fluctuations. Phys Rev Lett (2012) 109:137001. doi:10.1103/PhysRevLett.109.137001
15. Onari S, Yamakawa Y, Kontani H. High-TcSuperconductivity Near the Anion Height Instability in Fe-Based Superconductors: Analysis ofLaFeAsO1−xHx. Phys Rev Lett (2014) 112:187001. doi:10.1103/PhysRevLett.112.187001
16. Onari S, Yamakawa Y, Kontani H. Sign-Reversing Orbital Polarization in the Nematic Phase of FeSe Due to theC2Symmetry Breaking in the Self-Energy. Phys Rev Lett (2016) 116:227001. doi:10.1103/physrevlett.116.227001
17. Yamakawa Y, Onari S, Kontani H. Nematicity and Magnetism in FeSe and Other Families of Fe-Based Superconductors. Phys Rev X (2016) 6:021032. doi:10.1103/PhysRevX.6.021032
18. Yamakawa Y, Kontani H. Nematicity, Magnetism, and Superconductivity in FeSe under Pressure: Unified Explanation Based on the Self-Consistent Vertex Correction Theory. Phys Rev B (2017) 96:144509. doi:10.1103/PhysRevB.96.144509
19. Onari S, Kontani H. Origin of Diverse Nematic Orders in Fe-Based Superconductors: 45° Rotated Nematicity in AFe2As2(A=Cs,Rb). Phys Rev B (2019) 100:020507(R). doi:10.1103/physrevb.100.020507
20. Onari S, Kontani H. Hidden Antiferronematic Order in Fe-Based Superconductor BaFe2As2 and NaFeAs above TS. Phys Rev Res (2020) 2:042005(R). doi:10.1103/PhysRevResearch.2.042005
21. Jiang K, Hu J, Ding H, Wang Z. Interatomic Coulomb Interaction and Electron Nematic Bond Order in FeSe. Phys Rev B (2016) 93:115138. doi:10.1103/PhysRevB.93.115138
22. Fanfarillo L, Giovannetti G, Capone M, Bascones E. Nematicity at the Hund's Metal Crossover in Iron Superconductors. Phys Rev B (2017) 95:144511. doi:10.1103/PhysRevB.95.144511
23. Hsu FC, Luo JY, Yeh KW, Chen TK, Huang TW, Wu PM, et al. Superconductivity in the PbO-type Structure α-FeSe. Proc Natl Acad Sci U.S.A (2008) 105:14262–4. doi:10.1073/pnas.0807325105
24. Böhmer AE, Kreisel A. Nematicity, Magnetism and Superconductivity in FeSe. J Phys Condens Matter (2018) 30:023001. doi:10.1088/1361-648X/aa9caa
25. Kreisel A, Hirschfeld P, Andersen B. On the Remarkable Superconductivity of FeSe and its Close Cousins. Symmetry (2020) 12:1402. doi:10.3390/sym12091402
26. Shibauchi T, Hanaguri T, Matsuda Y. Exotic Superconducting States in FeSe-Based Materials. J Phys Soc Jpn (2020) 89:102002. doi:10.7566/jpsj.89.102002
27. Wang QY, Li Z, Zhang WH, Zhang ZC, Zhang JS, Li W, et al. Interface-Induced High-Temperature Superconductivity in Single Unit-Cell FeSe Films on SrTiO 3. Chin Phys. Lett. (2012) 29:037402. doi:10.1088/0256-307x/29/3/037402
28. Ge JF, Liu ZL, Liu C, Gao CL, Qian D, Xue QK, et al. Superconductivity above 100 K in Single-Layer FeSe Films on Doped SrTiO3. Nat Mater (2015) 14:285–9. doi:10.1038/nmat4153
29. Fan Q, Zhang WH, Liu X, Yan YJ, Ren MQ, Peng R, et al. Plain S-Wave Superconductivity in Single-Layer FeSe on SrTiO3 Probed by Scanning Tunnelling Microscopy. Nat Phys (2015) 11:946–52. doi:10.1038/nphys3450
30. Zhang Y, Lee JJ, Moore RG, Li W, Yi M, Hashimoto M, et al. Superconducting gap Anisotropy in Monolayer FeSe Thin Film. Phys Rev Lett (2016) 117:117001. doi:10.1103/PhysRevLett.117.117001
31. Miyata Y, Nakayama K, Sugawara K, Sato T, Takahashi T. High-temperature Superconductivity in Potassium-Coated Multilayer FeSe Thin Films. Nat Mater (2015) 14:775–9. doi:10.1038/nmat4302
32. Shimojima T, Suzuki Y, Sonobe T, Nakamura A, Sakano M, Omachi J, et al. Lifting of Xz/yz Orbital Degeneracy at the Structural Transition in Detwinned FeSe. Phys Rev B (2014) 90:121111(R). doi:10.1103/physrevb.90.121111
33. Nakayama K, Miyata Y, Phan GN, Sato T, Tanabe Y, Urata T, et al. Reconstruction of Band Structure Induced by Electronic Nematicity in an FeSe Superconductor. Phys Rev Lett (2014) 113:237001. doi:10.1103/physrevlett.113.237001
34. Suzuki Y, Shimojima T, Sonobe T, Nakamura A, Sakano M, Tsuji H, et al. Momentum-dependent Sign Inversion of Orbital Order in Superconducting FeSe. Phys Rev B (2015) 92:205117. doi:10.1103/PhysRevB.92.205117
35. Zhang Y, Yi M, Liu ZK, Li W, Lee JJ, Moore RG, et al. Distinctive Orbital Anisotropy Observed in the Nematic State of a FeSe Thin Film. Phys Rev B (2016) 94:115153. doi:10.1103/PhysRevB.94.115153
36. Yi M, Pfau H, Zhang Y, He Y, Wu H, Chen T, et al. Nematic Energy Scale and the Missing Electron Pocket in FeSe. Phys Rev X (2019) 9:041049. doi:10.1103/PhysRevX.9.041049
37. Xing RQ, Classen L, Chubukov AV. Orbital Order in FeSe: The Case for Vertex Renormalization. Phys Rev B (2018) 98:041108(R). doi:10.1103/PhysRevB.98.041108
38. Chubukov AV, Khodas M, Fernandes RM. Magnetism, Superconductivity, and Spontaneous Orbital Order in Iron-Based Superconductors: Which Comes First and Why? Phys Rev X (2016) 6:041045. doi:10.1103/PhysRevX.6.041045
39. Kawaguchi K, Yamakawa Y, Tsuchiizu M, Kontani H. Competing Unconventional Charge-Density-Wave States in Cuprate Superconductors: Spin-Fluctuation-Driven Mechanism. J Phys Soc Jpn (2017) 86:063707. doi:10.7566/jpsj.86.063707
40. Yamakawa Y, Kontani H. Spin-Fluctuation-Driven Nematic Charge-Density Wave in Cuprate Superconductors: Impact of Aslamazov-Larkin Vertex Corrections. Phys Rev Lett (2015) 114:257001. doi:10.1103/PhysRevLett.114.257001
41. Tsuchiizu M, Kawaguchi K, Yamakawa Y, Kontani H. Multistage Electronic Nematic Transitions in Cuprate Superconductors: A Functional-Renormalization-Group Analysis. Phys Rev B (2018) 97:165131. doi:10.1103/physrevb.97.165131
42. Onari S, Kontani H. SU(4) Valley+Spin Fluctuation Interference Mechanism for Nematic Order in Magic-Angle Twisted Bilayer Graphene: The Impact of Vertex Corrections. Phys Rev Lett (2022) 128:066401. doi:10.1103/PhysRevLett.128.066401
43. Hirata T, Yamakawa Y, Onari S, Kontani H. Unconventional Orbital Charge Density Wave Mechanism in the Transition Metal Dichalcogenide 1T−TaS2. Phys Rev Res (2021) 3:L032053. doi:10.1103/physrevresearch.3.l032053
44. Tazai R, Yamakawa Y, Onari S, Kontani H. Mechanism of Exotic Density-Wave and Beyond-Migdal Unconventional Superconductivity in Kagome Metal AV 3 Sb 5 (A = K, Rb, Cs). Sci Adv (2022) 8:eabl4108. doi:10.1126/sciadv.abl4108
45. Licciardello S, Buhot J, Lu J, Ayres J, Kasahara S, Matsuda Y, et al. Electrical Resistivity across a Nematic Quantum Critical point. Nature (2019) 567:213–7. doi:10.1038/s41586-019-0923-y
46. Coldea AI, Blake SF, Kasahara S, Haghighirad AA, Watson MD, Knafo W, et al. Evolution of the Low-Temperature Fermi Surface of Superconducting FeSe1−xSx across a Nematic Phase Transition. Npj Quant Mater (2019) 4:2. doi:10.1038/s41535-018-0141-0
47. Huang WK, Hosoi S, Čulo M, Kasahara S, Sato Y, Matsuura K, et al. Magnetization Switching Driven by Current-Induced Torque from Weakly Spin-Orbit Coupled Zr. Phys Rev Res (2020) 2:033367. doi:10.1103/PhysRevResearch.2.033367
48. Huang WK, Hosoi S, Čulo M, Kasahara S, Sato Y, Matsuura K, et al. Non-Fermi Liquid Transport in the Vicinity of the Nematic Quantum Critical point of Superconducting FeSe1−xSx. Phys Rev Res (2020) 2:033367. doi:10.1103/PhysRevResearch.2.033367
49. Mukasa K, Matsuura K, Qiu M, Saito M, Sugimura Y, Ishida K, et al. High-pressure Phase Diagrams of FeSe1−xTex: Correlation between Suppressed Nematicity and Enhanced Superconductivity. Nat Commun (2021) 12:381. doi:10.1038/s41467-020-20621-2
50. Mukasa K, Ishida K, Imajo S, Qiu MW, Saito M, Matsuura K, et al. Enhanced Superconducting Pairing Strength Near a Nonmagnetic Nematic Quantum Critical point. ArXiv (2022) 2202:11657. doi:10.48550/arXiv.2202.11657
51. Ishida K, Onishi Y, Tsujii M, Mukasa K, Qiu M, Saito M, et al. Pure Nematic Quantum Critical point Accompanied by a Superconducting Dome. ArXiv (2022) 2202:11674. doi:10.1073/pnas.2110501119
52. Kasahara S, Shi HJ, Hashimoto K, Tonegawa S, Mizukami Y, Shibauchi T, et al. Electronic Nematicity above the Structural and Superconducting Transition in BaFe2(As1−xP X )2. Nature (2012) 486:382–5. doi:10.1038/nature11178
53. Kim YK, Jung WS, Han GR, Choi KY, Chen CC, Devereaux TP, et al. Existence of Orbital Order and its Fluctuation in SuperconductingBa(Fe1−xCox)2As2Single Crystals Revealed by X-ray Absorption Spectroscopy. Phys Rev Lett (2013) 111:217001. doi:10.1103/physrevlett.111.217001
54. Thewalt E, Hayes IM, Hinton JP, Little A, Patankar S, Wu L, et al. Imaging Anomalous Nematic Order and Strain in Optimally Doped BaFe2(As,P)2. Phys Rev Lett (2018) 121:027001. doi:10.1103/physrevlett.121.027001
55. Shimojima T, Motoyui Y, Taniuchi T, Bareille C, Onari S, Kontani H, et al. Discovery of Mesoscopic Nematicity Wave in Iron-Based Superconductors. Science (2021) 373:1122–5. doi:10.1126/science.abd6701
56. Chu JH, Analytis JG, De Greve K, McMahon PL, Islam Z, Yamamoto Y, et al. In-Plane Resistivity Anisotropy in an Underdoped Iron Arsenide Superconductor. Science (2010) 329:824–6. doi:10.1126/science.1190482
57. Ren X, Duan L, Hu Y, Li J, Zhang R, Luo H, et al. Nematic Crossover inBaFe2As2under Uniaxial Stress. Phys Rev Lett (2015) 115:197002. doi:10.1103/PhysRevLett.115.197002
58. Man H, Zhang R, Park JT, Lu X, Kulda J, Ivanov A, et al. Direct Observation of Spin Excitation Anisotropy in the Paramagnetic Orthorhombic State of BaFe2−xNixAs2. Phys Rev B (2018) 97:060507(R). doi:10.1103/PhysRevB.97.060507
59. Wiecki P, Zhou R, Julien MH, Böhmer AE, Schmalian J. Edwards-Anderson Parameter and Local Ising Nematicity in FeSe Revealed via NMR Spectral Broadening. Phys Rev B (2021) 104:125134. doi:10.1103/PhysRevB.104.125134
60. Lahiri A, Klein A, Fernandes RM. Defect-induced Electronic Smectic State at the Surface of Nematic Materials. ArXiv (2021) 2111:00541. doi:10.48550/arXiv.2111.00541
61. Li J, Zhao D, Wu YP, Li SJ, Song DW, Zheng LX, et al. Reemergeing Electronic Nematicity in Heavily Hole-Doped Fe-Based Superconductors. ArXiv (2021) 1611:04694. doi:10.48550/arXiv.1611.04694
62. Liu X, Tao R, Ren M, Chen W, Yao Q, Wolf T, et al. Evidence of Nematic Order and Nodal Superconducting gap along [110] Direction in RbFe2As2. Nat Commun (2019) 10:1039. doi:10.1038/s41467-019-08962-z
63. Moroni M, Prando G, Aswartham S, Morozov I, Bukowski Z, Büchner B, et al. Charge and Nematic Orders in AFe2As2(A=Rb,Cs) Superconductors. Phys Rev B (2019) 99:235147. doi:10.1103/physrevb.99.235147
64. Ishida K, Tsujii M, Hosoi S, Mizukami Y, Ishida S, Iyo A, et al. Novel Electronic Nematicity in Heavily Hole-Doped Iron Pnictide Superconductors. Proc Natl Acad Sci U.S.A (2020) 117:6424–9. doi:10.1073/pnas.1909172117
65. Wiecki P, Haghighirad AA, Weber F, Merz M, Heid R, Böhmer AE. Dominant In-Plane Symmetric Elastoresistance in CsFe2As2. Phys Rev Lett (2020) 125:187001. doi:10.1103/PhysRevLett.125.187001
66. Wiecki P, Frachet M, Haghighirad AA, Wolf T, Meingast C, Heid R, et al. Emerging Symmetric Strain Response and Weakening Nematic Fluctuations in Strongly Hole-Doped Iron-Based Superconductors. Nat Commun (2021) 12:4824. doi:10.1038/s41467-021-25121-5
67. Borisov V, Fernandes RM, Valentí R. Evolution from B2g Nematics to B1g Nematics in Heavily Hole-Doped Iron-Based Superconductors. Phys Rev Lett (2019) 123:146402. doi:10.1103/PhysRevLett.123.146402
68. Wu YP, Zhao D, Wang AF, Wang NZ, Xiang ZJ, Luo XG, et al. Emergent Kondo Lattice Behavior in Iron-Based SuperconductorsAFe2As2(A=K, Rb, Cs). Phys Rev Lett (2016) 116:147001. doi:10.1103/PhysRevLett.116.147001
69. Civardi E, Moroni M, Babij M, Bukowski Z, Carretta P. Superconductivity Emerging from an Electronic Phase Separation in the Charge Ordered Phase of RbFe2As2. Phys Rev Lett (2016) 117:217001. doi:10.1103/PhysRevLett.117.217001
70. Baym G, Kadanoff LP. Conservation Laws and Correlation Functions. Phys Rev (1961) 124:287–99. doi:10.1103/physrev.124.287
71. Allen S, Tremblay AMS, Vilk YM. Theoretical Methods for Strongly Correlated Electrons. New-York: Springer-Verlag (2004).
72. Blaha P, Schwarz K, Tran F, Laskowski R, Madsen GKH, Marks LD. WIEN2k: An APW+lo Program for Calculating the Properties of Solids. J Chem Phys (2020) 152:074101. doi:10.1063/1.5143061
73. Mostofi AA, Yates JR, Pizzi G, Lee YS, Souza I, Vanderbilt D, et al. An Updated Version of Wannier90: A Tool for Obtaining Maximally-Localised Wannier Functions. Comput Phys Commun (2014) 185:2309–10. doi:10.1016/j.cpc.2014.05.003
74. Miyake T, Nakamura K, Arita R, Imada M. Comparison of Ab Initio Low-Energy Models for LaFePO, LaFeAsO, BaFe2As2, LiFeAs, FeSe, and FeTe: Electron Correlation and Covalency. J Phys Soc Jpn (2010) 79:044705. doi:10.1143/JPSJ.79.044705
75. Bickers NE, White SR. Conserving Approximations for Strongly Fluctuating Electron Systems. II. Numerical Results and Parquet Extension. Phys Rev B (1911) 43:8044–64. doi:10.1103/PhysRevB.43.8044
76. Kontani H, Yamakawa Y, Tazai R, Onari S. Odd-parity Spin-Loop-Current Order Mediated by Transverse Spin Fluctuations in Cuprates and Related Electron Systems. Phys Rev Res (2021) 3:013127. doi:10.1103/PhysRevResearch.3.013127
77. Nakayama K, Tsubono R, Phan GN, Nabeshima F, Shikama N, Ishikawa T, et al. Orbital Mixing at the Onset of High-Temperature Superconductivity in FeSe1−xTex/CaF2. Phys Rev Res (2021) 3:L012007. doi:10.1103/PhysRevResearch.3.L012007
78. Zhang P, Wang Z, Wu X, Yaji K, Ishida Y, Kohama Y, et al. Multiple Topological States in Iron-Based Superconductors. Nat Phys (2019) 15:41–7. doi:10.1038/s41567-018-0280-z
79. Wang Z, Zhang P, Xu G, Zeng LK, Miao H, Xu X, et al. Topological Nature of theFeSe0.5Te0.5superconductor. Phys Rev B (2015) 92:115119. doi:10.1103/PhysRevB.92.115119
80. Lohani H, Hazra T, Ribak A, Nitzav Y, Fu H, Yan B, et al. Band Inversion and Topology of the Bulk Electronic Structure in FeSe0.45Te0.55. Phys Rev B (2020) 101:245146. doi:10.1103/PhysRevB.101.245146
81. Yin ZP, Haule K, Kotliar G. Kinetic Frustration and the Nature of the Magnetic and Paramagnetic States in Iron Pnictides and Iron Chalcogenides. Nat Mater (2011) 10:932–5. doi:10.1038/nmat3120
82. Yamasaki A, Matsui Y, Imada S, Takase K, Azuma H, Muro T, et al. Electron Correlation in the FeSe Superconductor Studied by Bulk-Sensitive Photoemission Spectroscopy. Phys Rev B (2010) 82:184511. doi:10.1103/PhysRevB.82.184511
83. Watson MD, Haghighirad AA, Rhodes LC, Hoesch M, Kim TK. Electronic Anisotropies Revealed by Detwinned Angle-Resolved Photo-Emission Spectroscopy Measurements of Fese. New J Phys (2017) 19:103021. doi:10.1088/1367-2630/aa8a04
84. Yi M, Pfau H, Zhang Y, He Y, Wu H, Chen T, et al. Nematic Energy Scale and the Missing Electron Pocket in FeSe. Phys Rev X (2019) 9:041049. doi:10.1103/PhysRevX.9.041049
85. Huh SS, Seo JJ, Kim BS, Cho SH, Jung JK, Kim S, et al. Absence of Y-Pocket in 1-Fe Brillouin Zone and Reversed Orbital Occupation Imbalance in FeSe. Commun Phys (2020) 3:52. doi:10.1038/s42005-020-0319-1
86. Rhodes LC, Boker J, Muller MA, Eschrig M, Eremin IM. Non-local Dxy Nematicity and the Missing Electron Pocket in FeSe. npj Quan Mater (2021) 6:45. doi:10.1038/s41535-021-00341-6
87. Tazai R, Matsubara S, Yamakawa Y, Onari S, Kontani H. A Rigorous Formalism of Unconventional Symmetry Breaking in Fermi Liquid Theory and its Application to Nematicity in FeSe. ArXiv (2022) 2205:02280. doi:10.48550/arXiv.2205.02280
88. Moon SJ, Schafgans AA, Kasahara S, Shibauchi T, Terashima T, Matsuda Y, et al. Infrared Measurement of the Pseudogap of P-Doped and Co-doped High-TemperatureBaFe2As2Superconductors. Phys Rev Lett (2012) 109:027006. doi:10.1103/PhysRevLett.109.027006
89. Shimojima T, Sonobe T, Malaeb W, Shinada K, Chainani A, Shin S, et al. Pseudogap Formation above the Superconducting Dome in Iron Pnictides. Phys Rev B (2014) 89:045101. doi:10.1103/PhysRevB.89.045101
90. Shimojima T, Malaeb W, Nakamura A, Kondo T, Kihou K, Lee CH, et al. Antiferroic Electronic Structure in the Nonmagnetic Superconducting State of the Iron-Based Superconductors. Sci Adv (2017) 3:e1700466. doi:10.1126/sciadv.1700466
91. Yi M, Lu D, Chu JH, Analytis JG, Sorini AP, Kemper AF, et al. Symmetry-breaking Orbital Anisotropy Observed for Detwinned Ba(Fe 1- X Co X ) 2 as 2 above the Spin Density Wave Transition. Proc Natl Acad Sci U.S.A (2011) 108:6878–83. doi:10.1073/pnas.1015572108
92. Zhou R, Xing LY, Wang XC, Jin CQ, Zheng GQ. Orbital Order and Spin Nematicity in the Tetragonal Phase of the Electron-Doped Iron pnictidesNaFe1−xCoxAs. Phys Rev B (2016) 93:060502(R). doi:10.1103/PhysRevB.93.060502
93. Mizukami Y, Tanaka O, Ishida K, Tsujii M, Mitsui T, Kitao S, et al. Thermodynamic Signatures of Diagonal Nematicity in RbFe2As2 Superconductor. ArXiv (2021) 2108:13081. doi:10.48550/arXiv.2108.13081
Keywords: nematic order, smectic order, orbital order, bond order, quantum critical point, iron-based superconductors
Citation: Onari S and Kontani H (2022) Diverse Exotic Orders and Fermiology in Fe-Based Superconductors: A Unified Mechanism for B1g/B2g Nematicity in FeSe/(Cs,Rb)Fe2As2 and Smectic Order in BaFe2As2. Front. Phys. 10:915619. doi: 10.3389/fphy.2022.915619
Received: 08 April 2022; Accepted: 14 June 2022;
Published: 19 July 2022.
Edited by:
Laura Fanfarillo, International School for Advanced Studies (SISSA), ItalyReviewed by:
Avraham Klein, Ariel University, IsraelCopyright © 2022 Onari and Kontani. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Seiichiro Onari, b25hcmlAcy5waHlzLm5hZ295YS11LmFjLmpw
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.