
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 27 May 2022
Sec. Interdisciplinary Physics
Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.912229
This article is part of the Research Topic Advances in Memristor and Memristor-Based Applications View all 14 articles
In this paper, we rebuild a new meminductive chaotic circuit model based on a Wien-bridge oscillator. Due to the extreme multistability of the meminductive system, it can produce the phenomenon of many infinitely coexisting attractors. Systems that spontaneously produce coexisting oscillations are relatively rare in the study of meminductive circuit systems and are well suited as pseudo-random number generators (PRNG). In this study, a new weak signal detection model is established based on the proposed meminductive system. This detection model can detect boosting weak signals with different amplitudes. The trajectory of objects can be predicted effectively by the boosting line spectrum in the frequency domain. The experimental result shows the feasibility through which the meminductive multistable system is applied in the detection field.
Memristor, a nonlinear memory resistor, has been used extensively in recent studies. The concept of memristor first appeared in a paper by Chua [1]. Based on the relationship between electrical physical quantities, Chua outlines that there must be a set of relationships between the charge and the flux. In subsequent studies, Chua’s team defined the resistance-like relationship between them as memristor. Until 2008, according to the conceptual model of memristor, HP laboratory manufactured the first nanoscale memristor using TiO2 material [2]. It also confirms the correctness of Chua’s prediction. After further scientific certification, some researchers found that the volt-ampere characteristic curve of the memristor is a hysteresis loop due to its nonlinear characteristic [3–8]. Unlike normal volatile resistors, memristors are efficient at retaining energy, i.e. memristor is a component with a memory function. The memory properties of the memristor are a good match for the resistive components that will be used to build future artificial brains, for which it made headlines in scientific journals [9, 10]. Then, the Ventra team proposed the concept of meminductor [11], which adds better memory features to conventional storage devices.
Research on memristive circuit systems has made great progress, with continuous breakthroughs in memristive hardware [12–15]. The memristor oscillation circuit based on Chua’s circuit model has become a hotspot of nonlinear system research. Due to the more nonlinear parts of the memristor, it can often produce complex dynamic behavior and higher sequence complexity. Thus, the memristive dynamical system is widely used in the related fields of physics [16–19], computer science [20–24], and cryptography [25–28]. Ye et al constructed a memristive circuit model based on Wen’s bridge oscillating circuit. By replacing a memristor of the original 4D Wen’s bridge oscillator, the new circuit equations with a memristor have more nonlinear terms. Based on this, the dynamic behavior of the memristive circuit system becomes more complex, and there is even multi-attractor coexistence. There is even a phenomenon of multi-attractor coexistence [29]. Bao et al proposed an inductor-free memristive circuit using linear coupling of a BPF and found many coexisting infinite attractors by using numerical simulation [30]. There is a large amount of research on memristors in the existing literature. However, there are relatively few studies on meminductor, especially on the meminductive multi-stable system. Thus, it is very important to further explore complex dynamic behavior and the application of a memory-sensing system.
In this article, we focus on a novel meminductive chaotic system of extremely multistability and its application in signal detection. The article is organized as follows: in section 2, the meminductive equivalent circuit model is proposed. In section 3, the meminductive chaotic system model is built. In section 4, the proposed meminductive system is applied to weak signal detection. Finally, the chaotic attractors of the meminductive system are implemented by circuit experiment.
Based on the i-φ characteristics of meminductor, we have
in the formula above, i(t) and φ(t) are the current and magnetic flux flowing through the meminductor, and M(μ) reflects the inductive resistance of the meminductor. Then, we get
Based on Eqs 1, 2, the mathematical model of meminductor can be designed as
in which, aμ and bμ are the positive real numbers, and then we have
Based on the mathematical model of the meminductor above, the equivalent circuit model of the meminductor can be designed as shown in Figure 1. According to the relationships of all components reflected in Figure 1, we can achieve the i-φ characteristic of the meminductor:
According to Eqs 4, 5, aμ = R9/R8 and bμ = R9/R7. Set the component parameters in Figure 1 R1 = R3 = R4 = 200kΩ, R5 = R6 = R8 = R9 = 10kΩ, R2 = 1MΩ, R7 = 3kΩ, and C1 = C2 = 10nF. By using the circuit simulation software, as shown in Figure 2, we can get the v-i hysteresis loop under different frequencies.
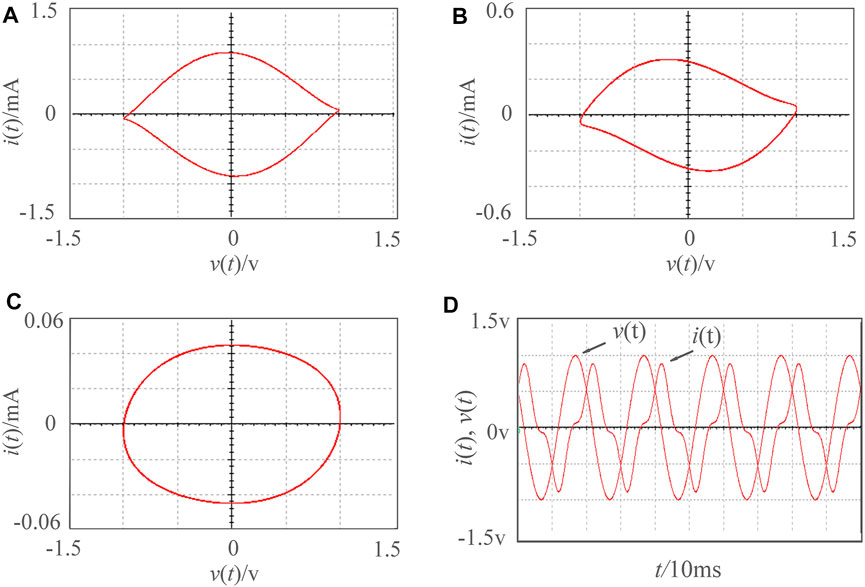
FIGURE 2. The v-i hysteresis loop of a meminductive equivalent circuit under different frequencies. (A) f = 50 Hz. (B) f = 70 Hz. (C) f = 180 Hz. (D) waveform of f = 50 Hz.
By building an RLC oscillation structure based on a Wien-bridge oscillator, a novel meminductive circuit model can be rebuilt. As reflected in Figure 3, the new meminductive circuit model has four resistors R1∼R4, three capacitors, one operational amplifier, two diodes, and one meminductor.
Based on the circuit model reflected in Figure 7, we can obtain the circuit equations
in Eq. 6, the equations of the diodes can be expressed as
in which, Ue shows the threshold voltage, ge is the conductance. Then, let u1 = Uex, u2 = Uey, u3 = Uez, φ = UeC1(R2R3)1/2v, ρ = UthC12R1R2w, ie = UegeH, t = C1(R1R2)1/2τ, c=(R1/R2)1/2, d = R4/R3, e=(R1R2)1/2ge, C1 = C2 = C3, a = UeC1R1R2a1, b = Ue3C15R13R23b1, L−1(ρ) = a+3bρ2, we have
Finally, we can get an equivalent mathematical model
According to the mathematical equations of the system (9), the dynamical behavior of the proposed system can be analyzed. When the system parameters are a = 40, b = 10, c = 0.6, d = 8, e = 30, the initial condition is (1,1,1,0.1,0.01). We can calculate Lyapunov exponents are Ly1 = 0.4403, Ly2 = 0.0127, Ly3 = 0, Ly4 = -0.4536, Ly5 = -35.18. This indicates the proposed system is a hyperchaotic circuit system.
Due to the initial value sensitivity of chaotic systems, the system model may generate resonance signals with some weak signals. The detection model of the weak signal can be built based on the system (9). In the process of signal detection, the test weak signal is often mixed with the noise signals. In particular, some noise signals have a close frequency to the test weak signal. The detection model can be expressed as
where K1 is the amplitude of the test weak signal, w1 is its angular frequency. K2 is the amplitude of the noise signal, w2 is its angular frequency, and is its initial phase. The newly constructed detection model (10) inherits the extremely multiple stability from the meminductive system (9). Let system parameter a = 40, b = 10, c = 0.6, d = 8, e = 30, C1 = 1, C2 = 2, w1 = 1, w2 = 2, φ = 0, and the initial conditions is (1,1,1,w(0),0.01). As shown in Figure 4, when w(0) = -0.1, 0.2, 0.5, 0.7, and 0.9 respectively, the detection model can produce infinite coexisting attractors. Figure 5 shows the boosting signals with different amplitudes when w(0) = 0.1, 0.2, 0.3, 0.4, 0.5 respectively.
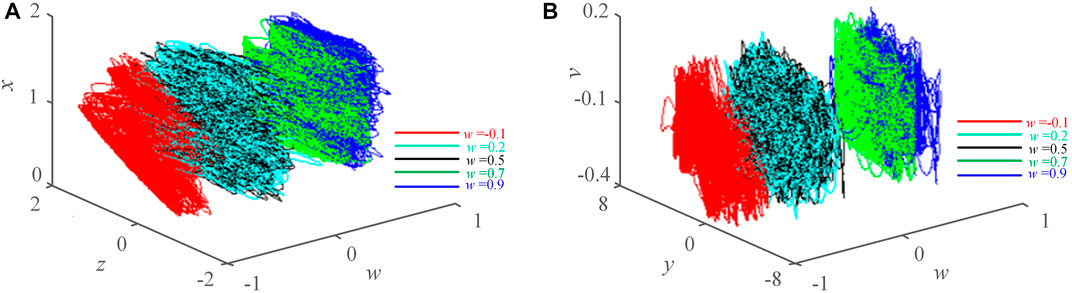
FIGURE 4. Infinitely coexisting attractors generated by the system (10). (A) x-z-w plane. (B) v-y-w plane.
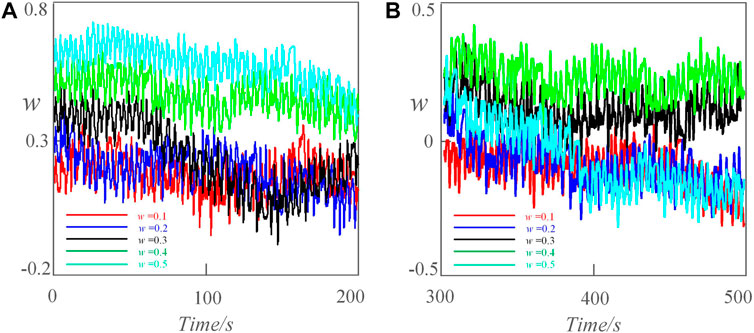
FIGURE 5. The boosting chaos signals of the time domain. (A) The boost signals on w direction at 0–200 s. (B) The boost signals on w direction at 300–500 s.
In the weak signal detection field, to understand the trajectory of the object producing the weak signal, the line spectrum in the frequency domain is often extracted. Keeping other parameters unchanged, let the initial value w = 0.1, 0.5, 1, 1.5, and 2 respectively, the line spectrum of the test signal in the frequency domain is reflected in Figure 6. As the initial condition w increases constantly, the corresponding amplitude of the sequence is boosting constantly, and the boosting signal can be detected within the frequency range 0–1 Hz. Due to the proposed meminductive system being extremely multistable, the useful signal can be detected within different amplitudes. Even if a detector in the amplitude range fails, the weak signals can also be detected in other amplitude ranges, which increases the fault tolerance of the detection process. These boosting signals show more useful information about the running object. Based on this key information, the trajectory of the object can be predicted.
Doing the circuit implementation to the system (9). Based on Eqs 8, 9, we have
in which,
Set t = KT, x = MX, y = MY, z = MZ, w = MW, v = MV, and set scale transformation factors M = 2 and K = 100, and we have
where,
In combination with the formula above, the equivalent circuit model of the system (9) can be designed as shown in Figure 7. Based on the equivalent circuit, as shown in Figure 8, the chaotic attractors can be implemented by multisim 14.0. The specific component parameters are shown in Table 1.
This proposes a new meminductive chaotic system of extreme multistability. Due to the constant shift of equilibrium with different initial values, the proposed meminductive chaotic system can generate many infinitely coexisting attractors. By introducing the model of weak signal and noise to the meminductive chaotic system, a new weak signal detection model is established. Because this detection model inherits the extreme multistability of the original meminductive system, it can detect boosting signals of different amplitudes at the same time. The spectral line in the frequency domain can effectively reflect the motion trajectory of the object generating a weak signal. Next, we will try to apply the proposed meminductive system to other related areas.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
BK: Conceptualization; Methodology; Data curation; Supervision; Investigation; Project administration; Writing—original draft; Writing—review and editing. WQ: Funding acquisition; Investigation; Project administration; Resources; Validation.
This work was supported by the National Natural Science Foundation of China (No: 12171004, 12026233, and 12026221).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Chua L. Memristor-The Missing Circuit Element. IEEE Trans Circuit Theor (1971) 18:507–19. doi:10.1109/tct.1971.1083337
3. Ma X, Li C, Wang R, Jiang Y, Leiet T. Memristive Computation-Oriented Chaos and Dynamics Control. Front Phys (2021) 27. doi:10.3389/fphy.2021.759913
4. Wu X, Wang H, He S. Localization of Hidden Attractors in Chua’s System with Absolute Nonlinearity and its FPGA Implementation. Front Phys (2021) 06. doi:10.3389/fphy.2021.788329
5. Wang N, Zhang G, Kuznetsov NV, Bao H. Hidden Attractors and Multistability in a Modified Chua's Circuit. Commun Nonlinear Sci Numer Simulation (2021) 92:105494. doi:10.1016/j.cnsns.2020.105494
6. Wang N, Li C, Bao H, Chen M, Bao B. Generating Multi-Scroll Chua's Attractors via Simplified Piecewise-Linear Chua's Diode. IEEE Trans Circuits Syst (2019) 66:4767–79. doi:10.1109/tcsi.2019.2933365
7. Wang N, Zhang G, Bao H. Bursting Oscillations and Coexisting Attractors in a Simple Memristor-Capacitor-Based Chaotic Circuit. Nonlinear Dyn (2019) 97:1477–94. doi:10.1007/s11071-019-05067-6
8. Wang N, Zhang G, Bao H. A Simple Autonomous Chaotic Circuit with Dead-Zone Nonlinearity. IEEE Trans Circuits Syst Express Briefs (2020) 67:3052–6. doi:10.1109/tcsii.2020.3005726
9. Li C, Li H, Xie W, Du J. A S-type Bistable Locally Active Memristor Model and its Analog Implementation in an Oscillator Circuit. Nonlinear Dyn (2021) 106:1041–58. doi:10.1007/s11071-021-06814-4
10. Li C, Yang Y, Yang X, Zi X, Xiao F. A Tristable Locally Active Memristor and its Application in Hopfield Neural Network. Nonlinear Dyn (2022) 108:1697–717. doi:10.1007/s11071-022-07268-y
11. Di Ventra M, Pershin YV, Chua LO. Circuit Elements with Memory: Memristors, Memcapacitors, and Meminductors. Proc IEEE (2009) 97:1717–24. doi:10.1109/jproc.2009.2021077
12. Ma X, Mou J, Liu J, Ma C, Yang F, Zhao X. A Novel Simple Chaotic Circuit Based on Memristor-Memcapacitor. Nonlinear Dyn (2020) 100:2859–76. doi:10.1007/s11071-020-05601-x
13. Ye X, Wang X, Gao S, Mou J, Wang Z, Yang F. A New Chaotic Circuit with Multiple Memristors and its Application in Image Encryption. Nonlinear Dyn (2020) 99:1489–506. doi:10.1007/s11071-019-05370-2
14. Ye X, Mou J, Luo C, Wang Z. Dynamics Analysis of Wien-Bridge Hyperchaotic Memristive Circuit System. Nonlinear Dyn (2018) 92:923–33. doi:10.1007/s11071-018-4100-x
15. Xiong L, Yang F, Mou J, An X, Zhang X. A Memristive System and its Applications in Red–Blue 3D Glasses and Image Encryption Algorithm with DNA Variation. Nonlinear Dyn (2022) 107:1–23. doi:10.1007/s11071-021-07131-6
16. Xiong L, Zhang X, Teng S, Qi L, Zhang P. Detecting Weak Signals by Using Memristor-Involved Chua's Circuit and Verification in Experimental Platform. Int J Bifurcation Chaos (2020) 30:2050193. doi:10.1142/s021812742050193x
17. Ye X, Wang X. Characteristic Analysis of A Simple Fractional-Order Chaotic System with Infinitely Many Coexisting Attractors and its DSP Implementation. Phys Scr (2020) 95:075212. doi:10.1088/1402-4896/ab8eec
18. Liu B, Ye X, Hu G. Design of a New 3D Chaotic System Producing Infinitely Many Coexisting Attractors and its Application to Weak Signal Detection. Int J Bifurcation Chaos (2021) 31:2150235. doi:10.1142/s0218127421502357
19. Xu S, Wang X, Ye X. A New Fractional-Order Chaos System of Hopfield Neural Network and its Application in Image Encryption”, ChaosA New Fractional-Order Chaos System of Hopfield Neural Network and its Application in Image Encryption. Solitons & FractalsChaos, Solitons & Fractals (2022) 157:111889. doi:10.1016/j.chaos.2022.111889
20. Zhou Y, Li C, Li W, Li H, Feng W, Qian K. Image Encryption Algorithm with circle index Table Scrambling and Partition Diffusion. Nonlinear Dyn (2021) 103:2043–61. doi:10.1007/s11071-021-06206-8
21. Li C-L, Zhou Y, Li H-M, Feng W, Du J-R. Image Encryption Scheme with Bit-Level Scrambling and Multiplication Diffusion. Multimed Tools Appl (2021) 80:18479–501. doi:10.1007/s11042-021-10631-7
22. Li X, Mou J, Banerjee S, Cao Y. An Optical Image Encryption Algorithm Based on Fractional-Order Laser Hyperchaotic System. Int J Bifurcation Chaos (2022) 32:2250035. doi:10.1142/s0218127422500353
23. Gao X, Mou J, Xiong L, Sha Y, Yan H, Cao Y. A Fast and Efficient Multiple Images Encryption Based on Single-Channel Encryption and Chaotic System. Nonlinear Dyn (2022) 108:613–36. doi:10.1007/s11071-021-07192-7
24. Gao X, Mou J, Banerjee S, Cao Y, Xiong L, Chen X. An Effective Multiple-Image Encryption Algorithm Based on 3D Cube and Hyperchaotic Map. J King Saud Univ - Comp Inf Sci (2022) 34:1535–51. doi:10.1016/j.jksuci.2022.01.017
25. Wang X, Wang X, Ma B, Li Q, Shi Y-Q. High Precision Error Prediction Algorithm Based on ridge Regression Predictor for Reversible Data Hiding. IEEE Signal Process Lett (2021) 28:1125–9. doi:10.1109/lsp.2021.3080181
26. Ma B, Shi YQ. A Reversible Data Hiding Scheme Based on Code Division Multiplexing. IEEE Trans.Inform.Forensic Secur. (2016) 11:1914–27. doi:10.1109/tifs.2016.2566261
27. Li Q, Wang X, Ma B, Wang X, Wang C, Gao S, et al. Concealed Attack for Robust Watermarking Based on Generative Model and Perceptual Loss. IEEE Trans Circuits Syst Video Technol (2021) 1. doi:10.1109/TCSVT.2021.3138795
28. Wang C, Ma B, Xia Z, Li J, Li Q, Shi Y-Q. Stereoscopic Image Description with Trinion Fractional-Order Continuous Orthogonal Moments. IEEE Trans Circuits Syst Video Technol (2022) 32:1998–2012. doi:10.1109/TCSVT.2021.3094882
29. Ye X, Wang X, Zhao H, Gao H, Zhang M. Extreme Multistability in a New Hyperchaotic Meminductive Circuit and its Circuit Implementation. Eur Phys J Plus (2019) 134:206. doi:10.1140/epjp/i2019-12535-0
Keywords: chaos, extremely multistability, weak signal detection, meminductor, equivalent circuit
Citation: Kang B and Qin W (2022) Detecting Boosting Weak Signal via A Meminductive Multistable Chaotic System. Front. Phys. 10:912229. doi: 10.3389/fphy.2022.912229
Received: 04 April 2022; Accepted: 20 April 2022;
Published: 27 May 2022.
Edited by:
Jun Mou, Dalian Polytechnic University, ChinaCopyright © 2022 Kang and Qin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wenjie Qin, d2VuamllcWluQGhvdG1haWwuY29t
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.