Low-Frequency Dual-Band Sound Absorption by Ultrathin Planar Wall Embedded With Multiple-Cavity Resonators

We report the numerical and experimental realization of a type of ultrathin planar wall with low-frequency dual-band sound absorption. The proposed planar wall is constructed by a periodic subwavelength unit cell (with a thickness of λ/19) which consists of two different multiple-cavity resonators embedded into a plate structure with a groove. The sound absorption of the wall exists in two working bands (IandII) below 600 Hz which are created by two different mechanisms. In addition to the band I created by a conventional resonance coupling of the two multiple-cavity resonators, it is worth noting that the band II is realized by a mutual resonance coupling between the resonators and groove structure. The fractional bandwidths of the bands I and II can reach about 34.1 and 10.4%, respectively. Furthermore, the application of the proposed ultrathin planar wall in the design of a barrier-free anechoic room with omnidirectional low-frequency dual-band sound absorption is further discussed in detail. The proposed planar wall has the advantages of ultrathin planar structure and omnidirectional low-frequency dual-band sound absorption, which provides diverse routes to design advanced sound-absorption structures in noise control and architectural acoustics.

Introduction

Low-frequency sound absorption has always been a research hotspot due to its wider applications in several important fields, including noise control, environmental protection, and architectural acoustics. In the recent years, the rapid development of metamaterial [1–10] and metasurface [11–18] structures have provided alternative ways to design advanced acoustic absorbers which effectively overcome the limitation of a relatively large size for conventional low-frequency sound absorbers [19–21].

By designing resonance-type unit cells with a subwavelength size, external sound energy can be absorbed in the unit cell based on different types of mechanisms, and part of energy is dissipated during its propagation inside the unit cell. So far, the previously demonstrated unit cells of sound absorbers mainly include Helmholtz resonators [22–26], Fabry-Perot resonators [27, 28], membrane resonators [29–31], split-ring resonators [32–34], coherent perfect absorbers [35, 36], and metasurface-based absorbers [37–42], and these types of sound absorbers can realize high-performance sound absorption with a subwavelength structure. However, most of these sound absorbers generally work in a single working band, and there still exist some difficulties in designing multiband sound absorbers.

To overcome this, by constructing a type of double-channel Mie resonator backed with a rigid wall [43], a multi-band sound absorber based on multi-order monopolar and dipolar resonances have been proposed. Additionally, a perforated composite Helmholtz-resonator [44] is designed by inserting several plates with a small hole into the interior of a Helmholtz resonator, and a multi-order sound absorption has been realized. Beyond that, other types of absorber structures, such as coiling-up space metasurfaces [45] by two nesting subchannels with a circular hole in series, checkerboard absorbers [46] composed of alternate distributions of inhomogeneous Helmholtz resonators with extended necks, and metaporous composite structures [47] by porous materials with Helmholtz and Fabry–Pérot resonances, can also be applied to the realization of dual- or multi-band sound absorption. In these demonstrated structures, dual- or multi-band sound absorption with high performance are realized. However, most of them are usually designed to be attached outside the wall, which greatly limits the use of space. Therefore, the design of low-frequency ultrathin planar wall with multi-band sound absorption becomes an urgent problem to be solved.

In this work, we propose an ultrathin planar wall with low-frequency dual-band sound absorption which is composed of a periodic unit cell designed by two different multiple-cavity resonators embedded into a plate structure with a groove. The designed wall can realize sound absorption in two working bands (I and II) below 600 Hz based on two different mechanisms. Besides the band I created by a conventional resonance coupling of the two multiple-cavity resonators, we here introduce a mutual resonance coupling between the resonators and groove structure to realize the band II. The fractional bandwidth of both bands can reach about 34.1 and 10.4%. The measured results agree well with the simulated ones. Finally, we simulate the sound absorption of the unit cell created by different incident angles, and discuss the application of the proposed wall in the design of a barrier-free anechoic room with omnidirectional low-frequency dual-band sound absorption in detail.

Design of Model

As schematically shown in Figure 1A, we propose a type of ultrathin planar wall composed of periodic unit cells, and the cross section of a unit cell with the width of D is shown in Figure 1B. We can see that the unit cell consists of two multiple-cavity resonators (denoted as MRs I and II) with the distance of a embedded into a plate structure with a groove. The multiple-cavity resonator is composed of a central circular cavity surrounded by 8 interconnected identical cavities which are separated by 4 channels with the width of w. Here, the thickness of cavity walls, the open width and the radial length of 8 inner cavities, the outer and inner radii of resonators, and the distances between the resonator and the bottom, left and top surfaces of the plate are t, b, d, R, r, l₁, l₂ and l₃, respectively. In addition to the parameters d and r of the MRs I (d₁ and r₁ ) and II (d₂ and r₂ ), the other parameters of both MRs are the same. The unit cell is made of epoxy resin based on the 3D printing technology, and its photograph is shown in Figure 1C. Here, we introduce the software of COMSOL Multiphysics to numerically design sound absorbers. Due to the sound absorption created by the thermoviscous energy loss in the unit cell, the module of Thermoviscous Acoustic-Solid Interaction is used inside the unit cell, and that of Acoustic Pressure module is adopted in the other parts of the model. Beyond that, the surfaces inside the unit cell are set as the thermoviscous acoustic boundary layers, and the thickness of the thermoviscous acoustic boundary layer is $d\upsilon =\sqrt{2\mu /\rho \omega }$ [37], in which the parameters µ, ρ and ω are the coefficient of dynamic viscosity, the density of air, and the angular frequency, respectively. In the simulations, the parameters R, r₁, r₂, d₁, d₂, t, b, w, a, l₁, l₂, l₃ and D are selected as 5.0 cm, 5.0 mm, 7.0 mm, 38.8 mm, 36.8 mm, 1.6 mm, 3.0 mm, 1.0 mm, 4.0 mm, 1.0 mm, 2.0 mm, 3.0 mm, and 31.0 cm, respectively, and the material parameters of air and epoxy resin are shown in Table 1.

FIGURE 1

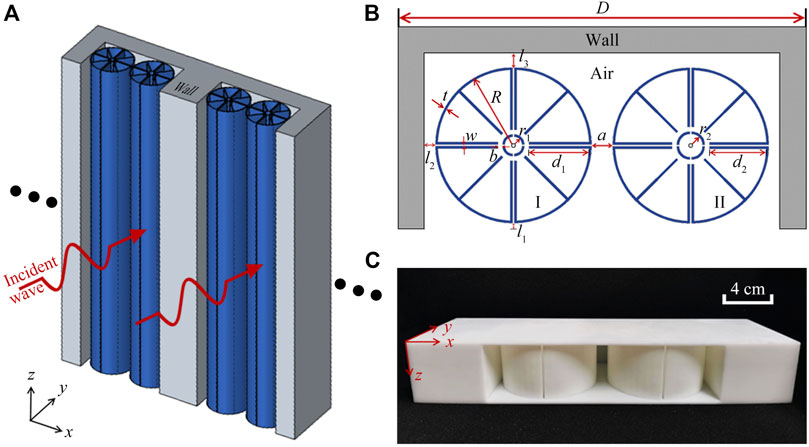
FIGURE 1. (A) Schematic of an ultrathin planar wall with sound absorption, which is composed of periodic unit cells. (B) Cross section of the unit cell, (C) and sample photograph.

TABLE 1

TABLE 1. Material parameters.

Performances and Mechanisms of Low-Frequency Dual-Band Sound Absorption

Here, we conduct an experiment to measure the performance of the design ultrathin planar wall. As shown in Figure 2A, the experiment is carried out in a straight waveguide with a size of 2 × 0.33 × 0.06 m³ which is fabricated with acrylic plates to satisfy the condition of sound hard boundary. The sample of the unit cell is made of epoxy resin by a 3D printing technology, which is placed at the right side of the waveguide. Additionally, a loudspeaker with the size of 4 × 4 cm² driven by a power amplifier is placed at the left side of the waveguide to obtain incident sound signals. Two 0.25-inch microphones (Brüel and Kjær type-4954, marked as Microphones 1 and 2) are inserted into the waveguide from two holes with the same size to experimentally detect sound signals. The measured data is recorded by the module of Brüel and Kjær 3160-A-022, and is analyzed by the software of PULSE Labshop.

FIGURE 2

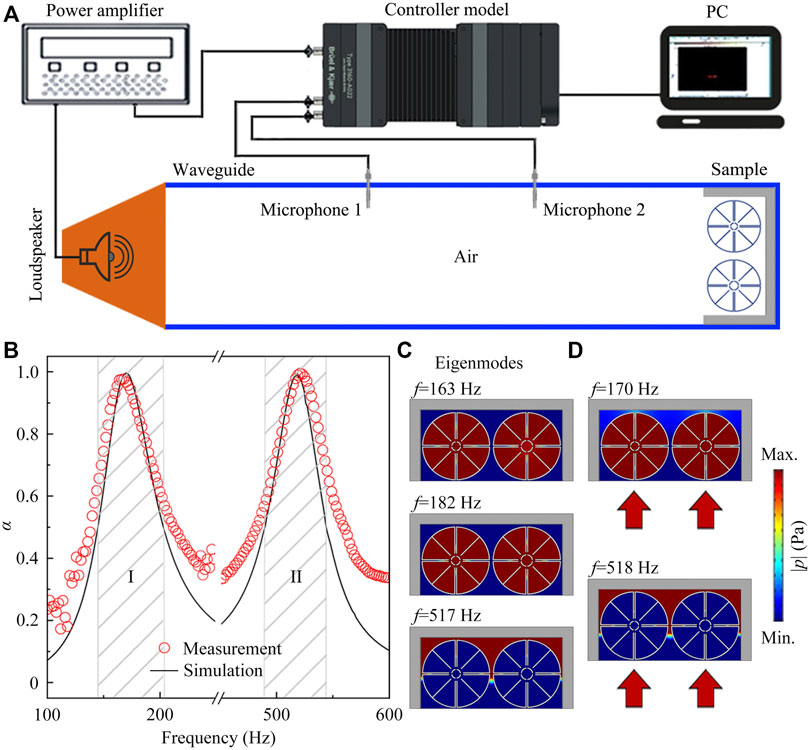
FIGURE 2. (A) Experimental set-up. (B) Measured and simulated sound absorption spectra, and black shaded regions are two working bands of the unit cell (I: 145–203 Hz, II: 490–544 Hz). (C) Simulated pressure amplitude eigenfunctions of the unit cell at 163 Hz, 182 Hz, and 517 Hz. (D) Simulated distributions of pressure amplitude in the unit cell created by a normal incidence of sound (red solid arrows) at 170 and 518 Hz.

Figure 2B shows the measured absorption spectra (red open circles) created by the sample, in which the corresponding simulated ones with the same conditions are also provided for comparison (black solid lines), and the parameters of the sample are the same as those in Figure 1. We can see that, there exist two absorption peaks around 170 and 518 Hz, and their maximum absorption coefficients can reach about 0.99 and 0.98, respectively, showing a typical characteristic of low-frequency dual-band sound absorption. Additionally, in the two black shaded regions (denoted as the bands I and II), the absorption coefficients are larger than 0.5, and thus the corresponding fractional bandwidths (the ratio of the bandwidth to the center frequency) can reach about 34.1 and 10.4%, respectively. The measured and simulated absorption spectra match well with each other. Moreover, the thickness of the unit cell is 104 mm, which is equal to λ/19 (λ is the wavelength), exhibiting a characteristic of ultrathin structure for the proposed wall.

To provide a further insight into its mechanism, we simulate pressure amplitude eigenfunctions of the unit cell around 170 and 518 Hz. As shown in Figure 2C, 3 types of eigenmodes exist at 163 Hz, 182 and 517 Hz. We can see that the distributions of pressure amplitude for the eigenmodes at 163 and 182 Hz are almost the same, and most of sound energy is concentrated into the cavities of the two MRs, showing that both eigenmodes are related to a resonance coupling of both MR structures. However, for the eigenmode at 517 Hz, the sound energy is mainly concentrated into the space between the MRs and groove structure, and little energy exists inside the cavity of both MRs. Thus, this eigenmode is determined by a mutual resonance coupling between the MRs and groove structure, which is different from the eigenmodes at 163 and 182 Hz. Figure 2D shows the pressure amplitude distributions in the unit cell created by the normal incidence of sound at the frequencies of both absorption peaks (170 and 518 Hz). We can see that the sound energy is mainly concentrated into the cavities of both MRs at 170 Hz, in which its distribution of pressure amplitude is the same as that of the eigenmodes at 163 and 182 Hz. It is therefore deduced that the absorption peak in the band I is created by the resonance coupling of both MRs. Additionally, the characteristics of the pressure amplitude distributions at 518 Hz are almost the same as those of the eigenmode at 517 Hz, indicating that the absorption peak in the band II is attributed to the mutual resonance coupling between the resonators and groove structure. Therefore, the observed dual-band sound absorption of the wall arises from two different mechanisms.

Moreover, we discuss the influences of the parameters r₁ and l₃ on the sound absorption of the unit cell in detail (see Supplementary Material), and the results show that the sound absorption in the band II can be modulated by simply adjusting both parameters r₁ and l₃, but that in the band I is only closely related to the parameter r₁, which provides the feasibility of modulating both working bands.

Application of Ultrathin Planar Wall in Barrier-Free Anechoic Room

Figures 3A,B show the simulated sound absorption spectra of the unit cell created by the incident waves with θ = 0°, 45° and 60° in the bands I and II, respectively, in which θ is defined as the angle between the incident direction and the normal line (shown in the inset in Figure 3A). We can see that, with the increase of the angle θ, the frequency of the absorption peak almost remains unchanged in the band I (Figure 3A), and that slightly moves to the high-frequency region in the band II (Figure 3B). Additionally, the absorption coefficients of these peaks are larger than 0.9, showing a high-performance sound absorption of the designed unit cell for different incident angles. Such a phenomenon provides a feasibility for constructing a barrier-free anechoic room.

FIGURE 3

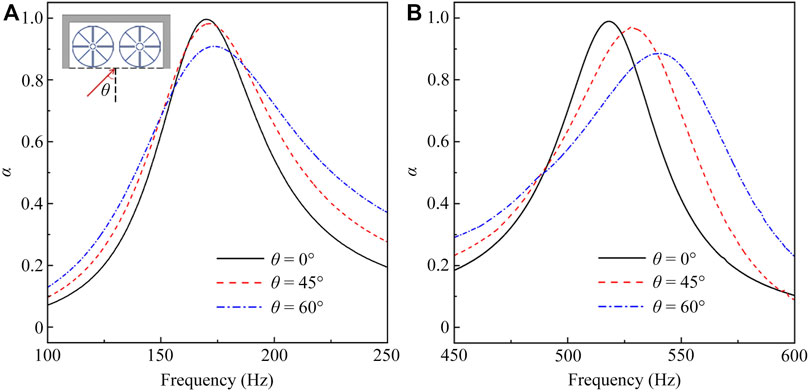
FIGURE 3. Simulated absorption spectra of the unit cell in the bands (A) I and (B) II with the incident angle θ = 0°, 45° and 60°.

Finally, we discuss the application of the designed unit cell in a barrier-free anechoic room. As shown in Figure 4A, the proposed structure of barrier-free anechoic room with the size of 3.41 × 3.41 m² is composed of 40 unit cells, in which the parameters of each unit cell (shown in the inset in Figure 4A) are the same as those in Figure 1B. Moreover, the module of Thermoviscous Acoustic-Solid Interaction is used inside the unit cells, while the module of Acoustic Pressure is adopted in the other parts of the model. Figures 4B,C show the simulated sound absorption spectra created by the barrier-free anechoic room, in which a cylindrical sound source is placed at the center (point O) of the room. We can see that, the absorption coefficients are larger than 0.5 in the black shaded regions around the bands I (149–194 Hz) and II (490–543 Hz). The maximum values of absorption coefficients are 0.98 and 0.96 at 173 and 519 Hz, respectively, and the corresponding fractional bandwidths can reach about 26.0 and 10.2%, showing a typical characteristic of omnidirectional low-frequency dual-band sound absorption.

FIGURE 4

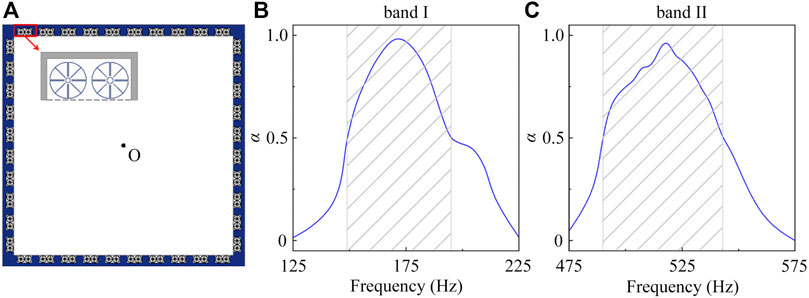
FIGURE 4. (A) Schematic of a barrier-free anechoic room with omnidirectional low-frequency dual-band sound absorption. A cylindrical sound source is located at the point O. Simulated absorption spectra created by the barrier-free anechoic room around the bands (B) I and (C) II. The absorption coefficients are larger than 0.5 in the black shaded regions.

To further present the performance of sound absorption, we also simulate the total pressure distributions and their corresponding reflected sound intensity distributions in the barrier-free anechoic room at 173 and 519 Hz, which are shown in Figures 5A–D. We can see that the total pressure distributions in the barrier-free anechoic room at both frequencies are obviously different from those in the room with hard boundaries (see Supplementary Material), but are similar to those in the free space (see Supplementary Material). Beyond that, the reflected sound intensity distributions created by the anechoic room are very weak, indicating that the sound energy are almost absorbed by the unit cell in all directions of the room, showing a typical characteristic of omnidirectional low-frequency dual-band sound absorption.

FIGURE 5

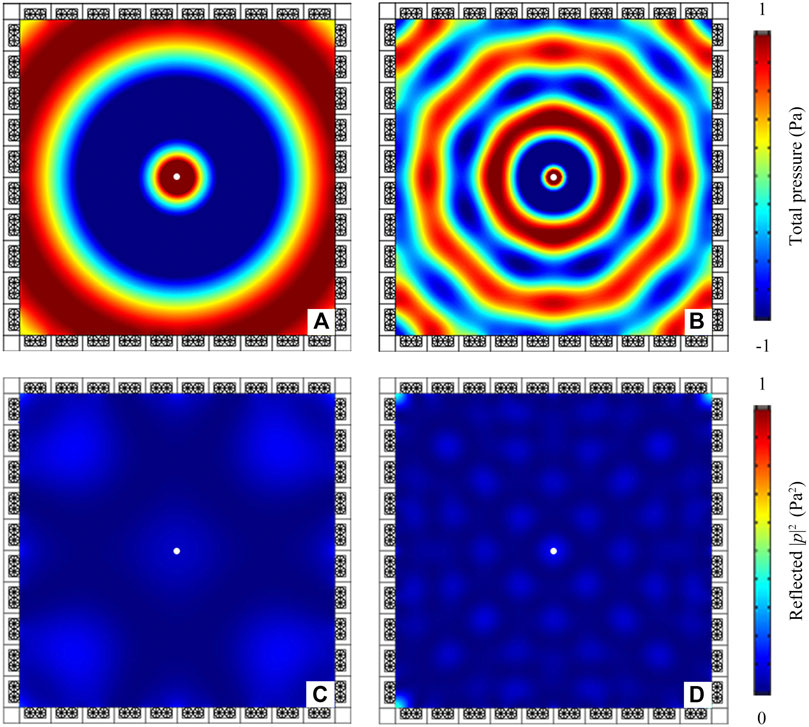
FIGURE 5. Simulated total pressure distributions in the barrier-free anechoic room at (A) 173 Hz and (B) 519 Hz, and its corresponding reflected intensity distributions at (C) 173 Hz and (D) 519 Hz. White points at the center of the room are the positions of cylindrical sound source.

To verify the robustness of the barrier-free anechoic room, we simulate the sound absorption spectra created by the anechoic room with a cylindrical sound source placed at the point O' (shown in Figure 6A), in which all parameters of the anechoic room remain unchanged. As shown in Figures 6B,C, the absorption coefficients are larger than 0.5 around the bands I (156–185 Hz) and II (501–534 Hz), which are shown in the black shaded regions, in which the maximum values of absorption coefficient can reach about 0.97 at 171 Hz and 0.96 at 519 Hz, and the corresponding fractional bandwidths are about 16.9 and 6.3%, respectively, showing high-robustness dual-band sound absorption of the designed room structure.

FIGURE 6

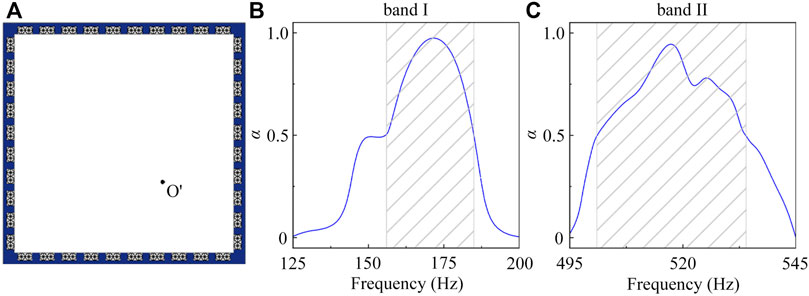
FIGURE 6. (A) Schematic of a barrier-free anechoic room with a cylindrical sound source placed at the point O'. Simulated absorption spectra created by the barrier-free anechoic room around the (B) bands I and (C) II. The absorption coefficients are larger than 0.5 in the black shaded regions.

Figure 7 shows the simulated total pressure distributions and their corresponding reflected sound intensity distributions created by the barrier-free anechoic room at 171 and 519 Hz. We can see that the characteristics of total pressure distributions and corresponding reflected intensity distributions are almost the same as that in Figure 5. Therefore, the proposed ultrathin planar wall with omnidirectional low-frequency dual-band sound absorption shows great potential for applications in architectural acoustics and noise control.

FIGURE 7

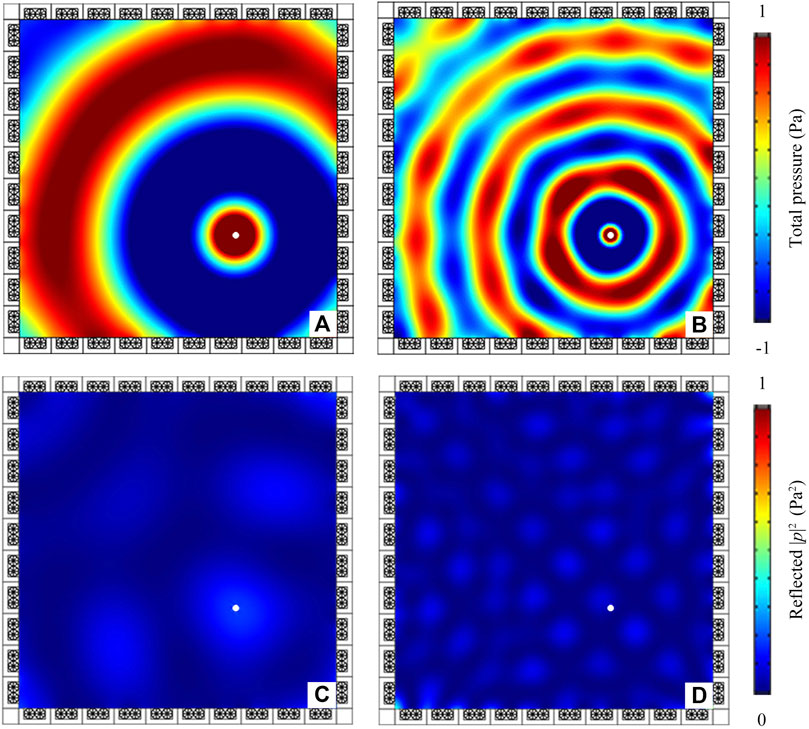
FIGURE 7. Simulated total pressure distributions created by the barrier-free anechoic room at (A) 171 Hz and (B) 519 Hz, and their corresponding reflected intensity distributions at (C) 171 Hz and (D) 519 Hz. White points represent the positions of cylindrical sound source.

Conclusion

In conclusions, we have demonstrated an ultrathin planar wall with low-frequency dual-band sound absorption. The results show that the sound absorption of the wall exists in two frequency bands (I: 145–203 Hz and II: 490–544 Hz) based on two different mechanisms. The band I is created by the conventional resonance coupling of the two multiple-cavity resonators, but it is worth noting that the band II is realized by the mutual resonance coupling between the resonators and groove structure. The corresponding fractional bandwidth of both bands can reach about 34.1 and 10.4%, and the measured and simulated results agree well with each other. Additionally, the influences of incident angles on the sound absorption of unit cell are simulated, and the characteristics of sound absorption almost remains unchanged with different incident angles. Finally, the application of the proposed ultrathin planar wall in the design of a barrier-free anechoic room is discussed in detail. The proposed ultrathin planar wall with the characteristic of omnidirectional low-frequency dual-band sound absorption has wide prospects in noise control and architectural acoustics.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

Y-WX and Y-JG contributed equally to this work.

Funding

This work was supported by the National Key Research and Development Program of China (Grant No. 2020YFC1512403), the National Natural Science Foundation of China (Grant Nos. 12174159 and 11834008), and the Practice Innovation Training Program Projects of Jiangsu Province (Grant No. 202110299082Z).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.911711/full#supplementary-material

References

1. Liu Z, Zhang X, Mao Y, Zhu YY, Yang Z, Chan CT, et al. Locally Resonant Sonic Materials. Science (2000) 289:1734–6. doi:10.1126/science.289.5485.1734

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Fang N, Xi D, Xu J, Ambati M, Srituravanich W, Sun C, et al. Ultrasonic Metamaterials with Negative Modulus. Nat Mater (2006) 5:452–6. doi:10.1038/nmat1644

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Liang Z, Li J. Extreme Acoustic Metamaterial by Coiling up Space. Phys Rev Lett (2012) 108:114301. doi:10.1103/PhysRevLett.108.114301

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Cummer SA, Christensen J, Alù A. Controlling Sound with Acoustic Metamaterials. Nat Rev Mater (2016) 1:16001. doi:10.1038/natrevmats.2016.1

CrossRef Full Text | Google Scholar

5. Ma G, Sheng P. Acoustic Metamaterials: From Local Resonances to Broad Horizons. Sci Adv (2016) 2:e1501595. doi:10.1126/sciadv.1501595

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Gao N, Lu K. An Underwater Metamaterial for Broadband Acoustic Absorption at Low Frequency. Appl Acoust (2020) 169:107500. doi:10.1016/j.apacoust.2020.107500

CrossRef Full Text | Google Scholar

7. Tsang L, Liao T-H, Tan S. Calculations of Bands and Band Field Solutions in Topological Acoustics Using the Broadband Green's Function-kkr-Multiple Scattering Method. Prog Electromagn Res (2021) 171:137–58. doi:10.2528/PIER21081706

CrossRef Full Text | Google Scholar

8. Jia D, Wang Y, Ge Y, Yuan S-Q, Sun H-X. Tunable Topological Refractions in Valley Sonic Crystals with Triple Valley Hall Phase Transitions. Prog Electromagn Res (2021) 172:13–22. doi:10.2528/PIER21102002

CrossRef Full Text | Google Scholar

9. Yan Q, Chen H, Yang Y. Non-Hermitian Skin Effect and Delocalized Edge States in Photonic Crystals with Anomalous Parity-Time Symmetry. Prog Electromagn Res (2021) 172:33–40. doi:10.2528/PIER21111602

CrossRef Full Text | Google Scholar

10. Gao N, Zhang Z, Deng J, Guo X, Cheng B, Hou H. Acoustic Metamaterials for Noise Reduction: A Review. Adv Mater Technol (2022) 2100698 [Epub ahead of print]. doi:10.1002/admt.202100698

CrossRef Full Text | Google Scholar

11. Li Y, Liang B, Gu Z-M., Zou X-Y, Cheng J-C. Reflected Wavefront Manipulation Based on Ultrathin Planar Acoustic Metasurfaces. Sci Rep (2013) 3:2546. doi:10.1038/srep02546

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Mei J, Wu Y. Controllable Transmission and Total Reflection through an Impedance-Matched Acoustic Metasurface. New J Phys. (2014) 16:123007. doi:10.1088/1367-2630/16/12/123007

CrossRef Full Text | Google Scholar

13. Tang K, Qiu C, Ke M, Lu J, Ye Y, Liu Z. Anomalous Refraction of Airborne Sound through Ultrathin Metasurfaces. Sci Rep (2014) 4:6517. doi:10.1038/srep06517

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Zhang H, Xiao Y, Wen J, Yu D, Wen X. Ultra-Thin Smart Acoustic Metasurface for Low-Frequency Sound Insulation. Appl Phys Lett (2016) 108:141902. doi:10.1063/1.4945664

CrossRef Full Text | Google Scholar

15. Assouar B, Liang B, Wu Y, Li Y, Cheng J-C, Jing Y. Acoustic Metasurfaces. Nat Rev Mater (2018) 3:460–72. doi:10.1038/s41578-018-0061-4

CrossRef Full Text | Google Scholar

16. Quan L, Sounas DL, Alù A. Nonreciprocal Willis Coupling in Zero-Index Moving Media. Phys Rev Lett (2019) 123:064301. doi:10.1103/PhysRevLett.123.064301

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Hu Z, He N, Sun Y, Jin Y, He S. Wideband High-Reflection Chiral Dielectric Metasurface. Prog Electromagn Res (2021) 172:51–60. doi:10.2528/PIER21121903

CrossRef Full Text | Google Scholar

18. Li Z, Cao G, Li C, Dong S, Deng Y, Liu X, et al. Non-Hermitian Electromagnetic Metasurfaces at Exceptional Points. Prog Electromagn Res (2021) 171:1–20. doi:10.2528/PIER21051703

CrossRef Full Text | Google Scholar

19. Zarek JHB. Sound Absorption in Flexible Porous Materials. J Sound Vib (1978) 61:205–34. doi:10.1016/0022-460X(78)90004-4

CrossRef Full Text | Google Scholar

20. Maa D-Y. Potential of Microperforated Panel Absorber. J Acoust Soc Am (1998) 104:2861–6. doi:10.1121/1.423870

CrossRef Full Text | Google Scholar

21. García-Chocano VM, Cabrera S, Sánchez-Dehesa J. Broadband Sound Absorption by Lattices of Microperforated Cylindrical Shells. Appl Phys Lett (2012) 101:184101. doi:10.1063/1.4764560

CrossRef Full Text | Google Scholar

22. Jiménez N, Huang W, Romero-García V, Pagneux V, Groby J-P. Ultra-Thin Metamaterial for Perfect and Quasi-Omnidirectional Sound Absorption. Appl Phys Lett (2016) 109:121902. doi:10.1063/1.4962328

CrossRef Full Text | Google Scholar

23. Li J, Wang W, Xie Y, Popa B-I, Cummer SA. A Sound Absorbing Metasurface with Coupled Resonators. Appl Phys Lett (2016) 109:091908. doi:10.1063/1.4961671

CrossRef Full Text | Google Scholar

24. Romero-García V, Theocharis G, Richoux O, Merkel A, Tournat V, Pagneux V. Perfect and Broadband Acoustic Absorption by Critically Coupled Sub-wavelength Resonators. Sci Rep (2016) 6:19519. doi:10.1038/srep19519

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Long H, Cheng Y, Liu X. Asymmetric Absorber with Multiband and Broadband for Low-Frequency Sound. Appl Phys Lett (2017) 111:143502. doi:10.1063/1.4998516

CrossRef Full Text | Google Scholar

26. Guan Y-J, Ge Y, Sun H-X, Yuan S-Q, Liu X-J. Low-Frequency, Open, Sound-Insulation Barrier by Two Oppositely Oriented Helmholtz Resonators. Micromachines (2021) 12:1544. doi:10.3390/mi12121544

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Zhang C, Hu X. Three-Dimensional Single-Port Labyrinthine Acoustic Metamaterial: Perfect Absorption with Large Bandwidth and Tunability. Phys Rev Appl (2016) 6:064025. doi:10.1103/PhysRevApplied.6.064025

CrossRef Full Text | Google Scholar

28. Yang M, Chen S, Fu C, Sheng P. Optimal Sound-Absorbing Structures. Horiz (2017) 4:673–80. doi:10.1039/c7mh00129k

CrossRef Full Text | Google Scholar

29. Mei J, Ma G, Yang M, Yang Z, Wen W, Sheng P. Dark Acoustic Metamaterials as Super Absorbers for Low-Frequency Sound. Nat Commun (2012) 3:756. doi:10.1038/ncomms1758

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Ma G, Yang M, Xiao S, Yang Z, Sheng P. Acoustic Metasurface with Hybrid Resonances. Nat Mater (2014) 13:873–8. doi:10.1038/NMAT3994

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Yang M, Li Y, Meng C, Fu C, Mei J, Yang Z, et al. Sound Absorption by Subwavelength Membrane Structures: A Geometric Perspective. Comptes Rendus Mécanique (2015) 343:635–44. doi:10.1016/j.crme.2015.06.008

CrossRef Full Text | Google Scholar

32. Wu X, Fu C, Li X, Meng Y, Gao Y, Tian J, et al. Low-Frequency Tunable Acoustic Absorber Based on Split Tube Resonators. Appl Phys Lett (2016) 109:043501. doi:10.1063/1.4959959

CrossRef Full Text | Google Scholar

33. Long H, Cheng Y, Tao J, Liu X. Perfect Absorption of Low-Frequency Sound Waves by Critically Coupled Subwavelength Resonant System. Appl Phys Lett (2017) 110:023502. doi:10.1063/1.4973925

CrossRef Full Text | Google Scholar

34. Gao N, Hou H, Zhang Y, Wu JH. Sound Absorption of a New Oblique-Section Acoustic Metamaterial with Nested Resonator. Mod Phys Lett B (2018) 32:1850040. doi:10.1142/s0217984918500409

CrossRef Full Text | Google Scholar

35. Wei P, Croënne C, Tak Chu S, Li J. Symmetrical and Anti-Symmetrical Coherent Perfect Absorption for Acoustic Waves. Appl Phys Lett (2014) 104:121902. doi:10.1063/1.4869462

CrossRef Full Text | Google Scholar

36. Song JZ, Bai P, Hang ZH, Lai Y. Acoustic Coherent Perfect Absorbers. New J Phys (2014) 16:033026. doi:10.1088/1367-2630/16/3/033026

CrossRef Full Text | Google Scholar

37. Li Y, Assouar BM. Acoustic Metasurface-Based Perfect Absorber with Deep Subwavelength Thickness. Appl Phys Lett (2016) 108:063502. doi:10.1063/1.4941338

CrossRef Full Text | Google Scholar

38. Chang H, Liu L, Zhang C, Hu X. Broadband High Sound Absorption from Labyrinthine Metasurfaces. AIP Adv (2018) 8:045115. doi:10.1063/1.5024303

CrossRef Full Text | Google Scholar

39. Wang X, Luo X, Zhao H, Huang Z. Acoustic Perfect Absorption and Broadband Insulation Achieved by Double-Zero Metamaterials. Appl Phys Lett (2018) 112:021901. doi:10.1063/1.5018180

CrossRef Full Text | Google Scholar

40. Long H, Shao C, Liu C, Cheng Y, Liu X. Broadband Near-Perfect Absorption of Low-Frequency Sound by Subwavelength Metasurface. Appl Phys Lett (2019) 115:103503. doi:10.1063/1.5109826

CrossRef Full Text | Google Scholar

41. Donda K, Zhu Y, Merkel A, Fan S-W, Cao L, Wan S, et al. Ultrathin Acoustic Absorbing Metasurface Based on Deep Learning Approach. Smart Struct (2021) 30:085003. doi:10.1088/1361-665X/ac0675

CrossRef Full Text | Google Scholar

42. Liu H, Wu JH, Ma F. High-efficiency Sound Absorption by a Nested and Ventilated Metasurface Based on Multi-Slit Synergetic Resonance. J Phys D Appl Phys (2021) 54:205304. doi:10.1088/1361-6463/abe6cd

CrossRef Full Text | Google Scholar

43. Long H, Gao S, Cheng Y, Liu X. Multiband Quasi-Perfect Low-Frequency Sound Absorber Based on Double-Channel Mie Resonator. Appl Phys Lett (2018) 112:033507. doi:10.1063/1.5013225

CrossRef Full Text | Google Scholar

44. Liu CR, Wu JH, Chen X, Ma F. A Thin Low-Frequency Broadband Metasurface with Multi-Order Sound Absorption. J Phys D Appl Phys (2019) 52:105302. doi:10.1088/1361-6463/aafaa3

CrossRef Full Text | Google Scholar

45. Chen S, Fan Y, Yang F, Jin Y, Fu Q, Zheng J, et al. Engineering Coiling‐Up Space Metasurfaces for Broadband Low‐Frequency Acoustic Absorption. Phys Status Solidi RRL (2019) 13:1900426. doi:10.1002/pssr.201900426

CrossRef Full Text | Google Scholar

46. Guo J, Fang Y, Jiang Z, Zhang X. Acoustic Characterizations of Helmholtz Resonators with Extended Necks and Their Checkerboard Combination for Sound Absorption. J Phys D Appl Phys (2020) 53:505504. doi:10.1088/1361-6463/abb5d8

CrossRef Full Text | Google Scholar

47. Zhou Y, Zhang X, Wang Y, Feng Y. Dual-Band Perfect Low-Frequency Acoustic Absorption Based on Metaporous Composite. Appl Phys Express (2021) 14:094003. doi:10.35848/1882-0786/ac1980

CrossRef Full Text | Google Scholar