Dynamical Analysis of Two-Dimensional Memristor Cosine Map

Research on discrete memristor models applied to discrete maps deserves more in-depth discussion. In this paper, a continuous memristor is introduced and the discrete memristor model is obtained by the forward Eulerian difference algorithmic discretization. This model is coupled to a cosine map to further obtain a two-dimensional memristor cosine map. The dynamical characteristics of the memristor cosine map are investigated through numerical simulations and other analytical methods. For example, the phase diagram, the bifurcation diagram, the Lyapunov exponential spectrum and the Spectral Entropy complexity with parameters, etc., In addition, multi-stability phenomena of the system are identified. The results show that the cosine map coupled with a discrete memristor has more complex dynamical behaviors and is more suitable for applications in cryptography.

Introduction

In 1963, the meteorologist Lorenz proposed the Lorenz model and the “butterfly effect” [1–3]. Since then, chaos theory has gradually entered the eyes of scholars. With a series of significant research results in the history of chaos, the study of chaos theory and chaos properties has become a major research hotspot [4–8]. In recent years, chaos science has interpenetrated with other disciplines, and breakthroughs have been made in chaotic synchronous control [9, 10], chaotic secure communication [11–14] and chaotic neural networks [15–18]. This has led to a wide range of applications of chaos theory in both natural and social sciences. Although some progress has been made in the study of chaos theory [19], its complexity is still not understood and how to chaoticize it is still a very interesting issue for scholars to explore further. Chaosification is the process of generating or enhancing the chaotic nature of a system. Chaosification can increase the complexity and unpredictability of a system, and making it more suitable for areas such as secure communications.

In 1971, Chua introduced the concept of memristors [20–22] and its associated theory. Unlike resistor, inductor and capacitor, memristor is the fourth fundamental element describing the relationship between charge and flux [23, 24]. The first report of the realisability of memristors from Hewlett-Packard (HP) Labs in 2008 [25]. The result quickly gained attention and caused a surge of research on memristors by scholars in various fields [26–28]. Compared to the other three fundamental components, the memristor has a very interesting property in that it is a non-linear component with a memory function [29]. It is because of the memory property of memristors that the research related to memristors reflects the cross-fertilisation of several disciplines. Memory properties have had a great impact on computer science, biology [30], neural networks [31] and communication engineering [32, 33]. The application of memristors to the construction of non-linear circuits and systems produces complex dynamical behaviors, and therefore memristors are widely used in the field of chaos [34, 35]. Currently, most of the research on chaotic systems based on memristors is focused on continuous chaotic systems. For example, [36] et al. proposed a novel simple chaotic circuit, which includes a memristor, a linear inductor and a memcapacitor. [37] constructed a deoxyribonucleic acid (DNA) encoding algorithm with memristor based chaotic system. [38] et al. reported a 3-D conservative memristive system with amplitude control. However, discrete chaotic systems have the advantages of simple model building and fast iteration [39–41]. Is it possible if memristor is applied to discrete chaotic systems? Some scholars have already studied the discretization of memristors to obtain discrete memristor models [42–45]. For example, [46] et al. discussed a second-order map model based on memristor. And to enhance the chaotic performance of the 1-D maps, [47] et al. proposed a chaotification method. These research results have laid a solid foundation for the application of memristors in discrete chaotic systems. There are still great prospects for introducing discrete memristor models into discrete chaotic maps. In this paper, a new memristor cosine map is proposed based on a one-dimensional cosine map coupled with a magnetically controlled memristor model. It is shown that the memristor cosine map has richer dynamical behaviors.

The rest of the paper is structured as follows. The discretized memristor model and the memristor cosine map model based on a one-dimensional cosine map are presented in the “System Model” section. This is followed by the “Dynamics Analysis” section, which describes the dynamical behaviors of the memristor cosine map as the parameters and initial values are varied. Finally, we summarized the conclusions drawn from the research in this paper and give directions for future research.

System Model

Model of Discrete Memristor

In this section, a triple magnetron memristor has been chosen, which can be expressed as

$\{\begin{array}{l}i\left(t\right)=W\left(\phi \right)v\left(t\right)\\ \frac{d\phi \left(t\right)}{dt}=v\left(t\right),\\ W\left(\phi \right)=\alpha +\beta {\phi }^2\end{array}(1)$

here, i(t) and v(t) are the input current and the output voltage of the memristor, respectively. W(φ) is a non-linear function about φ(t) with the same magnitude as the conductance value, called the amnesic conductance, indicating dependence on the control of the internal variable φ(t) of the memristor. And φ is the magnetic flux and represents the amount of internal magnetic flux change in the memristor. Then, α and β are the control parameters of the memristor.

First, discrete i(t), v(t), φ(t) by sampling at unit time n to obtain i_n, v_n and φ_n respectively. Then, one can discretize the memristor model described in Eq. 1 by using the forward Eulerian difference algorithm, the discrete memristor model can be obtained as

$\{\begin{array}{l}{i}_n=\left(\alpha +\beta {\phi }_n^2\right)v_n\\ {\phi }_{n+1}={\phi }_n+k{v}_n.\end{array}(2)$

Assuming that the sinusoidal current i_n = Hsin (ωn) is added to the model of the discrete memristor, the characteristics of the model are analyzed. Let α = 0.5, β = 0.5, and its characteristic curve can be obtained in Figure 1A. In order to further analyze this discrete memristor model, the voltammetric characteristic curves of the amnestic resistor obtained by taking different ω, H, and φ₀ respectively, are shown in Figures 1B–D.

FIGURE 1

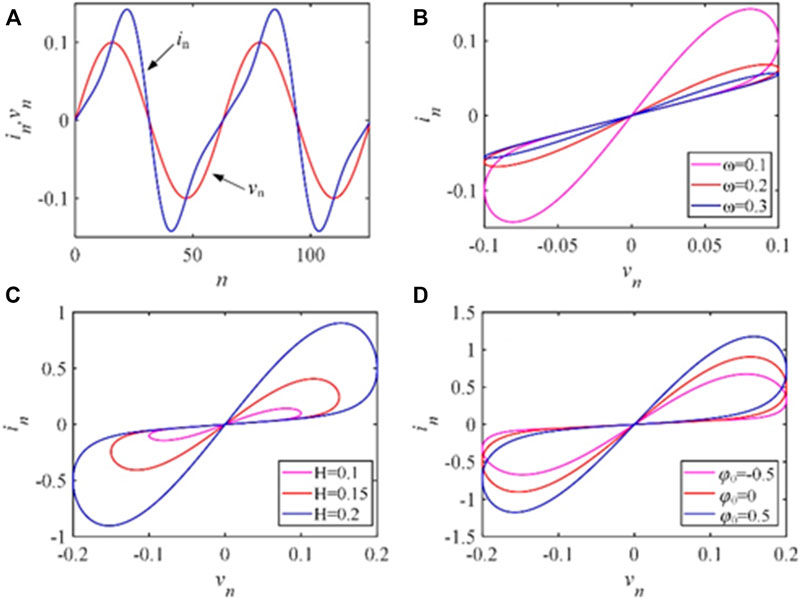
FIGURE 1. Characteristics of the discrete memristor when being applied to a discrete sinusoidal current i_n = Hsin (ωn), where α = 0.5 and β = 0.5. (A) Current and voltage sequences; (B) H = 0.1, φ0 = 0; (C) ω = 0.1, φ0 = 0; (D) H = 0.1, ω = 0.1.

Memristor-Coupled Map

A cosine map with a simple structure and few parameter variables was chosen and it was defined as

$x_{i+1}=a\cos \left(\pi x_i\right).(3)$

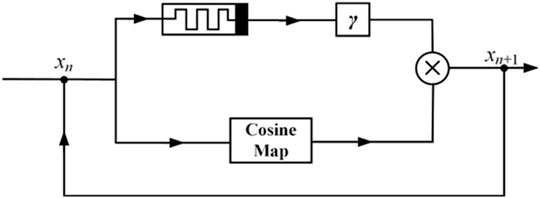
Based on the chaotic control method of modulation and coupling, coupling the discrete memristor model (2) with the cosine map (3), a new two-dimensional chaotic map model can be obtained. Figure 2 is a schematic diagram of the two-dimensional map coupled by the discrete memristor, where γ is the coupling parameter. The mathematical expression is

$\{\begin{array}{l}{x}_{n+1}=a\cos \left(\pi x_n\right)+\gamma x_n\left(\alpha +\beta y_n^2\right)\\ y_{n+1}=y_n+e{x}_n,\end{array}(4)$

where, a is the control parameter of the cosine map (3), α and β are the control parameters of the discrete memristor model (2), and e is the step length.

FIGURE 2

FIGURE 2. Structural diagram of the cosine map coupled by the discrete memristor.

Dynamical Analyses

Bifurcation and Lyapunov Exponent Analysis

In order to analyze the dynamical characteristics of this discrete chaotic map, the bifurcation diagram and the Lyapunov exponential spectrum of the map with respect to the parameter a are plotted as shown in Figure 3. Set the other parameters γ = −0.4, e = 0.02, α = 0.5 and β = 0.5, the initial value is (1, 1), the step size is 0.001. The discrete map has a number of divergent points as the parameter a varies in the range 0.25–1.363. Therefore, the range of parameter a is divided into three segments for analysis. When a ϵ (0.25, 0.66), the bifurcation diagram and Lyapunov exponent spectrum of the discrete system are shown in Figures 3A1,B1. As can be seen in the figure, the system has a clear multiplicative period bifurcation behavior. The map goes from two cycles to four cycles and then into a chaotic state. The bifurcation and LEs with the parameter a when a ϵ (0.67, 0.862) are plotted in Figures 3A2,B2. The simulation results show that the two correspond well. When the parameter a ϵ (0.875, 1.363), the bifurcation diagram and the Lyapunov exponent diagram of the chaotic map are drawn in Figures 3A3,B3. In addition, the trajectory of this map when taking different values of a is plotted as shown in Figure 4.

FIGURE 3

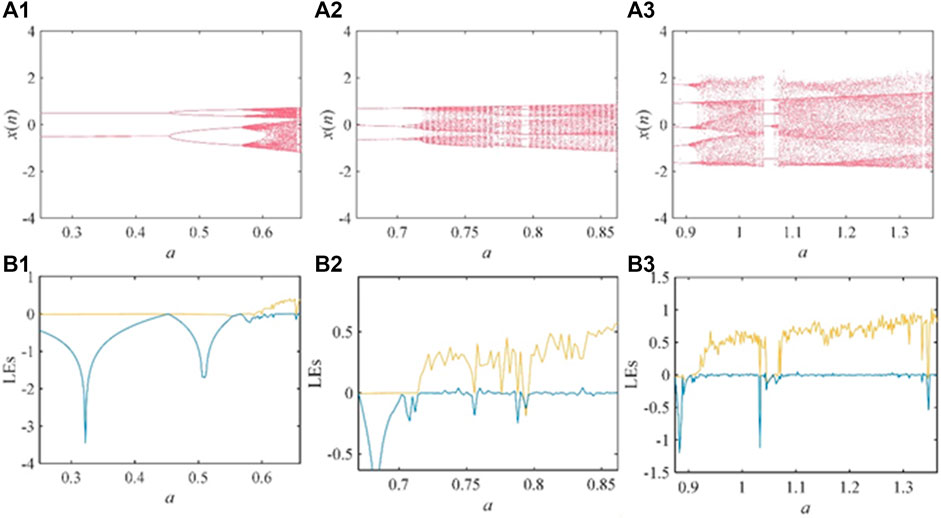
FIGURE 3. Bifurcation and LEs of the map with parameter a. (A1) a ϵ (0.25, 0.66); (A2) a ϵ (0.67, 0.862); (A3) a ϵ (0.875, 1.363); (B1) a ϵ (0.25, 0.66); (B2) a ϵ (0.67, 0.862); (B3) a ϵ (0.875, 1.363).

FIGURE 4

FIGURE 4. The phase space motion trajectory of this discrete system. (A) a = 0.3; (B) a = 0.5; (C) a = 0.6; (D) a = 0.65; (E) a = 0.7; (F) a = 0.85; (G) a = 0.9; (H) a = 1; (I) a = 1.2.

Spectral Entropy Complexity

The complexity of chaotic systems is a way to characterize the dynamical properties of chaotic systems. There are many algorithms to calculate the complexity value of chaotic systems, and where the complexity algorithm of the Spectral Entropy (SE) is used [48]. Its algorithm is described as follows.

First, for a pseudo-random sequence{x(m), m = 0, 1, 2, …, M-1} of length M, the DC part is removed through the following equation.

$x\left(m\right)=x\left(m\right)-\overline{x},(5)$

$\overline{x}=\frac{1}{M}{\displaystyle \sum _{m=0}^{M-1}x\left(m\right)}.(6)$

Second, performing the discrete Fourier transform on the sequence x(m),

$X\left(k\right)={\displaystyle \sum _{m=0}^{M-1}x\left(m\right)e^{-j\frac{2\pi }{M}mk}}={\displaystyle \sum _{m=0}^{M-1}x\left(m\right)W_M^{mk}},(7)$

Where, k = 0, 1, 2, …, M-1.

Third, for the transformed sequence X(k), take the first half for calculation. Based on the Paserval theorem, calculate the power spectrum value of one frequency point as

$p\left(k\right)=\frac{1}{N}{\left|X\left(k\right)\right|}^2,(8)$

Among them, k = 0, 1, 2, …, M/2-1, the overall power of the sequence is

$p_{tot}=\frac{1}{M}{\displaystyle \sum _{K=0}^{\raisebox{1ex}{$M$}\!\left/ \!\raisebox{-1ex}{$2$}\right.-1}{\left|X\left(K\right)\right|}^2}.(9)$

The relative power spectrum probability of the sequence is

$P_k=\frac{p\left(k\right)}{p_{tot}}=\frac{\frac{1}{M}{\left|X\left(k\right)\right|}^2}{\frac{1}{M}{\displaystyle \sum _{k=0}^{\raisebox{1ex}{$M$}\!\left/ \!\raisebox{-1ex}{$2$}\right.-1}{\left|X\left(k\right)\right|}^2}}=\frac{{\left|X\left(k\right)\right|}^2}{{\displaystyle \sum _{k=0}^{\raisebox{1ex}{$M$}\!\left/ \!\raisebox{-1ex}{$2$}\right.-1}{\left|X\left(k\right)\right|}^2}},(10)$

Fourth, calculate the spectral entropy as follows

$se=-{\displaystyle \sum _{k=0}^{\raisebox{1ex}{$M$}\!\left/ \!\raisebox{-1ex}{$2$}\right.-1}{p}_k}\ln P_k.(11)$

Finally, to facilitate the consideration, the spectral entropy is normalized

$SE\left(N\right)=\frac{se}{\ln \left(M/2\right)}.(12)$

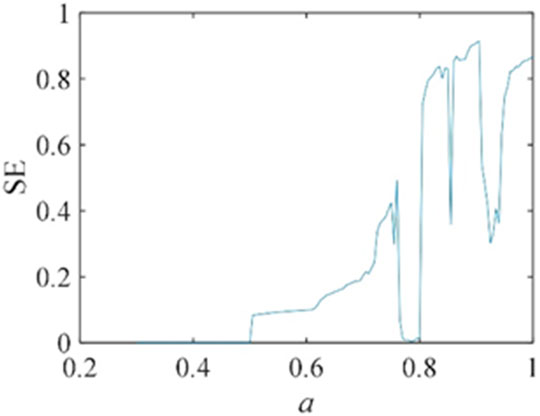
According to the above algorithm, the complexity curve of this discrete map with the parameter a is plotted in Figure 5. The vertical coordinates in the figure represent the SE complexity values corresponding to different values of a. A larger complexity value means that the sequence is closer to a random sequence and the system is more secure. Set γ = −0.4, e = 0.02, α = 0.5 and β = 0.5, and the initial value remains unchanged. When a ϵ (0.2, 0.5) Ս (0.76, 0.8), the complexity value of the discrete system is low and the system is in a periodic state. When a ϵ (0.8, 0.85) Ս (0.86, 0.9) Ս (0.95, 1), the complexity value of the discrete system is high and the system is in a chaotic state.

FIGURE 5

FIGURE 5. SE complexity diagrams of the map when the parameter a varies.

Coexisting Attractors

When the system parameters are fixed, changing the initial value gives two or more different attractors coexisting. This interesting phenomenon can also be called multi-stability. In general, multi-stable systems are more sensitive to initial values and are more secure in their application to cryptography and secure communications. In this section, the phenomenon of attractors coexistence can be observed in the course of the experiment. When a = 0.77, γ = −0.4, e = 0.01, α = 0.5 and β = 0.5, the bifurcation diagram of this map with the initial value x (0) is shown in Figure 6A. From the diagram, there are two different attractors for different initial values, and the phase diagram for the coexistence of the two attractors is drawn as shown in Figure 6B. The bifurcation diagram with the initial value x (0) is plotted in Figure 7A when a = 1.03, and other parameters remain unchanged. The coexistence of period four attractor and chaotic attractor can be observed in the bifurcation diagram. The plotted attractor coexistence phase diagram is shown in Figure 7B. In addition, let x (0) = 1, the bifurcation diagrams with the initial value y (0) are analyzed and the simulation results are shown in Figures 8A, 9A. Based on the two bifurcation diagrams, we take two sets of initial values (1, −1.5) and (1, 1). Then, the coexistence phase diagrams of the chaotic attractor with the period-3 attractor and the coexistence phase diagrams of two different chaotic attractors are plotted as shown in Figures 8B, 9B.

FIGURE 6

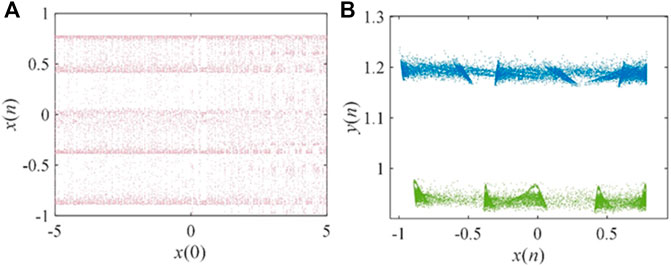
FIGURE 6. Experimental results graph when a = 0.77. (A) Bifurcation with initial value x (0); (B) Attractors coexistence phase diagram.

FIGURE 7

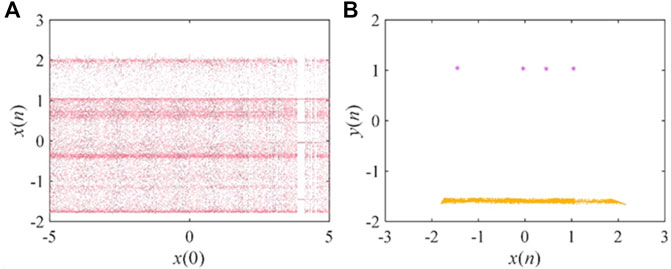
FIGURE 7. Experimental results graph when a = 1.03. (A) Bifurcation with initial value x (0); (B) Attractors coexistence phase diagram.

FIGURE 8

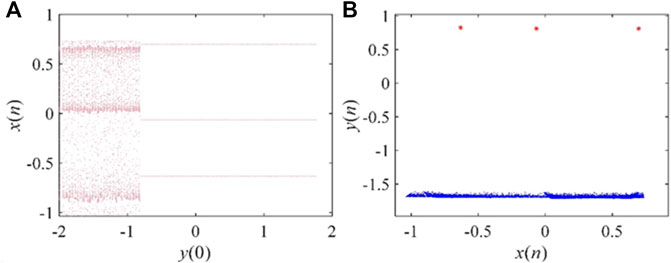
FIGURE 8. Experimental results graph when a = 0.69. (A) Bifurcation with initial value y (0); (B) Attractors coexistence phase diagram.

FIGURE 9

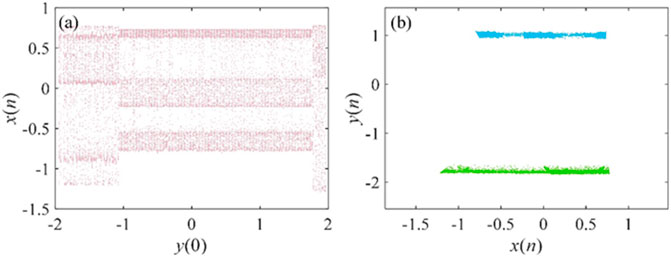
FIGURE 9. Experimental results graph when a = 0.72. (A) Bifurcation with initial value y (0); (B) Attractors coexistence phase diagram.

Conclusion

In this paper, a continuous magnetron memristor was chosen and the discrete memristor model was obtained by means of the forward Eulerian difference algorithm. The discrete memristor was coupled with a one-dimensional cosine map to obtain a new two-dimensional chaotic map. The dynamical characteristics of the discrete system were analyzed by computer simulations. The results of the study show that the newly constructed discrete system has complex dynamical behaviors, higher complexity, and a higher degree of initial value sensitivity. These findings suggest that the chaoticisation method of coupling discrete memristor with discrete maps is worthy of further research, and that the map after the introduction of the discrete memristor model is more suitable for applications in areas such as secure communications. In the future, other ways of implementing this discrete system will be considered and attempts will be made to explore its practical applications.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

XH designed and carried out experiments, data analyzed and manuscript wrote. XB and LX made the theoretical guidance for this paper. LR carried out experiment. All authors reviewed the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 62061014).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Adams TM, Stewart LD. Chaos Theory and Organizational Crisis: A Theoretical Analysis of the Challenges Faced by the New Orleans Police Department During Hurricane Katrina. Public Organiz Rev (2015) 15(3):415–31. doi:10.1007/s11115-014-0284-9

CrossRef Full Text | Google Scholar

2. Dong C, Sun K, He S, Wang H. A Hyperchaotic Cycloid Map with Attractor Topology Sensitive to System Parameters. Chaos (2021) 31(8):083132. doi:10.1063/5.0061519

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Gleick J, Glazier J, Gunaratne G. Chaos: Making a New Science. Phys Today (1988) 41(11):79. doi:10.1063/1.2811320

CrossRef Full Text | Google Scholar

4. Gu S, He S, Wang H, Du B. Analysis of Three Types of Initial Offset-Boosting Behavior for a New Fractional-Order Dynamical System. Chaos, Solit Fractals (2021) 143:110613. doi:10.1016/j.chaos.2020.110613

CrossRef Full Text | Google Scholar

5. Han X, Mou J, Liu T, Cao Y. A New Fractional-Order 2D Discrete Chaotic Map and its DSP Implement. Eur. Phys. J. Spec. Top. (2021) 230(21):3913–25. doi:10.1140/epjs/s11734-021-00331-6

CrossRef Full Text | Google Scholar

6. Kyriazis M. Practical Applications of Chaos Theory to the Modulation of Human Ageing: Nature Prefers Chaos to Regularity. Biogerontology (2003) 4(2):75–90. doi:10.1023/A:1023306419861

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Li X, Mou J, Cao Y, Banerjee S. An Optical Image Encryption Algorithm Based on a Fractional-Order Laser Hyperchaotic System. Int. J. Bifurc Chaos (2022) 32:32. doi:10.1142/S0218127422500353

CrossRef Full Text | Google Scholar

8. Yu F, Shen H, Zhang Z, Huang Y, Cai S, Du S. A New Multi-Scroll Chua's Circuit with Composite Hyperbolic Tangent-Cubic Nonlinearity: Complex Dynamics, Hardware Implementation and Image Encryption Application. Integration (2021) 81:71–83. doi:10.1016/j.vlsi.2021.05.011

CrossRef Full Text | Google Scholar

9. Karthikeyan A, Rajagopal K. Chaos Control in Fractional Order Smart Grid with Adaptive Sliding Mode Control and Genetically Optimized PID Control and its FPGA Implementation. Complexity (2017) 2017:1–18. doi:10.1155/2017/3815146

CrossRef Full Text | Google Scholar

10. Vaseghi B, Pourmina MA, Mobayen S. Secure Communication in Wireless Sensor Networks Based on Chaos Synchronization Using Adaptive Sliding Mode Control. Nonlinear Dyn(2017) 89(9):1689–704. doi:10.1007/s11071-017-3543-9

CrossRef Full Text | Google Scholar

11. Gao X, Mou J, Xiong L, Sha Y, Yan H, Cao Y. A Fast and Efficient Multiple Images Encryption Based on Single-Channel Encryption and Chaotic System. Nonlinear Dyn(2022) 108(1):613–36. doi:10.1007/s11071-021-07192-7

CrossRef Full Text | Google Scholar

12. He S, Sun K, Wu X. Fractional Symbolic Network Entropy Analysis for the Fractional-Order Chaotic Systems. Phys. Scr. (2020) 95(313pp):035220. doi:10.1088/1402-4896/ab46c9

CrossRef Full Text | Google Scholar

13. Li C-L, Zhou Y, Li H-M, Feng W, Du J-R. Image Encryption Scheme with Bit-Level Scrambling and Multiplication Diffusion. Multimed Tools Appl (2021) 80(12):18479–501. doi:10.1007/s11042-021-10631-7

CrossRef Full Text | Google Scholar

14. Zhou S, Wang X, Wang M, Zhang Y. Simple Colour Image Cryptosystem with Very High Level of Security. Chaos, Solit Fractals (2020) 141:110225. doi:10.1016/j.chaos.2020.110225

CrossRef Full Text | Google Scholar

15. Çelik V, Demir Y. Chaotic Fractional Order Delayed Cellular Neural Network. New Trends in Nanotechnology and Fractional Calculus Applications (2020):313–20. doi:10.1007/978-90-481-3293-5_27

CrossRef Full Text | Google Scholar

16. Rakkiyappan R, Preethi Latha V, Zhu Q, Yao Z. Exponential Synchronization of Markovian Jumping Chaotic Neural Networks with Sampled-Data and Saturating Actuators. Nonlinear Anal Hybrid Syst (2017) 24:28–44. doi:10.1016/j.nahs.2016.10.004

CrossRef Full Text | Google Scholar

17. Yu F, Zhang Z, Shen H, Huang Y, Cai S, Du S. FPGA Implementation and Image Encryption Application of a New PRNG Based on a Memristive Hopfield Neural Network with a Special Activation Gradient. Chin Phys. B (2022) 31:020505. doi:10.1088/1674-1056/ac3cb2

CrossRef Full Text | Google Scholar

18. Yu F, Zhang Z, Shen H, Huang Y, Cai S, Jin J, et al. Design and FPGA Implementation of a Pseudo-random Number Generator Based on a Hopfield Neural Network Under Electromagnetic Radiation. Front. Phys. (2021) 9:690651. doi:10.3389/fphy.2021.690651

CrossRef Full Text | Google Scholar

19. He S, Sun K, Mei X, Yan B, Xu S. Numerical Analysis of a Fractional-Order Chaotic System Based on Conformable Fractional-Order Derivative. Eur. Phys. J. Plus (2017) 132(1):36. doi:10.1140/epjp/i2017-11306-3

CrossRef Full Text | Google Scholar

20. Chua L. If It's Pinched It's a Memristor. Semicond. Sci. Technol. (2014) 29(10):104001. doi:10.1088/0268-1242/29/10/104001

CrossRef Full Text | Google Scholar

21. Bao H, Chen M, Wu H, Bao B. Memristor Initial-Boosted Coexisting Plane Bifurcations and its Extreme Multi-Stability Reconstitution in Two-Memristor-Based Dynamical System. Sci. China Technol. Sci. (2020) 63(04):603–13. doi:10.1007/s11431-019-1450-6

CrossRef Full Text | Google Scholar

22. Yu F, Kong X, Chen H, Yu Q, Cai S, Huang Y, et al. A 6D Fractional-Order Memristive Hopfield Neural Network and its Application in Image Encryption. Front. Phys. (2022) 10:847385. doi:10.3389/fphy.2022.847385

CrossRef Full Text | Google Scholar

23. Yuan F, Wang G, Wang X. Extreme Multistability in a Memristor-Based Multi-Scroll Hyper-Chaotic System. Chaos (2016) 26(7):073107–519. doi:10.1063/1.4958296

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Xiong L, Yang F, Mou J, An X, Zhang X. A Memristive System and its Applications in Red-Blue 3D Glasses and Image Encryption Algorithm with DNA Variation. Nonlinear Dyn(2022) 107(5):2911–33. doi:10.1007/s11071-021-07131-6

CrossRef Full Text | Google Scholar

25. Huang L-L, Liu S, Xiang J-H, Wang L-Y. Design and Multistability Analysis of Five-Value Memristor-Based Chaotic System with Hidden Attractors. Chin Phys. B (2021) 30(10):100506. doi:10.1088/1674-1056/ac1e13

CrossRef Full Text | Google Scholar

26. Ho Y, Huang GM, Li P. Dynamical Properties and Design Analysis for Nonvolatile Memristor Memories. IEEE Trans. Circuits Syst. I (2011) 58(4):724–36. doi:10.1109/TCSI.2010.2078710

CrossRef Full Text | Google Scholar

27. Kim H, Sah MP, Yang C, Cho S, Chua LO. Memristor Emulator for Memristor Circuit Applications. IEEE Trans. Circuits Syst. I (2012) 59(10):2422–31. doi:10.1109/TCSI.2012.2188957

CrossRef Full Text | Google Scholar

28. Xiong L, Zhang X, Teng S, Qi L, Zhang P. Detecting Weak Signals by Using Memristor-Involved Chua's Circuit and Verification in Experimental Platform. Int. J. Bifurc Chaos (2020) 30(13):2050193. doi:10.1142/S021812742050193X

CrossRef Full Text | Google Scholar

29. Kengne J. Periodicity, Chaos, and Multiple Attractors in a Memristor-Based Shinriki's Circuit. Chaos Interdiscip J Nonlinea (2015) 25:103126. doi:10.1063/1.4934653

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Li C, Yang Y, Yang X, Zi X, Xiao F. A Tristable Locally Active Memristor and its Application in Hopfield Neural Network. Nonlinear Dyn(2022) 108:1697–717. doi:10.1007/s11071-022-07268-y

CrossRef Full Text | Google Scholar

31. Sun J, Han G, Zeng Z, Wang Y. Memristor-Based Neural Network Circuit of Full-Function Pavlov Associative Memory With Time Delay and Variable Learning Rate. IEEE Trans. Cybern. (2019) 50(7):1–11. doi:10.1109/TCYB.2019.2951520

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Zhou Y, Li C, Li W, Li H, Feng W, Qian K. Image Encryption Algorithm with Circle Index Table Scrambling and Partition Diffusion. Nonlinear Dyn(2021) 103(2):2043–61. doi:10.1007/s11071-021-06206-8

CrossRef Full Text | Google Scholar

33. Zhou S, Wang X, Zhang Y, Ge B, Wang M, Gao S. A Novel Image Encryption Cryptosystem Based on True Random Numbers and Chaotic Systems. Multimed Syst (2021) 28:95–112. doi:10.1007/s00530-021-00803-8

CrossRef Full Text | Google Scholar

34. Ruan J, Sun K, Mou J, He S, Zhang L. Fractional-order Simplest Memristor-Based Chaotic Circuit with New Derivative. Eur. Phys. J. Plus (2018) 133(1):3. doi:10.1140/epjp/i2018-11828-0

CrossRef Full Text | Google Scholar

35. Liu W, Sun K, He S. SF-SIMM High-Dimensional Hyperchaotic Map and its Performance Analysis. Nonlinear Dyn(2017) 89(4):2521–32. doi:10.1007/s11071-017-3601-3

CrossRef Full Text | Google Scholar

36. Ma X, Mou J, Liu J, Ma C, Yang F, Zhao X. A Novel Simple Chaotic Circuit Based on Memristor-Memcapacitor. Nonlinear Dyn(2020) 100(3):2859–76. doi:10.1007/s11071-020-05601-x

CrossRef Full Text | Google Scholar

37. Yildirim M. DNA Encoding for RGB Image Encryption with Memristor Based Neuron Model and Chaos Phenomenon. Microelectron J (2020) 104:104878. doi:10.1016/j.mejo.2020.104878

CrossRef Full Text | Google Scholar

38. Zhang X, Li C, Dong E, Zhao Y, Liu Z. A Conservative Memristive System with Amplitude Control and Offset Boosting. Int. J. Bifurc Chaos (2022) 32(04):2250057. doi:10.1142/S0218127422500572

CrossRef Full Text | Google Scholar

39. Liu T, Banerjee S, Yan H, Mou J. Dynamical Analysis of the Improper Fractional-Order 2D-SCLMM and its DSP Implementation. Eur. Phys. J. Plus (2021) 136(5):1–17. doi:10.1140/epjp/s13360-021-01503-y

CrossRef Full Text | Google Scholar

40. Gao X, Mou J, Banerjee S, Cao Y, Xiong L, Chen X. An Effective Multiple-Image Encryption Algorithm Based on 3D Cube and Hyperchaotic Map. J King Saud Univ - Comput Inf Sci (2022) 34(4):1535–51. doi:10.1016/j.jksuci.2022.01.017

CrossRef Full Text | Google Scholar

41. Li Y, Li C, Zhang S, Chen GR, Zeng Z. A Self-Reproduction Hyperchaotic Map With Compound Lattice Dynamics. IEEE Trans. Ind. Electron. (2022) 1. doi:10.1109/TIE.2022.3144592

CrossRef Full Text | Google Scholar

42. Peng Y, Sun K, He S. A Discrete Memristor Model and its Application in Hénon Map. Chaos, Solit Fractals (2020) 137:109873. doi:10.1016/j.chaos.2020.109873

CrossRef Full Text | Google Scholar

43. Deng Y, Li Y. Bifurcation and Bursting Oscillations in 2D Non-autonomous Discrete Memristor-Based Hyperchaotic Map. Chaos, Solit Fractals (2021) 150:111064. doi:10.1016/j.chaos.2021.111064

CrossRef Full Text | Google Scholar

44. Li C, Li H, Xie W, Du J. A S-type Bistable Locally Active Memristor Model and its Analog Implementation in an Oscillator Circuit. Nonlinear Dyn(2021) 106(1):1041–58. doi:10.1007/s11071-021-06814-4

CrossRef Full Text | Google Scholar

45. Li Y, Li C, Zhao Y, Liu S. Memristor-Type Chaotic Mapping. Chaos (2022) 32(2):021104. doi:10.1063/5.0082983

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Peng Y, He S, Sun K. Chaos in the Discrete Memristor-Based System with Fractional-Order Difference. Results Phys (2021) 24:104106. doi:10.1016/j.rinp.2021.104106

CrossRef Full Text | Google Scholar

47. Wu C, Sun K, Xiao Y. A Hyperchaotic Map with Multi-Elliptic Cavities Based on Modulation and Coupling. Eur. Phys. J. Spec. Top. (2021) 230(7):2011–20. doi:10.1140/epjs/s11734-021-00126-9

CrossRef Full Text | Google Scholar

48. Ye X, Mou J, Luo C, Yang F, Cao Y. Complexity Analysis of a Mixed Memristive Chaotic Circuit. Complexity (2018) 2018:1–9. doi:10.1155/2018/8639470

CrossRef Full Text | Google Scholar