- Department of Physics, Xinzhou Teachers University, Xinzhou, China
We investigate the dynamics of rotating spin-orbit-coupled spin-1 Bose–Einstein condensates (BECs) in an in-plane gradient magnetic field, which is confined in an anharmonic trap. In the case of rotating spin-orbit-coupled spin-1 BECs with given parameters, the system evolves from initial disk-shaped condensates into drastic turbulent oscillations and ghost vortices on the surface of the component densities due to surface wave excitations and then into two final vortex necklaces along the azimuthal direction with an irregular density hole, in which the vortices differ by one quantum number in turn. For the case of rotating spin-orbit-coupled spin-1 BECs with in-plane gradient magnetic field, with the dynamic evolution, the system undergoes a transition from an initial central polar-core vortex to violent turbulent oscillations and then to a final vortex chain along the diagonal of BECs, with the remaining vortices symmetrically distributed on both sides in the individual component. In addition, the corresponding spin texture undergoes a transition from plane-wave phase to double half-antiskyrmion necklaces for the former case and a transition from a structure similar to a quadrupole magnetic field to a half-antiskyrmion chain with the rest of the half-antiskyrmions on both sides. During the dynamic evolution process, the angular momentum increases gradually and then approaches a convergent value.
1 Introduction
Spin-orbit coupling (SOC) in ultracold atomic gases has been realized experimentally in the last decade [1–3], which has greatly stimulated people’s interest in the study of spin-orbit-coupled quantum gases [4–6]. This new and controllable artificial SOC not only offers new possibilities for quantum simulations of spin quantum Hall effect [7, 8], topological insulators [9], and topological superconductors [10] but also provides a new direction for exploring exotic quantum phenomena, novel states of matter in the fields of ultracold atomic, molecular physics, and condensed matter physics [11–18].
A novel anharmonic trap (a harmonic trap with a quartic distortion) [19, 20], which confines the Bose–Einstein condensates (BECs) even if the rotation frequency exceeds the trapping frequency, has attracted great attention both in theory and experiment. Most research so far focuses on the ground-state properties of BECs in an anharmonic trap [20, 21], but there are few studies on the dynamics of BECs. In this work, we investigate the dynamics of rotating spin-orbit-coupled spin-1 BECs with an in-plane gradient magnetic field in an anharmonic trap. Our research can not only obtain the stable structures of the system but also survey the detailed physical process and interesting dynamic properties of the system from an initial quantum state to a non-equilibrium state evolution and then to a final equilibrium state, which provides a new direction for exploring quantum phenomena of spin-orbit-coupled BECs in an anharmonic trap. As a matter of fact, the interesting physical properties in dynamics of quantum systems have attracted considerable interest, which includes Zitterbewegung oscillation in quenched spin–orbit-coupled BECs [22] and dynamical phases in a quenched spin–orbit-coupled degenerate Fermi gas [23].
The study is organized as follows. The theoretical model is introduced in Section 2. In Section 3, we analyze and discuss the simulation results. Finally, we summarize our findings in Section 4.
2 Model
We consider a quasi-two-dimensional (quasi-2D) spin-orbit-coupled F = 1 spinor BECs with an in-plane gradient magnetic field in an anharmonic trap. In the mean-field framework, the dynamics of the system can be given by the dissipative Gross–Pitaevskii (GP) form [24–27].
Here, γ is the dissipation parameter. The model is a variation and generalization of that in BECs [24, 25, 28]. In addition, this model enables one not only to find the steady state of a rotating system but also to study the whole dynamical process toward the final steady state. Moreover, this model has considered the inevitable dissipation effects in actual cold atom experiments. When we switch off the dissipation term, the simulation based on the time-dependent GP equations shows that no steady state exists. In Equation 1, the Hamiltonian of the system can be written as H = H0 + Hint with
where
where ω⊥ is the radial trap frequency and
where ψj = N−1/2ahΨj (j = 0, ±1) denotes the dimensionless jth component wave function, and the total particle density is given by
For spin-1 BEC, the spin texture is defined as [33, 34].
The spatial distribution of the topological structure of the system is characterized by the topological charge density
with
The topological charge
3 Results and Discussion
In what follows, we study the dynamics of rotating spin-orbit-coupled spin-1 BECs without an in-plane gradient magnetic field and with an in-plane gradient magnetic field in an anharmonic trap. We can numerically solve the GP Eqs. 4–6 by using the split-step Fourier method [24, 25]. First, with the imaginary-time propagation method based on the Peaceman–Rachford method [35–37], the initial quantum state of the abovementioned two cases can be obtained for Ω = 0. The variation of nonzero γ does not change the dynamics of the vortex formation and the ultimate steady structure of the rotating system but only influences the relaxation time scale. In this work, we take γ = 0.03, which corresponds to a temperature of about 0.1 Tc. The relevant parameters are λ0 = 2000 and λ2 = −100, and the typical parameter of the anharmonic trap is chosen as μ =0.5.
3.1 Dynamics of Rotating Spin-Orbit-Coupled Spin-1 BECs in an Anharmonic Trap
It is to be noted that
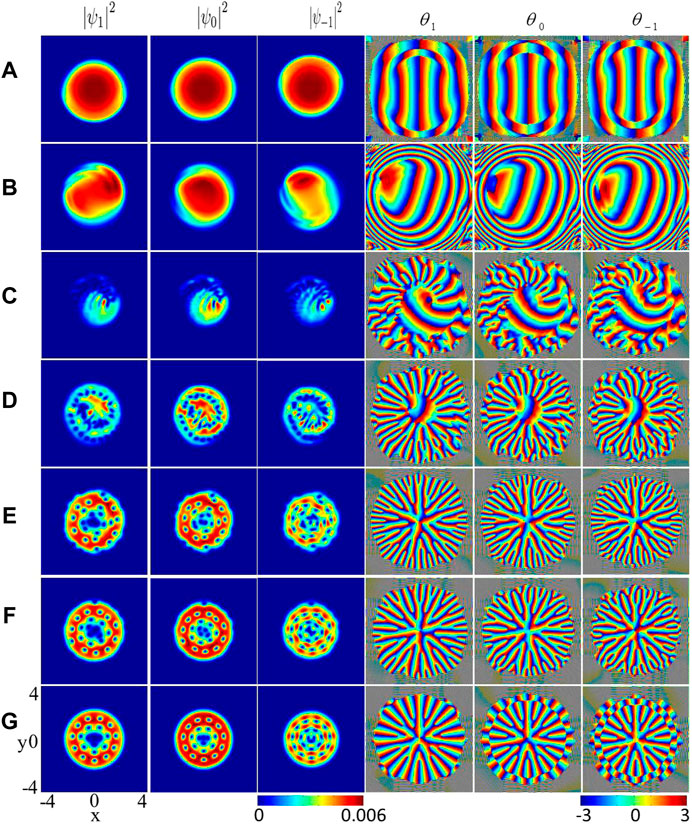
FIGURE 1. Dynamics evolution of rotated spin-orbit-coupled spin-1 BECs. The first to the third columns are the density distributions of three components
3.2 Dynamics of Rotating Spin-Orbit-Coupled Spin-1 BECs With In-Plane Gradient Magnetic Field in an Anharmonic Trap
Next, we study the dynamics of rotating spin-orbit-coupled spin-1 BECs with an in-plane gradient magnetic field in an anharmonic trap. In Figure 2A, we show the initial quantum state of spin-1 BECs with SOC strength k = 2 and in-plane quadrupole field strength B = 2. The vortices occur only in the central regions of the components mF = 1 and mF = −1, which form a polar-core vortex [41] with winding combination
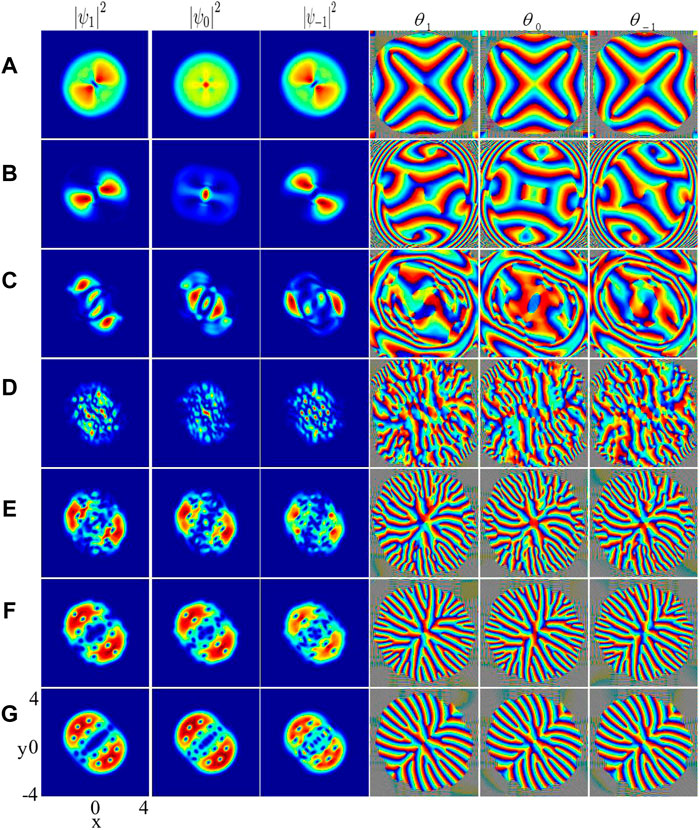
FIGURE 2. Dynamics evolution of rotated spin-orbit-coupled spin-1 BECs with an in-plane quadrupole field. The first to the third columns are the density distributions of three components
3.3 Spin Texture
The skyrmion is a type of topological soliton, which was originally suggested in nuclear physics by Skrme to elucidate baryons as a quasiparticle excitation with spins pointing in all directions to wrap a sphere [47]. A skyrmion can be viewed as the reverse of the local spin, and the spin-vector sweeps the whole unit sphere; therefore, its topological charge is Q = 1. As shown Figure 3 and Figure 4, we display the typical transitions of the topological charge density and spin texture. Displayed in Figures 3A,B are the topological charge density and the spin texture, and the corresponding density and phase distributions (t = 6) are given in Figure 1D. Figures 3C–G represent the typical local amplifications of the spin texture in Figure 3B, and Figure 3H shows the topological charge density of t = 11 (Figure 1E). Considering the limited resolution of the texture, in Figure 3I, we only show the spin texture in the core region, and the typical local amplifications of the full spin texture are given in Figures 3J–N. Our numerical calculation shows that Figures 3C–E and Figures 3J–M denote half-antiskyrmions [21, 48] with topological charge Q = −0.5, and Figures 3F,G and Figure 3N present antiskyrmions with topological charge Q = −1, which indicates that the spin texture in the process of evolution comprises different types of half-antiskyrmions (antimerons) and antiskyrmions. Due to the transitional spin texture being unstable, we cannot determine exactly what the topological defect is. Shown in Figures 3O,P are the topological density and spin texture of the steady state, and the local amplifications are given in Figures 3Q–U, Our calculation results demonstrate that the topological defect of the central region in the green spot is a hyperbolic antiskyrmion with unit topological charge Q = −1. The hyperbolic skyrmion and hyperbolic half-skyrmions have been reported in the literature [21, 47–49]. The topological defect in Figures 3Q–T is half-antiskyrmion (antimeron) with topological charge Q = −0.5, where different colors of dots represent half-antiskyrmions with different shapes. As seen from Figure 3O, there are seven half-skyrmions around the trap center, which develop into a half-antiskyrmion necklace structure along the azimuthal direction, and the external region of the cloud is occupied by a larger half-antiskyrmion necklace comprising eleven half-antiskyrmions, that is, the half-antiskyrmion necklace consists of two concentric annular half-antiskyrmions. In short, the spin texture undergoes a transition from an irregular antimeron and antiskyrmion structures to a double half-antiskyrmion necklace structure.
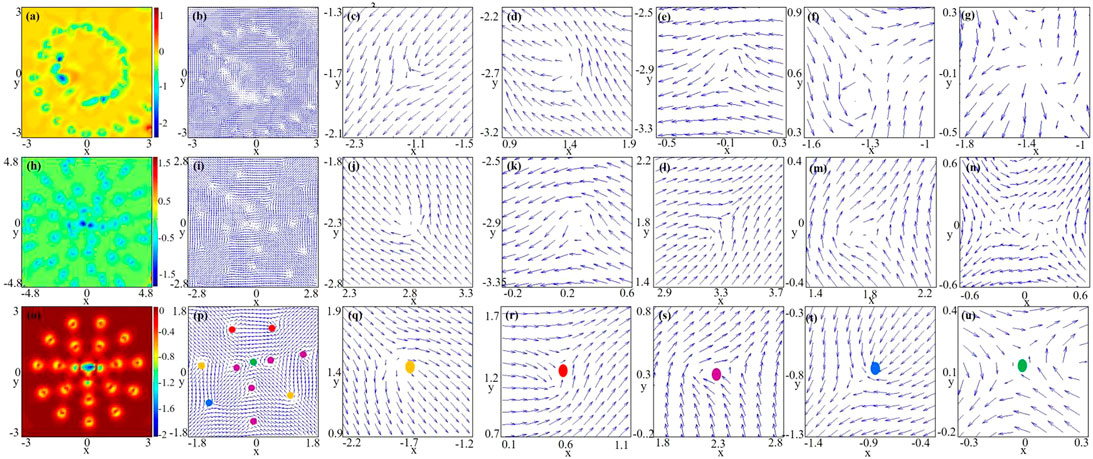
FIGURE 3. Transition of topological charge densities and spin textures in the anharmonic trap. (A–U) correspond to Figures 1D,E,G, respectively. The left two columns represent the topological charge densities and spin texture, and the right four columns denote the local enlargements of spin textures, respectively. (C–E), (I–M), (Q–T) denote half-antiskyrmions, and (F,G), (N,U) denote antiskyrmions. The unit length is a0.
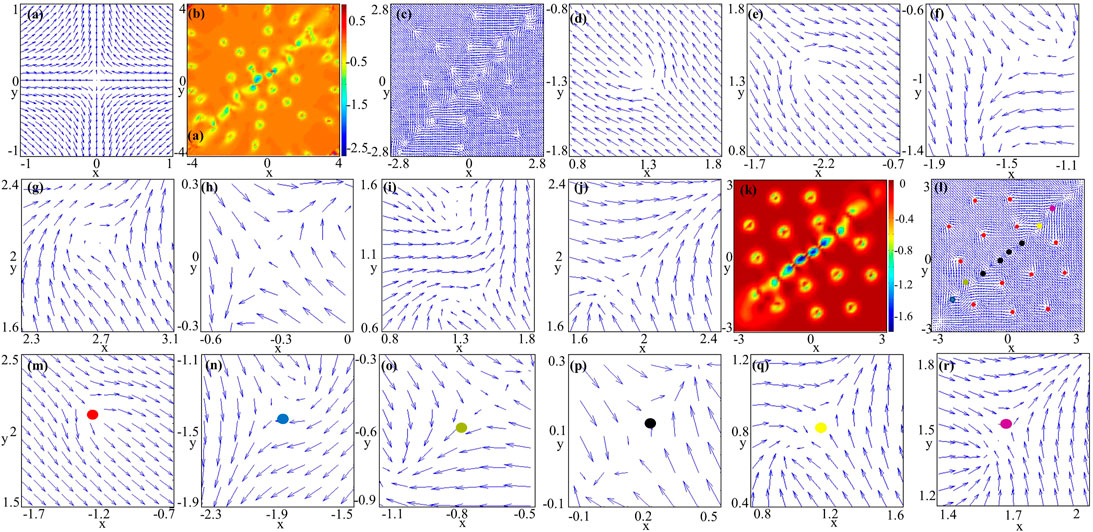
FIGURE 4. Transition of topological charge densities and spin textures. (A) is the texture of Figure 2A. (B–J) and (K–R) correspond to Figures 2F,G, respectively. (B,C) and (K,L) represent the topological charge densities and spin textures, and the rest represent the local enlargements of spin textures, which denote half-antiskyrmions, respectively. The unit length is a0.
Figure 4A shows the spin structure corresponding to Figure 2A, and it indicates that the spin of the initial state is fully magnetized into the plane and whose arrangement resembles the configuration of a quadrupole magnetic field. The center of the quadrupole magnetic field is a saddle point with the magnetic field strength being 0, which has no magnetization. However, due to the continuity of the wave function, the spin function S (r) in the center point must be continuous. If S (0) has a certain magnitude, it must point in a certain direction. However, due to the symmetry of the system, no matter S (0) choice, any direction will break the continuity of S (r) at the center point. So, S (0) can only take 0 to satisfy the continuity condition. Therefore, the components mF = 1 and mF = −1 form a central vortex core. To satisfy the conservation of angular momentum, the two vortices at the center of
The dynamic process can also be characterized by the time evolution of the average angular momentum per atom
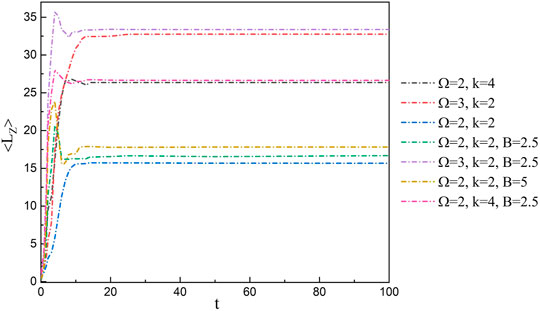
FIGURE 5. Time evolution of the average angular momentum per atom
4 Conclusion
To summarize, we investigate the dynamics of rotating spin-orbit-coupled spin-1 BECs in an in-plane gradient magnetic field, which is confined in an anharmonic trap. Such a system sustains peculiar and interesting dynamic behaviors due to the multicomponent-order parameters and the interplay among the in-plane quadrupole field, SOC, rotation, and dissipation. In order to study the dynamics, the system is rotated suddenly after the system has been prepared to an initial quantum state. For the case of rotating spin-orbit-coupled spin-1 BECs, with the dynamic evolution, the system transforms from initial disk-shaped condensates to drastic turbulent oscillations and ghost vortices on the surface of the component densities due to the surface wave excitations and then to two final steady vortex necklaces along the azimuthal direction with an irregular density hole, where the vortices in the three components differ by one quantum number in turn, whereas for the case of rotating spin-orbit-coupled spin-1 BECs with in-plane gradient magnetic field, the system evolves from an initial central polar-core vortex to violent turbulent oscillations and then to a final vortex chain along the diagonal of BECs, with the remaining vortices symmetrically distributed on both sides in the individual component. Simultaneously, the corresponding spin texture experiences a structural phase transition from plane-wave phase to double half-antiskyrmion necklaces for the former case and a transition from a structure similar to a quadrupole magnetic field to a vortex chain with half-antiskyrmions on both sides. In addition, the angular momentum increases gradually and then approaches a convergent value. These interesting findings provide new understanding and exciting perspectives for ultracold atomic gases and condensed matter physics. Although it may be a challenge to implement the present system experimentally, this system is theoretically feasible and can be achieved in principle. For instance, one may consider a spin-187Rb BEC [44, 50] or a spin-123Na BEC [51]. With the ongoing development of cold-atom experimental techniques, the system may be realized in the future and its novel quantum phases and dynamic properties are expected to be observed in experiments.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author Contributions
HY: Conceptualization, Formal analysis, Data curation, and Writing—review. QZ: Formal analysis. ZJ: Investigation, Supervision, and Writing—review editing.
Funding
This work was supported by Shanxi Education Department Fund (2020L0546).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Lin YJ, Jiménez-García K, Spielman IB. Spin-orbit-coupled Bose-Einstein Condensates. Nature 471 (2011) 83, 6.doi:10.1038/nature09887
2. Wu Z, Zhang L, Sun W, Xu XT, Wang BZ, Ji SC, et al. Realization of Two-Dimensional Spin-Orbit Coupling for Bose-Einstein Condensates. Science (2016) 354:83–8. doi:10.1126/science.aaf6689
3. Li JR, Lee J, Huang W, Burchesky S, Shteynas B, Top FÇ, et al. A Stripe Phase with Supersolid Properties in Spin-Orbit-Coupled Bose-Einstein Condensates. Nature (2017) 543:91–4. doi:10.1038/nature21431
4. Wang P, Yu ZQ, Fu Z, Miao J, Huang L, Chai S, et al. Spin-orbit Coupled Degenerate Fermi Gases. Phys Rev Lett (2012) 109:095301. doi:10.1103/PhysRevLett.109.095301
5. Cheuk LW, Sommer AT, Hadzibabic Z, Yefsah T, Bakr WS, Zwierlein MW. Spin-injection Spectroscopy of a Spin-Orbit Coupled Fermi Gas. Phys Rev Lett (2012) 109:095302. doi:10.1103/PhysRevLett.109.095302
6. Wang ZY, Cheng XC, Wang BZ, Zhang JY, Lu YH, Yi CR, et al. Realization of an Ideal Weyl Semimetal Band in a Quantum Gas with 3d Spin-Orbit Coupling. Science (2021) 372:271–6. doi:10.1126/science.abc0105
7. Kato YK, Myers RC, Gossard AC, Awschalom DD. Observation of the Spin Hall Effect in Semiconductors. Science (2004) 306:1910–3. doi:10.1126/science.1105514
8. Xiao D, Chang MC, Niu Q. Berry Phase Effects on Electronic Properties. Rev Mod Phys (2010) 82:1959–2007. doi:10.1103/revmodphys.82.1959
9. Qi XL, Zhang SC. Topological Insulators and Superconductors. Rev Mod Phys (2011) 83:1057–110. doi:10.1103/revmodphys.83.1057
10. Read N, Green D. Paired States of Fermions in Two Dimensions with Breaking of Parity and Time-Reversal Symmetries and the Fractional Quantum Hall Effect. Phys Rev B (2000) 61:10267–97. doi:10.1103/physrevb.61.10267
11. Zhai H. Degenerate Quantum Gases with Spin-Orbit Coupling: a Review. Rep Prog Phys (2015) 78:026001. doi:10.1088/0034-4885/78/2/026001
12. Sinha S, Nath R, Santos L. Trapped Two-Dimensional Condensates with Synthetic Spin-Orbit Coupling. Phys Rev Lett (2011) 107:270401. doi:10.1103/physrevlett.107.270401
13. Jiang X, Fan Z, Chen Z, Pang W, Li Y, Malomed BA. Two-dimensional Solitons in Dipolar Bose-Einstein Condensates with Spin-Orbit Coupling. Phys Rev A (2016) 93:023633. doi:10.1103/physreva.93.023633
14. Poon TFJ, Liu XJ. Quantum Spin Dynamics in a Spin-Orbit-Coupled Bose-Einstein Condensate. Phys Rev A (2016) 93:063420. doi:10.1103/physreva.93.063420
15. Kartashov YV, Konotop VV. Solitons in Bose-Einstein Condensates with Helicoidal Spin-Orbit Coupling. Phys Rev Lett (2017) 118:190401. doi:10.1103/physrevlett.118.190401
16. Liu CF, Juzeliūnas G, Liu WM. Spin-orbit Coupling Manipulating Composite Topological Spin Textures in Atomic-Molecular Bose-Einstein Condensates. Phys Rev A (2017) 95:023624. doi:10.1103/physreva.95.023624
17. Yang S, Wu F, Yi W, Zhang P. Two-body Bound State of Ultracold Fermi Atoms with Two-Dimensional Spin-Orbit Coupling. Phys Rev A (2019) 100:043601. doi:10.1103/physreva.100.043601
18. Wang JG, Li YQ. Vortex Lattices in a Rotating Spin-Orbit Coupled Spin-1/2 Bose-Einstein Condensates with Spatially Modulated Nonlinear Interaction. Results Phys (2020) 17:103099. doi:10.1016/j.rinp.2020.103099
19. Fetter AL, Jackson B, Stringari S. Rapid Rotation of a Bose-Einstein Condensate in a Harmonic Plus Quartic Trap. Phys Rev A (2005) 71:013605. doi:10.1103/physreva.71.013605
20. Su N, Wang Q, Hu J, Su X, H WL. Topological Defects in Rotating Spin-Orbit-Coupled Dipolar Spin-1 Bose-Einstein Condensates. J Phys B (2020) 53:215301. doi:10.1088/1361-6455/abb031
21. Shi CX, Wen L, Wang Q, Yang H, Wang H. Topological Defects of Spin-Orbit-Coupled Bose-Einstein in a Rotating Anharmonic Trap. J Phys Soc Jpn (2018) 87:094003. doi:10.7566/jpsj.87.094003
22. Qu C, Hamner C, Gong M, Zhang C, Engels P. Observation of Zitterbewegung in a Spin-Orbit-Coupled Bose-Einstein Condensate. Phys Rev A (2013) 88:021604. doi:10.1103/physreva.88.021604
23. Dong Y, Dong L, Gong M, Pu H. Dynamical Phases in Quenched Spin-Orbit-Coupled Degenerate Fermi Gas. Nat Commun (2015) 6:6103. doi:10.1038/ncomms7103
24. Wen L, Xiong H, Wu B. Hidden Vortices in a Bose-Einstein Condensate in a Rotating Double-Well Potential. Phys Rev A (2010) 82:053627. doi:10.1103/physreva.82.053627
25. Wen LH, Luo XB. Formation and Structure of Vortex Lattices in a Rotating Double-Well Bose-Einstein Condensate. Laser Phys Lett (2012) 9:618. doi:10.7452/lapl.201210044
26. Kasamatsu K, Tsubota M, Ueda M. Nonlinear Dynamics of Vortex Lattice Formation in a Rotating Bose-Einstein Condensate. Phys Rev A (2003) 67:033610. doi:10.1103/physreva.67.033610
27. Wang QB, Hu JG, Su XH, Wen LH. Dynamics of Rotating Spin-Orbit-Coupled Bose-Einstein Condensates in a Quasicrystalline Optical Lattice. Results Phys (2021) 20:103755. doi:10.1016/j.rinp.2020.103755
28. Tsubota M, Kasamatsu K, Ueda M. Vortex Lattice Formation in a Rotating Bose-Einstein Condensate. Phys Rev A (2002) 65:023603. doi:10.1103/physreva.65.023603
29. Kawaguchi Y, Ueda M. Spinor Bose-Einstein Condensates. Phys Rep (2012) 520:253. doi:10.1016/j.physrep.2012.07.005
30. Stamper-Kurn DM, Ueda M. Spinor Bose Gases: Symmetries, Magnetism, and Quantum Dynamics. Rev Mod Phys (2013) 85:1191. doi:10.1103/revmodphys.85.1191
31. Martikainen JP, Collin A, Suominen KA. Coreless Vortex Ground State of the Rotating Spinor Condensate. Phys Rev A (2002) 66:053604. doi:10.1103/physreva.66.053604
32. Lovegrove J, Borgh MO, Ruostekoski J. Energetically Stable Singular Vortex Cores in an Atomic Spin-1 Bose-Einstein Condensate. Phys Rev A (2012) 86:013613. doi:10.1103/physreva.86.013613
33. Mizushima T, Kobayashi N, Machida K. Coreless and Singular Vortex Lattices in Rotating Spinor Bose-Einstein Condensates. Phys Rev A (2004) 70:043613. doi:10.1103/physreva.70.043613
34. Kasamatsu K, Tsubota M, Ueda M. Spin Textures in Rotating Two-Component. Bose-Einstein condensates (2005) 71:043611. doi:10.1103/physreva.71.043611
35. Zhang Y, Mao L, Zhang C. Mean-field Dynamics of Spin-Orbit Coupled Bose-Einstein Condensates. Phys Rev Lett (2012) 108:035302. doi:10.1103/PhysRevLett.108.035302
36. Peaceman DW, Rachford HH. The Numerical Solution of Parabolic and Elliptic Differential Equations. J Soc Ind Appl Math (1955) 3:28. doi:10.1137/0103003
37. Wen L, Qiao Y, Xu Y, Mao L. Structure of Two-Component Bose-Einstein Condensates with Respective Vortex-Antivortex Superposition States. Phys Rev A (2013) 87:033604. doi:10.1103/physreva.87.033604
38. Wang C, Gao C, Jian CM, Zhai H. Spin-orbit Coupled Spinor Bose-Einstein Condensates. Phys Rev Lett (2010) 105:160403. doi:10.1103/physrevlett.105.160403
39. Yang H, Wang Q, Su N, Wen L. Topological Excitations in Rotating Bose-Einstein Condensates with Rashba-Dresselhaus Spin-Orbit Coupling in a Two-Dimensional Optical Lattice. Eur Phys J Plus (2019) 134:589. doi:10.1140/epjp/i2019-12988-y
40. Liu CF, M LW. Spin-orbit-coupling-induced Half-Skyrmion Excitations in Rotating and Rapidly Quenched Spin-1 Bose-Einstein Condensates. Phys Rev A (2012) 86:033602. doi:10.1103/physreva.86.033602
41. Sadler LE, Higbie JM, Leslie SR, Vengalattore M, Stamper-Kurn DM. Spontaneous Symmetry Breaking in a Quenched Ferromagnetic Spinor Bose-Einstein Condensate. Nature (2006) 443:312. doi:10.1038/nature05094
42. Wang JG, Yang SJ. Ground-state Phases of Spin-Orbit-Coupled Spin-1 Bose-Einstein Condensate in a Plane Quadrupole Field. J Phys.:Condens Matter (2018) 30:295404. doi:10.1088/1361-648x/aacc42
43. Li J, Liu WM. Ground State of Spin-Orbit Coupled Rotating Two-Component Bose-Einstein Condensate in Gradient Magnetic Field. Acta Phys Sin (2018) 67:110302. doi:10.7498/aps.67.20180539
44. Luo X, Wu L, Chen J, Guan Q, Gao K, Xu Z, et al. Tunable Atomic Spin-Orbit Coupling Synthesized with a Modulating Gradient Magnetic Field. Sci Rep (2016) 6:18983. doi:10.1038/srep18983
45. Xu ZF, You L, Ueda M. Atomic Spin-Orbit Coupling Synthesized with Magnetic-Feld-Gradient Pulses. Phys Rev A (2013) 87:063634. doi:10.1103/physreva.87.063634
46. Anderson BM, Spielman IB, Juzeliunas G. Magnetically Generated Spin-Orbit Coupling for Ultracold Atoms. Phys Rev Lett (2013) 111:125301. doi:10.1103/physrevlett.111.125301
47. Skyrme THR. A Unified Field Theory of Mesons and Baryons. Nucl Phys (1962) 31:556. doi:10.1016/0029-5582(62)90775-7
48. Kasamatsu K, Tsubota M, Ueda M. Vortex Molecules in Coherently Coupled Two-Component Bose-Einstein Condensates. Phys Rev Lett (2004) 93:250406. doi:10.1103/physrevlett.93.250406
49. Liu CF, Fan H, Zhang YC, Wang DS, Liu WM. Circular-hyperbolic Skyrmion in Rotating Pseudo-spin-1/2 Bose-Einstein Condensates with Spin-Orbit Coupling. Phys Rev A (2012) 86:053616. doi:10.1103/physreva.86.053616
50. Campbell DL, Price RM, Putra A, Valdés-Curiel A, Trypogeorgos D, Spielman IB. Magnetic Phases of Spin-1 Spin-Orbit-Coupled Bose Gases. Nat commun. (2016) 7:10897. doi:10.1038/ncomms10897
Keywords: spin-orbit-coupled Bose-Einstein condensates, Anharmonic trap, dynamics, vortex, skyrmion
Citation: Yang H, Zhang Q and Jian Z (2022) Dynamics of Rotating Spin-Orbit-Coupled Spin-1 Bose-Einstein Condensates With In-Plane Gradient Magnetic Field in an Anharmonic Trap. Front. Phys. 10:910818. doi: 10.3389/fphy.2022.910818
Received: 01 April 2022; Accepted: 06 June 2022;
Published: 13 July 2022.
Edited by:
Lauro Tomio, Sao Paulo State University, BrazilReviewed by:
Charles Reichhardt, Los Alamos National Laboratory (DOE), United StatesFarhad Sattari, University of Mohaghegh Ardabili, Iran
Copyright © 2022 Yang, Zhang and Jian . This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hui Yang, eWFuZ2h1aTIwMDMyMDAyQDE2My5jb20=
 Hui Yang
Hui Yang Qing Zhang
Qing Zhang