Entanglement Between Two Mechanical Oscillators in a Dual-Coupling Optomechanical System

In this study, we investigated the properties of entanglement of an optomechanical system including two mechanical oscillators, where two mechanical oscillators are coupled with the cavity field in different coupling modes: the interaction between one mechanical oscillator and cavity field is first-order coupling, and the interaction between the other and the cavity field is quadratic coupling. On the one hand, the entanglement between two mechanical oscillators is studied. The influence of the frequency of the cavity field, the mass of mechanical oscillators, and the temperature of mechanical oscillators on the entanglement between two mechanical oscillators are investigated. On the other hand, for the given parameters of the system, we also obtained the entanglement between the cavity field and the mechanical oscillator that has a quadratic coupling. Compared with the entanglement between microscopic particles, the stable macroscopic quantum entanglement between two mechanical oscillators has the characteristics of long existence life and can be reused, and it also plays an important role in quantum information processing and quantum network construction.

1 Introduction

As an important resource of quantum information processing, quantum entanglement has always been a research hotspot in the field of quantum physics. In recent decades, researchers have obtained quantum entanglement in different physical systems [1–5], such as atomic system, ion trap system, and photon system. People use quantum entanglement to realize quantum teleportation [6], quantum dense coding [7], quantum remote state preparation [8], and construction of quantum logic gate [9]. These applications fully show the importance of quantum entanglement in the process of quantum information processing. In addition, quantum entanglement can also explore the basic physical problems in quantum mechanics, such as implicit variable theory and quantum non-locality [10, 11]. In recent years, a new physical system, that is, a cavity optomechanical system [12], has emerged in the field of the research of quantum information processing. The cavity optomechanical system can effectively couple the degree of freedom of photon with the degree of freedom of the mechanical oscillator, which can bring many novel physical phenomena [13–15]. People can use the cavity optomechanical system to perform quantum precision measurement [16], and they can couple the atomic system [17] or quantum dot system [18] with a cavity optomechanical system to realize coupling of more degree of freedom. In the coupling system with multi-degree of freedom, researchers can obtain the quantum nonlinear phenomena such as optomechanical induced transparency [19] and optical bistability [20].

At present, the manipulation of cavity optomechanics has become a kind of quantum control technology, which has been widely extended and applied. Vitali and his coworkers from Italy realized the entanglement of the cavity field and mechanical oscillator in the cavity optomechanical system [21]. This research team also proposed the coupling among the optical cavity, moving cavity mirror, and microwave cavity, and entangled the optical cavity mode and microwave cavity mode with the help of a mechanical oscillator [22]. For further research, they extended to the multi-degree of the freedom coupling system [23], and realized the entanglement among atom, moving mirror, and cavity field by coupling the cavity field with atom and mechanical oscillator at the same time. It is reported in nature that the stable quantum entanglement between two mechanical oscillators is realized by using this coupling [24]. The experimental realization of this macroscopic superposition state and macroscopic quantum entanglement state has become a new important milestone in the field of quantum physics. Since we know that the quantum entanglement of this macroscopic steady-state system has the characteristics of a long lifetime and can be reused, this plays an important role in quantum information processing and quantum network construction.

In this study, we consider an optical cavity containing the two mechanical oscillators, where the two mechanical oscillators are in cases of linear and quadratic coupling, respectively. When the cavity is driven by a laser, we investigate the properties of entanglement of the system. For the multibody system, the values of the logarithmic negativity can determine whether the system has entanglement. By calculating the logarithmic negativity, we analyze the possibility of entanglement between two oscillators in different cases where we choose different cavity frequencies and different masses of oscillators. Compared with the existing reported works, we also studied the entanglement between a single oscillator and cavity field. The remainder of this study is organized as follows. In Section 2, we show the theoretical model of a dual-coupling optomechanical system where the two mechanical oscillators are coupled with the cavity field in different coupling modes. In Section 3, some numerical results are shown, and we discuss the possibility of entanglement for different physical parameters. Finally, the results are summarized in Section 4.

2 Theoretical Model

Here, we consider a Fabry–Pérot optical cavity in Figure 1, which is composed of two parallel mirrors separated by a certain distance. The reflectivity of the mirrors is nearly unity. The reflectivity of the left mirror is slightly lower than that of the right mirror whose reflectivity is one, so the light is emitted from the left. The stable standing wave can be produced in the optical cavity when we use an incident light field to drive the optical cavity. For the standing wave, its energy is not static but flowing periodically to and fro between wave antinode and wave node. Moreover, we know the change of energy of the wave node and the wave antinodes have their own characteristics. In this study, two partially transparent dielectric membranes are placed in the optical cavity, and they can be looked as mechanical oscillators under the interaction of radiation pressure. By analyzing the changes of the standing wave, it is well known that the optomechanical coupling between the mechanical mode of oscillators and the optical mode is related to the position of membranes [25]. If the membrane is placed in the vicinity of the wave antinode of the standing wave field, then the dependence of optomechanical coupling strength on position is mainly linear, and the quadratic term and higher-order terms can be ignored. If the membrane oscillates around the node, the quadratic term of optomechanical coupling strength is much larger than other terms. When the optical cavity is driven by a driving field with amplitude $E$ and frequency ${\omega }_p$, the Hamiltonian of the total system can be expressed as follows:

$\mathrm{\mathscr{H}}=\hslash {\mathrm{\Delta }}_0{a}^{†}a+\frac{\hslash {\omega }_m}{2}\left(p_1^2+q_1^2\right)+\frac{\hslash {\omega }_m}{2}\left(p_2^2+q_2^2\right)-\hslash G_1{a}^{†}a{q}_1+\hslash G_2{a}^{†}a{q}_2^2+i\hslash E\left(a^{†}-a\right),(1)$

where we also perform a rotation transformation about frequency ${\omega }_p$ of the driving field. The first term of Eq. 1 describes the energy of the cavity modes and gives the annihilation and creation operators of the cavity modes a and $a^{†}$ ([a, $a^{†}$] $=$ 1), ${\omega }_c$ and $\kappa$ are cavity frequency and attenuation rate, respectively, and ${\text{Δ}}_0={\omega }_c-{\omega }_p$ is the detuning with respect to the frequency of the incident driving field. The second and third terms give the energy of the mechanical oscillator modes, which are modeled as a harmonic oscillator with the same resonance frequency with ${\omega }_m$ and the effective mass $m$, and dimensionless positions and momentum operators $q_{l=\mathrm{1,2}}$, and $p_{l=\mathrm{1,2}}$ ([$q_l$, $p_l$ ] = $i\hslash$). The couplings of harmonic oscillators with the cavity field produced by the radiative pressure are shown in the fourth and fifth terms, where the coupling constants $G_1=$ (${\omega }_c/L$) $\sqrt{\hslash /m{\omega }_m}$ and $G_2=$ (${\omega }_c$/L²) $\times \hslash /m{\omega }_m$ (L is dependent on the effective length of the cavity geometry). Furthermore, we need to state that one follows a first-order coupling about the position and the other coupling is a quadratic coupling about the position. The last term describes the interaction of the cavity field with the incident driving laser with frequency ${\omega }_p$ and amplitude $E$, where the relation of the amplitude $E$ with the laser power $P$ is expressed as $\left|E\right|=\sqrt{2P\kappa /\hslash {\omega }_p}$. As long as one drives only the single cavity mode, the mechanical frequency ${\omega }_m$ is much smaller than the cavity free spectral range (FSR $\sim c/2L$). In this case, photon scattering from the driving modes to other cavity modes can be neglected.

FIGURE 1

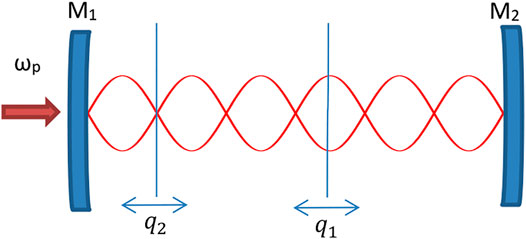
FIGURE 1. Schematic diagram of a Fabry–Pérot optical cavity coupling with two partially transparent dielectric membranes which can be looked as two oscillators. The positions of membranes 1 and 2 in cavity are expressed as $q_1$ and $q_2$, respectively.

Using the Heisenberg equation of motion, we can establish the evolution equation of the system operators. In addition, the dynamics of the total system also depends on the fluctuating dissipative processes affecting the optical and mechanical modes; that is, the corresponding damping and noise terms are also added to the evolution equation. Finally, the quantum Langevin equations of the system operators can be written as follows:

$\begin{array}{l}{\dot{q}}_1={\omega }_m{p}_1,\\ {\dot{q}}_2={\omega }_m{p}_2,\\ {\dot{p}}_1=-{\omega }_m{q}_1+G_1{a}^{†}a-{\gamma }_m{p}_1+\xi ,\\ {\dot{p}}_2=-{\omega }_m{q}_2-2G_2{a}^{†}a{q}_2-{\gamma }_m{p}_2+\xi ,\\ \dot{a}=-i{\mathrm{\Delta }}_{0}a+i{G}_{1}a{q}_1-i{G}_{2}a{q}_2^2+E-\kappa a+\sqrt{2\kappa }{a}^{in},\end{array}(2)$

where ${\gamma }_m$ is the mechanical damping rate, $a^{in}$ is an operator of the vacuum radiation input noise, and $\text{ξ}$ denotes the Hermitian Brownian noise operator. We can obtain correlation functions satisfied by these noise operators: the non-zero correlation function of $a^{in}$ is $\langle a^{in}\left(t\right)a^{in,†}\left(t^{\prime }\right)\rangle =\langle \delta \left(t-t^{\prime }\right)\rangle$ and the correlation functions of and the noise operator $\text{ξ}$ may be expressed as $\langle \xi \left(t\right)\xi \left(t^{\prime }\right)\rangle =\frac{{\gamma }_m}{{\omega }_m}{\displaystyle \int \frac{d\omega }{2\pi }{e}^{-i\omega \left(t-t^{\prime }\right)}}\omega \left[\coth \left(\frac{\hslash \omega }{2k_{B}T}\right)+1\right]$ ($k_B$ is the Boltzmann constant and $T$ is the temperature of the oscillators). For solving Eq. 2, we can rewrite each Heisenberg operator as a steady-state mean value of the $c$-number plus an additional fluctuation operator around the steady-state mean value:

$\begin{array}{l}a={\alpha }_S+\delta a,\\ q_l=q_{l,S}+\delta q_l,l=1, 2, \\ p_l=p_{l,S}+\delta p_l, l=1, 2,\end{array}(3)$

where we only consider the first-order terms in the fluctuations in Eq. 3. Substituting Eq. 3 into Eq. 2, we can obtain the equations satisfied by steady-state mean values $p_{1S}=$ 0, $p_{2S}=0$, $q_{1S}=\frac{G_1\left|{\alpha }_S\right|}{{\omega }_m}$, $q_{2S}=0$, and ${\alpha }_S= \frac{E}{\kappa +i\Delta }$, where $\text{Δ}={\text{Δ}}_0-\frac{G_1^2|{\alpha }_S{|}^2}{{\omega }_m}$ represents the effective cavity detuning. We also obtain the equations that the first-order fluctuation operators obey:

$\begin{array}{l}\delta {\dot{q}}_1={\omega }_m\delta p_1,\\ \delta {\dot{q}}_2={\omega }_m\delta p_2,\\ \delta {\dot{p}}_1=-{\omega }_m\delta q_1+G\delta X-{\gamma }_m\delta p_1+\xi ,\\ \delta {\dot{p}}_2=-[{\omega }_m+2G_2{\left|{\alpha }_s\right|}^2\delta q_2-2G^{\prime }{q}_{2s}\delta X-{\gamma }_m\delta p_2+\xi ,\\ \delta \dot{X}=\mathrm{\Delta }\delta Y-\kappa \delta X+\sqrt{2\kappa }{X}^{in},\\ \delta \dot{Y}=-\Delta \mathrm{\delta }X-\kappa \delta Y+G\delta q_1-2G^{\prime }{q}_{2s}\delta q_2+\sqrt{2\kappa }{Y}^{in},\end{array}(4)$

where and stand for the effective optomechanical coupling parameters. In the process of deriving Eq. 4, we assume the power of the incident driving field is large enough, that is, so we may neglect the nonlinear terms such as a† a and a q, and we only retain linear terms in Eq. 4. Comparing the coupling parameters as shown in Eq. 1, the effective optomechanical coupling parameters and become larger. In addition, we introduce the cavity field quadratures and as well as the corresponding quadratures of Hermitian input noise operators and. The existence of the driving field enhances the coupling between the oscillators and the cavity field; that is, the effective optomechanical coupling is helpful to produce significant optomechanical entanglement. Here, we consider the case where the system is in a steady state. We know that once the system enters a unique steady state, it no longer depends on the initial conditions since the quantum noise of the and is a zero mean quantum Gaussian noise, and the dynamics is linearized. In addition, the quantum steady state for the fluctuations can be expressed as a zero mean bipartite Gaussian state, and it is fully characterized by its 6 × 6 correlation matrix, where is the vector of the continuous variable fluctuation operator. Vector of the noise is written as, and the coefficient matrix of Eq. 4 is given by

$A=\left(\begin{array}{cccccc}0& {\omega }_m& 0& 0& 0& 0\\ -{\omega }_m& -{\gamma }_m& 0& 0& G& 0\\ 0& 0& 0& {\omega }_m& 0& 0\\ 0& 0& -\left[{\omega }_m+2G_2|{\alpha }_S{|}^2\right]& -{\gamma }_m& 0& 0\\ 0& 0& 0& 0& -\kappa & \mathrm{\Delta }\\ G& 0& 0& 0& -\mathrm{\Delta }& -\kappa \end{array}\right).(5)$

Equation 4 can be written in a compact form as $\dot{u}\left(t\right)=Au\left(t\right)+n\left(t\right)$. The solution of $u\left(t\right)$ can be expressed as $u\left(t\right)=M\left(t\right)u\left(0\right)+\underset{0}{\overset{t}{{\displaystyle \int }}}d{t}^{\prime }M\left(t^{\prime }\right)n\left(t-t^{\prime }\right)$, where $M\left(t\right)=\exp \left(At\right)$. Matrix element $V_{ij}={\displaystyle \sum _{k,l}{\displaystyle \underset{0}{\overset{\infty }{\int }}dt}}{\displaystyle \underset{0}{\overset{\infty }{\int }}d{t}^{\prime }}{M}_{ik}\left(t\right)M_{jl}\left(t^{\prime }\right){\Phi }_{k,l}\left(t-t^{\prime }\right)$, where ${\Phi }_{kl}\left(t-t^{\prime }\right)=\left(\langle n_k\left(t\right)n_l\left(t^{\prime }\right)\rangle +\langle n_l\left(t^{\prime }\right)n_k\left(t\right)\rangle \right)/2$ is the matrix of the stationary noise correlation function. Thermal noise $\xi$ (t) has non-zero correlation function $\langle \xi \left(t\right)\xi \left(t^{\prime }\right)+\langle \xi \left(t^{\prime }\right)\xi \left(t\right)\rangle /2\simeq {\gamma }_m\left(2{\overline{n}}_{th}+1\right)\delta \left(t-t^{\prime }\right)$, where ${\overline{n}}_{th}={\left(\exp \left\{\hslash {\omega }_m/k_{B}T\right\}-1\right)}^{-1}$ is the average number of thermal phonon number of the mechanical oscillators. According to the calculation for the stationary noise correlation function, we can obtain ${\Phi }_{kl}=D_{kl}\delta \left(t-t^{\prime }\right)$, where $D=Diag\left[0,{\gamma }_m\left(2\overline{n}+1\right),0,{\gamma }_m\left(2\overline{n}+1\right),\kappa ,\kappa \right]$ is a diagonal matrix and the correlation matrix becomes $V=$ ${\displaystyle \underset{0}{\overset{\infty }{\int }}dtM\left(t\right)DM{\left(t\right)}^T}$.

When the system reaches a steady state, we can let $M\left(t=\infty \right)$ be equal to zero. Steady-state correlation matrix $V$ can be obtained from the solution of the Lyapunov equation

$V{A}^T+AV=-D.(6)$

Correlation matrix $V$ is represented as six 2 $\times$ 2 matrices $K_{m_1}$, $L_{m_1{m}_2}$, $L_{c{m}_1}$, $K_{m_2}$, $L_{c{m}_2}$, and $K_c$,

$V=\left(\begin{array}{ccc}{K}_{m_1}& L_{m_1{m}_2}& L_{c{m}_1}\\ L_{m_1{m}_2}^T& K_{m_2}& L_{c{m}_2}\\ L_{c{m}_1}^T& L_{c{m}_2}^{\text{T}}& K_c\end{array}\right),(7)$

where subscripts $m_1$, $m_2$, and $c$ represent oscillator 1, 2, and cavity field, respectively, and superscript T represents the transpose of matrix. $K_{m_1}$, $K_{m_2}$, and $K_c$ stand for the variances of the mechanical oscillator mode 1, the mechanical oscillator mode 2, and the cavity field mode, respectively. $L_{m_1{m}_2}$, $L_{c{m}_1}$, and $L_{c{m}_2}$ represent the correlation between the mechanical oscillator modes 1 and 2, mechanical oscillator mode 1 and the cavity mode, and mechanical oscillator mode 2 and the cavity mode, respectively. In order to calculate quantitatively the entanglement between two modes, we considered the amount of logarithmic negativity $E_{\mathcal{N}}$, which may be expressed as [26, 27].

$E_{\mathcal{N}}=\max \left[0,-\ln 2{\mathit{\eta }}^{-}\right],(8)$

where ${\eta }^{-}\equiv 2^{-\frac{1}{2}}{\left\{-{\left[\Sigma {\left(V_{4\times 4}\right)}^2-4\det V_{4\times 4}\right]}^{1/2}+\Sigma \left(V_{4\times 4}\right)\right\}}^{1/2}$, where $V_{4\times 4}$ is a 4 $\times 4$ matrix. When we investigate the entanglement between two of the three modes, we choose matrix $V_{4\times 4}$ from correlation matrix $V$, and then we performed calculations on $\Sigma \left(V_{4\times 4}\right)$ and det $V_{4\times 4}$ based on the selected matrix. For example, if we want to discuss the entanglement between the two oscillators, the 4 $\times 4$ matrix from correlation matrix $V$ can be expressed as $\left(\begin{array}{cc}{K}_{m_1}& L_{m_1{m}_2}\\ L_{m_1{m}_2}^T& K_{m_2}\end{array}\right)$.

3 Results and Discussions

In this section, we will talk about the properties of the entanglement of the system. Here, values of physical parameters are based on Ref. [21]. Some common parameter values include Planck’s constant $h=6.6260689633\ast {10}^{-34} J\cdot s$, $\hslash =h/2\pi$, the speed of light in vacuum $c=299792458 m/s$, Boltzmann’s constant $k=1.380649\ast {10}^{-23} J/K$, the power of incident light $P=5\ast {10}^{-2} W$, the center wavelength of incident light $\lambda =8.1\ast {10}^{-7} m$, the length of cavity $L=1\ast {10}^{-3} m$, the damping rate $\frac{\gamma }{2\pi }=100 Hz$, the center frequency of incident light ${\omega }_0=\left(2\ast \pi \ast c\right)/\lambda$, the mean thermal excitation number $\overline{n}={\left(\exp \left\{\hslash {\omega }_m/k_{B}T\right\}-1\right)}^{-1}$, the decay rate of cavity $\kappa =\left(\pi \ast c\right)/\left(F\ast L\right)$, and the frequency of mechanical oscillator $\frac{{\omega }_m}{2\pi }={10}^{7}Hz$. First, we investigated the properties of the entanglement of the two oscillators based on the logarithmic negativity. Logarithmic negativity $E_N$ is plotted as a function of the normalization detuning $\Delta /{\omega }_m$ for the different cavity frequencies ${\omega }_c$ in Figure 2, where the values of mass of oscillators and the optical finesse are the same as those in Ref. 21: the mass of the oscillator $m=5\ast {10}^{-9}$ kg and the finesse $F=3.4\ast 10^4$. For a solid line, ${\omega }_c=3\ast {\omega }_0$; for a dash line, ${\omega }_c=3.5\ast {\omega }_0$; and for a dotted line, ${\omega }_c=4\ast {\omega }_0$.

FIGURE 2

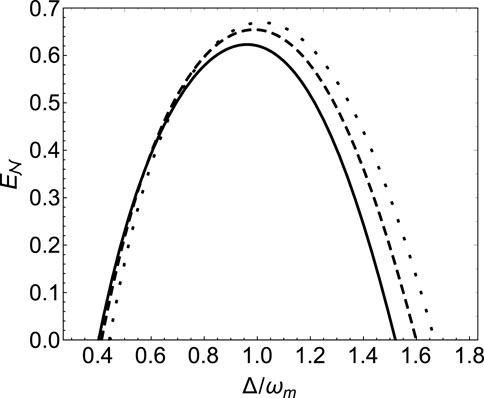
FIGURE 2. Logarithmic negativity $E_N$ is plotted as a function of the normalization detuning $\Delta /{\omega }_m$ for different cavity frequencies ${\omega }_c$. The solid line refers to ${\omega }_c=3\ast {\omega }_0$, the frequency corresponding to the dash line is $3.5\ast {\omega }_0$, and for the dotted line, ${\omega }_c=4\ast {\omega }_0$. The temperature is T = 0.4.

From Figure 2, we know that logarithmic negativity $E_N$ is greater than zero when the values of the normalization detuning are in a certain range; that is, the entanglement between the two oscillators exists in these specific ranges. Beyond the range, $E_N=0$, which means the entanglement between the two oscillators will vanish; that is, for the given oscillators, the realization of entanglement requires strict control of the frequency of the incident field. For different cavity frequencies, we can also know that the maximum values of the logarithmic negativity $E_N$ are different and the maximum values appear near the place where the normalization detuning is equal to 1. In addition, by changing the cavity frequencies, we can make the peak of the logarithmic negativity become larger, and the variation range of the maximum values is between 0.6 and 0.7. We also find the peak shifts slowly to the right with the increasing of the cavity field frequency.

Next, we show logarithmic negativity $E_N$ against temperature $T$ of the system temperature for different frequencies of cavity in Figure 3, where we let $\Delta /{\omega }_m=1$; the values of other parameters are the same as those mentioned in Figure 2. The entanglement between the two oscillators can be obtained within a certain temperature range. The overall trends of the logarithmic negativity $E_N$ against the temperature $T$ tell us that the entanglement between the two oscillators becomes weak with the increase in system temperature $T$, so a low temperature is a necessary condition to realize the entanglement of two thin dielectric membrane oscillators. A perfect entanglement requires the temperature of the oscillator to be close to 0 k; consequently, the cooling mechanical oscillator has become an important research field, which becomes the precondition of realizing entanglement and precise measurement in the cavity optomechanical system. From Figure 3, for ${\omega }_c=3\ast {\omega }_0$, $3.5\ast {\omega }_0$, and $4\ast {\omega }_0$, the entanglement between the two oscillators vanishes when the temperature of the system is $T>1.95$ K, 2.55 K, and 3.10 K, respectively.

FIGURE 3

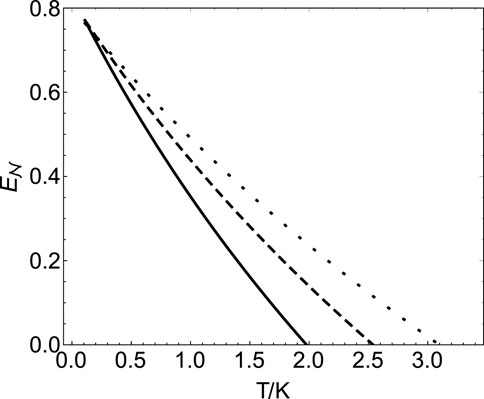
FIGURE 3. Plot of logarithmic negativity $E_N$ as a function of temperature $T$ of the system temperature. Normalization detuning $\Delta /{\omega }_m=1.0$, and the other parameters have the same values as those in Figure 2. The three curves correspond to different frequencies: for different cavity frequencies ${\omega }_c$. The solid line refers to ${\omega }_c=3{\omega }_0$, the frequency corresponding to the dash line is $3.5{\omega }_0$, and for the dotted line, ${\omega }_c=4{\omega }_0$.

In Figure 4, we plot the three curves that can show that logarithmic negativity $E_N$ changes with the normalization detuning $\Delta /{\omega }_m$ for different masses of oscillators (where we assume that the two oscillators have the same mass). Here, the mass of oscillators is equal to $m=5\ast {10}^{-9}$ kg, $10\ast {10}^{-9}$ kg, and $15\ast {10}^{-9}$ kg, respectively, ${\omega }_c=4\ast {\omega }_0$, and the values of other parameters are the same as those in Figure 2. These curves tell us that the masses of oscillators can affect the entanglement between two oscillators. For more massive oscillators, the maximum value of logarithmic negativity $E_N$ approaches 0.52. For the light oscillators, the maximum value of logarithmic negativity $E_N$ can reach 0.68, which means the entanglement can be easily realized for the light oscillators. Figure 4 also shows the entanglement only appears in a certain range of the normalization detuning. The maximum values of the three curves show that the maximally entangled case requires the value of the normalization detuning to be close to 1; that is, for the given cavity frequency and oscillators with a given mass, the realization of entanglement has high requirements for the control of the frequency of the incident field. The changes of entanglement with the temperature of the system are shown in Figure 5 for different masses of oscillators (concrete values of the parameters are indicated in Figure 5). For the light oscillators, we can obtain the entanglement in a wider range of temperature. For the mass of oscillators, $m=5\ast 10^\left(-9\right)$ kg, $10\ast 10^\left(-9\right)$ kg, and $15\ast 10^\left(-9\right)$ kg, and the entanglement between the two oscillators vanishes when the temperature of the system is $T>$ 3.10 K, 1.80 K, and $1.25$ K, respectively.

FIGURE 4

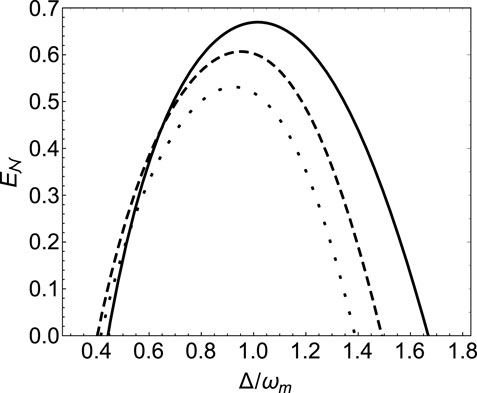
FIGURE 4. Logarithmic negativity $E_N$ as a function of the normalization detuning $\Delta /{\omega }_m$ for different masses of oscillators. The solid line refers to $m=5\ast {10}^{-9}$ kg, the mass corresponding to the dash line is $m=10\ast {10}^{-9}$ kg, and for the dotted line, $m=15\ast {10}^{-9}$ kg. The temperature is T = 0.4 K.

FIGURE 5

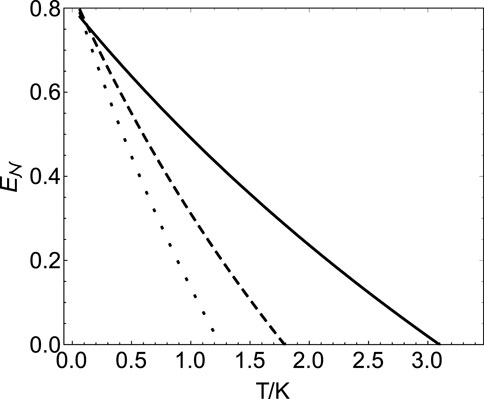
FIGURE 5. Logarithmic negativity $E_N$ as a function of the temperature for different masses of oscillators. The solid line refers to $m=5\ast {10}^{-9}$ kg, the mass corresponding to the dash line is $m=10\ast {10}^{-9}$ kg, and for the dotted line $m=15\ast {10}^{-9}$ kg. The normalization detuning is $\Delta /{\omega }_m$ = 1.

Finally, we investigate the entanglement between the oscillator and cavity mode. By calculating the correlation matrix, we can obtain the logarithmic negativity $E_N$ about the cavity mode and one of the oscillators. For comparing with the results published, we first consider the entanglement between the cavity mode and the oscillator that has a linear coupling with the cavity mode. The plot of logarithmic negativity $E_N$ changing with the normalized detuning for two different masses of the oscillator 5 and 50 ng is shown in Figure 6, where the values of other physical parameters are the same as those in Ref. [21]. These curves show that the entanglement between the cavity mode and the oscillator can be realized, and the entanglement is most easily obtained when the value of the normalized detuning is close to 1. It was also found that the oscillator with light mass can produce entanglement with the cavity mode in a wider frequency range. Based on the same physical parameters, our research results are similar to those in Vitali’s works [21]. We also investigated the dependence of entanglement between the cavity and single oscillator on the temperature of the system in Figure 7. For the light mechanical oscillator, we can achieve the entanglement between oscillator 1 and the cavity mode in a wider range of temperatures: for m = 5 ng, the temperature ranges from 0 to 23 Kelvin, while the temperature ranges from 0 to 2.3 Kelvin for m = 5 ng. Beyond these ranges, the entanglement vanishes. The optomechanical entanglement of cavity optomechanics with linear coupling has been reported in Vitali’s works [21]. From Figures 6, 7, we restudied the previous work about entanglement between two different modes. At the end of our study, we want to investigate the entanglement between oscillator 2 and the cavity mode. Logarithmic negativity $E_N$ changing with the temperature of oscillator is shown in Figure 8, where the mass of oscillator is 10 ng and the normalized detuning is equal to 1. The dash line and solid line correspond to ${\omega }_c=0.5\ast {\omega }_0$ and ${\omega }_c=1\ast {\omega }_0$, respectively. From Figure 8, we know that appropriate parameters can make the entanglement be produced between the cavity mode and oscillator 2. On comparing with Figure 3, in the ideal condition (temperature T = 0 K), logarithmic negativity $E_N$ can reach 1, which is greater than the value in Figure 3, where its value is 0.8. Figure 9 shows the plot of logarithmic negativity $E_N$ as a function of temperature of the system for the different masses of oscillators, where ${\omega }_c={\omega }_0$, the mass of oscillator with 10 ng is for the solid line, and m = 100 ng is for the dash line. In comparison with Figures 5, 7, logarithmic negativity $E_N$ in Figure 9 has a larger value in an ideal condition. Based on Figures 8, 9, we found that we can realize the entanglement between the cavity mode and oscillator 2 in a wider temperature range. For oscillator 2, it has a quadratic coupling with the cavity field. This kind of nonlinear effect is helpful in realizing the entanglement between the cavity mode and oscillator 2.

FIGURE 6

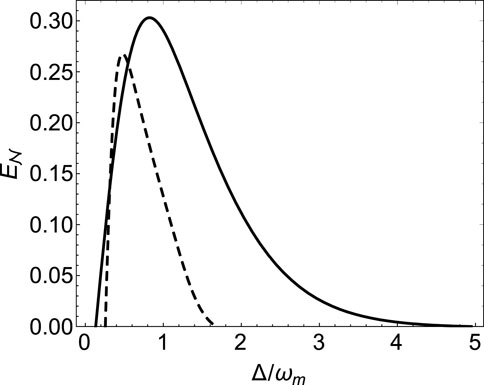
FIGURE 6. Logarithmic negativity $E_N$ as a function of the normalization detuning $\Delta /{\omega }_m$ for different masses of oscillators. The solid line refers to $m=5\text{ng}$, and the dash line stands for $m$ with 50 ng. The temperature of the system is T = 0.4 K.

FIGURE 7

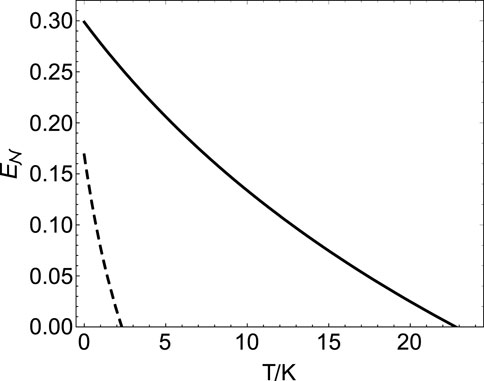
FIGURE 7. Logarithmic negativity $E_N$ as a function of temperature of the system for different masses of oscillators. The solid line refers to $m=5$ ng, the mass corresponding to the dash line is $m=50$ ng, and the normalization detuning $\frac{\Delta }{{\omega }_m}=1$.

FIGURE 8

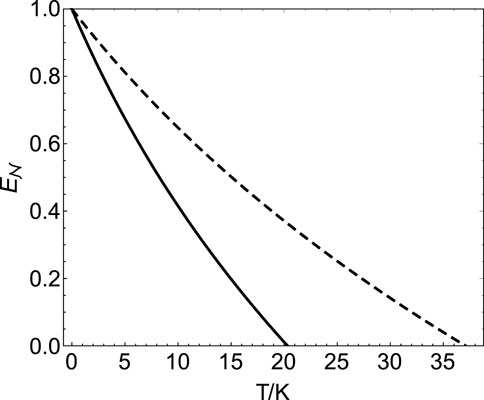
FIGURE 8. Logarithmic negativity $E_N$ as a function of temperature of the system for the different frequency of cavity field. The mass of oscillator is 10 ng, the normalized detuning is equal to 1. The dash line and solid line correspond to ${\omega }_c=0.5\ast {\omega }_0$ and ${\omega }_c=1\ast {\omega }_0$, respectively.

FIGURE 9

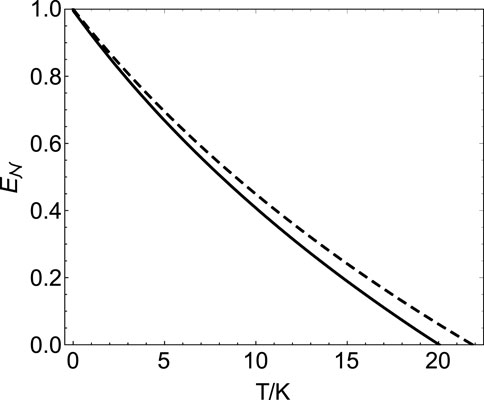
FIGURE 9. Logarithmic negativity $E_N$ as a function of temperature of the system for different masses of oscillator. When ${\omega }_c={\omega }_0$, the mass of oscillator with 10 ng is for the solid line, and m = 100 ng is for the dash line.

4 Conclusion

In summary, we have proposed to investigate the properties of quantum entanglement of the optomechanical system including two mechanical oscillators, where the two mechanical oscillators are coupled with the cavity field in different coupling modes: the interaction between mechanical oscillator 1 and the cavity field is first-order coupling, and mechanical oscillator 2 and the cavity field has a quadratic coupling. We mainly studied the entanglement between two mechanical oscillators with different coupling modes. The influences of the frequency of the cavity field and the mass of mechanical oscillators on the entanglement between two mechanical oscillators are investigated. We analyze in detail the characteristics of logarithmic negativity $E_N$ changing with the normalization detuning or temperature under the condition with given values of physical parameters. Our results show that the realization of entanglement requires the value of the normalization detuning close to 1; that is, we need to accurately control the frequency of the driving field. We also found that the realization of entanglement also has strict requirements on temperature. Beyond a certain temperature range, entanglement will disappear. On the other hand, for given parameters of the system, we also obtained the entanglement between the cavity field and the mechanical oscillator that has a quadratic coupling. The nonlinear effect is helpful for producing entanglement. We know that the amount of entanglement quantified by the logarithmic negativity is strongly dependent on the temperature of the oscillators. For the experiment, the choice of physical parameters is very important. The choice of our physical parameters is based on Ref. [21], where a concrete and a feasible experimental scheme is proposed. In addition, some cavity optomechanical experiments have been realized, and our choice of parameters is close to those of recently performed experiments [28, 29]. So we think our scheme has feasibility based on the current experiment about cavity optomechanics. Compared with the entanglement between microscopic particles, the stable macroscopic quantum entanglement between two mechanical oscillators has the characteristics of long existence life and can be reused, and it also plays an important role in quantum information processing and quantum network construction.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author Contributions

AC and TY conceived the physical model and the idea of the study, and YL and LD carried out the calculation and numerical analysis. YL and AC supervised the work. All authors contributed to the interpretation of the work and the preparation of the manuscript.

Funding

This study was funded by the National Natural Science Foundation of China (12005189, 12175199, and 12075209) and the Natural Science Foundation of Zhejiang Province (LZ20A040002).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Deb RN. Quantum Entanglement in Multiparticle Systems of Two-Level Atoms. Phys Rev A (2011) 84:032327. doi:10.1103/PhysRevA.84.032327

CrossRef Full Text | Google Scholar

2. Mirkhalaf SS, Smerzi A. Entanglement Detection in a Coupled Atom-Field System via Quantum Fisher Information. Phys Rev A (2017) 95:022302. doi:10.1103/PhysRevA.95.022302

CrossRef Full Text | Google Scholar

3. Yang W-X, Zhan Z-M, Li J-H. Efficient Scheme for Multipartite Entanglement and Quantum Information Processing with Trapped Ions. Phys Rev A (2005) 72:062108. doi:10.1103/PhysRevA.72.062108

CrossRef Full Text | Google Scholar

4. Bittencourt VASV, Bernardini AE, Blasone M. Quantum Transitions and Quantum Entanglement from Dirac-like Dynamics Simulated by Trapped Ions. Phys Rev A (2016) 93:053823. doi:10.1103/PhysRevA.93.053823

CrossRef Full Text | Google Scholar

5. Osawa S, Simon DS, Malinovsky VS, Sergienko AV. Controllable Entangled-State Distribution in a Dual-Rail Reconfigurable Optical Network. Phys Rev A (2021) 104:012617. doi:10.1103/PhysRevA.104.012617

CrossRef Full Text | Google Scholar

6. Wei H, Deng Z, Zhang X, Feng M. Transfer and Teleportation of Quantum States Encoded in Decoherence-free Subspace. Phys Rev A (2007) 76:054304. doi:10.1103/PhysRevA.76.054304

CrossRef Full Text | Google Scholar

7. Laurenza R, Lupo C, Lloyd S, Pirandola S. Dense Coding Capacity of a Quantum Channel. Phys Rev Res (2020) 2:023023. doi:10.1103/PhysRevResearch.2.023023

CrossRef Full Text | Google Scholar

8. Ra Y-S, Lim H-T, Kim Y-H. Remote Preparation of Three-Photon Entangled States via Single-Photon Measurement. Phys Rev A (2016) 94:042329. doi:10.1103/PhysRevA.94.042329

CrossRef Full Text | Google Scholar

9. Morachis Galindo D, Maytorena JA. Entangling Power of Symmetric Two-Qubit Quantum Gates and Three-Level Operations. Phys Rev A (2022) 105:012601. doi:10.1103/PhysRevA.105.012601

CrossRef Full Text | Google Scholar

10. Cavalcanti D, Guerini L, Rabelo R, Skrzypczyk P. General Method for Constructing Local Hidden Variable Models for Entangled Quantum States. Phys Rev Lett (2016) 117:190401. doi:10.1103/PhysRevLett.117.190401

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Shi F, Ye Z, Chen L, Zhang X. Strong Quantum Nonlocality in N-Partite Systems. Phys Rev A (2022) 105:022209. doi:10.1103/PhysRevA.105.022209

CrossRef Full Text | Google Scholar

12. Aspelmeyer M, Kippenberg TJ, Marquardt F. Cavity Optomechanics. Rev Mod Phys (2014) 86:1391–452. doi:10.1103/RevModPhys.86.1391

CrossRef Full Text | Google Scholar

13. Liu J, Zhou Y-H, Huang J, Huang J-F, Liao J-Q. Quantum Simulation of a Three-Mode Optomechanical System Based on the Fredkin-type Interaction. Phys Rev A (2021) 104:053715. doi:10.1103/PhysRevA.104.053715

CrossRef Full Text | Google Scholar

14. Deng ZJ, Yan X-B, Wang Y-D, Wu C-W. Optimizing the Output-Photon Entanglement in Multimode Optomechanical Systems. Phys Rev A (2016) 93:033842. doi:10.1103/PhysRevA.93.033842

CrossRef Full Text | Google Scholar

15. Huang S, Chen A. Mechanical Squeezing in a Dissipative Optomechanical System with Two Driving Tones. Phys Rev A (2021) 103:023501. doi:10.1103/PhysRevA.103.023501

CrossRef Full Text | Google Scholar

16. Sala K, Doicin T, Armour AD, Tufarelli T. Quantum Estimation of Coupling Strengths in Driven-Dissipative Optomechanics. Phys Rev A (2021) 104:033508. doi:10.1103/PhysRevA.104.033508

CrossRef Full Text | Google Scholar

17. Zhou L, Cheng J, Han Y, Zhang W. Nonlinearity Enhancement in Optomechanical Systems. Phys Rev A (2013) 88:063854. doi:10.1103/PhysRevA.88.063854

CrossRef Full Text | Google Scholar

18. Zhou B-y., Li G-x. Ground-state Cooling of a Nanomechanical Resonator via Single-Polariton Optomechanics in a Coupled Quantum-Dot-Cavity System. Phys Rev A (2016) 94:033809. doi:10.1103/PhysRevA.94.033809

CrossRef Full Text | Google Scholar

19. Huang S, Agarwal GS. Electromagnetically Induced Transparency with Quantized Fields in Optocavity Mechanics. Phys Rev A (2011) 83:043826. doi:10.1103/PhysRevA.83.043826

CrossRef Full Text | Google Scholar

20. Sete EA, Eleuch H. Controllable Nonlinear Effects in an Optomechanical Resonator Containing a Quantum Well. Phys Rev A (2012) 85:043824. doi:10.1103/PhysRevA.85.043824

CrossRef Full Text | Google Scholar

21. Vitali D, Gigan S, Ferreira A, Böhm HR, Tombesi P, Guerreiro A, et al. Optomechanical Entanglement between a Movable Mirror and a Cavity Field. Phys Rev Lett (2007) 98:030405. doi:10.1103/PhysRevLett.98.030405

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Vitali D, Tombesi P, Woolley MJ, Doherty AC, Milburn GJ. Entangling a Nanomechanical Resonator and a Superconducting Microwave Cavity. Phys Rev A (2007) 76:042336. doi:10.1103/PhysRevA.76.042336

CrossRef Full Text | Google Scholar

23. Genes C, Vitali D, Tombesi P. Emergence of Atom-Light-Mirror Entanglement inside an Optical Cavity. Phys Rev A (2008) 77:050307R. doi:10.1103/PhysRevA.77.050307

CrossRef Full Text | Google Scholar

24. Riedinger R, Wallucks A, Marinković I, Löschnauer C, Aspelmeyer M, Hong S, et al. Remote Quantum Entanglement between Two Micromechanical Oscillators. Nature (2018) 556:473–7. doi:10.1038/s41586-018-0036-z

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Bhattacharya M, Uys H, Meystre P. Optomechanical Trapping and Cooling of Partially Reflective Mirrors. Phys Rev A (2008) 77:033819. doi:10.1103/PhysRevA.77.033819

CrossRef Full Text | Google Scholar

26. Plenio MB. Logarithmic Negativity: a Full Entanglement Monotone that Is Not Convex. Phys Rev Lett (2005) 95:090503. doi:10.1103/PhysRevLett.95.090503

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Vidal G, Werner RF. Computable Measure of Entanglement. Phys Rev A (2002) 65:032314. doi:10.1103/PhysRevA.65.032314

CrossRef Full Text | Google Scholar

28. Kleckner D, Marshall W, de Dood MJA, Dinyari KN, Pors B-J, Irvine WTM, et al. High Finesse Opto-Mechanical Cavity with a Movable Thirty-Micron-Size Mirror. Phys Rev Lett (2006) 96:173901. doi:10.1103/PhysRevLett.96.173901

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Gigan S, Böhm HR, Paternostro M, Blaser F, Langer G, Hertzberg JB, et al. Self-cooling of a Micromirror by Radiation Pressure. Nature (2006) 444:67–70. doi:10.1038/nature05273

PubMed Abstract | CrossRef Full Text | Google Scholar