Experimental Demonstration of Self-Oscillation Microcomb in a Mode-Splitting Microresonator

Self-oscillation and bifurcation as many-body dynamics solutions in a high-Q microresonator have induced substantial interest in nonlinear optics and ultrafast science. Strong mode coupling between clockwise (CW) wave and counterclockwise (CCW) wave induces mode-splitting and optical self-oscillation in the optical cavity. This study experimentally demonstrates the self-oscillation microcomb formation in a microresonator with strong backward Rayleigh scattering. When a pump laser sweeps across a resonance, both spontaneous symmetry breaking (SSB) and self-oscillation phenomenon are observed. The breathing soliton and stable soliton state can switch to each other through careful tuning of the pump detuning. Our experiments provide a reliable scheme for breather soliton microcomb generation. Meanwhile, the rich physics process enhances the comprehension of nonlinear optics in a cavity.

Introduction

Optical Rayleigh backscatter is one widespread phenomenon in the optical system. In a microresonator, the Rayleigh backscatter can induce mode splitting and rich nonlinearities due to the linear coupling between CW and CCW propagating waves [1–3]. Meanwhile, the nonlinear coupling between CW and CCW waves can induce spontaneous symmetry breaking, self-switching of counterpropagating waves, and spontaneous chiral symmetry breaking, which have been experimentally demonstrated in ultrahigh-Q whispering-gallery-mode (WGM) microresonators [4–6]. The intrinsic mechanism is the different nonlinear phase shifts between the counterpropagating waves due to the cross-phase modulation (XPM) and self-phase modulation (SPM), which have been modeled based on the coupled-mode theory or coupled Lugiato–Lefever equations (LLEs) [7].

The optical field is greatly enhanced in a high-Q microresonator, which induces a low threshold four-wave mixing (FWM) for the microcomb formation [8]. The states of microcombs rely on the detuning of the continuous wave pump laser. To date, both stable solitons [9, 10] from soliton crystals [11–13] to soliton molecules [14, 15] and breathing solitons [16–19] have been discovered. Stable soliton microcombs (SMCs) [20–23] have become novel integrated broadband coherent optical sources that have shown great application prospects in a series of areas, such as dual-comb spectroscopy [24–26], ranging system [27, 28], high-speed communication systems [29, 30], and optical computing [31–33]. Breather soliton is a special soliton state with periodic energy exchange between the SMC and pump laser [16, 17] or another optical cavity mode [34, 35], which shows rich dynamics in cavity soliton physics. Recently, other types of soliton oscillations are also experimentally or theoretically studied. For example, forced oscillation is studied in a synthesized soliton crystal generation experiment due to the moving offset between the potential field and solitons [36]. In a counterpropagating Kerr soliton generation experiment, a relative motion between the counterpropagating solitons is observed due to the slight pump frequency difference [37]. Breather soliton via high-order dispersion is also theoretically studied [38]. Besides, self-oscillation performance and symmetry breaking via XPM or dual cavity are also demonstrated [39, 40]. For a microresonator with backward Rayleigh scattering, the interplay between counterpropagating waves introduces another degree of freedom affecting the microcomb formation [7]. A recent theoretical study shows a new type of soliton oscillation due to Rayleigh scattering instability [41]. The breathing frequency coincides with the Rayleigh scattering doublet splitting. A series of theoretical studies concern the generation of SMC in mode-splitting microresonators. All the studies show rich, dynamic processes in microresonators when the Rayleigh scattering is considered. However, there is still no experimental observation of mode-splitting induced breathing oscillations in an on-chip micro-ring resonator.

In this study, the dynamics of self-oscillation microcomb is studied based on the strong backward Rayleigh scattering. The CCW wave is suppressed while a high-power pump laser sweeps across the blue-detuned regime, which is regarded as SSB due to XPM between the counterpropagating waves. Once the pump laser enters the red-detuned regime, the power of counterpropagating waves inversely changes. The interplay of counterpropagating waves provides a novel mechanism for oscillated microcomb formation. Our results not only highlight the richness nonlinear dynamics for cavity physics research but also take the merits of simplicity for oscillated microcomb and breather soliton observations.

Principle

Figure 1A shows the microcomb formation in a microresonator with strong Rayleigh backscatter. Figure 1B shows the basic principle of microcomb generation with Rayleigh backscatter. Previous reports mainly focus on the case of weak Rayleigh backscatter, which has little influence on the SMC formation and survival. As a comparison, when a microresonator with strong backward Rayleigh scatter is pumped, part of the pump power is backward scattered and forms a CCW optical field in the microcavity. The counterpropagating fields experience an additional phase shift due to the XPM, which causes a larger frequency shift on the resonances and suppresses the CCW wave power increase when the pump locates at the blue-detuned regime. Hence, a strong SSB would be formed. Once the pump laser enters the red-detuned regime or frequency domain between two resonance modes, the power of counterpropagating waves will inversely change. Two counterpropagating microcombs will co-exist in the cavity. By considering the strong Rayleigh backscatter effect, the dynamics of microcomb formation can be modeled using the coupled normalized LLE:

$\frac{\mathit{d}{\mathit{A}}_{\mathit{c}\mathit{w}}}{\mathit{d}\mathit{T}}=-\left(\mathbf{1}+\mathit{i}\mathit{\delta }\mathit{\omega }\right){\mathit{A}}_{\mathit{c}\mathit{w}}+\mathit{i}\mathit{G}{\mathit{A}}_{\mathit{c}\mathit{c}\mathit{w}}+\mathit{i}{\mathit{d}}_2\frac{{\partial }^{\mathbf{2}}}{\partial {\varphi }^{\mathbf{2}}} {\mathit{A}}_{\mathit{c}\mathit{w}}+2\mathit{i}{\mathit{A}}_{\mathit{c}\mathit{w}}{\mathit{P}}_{\mathit{c}\mathit{c}\mathit{w}}+\mathit{f}+\mathit{i}{\mathit{A}}_{\mathit{c}\mathit{w}}{\mathit{A}}_{\mathit{c}\mathit{w}}{\mathit{A}}_{\mathit{c}\mathit{w}}^{\ast },(1)$

$\frac{\mathit{d}{\mathit{A}}_{\mathit{c}\mathit{c}\mathit{w}}}{\mathit{d}\mathit{T}}=-\left(\mathbf{1}+\mathit{i}\mathit{\delta }\mathit{\omega }\right){\mathit{A}}_{\mathit{c}\mathit{c}\mathit{w}}+\mathit{i}\mathit{G}{\mathit{A}}_{\mathit{c}\mathit{w}}+i{\mathit{d}}_{\mathbf{2}}\frac{{\partial }^{\mathbf{2}}}{\partial {\mathit{\varphi }}^{\mathbf{2}}} {\mathit{A}}_{\mathit{c}\mathit{c}\mathit{w}}+\mathbf{2}\mathit{i}{\mathit{A}}_{\mathit{c}\mathit{c}\mathit{w}}{\mathit{P}}_{\mathit{c}\mathit{w}}+\mathit{i}{\mathit{A}}_{\mathit{c}\mathit{c}\mathit{w}}{\mathit{A}}_{\mathit{c}\mathit{c}\mathit{w}}{\mathit{A}}_{\mathit{c}\mathit{c}\mathit{w}}^{\ast },(2)$

where $A_{cw,u}$ and $A_{ccw,u}$ are the CW and CCW optical fields, respectively, and $\delta \omega$ represents the normalized detuning between the pump and resonance. The normalized coupling rate between the CW and CCW fields is $G$ . $d_2$ describes the normalized second-order dispersion coefficient. $P_{cw}$ and $P_{ccw}$ are the averaged intra-cavity power for CW and CCW optical waves, respectively. In order to demonstrate the self-oscillation phenomenon, the cavity stability is analyzed firstly. We only consider the pump mode and neglect the cavity dispersion. The value of external pump f is 3. When the backward Rayleigh scattering is negligible and the value of G is 0, a standard bistable curve can be obtained while a high-power pump sweeps across a resonance, as shown in Figure 1C. By adding a dimension of the counterpropagating mode-coupling effect and when the value of G is 1, the coupled LLEs have multi-solutions, as shown in Figure 1D. Compared with the lower pump power case (inset of Figure 1D), the CCW field is no longer increasing with the CW field under high power pump conditions, which proves the occurrence of SSB in a counter mode coupled microresonator. The optical fields show much more complex dynamics. A stability analysis shows that the coupled LLEs have stable and oscillatory solutions, which are respectively corresponding to the stable and self-oscillation regime of the counterpropagating mode-coupling microresonator. The self-oscillation of the pump mode can induce oscillated microcomb formation, which provides a novel mechanism for breathing SMCs or self-oscillation microcomb generation.

FIGURE 1

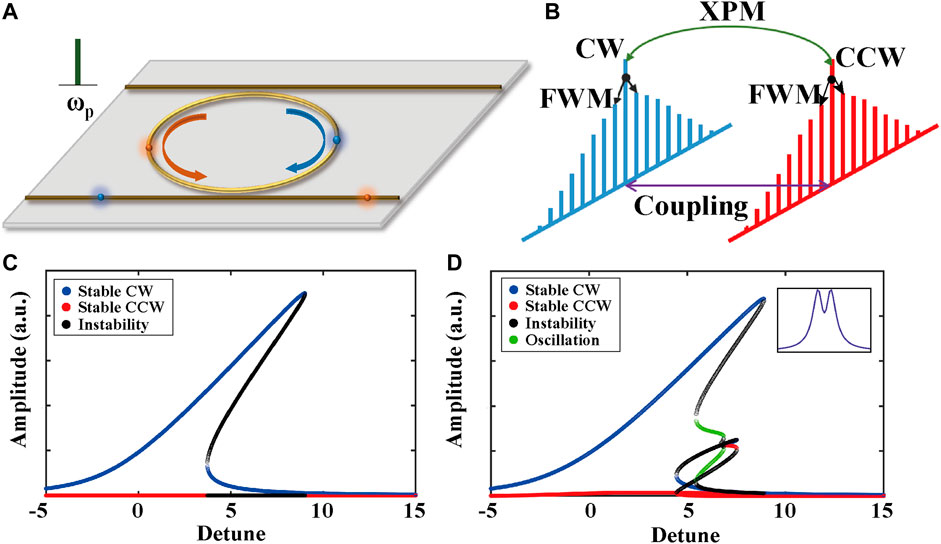
FIGURE 1. Comparison of SMC generation in negligible and strong counterpropagating mode-coupling effects in microresonators. (A) Schematic of SMC generation in a CW and CCW coupled microresonator. Two counterpropagating microcombs are spontaneously formed with a monochromatic pump at frequency ${\omega }_p$ . (B) Principle of coupled CW and CCW microcomb formation. The counterpropagating microcombs are linear and nonlinear coupled due to the Rayleigh backward scattering and XPM in the microresonator. When the microcomb forms in the cavity, the other frequency parts of CCW and CW waves are also linked by XPM and mode-coupling. (C,D) Effect of weak and strong counterpropagating mode-coupling on the transmission traces while a pump sweeps across a resonance. The values of weak mode-coupling and strong coupling are, respectively, 0 and 1. The value of the external pump $\mathit{f}$ is 3. Inset in (D) shows the linear transmission traces under lower pump power. For high pump power, the symmetry of resonance is spontaneously broken, which is indicated by suppression of the CCW power, and a multi-stable regime is formed. The green region supports the breathing microcomb solutions.

Experiment and Results

Figure 2A shows the setup of the experiment. The core device is a micro-ring resonator (MRR) with a free spectral range (FSR) of 200 GHz. Figure 2B shows the image of MRR, which is composed of a waveguide with a cross-section of 2 × 2 µm. The Q-factor of the MRR is 1.2 × 10⁶, whose resonances are split due to the strong backward Rayleigh scattering, as shown in Figure 2C. In order to monitor the coupling effect between the two counterpropagating waves in the MRR, the transmission power from the drop port (CW) and add port (CCW) are monitored simultaneously using a two-channel oscilloscope. When the power is about 150 mW, the powers of CW and CCW waves are monotonously increasing. Figure 2D shows the power traces while the pump sweeps across the resonances. There are no obvious nonlinear interactions between CW and CCW lights. When the on-chip pump power reaches 800 mW, a strong nonlinear coupling between CW and CCW waves occurs. Along with the pump detuning increase, there are obvious inflection points of the CCW power trace, as shown in Figure 2E. At this reflection point, the nonlinear coupling between the CW and CCW lights begins to dominate the optical field distribution, which induces power bifurcation of the counterpropagating waves. More interestingly, a rapid energy oscillation is observed. It is noted that microcomb is not formed at the self-oscillation region, where the CCW wave forms from the backward Rayleigh scattering field rather than external injection.

FIGURE 2

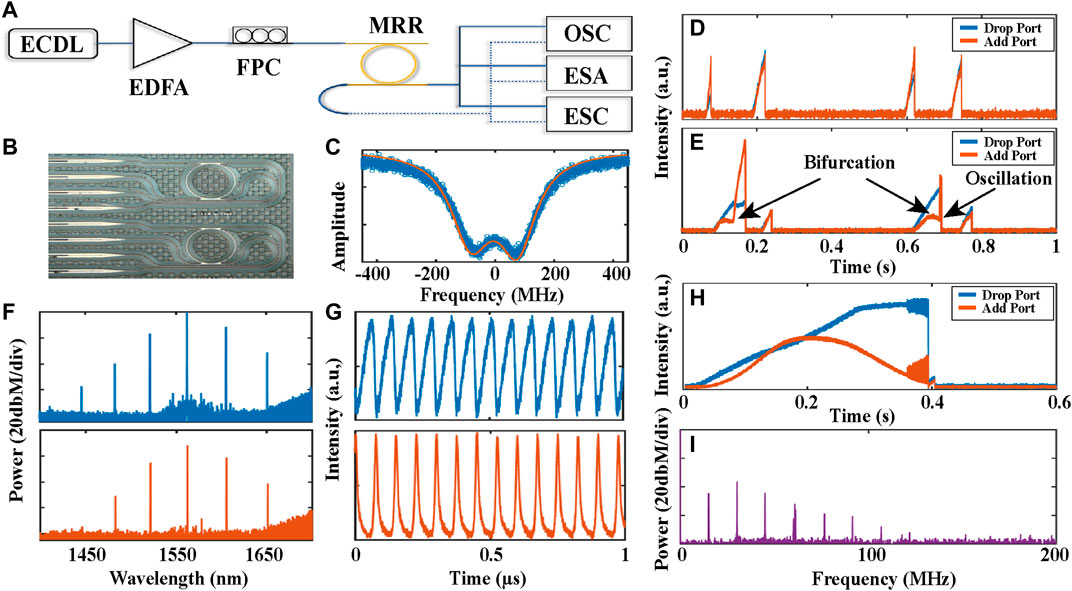
FIGURE 2. Experimental demonstration of spontaneous symmetry breaking induced self-oscillation cascade FWM in a micro-ring resonator with FSR of 200 G. (A) Experimental setup. An external cavity diode laser (ECDL) is employed to pump a micro-ring resonator (MRR), and the output lights from the drop port (CW) and add port (CCW) are monitored by an optical spectrum analyzer (OSA), an electrical spectrum analyzer (ESA), and an oscilloscope (OSC), respectively. EDFA: Erbium-doped fiber amplification, FPC: fiber polarization control. (B) Image of the MRR with a free spectral range of 200 GHz. (C) Transmission trace of a resonance that is split due to strong Rayleigh backward scattering. The Q-factor is ∼ 1.2×10⁶. (D,E) Measured transmission traces with on-chip power of 150 and 800 mW, respectively. Using low pump power, the CCW light is almost linearly increasing with the CW light. For a higher pump power (>500 mW), nonlinear coupling between the CW and CCW lights dominates the transmission character, which induces bifurcation and power oscillation. (F) Measured optical spectra of primary comb from drop port (top) and add port (bottom), respectively. (G) Measured waveforms of the CW and CCW microcombs showing the oscillation of the primary comb. The two waveforms are antiphase induced by the self-switching effect in the micro-cavity. (H) Power traces while the pump laser sweeps across a resonance. An obvious bifurcation is observed when the pump coupled into the resonance and power oscillation is formed at cascade FWM state. (I) Radio-frequency spectra of the self-oscillation cascade FWM comb.

The self-oscillation effect provides a novel mechanism for breathing microcomb formation. For microcomb generation in the microresonator, the on-chip power is boosted up to 1.0 W using a commercial EDFA and the polarization state is carefully tuned manually. Figure 2H shows the transmission traces of CW and CCW waves while the pump laser sweeps across a resonance of the MRR. The CW and CCW waves bifurcate at ∼ 0.2 s due to the strong XPM. Further increasing the pump detuning, a primary comb is formed, which accompanies strong power oscillation. Figure 2F and Figure 2G show the optical spectra and waveforms of CW and CCW waves, respectively. The CW and CCW waves oscillate out of phase. The optical state of the microcomb is the cascade FWM state. The oscillation is caused by the energy exchange between the CW and CCW waves, which is verified by the oscillation waveforms. Figure 2I shows the measured radio-frequency spectra, which indicates that the fundamental oscillation frequency is in the order of 10 MHz.

Figure 3A shows mode splitting at lower pump power, and the quality of the microresonator is 1.06 M. Figure 3B shows the output optical power traces of CW and CCW optical field while the on-chip power is amplified up to 1.0 W. Figure 3C and Figure 3D show the optical spectra of CW and CCW waves at different microcomb states, respectively. Power bifurcation phenomenon is observed at about −0.1 s. With the increase in intracavity power, the primary comb is formed with a frequency spacing of 11-FSR (Figure 3C(Ⅰ)). When the pump laser enters the red-detuning regime, the power of CW and CCW light changes inversely and keeps the intra-cavity optical power. Hence, the strong thermos-optics effect is avoided for stable soliton microcomb formation. According to the stability analysis, there are stable and oscillation SMC states while the pump locates at the soliton existing regime. Figure 3C(Ⅱ) presents the optical spectra of breathing perfect soliton crystals (PSC) after undergoing the stable soliton state. The oscillation perfect soliton crystal is caused by the energy exchange between the CW and CCW waves, which is proved by the antiphase oscillation of the measured optical power traces (Figure 3E and Figure 3F). The stable and breathing PSCs can be switched via slightly changing the pump detuning.

FIGURE 3

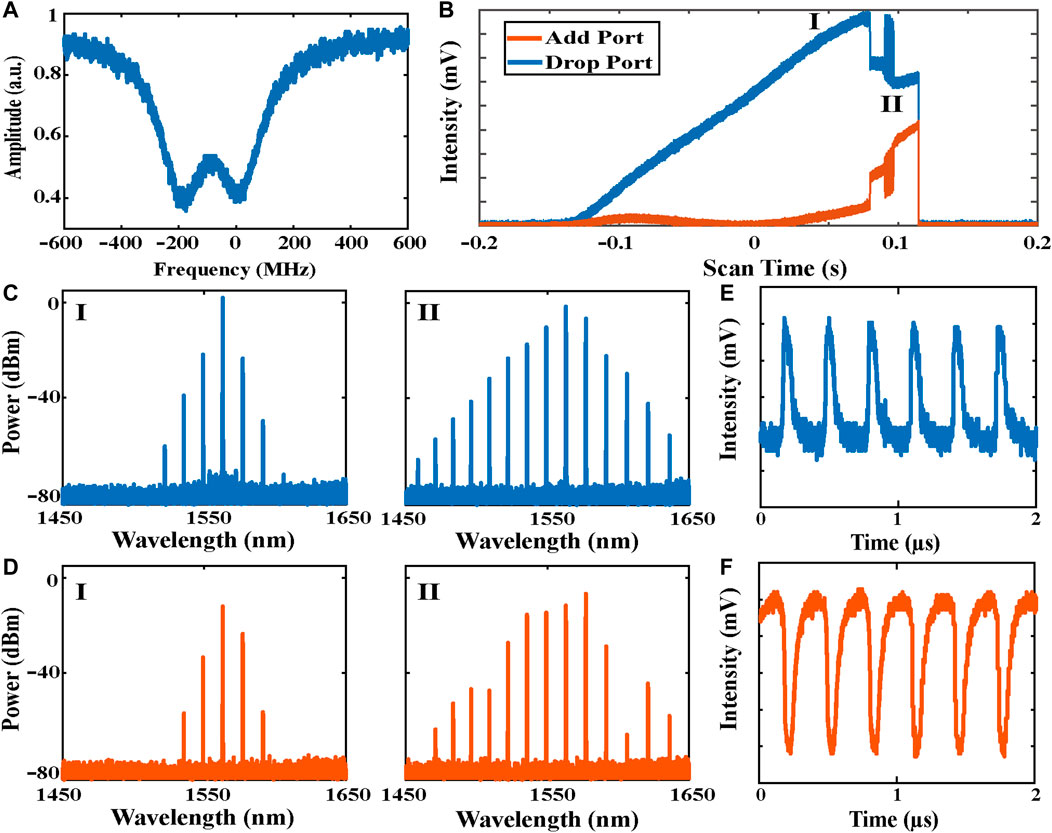
FIGURE 3. Breather soliton via SSB in the microresonator with FSR of 200 G. (A) Transmission trace of a resonance split due to backward Rayleigh scattering. (B) Measured power traces of CW and CCW via frequency tuning. States Ⅰ and Ⅱ are, respectively, in the cascade FWM state and breather perfect soliton crystal (PSC) state. Breather PSC (Ⅱ) is evolved from the turning pattern and low-noise modulation state. The power traces bifurcate at about −0.10 s. (C) Ⅰ and Ⅱ are, respectively, the optical spectrums of cascade FWM and breather PSC for CW waves. The frequency spacings of FWM and breather PSC are, respectively, 11-FSR and 9-FSR. (D) Optical spectrums of FWM and PSC for CCW waves. (E,F) Power traces of CW and CCW optical field at the breather soliton region.

The mode-splitting effect provides another mechanism to realize intracavity thermal balance for stably accessing soliton microcomb states. As shown in Figure 3B, the power of the CCW wave increases while the pump enters the red-detuned regime, which compensates for the power decrease in the CW waves. Continuously increasing the pump wavelength, the breather PSC would evolve into the multi-soliton, as shown in the second soliton step in Figure 3B. In this region, the power of CW and CCW waves demonstrate the antiphase exchange.

The self-thermal balance mechanism assisted mode splitting extends the soliton existing range, and no special experimental technique is demanded for SMC generation. The mode-splitting effect enriches the physics dynamics in microcomb generation. Both SSB and self-oscillation are observed due to the nonlinear interplay between two counterpropagating waves. The self-oscillation effect provides a novel mechanism for breathing SMC. Mode splitting could extend the breather soliton existence region.

Conclusion

In conclusion, we have experimentally demonstrated the self-oscillation microcomb generation in a microresonator with mode splitting due to strong Rayleigh backscatter. Due to the strong nonlinear coupling between CW and CCW waves, the CCW light is suppressed while the pump laser locates at the blue-detuned regime. Once the pump enters the red-detuned regime, the exchange power between CW and CCW waves would occur and realize the self-oscillation performances, which induces the oscillation of microcombs, including cascade FWM state and SMCs. The study provides a new mechanism of breathing SMC generation, which enriches the cavity soliton physics.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author Contributions

XW conceived the idea. XW, PX, YW, and WW performed the experiments and theoretical simulations. BL and SC designed and fabricated the microresonator. WZ and LW discussed the experimental results. WZ and WW supervised the whole project. All the authors contributed to the manuscript writing.

Funding

This study was supported by the National Natural Science Foundation of China (62075238) and the West Light Foundation of the Chinese Academy of Sciences (E0291113).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.908141/full#supplementary-material

References

1. Min B, Ostby E, Sorger V, Ulin-Avila E, Yang L, Zhang X, et al. High-Q Surface-Plasmon-Polariton Whispering-Gallery Microcavity. Nature (2009) 457:455–8. doi:10.1038/nature07627

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Kippenberg TJ, Spillane SM, Vahala KJ. Modal Coupling in Traveling-Wave Resonators. Opt Lett (2002) 27:1669–71. doi:10.1364/ol.27.001669

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Mazzei A, Götzinger S, de S. Menezes L, Zumofen G, Benson O, Sandoghdar V. Controlled Coupling of Counterpropagating Whispering-Gallery Modes by a Single Rayleigh Scatterer: A Classical Problem in a Quantum Optical Light. Phys Rev Lett (2007) 99:173603. doi:10.1103/PhysRevLett.99.173603

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Woodley MTM, Hill L, Del Bino L, Oppo G-L, Del’Haye P. Self-Switching Kerr Oscillations of Counterpropagating Light in Microresonators. Phys Rev Lett (2021) 126:043901. doi:10.1103/PhysRevLett.126.043901

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Cao Q-T, Wang H, Dong C-H, Jing H, Liu R-S, Chen X, et al. Experimental Demonstration of Spontaneous Chirality in a Nonlinear Microresonator. Phys Rev Lett (2017) 118:033901. doi:10.1103/PhysRevLett.118.033901

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Woodley MTM, Silver JM, Hill L, Copie F, Del Bino L, Zhang S, et al. Universal Symmetry-Breaking Dynamics for the Kerr Interaction of Counterpropagating Light in Dielectric Ring Resonators. Phys Rev A (2018) 98:053863. doi:10.1103/PhysRevA.98.053863

CrossRef Full Text | Google Scholar

7. Kondratiev NM, Lobanov VE. Modulational Instability and Frequency combs in Whispering-Gallery-Mode Microresonators with Backscattering. Phys Rev A (2020) 101:013816. doi:10.1103/PhysRevA.101.013816

CrossRef Full Text | Google Scholar

8. Del’Haye P, Schliesser A, Arcizet O, Wilken T, Holzwarth R, Kippenberg JT. Optical Frequency Comb Generation from a Monolithic Microresonator. Nature (2007) 450:1214–7. doi:10.1038/nature06401

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Herr T, Brasch V, Jost JD, Wang CY, Kondratiev NM, Gorodetsky ML, et al. Temporal Solitons in Optical Microresonators. Nat Photon (2014) 8:145–52. doi:10.1038/nphoton.2013.343

CrossRef Full Text | Google Scholar

10. Guo H, Karpov M, Lucas E, Kordts A, Pfeiffer MHP, Brasch V, et al. Universal Dynamics and Deterministic Switching of Dissipative Kerr Solitons in Optical Microresonators. Nat Phys (2017) 13:94–102. doi:10.1038/nphys3893

CrossRef Full Text | Google Scholar

11. Karpov M, Pfeiffer MHP, Guo H, Weng W, Liu J, Kippenberg TJ. Dynamics of Soliton Crystals in Optical Microresonators. Nat Phys (2019) 15:1071–7. doi:10.1038/s41567-019-0635-0

CrossRef Full Text | Google Scholar

12. Cole DC, Lamb ES, Del’Haye P, Diddams SA, Papp SB. Soliton Crystals in Kerr Resonators. Nat Photon (2017) 11:671–6. doi:10.1038/s41566-017-0009-z

CrossRef Full Text | Google Scholar

13. Wang W, Lu Z, Zhang W, Chu ST, Little BE, Wang L, et al. Robust Soliton Crystals in a Thermally Controlled Microresonator. Opt Lett (2018) 43:2002–5. doi:10.1364/ol.43.002002

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Weng W, Bouchand R, Lucas E, Obrzud E, Herr T, Kippenberg TJ. Heteronuclear Soliton Molecules in Optical Microresonators. Nat Commun (2020) 11(1):1–9. doi:10.1038/s41467-020-15720-z

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Weng W, Bouchand R, Kippenberg TJ. Formation and Collision of Multistability-Enabled Composite Dissipative Kerr Solitons. Phys Rev X (2020) X10:021017. doi:10.1103/PhysRevX.10.021017

CrossRef Full Text | Google Scholar

16. Yu M, Jang JK, Okawachi Y, Griffith AG, Luke K, Miller SA, et al. Breather Soliton Dynamics in Microresonators. Nat Commun (2017) 8:1–7. doi:10.1038/ncomms14569

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Lucas E, Karpov M, Guo H, Gorodetsky ML, Kippenberg TJ. Breathing Dissipative Solitons in Optical Microresonators. Nat Commun (2017) 8:1–11. doi:10.1038/s41467-017-00719-w

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Bao C, Jaramillo-Villegas JA, Xuan Y, Leaird DE, Qi M, Weiner AM. Observation of Fermi-Pasta-Ulam Recurrence Induced by Breather Solitons in an Optical Microresonator. Phys Rev Lett (2016) 117:163901. doi:10.1103/PhysRevLett.117.163901

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Wan S, Niu R, Wang Z-Y, Peng J-L, Li M, Li J, et al. Frequency Stabilization and Tuning of Breathing Solitons in Si3N4 Microresonators. Photon Res (2020) 8:1342–9. doi:10.1364/prj.397619

CrossRef Full Text | Google Scholar

20. Kippenberg TJ, Gaeta AL, Lipson M, Gorodetsky ML. Dissipative Kerr Solitons in Optical Microresonators. Science (2018) 361:129–62. doi:10.1126/science.aan8083

CrossRef Full Text | Google Scholar

21. Gaeta AL, Lipson M, Kippenberg TJ. Photonic-chip-based Frequency combs. Nat Photon (2019) 13:158–69. doi:10.1038/s41566-019-0358-x

CrossRef Full Text | Google Scholar

22. Wang W, Wang L, Zhang W. Advances in Soliton Microcomb Generation[J]. Adv Photon (2020) 3(2):034001. doi:10.1117/1.AP.2.3.034001

CrossRef Full Text | Google Scholar

23. Chang L, Liu S, Bowers JE. Integrated Optical Frequency Comb Technologies. Nat Photon (2022) 16:95–108. doi:10.1038/s41566-021-00945-1

CrossRef Full Text | Google Scholar

24. Yu M, Okawachi Y, Griffith AG, Picqué N, Lipson M, Gaeta AL. Silicon-chip-based Mid-infrared Dual-Comb Spectroscopy. Nat Commun (2018) 9:1–6. doi:10.1038/s41467-018-04350-1

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Suh M-G, Yang Q-F, Yang KY, Yi X, Vahala KJ. Microresonator Soliton Dual-Comb Spectroscopy. Science (2016) 354:600–3. doi:10.1126/science.aah6516

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Lin T, Dutt A, Joshi C, Ji X, Phare C, Okawachi Y, et al. Broadband Ultrahighresolution Chip-Scale Scanning Soliton Dual-Comb Spectroscopy. preprints, arxiv: 2001.00869v2 (2020).

Google Scholar

27. Suh M-G, Vahala KJ. Soliton Microcomb Range Measurement. Science (2018) 359:884–7. doi:10.1126/science.aao1968

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Trocha P, Karpov M, Ganin D, Pfeiffer MHP, Kordts A, Wolf S, et al. Ultrafast Optical Ranging Using Microresonator Soliton Frequency combs. Science (2018) 359:887–91. doi:10.1126/science.aao3924

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Marin-Palomo P, Kemal JN, Karpov M, Kordts A, Pfeifle J, Pfeiffer MHP, et al. Microresonator-based Solitons for Massively Parallel Coherent Optical Communications. Nature (2017) 546:274–9. doi:10.1038/nature22387

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Wang FX, Wang W, Niu R, Wang X, Zou CL, Dong CH, et al. Quantum Key Distribution with On‐Chip Dissipative Kerr Soliton. Laser Photon Rev (2020) 14:1900190. doi:10.1002/lpor.201900190

CrossRef Full Text | Google Scholar

31. Feldmann J, Youngblood N, Karpov M, Gehring H, Li X, Stappers M, et al. Parallel Convolutional Processing Using an Integrated Photonic Tensor Core. Nature (2021) 589:52–8. doi:10.1038/s41586-020-03070-1

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Xu X, Tan M, Corcoran B, Wu J, Boes A, Nguyen TG, et al. 11 TOPS Photonic Convolutional Accelerator for Optical Neural Networks. Nature (2021) 589(7840):44–51. doi:10.1038/s41586-020-03063-0

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Meng Y, Chen Y, Lu L, Ding Y, Cusano A, Fan JA, et al. Optical Meta-Waveguides for Integrated Photonics and beyond. Light Sci Appl (2021) 10(1):1–44. doi:10.1038/s41377-021-00655-x

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Guo H, Lucas E, Pfeiffer MHP, Karpov M, Anderson M, Liu J, et al. Intermode Breather Solitons in Optical Microresonators. Phys Rev X (2017) X7:041055. doi:10.1103/PhysRevX.7.041055

CrossRef Full Text | Google Scholar

35. Tikan A, Riemensberger J, Komagata K, Hönl S, Churaev M, Skehan C, et al. Emergent Nonlinear Phenomena in a Driven Dissipative Photonic Dimer. Nat Phys (2021) 17:604–10. doi:10.1038/s41567-020-01159-y

CrossRef Full Text | Google Scholar

36. Lu Z, Chen H-J, Wang W, Yao L, Wang Y, Yu Y, et al. Synthesized Soliton Crystals. Nat Commun (2021) 12:1–7. doi:10.1038/s41467-021-23172-2

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Bao C, Shen B, Suh M-G, Wang H, Şafak K, Dai A, et al. Oscillatory Motion of a Counterpropagating Kerr Soliton Dimer. Phys Rev A (2021) 103(1):L011501. doi:10.1103/PhysRevA.103.L011501

CrossRef Full Text | Google Scholar

38. Liu M, Huang H, Lu Z, Wang Y, Cai Y, Zhao W. Dynamics of Dark Breathers and Raman-Kerr Frequency combs Influenced by High-Order Dispersion. Opt Express (2021) 29(12):18095–107. doi:10.1364/oe.427718

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Xu G, Nielsen AU, Garbin B, Hill L, Oppo G-L, Fatome J, et al. Spontaneous Symmetry Breaking of Dissipative Optical Solitons in a Two-Component Kerr Resonator. Nat Commun (2021) 12:1–9. doi:10.1038/s41467-021-24251-0

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Yelo-Sarrión J, Parra-Rivas P, Englebert N, Arabí CM, Leo F, Gorza S-P. Self-Pulsing in Driven-Dissipative Photonic Bose-Hubbard Dimers. Phys Rev Res (2021) 3:L042031. doi:10.1103/PhysRevResearch.3.L042031

CrossRef Full Text | Google Scholar

41. Matsko AB, Maleki L. Bose-Hubbard Hopping Due to Resonant Rayleigh Scattering. Opt Lett (2017) 42:4764–7. doi:10.1364/ol.42.004764

PubMed Abstract | CrossRef Full Text | Google Scholar