Augmented reduced order models for turbulence

The authors introduce an augmented-basis method (ABM) to stabilize reduced-order models (ROMs) of turbulent incompressible flows. The method begins with standard basis functions derived from proper orthogonal decomposition (POD) of snapshot sets taken from a full-order model. These are then augmented with divergence-free projections of a subset of the nonlinear interaction terms that constitute a significant fraction of the time-derivative of the solution. The augmenting bases, which are rich in localized high wavenumber content, are better able to dissipate turbulent kinetic energy than the standard POD bases. Several examples illustrate that the ABM significantly out-performs L²-, H¹- and Leray-stabilized POD ROM approaches. The ABM yields accuracy that is comparable to constraint-based stabilization approaches yet is suitable for parametric model-order reduction in which one uses the ROM to evaluate quantities of interests at parameter values that differ from those used to generate the full-order model snapshots. Several numerical experiments point to the importance of localized high wavenumber content in the generation of stable, accurate, and efficient ROMs for turbulent flows.

1 Introduction

Parametric model-order reduction (pMOR) is a promising approach to leveraging high-performance computing (HPC) for design and analysis in fluid-thermal engineering applications. The governing equations in this context are the time-dependent incompressible Navier-Stokes equations (NSE) and the thermal transport equation.

${\partial }_t\mathit{u}+\mathit{u}\cdot \nabla \mathit{u}=-\nabla p+\nu {\nabla }^2\mathit{u}+\mathit{f},\nabla \cdot \mathit{u}=0,(1)$

${\partial }_{t}T+\mathit{u}\cdot \nabla T=\alpha {\nabla }^{2}T.(2)$

Where ν and α parameterize the PDEs and the forcing function f can be the Boussinesq approximation term, for example.¹ The equations are assumed to hold in a suitable domain Ω with appropriate initial and boundary conditions. The Galerkin statement is.

Find $({\partial }_t\mathit{u},p,{\partial }_{t}T)\in Y≔[{\mathbf{H}}_{\mathbf{0}}^{\mathbf{1}}\otimes L^2\otimes H_0^1]$ s.t. ∀(v, q, S) ∈ Y.

$\left(\mathit{v},{\partial }_t\mathit{u}\right)+\left(\mathit{v},\mathit{u}\cdot \nabla \mathit{u}\right)=\left(\nabla \cdot \mathit{v},p\right)-\nu \left(\nabla \mathit{v},\nabla \mathit{u}\right)+\left(\mathit{v},\mathit{f}\right),\left(q,\nabla \cdot \mathit{u}\right)=0,(3)$

$\left(S,{\partial }_{t}T\right)+\left(S,\mathit{u}\cdot \nabla T\right)=-\alpha \left(\nabla S,\nabla T\right).(4)$

Here, L² is the space of square-integrable functions on Ω; H¹ is the space of functions in L² whose gradient is also in L²; and $H_0^1$ is the space of functions in H¹ that vanish on subsets of the boundary, ∂Ω_D ⊂ ∂Ω, where homogeneous Dirichlet conditions are imposed. ${\mathbf{H}}_{\mathbf{0}}^{\mathbf{1}}$ is the vector counterpart to $H_0^1$.

To obtain a fully-accurate quantity of interest (QOI) such as friction factor, Nusselt number, or Strouhal number, one formally needs to obtain a full-order model (FOM) solution to the governing equations at discrete points in the parameter space of interest (e.g., spanned by a range of ν and α, of interest). Typically, the FOM constitutes a high-fidelity spectral- or finite-element solution to the governing equations, which can be expensive to solve, particularly for high Reynolds number cases that are typical of engineering applications. pMOR seeks to develop a sequence of reduced-order models (ROMs) that capture the behavior of the FOM and allow for parameter variation. For unsteady flows, the pMOR problem can be broken down into two subproblems: reproduction, wherein the ROM captures essential time-transient behavior of the FOM using the same parameter (anchor) point for each, and parametric variation, wherein the ROM is run at a different parametric point in order to predict the system behavior away from the anchor points at which the FOM simulation was conducted.

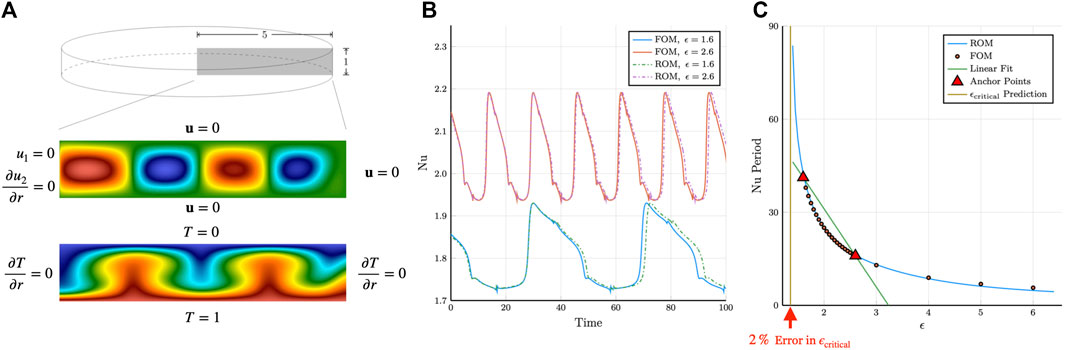
In this work, we focus primarily on the reproduction problem for challenging unsteady flows. We do, however, also consider pMOR, which we illustrate with an example from [1]. The thermal-fluids problem is the axisymmetric Rayleigh-Bénard configuration depicted in Figure 1A, which was studied by Tuckerman and Barkley [2,3]. The problem is parameterized by $ϵ=\frac{\mathrm{R}\mathrm{a}-\mathrm{R}{\mathrm{a}}_{\mathrm{c}}}{\mathrm{R}{\mathrm{a}}_{\mathrm{c}}}$, where Ra_c = 1734 is the critical Rayleigh number. The 2D axisymmetric domain has an aspect ratio of Γ = 5, shown in Figure 1A. For ϵ > 1.3843, traveling waves move towards the centerline axis with a period that depends on ϵ. We perform FOM calculations at two anchor points, ϵ = 1.6 and ϵ = 2.6, from which we collect snapshots (full flow/temperature fields). We apply proper orthogonal decomposition (POD) to the snapshot sets from each of the FOMs and use 20 POD modes from each to form a reduced-order subspace Z^N comprising N = 40 basis functions. These modes are used in the weak- (Galerkin-) formulation of the governing equations, where the solution is restricted to Z^N ⊂ Y. The low-dimensional ROM is able to capture short- and long-time behavior as shown in the Nusselt number reproduction traces in Figure 1B. Moreover, as shown in Figure 1C, the pMOR is able to accurately predict the period of the traveling wave solutions both inside and outside the ϵ range spanned by the anchor points. Note that as ϵ → 1.3843, the period goes to infinity and FOM simulations near this limit become intractable. The ROM, however, is able to predict this critical value of ϵ to within a few percent.

FIGURE 1

FIGURE 1. ROM application to axisymmetric Rayleigh–Bénard.

While pMOR is a promising approach for engineering analysis and design, it is well known that even the reproduction problem is challenging for the classical POD-Galerkin approach at high Reynolds numbers after the flow transitions to turbulence. One common issue with this class of problems is that the ROM solution approaches an unphysical attractor. This behavior is attributed to a lack of dissipation, given that the truncated POD space lacks high-wavenumber modes that are capable of dissipating energy. One can induce additional dissipation by including more modes but the cost is high. The convective tensor reduction requires storage of N³ entries for the advection operator with a corresponding work of 2N³ operations per timestep. While N = 100, with a cost of a two million operations per step and a million words in memory, may be tolerable, N = 400 with a cost of 128 million operations and 64 million words quickly makes pMOR less viable for running on a workstation, which is typically the target for this type of analysis tool.

Existing techniques for addressing the computational cost include the discrete empirical interpolation method (DEIM) [4], which effectively interpolates the convective term, and tensor decomposition, which aims to approximate the convective tensor by a low-rank tensor. We will show in our concluding examples that these methods will not, on their own, address the unphysical ROM dynamics. Stabilization of the ROM is critical and is the primary topic of this work. Several stabilization strategies are described in Section 2. The major contribution of this work is the development of a novel augmented-basis method (ABM), in which we add important modes to the standard POD bases. In many cases, the ABM increases both the stability and accuracy of the ROMs at a cost equivalent to standard POD approaches having the same total number of modes.

2 Background

The POD-Galerkin technique in fluid flow emerged from work to identify dominant flow features by [5] Model-reduction using POD modes as basis functions was introduced afterwards, with a comprehensive analysis appearing in a later monograph by [5].

More complex PDEs with non-affine parameter dependencies were addressed by [6] using decomposition of the nonlinearity based on the empirical interpolation method (EIM). In this approach, successive interpolation modes are chosen to eliminate the error between the targeted term in FOM and the ROM at “magic points” designated as points in Ω where the error of the current interpolant (i.e., the approximant of the next mode) is maximal. This method was further extended by [4] with a POD decomposition of the nonlinear term and the choice of points restricted to discrete points produced by the spatial discretization of the PDE, called discrete empirical interpolation method (DEIM). While these methods enable application of pMOR to nonlinear problems the issue of insufficient dissipation and feasible stabilization for the NSE persists.

Due to its approach of treating nonlinear terms, DEIM has the potential to address the high-cost issue of including more modes. DEIM replaces the third-order convective tensor with a collocation-like decomposition at the discrete magic points, which yields a reduction of computational complexity from O(N³) to O(N²). Accounting for the constants, evaluation of advection using DEIM with N = 200 modes would be equivalent to using the full tensor with N = 65. For the same cost, DEIM thus permits the use of a richer approximation space.

To certify that the error in the ROMs that are produced is smaller than the acceptable tolerance, error indicators have been developed based on the residual of the ROM solutions in the full-order model (FOM) space. Error indicators for coercive elliptic PDEs are described by [7]. An a posteriori error indicator for time-dependent NSE is described by [8] which is described as the dual-norm of the residual of the time-averaged momentum equation. This error indicator is evaluated by accumulation of residual contributions from each term in the momentum equation at each time-step. This metric provides an error estimate for time-dependent ROM solutions, while not a strict bound on the error, allows an efficient selection of anchor point selection for pMOR. We do not consider these further here, but they are an important component for efficient pMOR and are discussed in a companion paper [9].

For addressing the issue of stability, several modifications to the original POD Galerkin approach have been proposed [10]. proposed a modification of the POD mode generation in which the H¹ inner-product is used to produce the Gramian, rather than L² inner-product, to emphasize the importance of gradients in the FOM snapshots [11]. introduced Leray regularization in the context of ROM in which the advecting field is smoothed (conveniently, by truncation of the modes in the case of POD-ROM). This regularization enhances the stability property of the dynamical behavior; however, the optimal choice of regularization (e.g., number of modes to truncate or shape of transfer function) is not known a priori.

An alternative stabilization approach, introduced by [8], is to replace the discrete ODE system by a constrained minimization problem at each timestep. During the evolution of the system, the basis coefficients are bound by the minimum and maximum coefficient values observed in the snapshot projection onto the truncated POD space. (If the constraints are inactive, one recovers the standard Galerkin-based trajectory.) With this approach, the ROM tends to stay close to the dynamics of the FOM. A challenge, however, is that this approach requires ad hoc modification of the bounds for parametric values where the FOM snapshots are unavailable. Applications of several of these stabilization techniques may be found in [1].

Methods that address the stability issue by constructing basis functions that satisfy the energy-balance that closely match the POD basis is introduced by [12]. In this work, existing work on stabilizing linear time-invariant (LTI) systems by [13], which seeks optimal combinations of snapshots to produce dynamically stable ROMs, is combined with work by [14], in which the kinetic energy behavior is stabilized by introducing an empirical turbulence closure term in the ROM. In this combined method by Balajewicz, in a preprocessing step, an a priori nonlinear constrained optimization problem is solved that minimizes the difference between the energy captured by the new modes and the energy captured by the POD modes for a given N subject to constraints: the columns of the transformation matrix are orthonormal and the empirical kinetic energy-balance is satisfied. The result is a set of transformed POD modes that are augmented directly with dissipation modes (also taken as linear combinations of the snapshots). The author demonstrated that this approach offers significant improvement over the standard POD-Galerkin approach for a 2D lid-driven cavity problem and a 2D mixing layer. Also discovered was the fact that by ensuring the kinetic energy-balance is dissipative to an arbitrary degree, the ROM solution becomes stabilized. Thus, by encapsulating the method by this ROM training stage, the amount of appropriate dissipation to be prescribed in the constrained optimization step can be found to produce a stable ROM with mean TKE behavior close to that of the FOM.

Another basis augmentation approach, introduced by [15,16], uses a combination of L² POD modes and H¹ POD modes that are subsets of the originating snapshot set. The idea is to have a small number of L² POD modes capture the dominant energy-carrying features of the flow while the H¹ POD modes (containing small-scale features) provide the necessary dissipation that is not realized by the L² POD modes alone. The authors successfully applied this augmented basis to 3D turbulent flow in injectors.

In the next section, we introduce a novel augmented basis method, that is designed to address accuracy and stability of ROMs for turbulent flow. Rather than drawing upon the snapshot set, the augmenting vectors are derived from the nonlinear interaction terms that directly influence the time-derivative of the NSE. This augmented basis set does not require extensive training (i.e., ROM-parameter optimization) and can be used within a standard Galerkin-ROM setting.

3 Augmented basis method

To motivate the ABM, we consider the Leray-projected form of the NSE, in which the velocity field evolution is described as:

${\partial }_t\mathit{u}=\mathbb{P}\left[-\mathit{u}\cdot \nabla \mathit{u}+\nu {\nabla }^2\mathit{u}\right].(5)$

Here, the pressure has been formally eliminated and its effects are represented by an abstract operator, $\mathbb{P}$, sometimes called the Leray projector, which will project the operand onto a space of divergence-free fields. While the Leray projector is a projection using the H¹ inner-product, we will use the L² inner-product for our definition. For the discretized system, particularly with the P_NP_N−2 spectral element discretization, this operator is well-defined [17].

For the spectral element method (SEM), we look to find the solution in a finite-dimensional space, $X^{\mathcal{N}}$, comprising piecewise Nth-order tensor-product polynomial bases mapped from a reference unit cube to each of E spectral elements, for a total of $\mathcal{N}\approx E{N}^3$ degrees-of-freedom per field (in 3D). Finally, in the POD-Galerkin approach, we restrict our attention to solutions $Z^N\subset X^{\mathcal{N}}$, where the basis is generally formed from a proper orthogonal decomposition of a sequence of SEM solution snapshots, using the method introduced by [18].

The method of snapshots forms a basis from a linear combination of FOM solution fields (each involving $O(\mathcal{N})$ spectral element basis coefficients). One forms the Gramian matrix, whose first N eigenvectors (ranked by eigenvalues from largest to smallest) are used to determine the linear combination of the snapshots that forms the N-dimensional basis for the ROM approximation space, Z^N. Because the snapshots are (weakly) divergence-free, so are all elements of Z^N, which means that pressure drops out of the ordinary differential equation that governs the ROM. In this work, the velocity POD modes are denoted as ζ_i, and the thermal POD modes are denoted as θ_i. For both of these collections of modes, the i = 0 modes correspond to a lifting function that satisfies the boundary conditions and is always associated with a coefficient value of u₀ = 1 and T₀ = 1. The choice of the lifting function may be a solution to the Stokes problem, the Poisson equation, or the time-averaged solution. For the examples in Section 4, the lifting function is based on time-averaged FOM solutions. For the POD-ROM, the hierarchy of the spaces of interest is $Z^N\subset X^{\mathcal{N}}\subset Y$. For this work, we consider a FOM discretization that is well-resolved such that the projection error from Y to $X^{\mathcal{N}}$ is minimal. We next show how the Z^N space derived by the classical POD-Galerkin method can be augmented such that the time-evolution of the solution in the extended space better approximates the time-evolution of the solution in $X^{\mathcal{N}}$.

Assuming that the solution to Eq. 5 exists near t*, we can describe the local temporal behavior through a Taylor-series expansion involving a linear combination of all time-derivatives.

$\mathit{u}\left(\mathit{x},t^{\ast }+ϵ\right)=\mathit{u}\left(\mathit{x},t^{\ast }\right)+ϵ{\partial }_t\mathit{u}\left(\mathit{x},t^{\ast }\right)+\dots (6)$

$=\underset{\text{Snapshot}}{\underbrace{\mathit{u}\left(\mathit{x},t^{\ast }\right)}}+ϵ\mathbb{P}\left\{-\mathit{u}\cdot \nabla \mathit{u}+\nu {\nabla }^2\mathit{u}\right\}+\dots (7)$

Therefore, in addition to capturing the dominant modes of the snapshots, we propose to augment the POD basis set Z^N with modes that can accurately represent the order ϵ terms on the right-hand side of (7) in order to construct u (x, t* + ϵ). The consequence of not representing the O(ϵ) term is deviation in the trajectory of the physical solution and the projected (Galerkin) solution.

Consider a solution u that lives in Z^N, meaning $\mathit{u}={\sum }_{i=0}^N{u}_i{\mathit{\zeta }}_i$. Using (5), we can describe the time-derivative of the solution as

${\partial }_t\mathit{u}=\mathbb{P}\left[-\mathit{u}\cdot \nabla \mathit{u}+\nu {\nabla }^2\mathit{u}\right]=-\sum _{i,j=0}^N{u}_i{u}_j\mathbb{P}\left[{\mathit{\zeta }}_i\cdot \nabla {\mathit{\zeta }}_j\right]+\sum _{i=0}^N{u}_i\nu \mathbb{P}\left[{\nabla }^2{\mathit{\zeta }}_i\right](8)$

Thus, we can accurately describe the time-derivative with (N + 1)² terms for the nonlinear term and (N + 1) terms for the viscous operator.

We consider an example with Fourier basis to highlight this issue. When we have a band-limited solution state with the highest wavenumber k, the convection term would produce a solution at the next timestep of highest wavenumber 2k, which does not live in the original space. Thus, the wavenumber 2k behavior is never observed in the evolution of the projected Galerkin system. With an augmentation of the basis with the high-wavenumber modes, we will face the same issue through lack of 4k mode representation. This issue is of course recursive. We are helped, however, by the fact that the higher wavenumber modes have higher rates of dissipation. Continuation of this process will therefore eventually yield only marginal returns in improved solution fidelity. We shall see, however, that addition of just a few modes can have a significant impact on the overall ROM performance.

Because of nonlinear advection, the solution will evolve outside the N-dimensional span of Z^N. We note that as the basis includes more fine-scale components, the convective contribution becomes small relative to the diffusive contribution; thus, the solution becomes closed as the minimal grid-size approaches 0, as is the case in FOM solvers (i.e., the exact solution is band-limited). In the POD-ROM, however, the basis is typically far from completing the relevant approximation space and the addition of the modes $\mathbb{P}[{\mathit{\zeta }}_i\cdot \nabla {\mathit{\zeta }}_j]$ and $\mathbb{P}[{\nabla }^2{\mathit{\zeta }}_i]$ can provide an important first-order correction to Z^N.

For advection dominated problems, we can focus on the nonlinear contributions,

${\partial }_t\mathit{u}\approx \mathbb{P}\left[\mathit{u}\cdot \nabla \mathit{u}\right]=\sum _{j,k=0}^N{u}_j{u}_k\mathbb{P}\left[{\mathit{\zeta }}_k\cdot \nabla {\mathit{\zeta }}_j\right](9)$

Whenever we evolve the solution in the space Y, where the current solution lies in the truncated POD space Z^N, we see that the time derivative be reasonably represented with an additional (N + 1)² basis functions of the form ${\mathit{\varphi }}_{l=j+k(N+1)}=\mathbb{P}[{\mathit{\zeta }}_k\cdot \nabla {\mathit{\zeta }}_j]$. Obviously, this process is not closed, since more basis functions are required in the next timestep. Worse still, even starting with u ∈ Z^N, the required number of additional basis functions will be O(N²) if we include all terms in (9), which comes with an O(N⁶) computational cost that is untenable, even for a small number of POD modes, N. We therefore seek to augment the original POD basis with subsets of these evolution basis that are most relevant to the dynamics.

The first subset captures the interaction between the lifting function, ζ₀, and all other modes. This choice ensures that both the Taylor dispersion induced by the lifting function and the transport of the mean momentum by the POD modes are accurately captured. This choice is also rationalized by the fact that the lifting function is ever-present in the solution so its convective interaction is important in accurate reproduction of the time-evolution by the ROM. Thus, we add the modes $\mathbb{P}[{\mathit{\zeta }}_0\cdot \nabla {\mathit{\zeta }}_j+{\mathit{\zeta }}_j\cdot \nabla {\mathit{\zeta }}_0]$. Note that the two interactive terms can be combined because it is linear in each POD basis, ζ_j, meaning we only add N + 1 modes, which is still an O(N) augmentation.

Next, we extract the diagonal entries, $\mathbb{P}[{\mathit{\zeta }}_j\cdot \nabla {\mathit{\zeta }}_j]$. This choice is justified by the fact that for each mode, ζ_j, the mode that is the most correlated with it is itself (i.e., when other modes might have a phase-shift, or different temporal frequencies associated with it, the auto-correlation dominates other interactions). So we consider addition of these N modes with the total additional modes being 2N + 1.

For a thermal system with an advection-diffusion equation to describe its state, we can follow the same procedure as above for the lifting function interaction in the form of ζ₀ ⋅∇θ_j; however, the auto-interaction modes are not obvious. For this work, we will choose ζ_j ⋅∇θ_j, but there is no one-to-one correspondence between the dominant thermal modes and dominant velocity modes. One may come up with a more coherent substitute, but this choice remains an open question.

We note that ABM modes are not orthogonal in general, but are made orthogonal prior to running the ROM via eigendecomposition of the ROM mass matrix for numerical stability purposes. Disregarding round-off errors, the basis representation for a specific solution and test space do not affect the time-evolution of the solution for the standard POD-Galerkin ROM.

In summary, the ABM starts with N standard POD modes in Z^N and adds 2N + 1 modes corresponding to advection by the lifting function, $\mathbb{P}[{\mathit{\zeta }}_0\cdot \nabla {\mathit{\zeta }}_j+{\mathit{\zeta }}_j\cdot \nabla {\mathit{\zeta }}_0]$ and auto-advection, $\mathbb{P}[{\mathit{\zeta }}_j\cdot \nabla {\mathit{\zeta }}_j+{\mathit{\zeta }}_j\cdot \nabla {\mathit{\zeta }}_j]$, resulting in a total of $\widehat{N}=3N+1$ basis functions, which are used in a standard Galerkin formulation. We will use $\widehat{N}$ for the comparison against other (classic or stabilized) methods so that we have a fair cost comparison. The standard POD Galerkin ROM and ABM differ only in the choice of the underlying basis set.

4 Applications

We have demonstrated the effectiveness of the proposed augmentation method on several examples, including flow in a 2D Lid-Driven cavity (Re = 30, 000), 2D flow past baffles (Re = 800), 3D lid-driven cavity flow (Re = 10,000), flow over a hemisphere (Re = 2, 000), and turbulent pipe flow with forced convection for Re = 4,000 −10,000. For brevity, we here consider only the latter two. We will also use the 2D flow past a cylinder problem to demonstrate long-time stable ROM solutions by use of ABM. In the following, we denote the FOM solution with $(\tilde{\mathit{u}},\tilde{T})$ and the various ROM solutions with (u, T). Time averages are defined as $⟨\cdot ⟩=\frac{1}{\tau }{\int }_{t_0+\tau }^{\tau }\cdot dt$ with integration times, τ, prescribed on a case-by-base basis. There are plots that compare different ROM strategies: Standard POD Galerkin (L²-Glk), energy-based POD basis ($H_0^1$-Glk), Leray-filtered (L²-Lry), ABM with lifting function interaction (L²-Aug0), ABM with auto-interaction (L²-AugD), and ABM with both interactions (L²-AugC).

4.1 2D flow over a circular cylinder

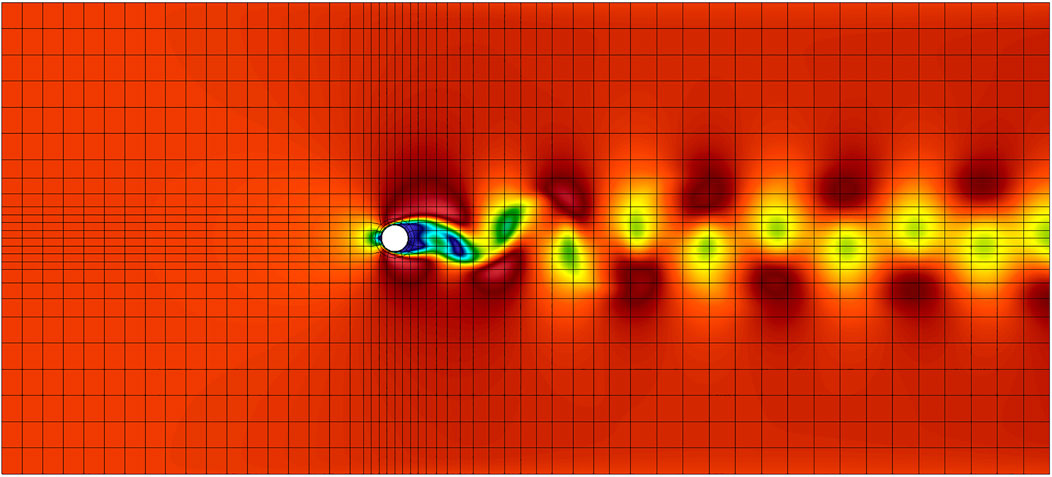
Before we compare the stabilization properties of ABM to other methods, we first investigate the long-time stability properties of ABM on the flow past a cylinder problem. Although this is a canonical problem that is used to demonstrate the model-order reduction capabilities of the POD-Galerkin approach, there are commonly observed instability issues for a large domain. This phenomenon is documented in [19–22]. To establish that ABM addresses this long-time stability issue observed in ROMs of low Reynolds number cylinder flows, we first take 200 snapshots of a flow past a cylinder problem over 200 CTUs. The domain and boundary conditions are of that specified in [20]. Figure 2 shows a velocity magnitude plot of a snapshot used to produce the ROMs.

FIGURE 2

FIGURE 2. Velocity magnitude plot of a flow past a cylinder snapshot (Re = 100)

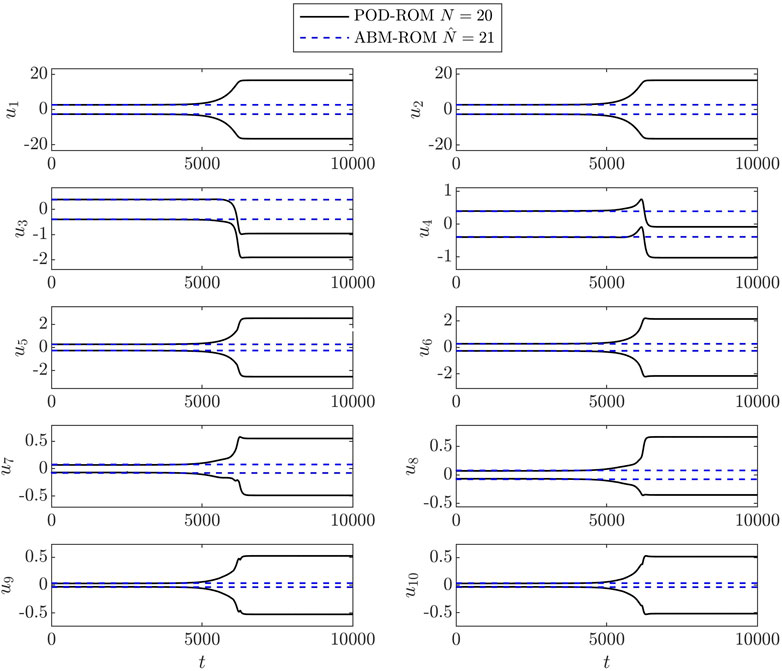
Figure 3 show reproduction of the 10 mode results in [20] with a difference in the ordering and signs of the POD modes stemming from the difference in snapshot count, snapshot timing, and possibly integration time for the mean flow which is used as the lifting function. For this problem, even if we increase the number of POD modes to N = 20, the growth of the instability is delayed, but is still present in the long-time solution as shown in Figure 4. Application of ABM to 10 originating POD modes resulting in a $\widehat{N}=21$ ROM produced a long-time result (over 20,000 CTUs) that is free from the type of instability observed in the N = 20 POD-ROM. The envelopes of the coefficient trajectories of this ABM-ROM are shown in Figure 5 on top of the POD-ROM result.

FIGURE 3

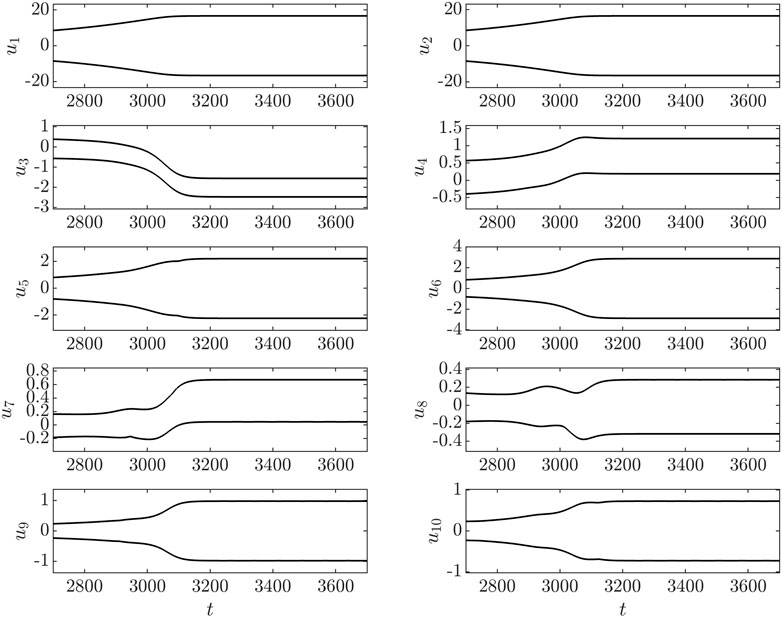
FIGURE 3. POD-ROM coefficient envelopes for flow past a cylinder (N = 10, t ∈ [2,700, 3,700], Re = 100)

FIGURE 4

FIGURE 4. POD-ROM coefficient envelopes for flow past a cylinder (N = 20, t ∈ [0, 10⁴], Re = 100)

FIGURE 5

FIGURE 5. ABM-ROM coefficient envelopes for flow past a cylinder (t ∈ [0, 2 × 10⁴], Re = 100)

With this example, we have demonstrated that ABM successfully address long-time stability issue observed in the low-dimensional models constructed by the POD-Galerkin methodology for the cylinder problem. In the next examples, we will show successful application of ABM to 3D turbulence problems.

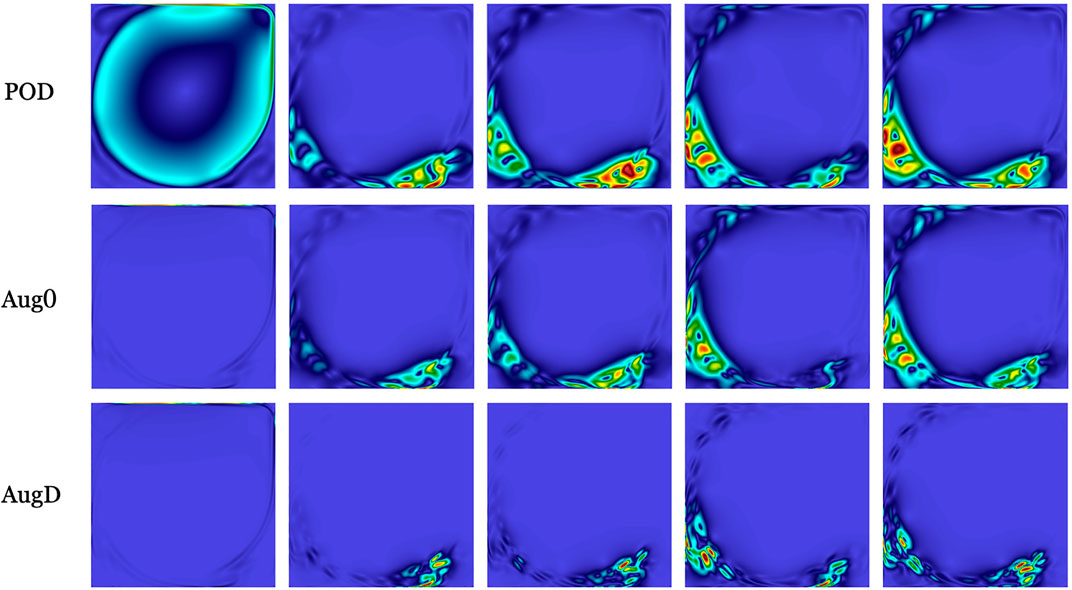
4.2 3D flow over a hemisphere

Figure 6 shows a snapshot of flow past a wall-mounted hemisphere of height D/2 at Re_D = DU/ν = 2000. A Blasius profile with boundary-layer thickness δ₉₉ = 0.6D is prescribed at the inlet, which 3.2D units upstream of the hemisphere center. Periodic boundary conditions are prescribed at ± 3.2D units in the spanwise direction and a stress-free condition is applied on the top surface, 3.2D units above the wall. Under these conditions, the flow exhibits periodic shedding of hairpin vortices, evidenced by the velocity distribution and λ₂ contours [23] in the hemisphere wake. The FOM, based on a spectral element mesh with $\mathcal{N}\approx 2$ million gridpoints was run for 100 convective time units (1 CTU = D/U) and 1,000 snapshots we collected to form the ROM POD bases.

FIGURE 6

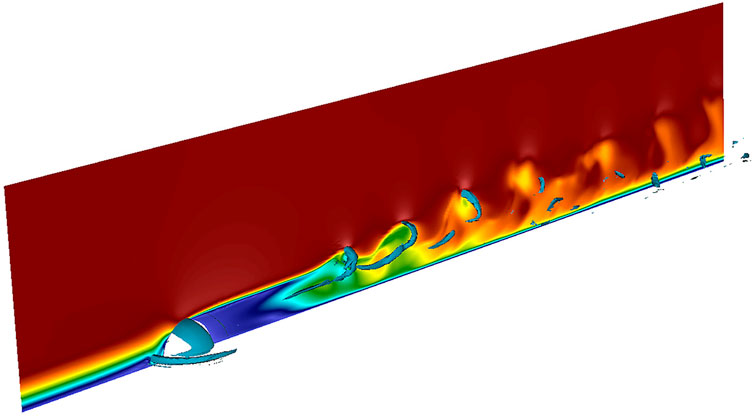
FIGURE 6. FOM velocity magnitude snapshot of flow over hemisphere (Re = 2,000) with overlaid λ₂ contour.

The mean-velocity error as a function of $\widehat{N}$ is shown in Figure 7 (left) for the five different ROMS. POD Galerkin with L² (L²–Glk) and $H_0^1$ ($H_0^1$–Glk) Gramians, Leray-regularized Galerkin (L²–Lry), Constrained-Galerkin (L²–Cst), and ABM with combined lifting- and diagonal-interactions (L²–AugC). The unstable L² and $H_0^1$ Galerkin results have several drop-outs for conditions that did not converge for this relatively high-Reynolds number application. Given enough basis functions, however, all cases converge, with the L²–Cst being the best performer for $\widehat{N}<120$. Both L²–Cst and L²–AugC yield mean-field errors $<.01$ for the majority of the cases, with L²–Cst generally being the best performer. Similar conclusions hold for the turbulence kinetic energy (TKE), the measure of kinetic energy contained in the fluctuations about the mean velocity field, shown in the right panel of 7. We reiterate that, while the constrained optimization solver performs well in the reproduction problem, it is not readily extended to pMOR because the parametric variation of the constraint limits is not known a priori.

FIGURE 7

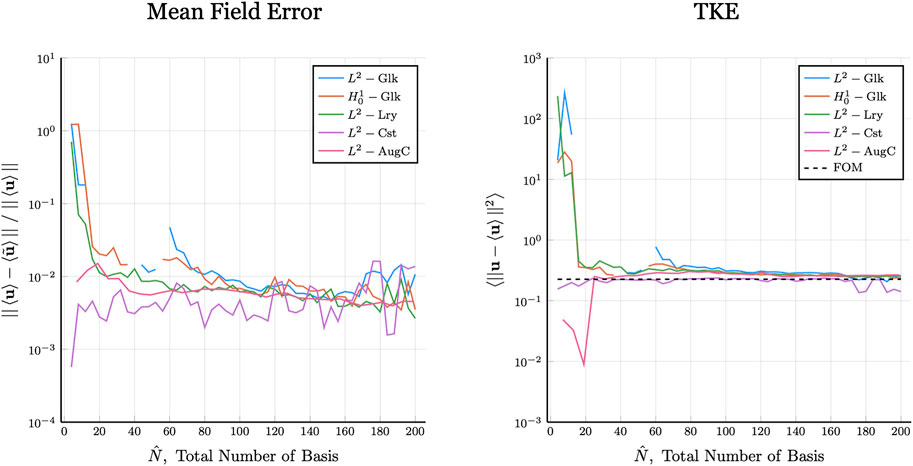
FIGURE 7. Flow over hemisphere (Re = 2,000): Mean and TKE error comparison, curve broken by blowup solution.

4.3 Forced convection in turbulent pipe flow

The next example is that of forced convection in turbulent pipe flow with Reynolds number Re = 4,000, 5300, and 10,000 (based on pipe diameter), and Prandtl number Pr = 1. All the cases use the same spectral element distribution with differing polynomial orders. The mesh consists of 12.5 million grid points for Re = 4,000 and 5300, and 24.5 million points for Re = 10,000. The periodic domain length is L = 4D, which is generally inadequate for a full DNS of turbulence but deemed sufficient for the numerical tests in this study. For Re = 4,000, 5300, and 10,000, the respective FOM Nusselt numbers are Nu = 16.38, 21.42, and 36.14, which is in good agreement with the Dittus-Boelter relationship, Nu = 0.023 Re^4/5 Pr^2/5. For all cases, the FOM is run until the solution is relaxed to a statistically steady state prior to gathering statistics or snapshot data. For each case, 1,000 snapshots are collected over 50 CTUs to form the Gramian, from which the POD basis is generated. Figure 8 shows typical snapshots of velocity magnitude and temperature that reveal the variation in range of scales for the different cases.

FIGURE 8

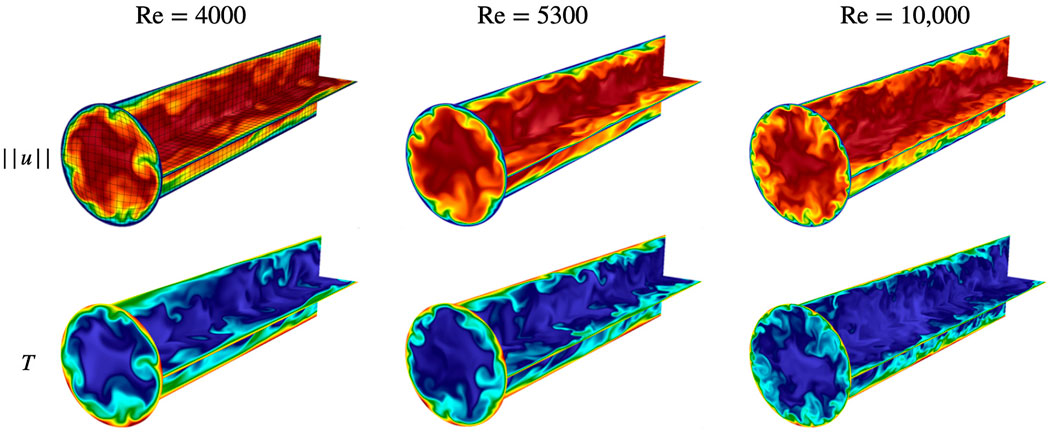
FIGURE 8. FOM velocity (top) and temperature (bottom) snapshots of 3D pipe flow at Re = 4,000, 5300, and 10,000.

The governing equations for the FOM are the incompressible Navier–Stokes equations and the thermal advection-diffusion equation. Because of the constant-flow rate and periodic restriction on the solutions, we provide a brief discussion of modifications to the standard equations for the FOM and their effect on the ROM formulation. We start with the Navier–Stokes equations:

$\frac{\partial \mathit{u}}{\partial t}+\mathit{u}\cdot \nabla \mathit{u}=-\nabla p+\nu {\nabla }^2\mathit{u}+\mathit{f}\left(\mathit{u}\right),\nabla \cdot \mathit{u}=0(10)$

Here, f(u) is a uniform forcing vector field function in the streamwise direction, $\widehat{\mathit{z}}$, that enforces a time-constant flow-rate. In the time-discrete problem, the forcing term effectively adds an impulse-response streamwise velocity field with boundary layer thickness proportional to $\sqrt{\nu \mathrm{\Delta }t}$. This impulse response is scaled appropriately at each time step to ensure that the mean velocity at each timestep conforms to the prescribed flow-rate. In the case of the ROM, the lifting function has the prescribed flow-rate and the remaining POD basis functions have zero flow-rate, meaning that the test-space Z^N only contains members with zero flow-rate. In the weak-form, the ROM forcing term therefore becomes

$\left(\mathit{v},\mathit{f}\right)={\int }_{\mathrm{\Omega }}\mathit{v}\cdot \mathit{f}dV=f_z\left({\int }_{\mathrm{\Omega }}{v}_{z}dV\right)=0.(11)$

Thus, the forcing term in the ROM formulation is zero.

The boundary conditions for the thermal problem are prescribed unit thermal flux on the walls. Therefore, we add a constant-slope ramp function γz such that the lifted temperature T, can be periodic in the domain. The equation becomes

$\frac{\partial T}{\partial t}+\mathit{u}\cdot \nabla \left(T+\gamma z\right)=\alpha {\nabla }^{2}T(12)$

To ensure that thermal energy is conserved in the domain we set $\gamma =\frac{P}{Q}=4$, where P is the circumference of the pipe and Q is the volumetric flow-rate.

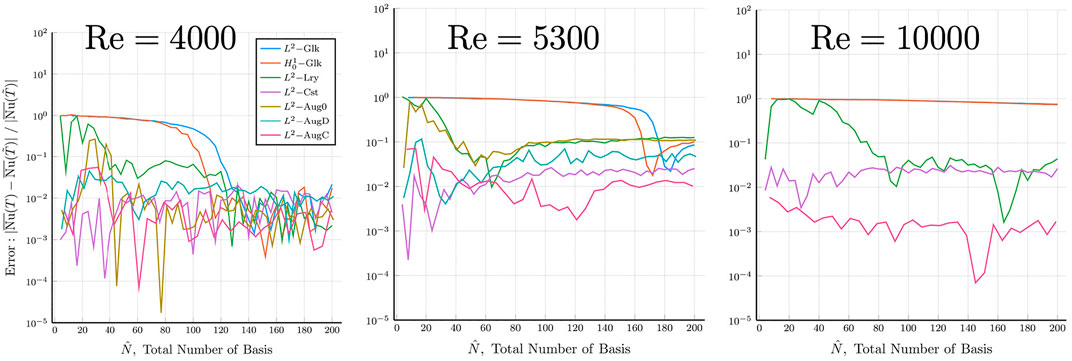
The results for the ROMs are presented in Figures 9–11, which show the error and variance for the velocity and temperature as well as the Nusselt number behavior as a function of the total number of modes. The mean Nusselt number definition is based on the time-averaged streamwise velocity and temperature,

$\overline{\mathrm{N}\mathrm{u}}=\frac{1}{\alpha \left(\overline{T_s}-\overline{T_b}\right)},\overline{T_s}={\int }_{\partial \mathrm{\Omega }}⟨T⟩dS,\overline{T_b}=\frac{{\int }_{\mathrm{\Omega }}⟨T⟩⟨u_z⟩dV}{{\int }_{\mathrm{\Omega }}⟨u_z⟩dV}.(13)$

The legends are ordered in the following manner: L² basis, $H_0^1$ basis, L² basis with Leray regularization, L² basis with constrained optimization, L² basis augmented with 0th-mode interaction, L² basis augmented with auto-correlation (diagonal), and L² basis augmented with combined 0th-mode and auto-correlation modes.

FIGURE 9

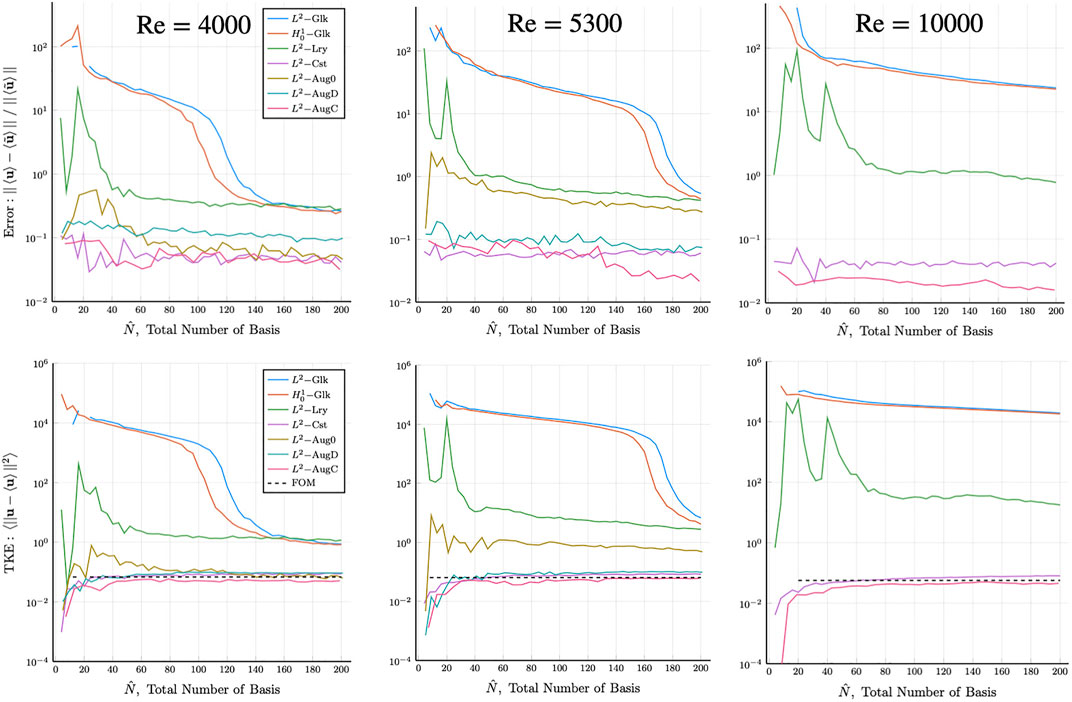
FIGURE 9. Pipe flow mean velocity error (top) and TKE results (bottom), for Re = 4,000, 5300, and 10,000 (FOM: τ = 50, ROM: τ = 500), curve broken by blowup solution.

FIGURE 10

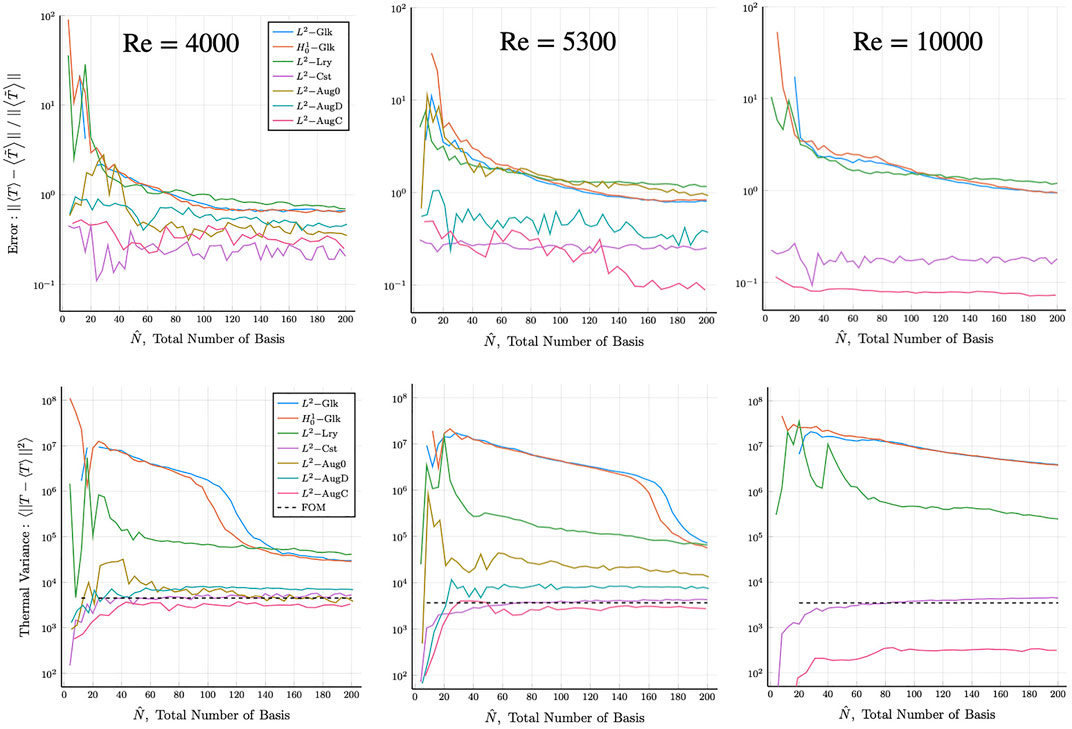
FIGURE 10. Pipe flow mean temperature error (top) and thermal variance results (bottom), for Re = 4,000, 5300, and 10,000 (FOM: τ = 50, ROM: τ = 500), curve broken by blowup solution.

FIGURE 11

FIGURE 11. Pipe flow error in Nusselt number for Re = 4,000, 5300, and 10,000.

A common observation for Figures 9–11 is nominal convergence for the Re = 4,000 case for the L², $H_0^1$, and Leray regularization methods, albeit to relatively large asymptotic values. As the Reynolds number increases, more modes are required for the L² and $H_0^1$ formulations to converge, with the required number of modes apparently exceeding $\widehat{N}=200$ for Re = 10,000. Clearly, Leray outperforms standard L² and $H_0^1$, but is inferior to L²–Cst and L²–AugC, with the latter two having mean velocity error of just a few percent at Re = 10,000 (Figure 9, top right). The thermal behavior is similar, save that the mean-field error (Figure 10, top) is above 10% with the exception of L²–AugC for Re = 10,000. Remarkably, this same case exhibits too little thermal variance, as seen in the lower right frame of Figure 10 (We explore this anomalous behavior in the next section.) On the other hand, the error in Nu for L²–AugC at Re = 10,000 is uniformly less than 1% (Figure 11).

We close this section with a remark about DEIM as a possible alternative to ABM. Although DEIM allows for larger number of modes in the ROM for a given cost, its accuracy will not surpass that of the underlying ROM formulation on which it is based. So, for a classic L²– or H¹–based formulation, DEIM will not yield an acceptable reconstruction result even at N = 200, whereas the constrained and ABM formulations realize convergence at much lower values of $\widehat{N}$ and much lower costs.

5 Discussion

The ABM has been remarkably successful in advancing our ability to apply ROMs to high-Reynolds number flows. Several observations point to the stabilization properties of the ABM, rather than its approximation quality, as the principal driver for its success. Inspection of the modes for several cases indicate that the augmenting modes in the ABM have high wavenumber content that is localized in Ω to regions of active flow dynamics. An example is illustrated in Figure 12, which shows the first 14 L²–AugC modes for the case of a lid-driven cavity at Re = 30, 000. For j = 0, … , 4, the first five POD modes, ζ_j ∈ Z^N, are in the top row; the first five 0-modes, $\mathbb{P}\left\{{\mathit{u}}_0\cdot \nabla {\mathit{u}}_j+{\mathit{u}}_j\cdot \nabla {\mathit{u}}_0\right\}$, are in the center row; and the first five diagonal-modes, $\mathbb{P}\left\{{\mathit{u}}_j\cdot \nabla {\mathit{u}}_j\right\}$, are in the lower row (The 0–0 mode is of course not used twice when forming the augmented basis.) We see that the auto-interaction modes in particular feature high wavenumber content in regions of Ω where the POD modes have significant amplitude. Although it is not shown here, the augmented bases develop high wavenumber content at a much faster rate (i.e., lower mode number) than their high mode-number POD counterparts, which explains why it takes so long for the standard POD Galerkin method to stabilize in the Re = 4,000, 5300, and 10,000 pipe flow cases of the preceding section. In this sense, the augmenting modes are more wavelet-like than Fourier-like and therefore quite efficient in providing a localized dissipation mechanism for quadratic interactions. Using these bases thus makes some sacrifice on approximation properties (because we use fewer POD modes, which are optimal in generating low-rank approximations to the snapshot space in the same spirit as low-rank SVD-based matrix decompositions) in favor of better stabilization. Despite this trade-off, the ABM generally yields a much better overall approximation of the dynamics than even its stabilized POD counterparts, as is evident in the turbulent pipe flow case. While not shown in this work, ABM-ROM constructed from pipe-flow at Re = 5300 snapshots were stable even with parametric variation (in Reynolds number), but accuracy in the Nusselt number prediction decreased as the Reynolds number moved away from 5300. How to address this phenomenon will be studied in subsequent works in the future.

FIGURE 12

FIGURE 12. Magnitude of POD and ABM modes for a regularized lid-driven cavity problem.

This stabilization hypothesis is supported by the graphs of Figure 13, which shows the amplitudes of the basis coefficients for POD and ABM Galerkin ROM solutions to pipe flow at Re = 5300 as a function of time and mode number. The coefficient evolutions are shown over three time windows [0, 10] [0, 100], and [0, 500], which reveal the growth and saturation of the amplitudes. We see that for the ABM (in the lowest row), the coefficients are all smaller than unity, save for the ζ₀ coefficient, which is unity (All modes have unit 2-norm, so the coefficients represent the true amplitude of each scaled mode.) The ABM results also show that most of the energy is in the POD bases, corresponding roughly to the lower third of the mode indices. By contrast, the coefficients for the standard POD Galerkin modes (top row) quickly saturate to amplitudes in excess of 100, and all modes are excited. As is well known from under-resolved Navier-Stokes simulations, there is an energy pile up—manifest as high amplitude modal coefficients—when the representation lacks high wavenumber bases capable of dissipating energy. The Leray-regularized coefficients (second row) exhibit a behavior similar to the standard Galerkin approach, save that the coefficients are much more controlled, which peak amplitudes much closer to unity. The constrained approach (third row) also exhibits chaotic coefficient behavior but at much more controlled amplitudes than either the standard or Leray cases. Remarkably, the evolution on the t = [0, 100] window indicates that the ABM coefficient behavior is nearly time periodic.

FIGURE 13

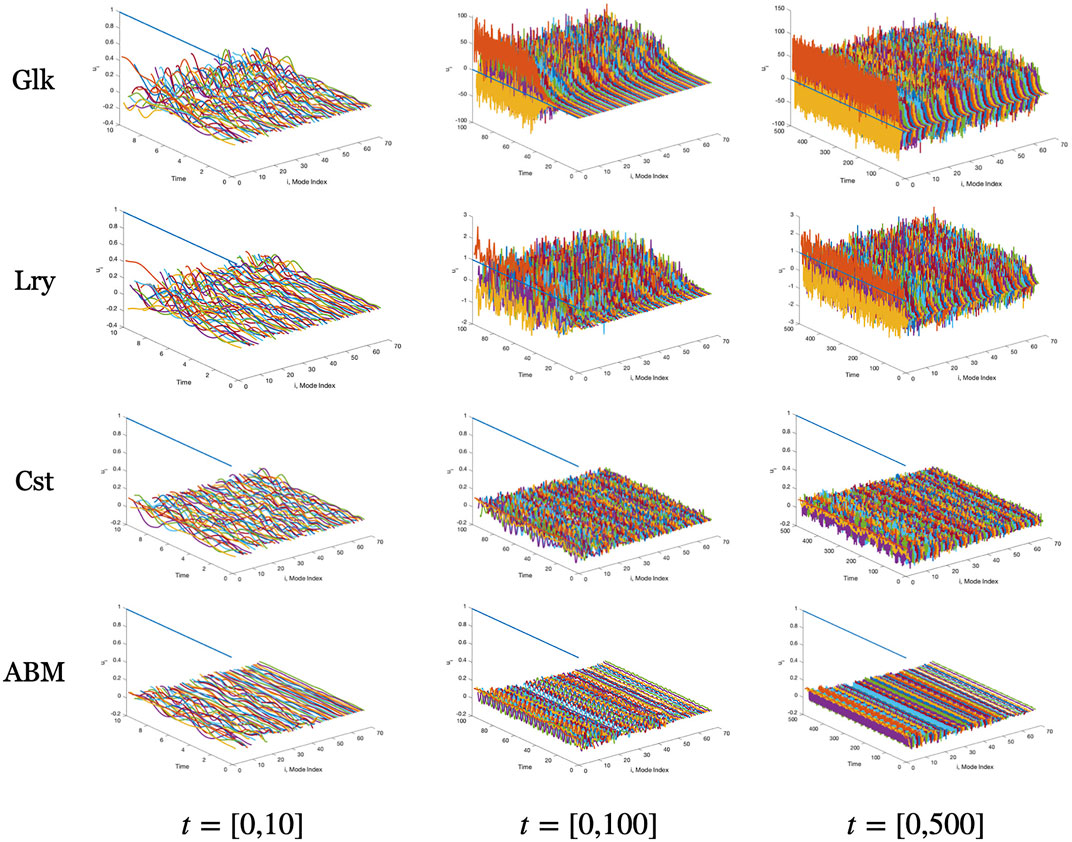
FIGURE 13. Temporal behavior of basis coefficients for standard POD (Glk), Leray-filtered (Lry), Constrained (Cst), and ABM-ROM solutions of turbulent pipe flow at Re = 5300 over (convective) time intervals t ∈ [0, 10] [0.100], and [0.500].

Another study to investigate the role of dissipation is illustrated in Figure 14. We focus initially on the upper left graph, which shows the mean-flow error for the standard POD-ROM case as a function of the number of modes $\widehat{N}=N$. The modes are drawn from a set of POD bases functions based on K snapshots, where K = 125, 250, 500, or 1,000. Whenever N = K it is clear that Z^N is equivalent to the snapshot space, which implies that the modes contain all the high frequency content present in the snapshots of a turbulent flow solution. We see that these cases have a lower error than cases where the number of modes is a relatively small fraction of the number of snapshots. The same trends are indicated in the TKE plots for the POD-ROM in the upper right graph. By contrast, the ABM-ROM needs very few total modes to yield a better estimate of the mean flow (lower left) and the best TKE predictions are obtained when the snapshot set is large (e.g., K ≥ 500 in the lower right graph). If we have too few modes in the snapshot space, along with the nonlinear augmentation modes, the ABM-ROM appears to be overly dissipative. Therefore, we suspect that using more snapshots to produce a more accurate POD series may ensure an accurate ROM reproduction for high Reynolds number pipe flow cases.

FIGURE 14

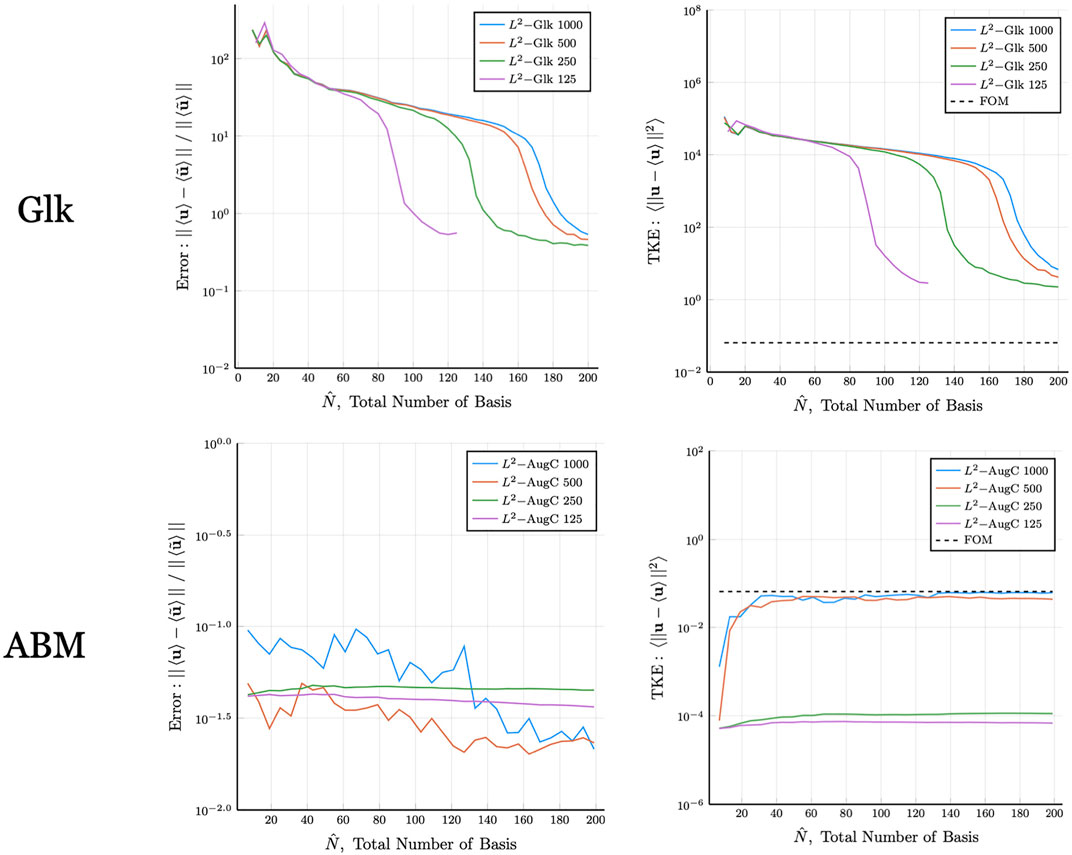
FIGURE 14. Convergence for mean velocity (left) and TKE (right) for turbulent pipe flow at Re = 5300 as a function of the number of modes for the POD-ROM (top) and ABM-ROM (bottom). The dimension of the snapshot space, K, is indicated in the legend.

The effectiveness of the ABM approach in a pMOR context is demonstrated by considering the pipe flow problem with two sets of snapshots at Re = 5300 and Re = 10,000. Combining 1,000 snapshots from each anchor point, we obtain 30 POD modes and 61 ABM modes using the average of the mean velocity solutions at the anchor points as the lifting function. Running this ROM for Re ∈ {4,000, 5000, … , 10,000} resulted in a parameteric behavior that is consistent with the physical flow: as Reynolds number is increased, the boundary layer thickness decreases according to the law of the wall and the turbulence fluctuation adjacent to the wall region increases. Figure 15 depict the mean axial flow profile. This profile was produced by an additional spatial averaging in the axial and azimuthal directions. More detailed analysis will be conducted in the future, but this preliminary example pMOR application provides evidence that ABM-ROM is a promising approach for pMOR of turbulent flows.

FIGURE 15

FIGURE 15. Time- and space-averaged axial velocity profiles for ABM-ROM pMOR.

6 Conclusion

We introduced a novel stabilization method, ABM, for ROM-based simulations of incompressible turbulent flows that augments the standard POD basis with approximate temporal derivatives. For a space of POD basis functions, Z^N = {ζ_i}, i = 0, … , N, we include and additional 2N + 1 functions that are the Leray (divergence-free) projections of the nonlinear interactions with the lifting mode, {ζ₀ ⋅∇ζ_i + ζ_i ⋅∇ζ₀}, and nonlinear auto-interactions, {ζ_i ⋅∇ζ_i}. With these basis functions, the ROM proceeds in the standard Galerkin fashion and is seen to dramatically outperform standard L²-and $H_0^1$-POD Galerkin ROM approaches as well as Leray-stabilized methods introduced by [1,11]. The ABM performs comparably to the constraint-based stabilization approach of [8], but the latter is restricted to the ROM reproduction problem (i.e., running at the same parameter points as the originating FOM) because, in a pMOR setting, the correct basis-coefficient limits are not known at training points other than the anchor points.

We showed that the auxiliary modes of the ABM have high wavenumber content that is localized to regions in Ω where flow gradients are large and thus provide efficient dissipation mechanisms that are lacking in standard POD bases. We further demonstrated that, for standard POD methods, having a more complete POD space (i.e., incorporating N ≈ K modes from a relatively small snapshot space of rank K) yields lower errors than having N′ > N POD modes from a larger snapshot space of rank K′ > N′. The reasoning is the same—the more complete space includes high wavenumber content in the ROM basis set that provides dissipation and hence stability. Analysis of the ROM coefficient time-traces for turbulent pipe flow at Re = 5300, illustrated that the amplitudes of all the modes for non-stabilized POD-ROM are orders of magnitude larger than their stabilized counterparts. While Leray-based stabilization mitigates this behavior, it still yields coefficient amplitudes that are roughly a factor of ten greater than observed in either the constrained or ABM-based formulations.

The ABM was also shown to be effective for predicting thermal QOIs such as Nusselt numbers. It was, however, a bit overly dissipative at Re = 10, 000. The study of the interplay between N and K indicates that this dissipation can be controlled with these two parameters and one might therefore use these parameters to gain insight to the root cause of the over-dissipation. Future work will include application of the ABM to higher Reynolds number flows and to more complex domains.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.

Author contributions

Research was performed by KK under advisement and direction of PF. The two authors both contributed to the production of the manuscript.

Funding

This work from NEUP with number DE NE0008780 for Turbulent Heat-Transfer ROM research was used. This research is supported by the DOE Office of Nuclear Energy under the Nuclear Energy University Program (Proj. No. DE_NE0008780). The research used resources at the Oak Ridge Leadership Computing Facility at Oak Ridge National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under Contract DE-AC05-00OR22725 and at the Argonne Leadership Computing Facility, under Contract DE- AC02-06CH11357.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹These equations are effectively in nondimensional form, which for forced conditions implies that ν = Re⁻¹, the inverse Reynolds number, and α = Pe⁻¹, the inverse Peclet number. For buoyancy-driven flows these parameters typically scale with Rayleigh number (Ra) and Prandtl number (Pr), with the precise definition dependent on the chosen scaling.

References

1. Kaneko K, Tsai P-H, Fischer P. Towards model order reduction for fluid-thermal analysis. Nucl Eng Des (2020) 370:110866. doi:10.1016/j.nucengdes.2020.110866

CrossRef Full Text | Google Scholar

2. Tuckerman L, Barkley D. Global bifurcation to traveling waves in axisymmetric convection. Phys Rev Lett (1988) 61:408–11. doi:10.1103/physrevlett.61.408

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Barkley D, Tuckerman L. Traveling waves in axisymmetric convection: The role of sidewall conductivity (1989).

Google Scholar

4. Chaturantabut S, Sorensen DC. Nonlinear model reduction via discrete empirical interpolation. SIAM J Scientific Comput (2010) 32:2737–64. 10.1137/090766498.(Accessed March 26, 2022)

CrossRef Full Text | Google Scholar

5. Holmes P, Lumley JL, Berkooz G. Turbulence, coherent structure, dynamical systems and symmetry. Cambridge University Press (1996). doi:10.1017/CBO9780511622700

CrossRef Full Text | Google Scholar

6. Barrault M, Maday Y, Nguyen N, Patera A. An ‘empirical interpolation’ method: Application to efficient reduced-basis discretization of partial differential equations. C R Math (2004) 339:667–72. doi:10.1016/j.crma.2004.08.006

CrossRef Full Text | Google Scholar

7. Veroy K, Rovas DV, Patera A. A posteriori Error estimation for reduced-basis approximation of parametrized elliptic coercive partial differential equations: “Convex inverse” bound conditioners. convex inverse” bound conditioners (2002) 8:1007–28. doi:10.1051/cocv:2002041

CrossRef Full Text | Google Scholar

8. Fick LH, Maday Y, Patera AT, Taddei T. A stabilized POD model for turbulent flows over a range of Reynolds numbers: Optimal parameter sampling and constrained projection. J Comput Phys (2018) 371:214–43. doi:10.1016/j.jcp.2018.05.027

CrossRef Full Text | Google Scholar

9. Tsai P-H, Fischer P. Parametric model-order-reduction development for unsteady convection. Front Phys (2022).

CrossRef Full Text | Google Scholar

10. Iollo A, Lanteri S, Desideri JA. Stability properties of POD-galerkin approximations for the compressible Navier-Stokes equations. Theor Comput Fluid Dyn (2000) 13:377–96. doi:10.1007/s001620050119

CrossRef Full Text | Google Scholar

11. Wells D, Wang Z, Xie X, Iliescu T. An evolve-then-filter regularized reduced order model for convection-dominated flows. Int J Numer Methods Fluids (2017) 84:598–615. doi:10.1002/fld.4363

CrossRef Full Text | Google Scholar

12. Balajewicz M. A new approach to model order reduction of the Navier-Stokes equations. Durham, NC: Duke University (2012). Ph.D. thesis.

Google Scholar

13. Amsallem D, Farhat C. Stabilization of projection-based reduced-order models. Int J Numer Methods Eng (2012) 91:358–77. doi:10.1002/nme.4274

CrossRef Full Text | Google Scholar

14. Cazemier W, Verstappen RWCP, Veldman AEP. Proper orthogonal decomposition and low-dimensional models for driven cavity flows. Phys Fluids (1998) 10:1685–99. doi:10.1063/1.869686

CrossRef Full Text | Google Scholar

15. Akkari N, Mercier R, Lartigue G, Moureau V (2017). Stable POD-Galerkin Reduced Order Models for unsteady turbulent incompressible flows. In 55th AIAA Aerospace Sciences Meeting (Grapevine, United States)

CrossRef Full Text | Google Scholar

16. Akkari N, Casenave F, Moureau V. Time stable reduced order modeling by an enhanced reduced order basis of the turbulent and incompressible 3d Navier–Stokes equations. Math Comput Appl (2019) 24:45. doi:10.3390/mca24020045

CrossRef Full Text | Google Scholar

17. Fischer P. An overlapping schwarz method for spectral element solution of the incompressible Navier–Stokes equations. J Comput Phys (1997) 133:84–101. doi:10.1006/jcph.1997.5651

CrossRef Full Text | Google Scholar

18. Sirovich L. Turbulence and the dynamics of coherent structures. I. Coherent structures. Q Appl Math (1987) 45:561–71. doi:10.1090/qam/910462

CrossRef Full Text | Google Scholar

19. Noack BR, Afanasiev K, Morzyński M, Tadmor G, Thiele F. A hierarchy of low-dimensional models for the transient and post-transient cylinder wake. J Fluid Mech (2003) 497:S0022112003006694–363. doi:10.1017/s0022112003006694

CrossRef Full Text | Google Scholar

20. Sirisup S, Karniadakis GE. A spectral viscosity method for correcting the long-term behavior of pod models. J Comput Phys (2004) 194:92–116. doi:10.1016/j.jcp.2003.08.021

CrossRef Full Text | Google Scholar

21. Akhtar I, Nayfeh AH, Ribbens CJ. On the stability and extension of reduced-order galerkin models in incompressible flows. Theor Comput Fluid Dyn (2009) 23:213–37. doi:10.1007/s00162-009-0112-y

CrossRef Full Text | Google Scholar

22. Hay A, Borggaard J, Akhtar I, Pelletier D. Reduced-order models for parameter dependent geometries based on shape sensitivity analysis. J Comput Phys (2010) 229:1327–52. doi:10.1016/j.jcp.2009.10.033

CrossRef Full Text | Google Scholar

23. Jeong J, Hussain F. On the identification of a vortex. J Fluid Mech (1995) 285:69–94. doi:10.1017/s0022112095000462

CrossRef Full Text | Google Scholar