The Roles of Information Diffusion on Financial Risk Spreading on Two-Layer Networks

The financial risk spreads widely on the financial network and the risk information diffuses broadly on the social networks. How the information diffusion affects the financial risk spreading still lacks mathematical study. This paper proposes a model to describe the coevolution of financial information diffusion and financial risk spreading on a two-layered network. We use a mean-field approach to describe the spreading dynamics and adopt extensive numerical simulations to simulate the dynamics. We find that financial information diffusion can suppress the financial risk generally. Notably, there exists an optimal information diffusion probability at which the financial risk is greatly suppressed. Our results may shed some light on controlling the financial risk spreading dynamics.

1 Introduction

Financial risk can spread in the financial networks, in which the nodes represent the financial institutions (e.g., banks) and edges stand for the loan relationships among that those financial institutions [1–4]. Generally, some poorly run enterprises may trigger a financial risk since they can not repay debts. As a result, those bad debts may result in their creditors being not ableunable to repay their debts, thus triggering cascading failures, and a global financial risk may arise. Investigating the financial risk spreading mechanisms and contagion models attracts the researchers from the field of network science and management science [5–8].

By using cascading failure or contagion models, extensive research revealed that the financial network topology markedly affects the spreading of financial risk [9–14]. Gai and Kapadia [15] investigated the financial risk spreading on the weighted directed network and revealed that the few hubs make the financial systems exhibit a robust-yet-fragile character. They used a generalized percolation theory to study the critical threshold point. Inspired by the phenomena in the field of epidemiology, Garas et al. [16] used the susceptible-infected-recovered (SIR) model and studiedy the probability of triggering the global crisis for different initial conditions. Huang et al. [17] investigated the financial risk spreading on the bipartite banking network and accurately predicted the failed banks with the natural failed banks after 2007.

The CEO (Chief Executive Officer) of the a financial institution will take measures to protect his/hertheir company from being infected based on his/her their risk perception. A CEO can percept the financial risk information from his/her CEO friends on the social network their CEO associates on social networks. How does that perceived information affect the financial risk spreading? To our best knowledge, there still lacks a systematical theoretical study on this is still lacking. Lin and Duan [18] revealed that the financial information spread dynamics depend on the topologies of the social network. To build a mathematical model to investigate the above stated problem, we will propose a coevolution spreading dynamics, which is inspired by information-epidemic coevolution spreading [19–25]. Granell et al. [21] used an unaware-aware-unaware–susceptible-infected-susceptible (UAU–SIS) model to study the effects of information diffusion on the epidemic spreading. They found that the epidemic spread size is greatly suppressed for large information diffusion probability.

The motivations of this paper have two aspectsare two-fold. On the one hand, the effects of the financial risk information diffusion on the financial risk spreading still are still lacking. On the other hand, the effects of heterogeneous CEO’s risk perception on the financial risk spreading need further investigation. In this paper, we will propose a mathematical model on two-layered networks to study the financial risk spreading, in which the financial risk spreading on the financial networks and the risk information diffuse diffusion on the CEOs social network are used. Different CEOs have different attitudes when receiving financial risk information, and we thus divide the CEOs into two types: risk aversion and risk patience. Therefore, the population is heterogeneous. Previous studies indicated that a heterogeneous population induces distinct spreading phenomena [26–28], such as the emergence of hybrid transition. Then we use a mean-field approach to describe the spreading dynamics and study the density of how each state evolves versus time. We find that the risk information spreading among CEOs can suppress the financial risk spreading through extensive numerical simulations. There is optimal information spreading probability at which the financial risk will be greatly suppressed. Finally, we find that the average degree of the two layers does not qualitatively affect the phenomena qualitatively.

The organizations of this paper are as follows This paper is organized as follows. In Section 2, we describe the spreading dynamics. In Section 3, we present the theory and numerical results. Finally, we make conclusions in Section 4.

2 Model Descriptions

In this section, we propose a systemic risk spreading model on a two-layered network (or multiplex networks [29–33]). We denote the two layers as A and B, respectively. We use layer B to denote the topology among banks. The nodes stand for financial institutions (e.g., banks), and the edge represents financial relationships (e.g., lending). Assuming there are N nodes in network B,. fFor layer A, we use it to describe the interactions among the CEOs of among the financial institutions. For each financial institution, there is only one CEO. Therefore, the nodes in two layers are matched one-to-one. An interlayer edge $e_{ij}^{\text{inter}}$ connecting two nodes i_A and i_B respectively in layers A and B represents the node i_A is the CEO of i_B.

We use an uncorrelated configuration model to describe the financial risk spreading dynamics on the two-layer networks by using a given degree distribution p_A (k_A) and p_B (k_B) for layers A and B, respectively. The average degree of layer A is $⟨k_A⟩={\sum }_{k_A}{p}_A(k_A)k_A$. Similarly, the mean degree of layer B can be expressed as $⟨k_B⟩={\sum }_{k_B}{p}_B(k_B)k_B$. The interlayer links are randomly connected one-to-one.

We simulate the financial risk spreading dynamics on the two-layer networks by using interacting spreading dynamics. The financial risk spreading on layer B follows a susceptible-infected-recovered-vaccination model, widely used to describe the failures and epidemics. A susceptible node means the financial institution is healthy (i.e., good financial condition) but can be infected once its infected neighbors cannot fulfill economic obligations. The infected node stands for the bad financial institution, and can not fulfill their economic obligations, and thus may transmit the financial risk to neighbors. The removed node means that a financial institution does not have any financial activities and can not trigger additional financial risk. The vaccination means that the financial institution has adopted measures to protect itself from being infected. On layer A, i.e., the CEO network where the information about the state of those financial conditions spreads, we divide the CEOs into two types: risk aversion and risk patience. A risk averse CEO means that he/shethey will take measures to protect his/hertheir financial institution from being infected once he/shethey obtains one piece of information from friends. Differently, a risk patient CEO takes measures only when he/she obtainsthey obtain ample information, i.e., T, from friends. For each CEO, they belonghe/she belongs to a risk aversion with probability p, and the remaining nodes 1 − p belong to the risk patience. We use a susceptible-informed-removed model to describe the information-spreading dynamics.

To stimulate the financial risk spreading, we randomly select one financial institution in layer B, and set it to be in the infected state. At each time state, the infected node j_B in layer B transmits the financial risk to each neighbor i_B with probability λ_B. If the infection is successful, its corresponding node i_A in layer A becomes informed, i.e., he/shethey know the “bad” information about his/hertheir financial institution, once i_A is in the susceptible state. The node j_B becomes a removed state with probability γ_B. On layer A, we use ℓ_A to record the number amount of the received information from neighbors for node j_A. We set ℓ_A = 0 initially, which means he/she doesthey do not know any information about the financial risk. At each time step, each node j_A transmits the information to every susceptible neighbor i_A with probability λ_A. If the node i_A obtains the information successfully, he/shethey becomes an informed state, and we set ℓ_A → ℓ_A + 1. If the node j_A represents a risk patient CEO, its corresponding node j_B becomes vaccination state with probability φ when ℓ_A ≥ T. If the node j_A is a risk aversion CEO, he/she becomesthey become vaccinated with probability φ. Therefore, the information spreading among the CEOs suppresses the financial risk spreading. The informed nodes become a recovered state with probability γ_A. The spreading dynamics evolve until there are no nodes in the infected or informed state in the system.

3 Results Analyses

We present the theoretical and Monte Carlo simulation results in this section. In Section 3.1, we present a heterogeneous mean-field theory to describe the evolution of the financial risk spreading dynamics in a two-layered network. Then, in Section 3.2, we use Monte Carlo simulation to study the model.

3.1 Theoretical Results

We here adopt a mean-field approach to study the evolution of the coupled dynamics. We assume there are no differences among the nodes. That is to say, different nodes in the same state have the same probability. Denoting S_A(t), ρ_A(t), and R_A(t) as the probability of a node in layer A is in the susceptible, infected, recovered, and vaccination state, while as B is in the susceptible, infected, recovered, and vaccination state as S_B(t), ρ_B(t), R_B(t), and V_B(t), respectively. Since each node can only be one of the three (or four) states in layer A (or layer B), we have

$\begin{array}{l}\hfill S_A\left(t\right)+{\rho }_A\left(t\right)+R_A\left(t\right)=1,\\ \hfill S_B\left(t\right)+{\rho }_B\left(t\right)+R_B\left(t\right)+V_B\left(t\right)=1.\end{array}(1)$

In the following, we investigate the rate equations of S_A(t), ρ_A(t), R_A(t), S_B(t), ρ_B(t), R_B(t), and V_B(t).

In the CEO network, i.e., layer A, the decrease of S_A(t) has two situations. Conversely, the susceptible node in layer A is informed by neighbors with probability ⟨k_A⟩λ_AS_A(t)ρ_A(t), where ⟨k_A⟩ is the mean degree of layer A. On the other hand, the corresponding node in layer B changes from susceptible state to infected. To compute the probability of this event, we should know that a node in layer A is a susceptible state, which means that its corresponding node in layer B is also in the susceptible state. Thus, we know the second event happens with probability ⟨k_B⟩λ_BS_A(t)ρ_B(t), where ⟨k_B⟩ is the mean degree of layer B. Combining the above two situations, we know the evolution of S_A(t) as

$\frac{d{S}_A\left(t\right)}{dt}=-S_A\left(t\right)\left[{\lambda }_A\langle k_A\rangle {\rho }_A\left(t\right)+{\lambda }_B\langle k_B\rangle {\rho }_B\left(t\right)\right].(2)$

For the evolution of ρ_A(t), the increase of ρ_A(t) equals to the decrease of S_A(t). The decrease of ρ_A(t) is γ_Aρ_A(t). We have

$\frac{d{\rho }_A\left(t\right)}{dt}=S_A\left(t\right)\left[{\lambda }_A\langle k_A\rangle {\rho }_A\left(t\right)+{\lambda }_B\langle k_B\rangle {\rho }_B\left(t\right)\right]-{\gamma }_A{\rho }_A\left(t\right).(3)$

Similarly, we know the evolution of R_A(t) is

$\frac{d{R}_A\left(t\right)}{dt}={\rho }_A\left(t\right).(4)$

We then investigate the financial risk spreading on layer B. The decrease of S_B(t) has two situations. For the first situation, a susceptible node in layer B is infected by neighbors with probability ⟨k_B⟩λ_BS_A(t)ρ_B(t). On the other hand, the susceptible node may become change to a vaccination state. If the susceptible state’s corresponding node in layer A is a risk aversion CEO, it becomes a vaccination state with probability φ⟨k_A⟩λ_AS_A(t)ρ_A(t). If the susceptible state’s corresponding node in layer A is a risk patient CEO, we should compute the obtained pieces of risk information at time step t. The probability that a susceptible node in layer A obtains m pieces of information at time t is

$h_m\left(t\right)=\left(\frac{\langle k_A\rangle }{m}\right){\left[u\left(t\right)\right]}^m{\left[1-u\left(t\right)\right]}^{\langle k_A\rangle -m},(5)$

where u(t) = ⟨k_A⟩λ_AS_A(t)ρ_A(t). Since the corresponding node in layer A of a susceptible node in layer B should receive at least T pieces of information when becoming to the vaccinated state, we have

$\mathrm{\Gamma }\left(t\right)=\left(1-p\right)\sum _{m\ge T}{h}_m\left(t\right).(6)$

Combining the above two situations, we know the evolution of S_B(t) as

$\frac{d{S}_B\left(t\right)}{dt}=-{\lambda }_B\langle k_B\rangle S_A\left(t\right){\rho }_B\left(t\right)-\phi \langle k_A\rangle {\lambda }_A{S}_A\left(t\right){\rho }_A\left(t\right)-\phi \mathrm{\Gamma }\left(t\right).(7)$

Similarly, we know the evolutions of ρ_B(t), R_B(t) and V_B(t) as

$\frac{d{\rho }_B\left(t\right)}{dt}={\lambda }_B⟨k_B⟩S_A\left(t\right){\rho }_B\left(t\right)-{\gamma }_B{\rho }_B\left(t\right),(8)$

$\frac{d{R}_B\left(t\right)}{dt}={\rho }_B\left(t\right),(9)$

and

$\frac{d{V}_B}{dt}=\phi ⟨k_A⟩{\lambda }_A{S}_A\left(t\right){\rho }_A\left(t\right)+\phi \mathrm{\Gamma }\left(t\right),(10)$

respectively. Numerically studying the above equations, we obtain the density of nodes in each state.

To obtain the percolation threshold point, we can investigate the linearizitionlinearization of Eqs 3, 8 when t → 0. We have S_A(t) → 1 and S_B(t) → 1. We know

$\begin{array}{ccc}\hfill \frac{d{\rho }_A\left(t\right)}{dt}& =\hfill & {\beta }_A⟨k_A⟩{\rho }_A\left(t\right)+{\beta }_B⟨k_B⟩{\rho }_B\left(t\right)-{\rho }_A\left(t\right),\hfill \\ \hfill \frac{d{\rho }_B\left(t\right)}{dt}& =\hfill & {\beta }_B⟨k_B⟩{\rho }_B\left(t\right)-{\rho }_B\left(t\right),\hfill \end{array}(11)$

where β_A = λ_A/γ_A and β_B = λ_B/γ_B are the rescaled infection probability. We rewrite Eq. 11 in matrix form as

$\frac{d\vec{\rho }}{dt}=C\vec{\rho }-\vec{\rho },(12)$

where $\vec{\rho }\equiv {({\rho }_A(t),{\rho }_B(t))}^T$, and

$C=\left(\begin{array}{cc}\hfill {\beta }_A⟨k_A⟩\hfill & \hfill {\beta }_B⟨k_B⟩\hfill \\ \hfill 0\hfill & \hfill {\beta }_B⟨k_B⟩\hfill \end{array}\right).(13)$

Since the financial risk spreading promotes the information diffusion in layer A, we know the information outbreak threshold is smaller than the financial risk breaks outs. The largest eigenvalue of C is

${\mathrm{\Lambda }}_C^1=\mathrm{m}\mathrm{a}\mathrm{x}\left\{{\beta }_A\langle k_A\rangle ,{\beta }_B\langle k_B\rangle \right\}.(14)$

The outbreak threshold of the information is

${\lambda }_c^{\mathcal{A}}=\frac{1}{{\mathrm{\Lambda }}_C^1}.(15)$

We cannot analytically obtain analytically a value for the financial risk globally outbreak threshold, and we can only obtain the numerical value.

3.2 Monte Carlo Simulation Results

We use a Monte Carlo simulation approach to study the financial risk spreading dynamics on the two-layered networks. For layers A and B, we use the homogeneous ER networks with a Poisson distribution $P_A(k_A)={⟨k_A⟩}^{k_A}/k_A!e^{-⟨k_A⟩}$ and $P_B(k_B)={⟨k_B⟩}^{k_B}/k_B!e^{-⟨k_B⟩}$ for networks A and B, respectively. For the given parameters, we perform it 2000 times and compute the average value in the following figures. We set the network sizes of networks A and B are N_A = 10⁴ and N_B = 10⁴, respectively.

We first introduce the methods to perform the Monte Carlo simulation for our suggested model.

i): Generating networks A and B according to the uncorrelated correlated model for the given degree distributions P_A (k_A) and P_B(k_B), respectively. For each CEO, we draw a probability q. If q ≤ p, the CEO belongs to thea risk aversion category. Otherwise, the CEO belongs to the risk patient.

ii): Randomly select a node in layer B and set it to be in the infected state.

iii): To stimulate the financial risk spreading, we randomly select one financial institution in layer B, and set it in to the infected state.

iv): Update the states of nodes in layer B. Each infected node j_B tries to transmit the risk to a susceptible neighbor i_B. Generating a random probability q, if q ≤ λ_B, node i_B becomes infected, and the corresponding node i_A becomes informed.

v): Recovery of each infected node j_B. Generating a random probability q, if q ≤ γ_B, node j_B becomes recovered.

vi): Update the states of nodes in layer A. Each informed node j_A tries to transmit the information to a susceptible neighbor i_A. Generating a random probability q, if q ≤ λ_A, node i_A becomes informed, and set ℓ_A → ℓ_A + 1. If i_A is a risk patient CEO, generating a random probability q and ℓ_A ≥ T, the node i_A change to a vaccination state when q ≤ φ. If i_A is a risk aversion CEO, i_A changes to vaccination state with probability φ.

vii): Recovery of each infected node j_A. Generating a random probability q, if q ≤ γ_A, node j_A becomes recovered.

viii): Repeat steps (iii)–(vii) until there is are no nodes in the informed and infected states.

In Figure 1, we first study the temporal evolution of the coevolution spreading dynamics on the homogeneous artificial networks. For the risk information spreading in the CEO network, i.e., layer A, the density of nodes in the informed state A, the density of nodes in the informed state ρ_A(t) first increases with time, then reaches a peak, and finally decreases to zero. We observe a similar phenomenaphenomenon for the evolution of financial risk ρ_B(t). Differently, ρ_A(t) reaches its peak is earlier than ρ_B(t), since the financial risk spreading dynamics promote the risk information spreading. However, the effects of the heterogeneous population of CEO networks do not become obvious, i.e., the fraction of individuals are the risk aversion CEOs. The evolutions of R_A(t) and R_B(t) increases with t continuously. We note that the more nodes belong to the risk aversion CEOs, the less financial risk outbreak size, i.e., the smaller R_B(t). Since This is because risk averse CEOs are more likely to take measures to protect themselves from being infected, resulting in a higher V_B(t).

FIGURE 1

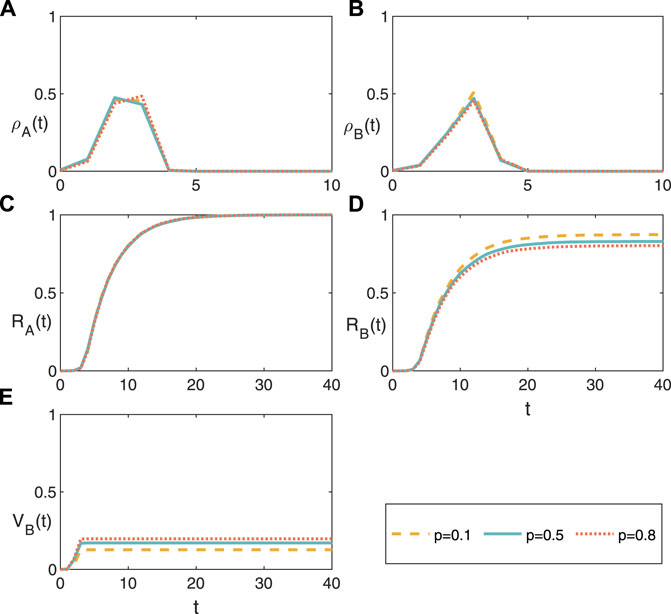
FIGURE 1. (Color online) Temporal evolutions of the spreading dynamics. The density of nodes in the (A) informed state ρ_A(t) of layer A, (B) infected state ρ_B(t) of layer B, (C) removed state R_A(t) of layer A, (D) removed state R_B(t) of layer B, and (E) vaccination state R_A(t) of layer (B). We set the average degree of the two layers as ⟨k_A⟩ = ⟨k_B⟩ = 10, information spreading probability λ_A = 0.5, financial risk probability λ_B = 0.8, T = 3, recovery probability γ_A = γ_B = 0.2, and φ = 0.9.

We then investigate the final financial risk spreading size R_B and final risk information spreading size R_A in Figure 2. Since the risk information spreading probability is set to be λ_B = 0.5 and λ_B = 0.8, we find that R_A is not affected by the heterogeneity of the CEO population (see Figures 2A,D). For the financial risk spreading, we find optimal risk information spreading probability at which R_B reaches a minimum value (see Figures 2B,E). Specifically, R_B first decreases with λ_A since the CEOs will take measures to protect themselves from being infected by the financial risk and will be immunized, as shown in Figures 2C,F. However, when λ_A is large enough, those risk patient CEOs will not be immunized since they can not obtain sufficient risk information from neighbors, thus inducing a higher values of R_B. We conclude that a reasonable information transmission probability helps us to decrease the financial risk spreading. In Figure 3, we further study the effects of the average degree of the two networks and find that the phenomenona is not affected qualitatively.

FIGURE 2

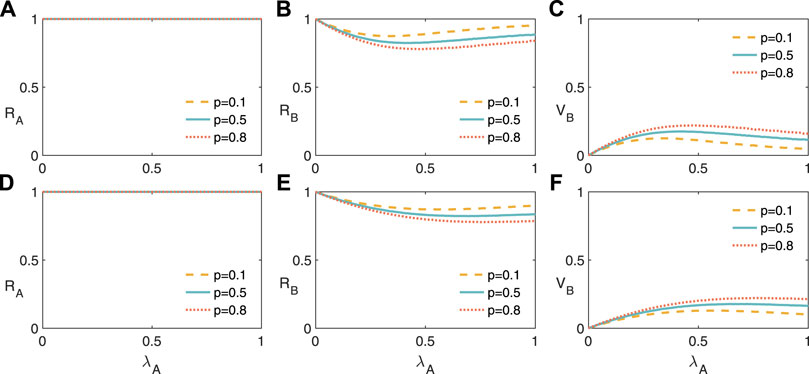
FIGURE 2. (Color online) The financial risk spreading on two-layer networks for a given values of financial risk transmission probability. Final information spreading size R_A (A), final financial risk spreading size R_B (B), and vaccination size R_B (C) versus information transmission probability λ_A with financial risk transmission probability λ_B = 0.5. R_A (D), R_B (B), and R_B (C) versus λ_A with λ_B = 0.8. We set the average degree of the two layers as ⟨k_A⟩ = ⟨k_B⟩ = 10, T = 3, recovery probability γ_A = γ_B = 0.2, and φ = 0.9.

FIGURE 3

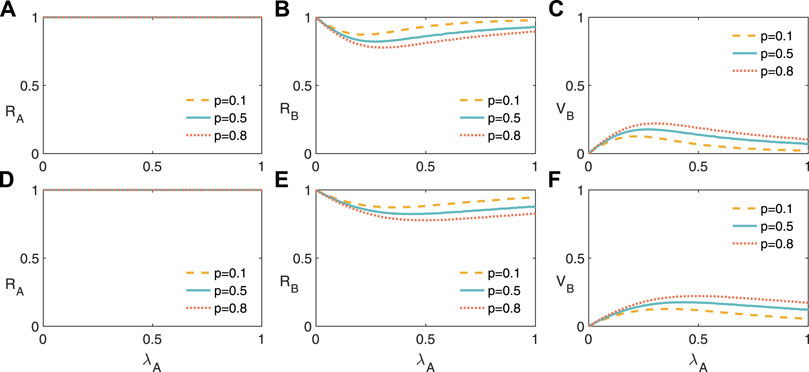
FIGURE 3. (Color online) The financial risk spreading on two-layer networks for a given values of financial risk transmission probability. Final information spreading size R_A (A), final financial risk spreading size R_B (B), and vaccination size R_B (C) versus information transmission probability λ_A with financial risk transmission probability λ_B = 0.5. R_A (D), R_B (B), and R_B (C) versus λ_A with λ_B = 0.8. We set the average degree of the two layers as ⟨k_A⟩ = 15, ⟨k_B⟩ = 10, T = 3, recovery probability γ_A = γ_B = 0.2, and φ = 0.9.

For a given information transmission probability λ_A, we investigate R_A, R_B, and V_B as a function of λ_B in Figure 4. Since λ_A are much larger than the risk outbreak threshold, R_A are not affected by p, i.e., the fraction of nodes belongs to the risk averse CEOs (see Figures 4A,D). RB first increases with as λ_B decreases, and finally increase, as shown in Figures 4B,E. That is to say, enlarging the financial risk spreading probability does not always enlarge increase the financial risk spreading. Since only the risk information and financial risk spreading have a compatible speed, the immunized nodes will be maximized (see Figures 4C,F). The average degree of the two networks does not qualitatively affect the phenomena in Figure 5.

FIGURE 4

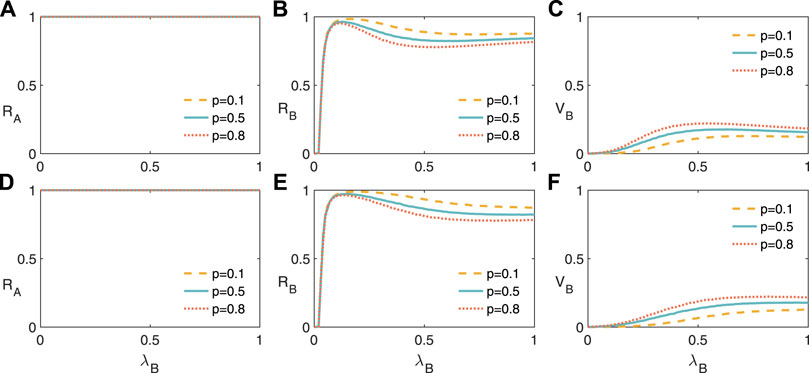
FIGURE 4. (Color online) The financial risk spreading on two-layer networks for a given values of financial risk transmission probability. Final information spreading size R_A (A), final financial risk spreading size R_B (B), and vaccination size R_B (C) versus information transmission probability λ_B with financial risk transmission probability λ_A = 0.5. R_A (D), R_B (B), and R_B (C) versus λ_B with λ_A = 0.8. We set the average degree of the two layers as ⟨k_A⟩ = ⟨k_B⟩ = 10, T = 3, recovery probability γ_A = γ_B = 0.2, and φ = 0.9.

FIGURE 5

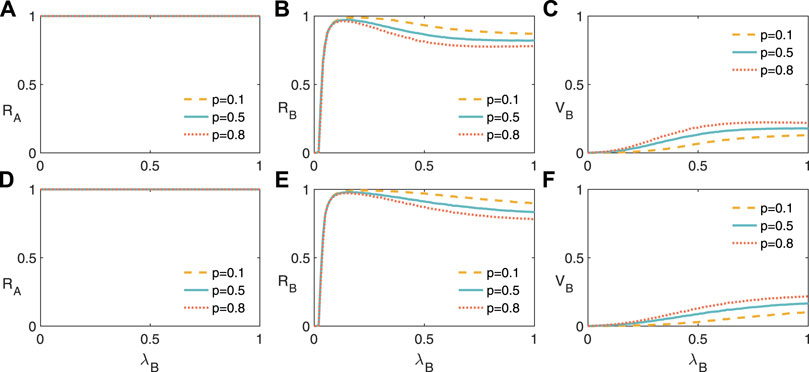
FIGURE 5. (Color online) The financial risk spreading on two-layer networks for a given values of financial risk transmission probability. Final information spreading size R_A (A), final financial risk spreading size R_B (B), and vaccination size R_B (C) versus information transmission probability λ_B with financial risk transmission probability λ_A = 0.5. R_A (D), R_B (B), and R_B (C) versus λ_B with λ_A = 0.8. We set the average degree of the two layers as ⟨k_A⟩ = 15, ⟨k_B⟩ = 10, T = 3, recovery probability γ_A = γ_B = 0.2, and φ = 0.9.

4 Conclusion

This paper uses a mathematical model to investigate the financial risk spreading on the multiplex networks. We first propose a model to describe the coevolution of financial information diffusion on the CEOs social network and financial risk spreading on the financial networks. For the CEOs, we divide them into two types and investigate the relatively fraction on the spreading dynamics. Using a mean-field approach, we study the evolution of the coevolution dynamics. We finally perform extensive numerical simulations. We find that the financial information diffusion suppresses the financial risk spreading. In addition, optimal information spreading probability exists, at which the financial risk will be greatly suppressed. Finally, we reveal that the networks average degree does not affect the above-presented phenomena qualitatively. The results presented in this paper may shed some light into on designing strategy to control the financial risk diffusion. How to develop a more accurate theory to study this model need further investigation.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

ML, LD, YL, and QX designed the research, performed the research, analysed the empirical data and wrote the paper.

Funding

This work was partially supported by Sichuan Science and Technology Program (No. 2020JDR0200) and National Social Science Foundation of China Western Project (No. 18XJY001).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Glasserman P, Young HP. How Likely Is Contagion in Financial Networks? J Banking Finance (2015) 50:383–99. doi:10.1016/j.jbankfin.2014.02.006

CrossRef Full Text | Google Scholar

2. Jorion P. Financial Risk Manager Handbook, Vol. 406. Hoboken, NJ, USA: John Wiley & Sons (2007).

Google Scholar

3. Alter A, Schüler YS. Credit Spread Interdependencies of European States and banks during the Financial Crisis. J Banking Finance (2012) 36:3444–68. doi:10.1016/j.jbankfin.2012.08.002

CrossRef Full Text | Google Scholar

4. Erb CB, Harvey CR, Viskanta TE. Political Risk, Economic Risk, and Financial Risk. Financial Analysts J (1996) 52:29–46. doi:10.2469/faj.v52.n6.2038

CrossRef Full Text | Google Scholar

5. Haldane AG, May RM. Systemic Risk in Banking Ecosystems. Nature (2011) 469:351–5. doi:10.1038/nature09659

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Elliott M, Golub B, Jackson MO. Financial Networks and Contagion. Am Econ Rev (2014) 104:3115–53. doi:10.1257/aer.104.10.3115

CrossRef Full Text | Google Scholar

7. Gai P, Haldane A, Kapadia S. Complexity, Concentration and Contagion. J Monetary Econ (2011) 58:453–70. doi:10.1016/j.jmoneco.2011.05.005

CrossRef Full Text | Google Scholar

8. Allen F, Babus A. The Network challenge: Strategy, Profit, and Risk in an Interlinked World (2009). p. 367.

Google Scholar

9. Glasserman P, Young HP. Contagion in Financial Networks. J Econ Lit (2016) 54:779–831. doi:10.1257/jel.20151228

CrossRef Full Text | Google Scholar

10. Caccioli F, Shrestha M, Moore C, Farmer JD. Stability Analysis of Financial Contagion Due to Overlapping Portfolios. J Banking Finance (2014) 46:233–45. doi:10.1016/j.jbankfin.2014.05.021

CrossRef Full Text | Google Scholar

11. Caccioli F, Farmer JD, Foti N, Rockmore D. Overlapping Portfolios, Contagion, and Financial Stability. J Econ Dyn Control (2015) 51:50–63. doi:10.1016/j.jedc.2014.09.041

CrossRef Full Text | Google Scholar

12. Kenett DY, Huang X, Vodenska I, Havlin S, Stanley HE. Partial Correlation Analysis: Applications for Financial Markets. Quantitative Finance (2015) 15:569–78. doi:10.1080/14697688.2014.946660

CrossRef Full Text | Google Scholar

13. Silva W, Kimura H, Sobreiro VA. An Analysis of the Literature on Systemic Financial Risk: A Survey. J Financial Stab (2017) 28:91–114. doi:10.1016/j.jfs.2016.12.004

CrossRef Full Text | Google Scholar

14. Battiston S, Caldarelli G, D’Errico M, Gurciullo S. Leveraging the Network: A Stress-Test Framework Based on DebtRank. Stat Risk Model (2016) 33:117–38. doi:10.1515/strm-2015-0005

CrossRef Full Text | Google Scholar

15. Gai P, Kapadia S. Contagion in Financial Networks. Proc R Soc A (2010) 466:2401–23. doi:10.1098/rspa.2009.0410

CrossRef Full Text | Google Scholar

16. Garas A, Argyrakis P, Rozenblat C, Tomassini M, Havlin S. Worldwide Spreading of Economic Crisis. New J Phys (2010) 12:113043. doi:10.1088/1367-2630/12/11/113043

CrossRef Full Text | Google Scholar

17. Huang X, Vodenska I, Havlin S, Stanley HE. Cascading Failures in Bi-partite Graphs: Model for Systemic Risk Propagation. Scientific Rep (2013) 3:1. doi:10.1038/srep01219

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Lin M, Duan L. Financial Risk Information Spreading on Metapopulation Networks. Complexity (2021) 2021:6654169. doi:10.1155/2021/6654169

CrossRef Full Text | Google Scholar

19. Wang W, Liu Q-H, Cai S-M, Tang M, Braunstein LA, Stanley HE. Suppressing Disease Spreading by Using Information Diffusion on Multiplex Networks. Scientific Rep (2016) 6:1. doi:10.1038/srep29259

CrossRef Full Text | Google Scholar

20. Wang W, Liu Q-H, Liang J, Hu Y, Zhou T. Coevolution Spreading in Complex Networks. Phys Rep (2019) 820:1–51. doi:10.1016/j.physrep.2019.07.001

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Granell C, Gómez S, Arenas A. Dynamical Interplay between Awareness and Epidemic Spreading in Multiplex Networks. Phys Rev Lett (2013) 111:128701. doi:10.1103/physrevlett.111.128701

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Soriano-Paños D, Ghanbarnejad F, Meloni S, Gómez-Gardeñes J. Markovian Approach to Tackle the Interaction of Simultaneous Diseases. Phys Rev E (2019) 100:062308. doi:10.1103/physreve.100.062308

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Wang Z, Xia C. Co-evolution Spreading of Multiple Information and Epidemics on Two-Layered Networks under the Influence of Mass media. Nonlinear Dyn (2020) 102:3039–52. doi:10.1007/s11071-020-06021-7

CrossRef Full Text | Google Scholar

24. Wu J, Zuo R, He C, Xiong H, Zhao K, Hu Z. The Effect of Information Literacy Heterogeneity on Epidemic Spreading in Information and Epidemic Coupled Multiplex Networks. Physica A: Stat Mech its Appl (2022) 596:127119. doi:10.1016/j.physa.2022.127119

CrossRef Full Text | Google Scholar

25. Sun C, Luo C. Co-evolution of Cooperation with Resource Allocation in Spatial Multigame Using Switching Control. Commun Nonlinear Sci Numer Simulation (2022) 107:106137. doi:10.1016/j.cnsns.2021.106137

CrossRef Full Text | Google Scholar

26. Wang W, Tang M, Shu P, Wang Z. Dynamics of Social Contagions with Heterogeneous Adoption Thresholds: Crossover Phenomena in Phase Transition. New J Phys (2016) 18:013029. doi:10.1088/1367-2630/18/1/013029

CrossRef Full Text | Google Scholar

27. Wang X, Lan Y, Xiao J. Anomalous Structure and Dynamics in News Diffusion Among Heterogeneous Individuals. Nat Hum Behav (2019) 3:709–18. doi:10.1038/s41562-019-0605-7

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Centola D. Research Handbook on Analytical Sociology. Cheltenham, UK: Edward Elgar Publishing (2021).

Google Scholar

29. Gomez S, Diaz-Guilera A, Gomez-Gardenes J, Perez-Vicente CJ, Moreno Y, Arenas A. Diffusion Dynamics on Multiplex Networks. Phys Rev Lett (2013) 110:028701. doi:10.1103/physrevlett.110.028701

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Menichetti G, Remondini D, Panzarasa P, Mondragón RJ, Bianconi G. Weighted Multiplex Networks. PloS one (2014) 9:e97857. doi:10.1371/journal.pone.0097857

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Battiston F, Nicosia V, Latora V. The New Challenges of Multiplex Networks: Measures and Models. Eur Phys J Spec Top (2017) 226:401–16. doi:10.1140/epjst/e2016-60274-8

CrossRef Full Text | Google Scholar

32. Lee K-M, Kim JY, Lee S, Goh K-I. Multiplex Networks. In: Networks of Networks: The Last Frontier of Complexity. Berlin, Germany: Springer (2014). p. 53–72. doi:10.1007/978-3-319-03518-5_3

CrossRef Full Text | Google Scholar

33. Osat S, Faqeeh A, Radicchi F. Optimal Percolation on Multiplex Networks. Nat Commun (2017) 8:1. doi:10.1038/s41467-017-01442-2

PubMed Abstract | CrossRef Full Text | Google Scholar