Asymmetric Quantum Steering Generated by Triple-Photon Down-Conversion Process With Injected Signals

Asymmetric quantum steering generated by the triple-photon down-conversion process in an injected signal optical cavity is investigated. The triple-photon down-conversion process can be realized in an optical superlattice by quasi-phase-matching technology. Asymmetric quantum steering can be obtained in this triple-photon down-conversion process. The direction of asymmetric quantum steering can be controlled by adjusting the parameters of the nonlinear process. The generation of asymmetric quantum steering in the present scheme has potential applications in quantum secret sharing and quantum networks.

1 Introduction

As an extension of the Einstein–Podolsky–Rosen (EPR) paradox [2], Schrödinger found the phenomenon of quantum steering in 1935 [1]. Quantum steering is a sufficient condition for quantum entanglement and a necessary condition for Bell nonlocality [3]. Wiseman et al. [4] gave a mathematically operable definition for quantum steering in 2007. In addition, they raised the question of whether there is asymmetric quantum steering, that is, A can steer B, but conversely B cannot steer A. According to Reid’s quantum steering criteria [5], this question was quickly answered both theoretically [6, 7] and experimentally [8]. The research shows that asymmetric quantum steering is a universal property, which does not depend on Gaussian measurement [9]. Intracavity second harmonic generation [10] and atomic Bose–Hubbard chain [11, 12] can produce asymmetric quantum steering based on continuous variables. The asymmetric quantum steering in four-mode cluster states was measured experimentally [13]. An optical parametric oscillator (OPO) is used in many quantum optical experiments [14]. For example, it can produce three-color entanglement [15, 16]. By using the two down-converted optical fields of a nondegenerate OPO, Ou et al. proposed that EPR steering was experimental feasible [17]. For both degenerate [18] and nondegenerate [19] cases, the nonlinear conversion efficiency can be improved by injecting signals into the low-frequency mode. He and Reid confirmed the existence of N-partite EPR steering and developed the concept of genuine N-partite EPR steering, and put forward the criteria for genuine multipartite EPR steering [20]. A scheme is proposed for experimental generation of a highly versatile and flexible repository of multipartite steering using an optical frequency comb and ultrafast pulse shaping [21]. Collective multipartite EPR steering can be generated by cascaded four-wave mixing of rubidium atoms [22]. The research on multipartite quantum steering has attracted much attention [23–28]. Olsen [29] used a nondegenerate parametric oscillator with an injected signal to show how the directionality and extent of the steering can be readily controlled for output modes. Wang and Li analyzed theoretically and experimentally bichromatic entanglement between the signal and the idle [30]. Kalaga and Leoński analyzed the relations between entanglement and steering for a two-mode mixed state [31] and three qubit system [32], respectively. Cao and Guo [33] not only provided the mathematical basis and characterization for Bell delocalization and EPR steering but also derived a sufficient condition to judge whether the state can be steered. Recently, the hybrid ferrimagnet–light system of two macroscopic magnons has made a huge breakthrough. Zheng et al. [34] found that entanglement can be significantly enhanced and strong two-way asymmetric quantum steering appears between two magnons.

Rojas González et al. [35] gave the first theoretical demonstration of continuous-variable triple-photon state quantum entanglement. They also found that quantum entanglement among the three modes disappeared in the case of spontaneous parametric triple-photon generation. However, the genuine triple-photon entanglement can be obtained in the case of injection signal [35]. Agustí et al. [36] showed that the state generated by a three-mode spontaneous parametric down-conversion (SPDC) was the non-Gaussian state, and the states that were generated by superconducting-circuit implementation of the three-mode SPDC had tripartite entanglement based on the criteria built from three-mode correlation functions. However, the quantum steering correlation, especially the asymmetric quantum steering correlation, in the triple-photon down-conversion process has not been studied. In this article, the asymmetric quantum steering generated by the triple-photon down-conversion process with two injected signals is investigated. We demonstrate that the asymmetric quantum steering can be generated by this nonlinear process and also show how to control the asymmetry of quantum steering by adjusting the intensity of the injected signals. Similar to quantum key distribution, in quantum secret sharing [37–39], the confidentiality of shared information does not depend on computational assumptions, but on the uncertainty and non-cloning of quantum mechanics. Xiang et al. [23] designed a protocol based on EPR steering and extended the protocol to three-user scenarios to distribute richer steerability properties including one-to-multimode steering and collective steering that can be used for one-sided device-independent quantum secret sharing. We think that the present scheme of the generation of asymmetric quantum steering has potential applications in quantum secret sharing and quantum networks.

2 Theory

The system consists of a nondegenerate OPO that is driven by an external coherent pump field with the frequency of ω₀. Triple-photon SPDC can be achieved in the optical cavity by using the quasi-phase-matching (QPM) technology [40]. The frequencies of the three parametric optical fields are ω₁, ω₂, and ω₃, respectively, which satisfies the energy conservation relationship ω₀ = ω₁ + ω₂ + ω₃. The phase mismatch in this nonlinear process is compensated by the reciprocal lattice vector provided by the optical superlattice. The interaction Hamiltonian for the triple-photon SPDC can be written as

${\mathcal{H}}_I=i\hslash \kappa {\widehat{a}}_0{\widehat{a}}_1^{†}{\widehat{a}}_2^{†}{\widehat{a}}_3^{†}+h.c.,(1)$

where κ represents the effective nonlinearity of optical superlattice that can be taken as real [41]. ${\widehat{a}}_i(i=\mathrm{0,1,2,3})$ is the bosonic annihilation operator of the cavity mode with the frequency ω_i. The Hamiltonian of the external input fields is

${\mathcal{H}}_{\mathit{ext}}=i\hslash \left({ϵ}_0{\widehat{a}}_0^{†}+{ϵ}_1{\widehat{a}}_1^{†}+{ϵ}_2{\widehat{a}}_2^{†}\right)+h.c.,(2)$

where ϵ₀ is the amplitude of pump. ϵ₁ and ϵ₂ represent the injected signal fields, and they are also considered to be real. If ϵ₁ = ϵ₂ = 0, it is the case of spontaneous down-conversion. Because there is no quantum correlation among the output optical fields in the spontaneous down-conversion case [35], in this work, we will study the asymmetric quantum steering characteristics among the output optical fields with two injected signals. We assume that all the optical fields are resonant in the cavity. Following the description of Lindblad superoperator, the losses of the optical fields in the cavity can be written as

$\mathcal{L}\widehat{\rho }={\gamma }_i\left(2{\widehat{a}}_i\widehat{\rho }{\widehat{a}}_i^{†}-{\widehat{a}}_i^{†}{\widehat{a}}_i\widehat{\rho }-\widehat{\rho }{\widehat{a}}_i^{†}{\widehat{a}}_i\right),(3)$

where γ_i (i = 0, 1, 2, 3) represents the cavity loss of the optical field with the frequency ω_i. $\widehat{\rho }$ is the system density matrix. The master equation of this system can be expressed as

$\frac{d\widehat{\rho }}{dt}=-\frac{i}{\hslash }\left[{\mathcal{H}}_I+{\mathcal{H}}_{\mathit{pump}},\widehat{\rho }\right]+\sum \mathcal{L}\widehat{\rho }.(4)$

One can obtain the Fokker–Planck equation in the positive-P representation for studying the characteristics of quantum steering [42, 43]. The third-order derivatives can be reasonably negligible. Then, the Fokker–Planck equation can be given as

$\begin{array}{ll}\hfill \frac{dP}{dt}& =\left\{-\left({ϵ}_0-{\gamma }_0{\alpha }_0-\kappa {\alpha }_1{\alpha }_2{\alpha }_3\right)\frac{\partial }{\partial {\alpha }_0}-\left({ϵ}_0^{\ast }-{\gamma }_0^{†}{\alpha }_0^{†}-\kappa {\alpha }_1^{†}{\alpha }_2^{†}{\alpha }_3^{†}\right)\frac{\partial }{\partial {\alpha }_0^{†}}\right\}\hfill \\ \hfill & -\left({ϵ}_1-{\gamma }_1{\alpha }_1+\kappa {\alpha }_0{\alpha }_2^{†}{\alpha }_3^{†}\right)\frac{\partial }{\partial {\alpha }_1}-\left({ϵ}_1^{\ast }-{\gamma }_1{\alpha }_1^{†}+\kappa {\alpha }_0^{†}{\alpha }_2{\alpha }_3\right)\frac{\partial }{\partial {\alpha }_1^{†}}\hfill \\ \hfill & -\left({ϵ}_2-{\gamma }_2{\alpha }_2+\kappa {\alpha }_0{\alpha }_2^{†}{\alpha }_3^{†}\right)\frac{\partial }{\partial {\alpha }_2}-\left({ϵ}_2^{\ast }-{\gamma }_2{\alpha }_2^{†}+\kappa {\alpha }_0^{†}{\alpha }_1{\alpha }_3\right)\frac{\partial }{\partial {\alpha }_2^{†}}\hfill \\ \hfill & -\left(-{\gamma }_3{\alpha }_3+\kappa {\alpha }_0{\alpha }_1^{†}{\alpha }_2^{†}\right)\frac{\partial }{\partial {\alpha }_3}-\left(-{\gamma }_3{\alpha }_3^{†}+\kappa {\alpha }_0^{†}{\alpha }_1{\alpha }_2\right)\frac{\partial }{\partial {\alpha }_3^{†}}\hfill \\ \hfill & +\frac{1}{2}\frac{{\partial }^2}{\partial {\alpha }_1\partial {\alpha }_2}\left(2\kappa {\alpha }_0{\alpha }_3^{†}\right)+\frac{1}{2}\frac{{\partial }^2}{\partial {\alpha }_1^{†}\partial {\alpha }_2^{†}}\left(2\kappa {\alpha }_0^{†}{\alpha }_3\right)+\frac{1}{2}\frac{{\partial }^2}{\partial {\alpha }_1\partial {\alpha }_3}\left(2\kappa {\alpha }_0{\alpha }_2^{†}\right)\hfill \\ \hfill & +\frac{1}{2}\frac{{\partial }^2}{\partial {\alpha }_1^{†}\partial {\alpha }_3^{†}}\left(2\kappa {\alpha }_0^{†}{\alpha }_2\right)+\frac{1}{2}\frac{{\partial }^2}{\partial {\alpha }_2\partial {\alpha }_3}\left(2\kappa {\alpha }_0{\alpha }_1^{†}\right)+\frac{1}{2}\frac{{\partial }^2}{\partial {\alpha }_1^{†}\partial {\alpha }_3^{†}}\left(2\kappa {\alpha }_0^{†}{\alpha }_1\right).\hfill \end{array}(5)$

Following the normal processing, the equations of motion of the cavity modes can be obtained as

$\begin{array}{cc}\hfill \frac{d{\alpha }_1}{dt}& ={ϵ}_1-{\gamma }_1{\alpha }_1+\kappa {\alpha }_0{\alpha }_2^{†}{\alpha }_3^{†}+\sqrt{2\kappa {\alpha }_0{\alpha }_3^{†}}{\eta }_1+\sqrt{2\kappa {\alpha }_0{\alpha }_2^{†}}{\eta }_2,\hfill \\ \hfill \frac{d{\alpha }_1^{†}}{dt}& ={ϵ}_1^{*}-{\gamma }_1{\alpha }_1^{†}+\kappa {\alpha }_0^{†}{\alpha }_2{\alpha }_{†}+\sqrt{2\kappa {\alpha }_0^{†}{\alpha }_3}{\eta }_1^{†}+\sqrt{2\kappa {\alpha }_0^{†}{\alpha }_2}{\eta }_2^{†},\hfill \\ \hfill \frac{d{\alpha }_2}{dt}& ={ϵ}_2-{\gamma }_2{\alpha }_2+\kappa {\alpha }_0{\alpha }_2^{†}{\alpha }_3^{†}+\sqrt{2\kappa {\alpha }_0{\alpha }_3^{†}}{\eta }_1+\sqrt{2\kappa {\alpha }_0{\alpha }_1^{†}}{\eta }_3,\hfill \\ \hfill \frac{d{\alpha }_2^{†}}{dt}& ={ϵ}_2^{*}-{\gamma }_2{\alpha }_2^{†}+\kappa {\alpha }_0^{†}{\alpha }_1{\alpha }_3+\sqrt{2\kappa {\alpha }_0^{†}{\alpha }_3}{\eta }_1^{†}+\sqrt{2\kappa {\alpha }_0^{†}{\alpha }_1}{\eta }_3^{†},\hfill \\ \hfill \frac{d{\alpha }_3}{dt}& =-{\gamma }_3{\alpha }_3+\kappa {\alpha }_0{\alpha }_1^{†}{\alpha }_2^{†}+\sqrt{2\kappa {\alpha }_0{\alpha }_2^{†}}{\eta }_2+\sqrt{2\kappa {\alpha }_0{\alpha }_1^{†}}{\eta }_3,\hfill \\ \hfill \frac{d{\alpha }_3^{†}}{dt}& =-{\gamma }_3{\alpha }_3^{†}+\kappa {\alpha }_0^{†}{\alpha }_1{\alpha }_2+\sqrt{2\kappa {\alpha }_0^{†}{\alpha }_2}{\eta }_2^{†}+\sqrt{2\kappa {\alpha }_0^{†}{\alpha }_1}{\eta }_3^{†},\hfill \\ \hfill \frac{d{\alpha }_0}{dt}& ={ϵ}_0-{\gamma }_0{\alpha }_0-\kappa {\alpha }_1{\alpha }_2{\alpha }_3,\frac{d{\alpha }_0^{†}}{dt}={ϵ}_0^{*}-{\gamma }_0^{†}{\alpha }_0^{†}-\kappa {\alpha }_1^{†}{\alpha }_2^{†}{\alpha }_3^{†}.\hfill \end{array}(6)$

The aforementioned eight coupled stochastic differential equations can be solved by the linearization method. One can expand the positive-P variables into their steady-state expectation values plus delta-correlated Gaussian fluctuation terms as α_i = A_i + δα_i (i = 0, 1, 2, 3) with δα_i ≪ A_i. A_i is the steady-state solution of the cavity mode ${\widehat{a}}_i$, which can be obtained when the noise terms are ignored by setting dα_i/dt = 0 in Eq. 6. Complex variable α_i corresponds to the normally ordered expectation value of the operator ${\widehat{a}}_i$. In this case, Eq. 6 can be linearized as

$\begin{array}{cc}\hfill \frac{d}{dt}\delta {\alpha }_1& =-{\gamma }_1\delta {\alpha }_1+\kappa A_2^{*}{A}_3^{*}\delta {\alpha }_0+\kappa A_0{A}_3^{*}\delta {\alpha }_2^{†}+\kappa A_0{A}_2^{*}\delta {\alpha }_3^{†}+\sqrt{2\kappa A_0{A}_3^{*}}{\eta }_1+\sqrt{2\kappa A_0{A}_2^{*}}{\eta }_2,\hfill \\ \hfill \frac{d}{dt}\delta {\alpha }_1^{†}& =-{\gamma }_1\delta {\alpha }_1^{†}+\kappa A_2{A}_3\delta {\alpha }_0^{†}+\kappa A_0^{*}{A}_3\delta {\alpha }_2+\kappa A_0^{*}{A}_2\delta {\alpha }_3+\sqrt{2\kappa A_0^{*}{A}_3}{\eta }_1^{†}+\sqrt{2\kappa A_0^{*}{A}_2}{\eta }_2^{†},\hfill \\ \hfill \frac{d}{dt}\delta {\alpha }_2& =-{\gamma }_2\delta {\alpha }_2+\kappa A_1^{*}{A}_3^{*}\delta {\alpha }_0+\kappa A_0{A}_3^{*}\delta {\alpha }_1^{†}+\kappa A_0{A}_1^{*}\delta {\alpha }_3^{†}+\sqrt{2\kappa A_0{A}_3^{*}}{\eta }_1+\sqrt{2\kappa A_0{A}_1^{*}}{\eta }_3,\hfill \\ \hfill \frac{d}{dt}\delta {\alpha }_2^{†}& =-{\gamma }_2\delta {\alpha }_2^{†}+\kappa A_1{A}_3\delta {\alpha }_0^{†}+\kappa A_0^{*}{A}_3\delta {\alpha }_1+\kappa A_0^{*}{A}_1\delta {\alpha }_3+\sqrt{2\kappa A_0^{*}{A}_3}{\eta }_1^{†}+\sqrt{2\kappa A_0^{*}{A}_1}{\eta }_3^{†},\hfill \\ \hfill \frac{d}{dt}\delta {\alpha }_3& =-{\gamma }_3\delta {\alpha }_3+\kappa A_1^{*}{A}_2^{*}\delta {\alpha }_0+\kappa A_0{A}_2^{*}\delta {\alpha }_1^{†}+\kappa A_0{A}_1^{*}\delta {\alpha }_2^{†}+\sqrt{2\kappa A_0{A}_2^{*}}{\eta }_2+\sqrt{2\kappa A_0{A}_1^{*}}{\eta }_3,\hfill \\ \hfill \frac{d}{dt}\delta {\alpha }_3^{†}& =-{\gamma }_3\delta {\alpha }_3^{†}+\kappa A_1{A}_2\delta {\alpha }_0^{†}+\kappa A_0^{*}{A}_2\delta {\alpha }_1+\kappa A_0^{*}{A}_1\delta {\alpha }_2+\sqrt{2\kappa A_0^{*}{A}_3}{\eta }_2^{†}+\sqrt{2\kappa A_0^{*}{A}_1}{\eta }_3^{†},\hfill \\ \hfill \frac{d}{dt}\delta {\alpha }_0& =-{\gamma }_0\delta {\alpha }_0-\kappa A_1{A}_2\delta {\alpha }_3-\kappa A_1{A}_3\delta {\alpha }_2-\kappa A_2{A}_3\delta {\alpha }_1,\hfill \\ \hfill \frac{d}{dt}\delta {\alpha }_0^{†}& =-{\gamma }_0\delta {\alpha }_0^{†}-\kappa A_1^{*}{A}_2^{*}\delta {\alpha }_3^{†}-\kappa A_1^{*}{A}_3^{*}\delta {\alpha }_2^{†}-\kappa A_2^{*}{A}_3^{*}\delta {\alpha }_1^{†}.\hfill \end{array}(7)$

The resulting equations can be written for the vector of fluctuation terms as

$d\delta \tilde{\alpha }=-\mathbf{A}\delta \tilde{\alpha }dt+\mathbf{B}dW,(8)$

where A is the drift matrix, B is the noise term that contains the steady-state solutions, and dW is a vector of Wiener increments [43]. The drift matrix A is obtained as

$\mathbf{A}=\left(\begin{array}{cccccccc}\hfill {\gamma }_0\hfill & \hfill 0\hfill & \hfill \kappa A_2{A}_3\hfill & \hfill 0\hfill & \hfill \kappa A_1{A}_3\hfill & \hfill -0\hfill & \hfill \kappa A_1{A}_2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\gamma }_0\hfill & \hfill 0\hfill & \hfill \kappa A_2^{*}{A}_3^{*}\hfill & \hfill 0\hfill & \hfill \kappa A_1^{*}{A}_3^{*}\hfill & \hfill 0\hfill & \hfill \kappa A_1^{*}{A}_2^{*}\hfill \\ \hfill -\kappa A_2^{*}{A}_3^{*}\hfill & \hfill 0\hfill & \hfill {\gamma }_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\kappa A_0{A}_3^{*}\hfill & \hfill 0\hfill & \hfill -\kappa A_0{A}_2^{*}\hfill \\ \hfill 0\hfill & \hfill -\kappa A_2{A}_3\hfill & \hfill 0\hfill & \hfill {\gamma }_1\hfill & \hfill -\kappa A_0{A}_3^{*}\hfill & \hfill 0\hfill & \hfill -\kappa A_0^{*}{A}_2\hfill & \hfill 0\hfill \\ \hfill -\kappa A_1^{*}{A}_3^{*}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\kappa A_0{A}_3^{*}\hfill & \hfill {\gamma }_2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\kappa A_0{A}_1^{*}\hfill \\ \hfill 0\hfill & \hfill -\kappa A_1{A}_3\hfill & \hfill -\kappa A_0{A}_3^{*}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\gamma }_2\hfill & \hfill -\kappa A_0^{*}{A}_1\hfill & \hfill -0\hfill \\ \hfill -\kappa A_1^{*}{A}_2^{*}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\kappa A_0{A}_2^{*}\hfill & \hfill 0\hfill & \hfill -\kappa A_0{A}_1^{*}\hfill & \hfill {\gamma }_3\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\kappa A_1{A}_2\hfill & \hfill -\kappa A_0^{*}{A}_2\hfill & \hfill 0\hfill & \hfill -\kappa A_0^{*}{A}_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\gamma }_3\hfill \end{array}\right).(9)$

Equation 8 can be solved via the Fourier transform. Then, one can obtain the intracavity spectra as

$\mathbf{S}\left(\omega \right)={\left(\mathbf{A}+i\omega \mathbf{I}\right)}^{-\mathrm{1}}\mathbf{B}{\mathbf{B}}^{\mathrm{T}}{\left({\mathbf{A}}^{\mathrm{T}}-i\omega \mathbf{I}\right)}^{-\mathrm{1}},(10)$

where ω is the Fourier analysis frequency and I is the identity matrix. According to the standard input–output relationship [44], the output spectra can be calculated through Eq. 10. The quadrature amplitude and phase can be defined as ${\widehat{X}}_j={\widehat{a}}_j+{\widehat{a}}_j^{†}$ and ${\widehat{Y}}_j=-i({\widehat{a}}_j-{\widehat{a}}_j^{†})$. We calculate S^q(ω) = QSQ^T, where Q is the block diagonal 8 × 8 matrix. Then, the output spectral variances and covariances for the cavity modes i and j can be obtained from S^q(ω). EPR steering can be demonstrated based on the Reid criterion, and the inferred variances are written as [5]

$\begin{array}{cc}\hfill V_{\inf }\left({\widehat{X}}_{ij}\right)& =V\left({\widehat{X}}_i\right)-\frac{{\left[V\left({\widehat{X}}_i,{\widehat{X}}_i\right)\right]}^2}{V\left({\widehat{X}}_j\right)},\hfill \\ \hfill V_{\inf }\left({\widehat{Y}}_{ij}\right)& =V\left({\widehat{Y}}_i\right)-\frac{{\left[V\left({\widehat{Y}}_i,{\widehat{Y}}_i\right)\right]}^2}{V\left({\widehat{Y}}_j\right)},\hfill \end{array}(11)$

where $V(\widehat{X},\widehat{Y})=⟨\widehat{X}\widehat{Y}⟩-⟨\widehat{X}⟩⟨\widehat{Y}⟩$ and $V_{\inf }({\widehat{X}}_{ij})$ denotes the variance of ${\widehat{X}}_i$ as inferred by measurement made of ${\widehat{X}}_j$. If the product of these two inferred variances is less than 1, one can say that mode i can be steered by the measurement of mode j, and EPR steering is demonstrated for the two cavity modes.

EPR_jk is the product of the ${\widehat{X}}_{jk}$ and ${\widehat{Y}}_{jk}$ inferred variance. However, EPR_jk is not always equal to EPR_kj. If one of EPR_jk and EPR_kj is more than or equal to 1 and the other is less than 1, there is asymmetric quantum steering between cavity modes k and j.

3 Results

Because asymmetric quantum steering between the other optical fields are not obvious enough, we only investigate the asymmetric quantum steering characteristics between the optical fields ${\widehat{a}}_0$ and ${\widehat{a}}_1$ and between the optical fields ${\widehat{a}}_1$ and ${\widehat{a}}_2$, respectively. In the following, we choose the pairs (ω₀, ω₁) and (ω₁, ω₂) to analyze the influences of the normalized analysis frequency ω/γ₀ and the injected signal amplitudes ϵ₁ and ϵ₂ on the asymmetric quantum steering.

Figure 1 depicts the values of EPR_jk and EPR_kj versus the normalized analysis frequency ω/γ₀. One can see that EPR₀₁ = 1, while EPR₁₀ < 1 in the whole range of the normalized analysis frequency, which shows that the output fields ${\widehat{a}}_0$ and ${\widehat{a}}_1$ exhibit asymmetric quantum steering. That is, the optical field ${\widehat{a}}_0$ can steer the optical field ${\widehat{a}}_1$, but ${\widehat{a}}_1$ cannot steer ${\widehat{a}}_0$. However, both EPR₁₂ and EPR₂₁ are less than 1, which shows that the output fields ${\widehat{a}}_1$ and ${\widehat{a}}_2$ do not exhibit asymmetric quantum steering. The optical fields ${\widehat{a}}_1$ and ${\widehat{a}}_2$ can be steered with each other.

FIGURE 1

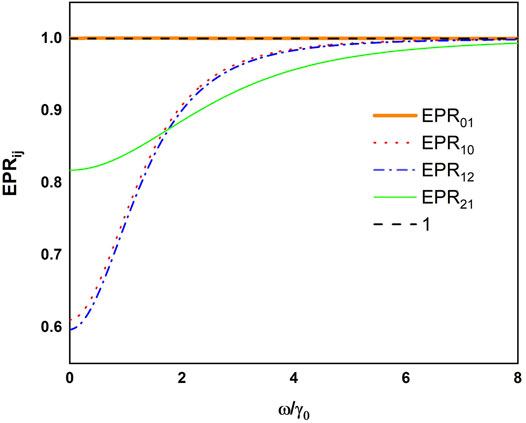
FIGURE 1. Values of EPR_jk and EPR_kj versus the normalized Fourier analysis frequency ω/γ₀ with γ₀=0.01, γ₁=2γ₀, γ₂=4γ₀, γ₃=3γ₀, κ =0.01, ϵ₀=0.45, ϵ₁=0.1, and ϵ₂=0.2.

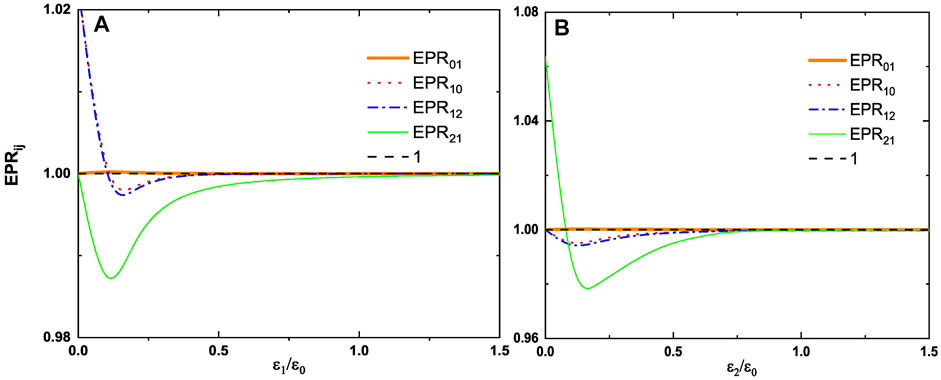
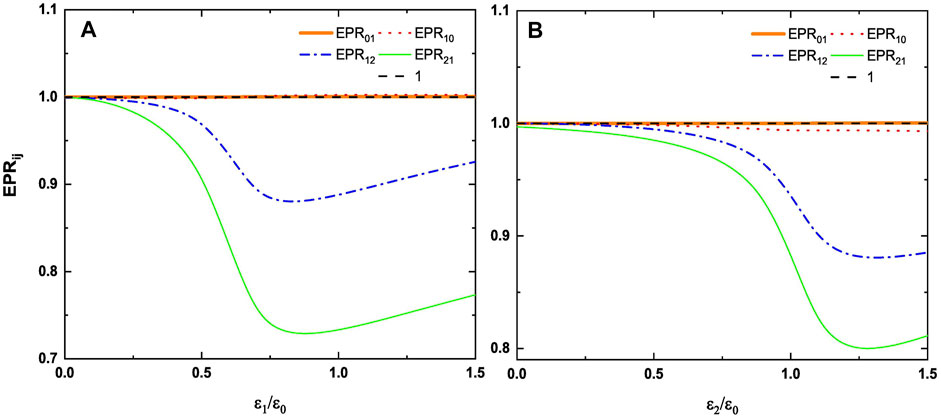
Figure 2 plots EPR_jk and EPR_kj versus 1) ϵ₁/ϵ₀ and 2) ϵ₂/ϵ₀ with ω = 8γ₀, γ₀ = 0.01, γ₁ = 0.02, γ₂ = 0.04, γ₃ = 0.03, and κ = 0.01. We found that by changing the amplitude of the injected signal ϵ₁or ϵ₂, one can control whether there is asymmetric quantum steering between the output modes. As shown in Figure 2A, EPR₂₁ is less than 1 and EPR₁₂ is more than 1 when ϵ₁/ϵ₀ < 0.13, which shows that the output fields ${\widehat{a}}_1$ and ${\widehat{a}}_2$ exhibit asymmetric quantum steering. When ϵ₁/ϵ₀ > 0.13, EPR₁₀ is less than 1 and EPR₀₁ is more than 1, which shows that the output fields ${\widehat{a}}_0$ and ${\widehat{a}}_1$ have asymmetric quantum steering in this range. Different from the case in Figure 2A, Figure 2B shows that the output fields ${\widehat{a}}_1$ and ${\widehat{a}}_2$ exhibit asymmetric quantum steering when ϵ₂ is small. However, the optical fields ${\widehat{a}}_0$ and ${\widehat{a}}_1$ have asymmetric quantum steering in the whole range of ϵ₂. This shows that the injected signal will affect the asymmetric quantum steering characteristics among the output optical fields. The influence of different cavity loss rates on quantum steering is also worth studying. Therefore, we choose a different set of γ_i to recalculate the quantum steering characteristics among the output optical fields.

FIGURE 2

FIGURE 2. Values of EPR_jk and EPR_kj versus (A) ϵ₁/ϵ₀ and (B) ϵ₂/ϵ₀, respectively.

Figure 3 shows the quantum steering of the output field $({\widehat{a}}_0,{\widehat{a}}_1)$ and $({\widehat{a}}_1,{\widehat{a}}_2)$ versus the normalized analysis frequency ω/γ₀ with a new set of γ_i. Asymmetric quantum steering does not exist between ${\widehat{a}}_0$ and ${\widehat{a}}_1$ only when ω is extremely small. Apart from that, ${\widehat{a}}_0$ and ${\widehat{a}}_1$ have asymmetric quantum steering. ${\widehat{a}}_1$ and ${\widehat{a}}_2$ have symmetric quantum steering in the whole range of ω which is similar to the case in Figure 1. However, the influences of ϵ₁ and ϵ₂ on the asymmetric quantum steering are different from the case in Figure 2. Figure 4A depicts the values of EPR_jk and EPR_kj versus ϵ₁/ϵ₀ with ω = 8γ₀, γ₀ = 0.1, γ₁ = 0.2, γ₂ = 0.4, γ₃ = 0.03, and κ = 0.01. One can see that ${\widehat{a}}_0$ and ${\widehat{a}}_1$ show asymmetric quantum steering when about ϵ₁/ϵ₀ < 0.7, and ${\widehat{a}}_1$ and ${\widehat{a}}_2$ have symmetric steering in the whole range. In Figure 4B, the quantum steering between ${\widehat{a}}_0$ and ${\widehat{a}}_1$ is always asymmetric, but the quantum steering between ${\widehat{a}}_1$ and ${\widehat{a}}_2$ is always symmetric in the whole range, which is different from the case in Figure 2. This may be due to the increase of the cavity loss rates, which affects the quantum properties of the output optical fields. Moreover, the injected signal of the optical field ${\widehat{a}}_1$ has a greater influence on the quantum steering than the injected signal of the optical field ${\widehat{a}}_2$. The asymmetry of quantum steering can be controlled by adjusting the intensities of the injected signals and the cavity loss rates.

FIGURE 3

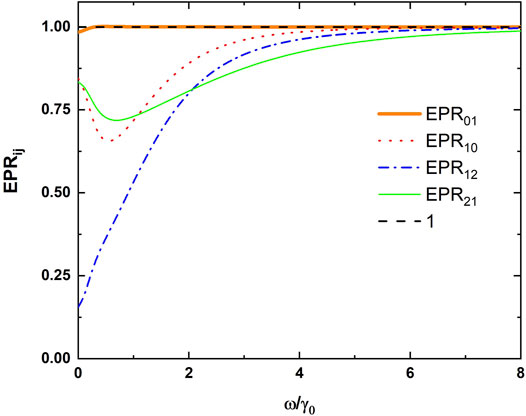
FIGURE 3. Values of EPR_jk and EPR_kj versus the Fourier analysis frequency ω with γ₀=0.1, γ₁=2γ₀, γ₂=4γ₀, γ₃=0.3γ₀, κ =0.01, ϵ₀=0.45, ϵ₁=0.1, and ϵ₂=0.2.

FIGURE 4

FIGURE 4. Values of EPR_jk and EPR_kj versus (A) ϵ₁/ϵ₀ and (B) ϵ₂/ϵ₀ with γ₀=0.1.

4 Conclusion

Asymmetric quantum steering produced by the triple-photon down-conversion process with two injected signals is investigated. Asymmetric quantum steering can be obtained in some parameter regimes between optical fields ${\widehat{a}}_0$ and ${\widehat{a}}_1$ or between ${\widehat{a}}_1$ and ${\widehat{a}}_2$. Both the loss rates of the cavity modes and the intensities of the injected signals have the influences on the asymmetric quantum steering among the output optical fields. Our scheme provides a new idea for generating asymmetric quantum steering, which has potential applications in quantum secret sharing and continuous variable teleportation.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author Contributions

TC wrote the manuscript. YY designed and directed the study. CX, KP, and AC contributed to the discussion and edited the manuscript.

Funding

This work is supported by the National Natural Science Foundation of China (No. 61975184) and the Science Foundation of Zhejiang Sci-Tech University (No. 19062151-Y).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Schrödinger E. Discussion of Probability Relations between Separated Systems. Proc Cambridge Philos Soc (1935) 31:555.

Google Scholar

2. Einstein A, Podolsky B, Rosen N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys Rev (1935) 47:777–80. doi:10.1103/physrev.47.777

CrossRef Full Text | Google Scholar

3. Jones SJ, Wiseman HM, Doherty AC. Phys Rev A (2007) 76:052116. doi:10.1103/physreva.76.052116

CrossRef Full Text

4. Wiseman HM, Jones SJ, Doherty AC. Steering, Entanglement, Nonlocality, and the Einstein-Podolsky-Rosen Paradox. Phys Rev Lett (2007) 98:140402. doi:10.1103/physrevlett.98.140402

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Reid MD. Demonstration of the Einstein-Podolsky-Rosen Paradox Using Nondegenerate Parametric Amplification. Phys Rev A (1989) 40:913–23. doi:10.1103/physreva.40.913

CrossRef Full Text | Google Scholar

6. Olsen MK, Bradley AS. Bright Bichromatic Entanglement and Quantum Dynamics of Sum Frequency Generation. Phys Rev A (2008) 77:023813. doi:10.1103/physreva.77.023813

CrossRef Full Text | Google Scholar

7. Midgley SLW, Ferris AJ, Olsen MK. Asymmetric Gaussian Steering: When Alice and Bob Disagree. Phys Rev A (2010) 81:022101. doi:10.1103/physreva.81.022101

CrossRef Full Text | Google Scholar

8. Händchen V, Eberle T, Steinlechner S, Samblowski A, Franz T, Werner RF, et al. Observation of One-Way Einstein-Podolsky-Rosen Steering. Nat Photon (2012) 6:596. doi:10.1038/NPHOTON.2012.202

CrossRef Full Text | Google Scholar

9. Bowles J, Vértesi T, Quintino MT, Brunner N. One-way Einstein-Podolsky-Rosen Steering. Phys Rev Lett (2014) 112:200402. doi:10.1103/physrevlett.112.200402

CrossRef Full Text | Google Scholar

10. Olsen MK. Asymmetric Gaussian Harmonic Steering in Second-Harmonic Generation. Phys Rev A (2013) 88:051802. doi:10.1103/physreva.88.051802

CrossRef Full Text | Google Scholar

11. Olsen MK. Spreading of Entanglement and Steering along Small Bose-Hubbard Chains. Phys Rev A (2015) 92:033627. doi:10.1103/physreva.92.033627

CrossRef Full Text | Google Scholar

12. Olsen MK. Asymmetric Steering in Coherent Transport of Atomic Population with a Three-Well Bose-Hubbard Model. J Opt Soc Am B (2015) 32:A15. doi:10.1364/josab.32.000a15

CrossRef Full Text | Google Scholar

13. Deng X, Xiang Y, Tian C, Adesso G, He Q, Gong Q, et al. Demonstration of Monogamy Relations for Einstein-Podolsky-Rosen Steering in Gaussian Cluster States. Phys Rev Lett (2017) 118:230501. doi:10.1103/physrevlett.118.230501

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Bachor HA. A Guide to Experiments in Quantum Optics. New York: Wiley VCH (1998).

Google Scholar

15. Coelho AS, Barbosa FAS, Cassemiro KN, Villar AS, Martinelli M, Nussenzveig P. Three-Color Entanglement. Science (2009) 326:823–6. doi:10.1126/science.1178683

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Yu YB, Wang HJ, Zhao JW. Analysis of Directly Produce Pump, Signal, and Idler Three-Color Continuous-Variable Entanglement. Eur Phys J D (2012) 66:18. doi:10.1140/epjd/e2011-20248-3

CrossRef Full Text | Google Scholar

17. Ou ZY, Pereira SF, Kimble HJ, Peng KC. Realization of the Einstein-Podolsky-Rosen Paradox for Continuous Variables. Phys Rev Lett (1992) 68:3663–6. doi:10.1103/physrevlett.68.3663

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Olsen MK, Dechoum K, Plimak LI. Degenerate Intracavity Parametric Processes with Injected Signal. Opt Commun (2003) 223:123–35. doi:10.1016/s0030-4018(03)01645-6

CrossRef Full Text | Google Scholar

19. Coutinho dos Santos B, Dechoum K, Khoury AZ, da Silva LF, Olsen MK. Quantum Analysis of the Nondegenerate Optical Parametric Oscillator with Injected Signal. Phys Rev A (2005) 72:033820. doi:10.1103/physreva.72.033820

CrossRef Full Text | Google Scholar

20. He QY, Reid MD. Genuine Multipartite Einstein-Podolsky-Rosen Steering. Phys Rev Lett (2013) 111:250403. doi:10.1103/physrevlett.111.250403

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Cai Y, Xiang Y, Liu Y, He QY, Treps N. Versatile Multipartite Einstein-Podolsky-Rosen Steering via a Quantum Frequency Comb. Phys Rev Res (2020) 2:032046(R). doi:10.1103/physrevresearch.2.032046

CrossRef Full Text | Google Scholar

22. Liu Y, Cai Y, Luo BS, Jin Y, Niu MQ, Li F, et al. Collective Multipartite Einstein-Podolsky-Rosen Steering via Cascaded Four-Wave Mixing of Rubidium Atoms. Phys Rev A (2021) 104:033704. doi:10.1103/physreva.104.033704

CrossRef Full Text | Google Scholar

23. Xiang Y, Su XL, Mišta L, Adesso G, He QY. Multipartite Einstein-Podolsky-Rosen Steering Sharing with Separable States. Phys Rev A (2019) 99:010104(R). doi:10.1103/physreva.99.010104

CrossRef Full Text | Google Scholar

24. Hao ZY, Sun K, Wang Y, Liu ZH, Yang M, Xu JS, et al. Demonstrating Shareability of Multipartite Einstein-Podolsky-Rosen Steering. Phys Rev Lett (2022) 128:120402. doi:10.1103/physrevlett.128.120402

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Gupta S, Das D, Majumdar AS. Distillation of Genuine Tripartite Einstein-Podolsky-Rosen Steering. Phys Rev A (2021) 104:022409. doi:10.1103/physreva.104.022409

CrossRef Full Text | Google Scholar

26. Teh RY, Gessner M, Reid MD, Fadel M. Full Multipartite Steering Inseparability, Genuine Multipartite Steering, and Monogamy for Continuous-Variable Systems. Phys Rev A (2022) 105:012202. doi:10.1103/physreva.105.012202

CrossRef Full Text | Google Scholar

27. Xiang Y, Liu Y, Cai Y, Li F, Zhang YP, He QY. Monogamy Relations within Quadripartite Einstein-Podolsky-Rosen Steering Based on Cascaded Four-Wave Mixing Processes. Phys Rev A (2020) 101:053834. doi:10.1103/physreva.101.053834

CrossRef Full Text | Google Scholar

28. Liu Y, Liang SL, Jin GR, Yu YB, Chen AX. Einstein-Podolsky-Rosen Steering in Spontaneous Parametric Down-Conversion Cascaded with a Sum-Frequency Generation. Phys Rev A (2020) 102:052214. doi:10.1103/physreva.102.052214

CrossRef Full Text | Google Scholar

29. Olsen MK. Controlled Asymmetry of Einstein-Podolsky-Rosen Steering with an Injected Nondegenerate Optical Parametric Oscillator. Phys Rev Lett (2017) 119:160501. doi:10.1103/physrevlett.119.160501

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Wang N, Li Y. Quantum Analysis and Experimental Investigation of the Nondegenerate Optical Parametric Oscillator with Unequally Injected Signal and Idler. Phys Rev A (2016) 93:013831.

CrossRef Full Text | Google Scholar

31. Kalaga JK, Leoński W. Quantum Steering Borders in Three-Qubit Systems. Quan Inf Process (2017) 16:175. doi:10.1007/s11128-017-1627-6

CrossRef Full Text | Google Scholar

32. Kalaga JK, Leoński W, Peřina JJ. Einstein-Podolsky-Rosen Steering and Coherence in the Family of Entangled Three-Qubit States. Phys Rev A (2018) 97:042110. doi:10.1103/physreva.97.042110

CrossRef Full Text | Google Scholar

33. Cao H, Guo Z. Characterizing Bell Nonlocality and EPR Steering. Sci China Phys Mech Astron (2019) 62:30311. doi:10.1007/s11433-018-9279-4

CrossRef Full Text | Google Scholar

34. Zheng SS, Sun FX, Yuan HY, Ficek Z, Gong QH, He QY. Enhanced Entanglement and Asymmetric EPR Steering between Magnons. Sci China Phys Mech Astron (2021) 64:210311. doi:10.1007/s11433-020-1587-5

CrossRef Full Text | Google Scholar

35. Rojas González EA, Borne A, Boulanger B, Levenson JA, Bencheikh K. Continuous-Variable Triple-Photon States Quantum Entanglement. Phys Rev Lett (2018) 120:043601. doi:10.1103/PhysRevLett.120.043601

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Agustí A, Sandbo Chang CW, Quijandría F, Johansson G, Wilson CM, Sabín C. Tripartite Genuine Non-gaussian Entanglement in Three-Mode Spontaneous Parametric Down-Conversion. Phys Rev Lett (2020) 125:020502. doi:10.1103/PhysRevLett.125.020502

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Gottesman D. Theory of Quantum Secret Sharing. Phys Rev A (2000) 61:042311. doi:10.1103/physreva.61.042311

CrossRef Full Text | Google Scholar

38. Dou Z, Xu G, Chen XB, Liu X, Yang YX. A Secure Rational Quantum State Sharing Protocol. Sci China Inf Sci (2018) 61:022501. doi:10.1007/s11432-016-9151-x

CrossRef Full Text | Google Scholar

39. Wang Y, Tian CX, Su Q, Wang MH, Su Xl. Sci China Inf Sci (2019) 62:072501. doi:10.1007/s11432-018-9705-x

CrossRef Full Text

40. Zhu SN, Zhu YY, Ming NB. Quasi-Phase-Matched Third-Harmonic Generation in a Quasi-Periodic Optical Superlattice. Science (1997) 278:843–6. doi:10.1126/science.278.5339.843

CrossRef Full Text | Google Scholar

41. Ferraro A, Paris MGA, Bondani M, Allevi A, Puddu E, Andreoni A. Three-mode Entanglement by Interlinked Nonlinear Interactions in Optical χ^(2) media. J Opt Soc Am B (2004) 21:1241. doi:10.1364/josab.21.001241

CrossRef Full Text | Google Scholar

42. Drummond PD, Gardiner CW. Generalised P-Representations in Quantum Optics. J Phys A: Math Gen (1980) 13:2353–68. doi:10.1088/0305-4470/13/7/018

CrossRef Full Text | Google Scholar

43. Gardiner CW. Quantum Noise. Berlin, Germany: Springer (1991).

Google Scholar

44. Gardiner CW, Collett MJ. Input and Output in Damped Quantum Systems: Quantum Stochastic Differential Equations and the Master Equation. Phys Rev A (1985) 31:3761–74. doi:10.1103/physreva.31.3761

CrossRef Full Text | Google Scholar