Background Noise Suppression of Optical Sectioning Structured Illumination Microscopy via Fourier Domain Reconstruction

Optical sectioning structured illumination microscopy (OS-SIM) has been attracting considerable interest in fast 3D microscopy. The reconstruction of optical sectioning images in the conventional method employs the root-mean-square (RMS) algorithm in the spatial domain, which is prone to residual background noise. To overcome this problem, we propose a Fourier domain based optical sectioning image reconstruction algorithm (termed Fourier-OS-SIM), which has an improved background noise suppression capability compared to the RMS algorithm. The experimental results verified the feasibility and the effectiveness of the algorithm. The improved performance of the Fourier-OS-SIM may find more applications in biomedical or industrial fields.

Introduction

Optical sectioning structured illumination microscopy (OS-SIM) [1] has drawn much attention due to the compact wide-field architecture, fast speed, and optical sectioning capability, compared to the prominent laser scanning confocal microscopy (LSCM) [2]. With the structured illumination pattern, OS-SIM enables to discriminate the in-focus portion and gets rid of the out-of-focus portion of the depth of field (DOF) of the objective lens. The RMS (root mean square) algorithm is a usually used method to recover an optically sectioned image by using three fringe illuminated raw images with a phase shift interval of 2π/3 [1, 3]. Firstly, every two of the three raw images subtract from each other. Then, these substractions are squared and summed up, and finally rooted to yield an optical sectioning image. It is worth noting that the RMS algorithm does not take noises into account. However, noises exist inevitably in the raw images, and they will cause a background noise after the RMS calculation. The background noise will become more evident when the raw SIM images have a low signal-to-noise ratio (SNR), which is usual in fluorescence imaging, where the weak signal from the labeled fluorophores is surrounded by strong background noise. OS-SIM is different from super-resolution SIM (SR-SIM) that aims to break the diffraction limit [4, 5]. Although OS-SIM and SR-SIM can perform on the same system, they are based on different principles and have distinct image reconstruction frameworks.

To mitigate the weakness of the RMS algorithm, some modified reconstruction methods have been proposed. Santos et al. introduced a HiLo microscopy using one uniform wide-field image and another structured illumination image as inputs [6, 7]. High- and low-pass filters were applied to extract the high and low frequencies of the in-focus information, which are then synthesized into a sectioned image. However, the parameters of the high- and low-pass filters need to be determined empirically [8]. Patorski et al. proposed a two-shot OS-SIM with a phase shift of π via Hilbert-Huang processing [9]. The subtraction of the two-shot images is decomposed into a series of bi-dimensional intrinsic mode functions (BIMFs) through fast and adaptive bi-dimensional empirical mode decomposition (FABEMD) [10] and then filtered selectively. The sectioned image is reconstructed using a 2D spiral Hilbert transform from the filtered outcome. Although selective filtration can remove noise and bias to a certain extent, the decomposition and the 2D spiral Hilbert transformation are time-consuming. Subsequently, Zhou et al. presented a 1D Hilbert transform reconstruction that dramatically simplifies the Hilbert-Huang processing approach [11]. Another advantage is that the phase shift of the two shots can be arbitrary rather than constant π. Despite the simplicity of procedure and robustness in phase shifting, the 1D Hilbert transform reconstruction is lousy in background noise suppression since there is no noise-relevant operation involved in this method. Recently, deep learning has significantly boosted the OS-SIM reconstruction speed and reduced the number of raw images requested [12, 13]. However, it needs enormous training datasets and an excel reconstruction algorithm in advance. The robustness of the deep learning networks remains a challenge for different imaging situations.

In this paper, we propose a Fourier domain based optical sectioning image reconstruction algorithm (termed Fourier-OS-SIM) with background noise suppression capability. The Fourier-OS-SIM outperforms background noise suppression for the sectioned images compared to the conventional RMS-based OS-SIM reconstruction method. The performance of the Fourier-OS-SIM can be enhanced by using fruitful frequency filters to reduce the image background further.

Principle of Fourier-OS-SIM

The intensity distribution of the illumination cosinusoidal fringe pattern employed in SIM is expressed as:

$I\left(r\right)=I_0\left[1+m\text{cos}\left(2\pi k_{0}r+\phi \right)\right],(1)$

where r indicates the coordinate in the object plane; I₀, m, k₀, and φ represent the mean intensity, modulation depth, spatial frequency, and initial phase, respectively. In the linear regime, the intensity of the fluorescence signal is proportional to the excitation illumination intensity. The image intensity distribution recorded in the camera plane can be written as:

$D\left(r\right)=\left[S\left(r\right)I\left(r\right)\right]\otimes PSF\left(r\right),(2)$

where S(r) represents the structure of the sample, PSF(r) is the point spread function of the imaging system, and the symbol $\otimes$ denotes the convolution operation. Substitution of Eq. 1 into Eq. 2 results in:

$D\left(r\right)=I_0\left\{S\left(r\right)\left[1+m\text{cos}\left(2\pi k_{0}r+\phi \right)\right]\right\}\otimes PSF\left(r\right).(3)$

Making the Fourier transform for Eq. 3, we obtain the following equation in the frequency domain:

$\tilde{D}\left(k\right)=I_0[\tilde{S}\left(k\right)+0.5m{e}^{-i\phi }\tilde{S}\left(k+k_0\right)+0.5m{e}^{i\phi }\tilde{S}\left(k-k_0\right)]OTF\left(k\right).(4)$

Here, the symbol ∼ represents the corresponding Fourier spectrum, k denotes the spatial frequency, OTF(k) is the optical transfer function formed by taking the Fourier transform of the PSF(r). $\tilde{\mathit{S}}\left(\mathit{k}\right)$ refers to the conventional wide-field spectrum. $\tilde{\mathit{S}}\left(\mathit{k}+{\mathit{k}}_0\right)$ and $\tilde{\mathit{S}}\left(\mathit{k}-{\mathit{k}}_0\right)$ correspond to spectra with frequencies shifted by a distance of ±k₀, respectively. Combining these three spectra into one will enlarge the object spectrum scope, indicating a resolution enhancement in the spatial domain.

To solve the three spectral items of $\tilde{S}\left(k\right)$, $\tilde{S}\left(k+k_0\right)$, and $\tilde{S}\left(k-k_0\right)$ in Eq. 4, the initial phase φ is generally varied three times through phase shifting. Specifically, three phase-shifting with an interval of 2π/3 is common-used. Such phase-shifting results in three raw images, forming an equation set:

$\{\begin{array}{c}{\tilde{D}}_1\left(k\right)=I_0\left[\tilde{S}\left(k\right)+0.5m{e}^{-i{\phi }_1}\tilde{S}\left(k+k_0\right)+0.5m{e}^{i{\phi }_1}\tilde{S}\left(k-k_0\right)\right]OTF\left(k\right)\\ {\tilde{D}}_2\left(k\right)=I_0\left[\tilde{S}\left(k\right)+0.5m{e}^{-i{\phi }_2}\tilde{S}\left(k+k_0\right)+0.5m{e}^{i{\phi }_2}\tilde{S}\left(k-k_0\right)\right]OTF\left(k\right)\\ {\tilde{D}}_3\left(k\right)=I_0\left[\tilde{S}\left(k\right)+0.5m{e}^{-i{\phi }_3}\tilde{S}\left(k+k_0\right)+0.5m{e}^{i{\phi }_3}\tilde{S}\left(k-k_0\right)\right]OTF\left(k\right)\end{array},(5)$

where φ₁ = φ₀; φ₂ = φ₀ + 2π/3; φ₃ = φ₀ + 4π/3. The solution of Eq. 5 is:

$\{\begin{array}{l}\tilde{S}\left(k\right)=\frac{1}{3I_0}\left[{\tilde{D}}_1\left(k\right)+{\tilde{D}}_2\left(k\right)+{\tilde{D}}_3\left(k\right)\right]/OTF\left(k\right)\hfill \\ \tilde{S}\left(k+k_0\right)=\frac{2e^{i{\phi }_0}}{3m{I}_0}\left[{\tilde{D}}_1\left(k\right)+e^{i\frac{2\pi }{3}}{\tilde{D}}_2\left(k\right)+e^{i\frac{4\pi }{3}}{\tilde{D}}_3\left(k\right)\right]/OTF\left(k\right)\hfill \\ \tilde{S}\left(k-k_0\right)=\frac{2e^{-i{\phi }_0}}{3m{I}_0}\left[{\tilde{D}}_1\left(k\right)+e^{i\frac{4\pi }{3}}{\tilde{D}}_2\left(k\right)+e^{i\frac{2\pi }{3}}{\tilde{D}}_3\left(k\right)\right]/OTF\left(k\right)\hfill \end{array}.(6)$

Making the inverse Fourier transform for Eq. 6, we get:

$\{\begin{array}{l}S\left(r\right)\otimes PSF\left(r\right)=\frac{1}{3I_0}\left[D_1\left(r\right)+D_2\left(r\right)+D_3\left(r\right)\right]\hfill \\ F{T}^{-1}\left\{\tilde{S}\left(k+k_0\right)\right\}\otimes PSF\left(r\right)=\frac{2e^{i{\phi }_0}}{3m{I}_0}\left[D_1\left(r\right)+e^{i\frac{2\pi }{3}}{D}_2\left(r\right)+e^{i\frac{4\pi }{3}}{D}_3\left(r\right)\right]\hfill \\ F{T}^{-1}\left\{\tilde{S}\left(k-k_0\right)\right\}\otimes PSF\left(r\right)=\frac{2e^{-i{\phi }_0}}{3m{I}_0}\left[D_1\left(r\right)+e^{i\frac{4\pi }{3}}{D}_2\left(r\right)+e^{i\frac{2\pi }{3}}{D}_3\left(r\right)\right]\hfill \end{array},(7)$

The first equation of Eq. 7 indicates that the conventional wide-field image can be reconstructed by summating the three raw images. Most notably, on the right side of the second and third equations, the terms of the square brackets identically represent the OS image, according to the RMS algorithm from the first report of OS-SIM [1]:

$\begin{array}{l}{D}_{os}\left(r\right)=\left|D_1\left(r\right)+e^{i\frac{2\pi }{3}}{D}_2\left(r\right)+e^{i\frac{4\pi }{3}}{D}_3\left(r\right)\right|\\ =\left|D_1\left(r\right)+e^{i\frac{4\pi }{3}}{D}_2\left(r\right)+e^{i\frac{2\pi }{3}}{D}_3\left(r\right)\right|\\ =\frac{\sqrt{2}}{2}\sqrt{{\left(D_2\left(r\right)-D_1\left(r\right)\right)}^2+{\left(D_3\left(r\right)-D_2\left(r\right)\right)}^2+{\left(D_1\left(r\right)-D_3\left(r\right)\right)}^2},\end{array}(8)$

where the symbol | | denotes the modulus operation. Combining Eqs 7 and 8, the OS image can be rewritten as:

$D_{os}\left(r\right)=\{\begin{array}{c}\left|\frac{3m{I}_0}{2e^{i{\phi }_0}}F{T}^{-1}\left\{\tilde{S}\left(k+k_0\right)\right\}\otimes PSF\left(r\right)\right|,or\\ \left|\frac{3m{I}_0}{2e^{-i{\phi }_0}}F{T}^{-1}\left\{\tilde{S}\left(k-k_0\right)\right\}\otimes PSF\left(r\right)\right|\end{array}.(9)$

Since $\tilde{\mathit{S}}\left(\mathit{k}+{\mathit{k}}_0\right)$ and $\tilde{\mathit{S}}\left(\mathit{k}-{\mathit{k}}_0\right)$ are symmetric to the original point, the two equations in Eq. 9 are equivalent. This implies the OS image is directly correlated to the acentric spectrum of $\tilde{\mathit{S}}\left(\mathit{k}+{\mathit{k}}_0\right)$ or $\tilde{\mathit{S}}\left(\mathit{k}-{\mathit{k}}_0\right)$. This provides an alternative way to reconstruct the OS image in the Fourier domain, which can apply filtering operation to reduce the background noise to enhance the performance of the OS image.

Experimental Verification

Experimental Setup

The experimental verification for the Fourier-OS-SIM is conducted in the home-built DMD-based LED illumination SIM microscope [14], whose scheme is illustrated in Figure 1. High brightness LED (center wavelength λ = 470 nm, LED4D251, Thorlabs, United States) is employed as the light source. After expanding and collimating, the LED beam incidents on the DMD chip (2,560 × 1,600 pixels, V-9001UV, ViALUX, Germany) at an angle of 24° with respect to the normal of the DMD panel. The rotation and phase-shifting of the fringe illumination are realized by rapidly refreshing the DMD patterns. In the binary pattern mode, the refreshing rate can reach 22 kHz. The objective lens (20×/NA0.45, Nikon, Japan) is used for fringe projection and imaging of samples. The sample is placed on an XYZ motorized translation stage for accurately positioning the observed target and axially scanning with a minimum step of 50 nm (M-405. DG, Physik Instruments Inc., Germany). The excited fluorescence light passes through the dichroic beamsplitter (edge 473–491 nm, Semorock, United States), the filter (490 nm long-pass, Semorock, United States), the zoom lens (70–300 mm, F/4–5.6, Nikon, Japan), and is recorded by the scientific CMOS camera (2,048 × 2,048 pixels, 100 fps, Orca Flash 4.0, Hamamatsu, Japan). The Arduino Uno board [15] with C++ programming triggers all the electric components in sequence.

FIGURE 1

FIGURE 1. The schematic of the DMD-based LED-illumination SIM microscope.

Background Noise Suppression via Fourier-OS-SIM

The experiment was performed with a mixed pollen grains specimen (Thermofisher). The autofluorescence signal was excited by the 470 nm LED light. The camera exposure time was 200 ms, and the field-of-view (FOV) area was measured to be 320 × 320 μm² by a micro ruler. We designed a 1D binary pattern with six pixels per period to produce the sinusoidal structured illumination fringe. The required three phase-shifts were realized by moving the fringe with a distance of two pixels for each step, corresponding to a 2π/3 interval. With the f = 400 mm collimated lens and the 20× objective lens, the six pixels per period fringe (DMD pixel size 7.56 μm) were demagnified into 1.134 μm/period in the sample plane. The system has an optical resolution of about 0.522 μm (λ/2NA). The structured illumination frequency is nearly half of the cut-off frequency, meeting with the optimal condition of the OS-SIM theory [3].

Figure 2 shows the reconstruction results of the wide-field, RMS algorithm, and the Fourier-OS-SIM for the same input of three phase-shifted fringe images. For the Fourier-OS-SIM image, we first conducted the input in the reconstruction framework of SR-SIM and then fused the extended spectra of $\tilde{S}\left(k+k_0\right)$ and $\tilde{S}\left(k-k_0\right)$ in Eq. 9. It should be noted that the spectra fusion process does not involve the spectrum of $\tilde{S}\left(k\right)$ so as to eliminate the deterioration from the out-of-focus background. It can be seen that the contrasts of Figures 2B,C are much better than that of Figure 2A, demonstrating the optical sectioning capacity of the RMS algorithm and the Fourier-OS-SIM. From the zoom-in parts, we can see that the inner circle area, which indicates the background, Figure 2C is darker than 2B, implying the background level of Fourier-OS-SIM is lower than that of RMS. The noise in Figure 2F is less intensive than 2E; thus, Figure 2F is sharper and smoother than 2E. The histograms of Figures 2E,F also reflect the noise degree, as shown in Figures 2G,H. The histogram of Figure 2G is more discrete and steeper than 2H, which means the noise of Fourier-OS-SIM is more modest than the RMS algorithm.

FIGURE 2

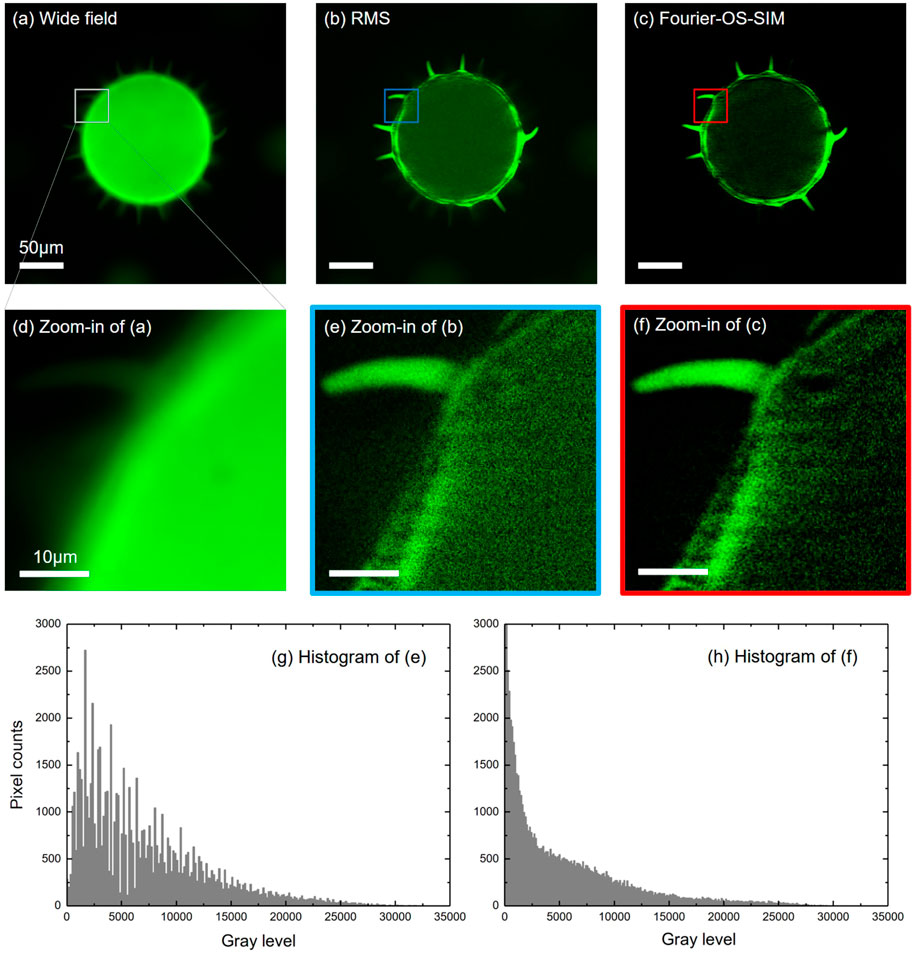
FIGURE 2. Experimental results of the Fourier-OS-SIM in comparison with the Wide-field and RMS algorithm for imaging pollen grains. (A–C): images of the Wide-field, RMS, and Fourier-OS-SIM, respectively. (D–F): the zoom-in parts of the marked areas indicated in (A–C). (G–H): the histograms of (E,F), respectively.

Additional Background Noise Suppression by Filtering

One significant advantage of OS-SIM in the frequency domain is that plenty of filters can suppress the random electrical noise and photon shot noise or compound in an image. Here, we take the simplest Gaussian low-pass filter as an example to enhance the performance of Fourier-OS-SIM image. The radius of the Gaussian low-pass filter was set to two pixels, considering that the imaging resolution is above six image pixels. Therefore, the filter does not harm the image signal. The filtered image of Figure 3C displays smoother than the original Fourier-OS-SIM image of Figure 3B; meanwhile, the details of Figure 3B are almost reserved. The SNR value was employed to evaluate the image quality. A reference image was pre-generated by subtracting the background of the wide-field image by using the ImageJ software (Biomedical imaging group, EPFL). The SNR value was calculated by using the SNR plugin of ImageJ. For comparison, a filtered RMS image is also presented in Figure 3D, which is applied with the same Gaussian filter. Although Figure 3D looks smoother than Figure 3C, the SNR of Figure 3C is much better than that of Figure 3D. From the SNR values in Figures 3A–D, we can see that the Fourier-OS-SIM image (SNR 7.97 dB) is better than the RMS image (4.43 dB); and the Fourier-OS-SIM image is further improved by applying an exemplified Gaussian filter (SNR increases from 7.97 to 15.57 dB). The intensity profiles along the marked lines in RMS, Fourier-OS-SIM, filtered Fourier-OS-SIM, and filtered RMS images are plotted as in Figures 3E–H. The curves present that the SNR of the Fourier-OS-SIM is superior to the RMS algorithm, especially after the Gaussian low-pass filtering.

FIGURE 3

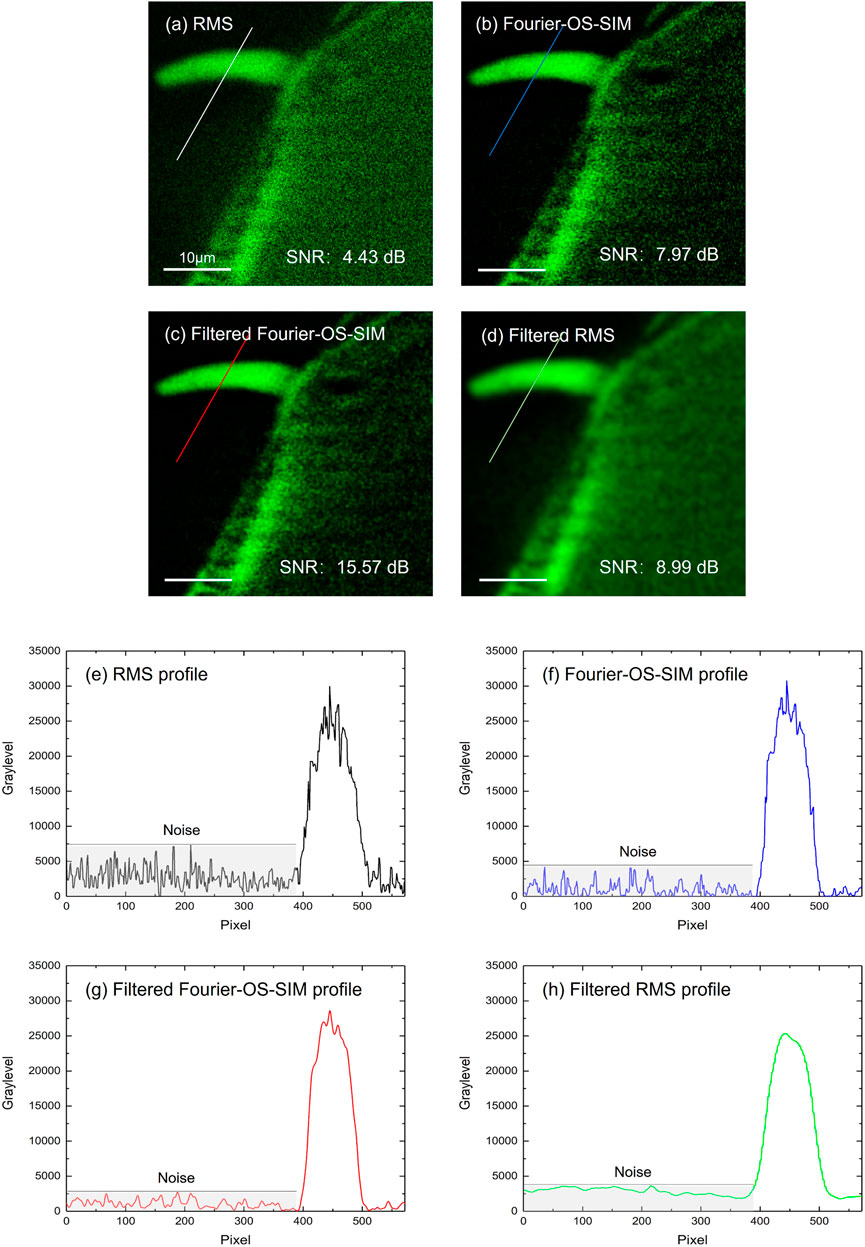
FIGURE 3. Fourier-OS-SIM images before and after Gaussian low-pass filtering compared to the RMS image. (A–D): images of the RMS, Fourier-OS-SIM before and after filtering, and the filtered RMS, respectively. (E–H): the intensity profiles along the marked lines in (A–D).

Image Reconstruction Accelerated by GPU

The drawback of the Fourier-OS-SIM is mainly related to the time-cost of the Fourier transform operation. To address this problem, we adopted the advanced GPU acceleration technology to boost the computational speed of Fourier transforms. An open-source library OpenCV [16] with Nvidia CUDA [17] support, was used to simplify the GPU acceleration. Three phase-shifted structured illumination images with 2,048 × 2,048 pixels were employed as the same input for Fourier-OS-SIM and RMS scripts. The scripts were written in C++ and operated in a workstation computer (Intel Xeon Silver 4114 CPU, 128GB RAM, Nvidia GeForce RTX 2080Ti graphic card, Windows 10 64 bit operation system). We iteratively ran the Fourier-OS-SIM, the accelerated Fourier-OS-SIM, and the RMS scripts 150 times, respectively, to record the reconstruction time. After acceleration, the Fourier-OS-SIM cost-time drops to 0.323 s from 1.591 s, achieving a nearly five folds boost. Although the accelerated Fourier-OS-SIM consuming time is still greater than RMS (0.026 s), the time gap is narrowed through GPU acceleration.

The Resultant 3D Imaging

3D imaging is reconstructed from the series of axially-scanned optically sectioned images. The optical sectioning enhancement efforts studied above can improve the performance of 3D images. We scanned the pollen sample by a step of 0.2 μm axially and sectioned 144 slices. Figures 4A,D present the maximum intensity projections (MIP) of the RMS and the Fourier-OS-SIM slice stacks visualized through 3D volume rendering, respectively. To demonstrate the superiority of the Fourier-OS-SIM more clearly, we zoomed in a rectangle ROI labeled in Figures 4A,D, as shown in Figures 4B,E accordingly. The intensity profiles along the same location lines in Figures 4B,E were plotted in Figures 4C,F. By comparing the two curves, we can see that the Fourier-OS-SIM curve is much smoother than the RMS, demonstrating a significant background noise suppression. The SNR values of Figures 4B,E support that the Fourier-OS-SIM algorithm is superior to the RMS algorithm.

FIGURE 4

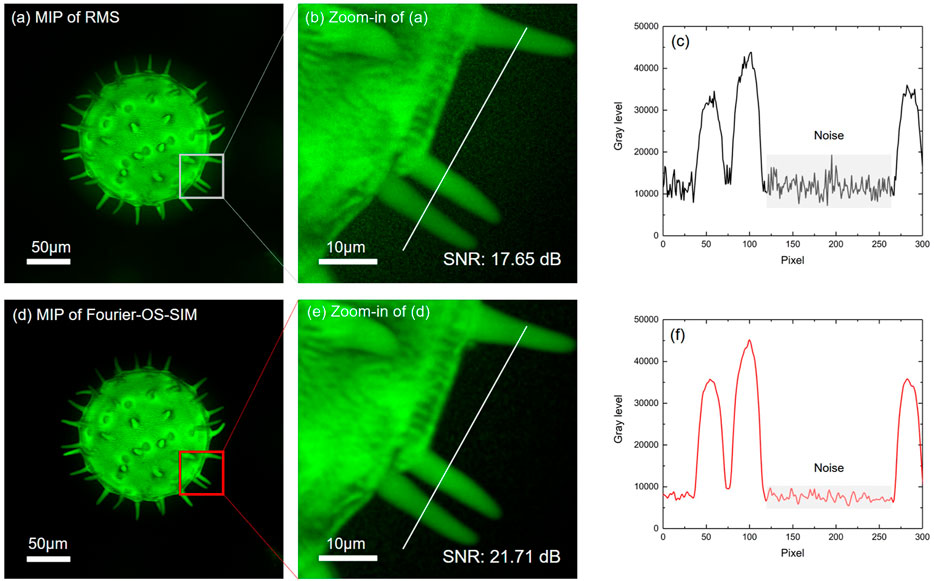
FIGURE 4. The MIPs of 3D images from the Fourier-OS-SIM and the RMS sectioned slice stacks. (A,D): the MIPs of the RMS and the Fourier-OS-SIM slice stacks visualized by 3D volume rendering, respectively. (B,E): the zoom-in images of the ROI in RMS and Fourier-OS-SIM 3D images. (C,F): the intensity profiles along the cut-lines in (B,E).

Conclusion

We have proposed a Fourier reconstruction scheme for optical sectioning SIM, termed Fourier-OS-SIM. In theory, an equivalent expression of the common-used RMS reconstruction algorithm has been deduced in light of the SR-SIM principle in the Fourier domain. In contrast to the RMS reconstruction approach, experimental results show that the Fourier-OS-SIM is more advanced at background noise suppression. More importantly, suppressing image background in the Fourier domain is more accessible and effective than in the spatial domain in general instances, because the Fourier-OS-SIM intrinsically operates in the Fourier domain, a frequency filter can be straightforwardly applied to suppress noise further. Thus, the Fourier-OS-SIM provides a new possibility that specific background noise suppression filters can be involved in this pipeline to suppress background noise further. The improved performance of Fourier-OS-SIM may find more applications in biomedical or industrial fields.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

BY conceived and supervised the project. SD, HW, and DD performed experiments. DD Wrote the programming scripts. JQ, TP, CB, and JM assisted to data analysis. SD and DD wrote the manuscript. All the authors contributed to discuss and revise the manuscript.

Funding

This work was supported by the National Key Research and Development Program of China (No. 2021YFF0700300) and the State Key Laboratory of Transient Optics and Photonics, Chinese Academy of Sciences (No. SKLST202006).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Neil MAA, Juškaitis R, Wilson T. Method of Obtaining Optical Sectioning by Using Structured Light in a Conventional Microscope. Opt Lett (1997) 22:1905–7. doi:10.1364/OL.22.001905

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Bayguinov PO, Oakley DM, Shih C-C, Geanon DJ, Joens MS, Fitzpatrick JAJ. Modern Laser Scanning Confocal Microscopy. Curr Protoc Cytometry (2018) 85:e39. doi:10.1002/cpcy.39

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Dan D, Yao B, Lei M. Structured Illumination Microscopy for Super-resolution and Optical Sectioning. Chin Sci Bull (2014) 59:1291–307. doi:10.1007/s11434-014-0181-1

CrossRef Full Text | Google Scholar

4. Gustafsson MGL. Surpassing the Lateral Resolution Limit by a Factor of Two Using Structured Illumination Microscopy. J Microsc (2000) 198:82–7. doi:10.1046/j.1365-2818.2000.00710.x

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Gao P, Yuan C. Resolution Enhancement of Digital Holographic Microscopy via Synthetic Aperture: a Review. Light Adv. Manuf. (2022) 3:1. doi:10.37188/lam.2022.006

CrossRef Full Text | Google Scholar

6. Santos S, Chu KK, Lim D, Bozinovic N, Ford TN, Hourtoule C, et al. Optically Sectioned Fluorescence Endomicroscopy with Hybrid-Illumination Imaging through a Flexible Fiber Bundle. J Biomed Opt (2009) 14:030502. doi:10.1117/1.3130266

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Lim D, Chu KK, Mertz J. Wide-field Fluorescence Sectioning with Hybrid Speckle and Uniform-Illumination Microscopy. Opt Lett (2008) 33:1819–21. doi:10.1364/ol.33.001819

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Shi R, Kong L. Evaluating Structured-Illumination Patterns in Optimizing Optical-Sectioning of HiLo Microscopy. J Phys D: Appl Phys (2021) 54:414001. doi:10.1088/1361-6463/ac153b

CrossRef Full Text | Google Scholar

9. Patorski K, Trusiak M, Tkaczyk T. Optically-sectioned Two-Shot Structured Illumination Microscopy with Hilbert-Huang Processing. Opt Express (2014) 22:9517–27. doi:10.1364/OE.22.009517

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Bhuiyan SMA, Adhami RR, Khan JF. A Novel Approach of Fast and Adaptive Bidimensional Empirical Mode Decomposition. In: IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2008). Las Vegas, NV, USA: IEEE (2008). doi:10.1109/ICASSP.2008.4517859

CrossRef Full Text | Google Scholar

11. Zhou X, Lei M, Dan D, Yao B, Qian J, Yan S, et al. Double-exposure Optical Sectioning Structured Illumination Microscopy Based on Hilbert Transform Reconstruction. PLoS One (2015) 10:e0120892. doi:10.1371/journal.pone.0120892

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Chai C, Chen C, Liu X, Lei Z. Deep Learning Based One-Shot Optically-Sectioned Structured Illumination Microscopy for Surface Measurement. Opt Express (2021) 29:4010–21. doi:10.1364/OE.415210

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Bai C, Qian J, Dang S, Peng T, Min J, Lei M, et al. Full-color Optically-Sectioned Imaging by Wide-Field Microscopy via Deep-Learning. Biomed Opt Express (2020) 11:2619–32. doi:10.1364/BOE.389852

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Dan D, Lei M, Yao B, Wang W, Winterhalder M, Zumbusch A, et al. DMD-based LED-Illumination Super-resolution and Optical Sectioning Microscopy. Sci Rep (2013) 3:1116. doi:10.1038/srep01116

PubMed Abstract | CrossRef Full Text | Google Scholar

15.Arduino Uno. Arduino UNO (2022). Available from: https://www.arduino.cc/en/Main/arduinoBoardUno> (Accessed March 20, 2022).

Google Scholar

16.Open Source Computer Vision Library. Open Source Computer Vision Library (2022). Available from: https://opencv.org/(Accessed March 20, 2022).

Google Scholar

17. Sanders J, Kandrot E. CUDA by Example: An Introduction to General-Purpose GPU Programming. Boston: Addison-Wesley Professional (2010).

Google Scholar