3D Organisation of Cells in Pseudostratified Epithelia

Introduction

Epithelia are common to all animals and plants, and play a key structural role in tissue morphogenesis and the development of organ shapes. With more than 90% of cancers being of epithelial origin [1], there is an urgent need to uncover the principles of epithelial organisation and understand the basis for epithelial integrity and homeostasis. Epithelia achieve their structural function via their polarity (Figure 1A). On the outward-facing apical side, cells form a virtually impermeable barrier via a cadherin-based adhesion belt and tight junctions, while, on their basal side, they bind tightly to the basal lamina, a thin sheet composed of extracellular matrix (ECM) proteins [2–5]. Additional cell-cell junction complexes along the lateral sides provide further mechanical stabilisation. Recent advances in imaging provide insight into the physical principles according to which cell connectivity is organised in epithelia, and how it changes during morphogenesis and concomitant cell shape transitions.

FIGURE 1

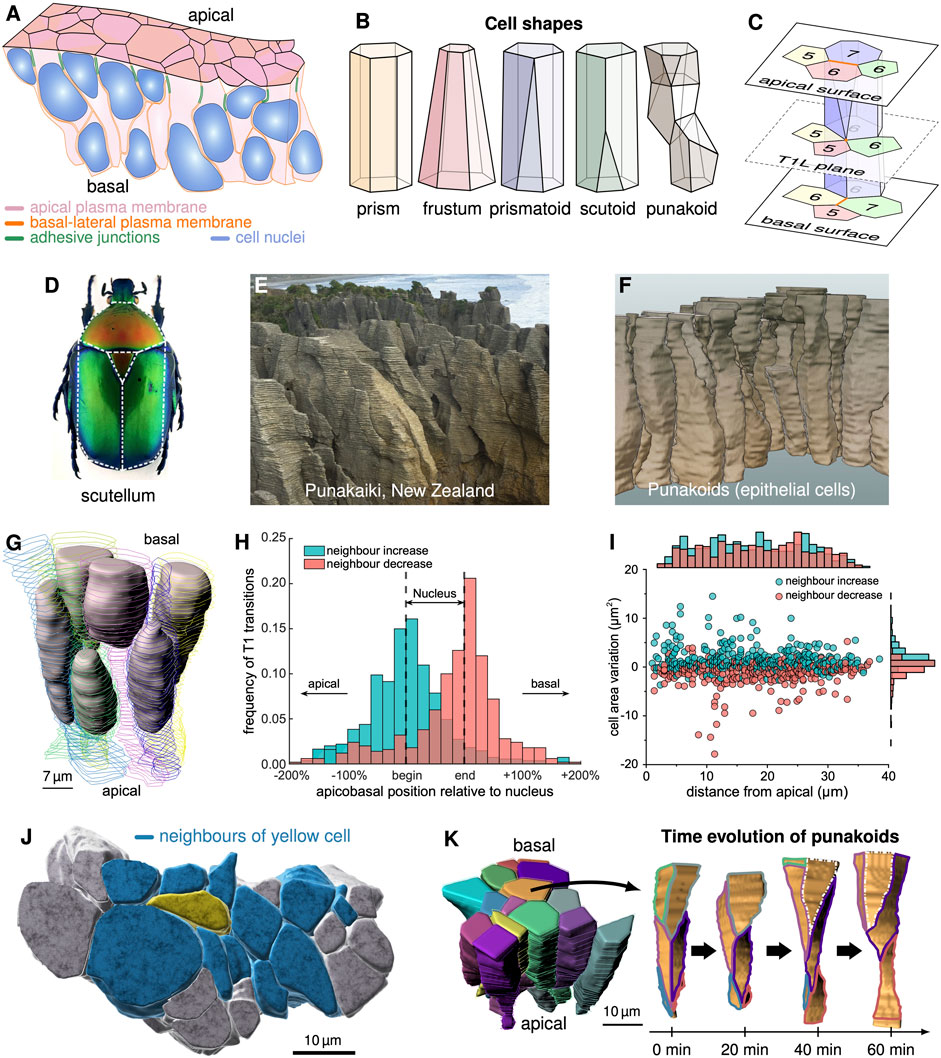
FIGURE 1. 3D epithelial cell shapes. (A) Pseudostratified epithelium with cell boundaries wrapping around wider nuclei. (B) Schematic depiction of cell shapes. (C) Cells alter their neighbour arrangements via T1L processes along the apical-basal axis. In a T1L process, two vertices that share an edge (orange) merge and decompose in a different direction such that neighbour relationships change. (D) The term scutoid was coined based on the shape of beetle scutum, scutellum and wings. (E) Pancake rocks at the beach of Punakaiki, NZ. (F) 3D segmented cells in the developing pseudostratified mouse lung epithelium (E12.5) resemble the Punakaiki rocks. (G) 3D shapes of 6 cells and their nuclei in an E12.5 pseudostratified mouse lung epithelium. (H) Neighbour relationships change predominantly at the apical and basal limits of the nuclei. (I) The lateral T1L processes are largely uniformly distributed along the apical-basal axis. Neighbour numbers tend to increase as cross-sectional cell area variation increases, and vice versa. (J) 3D cell neighbourship extends further than apparent on the surface. (K) Time evolution of the contact areas between the central cell (orange) and its neighbours in a patch of 15 epithelial cells (left) over 60 min of explant culture. (A, G–K) reproduced with modifications from [18], panel D from [15], published under the Creative Commons Attribution Non-Commercial 4.0 International License (CC BY-NC 4.0; https://creativecommons.org/licenses/by-nc/4.0/). Further reproduction of these panels would need to comply with the terms of this license.

3D Epithelial Cell Shapes

Since the advent of light microscopy, epithelial surfaces have been studied in great detail, and this has revealed tight cell packing in polygonal lattices along the entire apical-basal axis [6–19]. As 3D segmentation of cells has become possible only very recently [17, 18, 20–25], 3D cell shapes have long been depicted as prisms, which retain the same size and neighbour relationship along the entire apical-basal axis (Figure 1B). Cells in curved epithelial monolayers are commonly pictured as frusta (also termed bottle cells) as the apical and basal areas must differ. Differences in neighbour arrangements between the apical and basal side point to neighbour changes along the apical-basal axis in a range of epithelia [26]. Prismatoids accommodate the neighbour change at either surface. If the neighbour relationships change somewhere in between (Figure 1C), the cell shape is reminiscent of that formed by beetle scutum, scutellum and wings (Figure 1D), which led to the new term scutoid [15]. With up to 14 neighbour changes along the apical-basal axis [18], pseudostratified epithelial cells in developing mouse lungs, however, resemble more the pancake rock formations in Punakaiki at New Zealand’s west coast (Figure 1E) than the back of beetles (Figure 1D). This novel complex geometry may therefore better be referred to as punakoid (Figure 1F). The defining characteristics of punakoids are 1) a quasi-polygonal surface, 2) a well-defined cell axis (in the pseudostratified epithelia reviewed here, the apical-basal axis), and 3) multiple neighbour changes along the axis. Like scutoids, the faces of punakoids are not necessarily planar, the edges not necessarily straight, and the entire shape not necessarily convex. So far, punakoids were found in the embryonic mouse lung, and their prevalence in other pseudostratified epithelia, although likely, remains to be demonstrated.

As characteristic for pseudostratified epithelia [27], nuclei are found distributed along the entire apical-basal axis (Figure 1G) [18]. Neighbour changes occur mainly at the limits of the nuclei (Figure 1H), where the cross-sectional area changes the most [18]. An increase in the cross-sectional area correlates with a neighbour increase, and vice versa (Figure 1I). If the number of cells remains the same, neighbour relationships change via so-called T1 processes [28] (also referred to as rosette formation if more than four cells are involved [29]). We will refer to a neighbour transition along the apical-basal axis as lateral T1 process (T1L for short) (Figure 1C). The potentially large number of neighbour intercalations along their long axis lets the cells be in physical contact with others that, on the apical or basal surface, appear to be several cell diameters apart (Figure 1J). Cell-cell signalling can thus spread further than previously anticipated, and cells can read and average morphogen gradients over distances that were previously expected to require cell protrusions [30–33]. Much as on the apical surface [34], cell neighbour relationships further change dynamically over time along the entire apical-basal axis [17, 18] (Figure 1K), thereby further increasing the distance over which signals can be sensed, exchanged, and averaged. But what leads to these unexpectedly complex and dynamic 3D cell shapes, and what determines cell neighbour relationships?

Surface Area Minimisation

Epithelial cells are often compared to soap bubbles. Soap bubbles famously minimise their surface area and assume a spherical shape in isolation. Motivated by the tight packing of soap bubbles in foams, there has been a long-standing interest in optimal packing solutions that minimise the overall surface area. In the 19th century, Lord Kelvin proposed that tetrakaidekahedra minimise the overall surface area if all soap bubbles have the same volume. Flattened 14-sided tetrakaidecahedra with hexagonal apical and basal surfaces are found in the multi-layered, stratified epidermis of the skin [22]. However, a more efficient packing of equally sized cells has since been described [35], and the complex shapes of cells in single-layered pseudostratified epithelia (Figure 2A) certainly do not minimise the overall surface area for the given cell volume. What then governs their shape and neighbour relationships?

FIGURE 2

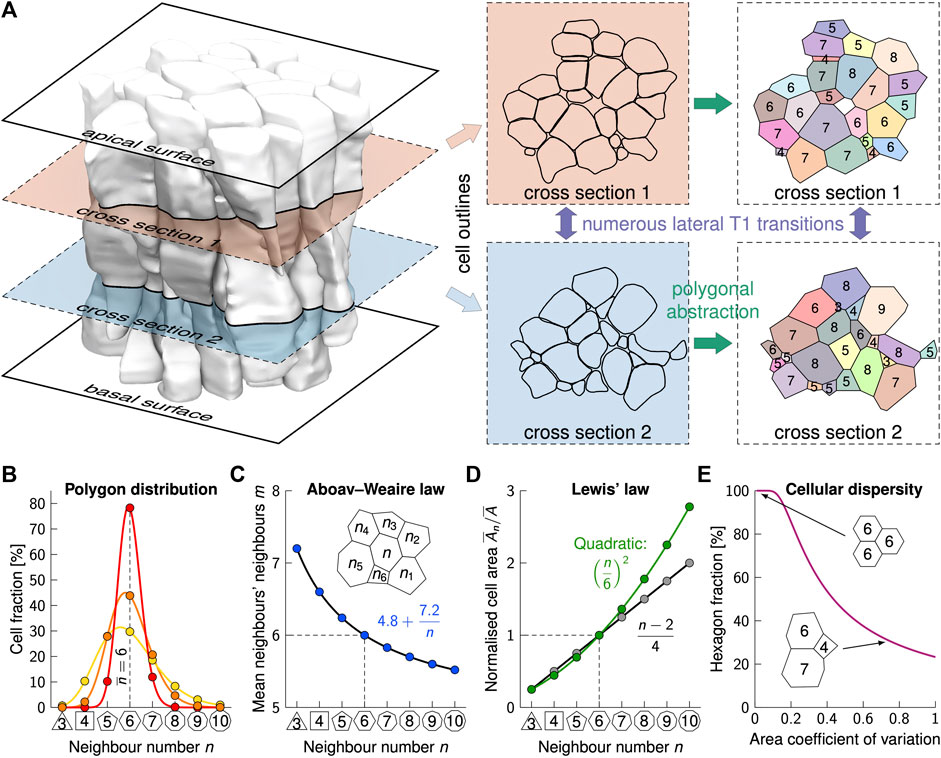
FIGURE 2. Phenomenological laws in epithelial cell arrangements. (A) Slicing through a mouse embryonic lung epithelium (shaded cells [18]) repeatedly along the apical-basal axis reveals the complex shape and packing structure of punakoids. Even over short distances, numerous T1L transitions occur, leading to vastly different cell neighbourships. Colours in the last column indicate cell identity, values are cross-sectional neighbour numbers. (B) The average neighbour number, $\overline{n}$, is (close to) six in all epithelia, even though the hexagon fraction and the neighbor number distribution vary. (C) All quantified epithelial tissues follow Aboav-Weaire’s law. (D) All quantified epithelial tissues follow either Lewis’ law (grey line), or the quadratic law (green line), or lie in between. (E) The hexagon frequency declines for increasing area variability according to the magenta curve.

Striking Regularities in Cell Arrangements

The 3D cell neighbour relationships can be understood by considering single 2D planes, perpendicular to the apical-basal cell axis [18]. In the following, we will therefore first discuss the neighbour relationships in these 2D planes (Figure 2).

Striking regularities that have long been known and that are found on all apical and basal surfaces studied to date [6–16, 19], have recently been reported also in all planes along the apical-basal axis (Figure 2A), even though neighbour relationships change between individual cells [18]. First and foremost, cells in any 2D plane have on average (close to) six neighbours, albeit the neighbour number distributions (Figure 2B) differ significantly among epithelia and between planes. This can be accounted to topological constraints in 2D contiguous polygonal lattices, and follows directly from Euler’s polyhedron formula [10, 36]. If three edges meet at each junction, the mean neighbour number in infinite lattices is exactly six, $\overline{n}=6$. The average declines as the number of edges per vertex increases, to $\overline{n}=4$ if four edges meet in each junction. Locally, the average deviates from six in epithelia (Figure 2C) and follows a phenomenological relationship known as Aboav-Weaire’s law [37],

$m=\frac{1}{n}{\displaystyle \sum _{i=1}^n{n}_i=a+\frac{b}{n}}(1)$

which relates the number of neighbours, n, of a central cell to the average one of its neighbours, $m$ (Figure 3C, inset). In epithelia, the parameter values fall into the range $a\in [4.5, 5.5]$ and b $\in [4.5, 9.5$] [38]. Finally, the relative average apical area, $\overline{A_n}$, of cells with n neighbours with respect to the average area of all cells, $\overline{A}$, linearly increases with n (Figure 2D, black line), a phenomenological relation termed Lewis’ law [6],

$\frac{\overline{A_n}}{\overline{A}}\approx \frac{(n-2)}{4}.(2)$

Initially, Lewis’ law has been accounted to entropy maximisation [36], but this has subsequently been ruled out [39, 40]. Many other hypotheses have been explored to explain epithelial organisation. According to topological arguments, sequential cell division results in the observed frequencies of neighbour numbers (Figure 2B) [10, 41]. However, this argument does not explain the emergence of cells with less than five neighbours, and predicts proliferative epithelial tissues to have about 45% hexagons. The hexagon frequencies, however, decrease with increasing variability in the cell cross-sectional areas (Figure 2E), and reported values range from 30 to 80% [14]. Contrary to the assumptions of the topological model, cells rearrange their boundaries until they reach a mechanical equilibrium [9]. By altering the relative cell-cell adhesion strength and cortical tension, the full range of neighbour relationships can be reproduced in vertex models and similar model setups [9, 14, 41–46]. In a small subset of the parameter space, Lewis’ law emerges [9, 43, 44]. Lewis’ law and the entire range of measured neighbour frequencies can be reproduced also using Voronoi tessellations, but again only for the subset of the parameter space that yields the right level of tessellation irregularity [13, 47]. So, why do all epithelia follow those two phenomenological laws?

Minimisation of the Lateral Cell-Cell Contact Energy Determines Cell Neighbour Relationships

As cells reach the mechanical equilibrium quickly (in less than a minute [9]), the polygonal lattices that one observes when cutting the epithelium in any plane (Figure 2A) represent a mechanical equilibrium, i.e., a state of minimal energy. At first sight, the highly irregular shapes of epithelial cells may appear inconsistent with surface energy minimisation, as observed in foam. However, by following Lewis’ law and Aboav-Weaire’s law, epithelial cells still minimise the lateral surface area for the given irregular cell volume distribution [14, 38]. Thus, in each plane along the apical-basal axis (Figure 2A), cells minimise the total perimeter for the enclosed cross-sectional areas.

As regular polygons have the smallest perimeter per enclosed area, a lattice composed of regular polygons will have the smallest total perimeter. If all cells had the same cross-sectional area, a regular hexagonal lattice would be most favourable. However, cellular processes constantly alter the cross-sectional areas, and the combined cell-cell contact surface energy is lower with mixed cross-sectional cell areas [14]. Even the hexagonal ommatidia in the Drosophila eye are each composed of 21 differently-sized apical cell areas, which are predominantly not hexagonal [48]. The arrangement into hexagonal ommatidia relies on the careful adjustment of cell adhesion, cortical tension, and cell dilation [49–51]. As mixed cross-sectional cell areas are most favourable, epithelial cells easily disperse from a clone with smaller cells, while they remain clustered without such a cell size difference relative to the surrounding tissue, potentially facilitating the spreading of tumour cells [16].

For the distribution of cross-sectional cell areas found in epithelial tissues, perfectly regular contiguous lattices cannot form. By following Aboav-Weaire’s law, the internal angles of the polygons are closest to those of a regular polygon while still adding up to 360° at each junction [38]. By following Lewis’ law, the side lengths are most similar [14]. Equal side lengths are obtained if the cross-sectional cell areas follow a quadratic relation (Figure 3D, green line) of the form

$\frac{\overline{A_n}}{\overline{A}}\approx \frac{n}{6}\frac{\text{tan} \left(\pi /6\right) }{\text{tan} \left(\pi /n\right) }\approx {\left(\frac{n}{6}\right)}^2.(3)$

The quadratic relationship, however, emerges only at a high area variability, as found on the apical side of embryonic lung tubes [14, 18]. Finally, a novel relationship that all epithelia follow emerges from the drive to the most regular polygonal shape, and relates the fraction of hexagons to the apical area variability, measured by the coefficient of variation (CV = std/mean) (Figure 2E) [14]. Interestingly, even puzzle cells in plants, which derive their name from their highly irregular shape, reminiscent of puzzle pieces, follow Lewis’ law [52]. This is still consistent with a minimisation of the cell perimeter because the puzzle shape emerges in an effort to minimise stress in large cross-sections only after the cells have stopped dividing and the neighbour relationships have been fixed by the rigid cell walls [53]. In summary, the minimisation of lateral cell-cell contact energy defines the polygonal shape of each cell cross-section, and thus the cell neighbour relationships. Changes in the relative cross-sectional areas along the apical-basal axis or over time drive cell neighbour changes [14, 18]. But why do the cross-sectional areas change–or differently put, what defines the 3D cell shape?

Impact of Tissue Curvature on Cell Neighbour Relationships

If the two principal curvatures of the tissue surface change differently along the apical-basal axis, such as in sufficiently thick epithelial tubes, then the cell aspect ratio changes along the apical-basal axis. To maintain a regular polygonal cross-sectional cell shape, neighbour relationships have to change. This curvature effect has been proposed to result in scutoid cell shapes in epithelial tubes [15]. Curvature-driven T1L processes should then on average occur more frequently, i.e., for lesser curvature fold-changes ${\kappa }_2/{\kappa }_1,$ the higher the cell neighbour number, n, in local cross sections [18]:

$\frac{{\kappa }_2}{{\kappa }_1}\left(n\right)={\left(1-\frac{\alpha \left(2+\text{cos} \alpha \right)}{n \text{sin} \alpha \left(1+2\text{cos} \alpha \right)}\right)}^{\pm \frac{\pi }{2}},\alpha =\frac{2\pi }{n}.(4)$

In the tubular embryonic mouse lung epithelium, no such systematic n-dependency is observed [18]. Moreover, in planar monolayers and in spherically shaped epithelia, where the principal curvatures change equally, T1L transitions are nonetheless still found [15, 18, 19]. Effects other than tissue curvature must thus dominate in these epithelia.

Determinants of 3D Cell Shape and Neighbour Relationships

The shape of cells in single-layered epithelia can range from a cuboidal to highly elongated columns with large aspect ratio, and apical or basal constriction can further affect the cell shape [20, 21, 54]. In highly elongated cells, the diameter of a spherical nucleus would be larger than the diameter of a cylindrical cell. Accordingly, both the cells and the nuclei deform [55]. The cell is wider where the nucleus is present, and the remaining part of the cell is necessarily much thinner (Figure 1G). At the apical and basal limits of the nucleus, there is a sharp change in the cell cross-sectional areas, and most changes in neighbour relationships are found in this transition zone (Figure 1H). Epithelia with an average cell diameter smaller than the maximal nuclear diameter can thus be expected to have many more neighbour changes than those with wider cells.

Given the narrow columnar shape, there is insufficient space to accommodate all nuclei simultaneously in the same plane. Accordingly, the nuclei of neighbouring cells are found at different positions along the apical-basal axis (Figures 1A,G) [18], a configuration referred to as pseudostratification [27]. As mitosis is restricted to the apical side [27, 56], nuclei actively move towards the apical side during the G2 phase, and are pushed towards the basal side as the cell exits mitosis, in a process called interkinetic nuclear migration (IKNM) [55, 57, 58]. As the nuclei translocate between the apical and basal side during the cell cycle, the cell cross-sectional areas and connectivities continuously change (Figure 1K). An increase in the cross-sectional area increases the chance of a neighbour increase and vice versa (Figure 1I). Neighbour changes are less frequent close to the basal surface of tube segments, where cells remain wider throughout the cell cycle, but are otherwise uniformly distributed along the apical-basal axis [18]. Consistent with a stochastic basis to the 3D organisation of epithelial cells, the number of T1L per cell is Poisson-distributed [18].

But why would epithelial cells adopt such an elongated cell shape? Independent of the increased number of dynamically changing cell contacts, a smaller cell diameter can increase the precision of morphogen-based patterning [30]. Interestingly, several diffusible morphogens and growth factors, including Fibroblastic Growth Factor (FGF), Sonic Hedgehog (SHH), Bone Morphogenetic Protein (BMP)/transforming growth factor-beta (TGF-β), and WNT, have been observed to affect cell height, presumably via an effect on cell tension and/or cell-cell adhesion [59–65]. Epithelial pseudostratification may thus have evolved to enable higher developmental patterning precision.

Discussion: Towards 3D Cell-Based Tissue Simulations of Epithelial Dynamics

As the complex, dynamic 3D organisation of cells in growing epithelia is governed by simple physical concepts, computer simulations present powerful tools to understand the emergent properties of epithelia [66], including IKNM and its effects [67–71]. Cellular Potts models, which represent a generalisation of the Ising model to cells, have long been used to simulate complex 3D cell shapes [72–74]. Vertex models have been developed to specifically represent epithelia in 3D, but without resolving the complex irregular shapes of epithelial cells [64, 75–77]. In 2D, several vertex-based models with higher cell boundary resolution have been developed to enable more complex cell shapes [78–82], and to represent individual cell boundaries and the interstitial volume [83–86]. A recent hybrid version between a spheroid and a vertex model allows for a 3D vertex model with an intermediate vertex that enables a neighbour transition along the apical-basal axis [87]. To make full use of the available 3D imaging data, efficient, high-resolution vertex-based simulation frameworks are now required. A first such simulation framework that represents cells by individual, deformable meshes has recently been developed [88, 89]. In combination with quantitative 3D imaging data, this now paves the way to a more detailed understanding of epithelial cell dynamics in development and disease. Vice versa, cell shape data can be used to infer force fields and to predict bias in cell division as cells divide perpendicular to the longest axis of their apical surface [41, 90–94]. With such tools at hand, it may become feasible to address open questions regarding the maintenance and loss of epithelial integrity and cell polarity, for instance in tumour growth and mesenchymal-to-epithelial transitions.

Data Availability Statement

Publicly available datasets were analyzed in this study. The data is available via openBIS: https://openbis-data-repo.ethz.ch/openbis/webapp/eln-lims/?user=observer&pass=openbis as dataset 2021_Gomez_3D_Cell_Neighbour_Dynamics.

Author Contributions

DI and RV wrote the review, RV generated the figures.

Funding

This work was funded by SNF Sinergia grant CRSII5_70930. Open access funding provided by ETH Zürich.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Harold F. Gómez, and Steve Runser for assistance in creating Figures 1F, 2A, respectively.

References

1. Hinck L, Näthke I. Changes in Cell and Tissue Organization in Cancer of the Breast and colon. Curr Opin Cel Biol (2014) 26:87–95. doi:10.1016/j.ceb.2013.11.003

CrossRef Full Text | Google Scholar

2. Shin K, Margolis B. ZOning Out Tight Junctions. Cell (2006) 126:647–9. doi:10.1016/j.cell.2006.08.005

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Drubin DG, Nelson WJ. Origins of Cell Polarity. Cell (1996) 84:335–44. doi:10.1016/s0092-8674(00)81278-7

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Rodriguez-Boulan E, Macara IG. Organization and Execution of the Epithelial Polarity Programme. Nat Rev Mol Cel Biol (2014) 15:225–42. doi:10.1038/nrm3775

CrossRef Full Text | Google Scholar

5. Walma DAC, Yamada KM: The extracellular matrix in development. Development. (2020) 147:dev175596.doi:10.1242/dev.175596

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Lewis FT. The Correlation between Cell Division and the Shapes and Sizes of Prismatic Cells in the Epidermis of Cucumis. Anat Rec (1928) 38:341–76. doi:10.1002/ar.1090380305

CrossRef Full Text | Google Scholar

7. Classen A-K, Anderson KI, Marois E, Eaton S. Hexagonal Packing of Drosophila wing Epithelial Cells by the Planar Cell Polarity Pathway. Develop Cel (2005) 9:805–17. doi:10.1016/j.devcel.2005.10.016

CrossRef Full Text | Google Scholar

8. Escudero LM, da F. Costa L, Kicheva A, Briscoe J, Freeman M, Babu MM. Epithelial Organisation Revealed by a Network of Cellular Contacts. Nat Commun (2011) 2:526. doi:10.1038/ncomms1536

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Farhadifar R, Röper J-C, Aigouy B, Eaton S, Jülicher F. The Influence of Cell Mechanics, Cell-Cell Interactions, and Proliferation on Epithelial Packing. Curr Biol (2007) 17:2095–104. doi:10.1016/j.cub.2007.11.049

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Gibson MC, Patel AB, Nagpal R, Perrimon N. The Emergence of Geometric Order in Proliferating Metazoan Epithelia. Nature (2006) 442:1038–41. doi:10.1038/nature05014

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Heller D, Hoppe A, Restrepo S, Gatti L, Tournier AL, Tapon N, et al. EpiTools: An Open-Source Image Analysis Toolkit for Quantifying Epithelial Growth Dynamics. Develop Cel (2016) 36:103–16. doi:10.1016/j.devcel.2015.12.012

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Etournay R, Popović M, Merkel M, Nandi A, Blasse C, Aigouy B, et al. Interplay of Cell Dynamics and Epithelial Tension during Morphogenesis of the Drosophila Pupal wing. Elife (2015) 4:e07090. doi:10.7554/eLife.07090

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Sánchez-Gutiérrez D, Tozluoglu M, Barry JD, Pascual A, Mao Y, Escudero LM. Fundamental Physical Cellular Constraints Drive Self-Organization of Tissues. EMBO J (2016) 35:77–88. doi:10.15252/embj.201592374

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Kokic M, Iannini A, Villa Fombuena G, Casares F, Iber D. Minimisation of Surface Energy Drives Apical Epithelial Organisation and Gives Rise to Lewis' Law. bioRxiv (2019). doi:10.1101/590729

CrossRef Full Text | Google Scholar

15. Gómez-Gálvez P, Vicente-Munuera P, Tagua A, Forja C, Castro AM, Letrán M, et al. Scutoids Are a Geometrical Solution to Three-Dimensional Packing of Epithelia. Nat Commun (2018) 9:2960. doi:10.1038/s41467-018-05376-1

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Ramanathan SP, Krajnc M, Gibson MC. Cell-Size Pleomorphism Drives Aberrant Clone Dispersal in Proliferating Epithelia. Develop Cel (2019) 51:49–61. doi:10.1016/j.devcel.2019.08.005

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Rupprecht J-F, Ong KH, Yin J, Huang A, Dinh H-H -Q, Singh AP, et al. Geometric Constraints Alter Cell Arrangements within Curved Epithelial Tissues. MBoC (2017) 28:3582–94. doi:10.1091/mbc.e17-01-0060

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Gómez HF, Dumond MS, Hodel L, Vetter R, Iber D. 3D Cell Neighbour Dynamics in Growing Pseudostratified Epithelia. Elife (2021) 10. doi:10.7554/eLife.68135

CrossRef Full Text | Google Scholar

19. Condic ML, Fristrom D, Fristrom JW. Apical Cell Shape Changes during Drosophila Imaginal Leg Disc Elongation: a Novel Morphogenetic Mechanism. Development (1991) 111:23–33. doi:10.1242/dev.111.1.23

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Krueger D, Tardivo P, Nguyen C, De Renzis S. Downregulation of Basal Myosin-II Is Required for Cell Shape Changes and Tissue Invagination. EMBO J (2018) 37. doi:10.15252/embj.2018100170

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Gelbart MA, He B, Martin AC, Thiberge SY, Wieschaus EF, Kaschube M. Volume Conservation Principle Involved in Cell Lengthening and Nucleus Movement during Tissue Morphogenesis. Proc Natl Acad Sci U.S.A (2012) 109:19298–303. doi:10.1073/pnas.1205258109

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Yokouchi M, Atsugi T, Logtestijn MV, Tanaka RJ, Kajimura M, Suematsu M, et al. Epidermal Cell Turnover across Tight Junctions Based on Kelvin's Tetrakaidecahedron Cell Shape. Elife (2016) 5. doi:10.7554/eLife.19593

CrossRef Full Text | Google Scholar

23. Sun Z, Amourda C, Shagirov M, Hara Y, Saunders TE, Toyama Y. Basolateral Protrusion and Apical Contraction Cooperatively Drive Drosophila Germ-Band Extension. Nat Cel Biol (2017) 19:375–83. doi:10.1038/ncb3497

CrossRef Full Text | Google Scholar

24. Cao J, Guan G, Ho VWS, Wong M-K, Chan L-Y, Tang C, et al. Establishment of a Morphological Atlas of the Caenorhabditis elegans Embryo Using Deep-Learning-Based 4D Segmentation. Nat Commun (2020) 11:6254. doi:10.1038/s41467-020-19863-x

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Guignard L, Fiúza UM, Leggio B, Laussu J, Faure E, Michelin G, et al. Contact Area-dependent Cell Communication and the Morphological Invariance of Ascidian Embryogenesis. Science (2020) 369:369. doi:10.1126/science.aar5663

CrossRef Full Text | Google Scholar

26. Gómez-Gálvez P, Vicente-Munuera P, Anbari S, Buceta J, Escudero LM. The Complex Three-Dimensional Organization of Epithelial Tissues. Development (2021) 148:148. doi:10.1242/dev.195669

CrossRef Full Text | Google Scholar

27. Norden C. Pseudostratified Epithelia - Cell Biology, Diversity and Roles in Organ Formation at a Glance. J Cel Sci (2017) 130:1859–63. doi:10.1242/jcs.192997

CrossRef Full Text | Google Scholar

28. Weaire D, Rivier N. Soap, Cells and Statistics-Random Patterns in Two Dimensions. Contemp Phys (1984) 25:59–99. doi:10.1080/00107518408210979

CrossRef Full Text | Google Scholar

29. Harding MJ, McGraw HF, Nechiporuk A. The Roles and Regulation of Multicellular Rosette Structures during Morphogenesis. Development (2014) 141:2549–2558. doi:10.1242/dev.101444

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Adelmann JA, Vetter R, Iber D. Impact of Cell Size on Morphogen Gradient Precision. bioRxiv (2022). doi:10.1101/2022.02.02.478800

CrossRef Full Text | Google Scholar

31. Hadjivasiliou Z, Hunter GL, Baum B. A New Mechanism for Spatial Pattern Formation via Lateral and Protrusion-Mediated Lateral Signalling. J R Soc Interf (2016) 13. doi:10.1098/rsif.2016.0484

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Cohen M, Georgiou M, Stevenson NL, Miodownik M, Baum B. Dynamic Filopodia Transmit Intermittent Delta-Notch Signaling to Drive Pattern Refinement during Lateral Inhibition. Develop Cel (2010) 19:78–89. doi:10.1016/j.devcel.2010.06.006

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Kornberg TB. Distributing Signaling Proteins in Space and Time: the Province of Cytonemes. Curr Opin Genet Develop (2017) 45:22–7. doi:10.1016/j.gde.2017.02.010

CrossRef Full Text | Google Scholar

34. Curran S, Strandkvist C, Bathmann J, de Gennes M, Kabla A, Salbreux G, et al. Myosin II Controls Junction Fluctuations to Guide Epithelial Tissue Ordering. Develop Cel (2017) 43:480–92. doi:10.1016/j.devcel.2017.09.018

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Weaire D, Phelan R. A Counter-example to Kelvin's Conjecture on Minimal Surfaces. Phil Mag Lett (1994) 69:107–10. doi:10.1080/09500839408241577

CrossRef Full Text | Google Scholar

36. Rivier N, Lissowski A. On the Correlation between Sizes and Shapes of Cells in Epithelial Mosaics. J Phys A: Math Gen (1982) 15:L143–L148. doi:10.1088/0305-4470/15/3/012

CrossRef Full Text | Google Scholar

37. Aboav DA. The Arrangement of Grains in a Polycrystal. Metallography (1970) 3:383–390. doi:10.1016/0026-0800(70)90038-8

CrossRef Full Text | Google Scholar

38. Vetter R, Kokic M, Gomez H, Hodel L, Gjeta B, Iannini A, et al. Aboave-Weaire's Law in Epithelia Results from an Angle Constraint in Contiguous Polygonal Lattices. bioRxiv (2019). doi:10.1101/591461

CrossRef Full Text | Google Scholar

39. Chiu SN. A Comment on Rivier's Maximum Entropy Method of Statistical Crystallography. J Phys A: Math Gen (1995) 28:607–15. doi:10.1088/0305-4470/28/3/015

CrossRef Full Text | Google Scholar

40. Chiu SN. Aboav-Weaire's and Lewis' Laws-A Review. Mater Characterization (1995) 34:149–65. doi:10.1016/1044-5803(94)00081-u

CrossRef Full Text | Google Scholar

41. Gibson WT, Veldhuis JH, Rubinstein B, Cartwright HN, Perrimon N, Brodland GW, et al. Control of the Mitotic Cleavage Plane by Local Epithelial Topology. Cell (2011) 144:427–38. doi:10.1016/j.cell.2010.12.035

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Naveed H, Li Y, Kachalo S, Liang J. Geometric Order in Proliferating Epithelia: Impact of Rearrangements and Cleavage Plane Orientation. Annu Int Conf IEEE Eng Med Biol Soc (2010) 2010:3808–11. doi:10.1109/IEMBS.2010.5627601

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Aegerter-Wilmsen T, Smith AC, Christen AJ, Aegerter CM, Hafen E, Basler K. Exploring the Effects of Mechanical Feedback on Epithelial Topology. Development (2010) 137:499–506. doi:10.1242/dev.041731

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Sahlin P, Jönsson H. A Modeling Study on How Cell Division Affects Properties of Epithelial Tissues under Isotropic Growth. PLoS One (2010) 5:e11750. doi:10.1371/journal.pone.0011750

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Tanaka S, Sichau D, Iber D. LBIBCell: a Cell-Based Simulation Environment for Morphogenetic Problems. Bioinformatics (2015). doi:10.1093/bioinformatics/btv147

CrossRef Full Text | Google Scholar

46. Conrad L, Runser SVM, Fernando Gómez H, Lang CM, Dumond MS, Sapala A, et al. The Biomechanical Basis of Biased Epithelial Tube Elongation in Lung and Kidney Development. Development (2021) 148:148. doi:10.1242/dev.194209

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Zhu HX, Thorpe SM, Windle AH. The Geometrical Properties of Irregular Two-Dimensional Voronoi Tessellations. Philosophical Mag A (2001) 81:2765–83. doi:10.1080/01418610010032364

CrossRef Full Text | Google Scholar

48. Carthew RW. Pattern Formation in the Drosophila Eye. Curr Opin Genet Develop (2007) 17:309–13. doi:10.1016/j.gde.2007.05.001

CrossRef Full Text | Google Scholar

49. Käfer J, Hayashi T, Marée AFM, Carthew RW, Graner F. Cell Adhesion and Cortex Contractility Determine Cell Patterning in the Drosophila Retina. Proc Natl Acad Sci U.S.A (2007) 104:18549–54. doi:10.1073/pnas.0704235104

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Hilgenfeldt S, Erisken S, Carthew RW. Physical Modeling of Cell Geometric Order in an Epithelial Tissue. Proc Natl Acad Sci U.S.A (2008) 105:907–11. doi:10.1073/pnas.0711077105

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Gallagher KD, Mani M, Carthew RW. Emergence of a Geometric Pattern of Cell Fates from Tissue-Scale Mechanics in the Drosophila Eye. eLife (2022) 11:11. doi:10.7554/eLife.72806

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Carter R, Sánchez-Corrales YE, Hartley M, Grieneisen VA, Marée AFM. Pavement Cells and the Topology Puzzle. Development (2017) 144:4386–97. doi:10.1242/dev.157073

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Sapala A, Runions A, Routier-Kierzkowska AL, Das Gupta M, Hong L, Hofhuis H, et al. Why Plants Make Puzzle Cells, and How Their Shape Emerges. Elife (2018) 7, e32794. doi:10.7554/eLife.32794

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Iber D. The Control of Lung Branching Morphogenesis. In: CTDB: Cellular Networks in Development, Vol. 143. Elsevier[Affolter M Series Editor (2021). p. 205–37. doi:10.1016/bs.ctdb.2021.02.002

CrossRef Full Text | Google Scholar

55. Lele TP, Dickinson RB, Gundersen GG. Mechanical Principles of Nuclear Shaping and Positioning. J Cel Biol (2018) 217:3330–42. doi:10.1083/jcb.201804052

CrossRef Full Text | Google Scholar

56. Gundersen GG, Worman HJ. Nuclear Positioning. Cell (2013) 152:1376–89. doi:10.1016/j.cell.2013.02.031

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Meyer EJ, Ikmi A, Gibson MC. Interkinetic Nuclear Migration Is a Broadly Conserved Feature of Cell Division in Pseudostratified Epithelia. Curr Biol (2011) 21:485–91. doi:10.1016/j.cub.2011.02.002

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Yanakieva I, Erzberger A, Matejčić M, Modes CD, Norden C. Cell and Tissue Morphology Determine Actin-dependent Nuclear Migration Mechanisms in Neuroepithelia. J Cel Biol (2019) 218:3272–89. doi:10.1083/jcb.201901077

CrossRef Full Text | Google Scholar

59. Gritli-Linde A, Bei M, Maas R, Zhang XM, Linde A, McMahon AP. Shh Signaling within the Dental Epithelium Is Necessary for Cell Proliferation, Growth and Polarization. Development (2002) 129:5323–37. doi:10.1242/dev.00100

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Widmann TJ, Dahmann C. Dpp Signaling Promotes the Cuboidal-To-Columnar Shape Transition of Drosophila wing Disc Epithelia by Regulating Rho1. J Cel Sci (2009) 122:1362–73. doi:10.1242/jcs.044271

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Kadzik RS, Cohen ED, Morley MP, Stewart KM, Lu MM, Morrisey EE. Wnt ligand/Frizzled 2 Receptor Signaling Regulates Tube Shape and branch-point Formation in the Lung through Control of Epithelial Cell Shape. Proc Natl Acad Sci U.S.A (2014) 111:12444–9. doi:10.1073/pnas.1406639111

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Kondo T, Hayashi S. Mechanisms of Cell Height Changes that Mediate Epithelial Invagination. Develop Growth Differ (2015) 57:313–323. doi:10.1111/dgd.12224

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Hirashima T, Matsuda M. ERK-mediated Curvature Feedback Regulates Branching Morphogenesis in Lung Epithelial Tissue. bioRxiv (2021). doi:10.1101/2021.07.11.451982

CrossRef Full Text | Google Scholar

64. Bielmeier C, Alt S, Weichselberger V, La Fortezza M, Harz H, Jülicher F, et al. Interface Contractility between Differently Fated Cells Drives Cell Elimination and Cyst Formation. Curr Biol (2016) 26:563–74. doi:10.1016/j.cub.2015.12.063

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Storgel N, Krajnc M, Mrak P, Strus J, Ziherl P. Quantitative Morphology of Epithelial Folds. Biophys J (2016) 110:269–77. doi:10.1016/j.bpj.2015.11.024

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Tanaka S. Simulation Frameworks for Morphogenetic Problems. Computation (2015) 3:197–221. doi:10.3390/computation3020197

CrossRef Full Text | Google Scholar

67. Kosodo Y, Suetsugu T, Suda M, Mimori-Kiyosue Y, Toida K, Baba SA, et al. Regulation of Interkinetic Nuclear Migration by Cell Cycle-Coupled Active and Passive Mechanisms in the Developing Brain. EMBO J (2011) 30:1690–704. doi:10.1038/emboj.2011.81

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Azizi A, Herrmann A, Wan Y, Buse SJ, Keller PJ, Goldstein RE, et al. Nuclear Crowding and Nonlinear Diffusion during Interkinetic Nuclear Migration in the Zebrafish Retina. Elife (2020) 9. doi:10.7554/eLife.58635

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Shinoda T, Nagasaka A, Inoue Y, Higuchi R, Minami Y, Kato K, et al. Elasticity-based Boosting of Neuroepithelial Nucleokinesis via Indirect Energy Transfer from Mother to Daughter. Plos Biol (2018) 16:e2004426. doi:10.1371/journal.pbio.2004426

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Carroll TD, Langlands AJ, Osborne JM, Newton IP, Appleton PL, Näthke I. Interkinetic Nuclear Migration and Basal Tethering Facilitates post-mitotic Daughter Separation in Intestinal Organoids. J Cel Sci (2017) 130:3862–3877. doi:10.1242/jcs.211656

CrossRef Full Text | Google Scholar

71. Guerrero P, Perez-Carrasco R, Zagorski M, Page D, Kicheva A, Briscoe J, et al. Neuronal Differentiation Influences Progenitor Arrangement in the Vertebrate Neuroepithelium. Development (2019) 146. doi:10.1242/dev.176297

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Hirashima T, Rens EG, Merks RMH. Cellular Potts Modeling of Complex Multicellular Behaviors in Tissue Morphogenesis. Develop Growth Differ (2017) 59:329–39. doi:10.1111/dgd.12358

CrossRef Full Text | Google Scholar

73. Starruss J, de Back W, Brusch L, Deutsch A. Morpheus: a User-Friendly Modeling Environment for Multiscale and Multicellular Systems Biology. Bioinformatics (2014) 30:1331–2. doi:10.1093/bioinformatics/btt772

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Swat MH, Thomas GL, Belmonte JM, Shirinifard A, Hmeljak D, Glazier JA. Multi-scale Modeling of Tissues Using CompuCell3D. Methods Cel Biol (2012) 110:325–66. doi:10.1016/b978-0-12-388403-9.00013-8

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Honda H, Tanemura M, Nagai T. A Three-Dimensional Vertex Dynamics Cell Model of Space-Filling Polyhedra Simulating Cell Behavior in a Cell Aggregate. J Theor Biol (2004) 226:439–53. doi:10.1016/j.jtbi.2003.10.001

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Rozman J, Krajnc M, Ziherl P. Collective Cell Mechanics of Epithelial Shells with Organoid-like Morphologies. Nat Commun (2020) 11:3805. doi:10.1038/s41467-020-17535-4

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Rauzi M, Hočevar Brezavšček A, Ziherl P, Leptin M. Physical Models of Mesoderm Invagination in Drosophila Embryo. Biophysical J (2013) 105:3–10. doi:10.1016/j.bpj.2013.05.039

CrossRef Full Text | Google Scholar

78. Palmieri B, Bresler Y, Wirtz D, Grant M. Multiple Scale Model for Cell Migration in Monolayers: Elastic Mismatch between Cells Enhances Motility. Sci Rep (2015) 5:11745. doi:10.1038/srep11745

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Kourouklis AP, Nelson CM. Modeling Branching Morphogenesis Using Materials with Programmable Mechanical Instabilities. Curr Opin Biomed Eng (2018) 6:66–73. doi:10.1016/j.cobme.2018.03.007

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Svoboda D, Necasova T, Tesarova L, Simara P. Tubular Network Formation Process Using 3D Cellular Potts Model. Lecture Notes Comput Sci (2018). doi:10.1007/978-3-030-00536-8_10

CrossRef Full Text | Google Scholar

81. Brown PJ, Green JEF, Binder BJ, Osborne JM. A Rigid Body Framework for Multicellular Modeling. Nat Comput Sci (2021) 1:754–66. doi:10.1038/s43588-021-00154-4

CrossRef Full Text | Google Scholar

82. Kim S, Pochitaloff M, Stooke-Vaughan GA, Campàs O. Embryonic Tissues as Active Foams. Nat Phys (2021) 17:859–66. doi:10.1038/s41567-021-01215-1

PubMed Abstract | CrossRef Full Text | Google Scholar

83. Tanaka S, Sichau D, Iber D. LBIBCell: a Cell-Based Simulation Environment for Morphogenetic Problems. Bioinformatics (2015) 31:2340–2347. doi:10.1093/bioinformatics/btv147

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Conradin R, Coreixas C, Latt J, Chopard B. PalaCell2D: A Framework for Detailed Tissue Morphogenesis. J Comput Sci (2021) 53. doi:10.1016/j.jocs.2021.101353

CrossRef Full Text | Google Scholar

85. Boromand A, Signoriello A, Lowensohn J, Orellana CS, Weeks ER, Ye F, et al. The Role of Deformability in Determining the Structural and Mechanical Properties of Bubbles and Emulsions. Soft Matter (2019) 15:5854–65. doi:10.1039/c9sm00775j

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Boromand A, Signoriello A, Ye F, O’Hern CS, Shattuck MD, Jamming of Deformable Polygons. Phys Rev Lett (2018) 121:248003. doi:10.1103/physrevlett.121.248003

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Ioannou F, Dawi MA, Tetley RJ, Mao Y, Muñoz JJ. Development of a New 3D Hybrid Model for Epithelia Morphogenesis. Front Bioeng Biotechnol (2020) 8:405. doi:10.3389/fbioe.2020.00405

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Van Liedekerke P, Neitsch J, Johann T, Warmt E, Gonzàlez-Valverde I, Hoehme S, et al. A Quantitative High-Resolution Computational Mechanics Cell Model for Growing and Regenerating Tissues. Biomech Model Mechanobiol (2020) 19:189–220. doi:10.1007/s10237-019-01204-7

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Hoehme S, Boettger J, Hammad S, Begher-Tibbe B, Bucur P, Vibert E, et al. A Predictive Computational Model Shows that Biomechanical Cell Cycle Progression Control Can Explain Liver Regeneration after Partial Hepatectomy (2021). hal-03136097f.

Google Scholar

90. Hertwig O. Das Problem der Befruchtung und der Isotropie des Eies. Eine Theorie der Vererbung. Jenaische Z Naturwissenschaft (1884) 18:274.

Google Scholar

91. Bosveld F, Markova O, Guirao B, Martin C, Wang Z, Pierre A, et al. : Epithelial Tricellular Junctions Act as Interphase Cell Shape Sensors to orient Mitosis. Nature (2016) 530:495–8. doi:10.1038/nature16970

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Minc N, Burgess D, Chang F. Influence of Cell Geometry on Division-Plane Positioning. Cell (2011) 144:414–426. doi:10.1016/j.cell.2011.01.016

PubMed Abstract | CrossRef Full Text | Google Scholar

93. Tang Z, Hu Y, Wang Z, Jiang K, Zhan C, Marshall WF, et al. Mechanical Forces Program the Orientation of Cell Division during Airway Tube Morphogenesis. Dev Cel (2018). doi:10.1016/j.devcel.2017.12.013

CrossRef Full Text | Google Scholar

94. Roffay C, Chan CJ, Guirao B, Hiiragi T, Graner F. Inferring Cell junction Tension and Pressure from Cell Geometry. Development (2021) 148:148. doi:10.1242/dev.192773

PubMed Abstract | CrossRef Full Text | Google Scholar