Acoustic Radiation Force and Torque Acting on Asymmetric Objects in Acoustic Bessel Beam of Zeroth Order Within Rayleigh Scattering Limit

1 Introduction

Acoustic manipulation of objects depends on their scattering response, when subjected to an external wave field [1–5]. Acoustic radiation force and radiation torque originated from the radiated momentum of the scattered waves, with both being proportional to the products of the scattered and of the incident fields [1, 3, 5–7]. The object-related factors determining these radiation force and torque include the material properties, dimensions, shape asymmetries, internal structure, and absorption capacity [1, 8–10]. Factors related to the surrounding fluid cover the viscosity, its density and compressibility, boundary conditions and the character of the wave front. Among these factors, the theoretical relation between shape asymmetry and wave front of the incident acoustic field is yet to be investigated.

Acoustic radiation force and torque applied to objects with axisymmetric geometries such as spheres, spheroids, Cassini ovals (red blood cell shape model) and others have been extensively investigated for travelling and standing plane waves, which are 1D propagating waves [1, 2, 5, 10, 12–15]. Analytical expressions of the force and torque were derived for such geometries using the partial-wave expansion method [7–9, 16–22]. The same analytical approach was used to study the radiation force and torque acting on axisymmetric objects due to acoustic Bessel beams of zeroth and first orders [11, 23–31]. Acoustic Bessel beams are of the 2D type of wave propagation, with an axisymmetric wave front that is characterised by an axis and a cone angle β, which indicates how much of wave propagation is along and normal to the beam axis, as shown in Figure 1A. Compared to the travelling plane waves, spherical objects of certain sizes can experience a pull radiation force in the opposite direction of the wave propagation, when positioned on the beam axis [30, 32]. For off-axis positions, the acoustic radiation force acts in the axial and transverse directions of the beam and there is an additional torque applied to the objects [25, 28]. These effects are examples of demonstrating the potential of controlling the acoustic manipulation of objects by changing the incident wave front.

FIGURE 1

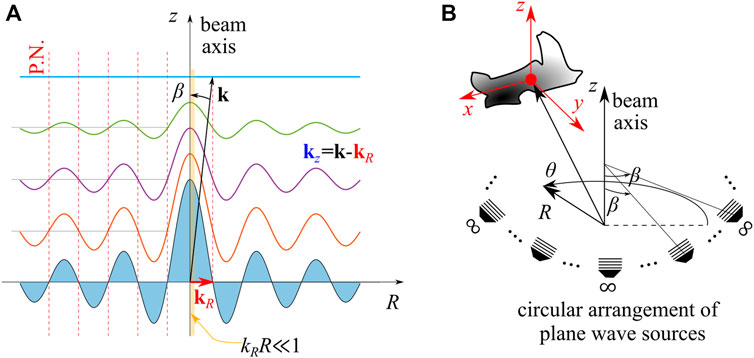
FIGURE 1. Acoustic Bessel beam of zeroth order in cylindrical coordinate system with beam axis aligned with the z-axis, (A) the wave front variation over a half wavelength in the z-direction, showing a travelling wave propagation, (B) the circular arrangement of sources at infinite distance emitting plane waves at angle β with respect to the z-axis to generate a Bessel beam of zeroth order [11]. The cylindrical coordinates (R, θ, z) of the position vector of an object with arbitrary shape located off-axis and the local Cartesian coordinate system are shown. The wave vector k and its components k_R and k_z and their relation with the cone angle β are shown in panel (A). The dotted lines in panel (A) shows the pressure nodes (P.N.) of the Bessel beam, implying a standing wave behaviour in the radial R-direction.

Asymmetry in the shape of an object changes the radiation force and torque applied to them by inducing the Willis coupling between the monopole-dipole scattering response and the incident velocity and pressure fields, respectively [33–35]. For objects within the Rayleigh scattering limit, the shape asymmetry manifests as non-zero coefficients of the polarizability tensor of up to dipole accuracy [5]. Analytical expressions of the radiation force and torque due to the shape asymmetry show the contribution from Willis coupling effects, compared to direct polarizability coefficients that are the diagonal sub-tensors of the polarizability tensor [5]. Since the acoustic polarization tensor is independent of the excitation type, the radiation force and torque of an object with an arbitrary shape in an acoustic Bessel beam of zeroth order can be investigated directly using the generic force and torque equations in Ref. [5].

In this paper, we investigate analytically the effects of a Bessel beam of zeroth order, as an axisymmetric case of non-planar travelling wave, on the acoustic radiation force and torque exerted on a object with arbitrary shape. This type of incident wave has a pressure anti-node on the axis, which can be considered as an approximate model for focused acoustic beams. It is assumed that there is no phase variation across the wavefront; however, the same analytical approach can be used to obtain the radiation force and torque for a vortex-type non-planar beam [36, 37]. The dependence of the radiation force and torque on the location of an object with respect to the beam axis are studied to provide insight about the acoustophoretic response of objects located off-axis. The objects are considered to be much smaller than the wavelength within the Rayleigh limit, and their polarizability tensor up to monopole-dipole approximation is given. Comparing the radiation force and torque induced by Bessel beam against those of the plane travelling wave provides insights about acoustic manipulation of objects with arbitrary shapes using non-planar engineered beams with potential implications for various fields of science and engineering, including the ultrasonic manipulation of biological structures.

2 Theory

The acoustic wave equations derived from the first-order approximation of the Navier-Stokes equations and in the zero viscosity limit are expressed [1, 2], as follows,

${\partial }_{tt}p=c_f^2{\nabla }^{2}p,\nabla p=-{\rho }_f{\partial }_t\mathbf{v},p=c_f^2\rho (1)$

where p, ρ and v denote the acoustic pressure, density and velocity fields, respectively, c_f and ρ_f are the speed of sound and the mean density of the fluid, respectively, ∇ denotes the spatial gradient operator, and ∂_t denotes the differentiation with respect to time t. The acoustic fields are time harmonic, e.g., p(x, t) = p(x)e^−jωt with x being the position vector, ω = 2πf and f denoting the wave frequency. We assume that the object size is within the Rayleigh limit, which is expressed as ka ≪ 1 with k = ω/c_f being the wavenumber and a being the characteristic length of the object.¹ Then, the scattered pressure field of such small object can be approximated by monopole-dipole partial fields [5, 34, 38], as follows,

$p_s\approx -{\omega }^2\mathrm{\Omega }MG+{\omega }^2\nabla \cdot \left[\mathrm{\Omega }\mathbf{D}G\right],G=\frac{e^{jkr}}{4\pi r}{e}^{-j\omega t},(2)$

where M and D are the volumetric monopole and dipole moments, Ω is the volume of the object, and G is the free-space Green’s function of the acoustic wave equation, Eq. 1. By employing the acoustic polarizability, the scattering moments M and D can be expressed in terms of the incident pressure and velocity fields [5], as follows,

$\begin{array}{ll}\hfill & \left[\begin{array}{c}\hfill M\hfill \\ \hfill \mathbf{D}\hfill \end{array}\right]=\widehat{\mathit{\alpha }}\left[\begin{array}{c}\hfill p_i\hfill \\ \hfill {\mathbf{v}}_i\hfill \end{array}\right],\widehat{\mathit{\alpha }}=\frac{1}{\mathrm{\Omega }}\left(\begin{array}{cc}\hfill {\widehat{\alpha }}_{pp}\hfill & \hfill {\widehat{\mathit{\alpha }}}_{pv}^T\hfill \\ \hfill {\widehat{\mathit{\alpha }}}_{vp}\hfill & \hfill {\widehat{\mathit{\alpha }}}_{vv}\hfill \end{array}\right),\hfill \\ \hfill {\widehat{\mathit{\alpha }}}_{pv}=& \left[\begin{array}{c}\hfill {\alpha }_{pv}^x\hfill \\ \hfill {\alpha }_{pv}^y\hfill \\ \hfill {\alpha }_{pv}^z\hfill \end{array}\right],{\widehat{\mathit{\alpha }}}_{vp}=\left[\begin{array}{c}\hfill {\alpha }_{vp}^x\hfill \\ \hfill {\alpha }_{vp}^y\hfill \\ \hfill {\alpha }_{vp}^z\hfill \end{array}\right],{\widehat{\mathit{\alpha }}}_{vv}=\left(\begin{array}{ccc}\hfill {\alpha }_{vv}^{xx}\hfill & \hfill {\alpha }_{vv}^{xy}\hfill & \hfill {\alpha }_{vv}^{xz}\hfill \\ \hfill {\alpha }_{vv}^{yx}\hfill & \hfill {\alpha }_{vv}^{yy}\hfill & \hfill {\alpha }_{vv}^{yz}\hfill \\ \hfill {\alpha }_{vv}^{zx}\hfill & \hfill {\alpha }_{vv}^{zy}\hfill & \hfill {\alpha }_{vv}^{zz}\hfill \end{array}\right),\hfill \end{array}(3)$

where $\widehat{\mathit{\alpha }}$ denotes the polarizability tensor, ${\widehat{\mathit{\alpha }}}_{pv}$ and ${\widehat{\mathit{\alpha }}}_{vp}$ are the Willis coupling coefficients, associated with the object’s shape asymmetry, while ${\widehat{\alpha }}_{pp}$ and ${\widehat{\mathit{\alpha }}}_{vv}$ are the direct polarization coefficients. The polarizability tensor is independent of the incident fields, neglecting non-linear scattering response or fluid properties, and describes the object’s scattering response as a function of its geometry, material properties, absorption and dissipation mechanisms within the fluid. A Cartesian description of these sub-tensors with respect to the coordinate system attached to the object, denoted by the hat ( ˆ ), is provided in Eq. 3. Considering the tensor properties under translation and rotation [22], the description of α in cylindrical coordinates, shown in Figure 1B, becomes

$\mathit{\alpha }=\left(\begin{array}{cc}\hfill {\widehat{\alpha }}_{pp}\hfill & \hfill {\widehat{\mathit{\alpha }}}_{pv}^T{\mathbf{R}}^T\hfill \\ \hfill \mathbf{R}{\widehat{\mathit{\alpha }}}_{vp}\hfill & \hfill \mathbf{R}{\widehat{\mathit{\alpha }}}_{vv}{\mathbf{R}}^T\hfill \end{array}\right),\mathbf{R}=\left(\begin{array}{ccc}\hfill {\mathbf{e}}_x\cdot {\mathbf{e}}_R\hfill & \hfill {\mathbf{e}}_y\cdot {\mathbf{e}}_R\hfill & \hfill 0\hfill \\ \hfill {\mathbf{e}}_x\cdot {\mathbf{e}}_{\theta }\hfill & \hfill {\mathbf{e}}_y\cdot {\mathbf{e}}_{\theta }\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right),(4)$

where R is the rotation tensor from the local Cartesian coordinates to the global cylindrical coordinates, and e denotes the unit basis vector in the direction indicated by its subscript. For the case of a sphere, the Willis coupling coefficients are zero and ${\widehat{\mathit{\alpha }}}_{vv}={\widehat{\alpha }}_{vv}\mathbf{I}$, with I denoting the identity tensor. For axisymmetric objects with a plane symmetry in the axis direction, e.g., prolate and oblate spheroids, Cassini ovals etc. [10], the Willis coupling coefficients become zero too, ${\alpha }_{vv}^{xx}={\alpha }_{vv}^{xx}\ne {\alpha }_{vv}^{zz}$, assuming the axis of symmetry is in the z-direction, and ${\alpha }_{vv}^{xy}={\alpha }_{vv}^{yx}={\alpha }_{vv}^{xz}={\alpha }_{vv}^{zx}={\alpha }_{vv}^{yz}={\alpha }_{vv}^{zy}=0$. In this study, we consider an object with arbitrary shape such that all the polarizability coefficients in Eq. 3 are non-zero, to provide a general formulation of acoustic radiation force and torque due to Bessel beams. Although we assume that the acoustic polarizability tensor is given, it can be obtained for objects with arbitrary shapes computationally using Boundary Element method [5, 39, 40], or Finite Element method [33, 41]. Here, we consider the zeroth order Bessel beam to derive the analytical expressions; however, the same formalism can be applied to Bessel beams of higher orders, or other non-planar beams regardless of the phase variation across the wavefront.

2.1 Acoustic Bessel Beam of Zeroth Order

The pressure field of an acoustic Bessel beam of zeroth order is expressed [11], as follows,

$p_i=A{J}_0{e}^{j{k}_{z}z}{e}^{-j\omega t},J_0=J_0\left(k_{R}R\right),R=\sqrt{x^2+y^2}(5)$

where J₀ denotes the regular Bessel function of zeroth order, and A is the magnitude of the wave. According to the representation of a Bessel beam using Durnin rings [42, 43],

$J_0\left(k_{R}R\right)=\frac{1}{2\pi }{\int }_0^{2\pi }{e}^{j\left(k_{R}x\cos \phi +k_{R}y\cos \phi \right)}d\phi ,(6)$

this type of incident beam can be generated from the superposition of plane travelling waves coming towards a given axis at an incidence angle of β, as illustrated in Figure 1B. The Bessel beam is of the travelling type along the beam axis, i.e., z-direction, while fixed pressure and velocity nodes are (standing wave profile) along the R-direction. This special acoustic beam is axisymmetric, which implies the same acoustic pressure for points that are at the same radius from the axis and ∂_θp = 0. The pressure nodes are indicated in Figure 1A, and a zone in the vicinity of the beam axis is shaded as a region of interest for investigating the radiation force and torque exerted off-axis objects. The velocity field of this Bessel beam and its spatial derivatives are as in the following,

$\begin{array}{l}\hfill \begin{array}{cc}\hfill \nabla p_i\cdot {\mathbf{e}}_z=& jAk\cos \beta J_0{e}^{j{k}_{z}z}{e}^{-j\omega t},\nabla p_i\cdot {\mathbf{e}}_R=-Ak\sin \beta J_1{e}^{j{k}_{z}z}{e}^{-j\omega t},\hfill \\ \hfill {\mathbf{v}}_i\cdot {\mathbf{e}}_z=& \frac{A}{{\rho }_f{c}_f}\cos \beta J_0{e}^{j{k}_{z}z}{e}^{-j\omega t},{\mathbf{v}}_i\cdot {\mathbf{e}}_R=\frac{jA}{{\rho }_f{c}_f}\sin \beta J_1{e}^{j{k}_{z}z}{e}^{-j\omega t},\hfill \\ \hfill \nabla {\mathbf{v}}_i:{\mathbf{e}}_z{\mathbf{e}}_z=& \frac{jAk}{{\rho }_f{c}_f}{\cos }^2\beta J_0{e}^{j{k}_{z}z}{e}^{-j\omega t},\nabla {\mathbf{v}}_i:{\mathbf{e}}_R{\mathbf{e}}_R=\frac{jAk}{{\rho }_f{c}_f}{\sin }^2\beta \left(J_0-\frac{J_1}{k_{R}R}\right)e^{j{k}_{z}z}{e}^{-j\omega t},\hfill \\ \hfill & \nabla {\mathbf{v}}_i:{\mathbf{e}}_R{\mathbf{e}}_z=\nabla {\mathbf{v}}_i:{\mathbf{e}}_z{\mathbf{e}}_R=\frac{-Ak}{2{\rho }_f{c}_f}\sin 2\beta J_1{e}^{j{k}_{z}z}{e}^{-j\omega t},\hfill \end{array}\end{array}(7)$

where : operator denotes inner product of two second-order tensors, $\nabla ={\partial }_R{\mathbf{e}}_R+\frac{1}{R}{\partial }_{\theta }{\mathbf{e}}_{\theta }+{\partial }_z{\mathbf{e}}_z$, and the dyadic products of the unit basis vectors are denoted by e_ze_R, e_ze_z, and e_Re_R. From Eq. 7, it can be seen that all the derivative fields are also axisymmetric, i.e., ∇v_i: e_Re_θ = ∇v_i: e_θe_z = ∇v_i: e_θe_θ = v_i ⋅e_θ = ∇p_i ⋅e_θ = 0. These field expressions of the Bessel beam of the zeroth order in Eqs 5, 7 are required to formulate the dependence of the radiation force and torque on cylindrical coordinates (R, θ, z) and cone angle β.

2.2 Acoustic Radiation Force and Torque

Acoustic radiation force and torque are exerted on an object within an incident field as a result of radiation stresses ⟨σ⟩ that can mathematically be expressed as follows,

$\langle \mathit{\sigma }\rangle =-\left[\frac{1}{2}{\kappa }_f\langle p^2\rangle -\frac{1}{2}{\rho }_f\langle v^2\rangle \right]\mathbf{I}-{\rho }_f\langle \mathbf{v}\mathbf{v}\rangle ,(8)$

where ${\kappa }_f=1/{\rho }_f{c}_f^2$ is the mean fluid compressibility, ⟨⟩ operator denotes a time-averaging over one wave period [2]. The first term on the right hand side of Eq. 8 is called radiation pressure that is generated by the radiated momentum of the scattered pressure field, and the second term represents the Reynolds stresses indicating the contribution from the object’s surface oscillations to the radiation momentum [1, 2, 5, 8, 9, 44]. Acoustic radiation force and torque are obtained from radiation stresses ⟨σ⟩, as follows,

$\mathbf{F}={\int }_{\mathrm{\Gamma }}\langle \mathit{\sigma }\rangle ·\mathbf{n}d\mathrm{\Gamma },\mathbf{T}={\int }_{\mathrm{\Gamma }}\mathbf{x}\times \left[\langle \mathit{\sigma }\rangle ·\mathbf{n}\right]d\mathrm{\Gamma },(9)$

where Γ denotes a surface enclosing the object and n is the outward normal vector of Γ surface. By using the far-field approach and integrating the stresses on any fictitious surface enclosing the object [2, 8, 45], the radiation force and torque exerted on an object with arbitrary shape and size in the Rayleigh scattering limit ka ≪ 1 is expressed [5], as follows,

$\begin{array}{l}\begin{array}{c}\mathbf{F}={\mathbf{F}}_d+{\mathbf{F}}_c,\hfill \\ {\mathbf{F}}_d=-{\langle \frac{{\alpha }_{pp}}{2{\rho }_f}\nabla \left[p_i^2\right]+j\omega {\mathit{\alpha }}_{vv}{\mathbf{v}}_i\cdot \nabla {\mathbf{v}}_i⟩}_{r=0},{\mathbf{F}}_c={\langle \frac{1}{{\rho }_f}{\mathit{\alpha }}_{pv}\cdot \left[p_i\nabla {\mathbf{v}}_i-{\mathbf{v}}_i\nabla p_i\right]⟩}_{r=0}.\hfill \\ \hfill \mathbf{T}={\mathbf{T}}_d+{\mathbf{T}}_c,\\ \hfill {\mathbf{T}}_d={⟨j\omega \left[{\mathit{\alpha }}_{vv}{\mathbf{v}}_i\right]\times {\mathbf{v}}_i⟩}_{r=0},{\mathbf{T}}_c={⟨j\omega p_i{\mathit{\alpha }}_{vp}\times {\mathbf{v}}_i⟩}_{r=0},\end{array}\hfill \end{array}(10)$

where d and c subscripts indicate the force and torque associated with direct polarization and Willis coupling, respectively. By substituting Eqs 5, 7 into Eq. 10 and using the reciprocity properties of the polarizability tensor [5, 22, 35, 38, 46], the analytical expressions of the force and torque are obtained, as in the following,

$\begin{array}{c}\hfill {\mathbf{F}}_d\cdot {\mathbf{e}}_z=-\frac{2E_{i}k}{{\rho }_f}\left[\frac{1}{{\kappa }_f}\text{Im}\left({\alpha }_{pp}\right)\cos \beta J_0^2+k{c}_f\text{Re}\left({\alpha }_{vv}^{zz}\right){\cos }^3\beta J_0^2+k{c}_f\text{Re}\left({\alpha }_{vv}^{RR}\right){\sin }^2\beta \cos \beta J_1^2\right],\\ \hfill {\mathbf{F}}_d\cdot {\mathbf{e}}_R=-\frac{2E_{i}k}{{\rho }_f}\left[-\frac{1}{{\kappa }_f}\text{Re}\left({\alpha }_{pp}\right)\sin \beta J_0{J}_1+k{c}_f\text{Re}\left({\alpha }_{vv}^{Rz}\right){\sin }^2\beta \cos \beta \left(J_0^2+J_1^2-\frac{J_0{J}_1}{k_{R}R}\right)\right.+\\ \hfill \left.k{c}_f\text{Im}\left({\alpha }_{vv}^{zz}\right){\cos }^2\beta \sin \beta J_0{J}_1-k{c}_f\text{Im}\left({\alpha }_{vv}^{RR}\right){\sin }^3\beta \left(J_0{J}_1-\frac{J_1^2}{k_{R}R}\right)\right],\end{array}(11)$

$\begin{array}{c}\hfill {\mathbf{F}}_c\cdot {\mathbf{e}}_z=-\frac{2E_{i}k}{{\rho }_f}\left[2c_f\text{Re}\left({\alpha }_{pv}^R\right)\sin \beta \cos \beta J_0{J}_1\right],\\ \hfill {\mathbf{F}}_c\cdot {\mathbf{e}}_R=-\frac{2E_{i}k}{{\rho }_f}\left[c_f\text{Im}\left({\alpha }_{pv}^R\right){\sin }^2\beta \left(J_0^2+J_1^2-\frac{J_0{J}_1}{k_{R}R}\right)\right],\end{array}(12)$

$\begin{array}{c}\hfill {\mathbf{T}}_d\cdot {\mathbf{e}}_z=-\frac{2E_{i}k}{{\rho }_f}\left[-c_f\text{Re}\left({\alpha }_{vv}^{\theta z}\right)\sin \beta \cos \beta J_0{J}_1+c_f\text{Im}\left({\alpha }_{vv}^{\theta R}\right){\sin }^2\beta J_1^2\right],\\ \hfill {\mathbf{T}}_d\cdot {\mathbf{e}}_{\theta }=-\frac{2E_{i}k}{{\rho }_f}\left[c_f\text{Re}\left({\alpha }_{vv}^{zz}\right)\sin \beta \cos \beta J_0{J}_1-c_f\text{Im}\left({\alpha }_{vv}^{zR}\right){\sin }^2\beta J_1^2+\right.\\ \hfill \left.c_f\text{Im}\left({\alpha }_{vv}^{Rz}\right){\cos }^2\beta J_0^2+c_f\text{Re}\left({\alpha }_{vv}^{RR}\right)\sin \beta \cos \beta J_0{J}_1\right],\\ \hfill {\mathbf{T}}_d\cdot {\mathbf{e}}_R=-\frac{2E_{i}k}{{\rho }_f}\left[-c_f\text{Im}\left({\alpha }_{vv}^{\theta z}\right){\cos }^2\beta J_0^2-c_f\text{Re}\left({\alpha }_{vv}^{\theta R}\right)\sin \beta \cos \beta J_0{J}_1\right],\end{array}(13)$

$\begin{array}{c}\hfill {\mathbf{T}}_c\cdot {\mathbf{e}}_z=-\frac{2E_{i}k}{{\rho }_f}\left[-\frac{1}{{\kappa }_f}\text{Re}\left({\alpha }_{vp}^{\theta }\right)\sin \beta J_0{J}_1\right],\\ \hfill {\mathbf{T}}_c\cdot {\mathbf{e}}_{\theta }=-\frac{2E_{i}k}{{\rho }_f}\left[\frac{1}{{\kappa }_f}\text{Re}\left({\alpha }_{vp}^z\right)\sin \beta J_0{J}_1+\frac{1}{{\kappa }_f}\text{Im}\left({\alpha }_{vp}^R\right)\cos \beta J_0^2\right],\\ \hfill {\mathbf{T}}_c\cdot {\mathbf{e}}_R=-\frac{2E_{i}k}{{\rho }_f}\left[\frac{1}{{\kappa }_f}\text{Im}\left({\alpha }_{vp}^{\theta }\right)\cos \beta J_0^2\right],\end{array}(14)$

where $E_i=A^2/4{\rho }_f{c}_f^2$ denotes the energy density of the incident Bessel beam. Both partial forces F_d and F_c have components only in z- and R-directions, which implies objects being pushed or pulled in axial and radial directions in an axisymmetric acoustic field. For the partial torques T_d and T_c, in addition to the component in the θ-direction, there exist two more components the z- and R-plane, which means a full 3D torque is induced by an axisymmetric acoustic field. This is in contrast to the case of a standing, plane wave, where only in-plane torque components are generated [5, 22]. Compared to a plane wave, this torque property of the Bessel beam shows that a 3D rotational manipulation an object with arbitrary shape can be realized even using 2D propagation type, axisymmetric beams. The real and imaginary parts of all polarizability coefficients, from the cylindrical description of the polarizability tensor in Eq. 4, are required to obtain the three components of the radiation torque; while only the z- and R-dependent coefficients are required to calculate both partial forces. This indicates the significance of accounting for the shape of the object to find the radiation force and torque in a Bessel beam of zeroth order.

3 Results

To further investigate the changes of Bessel radiation force and torque, we examine the expressions in Eqs 11–14 in four limit cases of (I) β = 0, i.e., plane travelling wave, (II) β tends to 0 corresponding to radially weak Bessel beam, (III) R = 0 indicating on-axis location of the object’s centroid, and (IV) k_RR ≪ 1, which is the vicinity of the axis, shown by the yellow-shaded strip in Figure 1A. For general off-axis locations, the force and torque should be obtained directly from Eqs 11–14.

3.1 Case I: β = 0 - Travelling Plane Wave

This case corresponds to zero radial variation of the wavefront k_R = 0, which means the Bessel beam degenerates to a travelling plane wave. By substituting sin β = 0, cos β = 1, J₀ = 1, J₁ = 0, and J₁/k_RR ≈ 1/2, the partial radiation forces and torques in Eqs 11–14 become

$\begin{array}{c}\hfill {\mathbf{F}}_d\cdot {\mathbf{e}}_z=-\frac{2E_{i}k}{{\rho }_f}\left[\frac{1}{{\kappa }_f}\text{Im}\left({\alpha }_{pp}\right)+k{c}_f\text{Re}\left({\alpha }_{vv}^{zz}\right)\right],{\mathbf{F}}_d\cdot {\mathbf{e}}_R=0,\end{array}(15)$

$\begin{array}{c}\hfill {\mathbf{F}}_c\cdot {\mathbf{e}}_z=0,{\mathbf{F}}_c\cdot {\mathbf{e}}_R=0,\end{array}(16)$

$\begin{array}{c}\hfill {\mathbf{T}}_d\cdot {\mathbf{e}}_z=0{\mathbf{T}}_d\cdot {\mathbf{e}}_{\theta }=-\frac{2E_{i}k}{{\rho }_f}{c}_f\text{Im}\left({\alpha }_{vv}^{Rz}\right),{\mathbf{T}}_d\cdot {\mathbf{e}}_R=-\frac{2E_{i}k}{{\rho }_f}\left[-c_f\text{Im}\left({\alpha }_{vv}^{\theta z}\right)\right],\end{array}(17)$

$\begin{array}{c}\hfill {\mathbf{T}}_c\cdot {\mathbf{e}}_z=0,{\mathbf{T}}_c\cdot {\mathbf{e}}_{\theta }=-\frac{2E_{i}k}{{\rho }_f}\frac{1}{{\kappa }_f}\text{Im}\left({\alpha }_{vp}^R\right){\mathbf{T}}_c\cdot {\mathbf{e}}_R=-\frac{2E_{i}k}{{\rho }_f}\frac{1}{{\kappa }_f}\text{Im}\left({\alpha }_{vp}^{\theta }\right).\end{array}(18)$

Equations 15–18 are identical to expressions in Eq. [26] of Ref. [5], verifying our formulation of the radiation force and torque under a Bessel beam at the limit case of β = 0. It is also found that Willis coupling effects show zero contribution to the force and only generates torque in the in-plane directions of a travelling plane wave. The forces and torques generated by a travelling plane wave are constant and independent of the location of the objects, meaning that the radiation force and torque fields are uniform and only depend on the polarizability response of the object.

3.2 Case II: β → 0 - Radially Weak Bessel Beam

This case corresponds to the long wavelength limit in the radial R direction, and k_R = k sin β ≈ kβ. This case is of interest since it represents relatively weaker propagation of acoustic energy in the R direction, i.e., the standing wave profile and fixed pressure and velocity nodes. By using the asymptotic approximation of the Bessel function in this limit, i.e., J₀ ≈ 1 and J₁ ≈ k_RR/2, sin β ≈ β, cos β ≈ 1 and β² ≪ β, Eqs 11–14 can be approximated, as follows,

$\begin{array}{c}\hfill {\mathbf{F}}_d\cdot {\mathbf{e}}_z=-\frac{2E_{i}k}{{\rho }_f}\left[\frac{1}{{\kappa }_f}\text{Im}\left({\alpha }_{pp}\right)+k{c}_f\text{Re}\left({\alpha }_{vv}^{zz}\right)\right],\\ \hfill {\mathbf{F}}_d\cdot {\mathbf{e}}_R=-\frac{2E_{i}k}{{\rho }_f}\left[-\frac{k}{2{\kappa }_f}\text{Re}\left({\alpha }_{pp}\right){\beta }^{2}R+\frac{k^2{c}_f}{2}\text{Im}\left({\alpha }_{vv}^{zz}\right){\beta }^{2}R+\frac{k{c}_f}{2}\text{Re}\left({\alpha }_{vv}^{Rz}\right){\beta }^2\right],\end{array}(19)$

$\begin{array}{c}\hfill {\mathbf{F}}_c\cdot {\mathbf{e}}_z=-\frac{2E_{i}k}{{\rho }_f}k{c}_f\text{Re}\left({\alpha }_{pv}^R\right){\beta }^{2}R,\\ \hfill {\mathbf{F}}_c\cdot {\mathbf{e}}_R=-\frac{2E_{i}k}{{\rho }_f}\frac{c_f}{2}\text{Im}\left({\alpha }_{pv}^R\right){\beta }^2,\end{array}(20)$

$\begin{array}{c}\hfill {\mathbf{T}}_d\cdot {\mathbf{e}}_z=-\frac{2E_{i}k}{{\rho }_f}\left[-\frac{k{c}_f}{2}\text{Re}\left({\alpha }_{vv}^{\theta z}\right){\beta }^{2}R\right],\\ \hfill {\mathbf{T}}_d\cdot {\mathbf{e}}_{\theta }=-\frac{2E_{i}k}{{\rho }_f}\left[\frac{k{c}_f}{2}\text{Re}\left({\alpha }_{vv}^{zz}+{\alpha }_{vv}^{RR}\right){\beta }^{2}R+c_f\text{Im}\left({\alpha }_{vv}^{Rz}\right)\right],\\ \hfill {\mathbf{T}}_d\cdot {\mathbf{e}}_R=-\frac{2E_{i}k}{{\rho }_f}\left[-c_f\text{Im}\left({\alpha }_{vv}^{\theta z}\right)-\frac{k{c}_f}{2}\text{Re}\left({\alpha }_{vv}^{\theta R}\right){\beta }^{2}R\right],\end{array}(21)$

$\begin{array}{c}\hfill {\mathbf{T}}_c\cdot {\mathbf{e}}_z=-\frac{2E_{i}k}{{\rho }_f}\left[-\frac{k}{2{\kappa }_f}\text{Re}\left({\alpha }_{vp}^{\theta }\right){\beta }^{2}R\right],\\ \hfill {\mathbf{T}}_c\cdot {\mathbf{e}}_{\theta }=-\frac{2E_{i}k}{{\rho }_f}\left[\frac{k}{2{\kappa }_f}\text{Re}\left({\alpha }_{vp}^z\right){\beta }^{2}R+\text{Im}\left({\alpha }_{vp}^R\right)\right],\\ \hfill {\mathbf{T}}_c\cdot {\mathbf{e}}_R=-\frac{2E_{i}k}{{\rho }_f}\frac{1}{{\kappa }_f}\text{Im}\left({\alpha }_{vp}^{\theta }\right).\end{array}(22)$

For a given cone angle β, we can see from Eqs 19–22 that the radiation force and torque spatially depend only on their radial coordinate R, changing linearly, while these fields are independent of the axial coordinate z, due to the travelling wave nature of propagation in this direction. Compared to the limit case of β = 0, it was found that the additional terms proportional to β² appear in the force and torque expressions T_c ⋅e_R, as result of the weak propagation in the R-direction, except for the radial component of the Willis coupling torque T_c ⋅e_R that remains unchanged. These analytical expressions reveal the sensitivity of the radiation force and torque, both direct and Willis coupling parts, to the change in the wave front that is the weak Bessel-type undulations. This provides β angle as another degree of freedom for manipulation of objects with arbitrary shape, using this type of radially weak Bessel beams.

3.3 Case III: On-Axis Object R = 0

There is a velocity node, corresponding to maximum pressure, on the axis of the zeroth-order Bessel beam. This is of interest since it is a relatively good example of focused acoustic beams that can be produced using a meta-lens [47] or a phased transducer array [48]. When the centroid of an object is located on the beam axis, the expressions of acoustic radiation force and torque in Eqs 11–14 are further simplified, as follows,

$\begin{array}{c}\hfill {\mathbf{F}}_d\cdot {\mathbf{e}}_z=-\frac{2E_{i}k}{{\rho }_f}\left[\frac{1}{{\kappa }_f}\text{Im}\left({\alpha }_{pp}\right)\cos \beta +k{c}_f\text{Re}\left({\alpha }_{vv}^{zz}\right){\cos }^3\beta \right],\\ \hfill {\mathbf{F}}_d\cdot {\mathbf{e}}_R=-\frac{2E_{i}k}{{\rho }_f}\left[\frac{k{c}_f}{2}\text{Re}\left({\alpha }_{vv}^{Rz}\right){\sin }^2\beta \cos \beta \right],\end{array}(23)$

$\begin{array}{c}\hfill {\mathbf{F}}_c\cdot {\mathbf{e}}_z=0\\ \hfill {\mathbf{F}}_c\cdot {\mathbf{e}}_R=-\frac{2E_{i}k}{{\rho }_f}\left[\frac{c_f}{2}\text{Im}\left({\alpha }_{pv}^R\right){\sin }^2\beta \right],\end{array}(24)$

$\begin{array}{c}\hfill {\mathbf{T}}_d\cdot {\mathbf{e}}_z=0\\ \hfill {\mathbf{T}}_d\cdot {\mathbf{e}}_{\theta }=-\frac{2E_{i}k}{{\rho }_f}\left[c_f\text{Im}\left({\alpha }_{vv}^{Rz}\right){\cos }^2\beta \right],\\ \hfill {\mathbf{T}}_d\cdot {\mathbf{e}}_R=-\frac{2E_{i}k}{{\rho }_f}\left[-c_f\text{Im}\left({\alpha }_{vv}^{\theta z}\right){\cos }^2\beta \right],\end{array}(25)$

$\begin{array}{c}\hfill {\mathbf{T}}_c\cdot {\mathbf{e}}_z=0\\ \hfill {\mathbf{T}}_c\cdot {\mathbf{e}}_{\theta }=-\frac{2E_{i}k}{{\rho }_f}\frac{1}{{\kappa }_f}\left[\text{Im}\left({\alpha }_{vp}^R\right)\cos \beta \right],\\ \hfill {\mathbf{T}}_c\cdot {\mathbf{e}}_R=-\frac{2E_{i}k}{{\rho }_f}\frac{1}{{\kappa }_f}\left[\text{Im}\left({\alpha }_{vp}^{\theta }\right)\cos \beta \right].\end{array}(26)$

From Eq. 23, we found that an object on the beam axis is subjected to only an axial force, i.e., in the z-direction as a result of the direct polarization.² Since the range of values of the cone angle is 0 ≤ β < π/2, cos β > 0 and the direction of the axial force is determined from the polarization coefficients, i.e., Im(α_pp) and $\text{Re}({\alpha }_{vv}^{zz})$, implying that some objects can experience pull-in effects from a Bessel beam of zeroth order at the ka ≪ 1 limit. The axial components of the Willis-coupling partial force F_c and both direct and Willis coupling torques T_d and T_c are zero. Equations 25, 26 show that the dependence of the direct and Willis coupling-induced torques on cone angle β are cos²β and cos β, respectively, implying that partial torque fields T_d and T_c are independent of each other and the shape asymmetry needs to be accounted for separately. Similarly, the partial force fields F_d and F_c are independent, as can be seen from Eqs 23, 24. Finally, the most significant contribution of the Willis coupling is the radial component of the radiation force, coming from F_c ⋅e_R, meaning that objects with shape asymmetry are pushed away from the beam axis in the direction that $\text{Im}({\alpha }_{pv}^R)$ is non-zero and maximum, if the radiation torque is accounted for. This depends on the orientation of the objects and its shape asymmetry with respect to the beam axis. For axisymmetric shapes with one degree of asymmetry along the axis of revolution, e.g., shapes of a Helmholtz resonator, unhealthy red blood cells [49], or a meta-atom with controlled Willis coupling [22], this radial force is zero if the axis of symmetry of the object is aligned with the beam axis. It is inferred that, in general, objects tends to be off-axis in such acoustic beams; hence, the axisymmetric wavefront provides the same level of control compared to a 2D arbitrary wavefront.

3.4 Case IV: Object in the Vicinity of the Beam Axis k_RR ≪ 1

We consider this special off-axis case such that k_RR ≪ 1, as shown by the yellow-shaded strip in Figure 1A. This condition applies to long wavelength limit ka ≪ 1, and we assume the radial distance is close to zero (vicinity of beam axis), while 0 ≤ β < π/2. By using the asymptotic approximation of Bessel functions J₀ and J₁, the radiation force and torque in Eqs 11–14 are approximated, as follows,

$\begin{array}{c}\hfill {\mathbf{F}}_d\cdot {\mathbf{e}}_z=-\frac{2E_{i}k}{{\rho }_f}\left[\frac{1}{{\kappa }_f}\text{Im}\left({\alpha }_{pp}\right)\cos \beta +k{c}_f\text{Re}\left({\alpha }_{vv}^{zz}\right){\cos }^3\beta +\frac{k^3{c}_f}{4}\text{Re}\left({\alpha }_{vv}^{RR}\right){\sin }^4\beta \cos \beta R^2\right],\\ \hfill {\mathbf{F}}_d\cdot {\mathbf{e}}_R=-\frac{2E_{i}k}{{\rho }_f}\left[-\frac{k}{2{\kappa }_f}\text{Re}\left({\alpha }_{pp}\right){\sin }^2\beta R+\frac{k^2{c}_f}{2}\text{Im}\left({\alpha }_{vv}^{zz}\right){\cos }^2\beta {\sin }^2\beta R+\right.\\ \hfill \left.\frac{k{c}_f}{2}\text{Re}\left({\alpha }_{vv}^{Rz}\right){\sin }^2\beta \cos \beta \left(1+\frac{k^2}{2}{\sin }^2\beta R^2\right)-\frac{k{c}_f}{4}\text{Im}\left({\alpha }_{vv}^{RR}\right){\sin }^4\beta R\right],\end{array}(27)$

$\begin{array}{c}\hfill {\mathbf{F}}_c\cdot {\mathbf{e}}_z=-\frac{2E_{i}k}{{\rho }_f}\left[k{c}_f\text{Re}\left({\alpha }_{pv}^R\right){\sin }^2\beta \cos \beta R\right],\\ \hfill {\mathbf{F}}_c\cdot {\mathbf{e}}_R=-\frac{2E_{i}k}{{\rho }_f}\left[c_f\text{Im}\left({\alpha }_{pv}^R\right){\sin }^2\beta \left(\frac{1}{2}+\frac{k^2{\sin }^2\beta }{4}{R}^2\right)\right],\\ \hfill {\mathbf{T}}_d\cdot {\mathbf{e}}_z=-\frac{2E_{i}k}{{\rho }_f}\left[-\frac{k{c}_f}{2}\text{Re}\left({\alpha }_{vv}^{\theta z}\right){\sin }^2\beta \cos \beta R+\frac{k^2{c}_f}{4}\text{Im}\left({\alpha }_{vv}^{\theta R}\right){\sin }^4\beta R^2\right],\end{array}(28)$

$\begin{array}{c}\hfill {\mathbf{T}}_d\cdot {\mathbf{e}}_{\theta }=-\frac{2E_{i}k}{{\rho }_f}\left[\frac{k{c}_f}{2}\text{Re}\left({\alpha }_{vv}^{zz}\right){\sin }^2\beta \cos \beta R-\frac{k^2{c}_f}{4}\text{Im}\left({\alpha }_{vv}^{zR}\right){\sin }^4\beta R^2+\right.\\ \hfill \left.c_f\text{Im}\left({\alpha }_{vv}^{Rz}\right){\cos }^2\beta +\frac{k{c}_f}{2}\text{Re}\left({\alpha }_{vv}^{RR}\right){\sin }^2\beta \cos \beta R\right],\\ \hfill {\mathbf{T}}_d\cdot {\mathbf{e}}_R=-\frac{2E_{i}k}{{\rho }_f}\left[-c_f\text{Im}\left({\alpha }_{vv}^{\theta z}\right){\cos }^2\beta -\frac{k{c}_f}{2}\text{Re}\left({\alpha }_{vv}^{\theta R}\right){\sin }^2\beta \cos \beta R\right],\end{array}(29)$

$\begin{array}{c}\hfill {\mathbf{T}}_c\cdot {\mathbf{e}}_z=-\frac{2E_{i}k}{{\rho }_f}\left[-\frac{k}{2{\kappa }_f}\text{Re}\left({\alpha }_{vp}^{\theta }\right){\sin }^2\beta R\right],\\ \hfill {\mathbf{T}}_c\cdot {\mathbf{e}}_{\theta }=-\frac{2E_{i}k}{{\rho }_f}\left[\frac{k}{2{\kappa }_f}\text{Re}\left({\alpha }_{vp}^z\right){\sin }^2\beta R+\text{Im}\left({\alpha }_{vp}^R\right)\cos \beta \right],\\ \hfill {\mathbf{T}}_c\cdot {\mathbf{e}}_R=-\frac{2E_{i}k}{{\rho }_f}\left[\frac{1}{{\kappa }_f}\text{Im}\left({\alpha }_{vp}^{\theta }\right)\cos \beta \right].\end{array}(30)$

From Eq. 30, it was found that the T_c ⋅e_R is constant and independent of the R-coordinate. Other components of the partial radiation force and torques change with the radial coordinate R, e.g., proportional to R and R². There are also some constant terms in F_d ⋅e_z, F_c ⋅e_R, T_d ⋅e_θ, T_d ⋅e_R, T_c ⋅e_θ, and T_c ⋅e_R, which provide the base value of these force and torque fields in the k_RR ≪ 1 region irrespective of the object’s radial location.

3.5 Numerical Analysis

To investigate the influence of non-planar wavefront of the zeroth order Bessel beam on the acoustic radiation force and torque, we consider an object with asymmetric shape such that major asymmetry occurs along the z-direction for θ = 0 and the polarizability coefficients become

$\begin{array}{cc}\hfill \frac{{\alpha }_{pp}}{{\mathrm{\Omega }}_s}=& 7.2\times 10^{-3}+0.0j,{\mathit{\alpha }}_{vp}=\frac{-j}{\omega {\rho }_f}{\mathit{\alpha }}_{pv}\hfill \\ \hfill \frac{{\mathit{\alpha }}_{pv}}{{\alpha }_{pp}}=& \left[\begin{array}{c}\hfill 8.4\times 10^{-4}+7.2\times 10^{-4}j\hfill \\ \hfill 3.4\times 10^{-10}-4.8\times 10^{-5}j\hfill \\ \hfill 0.0,-,7.4\times 10^{-2}j\hfill \end{array}\right],\hfill \\ \hfill \frac{{\mathit{\alpha }}_{vv}}{{\alpha }_{pp}}=& \left(\begin{array}{ccc}\hfill 1.0,\times ,10^{-4}-2.39j\hfill & \hfill 3.6\times 10^{-9}-2.89,\times ,10^{-5}j\hfill & \hfill 0.0,+,1.3\times 10^{-3}j\hfill \\ \hfill \hfill & \hfill 1.0,\times ,10^{-4}-2.39j\hfill & \hfill 5.0,\times ,10^{-8}-2.4\times 10^{-4}j\hfill \\ \hfill \text{Sym.}\hfill & \hfill \hfill & \hfill 1.0,\times ,10^{-4}-2.43j\hfill \end{array}\right).\hfill \end{array}(31)$

where Ω_s denote the volume of the object, and these values satisfy the acoustic energy balance, i.e., they are less than the maximum admissible polarizability [38]. Although these are just examples of the values of polarizability coefficients, they correspond to a sphere of size a with a blind circular hole which leads to the asymmetry along the hole axis [5], i.e., z-direction in this study. The non-zero coefficients with relatively smaller values correspond to the numerical discretization of this object for the calculation of monopole and dipole moments using Boundary Element Method, as outlined in Ref. 5. Nevertheless, these small values indicate the level of asymmetry in x- and y-directions, compared to the intended one in the z-direction.

The ratio of partial forces and torques in cases II to IV against the force and torque of a plane travelling wave, i.e., case I, is considered for comparison. The magnitude of the force and torque for case I are expressed, as follows,

$Q=\sqrt{\left({\mathbf{F}}_d+{\mathbf{F}}_c\right)\cdot \left({\mathbf{F}}_d+{\mathbf{F}}_c\right)},Z=\sqrt{\left({\mathbf{T}}_d+{\mathbf{T}}_c\right)\cdot \left({\mathbf{T}}_d+{\mathbf{T}}_c\right)}.(32)$

First, we investigate the case of weak Bessel beam, i.e., case II and Eqs 19–22, by choosing β = 5°, corresponding to k_R/k ≈ 0.1. The three components of the partial forces and torques are presented in Figure 2, for relatively large range of 0 < k_RR < π.

FIGURE 2

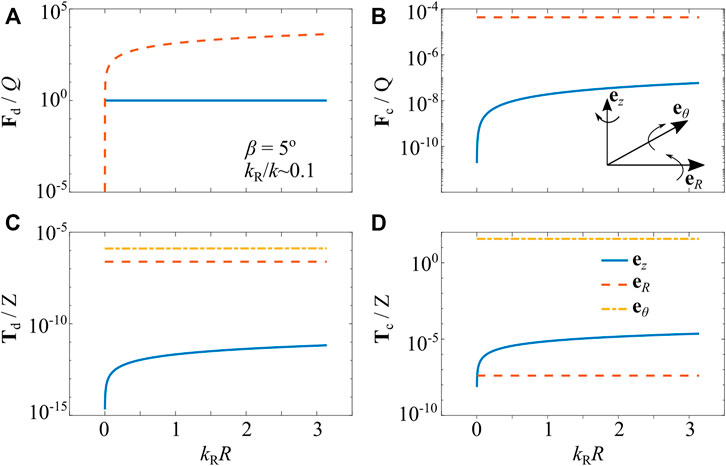
FIGURE 2. Partial forces, panels (A),(B), and torques, panels (C),(D), due to direct and Willis coupling acoustic polarization for a weak Bessel beam of β = 5° and k_R/K ≈ 0.1, with respect to the radial distance from the beam axis at R = 0 for the asymmetric object given by its polarizability coefficients in Eq. 31. The components of the forces and torques in the cylindrical coordinate system (e_R, e_θ, e_z) are shown by different line types. For the forces in panel (A),(B), the θ-component is zero. The magnitude of these forces are shown in the logarithmic scale to indicate the difference in orders of magnitude.

The direct partial force F_d shows a much larger radial component than the axial z-component, which is almost the same as the axial force component of a plane travelling wave, as shown in Figure 2A. Similar differences between components are observed in the Willis-coupling partial force F_c, as shown in Figure 2B; however, the contribution of F_c to the total force is negligible compared to F_d. It is noted that the only non-zero force component for the reference case of a plane travelling wave is the axial component of the direct partial force F_d ⋅e_z. In all cases I to IV, the force component in the θ-direction is always zero due to the axisymmetric wavefront of the Bessel beam. Comparing the partial torques in Figures 2C,D, we observed that the component in the θ-direction is the largest and the Willis coupling contribution is much larger than the direct partial torque. The R-component of the partial torques is of the same of order of magnitude, but the z- and θ-components of Willis coupling torque T_c are much larger than those of T_d. The force and torque components changes almost linearly with respect to the radial R-coordinate, except for R → 0 corresponding to region in the vicinity of the beam axis, i.e., R = 0. These results indicate that the effects of asymmetry of the object’s shape manifest as a relatively large torque component in the θ-direction, for Bessel beam of small β angle representing a weak non-planar travelling wave.

Next, the case of objects at the vicinity of the beam axis, i.e., case IV, is shown in Figure 3. The same object with polarizability tensor given in Eq. 31 is placed one radius a away from the beam axis, i.e., R/a = 1 corresponding to kR ≈ 0.03. The force and torque results are shown for cone angle β in the range of 0–90°. As shown in Figure 3A, the direct partial force F_d has a larger component in the radial R-direction. The component in the z-direction undergoes a sign reversal at β ≈ 78°, from opposite (pull) to same (push) as the wave propagation direction along the z-axis. The Willis coupling partial force F_c, shown in Figure 3B, is smaller than the F_d by several orders of magnitude and can be neglected. Comparing the partial torques T_d and T_c, shown in Figures 3C,D, respectively, it is observed that the asymmetry in shape results in relatively larger torque components in the θ-direction, and the magnitude increases as the cone angle β approaches π/2, corresponding to the limit of zero axial propagation. Finally, the significant difference between the magnitudes of the force and torque components correspond to the values of the polarizability coefficients for this study, which comes from a discretized geometry of a sphere with a blind circular hole. Nevertheless, they can be considered as an indication of the force and torque acting upon an object with asymmetric shape from several directions. Finally, our results show that the cone angle β can be used as a design parameter for axial manipulation using zeroth order Bessel beam.

FIGURE 3

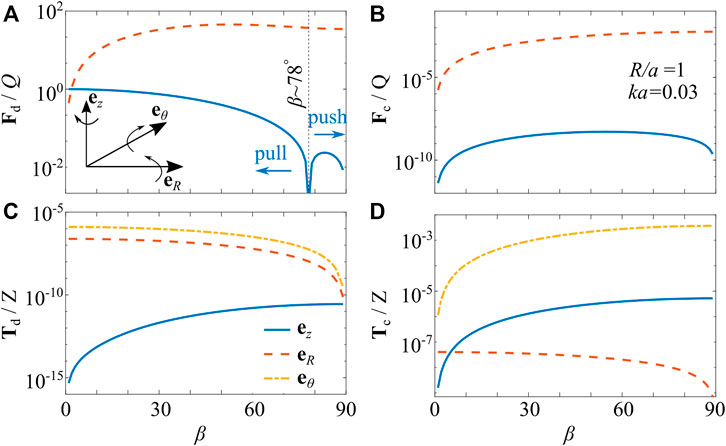
FIGURE 3. Partial forces, panels (A),(B), and torques, panels (C),(D), due to direct and Willis coupling acoustic polarization in the vicinity of the beam axis at R/a = 1 with a being the nominal radius of the asymmetric object given by its polarizability coefficients in Eq. 31. The results are shown for the entire range of 0 < β < 90° to demonstrate the effects of wave front deviating further from a plane (β = 0) on an asymmetric object of small size ka ≈ 0.03. The components of the forces and torques in the cylindrical coordinate system (e_R, e_θ, e_z) are shown by different line types. For the forces in panel (A),(B), the θ-component is zero. The magnitude of these forces are shown in the logarithmic scale to indicate the difference of orders of magnitude.

4 Conclusion

Acoustic radiation force and torque on objects with arbitrary shape were obtained by applying an acoustic Bessel beam of zeroth order, which has a pressure anti-node on the beam axis and fixed pressure nodes along the radial direction, as an estimate model of engineered non-planar beams using acoustic focusing techniques. To investigate the effects of this non-planar wavefront, analytical expressions of the radiation force and torque were derived by using the far-field approach, employing the polarizability concept, by remaining under the assumption of having a lossless fluid for sub-wavelength objects in the Rayleigh scattering limit. These expressions were verified by comparing against those for plane travelling waves in the limit case of zero cone angle β, which is a measure of energy propagation in the axial and radial directions. For cases of weak radial field, i.e., β tends to zero, it was found that additional terms proportional to β² emerges, compare to the case of a plane travelling wave, which implies the contribution from the weak radial field. We also showed that an asymmetric object located initially on the beam axis is pushed away from the axis due to the contribution of the Willis coupling partial force. Furthermore, an object located on the axis, where pressure is maximum, can experience a pull-in effect for certain values of direct polarizability coefficients and cone angle β. Finally, for off-axis cases in the vicinity of the beam axis, we found that the additional terms are proportional to R and R², compared to the case of plane travelling wave, showing the dependence on the radial position in a Bessel beam. These findings are of interest for applications of acoustic tweezing or levitation of thin elastic structures and biological samples with asymmetric geometries, using non-planar acoustic beams that can be produced by novel ultrasound meta-materials, in Space engineering and Bio-material engineering.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

SS contributed to conception and design of the study, conducted the theoretical analysis, organized the database, and wrote the first draft of the manuscript. SO contributed to the conception, provided resources and administered the project. Both read and revised the manuscript, and approved the submitted version.

Funding

This research has been financially supported by Australian Research Council Discovery Projects DP200101708 and DP200100358 and by the UTS Faculty of Engineering and IT as well as UTS Techlab.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors acknowledge preliminary discussions with David Powell and Yan Kei Chiang.

Footnotes

¹the dimension estimated by, e.g., dividing the object’s volume through its surface area for 3D objects.

²a combination of Im(α_pp) cos β and $\text{Re}({\alpha }_{vv}^{zz}){\cos }^3\beta$.

References

1. Doinikov AA. Acoustic Radiation Pressure on a Compressible Sphere in a Viscous Fluid. J. Fluid Mech. (1994) 267:1–22. doi:10.1017/s0022112094001096

CrossRef Full Text | Google Scholar

2. Bruus H. Acoustofluidics 7: The Acoustic Radiation Force on Small Particles. Lab Chip (2012) 12:1014–21. doi:10.1039/c2lc21068a

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Silva GT, Bruus H. Acoustic Interaction Forces between Small Particles in an Ideal Fluid. Phys Rev E Stat Nonlin Soft Matter Phys (2014) 90:063007. doi:10.1103/PhysRevE.90.063007

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Lima EB, Leão-Neto JP, Marques AS, Silva GC, Lopes JH, Silva GT. Nonlinear Interaction of Acoustic Waves with a Spheroidal Particle: Radiation Force and Torque Effects. Phys Rev Appl (2020) 13:064048. doi:10.1103/physrevapplied.13.064048

CrossRef Full Text | Google Scholar

5. Sepehrirahnama S, Oberst S, Chiang YK, Powell D. Acoustic Radiation Force and Radiation Torque beyond Particles: Effects of Nonspherical Shape and Willis Coupling. Phys. Rev. E (2021) 104:065003. doi:10.1103/PhysRevE.104.065003

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Settnes M, Bruus H. Forces Acting on a Small Particle in an Acoustical Field in a Viscous Fluid. Phys Rev E Stat Nonlin Soft Matter Phys (2012) 85:016327. doi:10.1103/PhysRevE.85.016327

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Sepehrirahnama S, Lim K-M, Chau FS. Numerical Analysis of the Acoustic Radiation Force and Acoustic Streaming Around a Sphere in an Acoustic Standing Wave. Phys Procedia (2015) 70:80–4. doi:10.1016/j.phpro.2015.08.047

CrossRef Full Text | Google Scholar

8. Doinikov AA. Acoustic Radiation Pressure on a Rigid Sphere in a Viscous Fluid. Proc R Soc Lond. Ser A Math Phys Sci (1994) 447:447–66.

Google Scholar

9. Sepehrirhnama S, Lim K-M. Generalized Potential Theory for Close-Range Acoustic Interactions in the Rayleigh Limit. Phys. Rev. E (2020) 102:043307. doi:10.1103/PhysRevE.102.043307

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Lima EB, Silva GT. Mean Acoustic Fields Exerted on a Subwavelength Axisymmetric Particle. J Acoust Soc Am (2021) 150:376–84. doi:10.1121/10.0005625

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Marston PL. Axial Radiation Force of a Bessel Beam on a Sphere and Direction Reversal of the Force. J Acoust Soc Am (2006) 120:3518–24. doi:10.1121/1.2361185

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Dual J, Hahn P, Leibacher I, Möller D, Schwarz T, Wang J. Acoustofluidics 19: Ultrasonic Microrobotics in Cavities: Devices and Numerical Simulation. Lab Chip (2012) 12:4010–21. doi:10.1039/c2lc40733g

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Leão-Neto JP, Hoyos M, Aider J-L, Silva GT. Acoustic Radiation Force and Torque on Spheroidal Particles in an Ideal Cylindrical Chamber. J Acoust Soc Am (2021) 149:285–95. doi:10.1121/10.0003046

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Foresti D, Nabavi M, Poulikakos D. On the Acoustic Levitation Stability Behaviour of Spherical and Ellipsoidal Particles. J. Fluid Mech. (2012) 709:581–92. doi:10.1017/jfm.2012.350

CrossRef Full Text | Google Scholar

15. Jerome TS, Ilinskii YA, Zabolotskaya EA, Hamilton MF. Acoustic Radiation Force on a Compressible Spheroid. J Acoust Soc Am (2020) 148:2403–15. doi:10.1121/10.0002277

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Hasegawa T, Yosioka K. Acoustic‐Radiation Force on a Solid Elastic Sphere. J Acoust Soc Am (1969) 46:1139–43. doi:10.1121/1.1911832

CrossRef Full Text | Google Scholar

17. Lopes JH, Azarpeyvand M, Silva GT. Acoustic Interaction Forces and Torques Acting on Suspended Spheres in an Ideal Fluid. IEEE Trans. Ultrason, Ferroelect., Freq. Contr. (2016) 63:186–97. doi:10.1109/tuffc.2015.2494693

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Sepehrirahnama S, Lim K-M, Chau FS. Numerical Study of Interparticle Radiation Force Acting on Rigid Spheres in a Standing Wave. J Acoust Soc Am (2015) 137:2614–22. doi:10.1121/1.4916968

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Sepehrirahnama S, Chau FS, Lim KM. Numerical Calculation of Acoustic Radiation Forces Acting on a Sphere in a Viscous Fluid. Phys Rev E Stat Nonlin Soft Matter Phys (2015) 92:063309. doi:10.1103/PhysRevE.92.063309

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Gong Z, Baudoin M. Acoustic Radiation Torque on a Particle in a Fluid: An Angular Spectrum Based Compact Expression. J Acoust Soc Am (2020) 148:3131–40. doi:10.1121/10.0002491

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Gong Z, Baudoin M. Equivalence between Angular Spectrum-Based and Multipole Expansion-Based Formulas of the Acoustic Radiation Force and Torque. J Acoust Soc Am (2021) 149:3469–82. doi:10.1121/10.0005004

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Sepehrirahnama S, Oberst S, Chiang Y, Powell D. Willis Coupling-Induced Acoustic Radiation Force and Torque Reversal (2021). 01354. arXiv preprint (2021) arXiv:2110. doi:10.48550/arXiv.2110.01354

CrossRef Full Text | Google Scholar

23. Marston PL. Axial Radiation Force of a Bessel Beam on a Sphere, Direction Reversal of the Force, and Solid Sphere Examples. J Acoust Soc Am (2007) 121:3109. doi:10.1121/1.4808510

CrossRef Full Text | Google Scholar

24. Mitri FG. Acoustic Radiation Force of High-Order Bessel Beam Standing Wave Tweezers on a Rigid Sphere. Ultrasonics (2009) 49:794–8. doi:10.1016/j.ultras.2009.07.006

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Silva GT. Off-axis Scattering of an Ultrasound Bessel Beam by a Sphere. IEEE Trans. Ultrason, Ferroelect., Freq. Contr. (2011) 58:298–304. doi:10.1109/tuffc.2011.1807

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Silva GT, Lobo TP, Mitri FG. Radiation Torque Produced by an Arbitrary Acoustic Wave. Epl (2012) 97:54003. doi:10.1209/0295-5075/97/54003

CrossRef Full Text | Google Scholar

27. Wijaya FB, Lim K-M. Numerical Calculation of Acoustic Radiation Force and Torque Acting on Rigid Non-spherical Particles. Acta Acustica united Acustica (2015) 101:531–42. doi:10.3813/aaa.918850

CrossRef Full Text | Google Scholar

28. Wijaya FB, Sepehrirahnama S, Lim K-M. Interparticle Force and Torque on Rigid Spheroidal Particles in Acoustophoresis. Wave Motion (2018) 81:28–45. doi:10.1016/j.wavemoti.2018.06.004

CrossRef Full Text | Google Scholar

29. Sepehrirahnama S, Lim KM. Acoustophoretic Agglomeration Patterns of Particulate Phase in a Host Fluid. Microfluid Nanofluidics (2020) 24:1–14. doi:10.1007/s10404-020-02397-5

CrossRef Full Text | Google Scholar

30. Zhang L, Marston PL. Geometrical Interpretation of Negative Radiation Forces of Acoustical Bessel Beams on Spheres. Phys. Rev. E (2011) 84:035601. doi:10.1103/PhysRevE.84.035601

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Fan X-D, Zhang L. Trapping Force of Acoustical Bessel Beams on a Sphere and Stable Tractor Beams. Phys. Rev. Appl (2019) 11:014055. doi:10.1103/PhysRevApplied.11.014055

CrossRef Full Text | Google Scholar

32. Marston PL. Negative Axial Radiation Forces on Solid Spheres and Shells in a Bessel Beam. J Acoust Soc Am (2007) 122:3162–5. doi:10.1121/1.2799501

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Jordaan J, Punzet S, Melnikov A, Sanches A, Oberst S, Marburg S. Measuring Monopole and Dipole Polarizability of Acoustic Meta-Atoms. Appl Phys Lett (2018) 113:224102. doi:10.1063/1.5052661

CrossRef Full Text | Google Scholar

34. Su X, Norris AN. Retrieval Method for the Bianisotropic Polarizability Tensor of Willis Acoustic Scatterers. Phys Rev B (2018) 98:174305. doi:10.1103/physrevb.98.174305

CrossRef Full Text | Google Scholar

35. Melnikov A, Chiang YK, Quan L, Oberst S, Alù A, Marburg S, et al. Acoustic Meta-Atom with Experimentally Verified Maximum Willis Coupling. Nat Commun (2019) 10:1–7. doi:10.1038/s41467-019-10915-5

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Gong Z, Baudoin M. Three-dimensional Trapping and Assembly of Small Particles with Synchronized Spherical Acoustical Vortices. Phys Rev Appl (2020) 14:064002. doi:10.1103/physrevapplied.14.064002

CrossRef Full Text | Google Scholar

37. Baudoin M, Thomas JL, Sahely RA, Gerbedoen JC, Gong Z, Sivery A, et al. Spatially Selective Manipulation of Cells with Single-Beam Acoustical Tweezers. Nat Commun (2020) 11:1–10. doi:10.1038/s41467-020-18000-y

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Quan L, Ra’di Y, Sounas DL, Alù A. Maximum Willis Coupling in Acoustic Scatterers. Phys Rev Lett (2018) 120:254301. doi:10.1103/physrevlett.120.254301

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Klaseboer E, Sepehrirahnama S, Chan DY. Space-time Domain Solutions of the Wave Equation by a Non-singular Boundary Integral Method and Fourier Transform. J Acoust Soc Am (2017) 142:697–707. doi:10.1121/1.4996860

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Gong Z, Marston PL, Li W. T-matrix Evaluation of Three-Dimensional Acoustic Radiation Forces on Nonspherical Objects in Bessel Beams with Arbitrary Order and Location. Phys Rev E (2019) 99:063004. doi:10.1103/PhysRevE.99.063004

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Chiang YK, Oberst S, Melnikov A, Quan L, Marburg S, Alù A, et al. Reconfigurable Acoustic Metagrating for High-Efficiency Anomalous Reflection. Phys Rev Appl (2020) 13:064067. doi:10.1103/physrevapplied.13.064067

CrossRef Full Text | Google Scholar

42. Jjja D. Exact Solutions for Nondiffracting Beams. I. The Scalar Theory. JOSA A (1987) 4:651–4.

Google Scholar

43. Marston PL. Scattering of a Bessel Beam by a Sphere. J Acoust Soc Am (2007) 121:753–8. doi:10.1121/1.2404931

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Doinikov AA. Acoustic Radiation Interparticle Forces in a Compressible Fluid. J Fluid Mech (2001) 444:1–21. doi:10.1017/s0022112001005055

CrossRef Full Text | Google Scholar

45. Sepehrirahnama S, Chau FS, Lim KM. Effects of Viscosity and Acoustic Streaming on the Interparticle Radiation Force between Rigid Spheres in a Standing Wave. Phys Rev E (2016) 93:023307. doi:10.1103/PhysRevE.93.023307

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Sieck CF, Alù A, Haberman MR. Origins of Willis Coupling and Acoustic Bianisotropy in Acoustic Metamaterials through Source-Driven Homogenization. Phys Rev B (2017) 96:104303. doi:10.1103/physrevb.96.104303

CrossRef Full Text | Google Scholar

47. Chiang YK, Quan L, Peng Y, Sepehrirahnama S, Oberst S, Alù A, et al. Scalable Metagrating for Efficient Ultrasonic Focusing. Phys Rev Appl (2021) 16:064014. doi:10.1103/physrevapplied.16.064014

CrossRef Full Text | Google Scholar

48. Polychronopoulos S, Memoli G. Acoustic Levitation with Optimized Reflective Metamaterials. Sci Rep (2020) 10:1–10. doi:10.1038/s41598-020-60978-4

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Lim G, Wortis M, Mukhopadhyay R. Stomatocyte–discocyte–echinocyte Sequence of the Human Red Blood Cell: Evidence for the Bilayer–Couple Hypothesis from Membrane Mechanics. Proc Natl Acad Sci (2002) 99:16766–9. doi:10.1073/pnas.202617299

PubMed Abstract | CrossRef Full Text | Google Scholar