- 1Department of Physics, University of Colorado Boulder, Boulder, CO, United States
- 2Center for Computational Biology, Flatiron Institute, New York, NY, United States
- 3Courant Institute, New York University, New York, NY, United States
- 4Department of Molecular, Cellular, and Developmental Biology, University of Colorado Boulder, Boulder, CO, United States
Living systems exhibit self-organization, a phenomenon that enables organisms to perform functions essential for life. The interior of living cells is a crowded environment in which the self-assembly of cytoskeletal networks is spatially constrained by membranes and organelles. Cytoskeletal filaments undergo active condensation in the presence of crosslinking motor proteins. In past studies, confinement has been shown to alter the morphology of active condensates. Here, we perform simulations to explore systems of filaments and crosslinking motors in a variety of confining geometries. We simulate spatial confinement imposed by hard spherical, cylindrical, and planar boundaries. These systems exhibit non-equilibrium condensation behavior where crosslinking motors condense a fraction of the overall filament population, leading to coexistence of vapor and condensed states. We find that the confinement lengthscale modifies the dynamics and condensate morphology. With end-pausing crosslinking motors, filaments self-organize into half asters and fully-symmetric asters under spherical confinement, polarity-sorted bilayers and bottle-brush-like states under cylindrical confinement, and flattened asters under planar confinement. The number of crosslinking motors controls the size and shape of condensates, with flattened asters becoming hollow and ring-like for larger motor number. End pausing plays a key role affecting condensate morphology: systems with end-pausing motors evolve into aster-like condensates while those with non-end-pausing crosslinking motor proteins evolve into disordered clusters and polarity-sorted bundles.
1 Introduction
Active matter is composed of energy-consuming units that generate activity through motility. Emergent behavior, like global contraction, collective motion, and turbulent flow underpin active matter systems [1–4]. Self-organization in active matter can form structures orders of magnitude larger than the size of a single particle [5–7]. Systems of attractively interacting colloidal particles exhibit phase coexistence, where a low-density vapor state surrounds a denser liquid, gel, or solid state [8–10]. Cytoskeletal filaments can undergo active condensation, by influence of transient crosslinking motors. Filaments condense into aster-like structures in the presence of end-pausing crosslinking motors [1, 7, 11, 12]. Active condensation may be considered a non-equilibrium analogue of micelle formation, where hydrophobic interactions between amphiphilic molecules lead to phase separation [13, 14]. In active condensation of filament asters, end-pausing crosslinking motors accumulate at filament tips, producing an effective attraction between filament ends. In the case of non-end-pausing crosslinking motors, the effective crosslink-mediated attraction is distributed along filament lengths, bundling adjacent filaments [2, 3, 5]. In the absence of end-pausing, crosslinking motors walk along filaments, generating rich dynamics from both extensile and contractile stresses [11].
While the bulk behavior of filament-motor assemblies has been extensively studied, the effects of confinement on such assemblies is not well studied. Confinement is biologically important as filaments and molecular motors self-assemble within the confines of cellular membranes and in the presence of organelles. Geometric constraints introduced by boundaries, both in cells and in microfabricated chambers, influence self-organization, leading to positioning and alignment of the cytoskeletal components [15–19]. Xenopus egg extract confined within small spherical droplets forms cortical and half-aster cytoskeletal structures [20, 21]. Microtubules under confinement with non-end-pausing motors generate vortices and continuous flows [22–24]. Boundaries alter the dynamics by blocking kinetic pathways, and therefore change the morphology of condensed structures. Despite previous work, our understanding of how confinement perturbs morphology of active condensates is limited [2, 20]. Improved understanding of the interplay between crosslinking motor activity and confinement in cytoskeletal active matter gives insight into their biological functionality in living organisms.
Here, we investigate the role of confinement on the active condensation of filaments and crosslinking motor proteins using large-scale Brownian Dynamics/kinetic Monte Carlo (BD/kMC) simulations. In particular, we consider spherical, cylindrical and planar confining geometries. We find that both geometry and confinement lengthscale affect condensate morphology. In systems with end-pausing motors, aster formation is inhibited at small confinement lengthscales. Spherically-confined systems assemble into both half and full asters. Cylindrically-confined systems condense into polarity-sorted bilayers at small confinement lengthscales and bottle brush-like states at large confinement lengthscales. Systems confined between planar surfaces condense into flattened asters at small confinement lengthscales. Under planar confinement, flattened asters become hollow and ring-like when the number of crosslinking motors is increased. For end-pausing crosslinking motors that walk to filament plus ends, motor accumulation induces a highly local effective attraction between filament plus ends that is analogous to the association of head and tail groups of amphiphilic molecules seen in micelle formation. In contrast, non-end-pausing crosslinking motors induce attraction between filaments distributed along their lengths. In the case of non-end-pausing crosslinking motors, and under planar confinement, filaments condense into disordered clusters at low filament packing fractions, and polarity-sorted bundles with high orientational order at high filament packing fractions.
2 Methods
2.1 Simulations
We use a Living ENsemble Simulator (aLENS), to simulate systems of filaments and crosslinking motors [25]. Filaments are modeled as rigid spherocylinders, with fixed length L0 = 0.25 μm and diameter D = 0.025 μm (aspect ratio 10), sterically interacting with each other. Each filament has a plus end and a minus end. The end-to-end filament length, when accounting for the hemispherical caps at both ends, is L = L0 + D = 0.275 μm. Crosslinking motors are modeled as Hookean springs connecting two binding sites or heads. Crosslinking motors do not sterically interact with each other. Filament motion, filament collision, and motor head binding/unbinding kinetics set the characteristic time scales for the system, with the timestep determined by the shortest time scale. In every timestep, aLENS calculates crosslinking motor diffusion and stepping, crosslinking motor binding/unbinding, and filament motion, in that order.
In this system, crosslinking motors can be unbound, singly bound, or doubly bound (crosslinking). Unbound crosslinking motors undergo Brownian motion. Singly bound crosslinking motors with one head bound to a filament and one unbound head, move on filaments with velocity vs. Doubly bound crosslinking motors have both heads bound to different filaments, and each head moves with velocity vf. Here, vf is the force-dependent stepping velocity that changes with the motor tether stretch [26].
The binding and unbinding of crosslinker motor heads is evaluated using a kinetic Monte Carlo algorithm that treats these as stochastic events. This algorithm satisfies detailed balance in the limit of non-walking heads. Motors are modeled explicitly, and transition between unbound, singly bound, and doubly bound states with time-independent transition rates R. State transitions are inhomogeneous Poisson processes, with the transition probability given by
Filaments move due to forces from crosslinking motors, steric interactions with other filaments and boundaries, and Brownian motion. Traditional simulation methods are based on interaction potentials between filaments [27], but this can lead to numerical instability and overlaps between filaments [28]. In contrast, aLENS treats filament steric interactions as non-overlapping constraints. A complementarity constraint, with interaction force γcol > 0 when the minimal distance Φcol = 0 (contact), and γcol = 0 when Φcol > 0 (no contact), is used. Crosslinking forces are modeled using an equality constraint that satisfies the Hookean spring model, γxl = −κ(lf − l0), where κ is the spring constant, lf is the spring length, and l0 is the spring rest length. Filament-boundary steric interactions are modeled in a similar fashion to filament-filament interactions, except that interaction forces only act on filaments. Integrating the equation of motion such that these constraints are satisfied for all possible collisions and crosslinking motors, filament positions and orientations can be evolved in time. For details on the simulation methods, we refer the reader to [25].
2.2 Confinement Boundaries
In this study, we confine systems of filaments and crosslinking proteins with variable geometry. For spherical confinement, we use a sphere where spatial constraints are three dimensional. For cylindrical confinement, we use a cylinder oriented along the z-axis. As a result, spatial constraints are two dimensional in the XY plane while periodic boundary conditions are enforced along the z-axis. For planar confinement, two planes with their normal vectors oriented along the z-axis are spaced with varying separation in z. Filaments lie between the two planes and experience spatial constraints in one dimension. We enforce periodic boundary conditions along the x and y-axes. When calculating the volume of a confined system, we use the end-to-end filament length L = 0.275 μm instead of L0 = 0.25 μm.
2.3 Initial Conditions
Filaments are initialized with an equal number oriented along the + z-axis and the − z-axis. Unless otherwise specified (as in the case of spherical confinement), our simulations contain N = 1,600 filaments. Each filament is a spherocylinder with volume
3 Results
3.1 Active Condensates in Confined Geometries
Filaments driven by crosslinking motor proteins can self-organize into large aggregates. We first consider plus-end-directed crosslinking motors. Motor heads that pause when they reach the filament plus end (Figure 1A) accumulate there. Filaments can then have a motor-rich end (the plus end in our model) and a motor-poor end (the minus end). Crosslinking produces effective attractive interactions between motor-rich filament plus ends, leading to condensation of motor-rich ends.
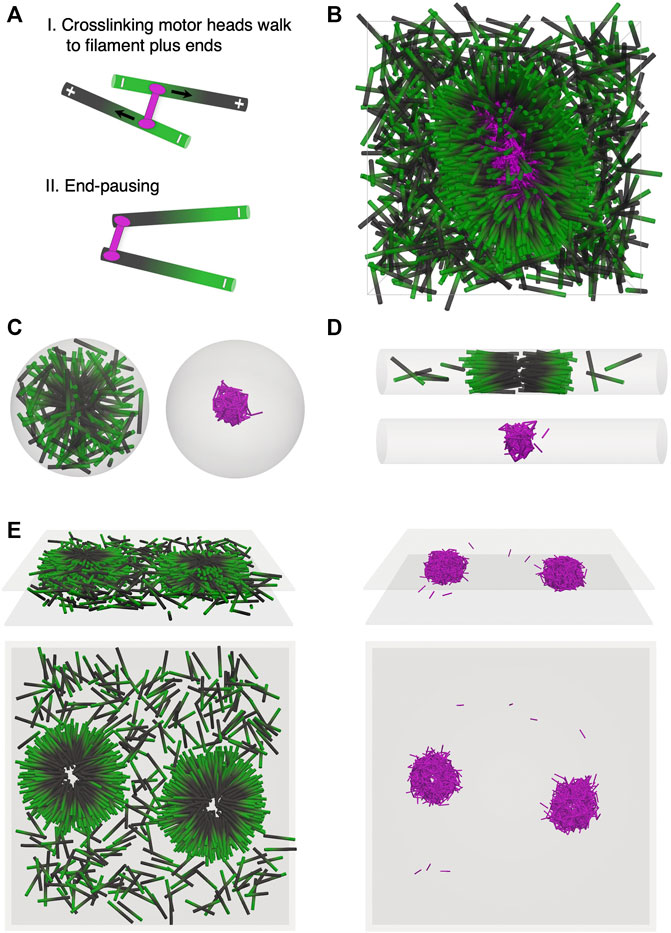
FIGURE 1. Self-organization of filaments and crosslinking motor proteins is affected by confinement geometry. (A) End-pausing crosslinking motors (pink) bind to filaments (minus end green, plus end black) and each motor head walks to the plus end of the filament to which it is bound. Upon reaching the plus end, the motor heads stop walking and pause there. (B–E) Simulation snapshots at a filament packing fraction of ϕ = 0.08. This corresponds to 1,600 filaments in B, D, E, and 181 filaments in C. The number of crosslinking motors in each geometry is three times the number of filaments. (B) Simulation snapshot of an unconfined system of filaments and crosslinking motors in a 3D periodic box. End pausing of crosslinking motor heads leads to tip accumulation of crosslinking motors on filament plus ends. (C) Spherical confinement. Filaments (left) self-organize into a symmetric 3D aster with the motors (right) forming a core near the center of the aster. (D) Cylindrical confinement. Filaments (top) form a polarity sorted bilayer oriented along the cylindrical axis. Motors (bottom) polarity sort the filaments. (E) Planar confinement. Filaments (left) self-organize into flattened asters due to activity of motors (right). Top (3D view) and bottom (top view).
In Figures 1B–E, we show results from simulations of systems containing filaments, at packing fraction ϕ = 0.08, and crosslinking motors. The number of crosslinking motors is equal to three times the number of filaments. Over time, motors bind to filaments, then walk and accumulate at the filament plus ends. In an unconfined system with N = 1,600 filaments and volume V = 2.6 µm3, end-pausing motors drive the formation of asters (Figure 1B, Supplementary Movie S1). Filament plus ends (black) are held together by a core of crosslinking motors (pink) with the filaments oriented radially inward. A fraction of the filaments with very few motors bound to them remain in an uncondensed “vapor” state.
Confinement can alter self-organization of filaments and motors by affecting aster positioning or even preventing full aster formation. To illustrate this, we first consider a sphere of diameter D = 3L and volume V ≈ 0.30 µm3. In this case, N = 181 filaments self-assemble into a spherically symmetric aster (Figure 1C, Supplementary Movie S2). When the confining boundary is a relatively narrow cylinder of diameter D = L, length 43.3 µm and volume V ≈ 2.6 µm3, filaments cannot form asters but instead condense Figure 1D into polarity-sorted bilayers (Figure 1D, Supplementary Movie S3). In the bilayer, filaments are aligned along the cylinder axis. Plus ends (black) are crosslinked by motors near the center of the bilayer, while minus ends are positioned on the outer edges of the condensate. For planar confinement with separation between the two surfaces H = L and volume V ≈ 2.6 µm3, flattened asters form (Figure 1E, Supplementary Movie S4). Filament plus ends are held together by a dense core of crosslinking motors. Filaments have a tendency to lie in planes parallel to the confining surfaces (Figure 1E, top left view).
3.2 Confinement Lengthscale Determines Morphology
The confinement lengthscale can affect condensate morphology by preventing the formation of the symmetric asters that are favored in bulk systems. We first investigate spherical confinement with a fixed filament packing fraction of ϕ = 0.08 for sphere diameters D in the range 1–3L (Figure 2A). In these three cases, we simulate N = 6, 53, and 181 filaments in spheres with volume V ≈ 0.01, 0.09, and 0.30 µm3 respectively. The ratio of the number of crosslinking motors to the number of filaments is
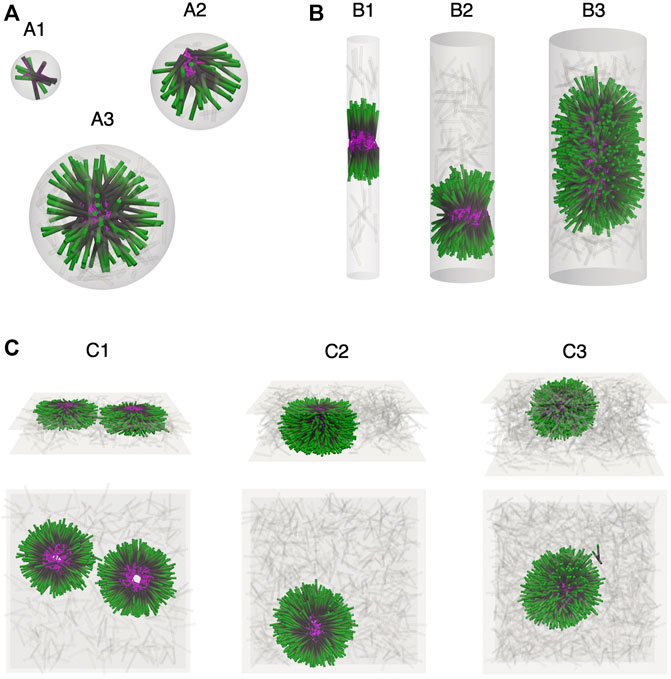
FIGURE 2. Confinement lengthscale alters filament self-organization and steady-state morphology. Simulation snapshots showing filaments (minus end green, plus end black) of length L and end-pausing crosslinking motors (pink). Filaments in the vapor have been grayed out. (A) Spherical confinement in a sphere of varying diameter D. (A1) D = L. Small spherical boundary inhibits extensile force generation of the motor proteins and no tip accumulation is observed. (A2) D = 2L. The confining sphere is just large enough to allow for extensile stress generation, and crosslinking motor proteins accumulate at filament plus ends to form a half aster whose core is visible at the edge of the sphere. (A3) D = 3L. Filaments self-assemble into a symmetric aster centered in the confining sphere. (B) Cylindrical confinement of 1,600 filaments and 4,800 crosslinking motors in cylinders of varying diameter D. Snapshots show a 2 µm long section of the simulation cylinder. (B1) D = L. Filaments form polarity-sorted bilayers, each one held together by a core of crosslinking motors. (B2) D = 2L. An asymmetric aster showing a degree of orientational alignment of microtubules along the axis of the cylinder. (B3) D = 3L. A bottle-brush-like aster with an elongated core of crosslinking motors. Filaments point radially in towards the surface of the crosslinker core. (C) Planar confinement of 1,600 filaments and 4,800 crosslinking motor proteins between two surfaces with separation H. (C1,C2) H = L and H = 2L. Flattened asters with a hollow filament core. (C3) H = 3L. The surface separation is large enough to accommodate a full, albeit slightly elongated, aster.
Cylindrical confinement can drive filament alignment along the cylinder axis. Figure 2B shows results from simulations of N = 1,600 filaments at a packing fraction of ϕ = 0.08 with
One-dimensional spatial constraints are modeled by confining the system between two hard planar surfaces. The degree of confinement is controlled by changing the separation H between the two surfaces. We investigate N = 1,600 filaments at a packing fraction of ϕ = 0.08 with
3.3 Ring-Like Asters Under Planar Confinement
Under planar confinement with surface separation H = L and system volume V ≈ 5.3 µm3, 1,600 filaments with packing fraction ϕ = 0.04 condense into flattened asters in the presence of end-pausing crosslinking motors. The observed morphologies depend on the crosslinking motor number ratio
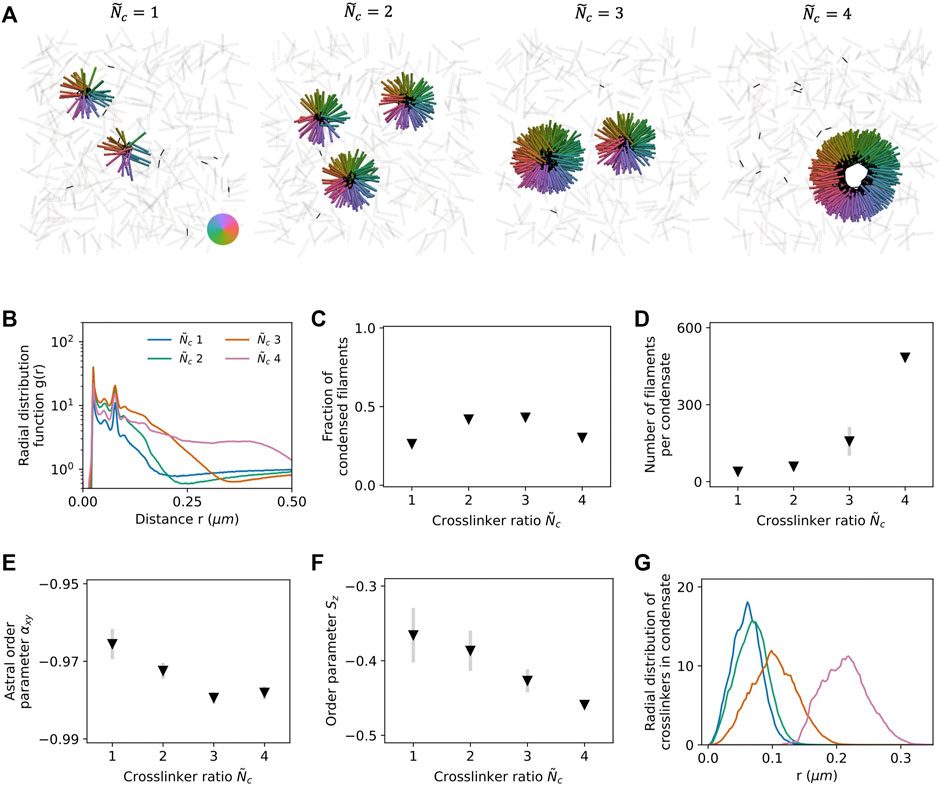
FIGURE 3. Filaments and end-pausing crosslinking motor proteins self-assemble into flower-like and ring-like asters when confined between two planar surfaces with separation H = L. (A) Simulation snapshots for varying crosslinker number ratio
Using Gaussian mixture models, we cluster filaments and identify the filament populations belonging to the condensed and vapor states (Supplementary Material). The fraction of condensed filaments increases with
Radial symmetry of the condensate is quantified by defining an astral order parameter
3.4 Polarity Sorted Condensates Formed by Non-End-Pausing Motors
Non-end-pausing crosslinking motors, including certain kinesins, do not exhibit tip accumulation on filaments. Instead of pausing upon reaching the filament plus end, both motor heads continue to walk and fall off of the filament. Consequently, the system is more active, and the kinetic pathways for system evolution are different than those in the case of end-pausing crosslinking motors [2, 3, 5]. Crosslinking and antiparallel sliding of anti-aligned filaments leads to extensile stress generation on the microscopic scale, and emergence of local order on the mesoscopic scale. Here, we study the effect of filament packing fraction ϕ and crosslinker number ratio
For a low filament packing fraction of ϕ = 0.04, filaments condense into orientationally-disordered clusters (Figure 4A top row, Supplementary Movie S7). Increasing
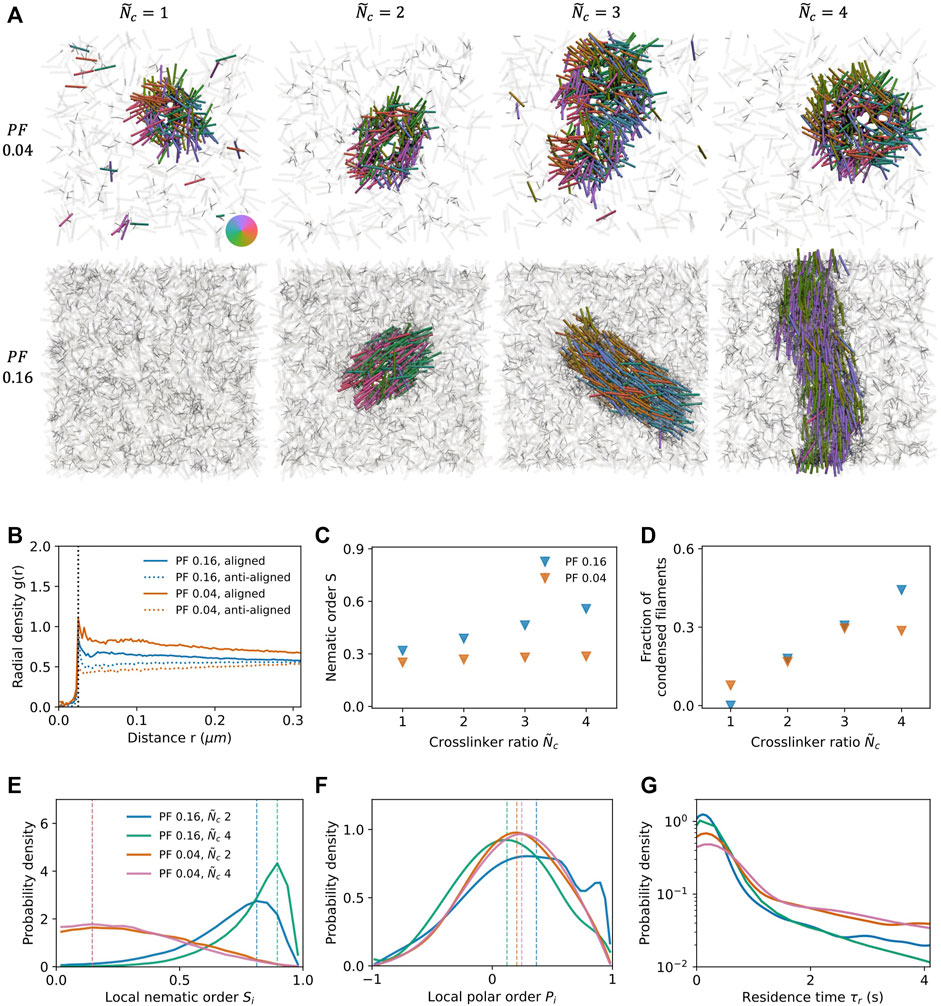
FIGURE 4. Condensate formation in the presence of non-end-pausing crosslinking motor proteins under planar confinement with surface separation H = L. (A) Simulation snapshots at packing fraction ϕ = 0.04 (top row) and 0.16 (bottom row) and varying crosslinker number ratio
We next measure the fraction of filaments in the condensed state as a function of
A second measure of orientational order is the local polar parameter Pi, which is a quantitative measure of the local polar alignment of a given filament i (Figure 4F, Supplementary Material). A system with a random mixture of aligned and anti-aligned filaments (as in a conventional nematic) would have Pi = 0, while a system where all filaments are perfectly aligned/anti-aligned would have Pi = ± 1. Polarity sorting in the system leads to probablility distributions with peaks at positive values of Pi (dashed lines). The distributions for ϕ = 0.04 are very similar, while for ϕ = 0.16 there are similarities and significant differences between the distributions for
Lastly, to quantify coherence, we measure the residence time τR of filaments in the condensed state (Figure 4G). In the low packing fraction systems, condensed filaments experience random directed motion within the orientationally-disordered condensate and consequently remain in the condensate for a relatively longer time. By contrast, the high degree of orientational order in the high packing fraction systems leads to coherent directed motion of filaments within the condensate, so that they can more easily be ejected from the condensate.
4 Discussion
Microbutule self-assembly is sensitive to spatial confinement. In vivo, there is interplay between cell shape and microtubule self-assembly, where cell shape affects microtubule orientational order [15, 16]. In vitro, assemblies of microtubules and end-pausing crosslinking motors form asters that are able to sense their surroundings and use that information for positioning [18]. Moreover, aster formation is perturbed in suspensions of Xenopus egg extract confined to spherical oil droplets, where microtubules self-assemble into cortical and half-aster states when the droplet size is small [20, 21]. Here, we find that fixed-length filaments assemble into half asters when the confinement diameter of the sphere is on the order of twice the length of a single filament. For smaller diameters, asters cannot form. For successful aster assembly, anti-aligned crosslinked filaments need to slide apart. This kinetic pathway requires that the diameter of the confining sphere be at least twice as long as the length of a single filament. When the confining diameter is three times the filament length, pairs of anti-aligned filaments remain unimpeded in both sliding apart and pivoting to form full asters.
In vitro, filament behavior and self-assembly in the presence of molecular motors is often studied in the presence of depleting agents [29]. Depleting agents, like PEG and methylcellulose, push filaments to the surface forming a thin layer, and increase the potential for filament interaction by forcing the filaments to lie in a single two-dimensional plane [30]. The use of a depletion agent effectively introduces a depletion interaction, which may be modeled in terms of an additional degree of spatial confinement. Here, we simulate filaments and crosslinking motor proteins confined between two planar surfaces. Under planar confinement, when the plate separation is equal to filament length, we find that systems of filaments and end-pausing crosslinking motors form flattened asters. Filaments in this condensed fraction have a tendency to align in the confinement plane, shown by a negative value for Sz. As the number of crosslinking motors is increased, we observe that the flattened aster dilates and becomes ring-like, with a hollow core that is free from both filaments and crosslinking motors. In experiments with Xenopus egg cytosol, taxol-stabilized microtubules self-assemble into both flattened ring-like and bilayer-like structures [31]. Simulations with higher number of filaments, and crosslinking motor proteins may yield assymetric condensates that resemble bilayers.
The coexistence of condensed and vapor phases in which most of the crosslinking motors accumulate in the condensed fraction bears an intriguing resemblance to amphiphile-based micelles. Instead of repulsive hydrophobic interaction due to chemical differences between head and tail groups, however, active condensates form due to localized crosslinker-mediated attractive interactions between filament plus ends. As a result, filament plus ends condense, while filament minus ends sterically repel each other, leading to micelle-like aster morphologies.
In the case of non-end-pausing crosslinking motors, the attractive interaction between filaments is no longer localized and is instead distributed along the length of the filament. Here, as expected, we find that filaments associate together into clusters or bundles. At low filament packing fraction, condensed clusters lack orientational order. Filaments prefer an isotropic distribution in this regime, and the addition of crosslinking motors introduces motility without affecting the local orientational order. Filaments form disordered clusters, and the variety of filament orientations mean that crosslinking motors have small overall displacement. This, in turn, allows crosslinking motors to aggregate together, enabling condensate formation. While the number of condensed filaments increases, the lack of orientational order persists when the crosslinker number ratio
The orientationally-ordered bundles for ϕ = 0.16 show an increase in aspect ratio with increasing
In summary, here we describe active condensate morphology in filament and crosslinking motor assemblies in a variety of geometries. Confinement can alter the self-organization of such assemblies by inhibiting certain kinetic pathways, in the case of spherical confinement. We find that self-assembled filament structures in the presence of end-pausing crosslinking motors are strongly dependent in their morphology to the type and degree of confinement. Flattened asters under planar confinement transition to a unique hollow and ring-like state. Planar-confined filament systems with non-end-pausing motors transition to a highly ordered and polarity-sorted nematic state upon increasing the filament packing fraction. The interplay between activity and confinement has significant implications for biological functionality. Our work shows the importance of how confinement can modify the morphology of active condensates.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
SA performed and analyzed the simulations, and wrote the manuscript. AL, MG, and MB edited the manuscript. WY and AL created the aLENS software used in these simulations. MS, MG, and MB supervised the project.
Funding
SA, AL, MG, and MB acknowledge support from NSF grants DMS-1821305, DMR-1420736, and NIH grant RGM124371A. MS acknowledges support from NSF grants DMR-2004469 and CMMI-1762506. This work utilized resources from the University of Colorado Boulder Research Computing Group, which is supported by the National Science Foundation (awards ACI-1532235 and ACI-1532236), the University of Colorado Boulder, and Colorado State University.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.897255/full#supplementary-material
References
1. Foster PJ, Fürthauer S, Shelley MJ, Needleman DJ. Active Contraction of Microtubule Networks. Elife (2015) 4:e10837. doi:10.7554/eLife.10837
2. Gompper G, Winkler RG, Speck T, Solon A, Nardini C, Peruani F, et al. The 2020 Motile Active Matter Roadmap. J Phys Condens Matter (2020) 32:193001. doi:10.1088/1361-648x/ab6348
3. Moore JM, Thompson TN, Glaser MA, Betterton MD. Collective Motion of Driven Semiflexible Filaments Tuned by Soft Repulsion and Stiffness. Soft Matter (2020) 16:9436–42. doi:10.1039/d0sm01036g
4. Bricard A, Caussin JB, Desreumaux N, Dauchot O, Bartolo D. Emergence of Macroscopic Directed Motion in Populations of Motile Colloids. Nature (2013) 503:95–8. doi:10.1038/nature12673
5. Roostalu J, Rickman J, Thomas C, Nédélec F, Surrey T. Determinants of Polar versus Nematic Organization in Networks of Dynamic Microtubules and Mitotic Motors. Cell (2018) 175:796–808. doi:10.1016/j.cell.2018.09.029
6. Redner GS, Hagan MF, Baskaran A. Structure and Dynamics of a Phase-Separating Active Colloidal Fluid. Phys Rev Lett (2013) 110:055701. doi:10.1103/PhysRevLett.110.055701
7. Ndlec FJ, Surrey T, Maggs AC, Leibler S. Self-organization of Microtubules and Motors. Nature (1997) 389:305–8. doi:10.1038/38532
8. Theurkauff I, Cottin-Bizonne C, Palacci J, Ybert C, Bocquet L. Dynamic Clustering in Active Colloidal Suspensions with Chemical Signaling. Phys Rev Lett (2012) 108:268303. doi:10.1103/physrevlett.108.268303
9. Palacci J, Sacanna S, Steinberg AP, Pine DJ, Chaikin PM. Living Crystals of Light-Activated Colloidal Surfers. Science (2013) 339:936–40. doi:10.1126/science.1230020
10. Fily Y, Marchetti MC. Athermal Phase Separation of Self-Propelled Particles with No Alignment. Phys Rev Lett (2012) 108:235702. doi:10.1103/physrevlett.108.235702
11. Lemma B, Mitchell NP, Subramanian R, Needleman DJ, Dogic Z. Active Microphase Separation in Mixtures of Microtubules and Tip-Accumulating Molecular Motors. arXiv preprint arXiv:2107.12281 (2021).
12. Surrey T, Nédélec F, Leibler S, Karsenti E. Physical Properties Determining Self-Organization of Motors and Microtubules. Science (2001) 292:1167–71. doi:10.1126/science.1059758
13. Lombardo D, Kiselev MA, Magazù S, Calandra P. Amphiphiles Self-Assembly: Basic Concepts and Future Perspectives of Supramolecular Approaches. Adv Condensed Matter Phys (2015) 2015. doi:10.1155/2015/151683
14. Israelachvili JN, Mitchell DJ, Ninham BW. Theory of Self-Assembly of Hydrocarbon Amphiphiles into Micelles and Bilayers. J Chem Soc Faraday Trans 2 (1976) 72:1525–68. doi:10.1039/f29767201525
15. Carazo-Salas RE, Nurse P. Self-organization of Interphase Microtubule Arrays in Fission Yeast. Nat Cel Biol (2006) 8:1102–7. doi:10.1038/ncb1479
16. Terenna CR, Makushok T, Velve-Casquillas G, Baigl D, Chen Y, Bornens M, et al. Physical Mechanisms Redirecting Cell Polarity and Cell Shape in Fission Yeast. Curr Biol (2008) 18:1748–53. doi:10.1016/j.cub.2008.09.047
17. Holy TE, Dogterom M, Yurke B, Leibler S. Assembly and Positioning of Microtubule Asters in Microfabricated chambers. Proc Natl Acad Sci U.S.A (1997) 94:6228–31. doi:10.1073/pnas.94.12.6228
18. Sulerud T, Sami AB, Li G, Kloxin A, Oakey J, Gatlin J. Microtubule-dependent Pushing Forces Contribute to Long-Distance Aster Movement and Centration in xenopus Laevis Egg Extracts. MBoC (2020) 31:2791–802. doi:10.1091/mbc.e20-01-0088
19. Islam MS, Kuribayashi-Shigetomi K, Kabir AMR, Inoue D, Sada K, Kakugo A. Role of Confinement in the Active Self-Organization of Kinesin-Driven Microtubules. Sensors Actuators B: Chem (2017) 247:53–60. doi:10.1016/j.snb.2017.03.006
20. Pinot M, Chesnel F, Kubiak JZ, Arnal I, Nedelec FJ, Gueroui Z. Effects of Confinement on the Self-Organization of Microtubules and Motors. Curr Biol (2009) 19:954–60. doi:10.1016/j.cub.2009.04.027
21. Gai Y, Setru S, Gouveia B, Stone H, Petry S. Self-organization of Microtubules in Cell-Sized Droplets. Bull Am Phys Soc (2019) 64.
22. Suzuki K, Miyazaki M, Takagi J, Itabashi T, Ishiwata Si. Spatial Confinement of Active Microtubule Networks Induces Large-Scale Rotational Cytoplasmic Flow. Proc Natl Acad Sci U.S.A (2017) 114:2922–7. doi:10.1073/pnas.1616001114
23. Fan Y, Wu KT, Aghvami SA, Fraden S, Breuer KS. Effects of Confinement on the Dynamics and Correlation Scales in Kinesin-Microtubule Active Fluids. Phys Rev E (2021) 104:034601. doi:10.1103/PhysRevE.104.034601
24. Wu KT, Hishamunda JB, Chen DT, DeCamp SJ, Chang YW, Fernández-Nieves A, et al. Transition from Turbulent to Coherent Flows in Confined Three-Dimensional Active Fluids. Science (2017) 355:eaal1979. doi:10.1126/science.aal1979
25. Yan W, Ansari S, Lamson A, Glaser MA, Betterton M, Shelley MJ. Alens: towards the Cellular-Scale Simulation of Motor-Driven Cytoskeletal Assemblies. arXiv preprint arXiv:2109.08206 (2021).
26. Gao T, Blackwell R, Glaser MA, Betterton MD, Shelley MJ. Multiscale Modeling and Simulation of Microtubule-Motor-Protein Assemblies. Phys Rev E Stat Nonlin Soft Matter Phys (2015) 92:062709. doi:10.1103/PhysRevE.92.062709
27. Nedelec F, Foethke D. Collective Langevin Dynamics of Flexible Cytoskeletal Fibers. New J Phys (2007) 9:427. doi:10.1088/1367-2630/9/11/427
28. Heyes DM, Melrose JR. Brownian Dynamics Simulations of Model Hard-Sphere Suspensions. J non-newtonian Fluid Mech (1993) 46:1–28. doi:10.1016/0377-0257(93)80001-r
29. Weirich KL, Dasbiswas K, Witten TA, Vaikuntanathan S, Gardel ML. Self-organizing Motors divide Active Liquid Droplets. Proc Natl Acad Sci U.S.A (2019) 116:11125–30. doi:10.1073/pnas.1814854116
30. Saito A, Farhana TI, Kabir AMR, Inoue D, Konagaya A, Sada K, et al. Understanding the Emergence of Collective Motion of Microtubules Driven by Kinesins: Role of Concentration of Microtubules and Depletion Force. RSC Adv (2017) 7:13191–7. doi:10.1039/c6ra27449h
31. Mitchison TJ, Nguyen P, Coughlin M, Groen AC. Self-organization of Stabilized Microtubules by Both Spindle and Midzone Mechanisms inXenopusegg Cytosol. MBoC (2013) 24:1559–73. doi:10.1091/mbc.e12-12-0850
32. Bolhuis P, Frenkel D. Tracing the Phase Boundaries of Hard Spherocylinders. J Chem Phys (1997) 106:666–87. doi:10.1063/1.473404
33. Prinsen P, Van Der Schoot P. Shape and Director-Field Transformation of Tactoids. Phys Rev E Stat Nonlin Soft Matter Phys (2003) 68:021701. doi:10.1103/PhysRevE.68.021701
Keywords: active matter, filaments, microtubules, self-organization, confinement, crosslinking motors, condensation
Citation: Ansari S, Yan W, Lamson AR, Shelley MJ, Glaser MA and Betterton MD (2022) Active Condensation of Filaments Under Spatial Confinement. Front. Phys. 10:897255. doi: 10.3389/fphy.2022.897255
Received: 15 March 2022; Accepted: 01 June 2022;
Published: 24 June 2022.
Edited by:
Kevin Mitchell, University of California, Merced, United StatesReviewed by:
Daniel Beller, University of California, Merced, United StatesJennifer L. Ross, Syracuse University, United States
Copyright © 2022 Ansari, Yan, Lamson, Shelley, Glaser and Betterton. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Saad Ansari, c2FhZC5hbnNhcmlAY29sb3JhZG8uZWR1
 Saad Ansari
Saad Ansari Wen Yan2
Wen Yan2