- 1Department of Automation, Shanghai Jiao Tong University, Shanghai, China
- 2Key Laboratory of System Control and Information Processing, Ministry of Education of China, Shanghai, China
- 3Shanghai Engineering Research Center of Intelligent Control and Management, Shanghai, China
- 4Department of Automation, Center for Intelligent and Networked Systems, Tsinghua University, Beijing, China
- 5Key Laboratory of Low-Dimensional Quantum Structures and Quantum Control of Ministry of Education, Key Laboratory for Matter Microstructure and Function of Hunan Province, Department of Physics and Synergetic Innovation Center for Quantum Effects and Applications, Hunan Normal University, Changsha, China
Recent progress has revealed that quantum systems with multiple position-dependent couplings, e.g., giant atoms, can exhibit some unconventional phenomena, such as non-exponential decay. However, their potential applications are still open questions. In this paper, we propose a giant-cavity-based quantum sensor for the first time, whose performance can be greatly enhanced compared to traditional cavity-based sensors. In our proposal, two cavities are coupled to a dissipative reservoir at multiple points while they couple to a gain reservoir in a single-point way. To detect an unknown parameter entering the sensor, a waveguide is coupled to one of the cavities where detecting fields can pass through for homodyne detection. We find that multiple position-dependent couplings can induce an inherent non-reciprocal coupling between the cavities, which can enhance the performance of sensors. Compared to the results in the work of Lau and Clerk, (Nat Commun, 2018, 9: 4,320), our output noise can remain at the shot noise level, which is about one order of magnitude lower. In addition, the signal-to-noise ratio per photon is also enhanced by about one order of magnitude. These results showed that the multiple-point coupling structure is beneficial to existing quantum devices.
1 Introduction
High-precision measurement of physical quantities lies in the core of metrology, e.g., gravitational wave detection [1, 2], nano-particle detection [3–6], thermal sensing [7], navigation [8, 9], and magnetometers [10–12]. Towards fundamental detection limits in weak-signal measurements, non-reciprocity [13] has become a powerful resource [14]. Since reciprocity is hard to break due to Lorentz theorem [15], many methods have been proposed for inducing non-reciprocity, for example, biasing with odd-symmetric quantities under time reversal [16], steering systems into exceptional points [17,18], constructing directional couplings [19], employing asymmetric or non-linear elements [20–29], or breaking the time-invariance of systems [30, 31].
Recent progress on quantum systems with multiple-point couplings (e.g., giant atoms [32–48]) provides a new possibility to acquire non-reciprocity. For example, when several giant atoms couple to a common reservoir, an indirect coupling among atoms can be built up via the shared reservoir. This indirect coupling depends on the arrangements of atoms and the relative phase between coupling points [36]. Therefore, one can construct an effective directional coupling between atoms by tuning the relative phase and adjusting the arrangements. It should be noticed that the non-reciprocity realized in this way is an inherent property of the system and it can be totally tuned by the relative phase, such that this method of acquiring non-reciprocity requires no other non-linear elements such as Faraday rotators [20, 21] or Josephson parametric converters [26, 28], and thus, it is easy to be integrated into an on-chip structure and flexible in experiments.
In this study, we propose a quantum sensor consisting of two giant cavities, where two coupled cavities couple to reservoirs at multiple points. We find that an inherent non-reciprocal coupling between cavities can be built up through a shared reservoir. Compared with the small-cavity-based structures in [14], i.e., cavities couple to reservoirs at a single point, the signal-to-noise ratio in our proposal can be improved by one order of magnitude. The study is organized as follows. In Section 2, we propose the theoretical model of the quantum sensor, including the Hamiltonian and equations of motion. Following the standard frame [14], we propose the performance indicator of sensors in Section 3, including signal, output noise, and signal-to-noise ratio per photon. The comparison with the sensor made up of small cavities is shown in Section 4. Finally, further discussion and conclusion are given in Section 5.
2 Model of Gaint-Cavity-Based Quantum Sensor
2.1 Hamiltonian
Generally speaking, a quantum sensor means the sensor utilizing quantum resources, such as quantum devices, quantum states, quantum effects, etc. [49, 50]. In [14], a paradigm in designing quantum sensors is proposed that several coupled cavities couple to a gain reservoir and a dissipative reservoir at a single point. Illuminated by this paradigm, the sensor we considered consists of a coupled double-cavity interacting with two reservoirs. The first cavity is coupled to a dissipative reservoir at x1 and x2, and the second cavity is coupled to it at x3 and x4, as shown in Figure 1. On the contrary, a gain reservoir couples to both cavities at the same point. In addition, a classical pump β with a noise input Bin enters the readout waveguide which only couples to the cavity 1, and its reflected field Bout is measured by homodyne detection. This model can be realized by superconducting quantum circuits, i.e., two LC resonators couple to three waveguides, where one of the waveguides is used for readout and the others are used as reservoirs. According to the model, the total Hamiltonian reads
where
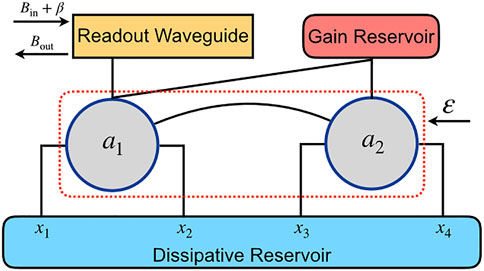
FIGURE 1. Schematic of the two giant-cavity quantum sensor. Both cavities couple to a dissipative reservoir at multiple points, i.e., x1 and x2 for cavity 1 (denoted by annihilation operator a1), x3 and x4 for cavity 2 (denoted by operator a2). The distance between the two points for one cavity is sufficiently large, which induces non-negligible time delays, such that it forms two giant cavities. As a result, the couplings between cavities and dissipative reservoir are position-dependent. On the contrary, both cavities couple to the gain reservoir at the same point. Also, a classical pump with an amplitude β and a noise input Bin is injected into the readout waveguide which only couples to the cavity 1. Its reflected field Bout is measured by homodyne detection. Initially, both reservoirs and the waveguide are prepared in the vacuum state. This sensor can reflect the external perturbation ɛ from the variations of the output Bout.
Equation 2a describes the free Hamiltonian of the two cavities, the readout waveguide, the gain and dissipative reservoirs with bosonic annihilation operators ai, bk, ck, and dk, respectively. Here, we have assumed that the perturbation ɛ is small enough such that Hij [ɛ] has a linear form1 [14, 51]
2.2 Langevin Equations
For the sake of sensing, we analyze how the output varies when the perturbation ɛ acts on the sensor, which can be done with the quantum Langevin equation. Before we proceed, we assume that the coupling points are equally spaced, i.e., d = x2 − x1 = x3 − x2 = x4 − x3. For simplicity, we let x1 = 0. Also, the linear dispersion relation holds in the dissipative reservoir, i.e., ωd,k = vgk with vg being the group velocity [48, 52, 53]. With the abovementioned assumptions, the equations of motion for two cavities take the form
where
with τ = d/vg being the time delay between the two neighboring points. Here,
are the inputs for the readout waveguide, gain, and dissipative reservoirs, respectively. In addition, the input-output relation for the field in the readout waveguide is given by
where
is the output field in the waveguide at a final time t1.
Using Fourier transformation, the delayed differential Eqs. 3a, 3b can be solved as
with
and
Here, I denotes a 2 × 2 identity matrix and χ[ω; ɛ] is the dimensionless state transfer matrix. Operators with a bar
We have provided a description of our sensor in the Heisenberg picture. From the above derivation, we can investigate how the unknown parameter affects the output of the detecting field. Different from the existing sensors, the dynamics of our sensor involve non-reciprocity induced by time-delayed terms which would improve the performance of the sensor.
3 Performance Evaluation of the Sensor
3.1 Homodyne Detection
As we have introduced, our sensor employs homodyne detection to extract the perturbation, where the photon current of the output field
is measured. All the information of ɛ is contained in the real part of eiφBout [t]. Note that the current is measured in a steady-state of the system such that we can evaluate the response of the system to the perturbation at the zero frequency; i.e., ω = 0. Also, for small ɛ, the expectation value of the output is assumed to be in a linear response to ɛ [14], i.e.,
where ⟨⋅⟩z denotes taking expectations at ɛ = z. Using this relation, the response coefficient λ reads
whose phase φ = − arg λ determines the angle in Eq. 13.
3.2 Signal, Noise, and Signal-to-Noise Ratio per Photon
To estimate the performance of the sensor, we further define a measurement operator m[ω] as the windowed Fourier transformation of current I [t], i.e.,
where the segment T should be much greater than 1/κ such that the sensor can reach the steady states during the measurement window. Under this condition, the integral limits can be extended to ±∞. Notably, this definition of m[ω] makes it have a unit of
The power associated with the signal can be defined as the square of the difference of measurement operator m [0] between the perturbed and unperturbed cases, i.e.,
In addition, the total average photon number induced by the classical input can be calculated as
where the mean-field approximation [55, 56] has been used. With this definitaion, the signal per photon can be expressed as
where we let
Similarly, the power of the output noise is defined as the fluctuation of the measurement operator m [0] in the unperturbed case; i.e.,
where
Combining Eqs. 19, 20, one can obtain the signal-to-noise ratio (SNR) per photon
which is the sensitivity of the sensor. Notably, the state transfer matrix
3.3 Corresponding Results for the Sensor Composed of Two Small Cavities
For comparison, we also consider the sensor made up of two small cavities that couple to the dissipative reservoir in a single-point way. This is a standard model of two-mode quantum sensors [14, 51], which is used as a benchmark. In this case, the second line in interaction Hamiltonian Eq. 2c is rewritten as
This induces a modification on Eq. 10
and Eq. 11
and the gain matrix GY (9) remains the same. Hereafter, we use superscript S to label the corresponding quantities of the sensor composed of small cavities.
An interesting fact is that, the third term in Eq. 20 then reduces to
4 Numerical Comparison of Giant vs. Small Sensors
To numerically estimate the performance of the sensor, we set the Hamiltonians Hf [0] and V as
which describes a common linear coupled-cavity system. For simplicity, we consider that both Yi and Zi are real. With these specific matrices, one can easily rewrite the state transfer matrix as
where Δ = ωL − ω1 and Δ12 = ω1 − ω2 are detunings,
We first plot the frequency responses of the relative signal per photon, noise, and SNR per photon of the sensor made up of two small cavities, as shown in Figure 2. We find that both the signal per photon and the noise reach the maximum value at the resonant point, as shown in Figure 2A,B, but does not the SNR per photon, as shown in Figure 2C. To characterize the influences of the loss γ, we replot the above quantities as the functions of γ at the resonant point Δ = 0, as shown in Figure 3. Hereafter, we only consider the responses at the resonant point. As the loss γ increases, both the signal per photon and the noise gradually increase until reaching their maximum values at γ ≃ 0.65Γ and then decrease, shown as the blue and red lines in Figure 3A. Especially, one can find that the output noise NS is always greater than the shot noise in the whole intervals of γ, which means that the shot noise is a fundamental limit of the output noise. Notably, this result also applies to the sensor made up of giant cavities, and we will discuss it later. Indeed, by rewriting Eq. 20 with the replacements
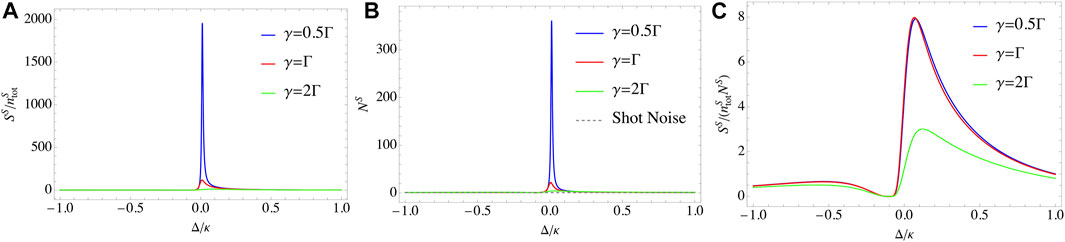
FIGURE 2. (Color online) Frequency responses of the relative signal per photon, noise, and SNR per photon. Parameters in plotting are Δ12 = 0 and J = Γ = 0.1κ. (A) Spectra of the relative signal per photon. The signal reaches the maximum at the resonant point and decreases as the loss γ increases. (B) Spectra of the relative noise. Similar to (A), the noise reaches the maximum at the resonant point and decreases as the loss γ increases. (C) Spectra of SNR per photon. SNR per photon does not reach its maximum value at the resonant point.
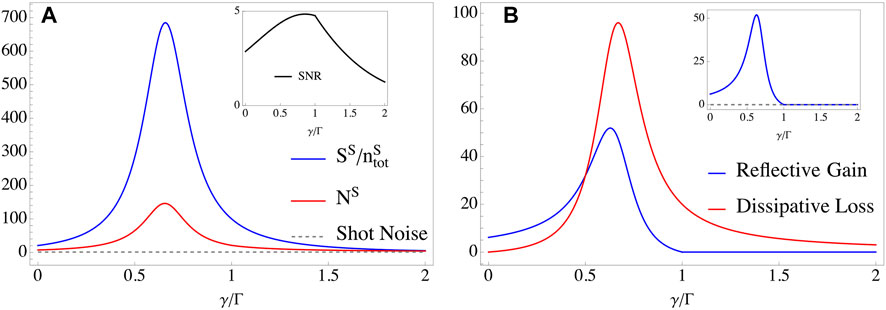
FIGURE 3. (Color online) Relative signal per photon and noise as functions of γ at the resonant point. Parameters in plotting are: Δ = Δ12 = 0, J = Γ = 0.1κ. (A) Both signal (blue line) and noise (red line) experience a process of first increase and then decrease, and reach their maximum value at γ ≃ 0.65Γ, but SNR (black line in inset) reaches the maximum value at γ ≃ 0.85Γ. In addition, the noise NS is always greater than the shot noise (Gray dotted line). (B) The reflective gain (Blue line, the second term in Eq. 20) and the dissipative loss (Red line, the third term in Eq. 20) as functions of γ with the replacement of matrix
With the previous results, we now turn to the sensor made up of two giant cavities. In contrast to the case we discussed in the last section, the dissipative matrix DZ additionally introduces a degree of freedom of the fixed phase ϕ (Δτ is zero at the resonant point), such that the relative signal per photon, noise, and SNR per photon have a response to ϕ, as shown Figure 4 where we also use the same parameters in plotting. Both the signal per photon and the noise experience a process of first increasing and then decreasing as the phase ϕ increases, as shown in Figure 4A,B. An interesting point is that, thanks to the phase ϕ, the output noise can remain at the shot noise level, e.g., N ≃ 1.12 at ϕ = 0.76π when γ = 0.5Γ (Blue line), N ≃ 1.03 at ϕ = 0.84π when γ = Γ (Red line) and N ≃ 1.00 at ϕ = 0.89π when γ = 2Γ (Green line), which are about one order of magnitude smaller than NS, as shown as the inset in Figure 4B. In Figure 4C, it shows that SNR per photon increases as the loss γ increases when ϕ ∈ [π, 2π], but indeed, SNR per photon reaches its maximum value at γ ≃ 2Γ. 2As we mentioned in the last section, the shot noise is the fundamental limit of the output noise for any sensor. This result also applies to our giant-cavity-based proposal, as shown in Figure 5. The reflective gain and dissipative loss cannot simultaneously be zero although they can be zero by adjusting the phase ϕ, which also explains why the noise is always greater than the shot noise in Figure 4B.
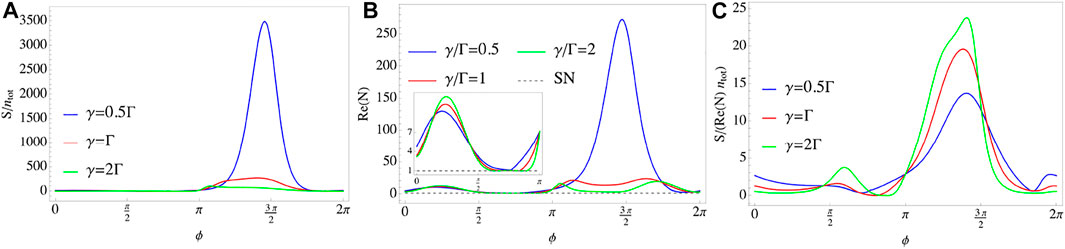
FIGURE 4. (Color online) Relative signal per photon, noise, and SNR per photon as the functions of ϕ at the resonant point. Parameters in plotting are: Δ = Δ12 = 0, J = Γ = 0.1κ. (A) The relative signal as the function of ϕ. As the loss γ increases, the maximum value of the signal decreases; (B) The relative noise as the function of ϕ. The term “SN” is the abbreviation for Shot Noise. Similar to (A), the noise also increases as the loss γ increases, and it is always greater than the shot noise. However, at some certain ϕ, the noise can remain at the shot noise level, e.g., N ≃ 1.12 at ϕ = 0.76π when γ = 0.5Γ, N ≃ 1.03 at ϕ = 0.84π when γ = Γ and N ≃ 1.00 at ϕ = 0.89π when γ = 2Γ. (C) The relative SNR per photon as the function of ϕ. Similar to (A) and (B), SNR per photon also increases as the loss γ increases.
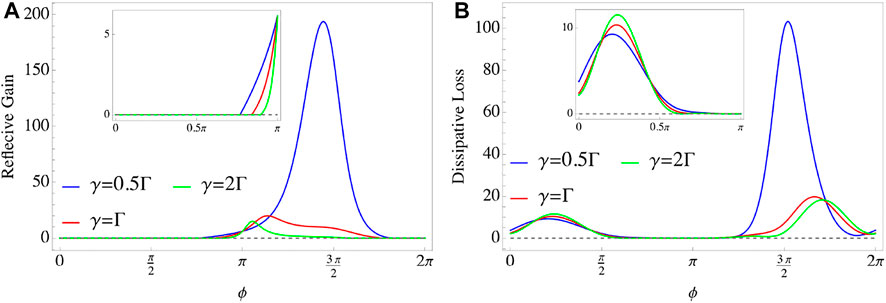
FIGURE 5. (Color online) Reflective gain (A) and dissipative loss (B) as the functions of ϕ. Parameters in plotting are: Δ = Δ12 = 0, J = Γ = 0.1κ. Both reflective gain and dissipative loss can be zero at some certain ϕ but they cannon be zero simultaneously, which is the reason why the noise is always greater than the shot noise in Figure 4B.
A clear comparison with the sensor made up of the small cavities is plotted in Figure 6. As Figure 6A shows, the signal per photon of giant-cavity proposal S/ntot can be about one order of magnitude greater than that of small-cavity proposal
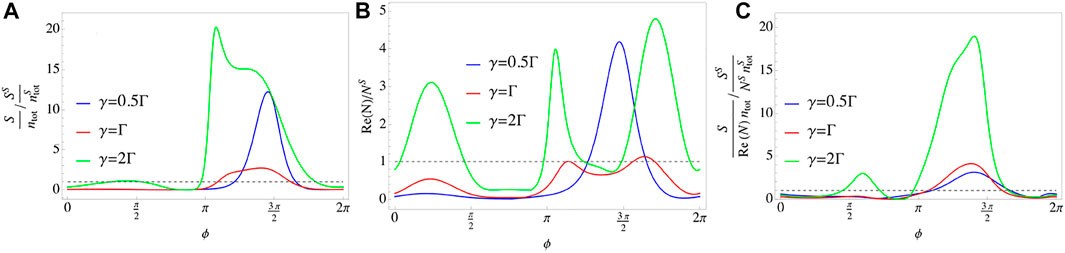
FIGURE 6. (Color online) The ratios of signal per photon (A), output noise (B) and SNR per photon (C) between sensors made up of giant and small cavities. Parameters in plotting are: Δ = Δ12 = 0 and J = Γ = 0.1κ. (A) For some certain intervals, e.g [π, 1.5π], the signals S/ntot are greater than
5 Conclusion and Future Works
In conclusion, we proposed a quantum sensor consisting of two giant cavities. By coupling cavities to a dissipative reservoir at multiple points, a non-reciprocal interaction can be engineered between the cavities and the common reservoir, which requires no non-linear elements. Compared to the standard two-mode quantum sensor [14], the output noise can remain at the shot noise level, which is reduced by about one order of magnitudes. And the signal-to-noise ratio per photon is also enhanced by about one order of magnitude. These results show that the giant-cavity-based sensor can effectively improve sensing precision.
A future direction is to consider how the non-Markovian effect affects the sensing performance. Since we only consider the cases at the resonant point, such that the non-Markovian effect depending on Δτ is neglected. However, this degree of freedom plays important roles in the deep non-Markovian regime τ ≫ 1/κ [35], e.g., it induces a non-exponential decay [37] and a multi-peak excitation spectrum [48]. Therefore, how these non-Markovian effects affect the sensing performance is an open question to be explored in the future, especially when a coherent feedback is applied to control the system [58–62]. A possible method to investigate the influences of the non-Markovian effect is utilizing the quantum simulation platform [63].
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
YZ and SX conceived the work. SX supervised the project. RW and ZP provided critical comments, suggestions, and text. YZ wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
Funding
This work was supported by the National Natural Science Foundation of China (NSFC) under Grants 61873162, 61973317, 61833010, 62173201, 12074117 and 12061131011. This work was also supported by the Open Research Project of the State Key Laboratory of Industrial Control Technology, Zhejiang University, China (No. ICT2022B47).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors thank Lei Du, Wenlong Li, Qiuyuan Cai, and Sulin Feng for the fruitful discussion.
Footnotes
1Since the perturbation is small enough, such that it can be expanded as a small quantity and kept to the first order.
2We have simulated SNR with γ ∈ {0.25Γ, 0.5Γ, Γ, 2Γ, 4Γ, 8Γ, 16Γ} and found SNR per photon is maximum at γ = 2Γ. For the sake of keeping the picture simple and clear, we do not show other curves in Figure 4C.
References
1. Schnabel R, Mavalvala N, McClelland DE, Lam PK. Quantum Metrology for Gravitational Wave Astronomy. Nat Commun (2010) 1:121. doi:10.1038/ncomms1122
2. Stray B, Lamb A, Kaushik A, Vovrosh J, Rodgers A, Winch J, et al. Quantum Sensing for Gravity Cartography. Nature (2022) 602:590–4. doi:10.1038/s41586-021-04315-3
3. Vollmer F, Arnold S, Keng D. Single Virus Detection from the Reactive Shift of a Whispering-Gallery Mode. Proc Natl Acad Sci U.S.A (2008) 105:20701–4. doi:10.1073/pnas.0808988106
4. Zhu J, Ozdemir SK, Xiao Y-F, Li L, He L, Chen D-R, et al. On-chip Single Nanoparticle Detection and Sizing by Mode Splitting in an Ultrahigh-Q Microresonator. Nat Photon (2010) 4:46–9. doi:10.1038/nphoton.2009.237
5. Zhao N, Hu J-L, Ho S-W, Wan JTK, Liu RB. Atomic-scale Magnetometry of Distant Nuclear Spin Clusters via Nitrogen-Vacancy Spin in diamond. Nat Nanotech (2011) 6:242–6. doi:10.1038/nnano.2011.22
6. Shi F, Kong X, Wang P, Kong F, Zhao N, Liu R-B, et al. Sensing and Atomic-Scale Structure Analysis of Single Nuclear-Spin Clusters in diamond. Nat Phys (2014) 10:21–5. doi:10.1038/nphys2814
7. Xu X, Chen W, Zhao G, Li Y, Lu C, Yang L. Wireless Whispering-Gallery-Mode Sensor for thermal Sensing and Aerial Mapping. Light Sci Appl (2018) 7:62. doi:10.1038/s41377-018-0063-4
8. Sánchez-Burillo E, Duch J, Gómez-Gardeñes J, Zueco D. Quantum Navigation and Ranking in Complex Networks. Sci Rep (2012) 2:605. doi:10.1038/srep00605
9. Marks P. Quantum Positioning System Steps in when Gps Fails. New Scientist (2014) 222:19. doi:10.1016/S0262-4079(14)60955-6
10. Li B-B, Bulla D, Prakash V, Forstner S, Dehghan-Manshadi A, Rubinsztein-Dunlop H, et al. Invited Article: Scalable High-Sensitivity Optomechanical Magnetometers on a Chip. APL Photon (2018) 3:120806. doi:10.1063/1.5055029
11. Li B-B, Bílek J, Hoff UB, Madsen LS, Forstner S, Prakash V, et al. Quantum Enhanced Optomechanical Magnetometry. Optica (2018) 5:850–6. doi:10.1364/OPTICA.5.000850
12. Yu C, Janousek J, Sheridan E, McAuslan DL, Rubinsztein-Dunlop H, Lam PK, et al. Optomechanical Magnetometry with a Macroscopic Resonator. Phys Rev Appl (2016) 5:044007. doi:10.1103/PhysRevApplied.5.044007
13. Sounas DL, Alù A. Non-reciprocal Photonics Based on Time Modulation. Nat Photon (2017) 11:774–83. doi:10.1038/s41566-017-0051-x
14. Lau H-K, Clerk AA. Fundamental Limits and Non-reciprocal Approaches in Non-Hermitian Quantum Sensing. Nat Commun (2018) 9:4320. doi:10.1038/s41467-018-06477-7
15. Potton RJ. Reciprocity in Optics. Rep Prog Phys (2004) 67:717–54. doi:10.1088/0034-4885/67/5/r03
16. Casimir HBG. On Onsager's Principle of Microscopic Reversibility. Rev Mod Phys (1945) 17:343–50. doi:10.1103/RevModPhys.17.343
17. Peng B, Özdemir ŞK, Lei F, Monifi F, Gianfreda M, Long GL, et al. Parity-time-symmetric Whispering-Gallery Microcavities. Nat Phys (2014) 10:394–8. doi:10.1038/nphys432310.1038/nphys2927
18. Peng B, Özdemir ŞK, Liertzer M, Chen W, Kramer J, Yılmaz H, et al. Chiral Modes and Directional Lasing at Exceptional Points. Proc Natl Acad Sci U.S.A (2016) 113:6845–50. doi:10.1073/pnas.1603318113
19. McDonald A, Clerk AA. Exponentially-enhanced Quantum Sensing with Non-Hermitian Lattice Dynamics. Nat Commun (2020) 11:5382. doi:10.1038/s41467-020-19090-4
20. Allen PJ. The Turnstile Circulator. IEEE Trans Microwave Theor Techn. (1956) 4:223–7. doi:10.1109/TMTT.1956.1125066
21. Auld BA. The Synthesis of Symmetrical Waveguide Circulators. IEEE Trans Microwave Theor Techn. (1959) 7:238–46. doi:10.1109/TMTT.1959.1124688
22. Scalora M, Dowling JP, Bowden CM, Bloemer MJ. The Photonic Band Edge Optical Diode. J Appl Phys (1994) 76:2023–6. doi:10.1063/1.358512
23. Tocci MD, Bloemer MJ, Scalora M, Dowling JP, Bowden CM. Thin‐film Nonlinear Optical Diode. Appl Phys Lett (1995) 66:2324–6. doi:10.1063/1.113970
24. Konotop VV, Kuzmiak V. Nonreciprocal Frequency Doubler of Electromagnetic Waves Based on a Photonic Crystal. Phys Rev B (2002) 66:235208. doi:10.1103/PhysRevB.66.235208
25. Zhukovsky SV, Smirnov AG. All-optical Diode Action in Asymmetric Nonlinear Photonic Multilayers with Perfect Transmission Resonances. Phys Rev A (2011) 83:023818. doi:10.1103/PhysRevA.83.023818
26. Abdo B, Sliwa K, Frunzio L, Devoret M. Directional Amplification with a Josephson Circuit. Phys Rev X (2013) 3:031001. doi:10.1103/PhysRevX.3.031001
27. Wang D-W, Zhou H-T, Guo M-J, Zhang J-X, Evers J, Zhu S-Y. Optical Diode Made from a Moving Photonic Crystal. Phys Rev Lett (2013) 110:093901. doi:10.1103/PhysRevLett.110.093901
28. Abdo B, Sliwa K, Shankar S, Hatridge M, Frunzio L, Schoelkopf R, et al. Josephson Directional Amplifier for Quantum Measurement of Superconducting Circuits. Phys Rev Lett (2014) 112:167701. doi:10.1103/PhysRevLett.112.167701
29. Fang K, Luo J, Metelmann A, Matheny MH, Marquardt F, Clerk AA, et al. Generalized Non-reciprocity in an Optomechanical Circuit via Synthetic Magnetism and Reservoir Engineering. Nat Phys (2017) 13:465–71. doi:10.1038/nphys4009
30. Xu Q, Schmidt B, Pradhan S, Lipson M. Micrometre-scale Silicon Electro-Optic Modulator. Nature (2005) 435:325–7. doi:10.1038/nature03569
31. Phare CT, Daniel Lee Y-H, Cardenas J, Lipson M. Graphene Electro-Optic Modulator with 30 GHz Bandwidth. Nat Photon (2015) 9:511–4. doi:10.1038/nphoton.2015.122
32. Kockum AF, Delsing P, Johansson G. Designing Frequency-dependent Relaxation Rates and Lamb Shifts for a Giant Artificial Atom. Phys Rev A (2014) 90:013837. doi:10.1103/PhysRevA.90.013837
33. Schuetz MJA, Kessler EM, Giedke G, Vandersypen LMK, Lukin MD, Cirac JI. Universal Quantum Transducers Based on Surface Acoustic Waves. Phys Rev X (2015) 5:031031. doi:10.1103/PhysRevX.5.031031
34. Manenti R, Kockum AF, Patterson A, Behrle T, Rahamim J, Tancredi G, et al. Circuit Quantum Acoustodynamics with Surface Acoustic Waves. Nat Commun (2017) 8:975. doi:10.1038/s41467-017-01063-9
35. Guo L, Grimsmo A, Kockum AF, Pletyukhov M, Johansson G. Giant Acoustic Atom: A Single Quantum System with a Deterministic Time Delay. Phys Rev A (2017) 95:053821. doi:10.1103/PhysRevA.95.053821
36. Kockum AF, Johansson G, Nori F. Decoherence-free Interaction between Giant Atoms in Waveguide Quantum Electrodynamics. Phys Rev Lett (2018) 120:140404. doi:10.1103/physrevlett.120.140404
37. Andersson G, Suri B, Guo L, Aref T, Delsing P. Non-exponential Decay of a Giant Artificial Atom. Nat Phys (2019) 15:1123–7. doi:10.1038/s41567-019-0605-6
38. Ekström MK, Aref T, Ask A, Andersson G, Suri B, Sanada H, et al. Towards Phonon Routing: Controlling Propagating Acoustic Waves in the Quantum Regime. New J Phys (2019) 21:123013. doi:10.1088/1367-2630/ab5ca5
39. Delsing P, Cleland AN, Schuetz MJA, Knörzer J, Giedke G, Cirac JI, et al. The 2019 Surface Acoustic Waves Roadmap. J Phys D: Appl Phys (2019) 52:353001. doi:10.1088/1361-6463/ab1b04
40. Kannan B, Ruckriegel MJ, Campbell DL, Kockum AF, Braumüller J, Kim DK, et al. Waveguide Quantum Electrodynamics with Superconducting Artificial Giant Atoms. Nature (2020) 583:775–9. doi:10.1038/s41586-020-2529-9
41. Kockum AF. Quantum Optics with Giant Atoms-The First Five Years. In: International Symposium on Mathematics, Quantum Theory, and Cryptography. Singapore: Springer (2021). p. 125–46. doi:10.1007/978-981-15-5191-8_12
42. Guo L, Kockum AF, Marquardt F, Johansson G. Oscillating Bound States for a Giant Atom. Phys Rev Res (2020) 2:043014. doi:10.1103/PhysRevResearch.2.043014
43. Vadiraj AM, Ask A, McConkey TG, Nsanzineza I, Chang CWS, Kockum AF, et al. Engineering the Level Structure of a Giant Artificial Atom in Waveguide Quantum Electrodynamics. Phys Rev A (2021) 103:023710. doi:10.1103/PhysRevA.103.023710
44. Du L, Cai M-R, Wu J-H, Wang Z, Li Y. Single-photon Nonreciprocal Excitation Transfer with Non-Markovian Retarded Effects. Phys Rev A (2021) 103:053701. doi:10.1103/PhysRevA.103.053701
45. Du L, Li Y. Single-photon Frequency Conversion via a Giant Λ -type Atom. Phys Rev A (2021) 104:023712. doi:10.1103/PhysRevA.104.023712
46. Du L, Zhang Y, Wu J-H, Kockum AF, Li Y. Giant Atoms in Synthetic Frequency Dimensions. arXiv: 2111.05584 (2021).
47. Cai QY, Jia WZ. Coherent Single-Photon Scattering Spectra for a Giant-Atom Waveguide-QED System beyond the Dipole Approximation. Phys Rev A (2021) 104:033710. doi:10.1103/PhysRevA.104.033710
48. Zhu Y, Wu R, Xue S. Spatial Non-Locality Induced Non-Markovian EIT in a Single Giant Atom. arXiv: 2106.05020 (2021).
49. Pezzè L, Smerzi A, Oberthaler MK, Schmied R, Treutlein P. Quantum Metrology with Nonclassical States of Atomic Ensembles. Rev Mod Phys (2018) 90:035005. doi:10.1103/RevModPhys.90.035005
50. Degen CL, Reinhard F, Cappellaro P. Quantum Sensing. Rev Mod Phys (2017) 89:035002. doi:10.1103/RevModPhys.89.035002
51. Bao L, Qi B, Dong D, Nori F. Fundamental Limits for Reciprocal and Nonreciprocal Non-Hermitian Quantum Sensing. Phys Rev A (2021) 103:042418. doi:10.1103/PhysRevA.103.042418
52. Shen J-T, Fan S. Theory of Single-Photon Transport in a Single-Mode Waveguide. I. Coupling to a Cavity Containing a Two-Level Atom. Phys Rev A (2009) 79:023837. doi:10.1103/PhysRevA.79.023837
53. Zhu YT, Jia WZ. Single-photon Quantum Router in the Microwave Regime Utilizing Double Superconducting Resonators with Tunable Coupling. Phys Rev A (2019) 99:063815. doi:10.1103/PhysRevA.99.063815
54. Clerk AA, Devoret MH, Girvin SM, Marquardt F, Schoelkopf RJ. Introduction to Quantum Noise, Measurement, and Amplification. Rev Mod Phys (2010) 82:1155–208. doi:10.1103/RevModPhys.82.1155
55. Huang S, Agarwal GS. Reactive-coupling-induced normal Mode Splittings in Microdisk Resonators Coupled to Waveguides. Phys Rev A (2010) 81:053810. doi:10.1103/PhysRevA.81.053810
56. Qu K, Agarwal GS. Phonon-mediated Electromagnetically Induced Absorption in Hybrid Opto-Electromechanical Systems. Phys Rev A (2013) 87:031802. doi:10.1103/PhysRevA.87.031802
57. Weis S, Rivière R, Deléglise S, Gavartin E, Arcizet O, Schliesser A, et al. Optomechanically Induced Transparency. Science (2010) 330:1520–3. doi:10.1126/science.1195596
58. Xue S-B, Wu R-B, Zhang W-M, Zhang J, Li C-W, Tarn T-J. Decoherence Suppression via Non-Markovian Coherent Feedback Control. Phys Rev A (2012) 86:052304. doi:10.1103/PhysRevA.86.052304
59. Xue S, Petersen IR. Realizing the Dynamics of a Non-Markovian Quantum System by Markovian Coupled Oscillators: a Green's Function-Based Root Locus Approach. Quan Inf Process (2016) 15:1001–18. doi:10.1007/s11128-015-1196-5
60. Xue S, Wu R, Hush MR, Tarn T-J. Non-Markovian Coherent Feedback Control of Quantum Dot Systems. Quan Sci. Technol. (2017) 2:014002. doi:10.1088/2058-9565/aa6125
61. Xue S, Hush MR, Petersen IR. Feedback Tracking Control of Non-Markovian Quantum Systems. IEEE Trans Contr Syst Technol (2017) 25:1552–63. doi:10.1109/TCST.2016.2614834
62. Xue S, Nguyen T, James MR, Shabani A, Ugrinovskii V, Petersen IR. Modeling for Non-Markovian Quantum Systems. IEEE Trans Contr Syst Technol (2020) 28:2564–71. doi:10.1109/TCST.2019.2935421
Keywords: giant cavities, quantum sensors, SNR (signal-to-noise ratio), non-Markovian quantum systems, quantum metrology, waveguide quantum electrodynamics, homodyne detection, position-dependent coupling
Citation: Zhu YT, Wu RB, Peng ZH and Xue S (2022) Giant-Cavity-Based Quantum Sensors With Enhanced Performance. Front. Phys. 10:896596. doi: 10.3389/fphy.2022.896596
Received: 15 March 2022; Accepted: 02 May 2022;
Published: 27 June 2022.
Edited by:
Andrew D. Greentree, RMIT University, AustraliaCopyright © 2022 Zhu, Wu, Peng and Xue. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shibei Xue, c2hieHVlQHNqdHUuZWR1LmNu
 Y. T. Zhu
Y. T. Zhu R. B. Wu
R. B. Wu Z. H. Peng
Z. H. Peng Shibei Xue
Shibei Xue