Beam Manipulations With Compact Planar Dielectric Pancharatnam–Berry Phase Devices

The growth spurt of novel planar optical devices in recent years has been greatly facilitated by the rapid development of artificial material designing and nanoprocessing technology. Traditional optical phase gradient devices cannot be scaled down to sub-wavelength size due to the confinement of the optical path difference required for versatile phase manipulation, so new strategies are urgently needed to design compact planar devices. Here, we develop a series of novel compact planar devices that break the thickness limitation by taking advantage of the superpositionable, polarization-dependent properties of the Pancharatnam–Berry phase. Among them, representative compact devices are fabricated using well-designed dielectric glass plates. Our compact devices therefore offer a novel and simple scheme to circumvent the accumulation of transmission loss in a cascade system of phase gradient devices.

Introduction

Planar optical devices have drawn much attention in recent years because of the development of two-dimensional (2D) structures including photonic crystals [1], nematic liquid crystal slabs [2], and metasurfaces [3–5]. By arranging building units in a sub-wavelength scale, artificial 2D structures present unprecedented performances in shaping the optical wave front. A variety of novel optical planar devices have been proposed, including holographic metasurfaces [6], ultrathin optical lens [7], and switchable devices [8, 9]. Different from general ultrathin planar devices, Pancharatnam–Berry (PB) phase [10] elements define the phase front of light spatially by molding the state of polarization (SOP) [11, 12]. Moreover, for most PB phase elements, the imposed phase can be modulated by just varying the incident state, which therefore offers a useful degree of freedom for light manipulation. Devices including optical planar lens [13, 14], vortex and vector beam generators [15–18], and linear gratings [19, 20] have been realized based on this principle. However, the cascading of planar PB phase devices is still restricted in practical applications mostly because of the low transmission rate of a single device. Although reflective devices have been demonstrated with high efficiency [21], they unavoidably increase the complexity in the cascading system. Dielectric planar devices exhibited high transmission efficiency to a larger extent [22, 23]; however, the series cascading of separated elements requires meticulous alignment in addition.

In this work, we developed a series of novel compact devices based on the mechanism of PB phase superposition. By integrating several phase diagrams, a single-PB phase device can be used to replace several separated elements while keeping the transmission rate. Moreover, the polarization-dependent property is considered in all designs. We further verified our designs by constructing several practical devices including the vortex beam splitter, Laguerre–Gaussian (LG) mode and Hermite–Gaussian (HG) mode convertor, high-order Bessel–Gaussian generator, and spin angular momentum–orbital angular momentum (SAM-OAM) multiplexer. Benefitting from the superposability provided by spin, our compact planar dielectric devices may promote the development of integrating optics.

The Superposition of Pancharatnam–Berry Phase

Light manipulation is significantly based on phase controlling. Conventional optical devices are obtained mostly by sculpting the contour profiles of bulk glasses, which impart a fixed phase distribution to the passing beam. The variation of the optical path length will lead to the change in the dynamical phase as $\left(\omega /c\right)n\cdot \Delta x$, where $\Delta x$ is the effective optical path, $n$ is the refractive index of material, $\omega$ is the angular frequency of light, and $c$ is speed of light in vacuum. It is clear that the change in the dynamical phase is proportional to the effective optical path afforded by the device. Thus, a given shape will be configured to get a phase gradient device, which is usually a great challenge for processing devices working in visible light. Moreover, as the full phase manipulation requires phase control from 0 to $2\pi$, the thickness of the conventional device should be greater than the effective wavelength ${\lambda }_0/n$ (${\lambda }_0$ is the operating wavelength in vacuum), which therefore restricts the miniaturization of these devices.

Different from the conventional dynamical phase accumulated with the propagation of light, planar optical devices provide an abrupt phase change through sub-wavelength unit cells. The unit geometry of size, thickness, orientation, and shape can be adjusted to tune the additional phase [5]. Moreover, external fields and environment changes can also be introduced to control the response of each unit [8, 9]. PB phases are obtained by ordering the evolution of polarization, which is usually related to the responses of building units controlled by their orientations [3, 6, 7]. A schematic example of polarization evolution in the birefringence material is depicted in Figure 1A. The middle panel shows a material arranged with rotational optical axes in a preferred direction, and the phase retardation is defined as $\pi$. Dash arrow lines represent the orientations of local optical axes, and short black arrows show the instant electric filed vectors. For a circularly polarized incident beam (left and right circular polarizations are represented by red and blue circles, respectively), the instant electric field vectors will be modulated according to the orientation of local optical axes. For a circularly polarized beam, it is well known that the temporal trace of the electric field vector represents the SOP, and the instant orientation reflects its phase. Therefore, the phase changes can be mapped to the orientation of local optical axes one by one, respectively.

FIGURE 1

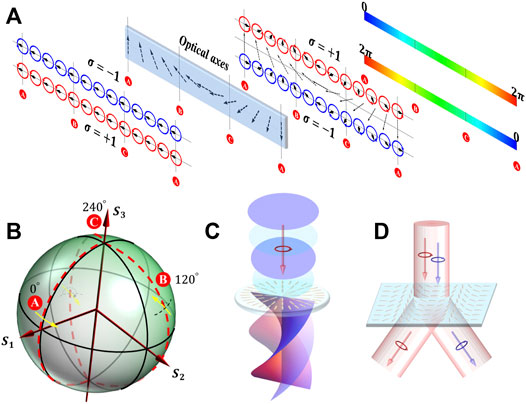
FIGURE 1. (A) Polarization evolutions under the modulation of artificial materials with spatially varying optical axes are constructed. The input and output SOPs are depicted in the first and third panels, respectively; red and blue circles represent the right- and left-circular polarizations, respectively; short arrows enclosed by these circles are the representations of instantaneous electric field vectors (corresponding to the phase shown in the fourth panel); dash arrow lines in the second panel show the orientations of local optical axes. It is shown that the circular polarization is reversed after passing through the material, and the orientation of the instantaneous electric field vectors is ordered by the orientation of local optical axes. (B) The Poincaré sphere are established to exhibit the evolution of SOP. Three evolving routes marked in red A, B, and C in the sphere highlight the evolutions under the optical axes with orientation angles $0^{°}$, ${60}^{°}$, and ${120}^{°}$, respectively. As the surface area enclosed by evolving routes on the Poincaré sphere determines the change of the geometric PB phase, the final phase values along these three evolving routes from the same direction are represented as ${\Phi }_0\pm 0^{°}$, ${\Phi }_0\pm {120}^{°}$, and ${\Phi }_0\pm {240}^{°}$, respectively. Yellow arrows represent the output orientation of the instantaneous electric field vectors. (C) and (D) Examples of constructed PB phase devices: vortex beam generator and circular polarization splitter. Short rods in the plates show the orientation of the local optical axes, where right- and left-circular polarizations are marked with red and blue arrows, respectively.

To precisely calculate the phase changes, a Poincaré sphere is applied to concretize the polarization space, which is a unit sphere involving all the homogenous polarization states, as shown in Figure 1B. Normalized Stokes parameters ($S_1$, $S_2$, and $S_3$) are the reference coordinates to characterize polarization states. Left and right circular polarizations are the orthogonal basis sets of the whole space, which are located at north ($0, 0, 1$) and south ($0, 0, -1$) poles, respectively. According to Berry’s theory [9], cyclic evolution of polarization states will lead to a phase change equaling half of the solid angle enclosed by the evolving route in the polarization space. Thus, the additional geometric phase can be deduced as $\phi =\Omega /2$, where $\Omega$ is the solid angle enclosed by the evolving route in the parameter space. Three representative evolving routes from the north to the south pole are marked in red A, B, and C in Figure 1B (the corresponding states are marked in Figure 1A). It is found that to choose a different departure route from the north to the south pole, the corresponding orientation of local optical axes is half the longitude (${\tan }^{-1}\left(S_2/S_1\right)$) of the corresponding routes on the Poincaré sphere.

The evolutions can be retrieved mathematically by the Jones calculus, which is a universal tool to analyze light propagation in different materials. The Jones matrix for a homogenous wave plate with a fixed optical axis ($x$ axis) can be written as

$J=\left[\begin{array}{cc}{t}_x\exp \left(-i\Phi /2\right)& 0\\ 0& t_y\exp \left(i\Phi /2\right)\end{array}\right],(1)$

where $t_x$ and $t_y$ are the transmission coefficients along $x$ and $y$ axes, respectively; $\Phi$ is the phase retardation of the birefringence material. For an inhomogeneous artificial material, the local optical axes are different in each position; thus, a rotation matrix can be used to adjust the Jones matrix.

$\mathrm{\Theta }\left(\alpha \right)=\left[\begin{array}{cc}\cos \alpha & \sin \alpha \\ -\sin a& \cos \alpha \end{array}\right],(2)$

where $\alpha$ represents the orientation of the optical axis with respect to the horizontal direction. Incident polarization $|P_{in}\rangle$ can be represented as

$|{\mathrm{P}}_{in}=\left[\begin{array}{c}\cos \theta \\ {\mathrm{e}}^{i\delta }\sin \theta \end{array}\right]E_0{\mathrm{e}}^{-i\phi },(3)$

where $E_0$ is the field intensity, $\phi$ is the phase term, $\theta$ is the orientation of incident polarization, and $\delta$ is the phase difference between $x$ and $y$ components. When $\delta =\pm \pi /2$ and $\theta =\pm \pi /4$, $|P_{in}\rangle$ is selected to be circular polarizations $|L/R\rangle ={\left(\begin{array}{cc}1& \pm i\end{array}\right)}^T$, where the intensity and phase factor are omitted. Therefore, the emerging field can be calculated by multiplying them together:

$\begin{array}{l}|{\mathrm{P}}_{\mathrm{o}\mathrm{u}\mathrm{t}}=\mathrm{\Theta }{\left(\alpha \right)}^{-1}\cdot J\cdot \mathrm{\Theta }\left(\alpha \right)\cdot |L/R\\ ={\eta }_{L/R}|L/R{\mathrm{e}}^{-i\left(-2\phi -\frac{\Phi }{2}\right)}+{\eta }_{R/L}|R/L{\mathrm{e}}^{-i\left(2\alpha -2\phi -\frac{\Phi }{2}\right)},\end{array}(4)$

where ${\eta }_{L/R}=\left[t_x+t_y\exp \left(-i\Phi \right)\right]/2$ and ${\eta }_{R/L}=\left[t_x-t_y\exp \left(-i\Phi \right)\right]/2$. Thus, the output field can be divided into a polarization invariant part and a reversed part, and the reversed part obtains an additional phase:

$\mathrm{\Delta }\Psi =-2\sigma \alpha .(5)$

As the additional phase is related to the orientation of local optical axes, elements requiring complex phase modulation can be achieved without increasing the processing precision by using the PB phase. Theoretically, cascading of optical phase gradient devices equals the superposition of phases provided by each single element. Thus, the integration of a finite number of phase gradient elements can be achieved by constructing a device with the superposed phase profile. As the periodicity of the phase value, the superposed phase profile can be reduced to the interval $\left[\begin{array}{cc}0, & 2\pi \end{array}\right]$, which corresponds to the local optical axes orientated in $\left[\begin{array}{cc}0,& \pi \end{array}\right]$ according to Eq. (5).

Figure 2 shows a simple example to explain our principle. The vortex beam generator (Figure 1A) and circular polarization splitter (Figure 1B) are integrated to get a polarization (spin)-dependent vortex beam splitter (Figure 1C). Figure 2A shows the phase profile ${\Psi }_1\left(x,y\right)=l\cdot {\tan }^{-1}\left(y/x\right)$ (here $l=1$, and $x$ and $y$ are the Cartesian coordinates), which enables the conversion from a general beam to a vortex beam carrying OAM $l\hslash$ ($\hslash$ is the reduced Plank constant). Figure 2B shows the phase profile ${\Psi }_2\left(x,y\right)=2\pi \cdot x/\Lambda$ ($\Lambda$ is the phase period), which could deflect the beam with an angle $k_0^{-1}\cdot 2\pi /\Lambda$ ($k_0^{-1}={\lambda }_0/2\pi$, ${\lambda }_0$ is the operating wavelength). The superposed phase is given as follows:

${\Psi }_{1+2}\left(x,y\right)={\Psi }_1\left(x,y\right)+{\Psi }_2\left(x,y\right),(6)$

which is shown in Figure 2C. A representative point ($\Lambda /5$, $\Lambda /5\cdot \tan \pi /8$) (red dots in Figures 2A–C) is chosen to present the expected evolving routes on the Poincaré sphere (as shown Figures 2D–F). To construct the integrated device, the required optical axis distribution is deduced according to Eq. 5 as follows:

${\alpha }_{1+2}\left(x,y\right)={\alpha }_1\left(x,y\right)+{\alpha }_2\left(x,y\right)=\frac{1}{2}\cdot {\Psi }_{1+2}\left(x,y\right).(7)$

FIGURE 2

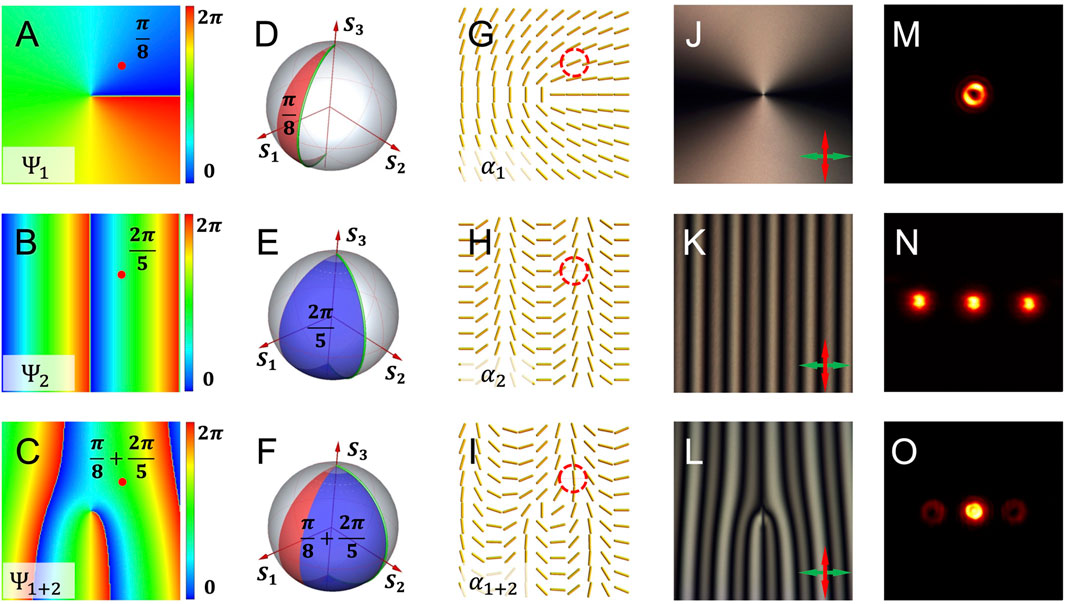
FIGURE 2. Design process of a vortex beam splitter is decomposed to demonstrate the principle of PB phase integration. (A–C) Superposition of a vortex phase (A) and a linear gradient phase (B) shows a fork-shaped phase (C). A selected point is highlighted with a red dot to show the superposition of phase values. (D–F) Poincaré spheres demonstrate the polarization evolving routes (green longitude lines) for the desired phase changes (colored regions) corresponding to the specific point in (A–C), respectively. It is shown that the phase changes can be achieved by controlling the evolving routes. (G–I) Desired distributions of the optical axes are painted, which correspond to the devices with phase profiles exhibited in the first column. (J–L) Polariscopic analyses are applied to verify the distributions of local optical axes. Red and green arrows represent the orientation of incident polarization and the analyzer, respectively. (M–O) Experimental intensities obtain by testing the corresponding devices.

Figures 2G–I are the expected optical axis distributions of the corresponding phase profiles.

To verify our designs, the femtosecond laser writing technique is applied to obtain the dielectric planar samples operating in a wavelength of $632.8nm$. Sub-wavelength gratings are constructed under the laser writing, which can be treated as a uniaxial crystal with optical fast and slow axes perpendicular and parallel to the gratings, respectively. The local orientation of the gratings can be modulated by rotating the polarization of the writing beam. To examine the orientation of the local optical axes without destroying the structures, polariscopic analyses are implemented in our experiments, which record the microscopic images of the structure under crossed polarizers. Figures 2J–L are the polariscopic analysis results of our samples, which show a good agreement with the expected optical axis distributions (Figures 2G–I). Figures 2M–O are the experimental intensities obtained by our planar devices. The ring-shaped distributions in Figures 2M,O represent the generation of a vortex beam. The middle spots in Figures 2N,O are the transmitted part of light due to the defects in our samples.

Results

To show the ability of our principles for designing complicated planar devices, several compact PB phase devices are constructed as follows. First, we constructed a convertor for the LG and HG modes. Both modes are the acceptable forms of transverse distributions of the electric field in laser cavities [24], enabling unique practical applications in particle manipulation [25, 26], light communication [27], and laser processing [28]. The LG mode can be decomposed into a set of HG modes with the same order, and vice versa [29]. In traditional optics, a pair of cylindrical lenses can realize the conversion between LG and HG modes [30]. However, this kind of convertor cannot be miniaturized as suitable separation between the lenses should be maintained to achieve the transform.

LG-HG Mode Convertor

Both LG and HG modes are widely used in laser applications. However, the conversion between them does not seem straightforward because different sources are always needed to produce these two modes in practical experiments. Most recently, a PB phase device for the conversion between the general Gaussian mode and the HG mode has been proposed [31]. Thus, in the optical integration way, the convertor for the LG and HG modes can be achieved by cascading two independent devices: an LG-to-Gaussian mode converter and a Gaussian-to-HG mode converter. The example of phase profiles of these two devices is demonstrated in Figure 3A (for HG₁₁) and Figure 3B (for LG₀₁). Following the designing principles introduced previously, the superposed phase profile and corresponding optical axis distribution are presented in Figures 3C,D. Figure 3E,F show the polariscopic analysis results under parallel and perpendicular linear polarizers, respectively. Then, the convertor is examined by an HG₁₁ (Figure 3G) beam and an LG₀₁ (Figure 3J) beam. Intensities shown in Figures 3H,K present the results of obtained LG₀₁ and HG₁₁ modes, respectively. To further verify the results, interference experiments with a general Gaussian beam are implemented. A typical fork-shaped dislocation shown in Figure 3I confirms the existence of the LG₀₁ mode. The mismatches of fringe arrays in Figures 3L,M represent the phase mutation in the direction orthogonal to the fringes in the tested field, which verifies that the converted field is an HG₁₁ mode.

FIGURE 3

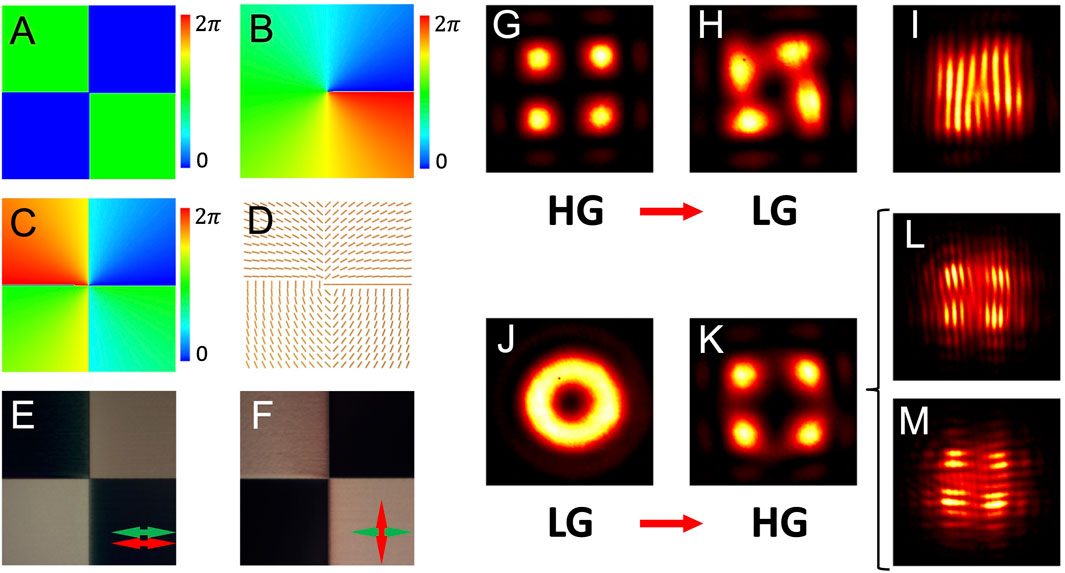
FIGURE 3. (A–C) Phase profiles of the HG₁₁ mode, LG₀₁ mode, and integrated phase. (D) Distribution of local optical axes of the desired mode converter. (E,F) Polariscopic analysis results of the constructed device. Red and green arrows indicate the orientations of the incident polarization state and the orientation of the analyzer. (G–I) Experimental intensities obtained when the device is working as an HG-to-LG mode converter. The incident HG₁₁ mode (G) and obtained LG₀₁ mode (H) are demonstrated. Interference fringes (I) imply the phase singularity in the obtained LG₀₁ mode. (J–M) Experimental intensities obtained when the device is working as an LG-to-HG mode converter. (J,K) are the intensity patterns of the incident and obtained beams. (L,M) Phase mutations in horizontal and vertical directions, respectively.

Higher Order BG Beam Generator

Second, we build a higher order Bessel–Gaussian (BG) beam generator. OAM provides an infinite volume for data coding and shows a new degree of freedom in light manipulation, which is substantially determined by the spatial property of the beam [21]. Vortex beam possessing winding phase distribution around its central axis is inherently endowed with a non-zero OAM [32]. Generally, the PB phase arises from the spin (polarization)–orbit interactions in light, thus presenting good ability in controlling these two degrees of freedom. In particular, the PB phase is widely applied in the design of vortex devices in planar optics. BG beams provide an alternative solution for OAM-carrying beams [33]. A zero-order BG beam possess a bright central spot, while higher order BG beams show a dark center as the presentation of phase singularity. Similar to the higher order LG mode, the higher order BG beams possess a vortex phase term $\exp \left(il\phi \right)$. Thus, $l\hslash$ units of OAM are accompanied with the $l$-order BG beam. Moreover, benefiting from the property of nearly non-diffraction and self-reconstruction, higher order BG beams have found great potential in the optical imaging [34, 35], micromanipulation [36], and quantum communication [37]. In conventional optics, the zero-order BG beam can be produced by the combination of a ring slit aperture and a lens with a fixed separation or by the axicons. However, the higher order BG beams cannot be obtained with a single device. Thus, designing a compact device to generate higher order BG beams is of great importance.

The phase profile of a typical zero-order BG mode is a set of equal-width concentric annuluses, where the adjacent annuluses are endowed with distinct phase values in a difference $\pi$ as the example in Figure 4B. To get the higher order modes, the vortex phase term (Figure 4A) should be added to the zero-order BG mode. Thus, we get the superposed phase as demonstrated in Figure 4C. According to Eq. 5, the local optical axis distributions are depicted in Figures 4D–F. Dielectric examples are fabricated to verify these designs. Polariscopic analysis results in Figures 4G–I suggest the real distributions of the local optical axes, and their corresponding experimental intensities in Figures 4J–M clearly verify the ability of the compact devices. As can be seen, the zero-order BG mode result (Figure 4J) shows a typical BG intensity with equal-energy annuluses. The higher order mode results (Figure 4L,M) exhibit dark centers, implying the existence of phase singularity. In particular, the comparison between Figure 4K,M shows that the quality of the compact device is better than the cascading of two elements, where Figure 4M is the result of the cascaded examples (Figures 4G,H).

FIGURE 4

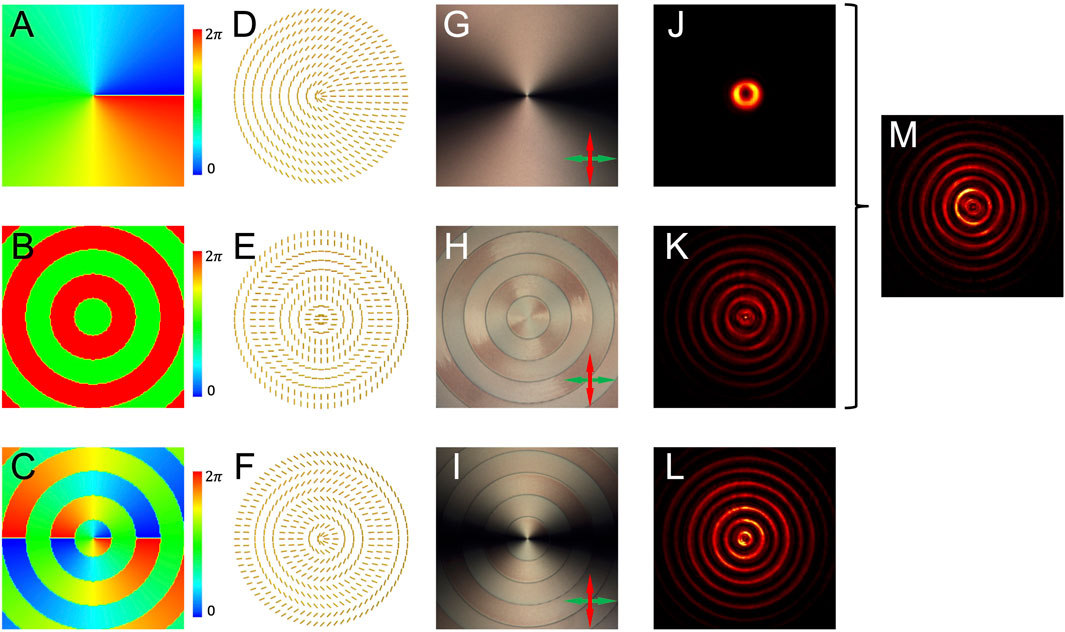
FIGURE 4. (A–C) Phase profiles of vortex, zero-order BG, and first-order BG beams. (D–F) Local optical axis distributions of expected PB phase devices corresponding to the phase profiles in the first column. (G–I) Polariscopic analysis results. (J–L) Experimental intensities obtained by using the samples corresponding to (G–I). (M) Intensity recorded when the vortex (G) and zero-order BG (H) generators are cascaded to get the first-order BG.

Compact SAM-OAM Multiplexer

The last example is an attempt to construct a compact SAM-OAM splitter. The SAM and OAM multiplexing techniques promise to enlarge the capacity of light communications in the fiber and free space. However, the splitting of different OAM modes is still complicated. A general way is to use the phase plates with particular profiles to split the modes one by one [24], which is too complicated to integrate in planar optical devices. Fork-shaped phase devices (similar to our example shown in Figure 2) have been proposed to divide the different OAM modes simultaneously [38]. However, these devices are restricted to split the opposite OAM modes in the same order. In particular, when SAM is considered in the system, the splitting system will become more and more complicated with the increasing of SAM and OAM channels.

Here, we show the solution by using a compact planar dielectric device. Figure 5 is the compact SAM and OAM splitter. As mentioned before, the linear gradient PB phase device (Figure 1D) can be used to separate different SAM states. However, in this case, the different SAM states are deflected to opposite directions. To solve this problem, we divide the phase plane to different annuluses, the phase gradients in different districts are varied and the signs of the gradients are opposite in the adjacent districts. To involve the different OAM states, each district is assigned with a vortex phase with different topological charges. Thus, the constructed phase is shown in Figure 5A, where the phase plane is divided in two districts for OAM states $\left|l\right|=1$ and $\left|l\right|=2$. Corresponding optical axis distribution and polariscopic analysis results are demonstrated in Figure 5B–D, respectively. The output intensities obtained by the sample, when a general Gaussian beam is illuminated, are exhibited in Figures 5E–I, where Figures 5F–I show the normalized intensities of all the separated modes. To verify their SAM and OAM states, the interference experiments are implemented for each split mode, as shown in Figure 5J–M. The fringe patterns show fork-shaped mismatches in the center, of which the number of staggered fringes imply their topological charge and the directions of fork are related to their sign of phase gradient (namely, SAM states in this case).

FIGURE 5

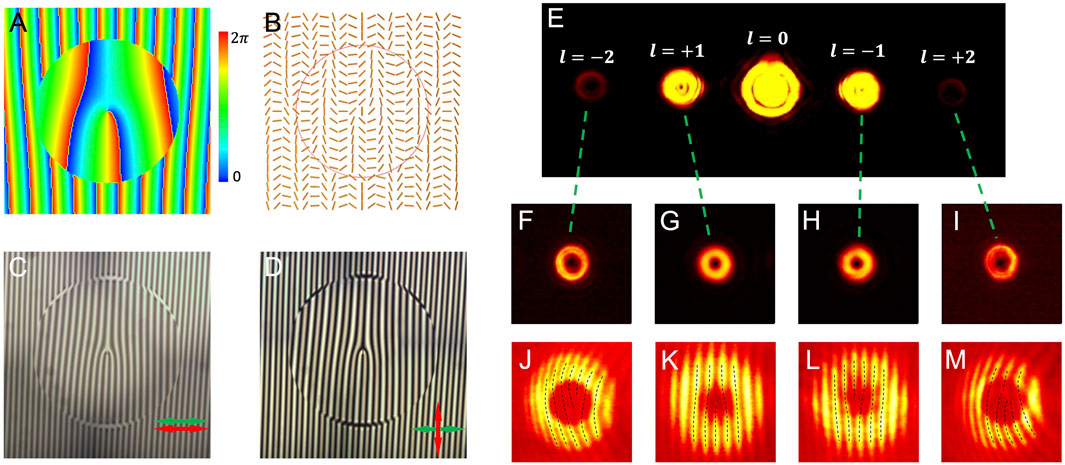
FIGURE 5. (A) Phase profile with two distinct parts along its radial direction. The inner part is designed with OAM $l=1$ and linear gradient with period $\Lambda =180\mu m$, while the outer part with $l=-2$ and $\Lambda =180\mu m$. (B) Desired local optical axis distribution. (C,D) Polariscopic analysis pictures of the real splitter. (E) Intensity pattern observed when a Gaussian beam impinges the splitter. (F–I) Individual intensity patterns recorded for each separated mode by filtering the other parts of the output light. Ring patterns with a dark center are demonstrated. (J–M) Interferences with a general Gaussian beam are implemented, which imply the SAM and OAM modes of each component. The mismatches in interference fringes indicate the order of topological charge (OAM), while the orientation of the fork patterns reveals its sign (SAM).

Methods

Dielectric Samples

The fabricated samples were constructed inside a silicon dioxide glass substrate. A polarized high-power femtosecond laser source was focused to a point under the surface of the substrate to induce the sub-wavelength grating. The process could be understood in an interference mechanism. A plasma electron wave would present in the glass after absorbing the energy of the photons of the writing beam. Components of the plasma electron wave in the plane of incident polarization would interfere with the writing beam. Thus, the negative electrons included in the illuminated area were redistributed, which led to the rearrangement of ionized oxide atoms. The structure was “frozen” after reaching the hot equilibrium, and finally, a grating in size comparable with the wavelength of writing laser was exhibited. The grating structure led to the birefringence of light in a specific wavelength. The effective ordinary and extraordinary refractive indexes could be obtained after a linear approximation:

$n_o=\sqrt{f{n}_1^2-\left(1-f\right)n_2^2},n_e=\sqrt{\frac{n_1^2{n}_2^2}{f{n}_2^2-\left(1-f\right)n_1^2}},$

where $n_o$ and $n_e$ refer to the ordinary and extraordinary refractive indexes, respectively; $n_1$ and $n_2$ are the actual refractive indexes of grain and ridge of grating, respectively; and $f$ is the fill factor. Thus, the phase retardation was calculated as $2\pi \left(n_e-n_o\right)h/\lambda$, where $h$ is the writing depth and $\lambda$ is the operating wavelength. The direction of the nano grating structures can be controlled by changing the polarization of the writing laser. Samples applied in this work were fabricated in Altechna R&D. The glass substrates had a round shape with a diameter equal to 25.4 mm and a thickness of 3 mm. The constructed structures possessed a clear aperture of 8 mm. Uniform phase retardation ($\pi$ at $632.8nm$) was fixed for all the samples.

Polariscopic Analyses

The polariscopic analyses were implemented under a polarized light microscope. The incident and detect polarizations were both adjusted by a flat polarizer. A digital camera recorded the pictures behind the eyepiece lens, and the magnification time was $10\times$.

Discussions and Conclusion

We have developed a convenient way to construct compact planar PB phase devices by integrating the phase profiles of separated elements. The superposition of PB phases is theoretically analyzed through the Poincaré sphere method. Several proof-of-principle devices are constructed by using the high-transmission efficiency dielectric sub-wavelength structures. The intensity distributions modulated by the conceived devices show a good agreement with expectations. It is worth noting that our principles are not limited to realize a particular planar device, which provides an intuitive way to construct novel PB phase elements and demonstrates a way to circumvent the higher transmission loss in a complex optical system. It can be applied to simplify all the cascaded phase-controlling elements in optical circuits. Our reported general principles extend the way to realize complicated planar devices, ushering in the area of light manipulation and communications.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work is supported by the National Natural Science Foundation of China (Grant Nos. 11904238, 11734012, and 12074267).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Chow E, Lin SY, Johnson SG, Villeneuve PR, Joannopoulos JD, Wendt JR, et al. Three-dimensional Control of Light in a Two-Dimensional Photonic crystal Slab. Nature (2000) 407:983–6. doi:10.1038/35039583

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Hikmet RAM, Kemperman H. Electrically Switchable Mirrors and Optical Components Made from Liquid-crystal Gels. Nature (1998) 392:476–9. doi:10.1038/33110

CrossRef Full Text | Google Scholar

3. Yu N, Capasso F. Flat Optics with Designer Metasurfaces. Nat Mater (2014) 13:139–50. doi:10.1038/nmat3839

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Meinzer N, Barnes WL, Hooper IR. Plasmonic Meta-Atoms and Metasurfaces. Nat Photon (2014) 8:889–98. doi:10.1038/nphoton.2014.247

CrossRef Full Text | Google Scholar

5. Kildishev AV, Boltasseva A, Shalaev VM. Planar Photonics with Metasurfaces. Science (2013) 339:1232009. doi:10.1126/science.1232009

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Huang L, Chen X, Mühlenbernd H, Zhang H, Chen S, Bai B, et al. Three-dimensional Optical Holography Using a Plasmonic Metasurface. Nat Commun (2013) 4:2808. doi:10.1038/ncomms3808

CrossRef Full Text | Google Scholar

7. Aieta F, Genevet P, Kats MA, Yu N, Blanchard R, Gaburro Z, et al. Aberration-free Ultrathin Flat Lenses and Axicons at Telecom Wavelengths Based on Plasmonic Metasurfaces. Nano Lett (2012) 12:4932–6. doi:10.1021/nl302516v

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Zheludev NI, Kivshar YS. From Metamaterials to Metadevices. Nat Mater (2012) 11:917–24. doi:10.1038/nmat3431

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Li L, Jun Cui T, Ji W, Liu S, Ding J, Wan X, et al. Electromagnetic Reprogrammable Coding-Metasurface Holograms. Nat Commun (2017) 8:197. doi:10.1038/s41467-017-00164-9

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Berry MV. The Adiabatic Phase and Pancharatnam's Phase for Polarized Light. J Mod Opt (1987) 34:1401–7. doi:10.1080/09500348714551321

CrossRef Full Text | Google Scholar

11. Bomzon Ze., Biener G, Kleiner V, Hasman E. Space-variant Pancharatnam-Berry Phase Optical Elements with Computer-Generated Subwavelength Gratings. Opt Lett (2002) 27:1141–3. doi:10.1364/OL.27.001141

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Maguid E, Yulevich I, Veksler D, Kleiner V, Brongersma ML, Hasman E. Photonic Spin-Controlled Multifunctional Shared-Aperture Antenna Array. Science (2016) 352:1202–6. doi:10.1126/science.aaf3417

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Hasman E, Kleiner V, Biener G, Niv A. Polarization Dependent Focusing Lens by Use of Quantized Pancharatnam-Berry Phase Diffractive Optics. Appl Phys Lett (2003) 82:328–30. doi:10.1063/1.1539300

CrossRef Full Text | Google Scholar

14. Chen X, Huang L, Mühlenbernd H, Li G, Bai B, Tan Q, et al. Dual-polarity Plasmonic Metalens for Visible Light. Nat Commun (2012) 3:1198. doi:10.1038/ncomms2207

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Beresna M, Gecevičius M, Kazansky PG, Gertus T. Radially Polarized Optical Vortex Converter Created by Femtosecond Laser Nanostructuring of Glass. Appl Phys Lett (2011) 98:201101. doi:10.1063/1.3590716

CrossRef Full Text | Google Scholar

16. Liu Y, Ling X, Yi X, Zhou X, Luo H, Wen S. Realization of Polarization Evolution on Higher-Order Poincaré Sphere with Metasurface. Appl Phys Lett (2014) 104:191110. doi:10.1063/1.4878409

CrossRef Full Text | Google Scholar

17. Li S, Li X, Zhang L, Wang G, Zhang L, Liu M, et al. Efficient Optical Angular Momentum Manipulation for Compact Multiplexing and Demultiplexing Using a Dielectric Metasurface. Adv Opt Mater. (2020) 8:1901666. doi:10.1002/adom.201901666

CrossRef Full Text | Google Scholar

18. Jin Z, Janoschka D, Deng J, Ge L, Dreher P, Frank B, et al. Phyllotaxis-inspired Nanosieves with Multiplexed Orbital Angular Momentum. eLight (2021) 1:1–11. doi:10.1186/s43593-021-00005-9

CrossRef Full Text | Google Scholar

19. Ding X, Monticone F, Zhang K, Zhang L, Gao D, Burokur SN, et al. Ultrathin Pancharatnam-Berry Metasurface with Maximal Cross-Polarization Efficiency. Adv Mater (2015) 27:1195–200. doi:10.1002/adma.201405047

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Ling X, Zhou X, Yi X, Shu W, Liu Y, Chen S, et al. Giant Photonic Spin Hall Effect in Momentum Space in a Structured Metamaterial with Spatially Varying Birefringence. Light Sci Appl (2015) 4–e290. doi:10.1038/lsa.2015.63

CrossRef Full Text | Google Scholar

21. Zheng G, Mühlenbernd H, Kenney M, Li G, Zentgraf T, Zhang S. Metasurface Holograms Reaching 80% Efficiency. Nat Nanotechnol (2015) 10:308–12. doi:10.1038/nnano.2015.2

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Lin D, Fan P, Hasman E, Brongersma ML. Dielectric Gradient Metasurface Optical Elements. Science (2014) 345:298–302. doi:10.1126/science.1253213

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Yi X, Ling X, Zhang Z, Li Y, Zhou X, Liu Y, et al. Generation of Cylindrical Vector Vortex Beams by Two Cascaded Metasurfaces. Opt Express (2014) 22:17207–15. doi:10.1364/OE.22.017207

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Allen L, Padgett MJ, Babiker M. IV the Orbital Angular Momentum of Light. Prog Opt (1999) 39:291–372. doi:10.1016/S0079-6638(08)70391-3

CrossRef Full Text | Google Scholar

25. Padgett M, Bowman R. Tweezers with a Twist. Nat Photon (2011) 5:343–8. doi:10.1038/nphoton.2011.81

CrossRef Full Text | Google Scholar

26. Paterson L, MacDonald MP, Arlt J, Sibbett W, Bryant PE, Dholakia K. Controlled Rotation of Optically Trapped Microscopic Particles. Science (2001) 292:912–4. doi:10.1126/science.1058591

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Wang J, Yang J-Y, Fazal IM, Ahmed N, Yan Y, Huang H, et al. Terabit Free-Space Data Transmission Employing Orbital Angular Momentum Multiplexing. Nat Photon (2012) 6:488–96. doi:10.1038/nphoton.2012.138

CrossRef Full Text | Google Scholar

28. Toyoda K, Miyamoto K, Aoki N, Morita R, Omatsu T. Using Optical Vortex to Control the Chirality of Twisted Metal Nanostructures. Nano Lett (2012) 12:3645–9. doi:10.1021/nl301347j

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Beijersbergen MW, Allen L, Van der Veen HELO, Woerdman JP. Astigmatic Laser Mode Converters and Transfer of Orbital Angular Momentum. Opt Commun (1993) 96:123–32. doi:10.1016/0030-4018(93)90535-D

CrossRef Full Text | Google Scholar

30. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital Angular Momentum of Light and the Transformation of Laguerre-Gaussian Laser Modes. Phys Rev A (1992) 45:8185–9. doi:10.1103/PhysRevA.45.8185

PubMed Abstract | CrossRef Full Text | Google Scholar

31. He Y, Liu Z, Liu Y, Zhou J, Ke Y, Luo H, et al. Higher-order Laser Mode Converters with Dielectric Metasurfaces. Opt Lett (2015) 40:5506–9. doi:10.1364/OL.40.005506

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Bliokh KY, Rodríguez-Fortuño FJ, Nori F, Zayats AV. Spin-orbit Interactions of Light. Nat Photon (2015) 9:796–808. doi:10.1038/nphoton.2015.201

CrossRef Full Text | Google Scholar

33. McGloin D, Dholakia K. Bessel Beams: Diffraction in a New Light. Contemp Phys (2005) 46:15–28. doi:10.1080/0010751042000275259

CrossRef Full Text | Google Scholar

34. Planchon TA, Gao L, Milkie DE, Davidson MW, Galbraith JA, Galbraith CG, et al. Rapid Three-Dimensional Isotropic Imaging of Living Cells Using Bessel Beam Plane Illumination. Nat Methods (2011) 8:417–23. doi:10.1038/nmeth.1586

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Fahrbach FO, Gurchenkov V, Alessandri K, Nassoy P, Rohrbach A. Self-reconstructing Sectioned Bessel Beams Offer Submicron Optical Sectioning for Large fields of View in Light-Sheet Microscopy. Opt Express (2013) 21:11425–40. doi:10.1364/OE.21.011425

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Garcés-Chávez V, McGloin D, Melville H, Sibbett W, Dholakia K. Simultaneous Micromanipulation in Multiple Planes Using a Self-Reconstructing Light Beam. Nature (2002) 419:145–7. doi:10.1038/nature01007

PubMed Abstract | CrossRef Full Text | Google Scholar

37. McLaren M, Mhlanga T, Padgett MJ, Roux FS, Forbes A. Self-healing of Quantum Entanglement after an Obstruction. Nat Commun (2014) 5:3248. doi:10.1038/ncomms4248

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Padgett M, Allen L. Light with a Twist in its Tail. Contemp Phys (2000) 41:275–85. doi:10.1080/001075100750012777

CrossRef Full Text | Google Scholar