Nonreciprocal Waveguide-QED for Spinning Cavities with Multiple Coupling Points

We investigate chiral emission and the single-photon scattering of spinning cavities coupled to a meandering waveguide at multiple coupling points. It is shown that nonreciprocal photon transmissions occur in the cavities-waveguide system, which stems from interference effects among different coupling points, and frequency shifts induced by the Sagnac effect. The nonlocal interference is akin to the mechanism in giant atoms. In the single-cavity setup, by optimizing the spinning velocity and number of coupling points, the chiral factor can approach 1, and the chiral direction can be freely switched. Moreover, destructive interference gives rise to the complete photon transmission in one direction over the whole optical frequency band, with no analogy in other quantum setups. In the multiple-cavity system, we also investigate the photon transport properties. The results indicate a directional information flow between different nodes. Our proposal provides a novel way to achieve quantum nonreciprocal devices, which can be applied in large-scale quantum chiral networks with optical waveguides.

1 Introduction

Waveguide quantum electrodynamics (QED) has emerged as an excellent platform for studying the interactions between atoms and itinerant photons in the past 2 decades [1–3]. A one-dimensional waveguide supports a continuum of photon modes with a strong transverse confinement, and is applicable to significantly enhance light-matter interactions [3]. Moreover, waveguide-QED systems serve as quantum channels in quantum networks, which can be realized in both natural and artificial systems, such as trapped atoms (quantum dots) interacting with nanofibers [4–8] and superconducting qubits coupled with transmission lines [9–11]. To date, a great deal of quantum optical effects have been revealed in waveguide-QED systems, including controlling single-photon scattering [12–16], photon-mediated long-range interactions [17–20] and directional photon emission [21, 22].

In traditional waveguide QED, atoms are commonly considered as point-like dipoles and coupled to the waveguide at a single point. However, an emergent class of artificial atoms, called giant atoms, break down this dipole approximation. Their sizes are comparable to the wavelength of photons (phonons) interacted [23–35]. Recent experiments have demonstrated that superconducting artificial atoms can be successfully coupled with propagating surface acoustic waves at several points [36–38]. The self-interference effects among multiple points dramatically modify the emission behaviors of giant atoms, such as frequency-dependent decay rates [23, 24], decoherence-free dipole-dipole interactions [25, 26], and nonreciprocal photon transport [30, 31]. All the above achievements indicate potential applications in quantum information processing.

Optical nonreciprocity allows photons to pass through from one side but blocks it from the opposite direction, which is requisite for preventing the information back flow in quantum network. At optical frequencies, magneto-optical Faraday effect is often applied to achieve optical nonreciprocity, which is lossy and cannot be integrated effectively on a chip [39, 40]. Therefore, several magnetic-free nonreciprocal proposals were developed. Their mechanisms include optical nonlinearity [41, 42], dynamic spatiotemporal modulation [43–45], and atomic reservoir engineering [46]. Recently, the whispering-gallery-mode resonators with mechanical rotation provide another approach to study many quantum nonreciprocal phenomena [47–50]. The simplest implementation contains a spinning resonator and a stationary tapered fiber. The rotation leads to Sagnac effect and shifts the frequency of the optical mode. Compared with previous studies, the nonreciprocal transmission of light has been achieved in experiment with very high isolation (about 99.6%) [51]. In early studies, spinning resonators, similar to small atoms, typically couple to waveguides at a single point. Nevertheless, multiple-point coupling in spinning resonator-waveguide systems has not been considered, and the photon emission and transport properties in this system are worth being explored.

In this work, we address this issue by considering spinning resonators interacting with a meandering waveguide at multiple coupling points. Such resonators are akin to the “giant atoms,” but with mechanical rotation. First, in the single-cavity setup, the complete unidirectional transparency over the whole optical frequency band is observed, which can be realized by considering the spinning resonator and multiple-point coupling simultaneously, with no analogy in other quantum setups. This phenomenon results from the interference effects among different coupling points and mode frequency shifts led by the Sagnac effect. Additionally, the chiral emission direction is switchable by simply changing the rotation direction and speed. Afterward, we extend to two-cavity system, where each resonator interacts with two separate points. The phase factors and the coupling strengths between the CW and CCW modes can significantly modulate the nonreciprocal transmission behaviors, which implies chiral photon transfer among different points. Employing spinning resonators as quantum nodes, those results obtained in this paper might have potential applications in large-scale chiral quantum networks.

The paper is organized as follows: in Section 2, we present the single-spinning-resonator model and give the motional equations. The chiral emission and nonreciprocal transmission by tuning spinning velocity or number of coupling points are also discussed. In Section 3, we extend to two separate spinning resonators interacting with several coupling points. Both analytical and numerical results for the weak-field transmission are obtained. Finally, the conclusions are given in Section 4.

2 A Spinning Resonator Interacting With Multiple Points

2.1 Hamilton and Motional Equations

Here we first consider a spinning optical resonator evanescently coupled to a meandering optical waveguide at N coupling points, as shown in Figure 1. The resonator is rotated and the waveguide is stationary. The separation distance between different coupling points on the waveguide is denoted by L = x_m − x_n. We assume the coherence length of photons in the waveguide is larger than the smallest distance L_min, and therefore we can ignore the non-Markovian retarded effects [19, 52]. The nonspinning resonator, for example, a whispering-gallery-mode resonator with a resonant frequency ω_c, simultaneously supports both clockwise (CW) and counter-clockwise (CCW) travelling modes. The CW and CCW modes couple to each other through a scatterer or induced by surface roughness [53, 54], which results in an optical mode splitting. When the optical resonator rotates in one direction at an angular velocity Ω, the propagating effects of the CW and CCW modes are different, leading to an opposite Sagnac-Fizeau shift in resonant frequencies, i.e., ω_c → ω_c + Δ_F, with [55].

${\mathrm{\Delta }}_F=\pm \frac{nR\mathrm{\Omega }{\omega }_c}{c}\left(1-\frac{1}{n^2}-\frac{\lambda }{n}\frac{dn}{d\lambda }\right),(1)$

where n is the refractive index of the dielectric material, R is the radius of the optical resonator, and c (λ) is the velocity (wavelength) of light in vacuum. The dispersion term λdn/ndλ, denoting the relativistic origin of the Sagnac effect [51, 55], is very small in typical materials compared to the value of (1–1/n²). In the following we assume the resonator rotates along the CCW direction, hence Δ_F > 0 (Δ_F < 0) represents the case of the driving field coming from the left-hand (right-hand) side. The resonant frequencies of the CW and CCW modes in this situation are ω_cw = ω_c + Δ_F and ω_ccw = ω_c − Δ_F, respectively.

FIGURE 1

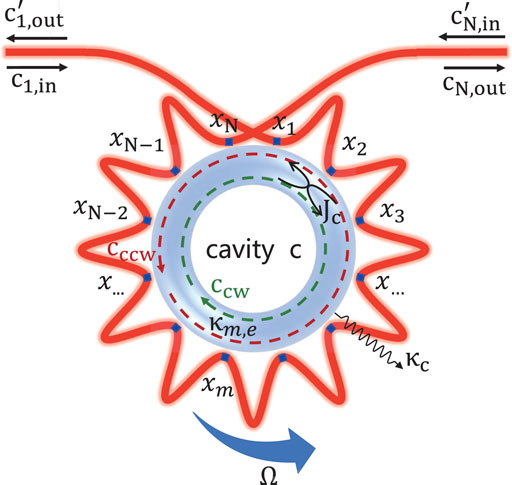
FIGURE 1. (Color online) Schematic of a spinning resonator coupled to a meandering waveguide at multiple coupling points x_m with the external loss rate κ_m,e. The resonator rotates along the CCW direction with an angular speed Ω. The CW and CCW modes of the resonator couple to each other with strength J. The intrinsic decay rate of the resonator is κ_c.

In our consideration, the Hamiltonian of the spinning resonator can be written as (ℏ = 1)

$H_c=\left({\omega }_c+{\mathrm{\Delta }}_F\right)c_{\text{cw}}^{†}{c}_{\text{cw}}+\left({\omega }_c-{\mathrm{\Delta }}_F\right)c_{\text{ccw}}^{†}{c}_{\text{ccw}}+J\left(c_{\text{cw}}^{†}{c}_{\text{ccw}}+c_{\text{ccw}}^{†}{c}_{\text{cw}}\right).(2)$

Here c_cw and c_ccw ($c_{\text{cw}}^{†}$ and $c_{\text{ccw}}^{†}$) are the annihilation (creation) operators of the CW and CCW modes, respectively. The coupling strength J denotes the interaction between these two modes induced by optical backscattering. The CW (CCW) mode can only be driven by an optical field coming from the left (right) side of the waveguide, own to the directionality of travelling wave modes in the resonator. The driving Hamiltonian is

$H_d=i\sum _{m=1}^N\sqrt{{\kappa }_{m,e}}{c}_{m,\text{in}}\left(c_{\text{cw}}^{†}-c_{\text{cw}}\right)+i\sum _{m=1}^N\sqrt{{\kappa }_{m,e}}{c}_{m,\text{in}}^{\prime }\left(c_{\text{ccw}}^{†}-c_{\text{ccw}}\right),(3)$

where c_m,in and $c_{m,\text{in}}^{\prime }$ are the input fields coming from the left and right sides at coupling point x_m, respectively. According to Fermi’s golden rule [56], ${\kappa }_{m,e}=2\pi g_m^2\mathcal{D}(\omega )$ describes the spontaneous emission of the resonator modes into the waveguide at coupling point x_m, with g_m being the resonator-waveguide coupling strength and $\mathcal{D}(\omega )$ being the photon density of states in the waveguide. In the presence of decay channels, the effective non-Hermitian Hamiltonian of the whole system is given by

$H_1=H_c+H_d-i{\mathrm{\Gamma }}_c\left(c_{\text{cw}}^{†}{c}_{\text{cw}}+c_{\text{ccw}}^{†}{c}_{\text{ccw}}\right),(4)$

with

${\mathrm{\Gamma }}_c=\frac{{\kappa }_c}{2}+\sum _{m=1}^N\frac{{\kappa }_{m,e}}{2},(5)$

where Γ_c is the total decay rate of the resonator mode, and κ_c is the intrinsic decay rate of the resonator.

According to the Heisenberg motional equations, the dynamic equations of the CW and CCW modes are yielded by

$\begin{array}{cc}\hfill \frac{d{c}_{\text{cw}}}{dt}& =-\left[i\left({\omega }_c+{\mathrm{\Delta }}_F\right)+{\mathrm{\Gamma }}_c\right]c_{\text{cw}}-iJ{c}_{\text{ccw}}+\sum _{m=1}^N\sqrt{{\kappa }_{m,e}}{c}_{m,\text{in}},\hfill \\ \hfill \frac{d{c}_{\text{ccw}}}{dt}& =-\left[i\left({\omega }_c-{\mathrm{\Delta }}_F\right)+{\mathrm{\Gamma }}_c\right]c_{\text{ccw}}-iJ{c}_{\text{cw}}+\sum _{m=1}^N\sqrt{{\kappa }_{m,e}}{c}_{m,\text{in}}^{\prime }.\hfill \end{array}(6)$

Note that k_cw = (ω_c + Δ_F)/c and k_ccw = (ω_c − Δ_F)/c are approximately regarded as the central mode vector of right-going and left-going photon in the waveguide emitted by the resonator [23], respectively. Different from the case without rotation, the accumulated phase shifts between neighbor coupling points for opposite propagation directions of the photons are distinct. As given in Refs. [17, 57–59], the local input-output relations for the CW and CCW modes at each coupling point x_m are written as

$\begin{array}{cc}\hfill c_{m,\text{out}}& =c_{m,\text{in}}-\sqrt{{\kappa }_{m,e}}{c}_{\text{cw}},c_{m+1,\text{in}}=c_{m,\text{out}}{e}^{i{k}_{\text{cw}}\left(x_{m+1}-x_m\right)},\hfill \\ \hfill c_{m,\text{out}}^{\prime }& =c_{m,\text{in}}^{\prime }-\sqrt{{\kappa }_{m,e}}{c}_{\text{ccw}},c_{m,\text{in}}^{\prime }=c_{m+1,\text{out}}^{\prime }{e}^{i{k}_{\text{ccw}}\left(x_{m+1}-x_m\right)}.\hfill \end{array}(7)$

Substituting Eq. 7 into Eq. 6, we obtain the effective dynamic equations

$\begin{array}{cc}\hfill \frac{d{c}_{\text{cw}}}{dt}=& -\left[i\left({\omega }_c+{\mathrm{\Delta }}_F\right)+{\mathrm{\Gamma }}_c+\sum _{m>n=1}^N\sqrt{{\kappa }_{m,e}{\kappa }_{n,e}}{e}^{i{k}_{\text{cw}}\left(x_m-x_n\right)}\right]c_{\text{cw}}-iJ{c}_{\text{ccw}}\hfill \\ \hfill & +\sum _{m=1}^N\sqrt{{\kappa }_{m,e}}{e}^{i{k}_{\text{cw}}\left(x_m-x_1\right)}{c}_{1,\text{in}},\hfill \\ \hfill \frac{d{c}_{\text{ccw}}}{dt}=& -\left[i\left({\omega }_c-{\mathrm{\Delta }}_F\right)+{\mathrm{\Gamma }}_c+\sum _{m>n=1}^N\sqrt{{\kappa }_{m,e}{\kappa }_{n,e}}{e}^{i{k}_{\text{ccw}}\left(x_m-x_n\right)}\right]c_{\text{ccw}}-iJ{c}_{\text{cw}}\hfill \\ \hfill & +\sum _{m=1}^N\sqrt{{\kappa }_{m,e}}{e}^{i{k}_{\text{ccw}}\left(x_N-x_m\right)}{c}_{N,\text{in}}^{\prime }.\hfill \end{array}(8)$

The total input-output relations of this system take the form

$\begin{array}{cc}\hfill c_{N,\text{out}}& =c_{1,\text{in}}{e}^{i{k}_{\text{cw}}\left(x_N-x_1\right)}-\sum _{m=1}^N\sqrt{{\kappa }_{m,e}}{e}^{i{k}_{\text{cw}}\left(x_N-x_m\right)}{c}_{\text{cw}},\hfill \\ \hfill c_{1,\text{out}}^{\prime }& =c_{N,\text{in}}^{\prime }{e}^{i{k}_{\text{ccw}}\left(x_N-x_1\right)}-\sum _{m=1}^N\sqrt{{\kappa }_{m,e}}{e}^{i{k}_{\text{ccw}}\left(x_m-x_1\right)}{c}_{\text{ccw}}.\hfill \end{array}(9)$

Eq. 8 exhibits a self-coupling in the CW or CCW mode, which arises from the self interference effects of reemitted photons between different connection points. Moreover, the Sagnac effect and the self-interference effects may significantly affect the optical properties of the system. We note that only when the resonator is nonspinning, the system is reciprocal. Based on these derivations, we will investigate the photon emission and transport properties in this system.

2.2 Phase Controlled Chiral Emission

In the giant-atom waveguide-QED systems, the multiple coupling points result in a frequency-dependent decay rate and Lamb shift for a giant atom [23, 60]. Similarly, the interference effects induced by multiple coupling points in our system also give a modification of the frequency shift Δ_j and decay rate Γ_j for the CW and CCW mode. According to Eq. 8, we have

${\mathrm{\Delta }}_j=\sum _{m>n=1}^N\sqrt{{\kappa }_{m,e}{\kappa }_{n,e}}\sin \left({\varphi }_{mn}^j\right),{\mathrm{\Gamma }}_j={\mathrm{\Gamma }}_c+\sum _{m>n=1}^N\sqrt{{\kappa }_{m,e}{\kappa }_{n,e}}\cos \left({\varphi }_{mn}^j\right).(10)$

where ${\varphi }_{mn}^j=k_j(x_m-x_n)$ with j = cw, ccw.

Here we consider the maximally symmetric case, in which decay rates of the resonator modes into the waveguide are the same at each coupling point with κ_m,e = κ_e and the distance between neighboring coupling points is identical with x_m+1 − x_m = d. Then we can set x_m − x_n = (m − n)d and θ_j = k_jd. Similar to the Lamb shift and decay rate in atomic physics, Eq. 10 becomes

${\mathrm{\Delta }}_j=\frac{{\kappa }_e}{2}\left[\frac{N\sin \left({\theta }_j\right)-\sin \left(N{\theta }_j\right)}{1-\cos \left({\theta }_j\right)}\right],{\mathrm{\Gamma }}_j=\frac{{\kappa }_c}{2}+\frac{{\kappa }_e}{2}\left[\frac{1-\cos \left(N{\theta }_j\right)}{1-\cos \left({\theta }_j\right)}\right].(11)$

We begin to discuss the effects of the rotation speed and number of coupling points on the emission properties under the condition of κ_c = 0. When the resonator is nonspinning with Ω = 0, the CW and CCW modes are degenerate with the Fizeau drag Δ_F = 0 and ω_ccw = ω_cw = ω_c. As increasing the rotation speed Ω, the Sagnac-Fizeau shift described by Eq. 1 linearly increases, as given in Supplementary Material. In our calculations, we choose the related parameters as follows: λ = 1,550 nm, R = 4.73 mm, and n = 1.4. For Ω = 0.97 GHz, we have Δ_F/ω_c = ±0.05 and (RΩ)/c ≈ 0.015. For the spinning resonator with a single coupling point (N = 1), Eq. 11 gives the results of Δ_cw = Δ_ccw = 0 and Γ_cw = Γ_ccw = (κ_c + κ_e)/2. When increasing the number of coupling points, the frequency shifts and decay rates for the CW and CCW modes have an opposite shift due to the rotation.

In Figures 2A,B, frequency shifts Δ_j and decay rates Γ_j are plotted as a function of the phase θ_c = ω_cd/c with N = 10 and Ω = 0.97 GHz. The frequency shifts Δ_cw and Δ_ccw take negative and positive values with the maximum at about 0.6Γ_max. Given that Δ_cw (Δ_ccw) is zero, the decay rate Γ_cw (Γ_ccw) reaches its highest magnitude at θ_c = 0.95 × 2π (θ_c = 1.05 × 2π). For θ_c = 0.95 × 2π, the accumulated phase of photons propagating along the CCW direction leads to Γ_ccw = 0, which arises from the destructive interference effects among the coupling points. In this case, the CCW mode of the resonator is decoupled from the waveguide. Moreover, there are a lot of additional lower and local maximum values in the decay rates. The phase θ_c of the local minima between these maxima scales with (1/N + Δ_F/ω_c). Note that the rotation speed and number of coupling points make a big difference in the values of Γ_cw and Γ_ccw. Narrower resonances can be found in the decay rates when we consider more coupling points.

FIGURE 2

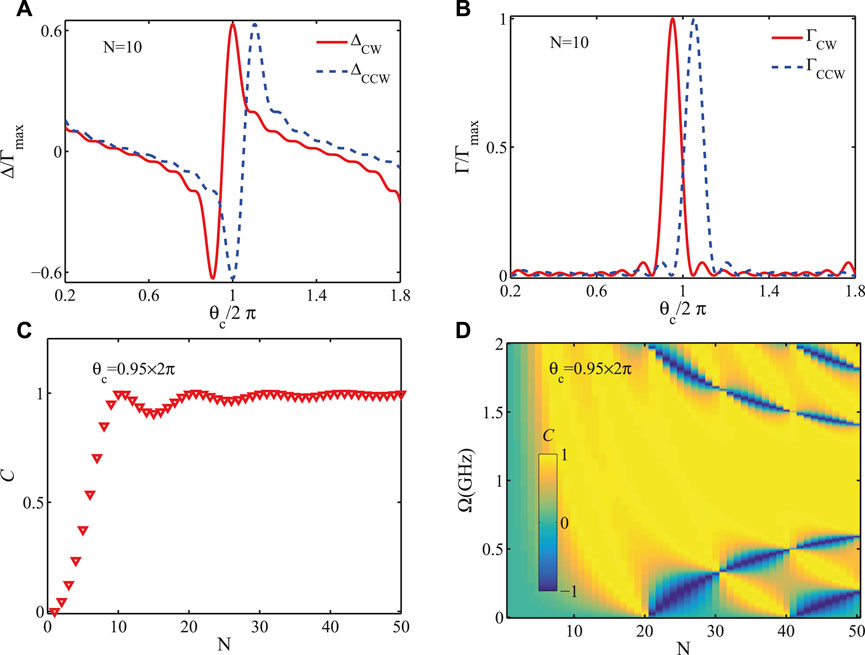
FIGURE 2. (Color online) The frequency shifts Δ_j (A) and the decay rates Γ_j (B) for the CW and CCW modes versus phase θ_c = ω_cd/c for N = 10 and Ω = 0.97 GHz. The maximum decay rate Γ_cw is used for normalization. (C) The chiral factor $\mathcal{C}$ changes with number of coupling points N. (D) The chiral factor $\mathcal{C}$ versus N and rotation speed Ω are plotted. Other parameters are set as: λ = 1,550 nm, R = 4.73 mm, n = 1.4, and κ_c = 0.

In order to study the emission properties more clearly, for a special frequency we define the chirality parameter $\mathcal{C}$ as

$\mathcal{C}=\frac{{\mathrm{\Gamma }}_{\text{cw}}-{\mathrm{\Gamma }}_{\text{ccw}}}{{\mathrm{\Gamma }}_{\text{cw}}+{\mathrm{\Gamma }}_{\text{ccw}}},(12)$

where $\mathcal{C}=1$ $(\mathcal{C}=-1)$ implies a truly unidirectional excitation of the right-going (left-going) photon, and $\mathcal{C}=0$ denotes the photon coupling into the waveguide without preference in both propagating directions. Figure 2C depicts the chiral factor $\mathcal{C}$ changing with number of coupling points N. When N = 1, the chiral factor is $\mathcal{C}=0$. For θ_c = 0.95 × 2π, as increasing number of coupling points N, the chirality factor $\mathcal{C}$ first goes up and then oscillates slowly with a relative larger value around 1. Note that $\mathcal{C}=1$ is obtained for N = 10, corresponding to Γ_cw = 50κ_e and Γ_ccw = 0. The essence of the chirality is that accumulated phases for photons propagating in CW and CCW directions are different. By tuning the phase shift θ_c, for example, θ_c = 1.05 × 2π, the photon emission direction is totally switched. Figure 2D shows the chiral factor $\mathcal{C}$ as functions of number of coupling points N and rotation speed Ω for θ_c = 0.95 × 2π. By optimizing the rotation speed and number of coupling points, the chiral factor $\mathcal{C}$ can approach 1, and the chiral direction can be freely switched. Moreover, the directional emission will be realized in a large parameter regime.

2.3 Nonreciprocal Photon Transmission

Now we study how the rotation velocity and number of coupling points affect the optical response of the spinning resonator. We consider the resonator is excited by an external input signal in the CW direction with frequency ω_l and amplitude ɛ. In this case, the input signal from the left side is given by $c_{1,\text{in}}+\epsilon e^{-i{\omega }_{l}t}$, with c_1,in being the vacuum input signal, while the input signal from the right side only contains the vacuum input field $c_{N,\text{in}}^{\prime }$. In the rotating frame at the driving frequency ω_l, the steady-state solutions of Eq. 8 can be written as

$\begin{array}{c}\hfill ⟨c_{\text{cw}}⟩=\frac{\left[i\left({\mathrm{\Delta }}_c-{\mathrm{\Delta }}_F+{\mathrm{\Delta }}_{\text{ccw}}\right)+{\mathrm{\Gamma }}_{\text{ccw}}\right]{\sum }_{m=1}^N\sqrt{{\kappa }_{m,e}}{e}^{i{k}_{\text{cw}}\left(x_m-x_1\right)}\epsilon }{\left[i\left({\mathrm{\Delta }}_c-{\mathrm{\Delta }}_F+{\mathrm{\Delta }}_{\text{ccw}}\right)+{\mathrm{\Gamma }}_{\text{ccw}}\right]\left[i\left({\mathrm{\Delta }}_c+{\mathrm{\Delta }}_F+{\mathrm{\Delta }}_{\text{cw}}\right)+{\mathrm{\Gamma }}_{\text{cw}}\right]+J^2}.\end{array}(13)$

Here Δ_c = ω_c − ω_l is the detuning between the resonator without rotation and the driving field. The transmission rate of the input signal is given by

$\begin{array}{c}\hfill T_L={\left|\frac{⟨c_{N,\text{out}}⟩}{\epsilon }\right|}^2={\left|1-\frac{\left[i\left({\mathrm{\Delta }}_c-{\mathrm{\Delta }}_F+{\mathrm{\Delta }}_{\text{ccw}}\right)+{\mathrm{\Gamma }}_{\text{ccw}}\right]{\sum }_{m,n=1}^N\sqrt{{\kappa }_{m,e}{\kappa }_{n,e}}{e}^{i{k}_{\text{cw}}\left(x_m-x_n\right)}}{\left[i\left({\mathrm{\Delta }}_c-{\mathrm{\Delta }}_F+{\mathrm{\Delta }}_{\text{ccw}}\right)+{\mathrm{\Gamma }}_{\text{ccw}}\right]\left[i\left({\mathrm{\Delta }}_c+{\mathrm{\Delta }}_F+{\mathrm{\Delta }}_{\text{cw}}\right)+{\mathrm{\Gamma }}_{\text{cw}}\right]+J^2}\right|}^2.\end{array}(14)$

Similarly, we also consider the case of an external input signal coming from the right side of the waveguide with ${\epsilon }^{\prime }{e}^{-i{\omega }_{l}t}$. By solving the steady-state solutions of Eq. 8, we obtain

$⟨c_{\text{ccw}}⟩=\frac{\left[i\left({\mathrm{\Delta }}_c+{\mathrm{\Delta }}_F+{\mathrm{\Delta }}_{\text{cw}}\right)+{\mathrm{\Gamma }}_{\text{cw}}\right]{\sum }_{m=1}^N\sqrt{{\kappa }_{m,e}}{e}^{i{k}_{\text{ccw}}\left(x_N-x_m\right)}{\epsilon }^{\prime }}{\left[i\left({\mathrm{\Delta }}_c-{\mathrm{\Delta }}_F+{\mathrm{\Delta }}_{\text{ccw}}\right)+{\mathrm{\Gamma }}_{\text{ccw}}\right]\left[i\left({\mathrm{\Delta }}_c+{\mathrm{\Delta }}_F+{\mathrm{\Delta }}_{\text{cw}}\right)+{\mathrm{\Gamma }}_{\text{cw}}\right]+J^2}.(15)$

The transmission rate of the input signal is written as

$T_R={\left|\frac{⟨c_{1,\text{out}}^{\prime }⟩}{{\epsilon }^{\prime }}\right|}^2={\left|1-\frac{\left[i\left({\mathrm{\Delta }}_c+{\mathrm{\Delta }}_F+{\mathrm{\Delta }}_{\text{cw}}\right)+{\mathrm{\Gamma }}_{\text{cw}}\right]{\sum }_{m,n=1}^N\sqrt{{\kappa }_{m,e}{\kappa }_{n,e}}{e}^{i{k}_{\text{ccw}}\left(x_m-x_n\right)}}{\left[i\left({\mathrm{\Delta }}_c-{\mathrm{\Delta }}_F+{\mathrm{\Delta }}_{\text{ccw}}\right)+{\mathrm{\Gamma }}_{\text{ccw}}\right]\left[i\left({\mathrm{\Delta }}_c+{\mathrm{\Delta }}_F+{\mathrm{\Delta }}_{\text{cw}}\right)+{\mathrm{\Gamma }}_{\text{cw}}\right]+J^2}\right|}^2.(16)$

A nonreciprocal photon transmission with T_R ≠ T_L can be observed when the resonator is spinning. This fact is due to the different numerators in Eqs 13, 15. For the maximally symmetric case, we have

${\mathrm{\Gamma }}_j^{\prime }=\sum _{m,n=1}^N\sqrt{{\kappa }_{m,e}{\kappa }_{n,e}}{e}^{i{k}_j\left(x_m-x_n\right)}={\kappa }_e\left[\frac{1-\cos \left(N{\theta }_j\right)}{1-\cos \left({\theta }_j\right)}\right].(17)$

For J = 0, the incident photon will be transmitted and absorbed with reflection being zero. In this scenario, the transmission curve T_L represents a Lorentzian line shape centered at Δ_c = −(Δ_F + Δ_cw) with a linewidth Γ_cw. For N = 1, we obtain Δ_c = −Δ_F and Γ_cw = (κ_c + κ_e)/2. The transmission dip is around 0. For multiple coupling points, as discussed above, Δ_cw and Γ_cw vary periodically with phase θ_c. The transmission rate T_L versus the detuning Δ_c and the phase θ_c are plotted in Figure 3A. It shows that θ_c will dramatically modify the transmission window. As we increase θ_c, the position of the transmission dip has a red-shift. When the phase θ_cw is 2π/N, the transmission dip disappears totally with T = 1, which means the resonator cannot be excited by the external field and corresponds to the optical dark state. This phenomenon arises from the destructive interferences in the multiple coupling points, which can be explained by Eq. 17. Moreover, the mode splitting is observed in some parameter range in Figure 3B when J = 5κ_e. The asymmetry of the two dips results from different decay rates and frequency shifts of these two modes.

FIGURE 3

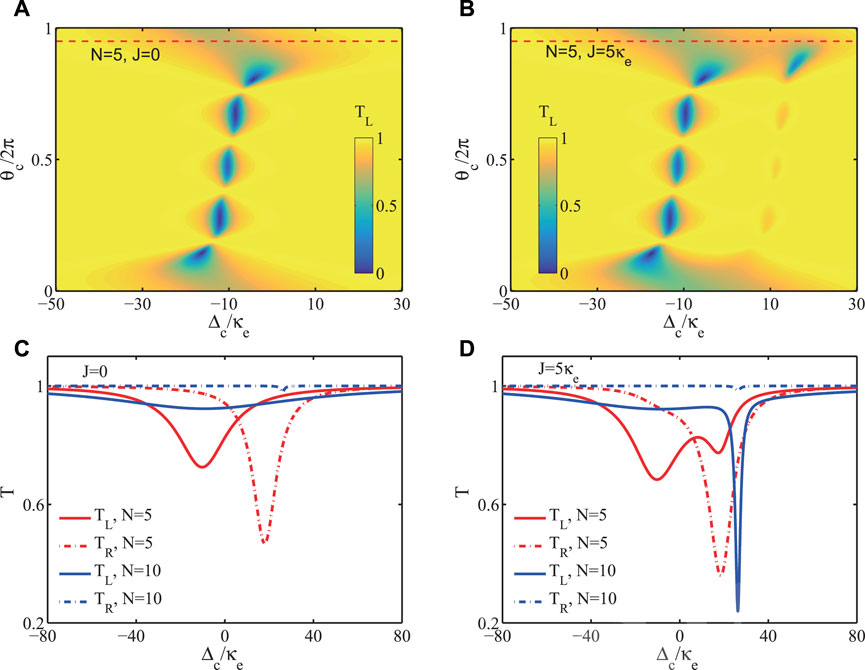
FIGURE 3. (Color online) Transmission rate T_R versus detuning Δ_c/κ and phase θ_c/2π for different coupling stengths: (A) J = 0, and (B) J = 5κ_e. Profiles of T_R and T_L versus Δ_c/κ with θ_c = 0.95 × 2π: (C) J = 0 and (D) J = 5κ_e. Other parameters are set as: κ_e = 5 × 10⁻³ω_c, Ω = 0.97 GHz, and κ_c = 2κ_e.

In Figures 3C,D, we plot the transmission rates T_L and T_R when the incident photon coming from the left side and right sides versus the detuning Δ_c for θ = 0.95 × 2π. It shows that T_L can be larger or smaller than T_R for N = 5. In other words, the nonreciprocal transmission is clearly observed due to the rotation. The interference effects between coupling points enable the transmission dips asymmetric with different linewidths. For N = 10, the decay rate of the CCW mode is very small, which leads to the complete photon transmission with T_R = 1. Moreover, a sharp dip appears in the transmission spectra T_L for J = 5κ_e. Note that the phase θ_c can also be used to adjust the nonreciprocal transmission behavior.

3 Two Spinning Resonators Interacting With Multiple Points

3.1 Hamiltonian and Dynamic Equations

The single-photon transport properties in a one-dimensional waveguide interacted with two giant atoms for three distinct topologies have been discussed in Ref. [61]. To study potential applications of the spinning resonator with multiple coupling points in large-scale quantum chiral networks, we now consider two separate spinning resonators evanescently coupled to a meandering waveguide at several different connection points. As shown in Figure 4, the optical resonator a (b) simultaneously supports both clockwise and counter-clockwise travelling optical modes. The creation operators of the CW and CCW modes are denoted by $a_{\text{cw}}^{†}$ and $a_{\text{ccw}}^{†}$ ($b_{\text{cw}}^{†}$ and $b_{\text{ccw}}^{†}$), respectively. The optical resonator a (b), with stationary resonant frequency ω_a (ω_b) and intrinsic decay rate κ_a (κ_b), rotates along the CCW direction by an angular velocity Ω_a (Ω_b). Owing to the rotation, the resonant frequencies of the CW and CCW modes in the resonator become ω_i,cw = ω_i + Δ_F,i and ω_i,ccw = ω_i − Δ_F,i with the subscript i = a, b, where Δ_F,i is given by Eq. 1. The resonator a (b) is coupled to the bent waveguide at connection points $x_1^a$ and $x_2^a$ ($x_1^b$ and $x_2^b$). The phase factor ϕ_i is calculated as $k(x_1^i-x_2^i)$when an optical signal travelling between them, and the phase factor when photons travelling from resonator a to resonator b is ${\varphi }_L=k(x_1^b-x_2^a)$. Here we note that there is no direct coupling between cavity a and cavity b due to the absence of the modal overlap.

FIGURE 4

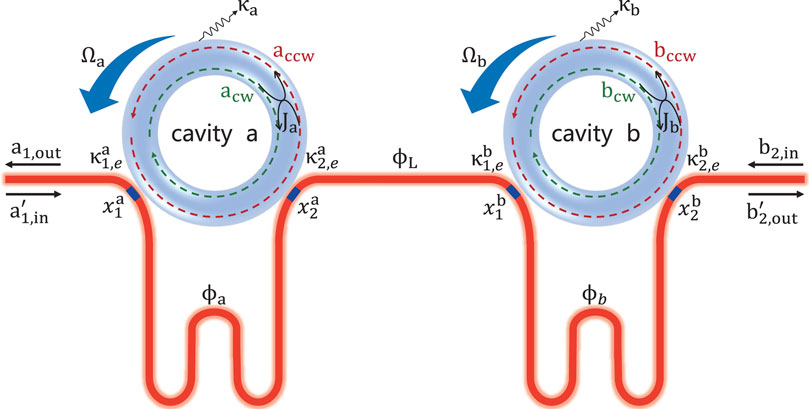
FIGURE 4. (Color online) Schematic of two separate spinning resonators coupled to a meandering waveguide at several coupling points $x_i^a$ and $x_i^b$ with i = 1, 2. The resonator a (b) with the intrinsic decay rate κ_a (κ_b) rotates along the CCW direction at an angular speed Ω_a (Ω_b). The CW and CCW modes of the resonator a (b) couple to each other with strength J_a (J_b). The external loss rates at coupling points $x_i^a$ and $x_i^b$ are ${\kappa }_{i,e}^a$ and ${\kappa }_{i,e}^b$, respectively. For the photon in the waveguide, the distance between neighboring coupling points results in different propagation phases denoting by ϕ_a, ϕ_L, and ϕ_b. Note that $\{a_{1,\text{in}}^{\prime },b_{2,\text{in}}\}$ and $\{b_{2,\text{out}}^{\prime },a_{1,\text{out}}\}$ are the input and output operators of optical fields towards and away the resonators.

The Hamiltonian of these two spinning resonators are given by

$H_c^{\prime }=\sum _{j=\text{cw},\text{ccw}}\left({\omega }_{a,j}{a}_j^{†}{a}_j+{\omega }_{b,j}{b}_j^{†}{b}_j\right)+J_a\left(a_{\text{cw}}^{†}{a}_{\text{ccw}}+a_{\text{ccw}}^{†}{a}_{\text{cw}}\right)+J_b\left(b_{\text{cw}}^{†}{b}_{\text{ccw}}+b_{\text{ccw}}^{†}{b}_{\text{cw}}\right).(18)$

Here J_a (J_b) is the coupling strength between the CW and CCW modes of the resonator a (b). The CCW (CW) modes in the resonators can only be driven by an optical field coming from the left (right) side of the waveguide. The amplitudes of the input fields at different coupling points are denoted by a_m,in, b_m,in, $a_{m,\text{in}}^{\prime }$, and $b_{m,\text{in}}^{\prime }$ with m = 1, 2. The driving fields give the Hamiltonian

$\begin{array}{ll}\hfill H_d^{\prime }& =i\sum _{m=1}^2\sqrt{{\kappa }_{m,e}^a}{a}_{m,\text{in}}\left(a_{\text{cw}}^{†}-a_{\text{cw}}\right)+i\sum _{m=1}^2\sqrt{{\kappa }_{m,e}^a}{a}_{m,\text{in}}^{\prime }\left(a_{\text{ccw}}^{†}-a_{\text{ccw}}\right)\hfill \\ \hfill & +i\sum _{m=1}^2\sqrt{{\kappa }_{m,e}^b}{b}_{m,\text{in}}\left(b_{\text{cw}}^{†}-b_{\text{cw}}\right)+i\sum _{m=1}^2\sqrt{{\kappa }_{m,e}^b}{b}_{m,\text{in}}^{\prime }\left(b_{\text{ccw}}^{†}-b_{\text{ccw}}\right).\hfill \end{array}(19)$

The non-Hermitian Hamiltonian of the whole system can be given by

$H_2=H_c^{\prime }+H_d^{\prime }-i{\mathrm{\Gamma }}_a\left(a_{\text{cw}}^{†}{a}_{\text{cw}}+a_{\text{ccw}}^{†}{a}_{\text{ccw}}\right)-i{\mathrm{\Gamma }}_b\left(b_{\text{cw}}^{†}{b}_{\text{cw}}+b_{\text{ccw}}^{†}{b}_{\text{ccw}}\right),(20)$

where ${\mathrm{\Gamma }}_i=({\kappa }_i+{\kappa }_{1,e}^i+{\kappa }_{2,e}^i)/2$ and i = a, b. Note that κ_a (κ_b) is the intrinsic optical loss of the resonator a (b), ${\kappa }_{1,e}^i$ and ${\kappa }_{2,e}^i$ are the waveguide-resonator coupling rates at coupling points $x_1^i$ and $x_2^i$, respectively.

The effective dynamic evolution equations of the cavity modes can be written as

$\begin{array}{cc}\hfill \frac{d{a}_{\text{cw}}}{dt}=& -\left[i\left({\omega }_a+{\mathrm{\Delta }}_{F,a}\right)+{\mathrm{\Gamma }}_a+\sqrt{{\kappa }_{1,e}^a{\kappa }_{2,e}^a}{e}^{i{\varphi }_{a,\text{cw}}}\right]a_{\text{cw}}-i{J}_a{a}_{\text{ccw}}-F_{\text{cw}}{b}_{\text{cw}}\hfill \\ \hfill & +\left[\sqrt{{\kappa }_{1,e}^a}{e}^{i\left({\varphi }_{a,\text{cw}}+{\varphi }_{L,\text{cw}}+{\varphi }_{b,\text{cw}}\right)}+\sqrt{{\kappa }_{2,e}^a}{e}^{i\left({\varphi }_{L,\text{cw}}+{\varphi }_{b,\text{cw}}\right)}\right]b_{2,\text{in}},\hfill \\ \hfill \frac{d{a}_{\text{ccw}}}{dt}=& -\left[i\left({\omega }_a-{\mathrm{\Delta }}_{F,a}\right)+{\mathrm{\Gamma }}_a+\sqrt{{\kappa }_{1,e}^a{\kappa }_{2,e}^a}{e}^{i{\varphi }_{a,\text{ccw}}}\right]a_{\text{ccw}}-i{J}_a{a}_{\text{cw}}\hfill \\ \hfill & +\left(\sqrt{{\kappa }_{1,e}^a}+\sqrt{{\kappa }_{2,e}^a}{e}^{i{\varphi }_{a,\text{ccw}}}\right)a_{1,\text{in}}^{\prime },\hfill \\ \hfill \frac{d{b}_{\text{cw}}}{dt}=& -\left[i\left({\omega }_b+{\mathrm{\Delta }}_{F,b}\right)+{\mathrm{\Gamma }}_b+\sqrt{{\kappa }_{1,e}^b{\kappa }_{2,e}^b}{e}^{i{\varphi }_{b,\text{cw}}}\right]b_{\text{cw}}-i{J}_b{b}_{\text{ccw}}\hfill \\ \hfill & +\left(\sqrt{{\kappa }_{1,e}^b}{e}^{i{\varphi }_{b,\text{cw}}}+\sqrt{{\kappa }_{2,e}^b}\right)b_{2,\text{in}},\hfill \\ \hfill \frac{d{b}_{\text{ccw}}}{dt}=& -\left[i\left({\omega }_b-{\mathrm{\Delta }}_{F,b}\right)+{\mathrm{\Gamma }}_b+\sqrt{{\kappa }_{1,e}^b{\kappa }_{2,e}^b}{e}^{i{\varphi }_{b,\text{ccw}}}\right]b_{\text{ccw}}-i{J}_b{b}_{\text{cw}}-F_{\text{ccw}}{a}_{\text{ccw}}\hfill \\ \hfill & +\left[\sqrt{{\kappa }_{1,e}^b}{e}^{i\left({\varphi }_{a,\text{ccw}}+{\varphi }_{L,\text{ccw}}\right)}+\sqrt{{\kappa }_{2,e}^b}{e}^{i\left({\varphi }_{a,\text{ccw}}+{\varphi }_{L,\text{ccw}}+{\varphi }_{b,\text{ccw}}\right)}\right]a{\prime }_{1,\text{in}},\hfill \end{array}(21)$

where

$\begin{array}{ll}\hfill F_j=& \sqrt{{\kappa }_{1,e}^a{\kappa }_{1,e}^b}{e}^{i\left({\varphi }_{a,j}+{\varphi }_{L,j}\right)}+\sqrt{{\kappa }_{1,e}^a{\kappa }_{2,e}^b}{e}^{i\left({\varphi }_{a,j}+{\varphi }_{L,j}+{\varphi }_{b,j}\right)}\hfill \\ \hfill & +\sqrt{{\kappa }_{2,e}^a{\kappa }_{1,e}^b}{e}^{i{\varphi }_{L,j}}+\sqrt{{\kappa }_{2,e}^a{\kappa }_{2,e}^b}{e}^{i\left({\varphi }_{L,j}+{\varphi }_{b,j}\right)}.\hfill \end{array}(22)$

Note that F_cw (F_ccw) denotes the effective unidirectional coupling strength between the CW (CCW) modes of these two resonators. The total input-output relations of this system take the form

$\begin{array}{cc}\hfill a_{1,\text{out}}=& b_{2,\text{in}}{e}^{i\left({\varphi }_{a,\text{cw}}+{\varphi }_{L,\text{cw}}+{\varphi }_{b,\text{cw}}\right)}-\left(\sqrt{{\kappa }_{1,e}^a}+\sqrt{{\kappa }_{2,e}^a}{e}^{i{\varphi }_{a,\text{cw}}}\right)a_{\text{cw}}\hfill \\ \hfill & -\left[\sqrt{{\kappa }_{1,e}^b}{e}^{i\left({\varphi }_{a,\text{cw}}+{\varphi }_{L,\text{cw}}\right)}+\sqrt{{\kappa }_{2,e}^b}{e}^{i\left({\varphi }_{a,\text{cw}}+{\varphi }_{L,\text{cw}}+{\varphi }_{b,\text{cw}}\right)}\right]b_{\text{cw}},\hfill \\ \hfill b_{2,\text{out}}^{\prime }=& a_{1,\text{in}}^{\prime }{e}^{i\left({\varphi }_{a,\text{ccw}}+{\varphi }_{L,\text{ccw}}+{\varphi }_{b,\text{ccw}}\right)}-\left(\sqrt{{\kappa }_{2,e}^b}+\sqrt{{\kappa }_{1,e}^b}{e}^{i{\varphi }_{b,\text{ccw}}}\right)b_{\text{ccw}}\hfill \\ \hfill & -\left(\sqrt{{\kappa }_{2,e}^a}{e}^{i\left({\varphi }_{L,\text{ccw}}+{\varphi }_{b,\text{ccw}}\right)}+\sqrt{{\kappa }_{1,e}^a}{e}^{i\left({\varphi }_{a,\text{ccw}}+{\varphi }_{L,\text{ccw}}+{\varphi }_{b,\text{ccw}}\right)}\right)a_{\text{ccw}}.\hfill \end{array}(23)$

By using Eqs 21, 23, we can investigate the photon transport properties of this system in the steady state.

3.2 Nonreciprocal Photon Transmission

In the following, we consider the input signal only comes from one side of the waveguide. Supposed that an external input signal b_2,in is injected from the right side of the waveguide with $\epsilon e^{-i{\omega }_{l}t}$, where ɛ and ω_l are the amplitude and frequency of the driving field, respectively. In the rotating frame at the driving frequency ω_l, the steady-state solutions of the CW resonator modes in Eq. 21 are solved as

$\begin{array}{cc}\hfill \langle a_{\text{cw}}\rangle & =\frac{U_{\text{ccw}}\left(V_{\text{cw}}{V}_{\text{ccw}}+J_b^2\right)A_{\text{cw}}-U_{\text{ccw}}{V}_{\text{ccw}}{F}_{\text{cw}}{B}_{\text{cw}}}{\left(U_{\text{cw}}{U}_{\text{ccw}}+J_a^2\right)\left(V_{\text{cw}}{V}_{\text{ccw}}+J_b^2\right)+J_a{J}_b{F}_{\text{cw}}{F}_{\text{ccw}}}\epsilon ,\hfill \\ \hfill \langle b_{\text{cw}}\rangle & =\frac{V_{\text{ccw}}\left(U_{\text{cw}}{U}_{\text{ccw}}+J_a^2\right)B_{\text{cw}}+J_a{J}_b{F}_{\text{ccw}}{A}_{\text{cw}}}{\left(U_{\text{cw}}{U}_{\text{ccw}}+J_a^2\right)\left(V_{\text{cw}}{V}_{\text{ccw}}+J_b^2\right)+J_a{J}_b{F}_{\text{cw}}{F}_{\text{ccw}}}\epsilon ,\hfill \end{array}(24)$

where

$\begin{array}{cc}\hfill U_{\text{cw}}& =i\left({\mathrm{\Delta }}_a+{\mathrm{\Delta }}_{F,a}\right)+{\mathrm{\Gamma }}_a+\sqrt{{\kappa }_{1,e}^a{\kappa }_{2,e}^a}{e}^{i{\varphi }_{a,\text{cw}}},\hfill \\ \hfill U_{\text{ccw}}& =i\left({\mathrm{\Delta }}_a-{\mathrm{\Delta }}_{F,a}\right)+{\mathrm{\Gamma }}_a+\sqrt{{\kappa }_{1,e}^a{\kappa }_{2,e}^a}{e}^{i{\varphi }_{a,\text{ccw}}},\hfill \\ \hfill V_{\text{cw}}& =i\left({\mathrm{\Delta }}_b+{\mathrm{\Delta }}_{F,b}\right)+{\mathrm{\Gamma }}_b+\sqrt{{\kappa }_{1,e}^b{\kappa }_{2,e}^b}{e}^{i{\varphi }_{b,\text{cw}}},\hfill \\ \hfill V_{\text{ccw}}& =i\left({\mathrm{\Delta }}_b-{\mathrm{\Delta }}_{F,b}\right)+{\mathrm{\Gamma }}_b+\sqrt{{\kappa }_{1,e}^b{\kappa }_{2,e}^b}{e}^{i{\varphi }_{b,\text{ccw}}},\hfill \\ \hfill A_{\text{cw}}& =\sqrt{{\kappa }_{1,e}^a}{e}^{i\left({\varphi }_{a,\text{cw}}+{\varphi }_{L,\text{cw}}+{\varphi }_{b,\text{cw}}\right)}+\sqrt{{\kappa }_{2,e}^a}{e}^{i\left({\varphi }_{L,\text{cw}}+{\varphi }_{b,\text{cw}}\right)},\hfill \\ \hfill A_{\text{ccw}}& =\sqrt{{\kappa }_{1,e}^a}+\sqrt{{\kappa }_{2,e}^a}{e}^{i{\varphi }_{a,\text{ccw}}},\hfill \\ \hfill B_{\text{cw}}& =\sqrt{{\kappa }_{1,e}^b}{e}^{i{\varphi }_{b,\text{cw}}}+\sqrt{{\kappa }_{2,e}^b},\hfill \\ \hfill B_{\text{ccw}}& =\sqrt{{\kappa }_{1,e}^b}{e}^{i\left({\varphi }_{a,\text{ccw}}+{\varphi }_{L,\text{ccw}}\right)}+\sqrt{{\kappa }_{2,e}^b}{e}^{i\left({\varphi }_{a,\text{ccw}}+{\varphi }_{L,\text{ccw}}+{\varphi }_{b,\text{ccw}}\right)}.\hfill \end{array}(25)$

Here, Δ_a = ω_a − ω_l (Δ_b = ω_b − ω_l) is the detuning between the resonator a (b) without rotation and the driving field. According to Eq. 23, the transmission rate of the output port a_1,out for the input signal b_2,in can be defined as $T_R={\left|⟨a_{1,\text{out}}⟩/\epsilon \right|}^2$.

Similarly, when an external input signal is injected from the left side of the waveguide with ${\epsilon }^{\prime }{e}^{-i{\omega }_{l}t}$, the steady-state solutions of the CCW resonator modes in Eq. 21 are also solved as

$\begin{array}{cc}\hfill \langle a_{\text{ccw}}\rangle & =\frac{U_{\text{cw}}\left(V_{\text{cw}}{V}_{\text{ccw}}+J_b^2\right)A_{\text{ccw}}+J_a{J}_b{F}_{\text{cw}}{B}_{\text{ccw}}}{\left(U_{\text{cw}}{U}_{\text{ccw}}+J_a^2\right)\left(V_{\text{cw}}{V}_{\text{ccw}}+J_b^2\right)+J_a{J}_b{F}_{\text{cw}}{F}_{\text{ccw}}}{\epsilon }^{\prime },\hfill \\ \hfill \langle b_{\text{ccw}}\rangle & =\frac{V_{\text{cw}}\left(U_{\text{cw}}{U}_{\text{ccw}}+J_a^2\right)B_{\text{ccw}}-U_{\text{cw}}{V}_{\text{cw}}{F}_{\text{ccw}}{A}_{\text{ccw}}}{\left(U_{\text{cw}}{U}_{\text{ccw}}+J_a^2\right)\left(V_{\text{cw}}{V}_{\text{ccw}}+J_b^2\right)+J_a{J}_b{F}_{\text{cw}}{F}_{\text{ccw}}}{\epsilon }^{\prime },\hfill \end{array}(26)$

Once again, the transmission rate of the ouput port $b_{2,\text{out}}^{\prime }$ is given by $T_L=|⟨b_{2,\text{out}}^{\prime }⟩/{\epsilon }^{\prime }{|}^2$.

In the following, we choose the related parameters as follows: ω_a = ω_b = ω_c, Ω_a = Ω_b = 0.97 GHz, ${\kappa }_{m,e}^a={\kappa }_{m,e}^b=\kappa$, κ_a = κ_b = 0.5κ, κ = 5 × 10⁻³ω_c and ϕ_L,cw = π. Thus, Δ_a = Δ_b = Δ_c and Δ_F,a = Δ_F,b. We first consider the CW and CCW modes decoupling, i.e., J_a = J_b = 0. In Figures 5A,B, we plot the transmission rates T_R and T_L versus the detuning Δ_c/κ and the phase ϕ_b,cw/π for ϕ_a,cw = π. According to Eqs 23, 24, the transmission rate T_R represents a Lorentzian line shape centered at Δ_c = −Δ_F − κ sin (ϕ_b,cw) with a linewidth Γ_b + κ cos (ϕ_b,cw). However, the behavior of transmission rate T_L is different. A mode splitting may appear around Δ_c = Δ_F, which implies indirect coherent coupling between the CCW modes of these two resonators is achieved. The reason behind this phenomenon is that the phase ϕ_a,ccw is not equal to π own to the rotation. Moreover, the phase ϕ_b,cw can significantly change the transmission windows with a period 2π. To give more details, in Figures 5C,D we plot the profiles of T_R and T_L changing with Δ_c/κ for ϕ_b,cw = π and ϕ_b,cw = 1.5π. By contrast, one finds that for ϕ_b,cw = π, the CW modes decouple to the waveguide corresponding to an optical dark state with T_R = 1, while the CCW modes are excited with a transmission dip in T_L. For ϕ_b,cw = 1.5π, strong coupling with a double-dip-type curve in T_L can be realized. The photon nonreciprocal transmission behavior is observed due to the Sagnac effects and the interference effects among multiple coupling points. Note that for ϕ_b,cw = π, similar results are obtained by tuning the phase ϕ_a,cw.

FIGURE 5

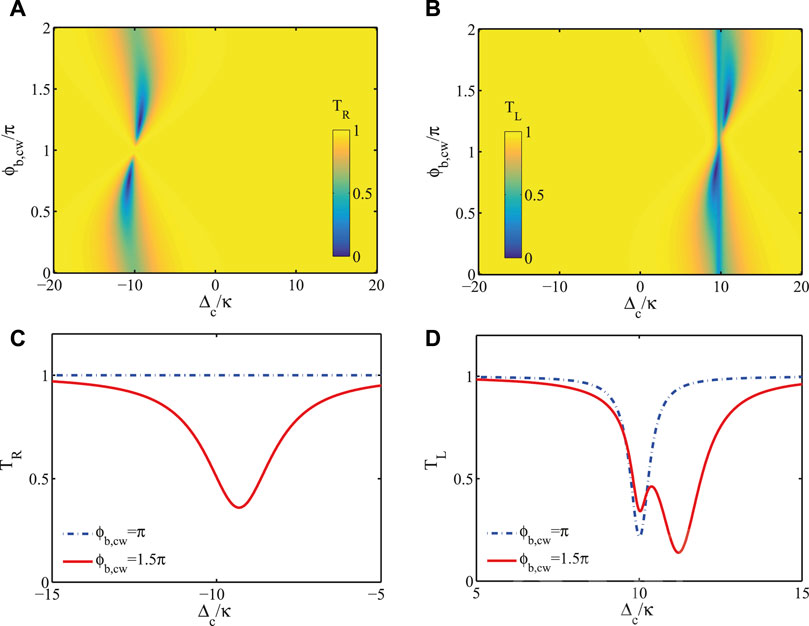
FIGURE 5. (Color online) Transmission rates T_R (A) and T_L (B) versus the detuning Δ_c/κ and the phase ϕ_b,cw/π. The corresponding transmission rates as a function of detuning Δ_c/κ for different phases ϕ_b,cw/π are plotted in (C,D). The parameters are set as: κ = 5 × 10⁻³ω_c, Ω = 0.97 GHz, ${\kappa }_{j,e}^i=\kappa$, κ_i = 0.5κ, and ϕ_a,cw = ϕ_L,cw = π with i = a, b and j = 1, 2.

In Figures 6A,B, we plot the transmission rates T_R and T_L versus the detuning Δ_c/κ for different J_b. For J_b = 10κ, the transmission spectra display an asymmetric four-dips structure. When decreasing J_b, the transmission dips can be suppressed. Moreover, T_L is always larger (smaller) than T_R in the region of Δ_c < 0 (Δ_c > 0). In order to describe the nonreciprocity clearly, we define the isolation ratio as

$\mathcal{I}\left(\text{dB}\right)=-10\times {\log }_{10}\frac{T_L}{T_R}.(27)$

In Figure 7, the isolation ratio $\mathcal{I}$ changing with the detuning Δ_c/κ and the coupling strength J_b is plotted. It shows that for J_b = 0 the ratio achieves $\mathcal{I}\approx 10\text{dB}$ $(\mathcal{I}\approx -5\text{dB})$ when fixing Δ_c = 11κ (Δ_c = −11.5κ). As we increase J_b, a larger mode splitting for Δ_c > 0 is observed. For J_b = 10κ, the ratio reaches $\mathcal{I}\approx 17\text{dB}$ when Δ_c is set as 15κ. In this case, the photons coming from the left side are blocked, which implies a directional photon transfer between different coupling points. Therefore, the nonreciprocal transmission behavior is also controlled by adjusting the coupling strengths between the CW and CCW modes and the detuning Δ_c.

FIGURE 6

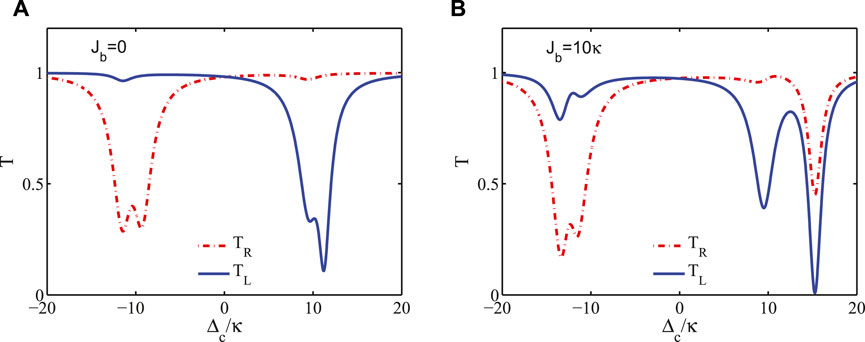
FIGURE 6. (Color online) The transmission rates T_R and T_L versus the detuning Δ_c/κ for (A) J_b = 0 and (B) J_b = 10κ. The parameters are set as: κ = 5 × 10⁻³ω_c, Ω = 0.97 GHz, ${\kappa }_{j,e}^i=\kappa$, κ_i = 0.5κ, J_a = 2κ, ϕ_a,cw = 0.5π, ϕ_L,cw = π, and ϕ_b,cw = 1.5π with i = a, b and j = 1, 2.

FIGURE 7

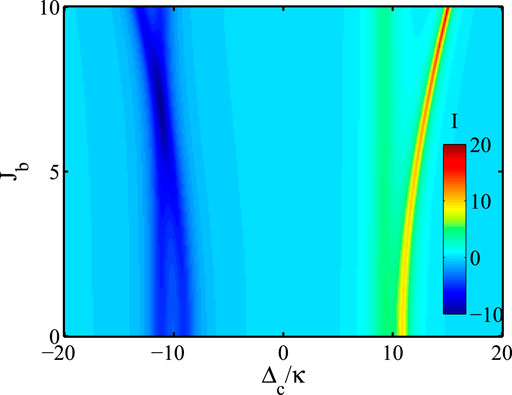
FIGURE 7. (Color online) The isolation ratio $\mathcal{I}$ as functions of the detuning Δ_c/κ and the coupling strength J_b. The parameters are set as: κ = 5 × 10⁻³ω_c, Ω = 0.97 GHz, ${\kappa }_{j,e}^i=\kappa$, κ_i = 0.5κ, J_a = 2κ, ϕ_a,cw = 0.5π, ϕ_L,cw = π, and ϕ_b,cw = 1.5π with i = a, b and j = 1, 2.

4 Conclusion

In conclusion, we have explored the photon emission and transport properties of spinning resonators coupled to a meandering waveguide at multiple coupling points. We demonstrate that the accumulated phases between multiple coupling points for photons propagating in CW and CCW directions are different. Both “giant-atoms” induced interference effects and mode frequency shifts led by the Sagnac effect dramatically modify photon transport properties. The emission direction and rates can be tuned by changing the spinning speed or number of coupling points. Moreover, the complete photon transmission over the whole optical frequency band led by destructive interference is observed, when photons coming from the right hand of the waveguide. This nonreciprocal phenomenon is very different from that observed in other optical systems. We have also studied the extended two-cavity system. The nonreciprocal photon transmission is controlled by changing the phases among adjacent coupling points or coupling strengths between the CW and CCW modes. By extending our proposal to multiple cavities interacting with multiple points, one can implement a multi-node chiral quantum network. In experiment, such a system with a spinning spherical resonator coupling to a stationary taper has been realized, where the angular speed is about 6.6 kHz [51]. The silica nanoparticle rotating with frequency exceeding 1 GHz has also been reported [62]. Therefore, we believe our theoretical proposals can be realized under current experimental approach. Those results in our paper provide a novel way to engineer rotatable nonreciprocal optical devices, which can be exploited for the realization of large-scale quantum networks and quantum information processing.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

XW contributed to conception. WL performed the numerical simulations and produced the first draft. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

WL was supported by the Natural Science Foundation of Henan Province (No. 222300420233). XW was supported by the National Natural Science Foundation of China (NSFC) (Nos. 12174303 and 11804270) and the China Postdoctoral Science Foundation (No. 2018M631136).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.894115/full#supplementary-material

Supplementary Figure S1 | The Sagnac-Fizeu shift Δ_F as a function of the spinning angular velocity Ω for the CW (red line) and CCW (blue line) mode. Other related parameters are Λ = 1550∼nm, R = 4.73∼nm, and n = 1.4.

References

1. Zheng H, Gauthier DJ, Baranger HU. Waveguide-QED-based Photonic Quantum Computation. Phys Rev Lett (2013) 111:090502. doi:10.1103/PhysRevLett.111.090502

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Liao Z, Zeng X, Nha H, Zubairy MS. Photon Transport in a One-Dimensional Nanophotonic Waveguide QED System. Phys Scr (2016) 91:063004. doi:10.1088/0031-8949/91/6/063004

CrossRef Full Text | Google Scholar

3. Roy D, Wilson CM, Firstenberg O. Colloquium : Strongly Interacting Photons in One-Dimensional Continuum. Rev Mod Phys (2017) 89:021001. doi:10.1103/RevModPhys.89.021001

CrossRef Full Text | Google Scholar

4. Akimov AV, Mukherjee A, Yu CL, Chang DE, Zibrov AS, Hemmer PR, et al. Generation of Single Optical Plasmons in Metallic Nanowires Coupled to Quantum Dots. Nature (2007) 450:402–6. doi:10.1038/nature06230

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Vetsch E, Reitz D, Sagué G, Schmidt R, Dawkins ST, Rauschenbeutel A. Optical Interface Created by Laser-Cooled Atoms Trapped in the Evanescent Field Surrounding an Optical Nanofiber. Phys Rev Lett (2010) 104:203603. doi:10.1103/PhysRevLett.104.203603

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Goban A, Hung C-L, Yu S-P, Hood JD, Muniz JA, Lee JH, et al. Atom-light Interactions in Photonic Crystals. Nat Commun (2014) 5:1–9. doi:10.1038/ncomms4808

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Goban A, Hung C-L, Hood JD, Yu S-P, Muniz JA, Painter O, et al. Superradiance for Atoms Trapped along a Photonic crystal Waveguide. Phys Rev Lett (2015) 115:063601. doi:10.1103/PhysRevLett.115.063601

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Corzo NV, Gouraud B, Chandra A, Goban A, Sheremet AS, Kupriyanov DV, et al. Large Bragg Reflection from One-Dimensional Chains of Trapped Atoms Near a Nanoscale Waveguide. Phys Rev Lett (2016) 117:133603. doi:10.1103/PhysRevLett.117.133603

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Astafiev O, Zagoskin AM, Abdumalikov AA, Pashkin YA, Yamamoto T, Inomata K, et al. Resonance Fluorescence of a Single Artificial Atom. Science (2010) 327:840–3. doi:10.1126/science.1181918

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Van Loo AF, Fedorov A, Lalumière K, Sanders BC, Blais A, Wallraff A. Photon-mediated Interactions between Distant Artificial Atoms. Science (2013) 342:1494–6. doi:10.1126/science.1244324

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Hoi I-C, Palomaki T, Lindkvist J, Johansson G, Delsing P, Wilson CM. Generation of Nonclassical Microwave States Using an Artificial Atom in 1D Open Space. Phys Rev Lett (2012) 108:263601. doi:10.1103/PhysRevLett.108.263601

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Shen JT, Fan S. Coherent Photon Transport from Spontaneous Emission in One-Dimensional Waveguides. Opt Lett (2005) 30:2001. doi:10.1364/OL.30.002001

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Zhou L, Gong ZR, Liu Y-x., Sun CP, Nori F. Controllable Scattering of a Single Photon inside a One-Dimensional Resonator Waveguide. Phys Rev Lett (2008) 101:100501. doi:10.1103/PhysRevLett.101.100501

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Witthaut D, Sørensen AS. Photon Scattering by a Three-Level Emitter in a One-Dimensional Waveguide. New J Phys (2010) 12:043052. doi:10.1088/1367-2630/12/4/043052

CrossRef Full Text | Google Scholar

15. Huang J-F, Shi T, Sun CP, Nori F Controlling Single-Photon Transport in Waveguides with Finite Cross Section. Phys Rev A (2013) 88:013836. doi:10.1103/PhysRevA.88.013836

CrossRef Full Text | Google Scholar

16. Liao Z, Nha H, Zubairy MS. Dynamical Theory of Single-Photon Transport in a One-Dimensional Waveguide Coupled to Identical and Nonidentical Emitters. Phys Rev A (2016) 94:053842. doi:10.1103/PhysRevA.94.053842

CrossRef Full Text | Google Scholar

17. Xiao Y-F, Li M, Liu Y-C, Li Y, Sun X, Gong Q. Asymmetric Fano Resonance Analysis in Indirectly Coupled Microresonators. Phys Rev A (2010) 82:065804. doi:10.1103/PhysRevA.82.065804

CrossRef Full Text | Google Scholar

18. Li B-B, Xiao Y-F, Zou C-L, Jiang X-F, Liu Y-C, Sun F-W, et al. Experimental Controlling of Fano Resonance in Indirectly Coupled Whispering-Gallery Microresonators. Appl Phys Lett (2012) 100:021108. doi:10.1063/1.3675571

CrossRef Full Text | Google Scholar

19. Sinha K, Meystre P, Goldschmidt EA, Fatemi FK, Rolston SL, Solano P. Non-Markovian Collective Emission from Macroscopically Separated Emitters. Phys Rev Lett (2020) 124:043603. doi:10.1103/PhysRevLett.124.043603

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Yu Y, Ma F, Luo X-Y, Jing B, Sun P-F, Fang R-Z, et al. Entanglement of Two Quantum Memories via Fibres over Dozens of Kilometres. Nature (2020) 578:240–5. doi:10.1038/s41586-020-1976-7

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Mitsch R, Sayrin C, Albrecht B, Schneeweiss P, Rauschenbeutel A. Quantum State-Controlled Directional Spontaneous Emission of Photons into a Nanophotonic Waveguide. Nat Commun (2014) 5:1–5. doi:10.1038/ncomms6713

CrossRef Full Text | Google Scholar

22. Le Feber B, Rotenberg N, Kuipers L. Nanophotonic Control of Circular Dipole Emission. Nat Commun (2015) 6:1–6. doi:10.1038/ncomms7695

CrossRef Full Text | Google Scholar

23. Frisk Kockum A, Delsing P, Johansson G. Designing Frequency-dependent Relaxation Rates and Lamb Shifts for a Giant Artificial Atom. Phys Rev A (2014) 90:013837. doi:10.1103/PhysRevA.90.013837

CrossRef Full Text | Google Scholar

24. Guo L, Grimsmo A, Kockum AF, Pletyukhov M, Johansson G. Giant Acoustic Atom: a Single Quantum System with a Deterministic Time Delay. Phys Rev A (2017) 95:053821. doi:10.1103/PhysRevA.95.053821

CrossRef Full Text | Google Scholar

25. Kockum AF, Johansson G, Nori F. Decoherence-free Interaction between Giant Atoms in Waveguide Quantum Electrodynamics. Phys Rev Lett (2018) 120:140404. doi:10.1103/PhysRevLett.120.140404

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Kannan B, Ruckriegel MJ, Campbell DL, Frisk Kockum A, Braumüller J, Kim DK, et al. Waveguide Quantum Electrodynamics with Superconducting Artificial Giant Atoms. Nature (2020) 583:775–9. doi:10.1038/s41586-020-2529-9

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Zhao W, Wang Z. Single-photon Scattering and Bound States in an Atom-Waveguide System with Two or Multiple Coupling Points. Phys Rev A (2020) 101:053855. doi:10.1103/PhysRevA.101.053855

CrossRef Full Text | Google Scholar

28. Frisk Kockum A. Quantum Optics with Giant Atoms-The First Five Years. In: International Symposium on Mathematics, Quantum Theory, and Cryptography. Singapore: Springer (2021). p. 125–46. doi:10.1007/978-981-15-5191-8_12

CrossRef Full Text | Google Scholar

29. Yu H, Wang Z, Wu J-H. Entanglement Preparation and Nonreciprocal Excitation Evolution in Giant Atoms by Controllable Dissipation and Coupling. Phys Rev A (2021) 104:013720. doi:10.1103/PhysRevA.104.013720

CrossRef Full Text | Google Scholar

30. Du L, Chen Y-T, Li Y. Nonreciprocal Frequency Conversion with Chiral Λ -type Atoms. Phys Rev Res (2021) 3:043226. doi:10.1103/PhysRevResearch.3.043226

CrossRef Full Text | Google Scholar

31. Du L, Cai M-R, Wu J-H, Wang Z, Li Y. Single-photon Nonreciprocal Excitation Transfer with Non-markovian Retarded Effects. Phys Rev A (2021) 103:053701. doi:10.1103/PhysRevA.103.053701

CrossRef Full Text | Google Scholar

32. Wang X, Liu T, Kockum AF, Li H-R, Nori F. Tunable Chiral Bound States with Giant Atoms. Phys Rev Lett (2021) 126:043602. doi:10.1103/PhysRevLett.126.043602

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Wang X, Li HR. Chiral Quantum Network with Giant Atoms (2021). arXiv preprint arXiv:2106.13187.

Google Scholar

34. Soro A, Kockum AF. Chiral Quantum Optics with Giant Atoms. Phys Rev A (2022) 105:023712. doi:10.1103/PhysRevA.105.023712

CrossRef Full Text | Google Scholar

35. Du L, Chen YT, Zhang Y, Li Y. Giant Atoms with Time-dependent Couplings (2022). arXiv preprint arXiv:2201.12575.

Google Scholar

36. Gustafsson MV, Aref T, Kockum AF, Ekström MK, Johansson G, Delsing P. Propagating Phonons Coupled to an Artificial Atom. Science (2014) 346:207–11. doi:10.1126/science.1257219

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Manenti R, Kockum AF, Patterson A, Behrle T, Rahamim J, Tancredi G, et al. Circuit Quantum Acoustodynamics with Surface Acoustic Waves. Nat Commun (2017) 8:1–6. doi:10.1038/s41467-017-01063-9

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Andersson G, Suri B, Guo L, Aref T, Delsing P. Non-exponential Decay of a Giant Artificial Atom. Nat Phys (2019) 15:1123–7. doi:10.1038/s41567-019-0605-6

CrossRef Full Text | Google Scholar

39. Goto T, Dorofeenko AV, Merzlikin AM, Baryshev AV, Vinogradov AP, Inoue M, et al. Optical Tamm States in One-Dimensional Magnetophotonic Structures. Phys Rev Lett (2008) 101:113902. doi:10.1103/PhysRevLett.101.113902

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Khanikaev AB, Mousavi SH, Shvets G, Kivshar YS. One-way Extraordinary Optical Transmission and Nonreciprocal Spoof Plasmons. Phys Rev Lett (2010) 105:126804. doi:10.1103/PhysRevLett.105.126804

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Fan L, Wang J, Varghese LT, Shen H, Niu B, Xuan Y, et al. An All-Silicon Passive Optical Diode. Science (2012) 335:447–50. doi:10.1126/science.1214383

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Cao Q-T, Wang H, Dong C-H, Jing H, Liu R-S, Chen X, et al. Experimental Demonstration of Spontaneous Chirality in a Nonlinear Microresonator. Phys Rev Lett (2017) 118:033901. doi:10.1103/PhysRevLett.118.033901

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Lira H, Yu Z, Fan S, Lipson M. Electrically Driven Nonreciprocity Induced by Interband Photonic Transition on a Silicon Chip. Phys Rev Lett (2012) 109:033901. doi:10.1103/PhysRevLett.109.033901

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Estep NA, Sounas DL, Soric J, Alù A. Magnetic-free Non-reciprocity and Isolation Based on Parametrically Modulated Coupled-Resonator Loops. Nat Phys (2014) 10:923–7. doi:10.1038/nphys3134

CrossRef Full Text | Google Scholar

45. Sounas DL, Alù A. Non-reciprocal Photonics Based on Time Modulation. Nat Photon (2017) 11:774–83. doi:10.1038/s41566-017-0051-x

CrossRef Full Text | Google Scholar

46. Lu X, Cao W, Yi W, Shen H, Xiao Y. Nonreciprocity and Quantum Correlations of Light Transport in Hot Atoms via Reservoir Engineering. Phys Rev Lett (2021) 126:223603. doi:10.1103/PhysRevLett.126.223603

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Jing H, Lü H, Özdemir SK, Carmon T, Nori F. Nanoparticle Sensing with a Spinning Resonator. Optica (2018) 5:1424–30. doi:10.1364/OPTICA.5.001424

CrossRef Full Text | Google Scholar

48. Li B, Huang R, Xu X, Miranowicz A, Jing H. Nonreciprocal Unconventional Photon Blockade in a Spinning Optomechanical System. Photon Res (2019) 7:630–41. doi:10.1364/PRJ.7.000630

CrossRef Full Text | Google Scholar

49. Huang R, Miranowicz A, Liao J-Q, Nori F, Jing H. Nonreciprocal Photon Blockade. Phys Rev Lett (2018) 121:153601. doi:10.1103/PhysRevLett.121.153601

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Jiao Y-F, Zhang S-D, Zhang Y-L, Miranowicz A, Kuang L-M, Jing H. Nonreciprocal Optomechanical Entanglement against Backscattering Losses. Phys Rev Lett (2020) 125:143605. doi:10.1103/PhysRevLett.125.143605

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Maayani S, Dahan R, Kligerman Y, Moses E, Hassan AU, Jing H, et al. Flying Couplers above Spinning Resonators Generate Irreversible Refraction. Nature (2018) 558:569–72. doi:10.1038/s41586-018-0245-5

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Fang Y-LL, Baranger HU Waveguide QED: Power Spectra and Correlations of Two Photons Scattered off Multiple Distant Qubits and a Mirror. Phys Rev A (2015) 91:053845. doi:10.1103/PhysRevA.91.053845

CrossRef Full Text | Google Scholar

53. Zhu J, Özdemir SK, Xiao Y-F, Li L, He L, Chen D-R, et al. On-chip Single Nanoparticle Detection and Sizing by Mode Splitting in an Ultrahigh-Q Microresonator. Nat Photon (2010) 4:46–9. doi:10.1038/nphoton.2009.237

CrossRef Full Text | Google Scholar

54. Özdemir ŞK, Zhu J, Yang X, Peng B, Yilmaz H, He L, et al. Highly Sensitive Detection of Nanoparticles with a Self-Referenced and Self-Heterodyned Whispering-Gallery Raman Microlaser. Proc Natl Acad Sci U.S.A (2014) 111:E3836–E3844. doi:10.1073/pnas.1408283111

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Malykin GB. The Sagnac Effect: Correct and Incorrect Explanations. Phys.-Usp. (2000) 43:1229–52. doi:10.1070/pu2000v043n12abeh000830

CrossRef Full Text | Google Scholar

56. Fermi E. Quantum Theory of Radiation. Rev Mod Phys (1932) 4:87–132. doi:10.1103/RevModPhys.4.87

CrossRef Full Text | Google Scholar

57. Xiao Y-F, Gaddam V, Yang L. Coupled Optical Microcavities: an Enhanced Refractometric Sensing Configuration. Opt Express (2008) 16:12538–43. doi:10.1364/OE.16.012538

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Xu S, Fan S. Fano Interference in Two-Photon Transport. Phys Rev A (2016) 94:043826. doi:10.1103/PhysRevA.94.043826

CrossRef Full Text | Google Scholar

59. Du L, Wang Z, Li Y. Controllable Optical Response and Tunable Sensing Based on Self Interference in Waveguide QED Systems. Opt Express (2021) 29:3038–54. doi:10.1364/OE.412996

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Cai QY, Jia WZ. Coherent Single-Photon Scattering Spectra for a Giant-Atom Waveguide-QED System beyond the Dipole Approximation. Phys Rev A (2021) 104:033710. doi:10.1103/PhysRevA.104.033710

CrossRef Full Text | Google Scholar

61. Feng SL, Jia WZ. Manipulating Single-Photon Transport in a Waveguide-QED Structure Containing Two Giant Atoms. Phys Rev A (2021) 104:063712. doi:10.1103/PhysRevA.104.063712

CrossRef Full Text | Google Scholar

62. Reimann R, Doderer M, Hebestreit E, Diehl R, Frimmer M, Windey D, et al. GHz Rotation of an Optically Trapped Nanoparticle in Vacuum. Phys Rev Lett (2018) 121:033602. doi:10.1103/PhysRevLett.121.033602

PubMed Abstract | CrossRef Full Text | Google Scholar