OSAFT Library: An Open-Source Python Library for Acoustofluidics

In this article, we present the Open-Source AcoustoFluidics Theories (OSAFT) library (version 0.9.14), a Python library for acoustofluidics. The focus of the library is the classical problem of a particle suspended in a fluid and subjected to an incident acoustic wave. The Python code provides easy access to a number of theories describing acoustic scattering, acoustic streaming, and most importantly the acoustic radiation force exerted on the particle. At the time of submission of this article, six different theoretical models and various limiting cases thereof are available. All are treating the problem of a single, spherical particle in an infinite 3D-domain subjected to an incident plane standing or plane traveling wave. The implementations of further theories are currently under development. Our code is designed to be extensible. A library of fluid and solid material models facilitates the implementation of new theories. A unified application programming interface (API), which is used across all models, makes comparisons between different theories straightforward. Such comparisons can be made directly by the user or through the plotting capabilities of our library. The code is distributed through Python’s standard software repository PyPi. Illustrative examples on the project’s website serve as a starting point for learning the library’s API. For a more in-depth understanding of the code, complete documentation of the codebase, directed at users as well as future collaborators, is available online. In an effort to make the library as extensive as possible, the authors of this article are looking for collaborators on the project.

1 Introduction

A particle or a droplet suspended in a fluid and subjected to an acoustic wave will experience a force that can lead to a drift of the particle in the surrounding medium. This force is called acoustic radiation force (ARF). It results from the scattering of the acoustic wave on the particle. More precisely, the force can be described as a time-averaged, nonlinear effect stemming from the interaction of the incident and scattered acoustic field [1]. In a general form, the force can be written as the time-averaged integral of the stress tensor σ_ij over the moving surface of the particle S(t)

$F_i^{\text{rad}}={\int }_{S\left(t\right)}{\sigma }_{ij}\left(t\right)n_j\left(t\right)ds(1)$

where n_j is the surface normal vector, and ⟨⋅⟩ denotes the time-average. Here summation over repeated indices is assumed. In 1934, King published the first theoretical treatment of the ARF [1]. In his seminal work, he describes the ARF exerted on a rigid sphere in an inviscid fluid. King solves the scattering problem in the near-field using the multipole expansion technique, which allows him to find a theoretical expression for the ARF in a plane standing and a plane traveling wave field. In 1955, Yosioka and Kawasima extended King’s work to compressible spheres [2]. Their paper includes the important formula that describes the ARF on small compressible particles in a standing wave field

$F^{\text{rad}}=4\pi R^3{k}_{\text{f}}\bar{E}\mathrm{\Phi }\sin \left(2k_{\text{f}}h\right)(2)$

where R is the particle radius, k_f the acoustic wavenumber in the inviscid fluid, and h is the distance between the particle and the pressure node of the standing wave field. Φ is the density-compressibility factor which, in more recent works, is mostly termed the acoustic contrast factor. $\bar{E}$ denotes the average acoustic energy density in the plane standing wave field. It can be expressed in terms of the pressure amplitude of the incident field p_a, the fluid density ρ_f, and the speed of sound in the fluid c_f

$\bar{E}=\frac{p_{\text{a}}^2}{4{\rho }_{\text{f}}{c}_{\text{f}}^2}.(3)$

Already lesser known is the fact that both King and Yosioka and Kawasima provide a general solution in their paper that is not limited to the small-particle regime, which, in the case of Yosioka and Kawasima, allows for investigations of the influence of particle resonances on the ARF. A theoretically different approach was chosen by Gor’kov, who computes the ARF on a small, compressible particle in the far-field [3]. This elegant mathematical trick allows Gor’kov in his famous 1962 paper to sidestep the often cumbersome modal decomposition of the incident field. Gor’kov is able to write the ARF in a standing wave field as a potential force

${\mathit{F}}^{\text{rad}}=2\pi R^3{\rho }_{\text{f}}\nabla \left\{\frac{\langle p_{\text{in}}^2\rangle }{3{\rho }_{\text{f}}^2{c}_{\text{f}}^2}{f}_1-\frac{\langle v_{\text{in}}^2\rangle }{2}{f}_2\right\},(4)$

where p_in and v_in are the incident pressure and velocity fields, respectively. f₁, the monopole coefficient, and f₂, the dipole coefficient, are closely related to the acoustic contrast factor introduced above

$\mathrm{\Phi }=\frac{1}{3}{f}_1+\frac{1}{2}{f}_2(\mathrm{5a})$

$f_1=1-\frac{c_{\text{f}}^2{\rho }_{\text{f}}}{c_{\text{p}}^2{\rho }_{\text{p}}}(\mathrm{5b})$

$f_2=\frac{2\left({\rho }_{\text{p}}-{\rho }_{\text{f}}\right)}{2{\rho }_{\text{p}}+{\rho }_f}(\mathrm{5c})$

where c_p and ρ_p are the speed of sound and the density of the particle, respectively. In the following years, the theory on the ARF has been extended in many publications. Following the footsteps of King, Yosioka, and Kawasima, Hasegawa et al. extended the theory to linear-elastic, solid particles [4], absorbing solid particles [5], and to quasi-stationary waves [6]. To the authors’ best knowledge, the first formulation of the ARF in a standing wave field that includes the fluid viscosity was given by Danilov [7]. His theory was later generalized by Doinikov, who published several articles treating the case of a viscous fluid [8, 9], a thermoviscous fluid [10–12] and most recently a viscoelastic fluid [13]. Using a similar approach as Gor’kov, Settnes and Bruus also found an expression for the ARF in a viscous fluid [14]. Karlsen and Bruus later extended the theory to thermoviscous fluids [15].

In the interest of brevity, our discussion of the ARF is limited to articles which assume that perturbation theory can be employed to compute the ARF. Furthermore, we restricted ourselves to publications treating the problem of a single, spherical, homogeneous particle that provide a solution for the plane standing wave case. And even so our summary is far from complete. A large number of articles discussing only progressive waves exist that were omitted here. Moreover, theories for non-spherical objects, multi-particle setups, non-homogeneous particles, non-symmetrical wavefronts, and theories where the assumptions of perturbation theory do not hold have been developed, and we refer the reader to the review by Doinikov who has written the most recent review on ARF theories the authors know of [16].

Even if we restrict ourselves to this very specific setup, a vast number of different theories exist, many of which come with special solutions that only hold in certain limiting cases. It becomes clear that choosing the most suitable model to fit a physical problem, for example to interpret experimental results, validate a numerical simulation, or during the design process of an acoustofluidic device, is not straightforward. The issue is amplified since the formulations for the ARF in some theories are long, complicated expressions and code that implements these formulas is not readily available online. Furthermore, different mathematical conventions used in publications further complicate the comparison between different models.

In this article, we describe the OSAFT library, an open-source Python library that tackles the problem at hand. When starting with the development, we had four main goals in mind: Our library should be 1) accessible, 2) extensive, 3) easy to use, and 4) all formulas should be implemented correctly.

We make our library accessible by using the Python programming language, which is widely used and available to download for free. The library is available through Python’s standard software repository PyPi, which simplifies the installation process [17].

The project is meant to be as extensive as possible. At the time of publication of this article, theories from six different models are implemented: King (1934), Yosioka and Kawasima (1955), Gor’kov (1962), Doinikov (1994, rigid particle), Doinikov (1994, compressible particle), and Settnes and Bruus (2012). A more detailed list containing the references is found in Table 1. A library for fluid and solid material models, a large number of often used mathematical functions, and standard definitions of physical properties of the acoustic field facilitate the implementation of new theories. For models that share a similar theoretical approach, such as multipole expansion theories, base classes for the computation of the scattering and streaming fields are available. These base classes provide essential methods and structures needed for the implementation of new theories.

TABLE 1

TABLE 1. Overview of available models and their implemented solutions in the OSAFT library (SC stands for acoustic scattering and AS for acoustic streaming). Note, here we take advantage of the fact that the 2-parameter-material model of a compressible sphere defined by the speed of sound c_s and the density ρ_s is equivalent to the material model of an inviscid fluids. Theresfore, the InviscidFluid class is used also as material model class for the scatterer in some theories.

The library is easy to use thanks to a standardized API that is applied across all models. During the implementation of the code mathematical definitions and variable names are unified across different theories. Using the integrated plotting capabilities of the library, different models can easily be compared. Examples are given in Section 3. Beyond simple line plots of the ARF, plots and animations of the scattering fields are possible, if the field can be inferred from a given theory. These scattering plots allow for a visual understanding of the influence of parameters, such as relative particle size or boundary layer thickness. The project’s documentation website [18] provides an installation tutorial¹, a complete documentation of the codebase, and example scripts that serve as a starting point for learning the library’s API².

Last but not least, our priority is the correctness of the code. We achieve this by employing different types of unittesting. Simple typos and bugs are discovered through redundant implementation of code in the test scripts. More involved errors are found through a comparison of different models that converge in limiting cases. This technique not only helped us discover bugs in our code but actually revealed errors in the publications themselves. The unittesting scheme is described in Section 2.2, the errors we found in the publications are discussed in Section 3.4.

Lastly, we want to emphasize the open-source character of the project. The library is not only meant to be free to download with a fully accessible codebase, but collaboration on the project is possible and explicitly welcomed. The collaboration is organized through the project’s online repository [19], where unpublished versions of the code are available, questions can be asked, and collaborator status can be requested.

2 Methods

2.1 Code Structure

Different theories describing the ARF vary in the combination of the material model for the scatterer and for the surrounding medium, the incident wave type, and, lastly, what assumptions are made and how calculations are carried out. For example, both Yosioka and Kawasima [2] and Gor’kov [3] assume an inviscid fluid for the surrounding medium and a compressible sphere as a scatterer. Nevertheless, they derive different solutions because of their calculation paths. Here, different does not mean inconsistent numerical results but different scope of application. Table 1 lists the currently available models in the library and also the classes/models they assume for the fluid and the particle. It can be seen that many models share common features.

We take advantage of this by defining basic core features that can be used throughout the library. In addition, the usage of inheritance reduces the number of duplicated code. For example, the class ViscoelasticFluid is an extension of ViscousFluid which in turn inherits from InviscidFluid. Here and in the following, expressions written in monospace font are actual methods, classes, and class attributes defined in the library. A similar inheritance scheme is in place for the implemented solid types (ElasticSolid inherits from RigidSolid). Each model also needs an acoustic background field which we implemented through the class BackgroundField. All of those core features are defined once and used multiple times throughout the library.

The core of the OSAFT library are the implemented theories themselves. In order to unify the interface for the user, we defined base classes for the scattering field, the streaming field, and the ARF with templated methods that need to be implemented. E.g., all classes for the ARF need to inherit at least from BaseARF which has a templated empty compute_arf() method. Therefore, each ARF implementation needs to have at least this method which simplifies usage.

For theories that not only provide expressions for the ARF but also for the acoustic scattering and acoustic streaming fields, the inheritance scheme is a bit more advanced. Figure 1 depicts the inheritance scheme for a model with a scattering, a streaming, and an ARF solution. The classes with “Base” as prefix are base classes with unified templated methods. As before, the templated methods ensure that the user has the same interface for every scattering and streaming model.

FIGURE 1

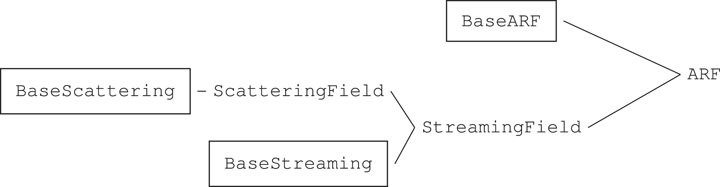
FIGURE 1. Inheritance diagram for model which has a scattering solution, a streaming solution, and an ARF solution. The boxed classes represent base classes given within the library.

We use code inheritance for the solutions instead of composition because it also reflects the physical world. The solution for the streaming field depends on the solution for the scattering field. And the ARF depends on the solution for the scattering field and sometimes on the solution for the streaming field. For a model, that does not need these three classes because it only provides an expression for the ARF, e.g., [3], the ARF class only inherits from BaseARF.

Composition is used when building the solution class from the material model classes and the incident field class. As shown in Table 1, all implemented models have a fluid attribute, a scatterer attribute, and an incident field attribute that are predefined classes in the library.

The solution classes, which implement a theory from acoustofluidics, contain many attributes representing physical entities in a theoretical model. The values of these attributes are connected to each other through complex patterns of interdependence. This can lead to problems since the change of an attribute value needs to be reflected in all dependent attributes. In the OSAFT library we tackle this problem by implementing the observer design pattern [20]. We differentiate between PassiveVariable and ActiveVariable. A PassiveVariable can be understood as a model input that does not depend on any other variables, e.g., the particle radius R or the speed of sound in the fluid surrounding the particle c_f. An ActiveVariable, on the other hand, is a quantity that depends directly or indirectly on a PassiveVariable, e.g., the viscous boundary layer thickness $\delta =\sqrt{2{\eta }_{\text{f}}/\omega {\rho }_{\text{f}}}$ or the linear scattering coefficients of a scattering field. Note that the design pattern is not limited to a two-level hierarchy but an ActiveVariable can also depend on another ActiveVariable. Whenever a variable changes its value, it notifies all dependent ActiveVariable. This notification does not trigger an immediate recomputation of the ActiveVariable, but the value is recomputed only if the attribute is accessed. The recomputed value is then stored in memory for later retrieval.

For a simple ActiveVariable like the boundary layer thickness, the observer design pattern might not improve the efficiency of the code since the design pattern itself introduces an overhead. However, beyond simple numerical values an ActiveVariable can store arrays of values or whole data structures, for which the recomputation is significantly slower than our observer design pattern. This is in particular relevant for the plotting of acoustic fields or for the computation of the ARF in complex models where during numerical integration certain values are accessed many times.

2.2 Code Validation

Besides implementing the formulas from a theory, an equally important part is the validation of the implemented code and the protection against unintended changes. We validate our code with a so-called unittest procedure that we explain in the following. Our test suite is based on Python’s built-in unittest library.

Most of our tests are a numeric comparison between two values. This numeric test compares the relative difference between two values x₁, x₂ to a threshold ϵ

$\frac{\left|x_1-x_2\right|}{\min \left\{\left|x_1\right|,\left|x_2\right|\right\}}<ϵ.(6)$

The test passes if our measure is smaller than ϵ and fails otherwise. Our default value for the threshold ϵ is 10^–10 but it can be adapted if needed. For the parts of the code where we cannot compare numeric values, like the plotting module, we check if the code (a) runs without raising errors—a runtime error like dividing by zero or executing false code leads to a failing unittesting procedure—and (b) produces the expected output by visual inspection.

With the numeric tests we can validate our code on three different levels of abstraction. The first one is the implementation level. On this level we implement each method again in the testing part and test the numeric values against each other. This testing level ensures that the methods are free of simple bugs, such as typos or missing terms in an expression. The next testing level is the structural level. On this level we check the dependencies of an ActiveVariable. On the testing site the methods and properties are implemented again, but this time in such a way that their return values are recomputed every time a method is called. By changing the parameters one after the other and by comparing the numeric values from the production code and testing code after each change we can ensure that all dependencies are set correctly, because a failed test directly implies that a dependency is missing. The last testing level is what we call the physical unittesting. Here, we differentiate between model-to-model testing and boundary condition testing. In the former, we compare different formulations of the ARF to each other. These can either be expressions from two separate publications or different solutions describing special cases within one article. To validate expressions against each other we make use of the fact that different expressions will converge to each other in certain limiting cases and thus will yield consistent results.

One of those model-to-model testing relations is shown in Figure 2. It depicts the relationship between Yosioka and Kawasima’s general solution [2] to King [1], Gor’kov [3], and the special cases from Yosioka and Kawasima’s theory. For this specific case, we set the relative numeric threshold ϵ of Eq. 6 to a value of 10^–3. An ϵ value of 10^–3 implies that the relative error between two models is less than 0.1%. We use this model-to-model ARF comparison as often as possible and not only for Yosioka and Kawasima’s general solution.

FIGURE 2

FIGURE 2. Relationship between Yosioka and Kawasima’s general solution and other theories and special cases. The rounded boxes indicate if a special case of a theory is assumed. The condition on the connection arrows indicate when the general solution is equal to the others. c_p, ρ_p and R are the sound speed, the density, and the radius of the particle, respectively; c_f, ρ_f, and k_f are the speed of sound, the density and the wavenumber in the fluid, respectively.

The latter type of physical unittesting is to verify the boundary conditions for the scattering and streaming solution. E.g., in [8] Doinikov assumes a rigid particle and a viscous fluid. In order to solve the first-order fields a set of boundary conditions must be fulfilled at the fluid-particle interface. For the case of a rigid particle and a viscous fluid, the fluid velocity v_f and the particle velocity v_p must be equal in magnitude and direction

${\mathrm{v}}_{\text{f}}={\mathrm{v}}_{\text{p}}\text{at\hspace{0.17em}surface\hspace{0.17em}of\hspace{0.17em}particle}.(7)$

For every scattering and streaming solution in the library, we test these velocity boundary conditions.

Lastly, it is also possible to measure how much of the production code is covered with unittests. This measure is the so-called coverage which is given as a percentage. A value of 50% coverage means that half of the total lines of code got executed at least once during the unittesting procedure. A high coverage value does not imply that the tested code is necessarily right but that the main part of the code got executed and passed all tests. Our code coverage is greater than 99%. Considering our three abstractions levels of unittesting and the almost perfect coverage percentage, we are confident that we have limited errors in our code to an absolute minimum.

2.3 Code Infrastructure and Dependencies

The library is listed in Python’s package index PyPi [17] ³ and can be installed on any machine running Python 3.9 or newer using pip. The minimal requirements for being officially listed on PyPi are: 1) code written in Python, 2) a setup script which handles the installation on the client machine, 3) a readme file with an overview of the scope of the package, 4) an open source license (here: GNU Lesser General Public Licence v3 ⁴). The current version of the OSAFT library (0.9.14) itself depends on four common third-party packages that are also distributed through PyPi: Matplotlib (3.5.1) [21], NumPy (1.22) [22], SciPy (1.8.0) [23], and SymPy (1.7.1) [24], where the numbers in parentheses indicate the versions of the packages that are used. During the installation process these dependencies are automatically installed.

As version control software we use Git⁵ and the code is hosted on Gitlab [19] ⁶. There not only the published code is available, but also extensions to the library that are currently under development. In forums, future models, bugs that need fixing, and planned new features are reviewed openly. In order to contribute, one needs to create an account and ask to be added to the group of developers. However, the code itself and discussions are visible without such an account.

Adding new lines of code or changing existing code is only possible with so-called merge requests. These requests are similar to the peer review process for scientific publications. During the merge request, changes to the code are reviewed, discussed, and, if needed, altered. This process is again visible to anybody (no account needed). There are three requirements before the changes get accepted into the existing production code: 1) New unittests must be implemented that validate the changes to the code; 2) The test suite must pass all its tests (including the new ones); 3) The changes must be approved by at least one of the maintainers of the code. A maintainer of the code (as of now Jonas Fankhauser and Christoph Goering) cannot self approve their own merge requests.

We document the library with documentation strings (docstrings) within the code. For that we use Sphinx⁷ which generates a user-friendly documentation website from the docstrings [18]. Most integrated development environments (IDEs) like PyCharm or Visual Studio Code, can also parse the docstrings and display them directly to the user to increase productivity. Finally, our documentation includes so-called typehints. Typehints are additional information strings that define what type (e.g., integer, float, list) the inputs or the return value of a method is expected to be. In Python, those types are not enforced, but modern IDEs can warn the user if the used type conflicts with the expected type. This again increases productivity.

3 Results

In the first three parts of this section, three examples illustrate possible applications of the OSAFT library. In the last section, the unittesting is discussed, and we show how our physical unittesting led to the discovery of errors in two research articles. All the code examples and plots in this section have been generated using the OSAFT library and the source code to reproduce them is given in the Supplementary Material. The arrow -> indicates the return value of a function to differentiate it from variable assignment with the equal sign = .

3.1 Small Polystyrene Particle in Water

In our first example, we compute the ARF on a 1 µm polystyrene particle in a 1 MHz standing wave field. The surrounding medium is water, the pressure amplitude of the incident field is p_in = 1 bar, and the particle is positioned halfway between velocity node and anti-node in the standing wave field, where the ARF reaches a maximum. The material parameters for all the examples can be found in Table 2. In this classical example for the computation of the ARF in acoustofluidics, different theories are expected to give an accurate estimation of the ARF. Here, we compare the models from Yosioka and Kawasima (Eq. 44 in [2]), Gor’kov (Eq. 13 in [3]), and Settnes and Bruus (Eq. 20 in [14]) to each other. While the former two assume an inviscid fluid for the surrounding medium, the model by Settnes and Bruus also models the fluid shear viscosity, which is included in our calculation. However, we are going to show that the influence of the viscosity is small and all three models return very similar results. In our example, we are in the small-particle limit which can easily be verified using the library by evaluating the product of the wavenumber in the fluid k_f and the particle radius R. E.g. using the solution class from Yosioka, we compute the product to be:

TABLE 2

TABLE 2. Table of material properties used in Section 3 at 25°C and 1 atm.

yosioka.k_f * yosioka.R_0 -> 0.0004

Therefore, both the model from Gor’kov and the model by Settnes and Bruus can be used to compute the ARF, which are both only valid in the small-particle limit. Evaluating the ARF for the three models using the OSAFT library yields:

yosioka.compute_arf() -> 1.228e-15

gorkov.compute_arf() -> 1.228e-15

settnes.compute_arf() -> 1.229e-15

And indeed, we were able to confirm that the three models are as expected in excellent agreement for the given example.

3.2 HFE Oil Droplet in Water

In the second example, the ARF exerted on a droplet of inviscid HFE oil in a 5 MHz standing wave field suspended in water is evaluated. The pressure amplitude is set to be p_in = 1 bar and the droplet is placed halfway between velocity node and anti-node of the field h = c_f/(8f). As we have shown in our first example, the influence of viscosity in water is small in this case and only the models from King (Eq. 74 in [1]), Yosioka and Kawasima (Eq. (44) in [2]), and Gor’kov (Eq. 13 in [3]) are compared, which all assume an inviscid fluid (see Table 1).

Figure 3A shows the dependency of the ARF on the particle size in the long-wavelength regime. The particle radius, ranging from R = 1–15 μm, is small in comparison to the acoustic wavelength in the fluid λ_f = 296 μm. The model from King deviates from the other and predicts the wrong direction for the ARF. This has to be expected since King’s theory computes the ARF on a rigid particle and thus only provides an accurate estimate of the ARF if the particle compressibility is much lower than the compressibility of the fluid. That this is not the case here can easily be verified using the library

FIGURE 3

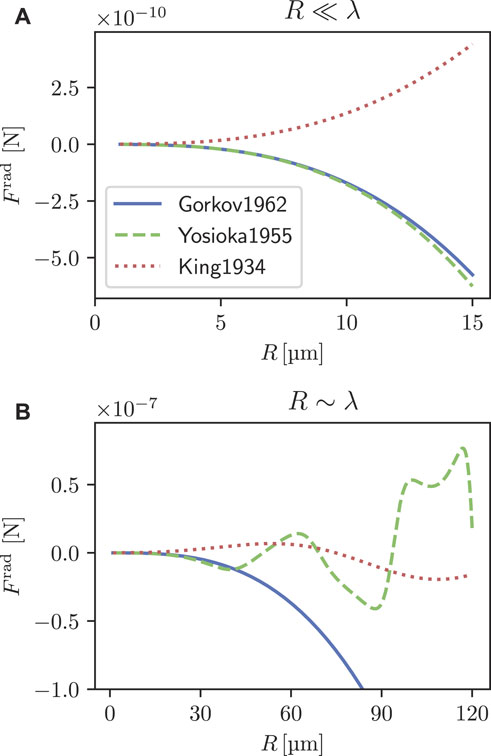
FIGURE 3. Acoustic radiation force on an HFE oil droplet suspended in water placed halfway between the velocity node and the anti-node of a standing wave field in the long-wavelength regime (A) and the intermediate wavelength regime (B).

yosioka.scatterer.kappa_f -> 1.42e-09

yosioka.fluid.kappa_f -> 4.47e-10

where scatterer.kappa_f and fluid.kappa_f return the droplet and the fluid compressibility, respectively. In the long-wavelength limit, the influence of the compressibility ratio and the density ratio between fluid and droplet can also be estimated by evaluating the scattering coefficients f₁ and f₂ in the model from Gor’kov from Eq. 4. The coefficient f₁ represents the contribution of the acoustic monopole to the ARF and is thus related to the compressibility ratio between fluid and droplet. The dipole coefficient f₂, on the other hand, depends on the density ratio. Evaluating these two coefficients with the OSAFT library reveals that indeed the contribution of the monopole scattering to ARF is significant, confirming our finding:

gorkov.f_1 - > -2.18

gorkov.f_2 -> 0.29

The models from Gor’kov and from Yosioka and Kawasima take the particle compressibility into account, and they are in good agreement in the small particle limit.

Increasing the particle radius further, the assumption of a small particle compared to the wavelength no longer holds. In this intermediate regime, displayed in Figure 3B, higher-order eigenmodes of the droplet start contributing to the ARF. The model of Gor’kov is limited to the small-particle regime and neglects the influence of these modes. Therefore, it fails to describe the ARF accurately for particles larger than 40 µm. As opposed to Gor’kov’s model, the general solution provided by Yosioka and Kawasima is not restricted, and it is possible to compute the ARF for larger particles and droplets. The figure further shows that the ARF does no longer scale with the particle volume in this regime which explains why the force is usually less relevant for applications here than in the long-wavelength limit.

Beyond plots of the ARF, with the OSAFT library it is possible to plot and animate the oscillatory motion of a particle in the acoustic field. Figure 4 shows the exaggerated droplet oscillation mode at three different radii plotted according to the theory of Yosioka and Kawasima. For a small droplet (R = 1 μm) the oscillations are dominated by the dipole mode, where the droplet moves back and forth as a rigid body. Increasing the particle size to R = 30 μm, the monopole (breathing) mode of the droplet starts contribution to the oscillations. Finally, at R = 90 μm the oscillation is composed of a complex superposition of droplet eigenmodes. It becomes clear why in this regime the model from Gor’kov no longer accurately describes the ARF. It has to be mentioned, however, that when drawing a direct connection between contributing eigenmodes in the oscillation and the ARF, one has to be cautious. While for example for an air bubble in water the ARF will indeed have a peak at its first eigenfrequency (see Section 3.4), the mode dominating the oscillation does not necessarily have to dominate the ARF. The oscillations are a result of the linear scattering process, while the ARF is an inherently nonlinear effect. And indeed, the fact that this direct connection can not be made was already shown in the example at hand. While the motion of the small droplet in Figure 4 is dominated by the dipole mode, we have shown that the monopole mode contributes more significantly to the ARF, when we evaluated the scattering coefficients in the model from Gor’kov.

FIGURE 4

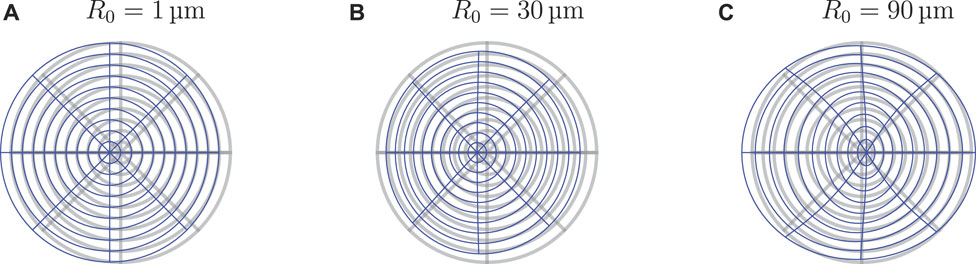
FIGURE 4. Modes of oscillation of an HFE droplet of different radii. The droplet is suspended in water and subjected to a standing wave at f = 5 MHz. Depending on the droplet size different mode participate in the oscillations: (A) dipole mode, (B) superposition of monopole and dipole mode, (C) complex superposition of multiple droplet eigenmodes.

3.3 Copper Particle in a Viscous Oil

In our second example, we compared theories that describe different limiting cases. The choice of an appropriate theory for a given problem was straightforward, since the theories from Gor’kov and Yosioka and Kawasima agree in their respective limits. Our third example describes a use case of the OSAFT library where this choice is more delicate. For certain parameters, different theories describing the same limiting case might yield different results. An example of this is given in the article from Baasch et al. [25], where they compare the theories from Doinikov (Eq. 5.15 together with Eqs 6.1–6.8 in [8]) and Settnes and Bruus (Eq. 20 in [14]) with a finite element simulation. In this section, we will revisit an example from their article.

The influence of viscosity shall be investigated for a copper particle in a viscous oil. Again, the particle is placed in a standing wave field between velocity node and anti-node with f = 0.5 MHz and p_in = 1 bar. The viscosity of the oil is changing from η_oil = 0 mPa s to 100 mPa s. We are comparing the model from Doinikov [8], who derives an expression for the ARF on a rigid particle in a viscous fluid in the long-wavelength limit, to the model from Settnes and Bruus [14], who compute the ARF on a compressible particle in a viscous fluid in the same limit. Here, long-wavelength means that the wavelength λ_f is large compared to both the particle radius (R ≪ λ_f) and the viscous boundary layer thickness (δ ≪ λ_f) defined in Section 2.1. Both models do not impose a restriction on the ratio R/δ. We compute the ARF in the regime where the boundary layer thickness and the particle radius are of the same order δ ∼ R. The ratio between boundary layer and radius can easily be computed using the library. For a viscosity of η_oil = 30 mPa s this ratio is:

settnes.R_0/settnes. delta -> 0.91

The boundary layer thickness is also drawn in the scattering field plot in Figure 5B, where the influence of viscosity on the first-order velocity is illustrated.

FIGURE 5

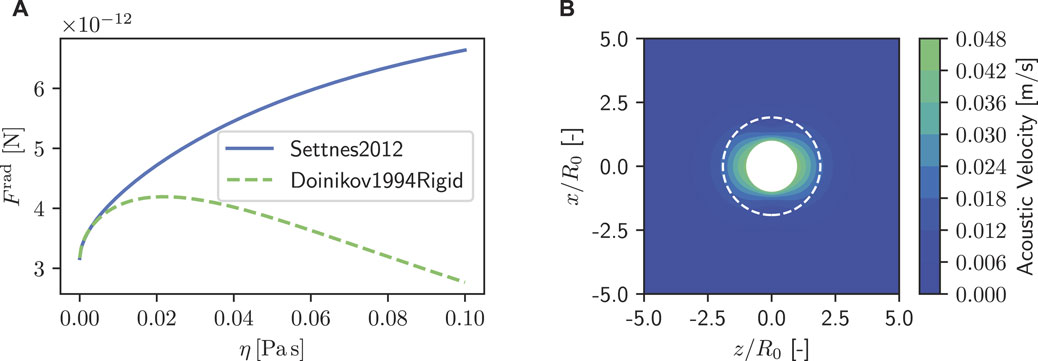
FIGURE 5. Copper particle in a viscous oil placed half way between the velocity node and the velocity anti-node of a f = 0.5 MHz standing wave field. (A) Comparison of the ARF in the model from Doinikov [8] and from Settnes and Bruus [14]. (B) Velocity amplitudes of the scattered acoustic field around the particle for η_oil = 30 mPa s plotted using the model by Doinikov. The dotted line represents the boundary layer thickness δ.

A comparison of the values for the ARF in the two models is depicted in Figure 5B. For a small viscosity, the two models are in good agreement. This is because the compressibility of copper is small compared to the compressibility of water, thus the rigid particle assumption from Doinikov’s model is accurate. If the viscosity is increased the two models start diverging. The model by Settnes and Bruus predicts an increasing ARF with increasing viscosity. In the model by Doinikov the ARF reaches a maximum at around η_oil = 20 mPa s and then decreases again. At η_oil = 100 mPa s the models differ already by a factor of two. According to Baasch et al., the two models disagree in the case of heavy particles in viscous fluids because of the influence of the so-called microstreaming around the particle on the ARF [25]. In the model by Doinikov the microstreaming contributes to the ARF while it is neglected in the model by Settnes and Bruus.

The example illustrates that the choice of the most suitable model can be crucial and theories might return significantly different results in certain cases. The intention of the OSAFT library is not to decide which theory is correct, but it rather provides a platform to easily compare different results. It is left to the user to decide what theory most accurately describes their problem statement and thus should be used for the interpretation of experimental results or the validation of numerical simulations.

3.4 Errors in Publications Discovered Through Testing

The unittesting described in Section 2.2 was designed to detect errors in our implementation of the theories. However, beyond finding bugs in our code the physical unittesting allowed us to find errors and typos in the research articles themselves. The discovered errors are corrected in the following paragraph.

A first error was found in the expression for the ARF for a small bubble in a standing wave field in the article by Yosioka and Kawasima [2]. As illustrated in Figure 2, Yosioka and Kawasima provide a general expression for the ARF and then derive limiting cases thereof. Such a limiting case is the ARF on a small bubble, where the wavelength is large compared to the radius (R ≪ λ_f) and the bubble is light in comparison to its surrounding medium (ρ_p/ρ_f ≪ 1). In our testing scheme, the parameters are set such that these two assumptions are fulfilled. Then results from the general and the special solution are compared. An example is given in Figure 6 where the ARF for an air bubble in water placed between velocity node and anti-node of a standing wave is computed. The plot displays a large discrepancy between the two solutions. This discrepancy was also detected in our testing scheme and the error was finally found in Eq. 75 from the article. The corrected expression is

$F=\frac{\sigma {\left(k^{*}a\right)}^3\left[3\lambda -{\left(k^{*}a\right)}^2\right]}{{\sigma }^2{\left(k^{*}a\right)}^6+{\left[3\lambda -{\left(k^{*}a\right)}^2\right]}^2}.(8)$

where indicates the term containing the error. The reader is referred to the referenced article for the description of the symbols used in the Eq. 2. We later found that the error has already been described by Lee and Wang [26].

FIGURE 6

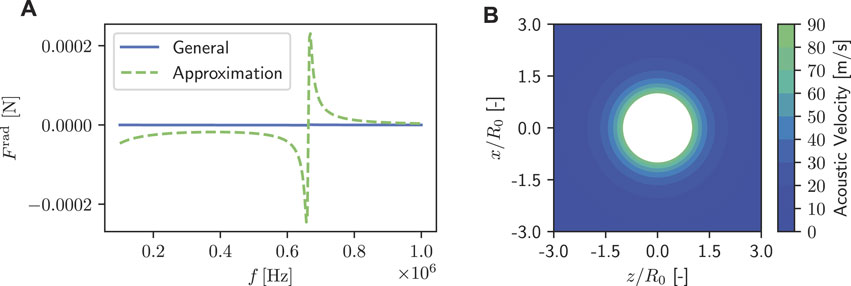
FIGURE 6. ARF on an air bubble in water halfway between the velocity node and the velocity anti-node: (A) Comparison of the correct general expression of the ARF (solid, blue) and the erroneous small bubble approximation (dashed, green). The general solution shows the same peaks at resonance but its magnitude is over two orders of magnitude smaller. The corrected small bubble solution is not plotted since it is in very good agreement with the general solution. (B) Velocity amplitudes of the scattered acoustic field close to resonance. At resonance, the acoustic scattering is dominated by the monopole mode.

Another error was discovered through the automated testing of the boundary conditions at the fluid-particle interface in the publication by Doinikov [8]. If the expressions for the particle velocity and the fluid velocity are evaluated the results do not match at the interface r = R. The error was located in the linear scattering coefficients and corrected expressions for Eqs 3.14, 3.15, 3.18, 3.19, 3.21 in [8] are

${\alpha }_1=-\left[\left.{\mu }_1{\mu }_3+2\left(1-{\lambda }^2\right)\right]j_1\left(x\right)h_1\left(x_v\right)\right]/{\mu }_4(\mathrm{9a})$

${\beta }_1=-\left(1-\lambda \right)\left[{\mu }_1{h}_1\left(x\right)-{\mu }_2{j}_1\left(x\right)\right]/{\mu }_4(\mathrm{9b})$

${\mu }_3=\left(1+2\lambda \right)h_1\left(x_v\right)+x_v{h}_1^{\prime }\left(x_v\right)(\mathrm{9c})$

${\mu }_4={\mu }_2{\mu }_3+2\left(1-{\lambda }^2\right)h_1\left(x\right)h_1\left(x_v\right)(\mathrm{9d})$

${\beta }_n=-\left[x{j}_n^{\prime }\left(x\right)h_n\left(x\right)-x{j}_n\left(x\right)h_n^{\prime }\left(x\right)\right]/{\xi }_n.(9e)$

Again, we refer the reader to the article for the variable definitions [8]. The error was since confirmed by the author, and it has to be mentioned that the error did not propagate to the arguably much more important expressions for the ARF given in the article.

4 Conclusion

In this manuscript, we presented the open-source Python library OSAFT. The library is an extendable collection of some of the most widely used theories for the computation of the ARF in acoustofluidics. It provides an easy way for researchers to evaluate different theories and compare their results. On three examples, we illustrated how such a comparison might look like. Firstly, we computed the ARF on a polystyrene particle in water subjected to an acoustic standing wave. In this classical example the models from Yosioka and Kawasima [2], Gor’kov [3], and Settnes and Bruus [14] were in excellent agreement. By contrast, in our study of an HFE droplet in water we explained how the selection of the most suitable theory can be crucial to get accurate estimates for the ARF. When plotting the ARF according to the models from King [1], Yosioka and Kawasima [2], and Gor’kov [3], it was revealed how the assumptions made in respective theories are reflected in the values the ARF takes. Lastly, we investigated a copper particle in a viscous oil. Comparing the model from Doinikov [8] with the model from Settnes and Bruus [14] exposed a discrepancy for the value of the ARF, even though the two models should be in good agreement for the given parameters. The example illustrated that it is not only different assumptions made in the theories that can lead to different results but in certain cases models might actually be inconsistent with one another. We believe that this further proves how relevant the selection of a fitting theory can be when researchers interpret experimental results or validate a numerical simulation using these theories.

Furthermore, we introduced our testing scheme consisting of numeric, structural, and physical unittesting. All three testing levels are aiming at different types of possible errors and bugs in our library. Beyond that, the physical testing allowed us not only to find bugs in the code, but we discovered errors in the research articles by Yosioka and Kawasima [2] and Doinikov [8] that we corrected in this manuscript.

In our examples, we showed how plotting of the acoustic scattering field in the fluid and particle oscillation modes can illustrate physical quantities like the boundary layer thickness and the contribution of eigenmodes to particle oscillations. We believe that this can make the library relevant not only for research but for teaching as well. For the latter, the library is in particular fitting since it is written in the widely used programing language Python that is taught in most physics and engineering undergraduate programs today. Also, the OSAFT library is available to download for free and easily installed using pip.

We provide the full source code of the examples shown in this article in the Supplementary Material and some more on the project’s documentation website [18]. These examples are meant as a starting point for learning the library’s API. In addition, the website provides an installation tutorial and the extensive documentation of the codebase. This documentation provides in-depth explanation of all user-facing methods and classes. Therefore, the documentation is not only suitable for users, but also meant to bring future collaborators up to speed.

Our goal, to make our code accessible and easy to use, is also reflected in the observer design pattern that has been applied across the whole codebase. The user can easily change a parameter of an already initialized solution and the dependent variables are automatically updated. This simplifies for example the plotting of the ARF over a parameter range. Moreover, the observer design pattern stores values of quantities to speed up their retrieval. This will prove relevant when more complex theories are implemented that require numerical integration.

While improving the usability of the library, the observer pattern is also responsible for the limited flexibility when initializing class instances. For example, in the current version all parameters of the class InviscidFluid depend on the density ρ_f and the speed of sound c_f. However, instead of c_f one could also use the compressibility κ_f together with ρ_f to fully define the properties of an inviscid fluid. In the current implementation κ_f is a dependent ActiveVariable and can therefore not be set directly. Consequently, for now, the class InviscidFluid can only be initialized with the parameter pair ρ_f and c_f. An issue that we are planning to tackle in the near future.

Another limitation of the code is the number of theories in the library. Currently, the model from Hasegawa and Yosioka [4] and the viscoelastic model from Doinikov [13] are being implemented, and they will be released in future versions. For the codebase to be as extensive as possible, we again emphasize the open-source character of the library. Interested readers are welcomed to visit our software repository [19] and to become a contributor to the OSAFT project.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.

Author Contributions

JF and CG wrote the manuscript together. Both contributed significantly to the library’s code base. JD supervised the project, contributed significantly to the writing of the manuscript and was involved the development of the library.

Funding

Open access funding provided by ETH Zürich.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to thank Cyrill Mast and David Ruckstuhl for their contributions to the OSAFT library during their student projects.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.893686/full#supplementary-material

Footnotes

¹https://osaft.readthedocs.io/en/stable/installation.html.

²https://osaft.readthedocs.io/en/stable/examples/index.html.

³https://pypi.org/project/osaft/.

⁴https://www.gnu.org/licenses/lgpl-3.0.

⁵https://git-scm.com.

⁶https://gitlab.com.

⁷https://www.sphinx-doc.org/.

References

1. King LV. On the Acoustic Radiation Pressure on Spheres. Proc R Soc Lond A (1934) 147:212–40. doi:10.1098/rspa.1934.0215

CrossRef Full Text | Google Scholar

2. Yosioka K, Kawasima Y. Acoustic Radiation Pressure on a Compressible Sphere. Acta Acustica united with Acustica (1955) 5:167–73.

Google Scholar

3. Gor’kov L. On the Forces Acting on a Small Particle in an Acoustical Field in an Ideal Fluid. Soviet Phys Doklady (1962) 6:773–5.

Google Scholar

4. Hasegawa T, Yosioka K. Acoustic‐Radiation Force on a Solid Elastic Sphere. The J Acoust Soc America (1969) 46:1139–43. doi:10.1121/1.1911832

CrossRef Full Text | Google Scholar

5. Hasegawa T, Watanabe Y. Acoustic Radiation Pressure on an Absorbing Sphere. J Acoust Soc America (1978) 63:1733–7. doi:10.1121/1.381912

CrossRef Full Text | Google Scholar

6. Hasegawa T. Acoustic Radiation Force on a Sphere in a Quasistationary Wave Field-Theory. J Acoust Soc America (1979) 65:32–40. doi:10.1121/1.382263

CrossRef Full Text | Google Scholar

7. Danilov S. The Mean Force Acting on a Small Body in an Axisymmetric Sound Field in a Real Medium. Fluid Dyn (1986) 21:812–20.

Google Scholar

8. Doinikov AA. Acoustic Radiation Pressure on a Rigid Sphere in a Viscous Fluid. Proc R Soc Lond A (1994) 447:447–66. doi:10.1098/rspa.1994.0150

CrossRef Full Text | Google Scholar

9. Doinikov AA. Acoustic Radiation Pressure on a Compressible Sphere in a Viscous Fluid. J Fluid Mech (1994) 267:1–22. doi:10.1017/S0022112094001096

CrossRef Full Text | Google Scholar

10. Doinikov AA. Acoustic Radiation Force on a Spherical Particle in a Viscous Heat-Conducting Fluid. I. General Formula. J Acoust Soc America (1997) 101:713–21. doi:10.1121/1.418035

CrossRef Full Text | Google Scholar

11. Doinikov AA. Acoustic Radiation Force on a Spherical Particle in a Viscous Heat-Conducting Fluid. Ii. Force on a Rigid Sphere. J Acoust Soc America (1997) 101:722–30. doi:10.1121/1.418036

CrossRef Full Text | Google Scholar

12. Doinikov AA. Acoustic Radiation Force on a Spherical Particle in a Viscous Heat-Conducting Fluid. Iii. Force on a Liquid Drop. J Acoust Soc America (1997) 101:731–40. doi:10.1121/1.417961

CrossRef Full Text | Google Scholar

13. Doinikov AA, Fankhauser J, Dual J. Nonlinear Dynamics of a Solid Particle in an Acoustically Excited Viscoelastic Fluid. Ii. Acoustic Radiation Force. Phys Rev E (2021) 104:065108. doi:10.1103/PhysRevE.104.065108

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Settnes M, Bruus H. Forces Acting on a Small Particle in an Acoustical Field in a Viscous Fluid. Phys Rev E (2012) 85:016327. doi:10.1103/PhysRevE.85.016327

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Karlsen JT, Bruus H. Forces Acting on a Small Particle in an Acoustical Field in a Thermoviscous Fluid. Phys Rev E Stat Nonlin Soft Matter Phys (2015) 92:043010. doi:10.1103/PhysRevE.92.043010

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Doinikov AA. Acoustic Radiation Forces: Classical Theory and Recent Advances. In: Recent Research Developments in Acoustics. Kerala, India: Transworld Research Network, 1 (2003). p. 39–67.

Google Scholar

17.[Dataset] Fankhauser J, Goering C. Pipy Website of Osaft (2022). online https://pypi.org/project/osaft/ (Accessed April 20, 2020).

Google Scholar

18.[Dataset] Fankhauser J, Goering C. Welcome to Osaft’s Documentation! (2022). online https://osaft.readthedocs.io/en/stable/ (Accessed April 20, 2020).

Google Scholar

19.[Dataset] Fankhauser J, Goering C. Gitlab Repository of Osaft (2022). online https://gitlab.com/acoustofluidics/osaft (Accessed April 20, 2020).

Google Scholar

20. Gamma E, Helm R, Johnson R, Vlissides J. Design Patterns: Elements of Reusable Object-Oriented Software. USA: Addison-Wesley Longman Publishing Co., Inc. (1995).

Google Scholar

21. Hunter JD. Matplotlib: A 2d Graphics Environment. Comput Sci Eng (2007) 9:90–5. doi:10.1109/MCSE.2007.55

CrossRef Full Text | Google Scholar

22. Harris CR, Millman KJ, van der Walt SJ, Gommers R, Virtanen P, Cournapeau D, et al. Array Programming with NumPy. Nature (2020) 585:357–62. doi:10.1038/s41586-020-2649-2

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat Methods (2020) 17:261–72. doi:10.1038/s41592-019-0686-2

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Meurer A, Smith CP, Paprocki M, Čertík O, Kirpichev SB, Rocklin M, et al. Sympy: Symbolic Computing in python. PeerJ Comput Sci (2017) 3:e103. doi:10.7717/peerj-cs.103

CrossRef Full Text | Google Scholar

25. Baasch T, Pavlic A, Dual J. Acoustic Radiation Force Acting on a Heavy Particle in a Standing Wave Can Be Dominated by the Acoustic Microstreaming. Phys Rev E (2019) 100:061102. doi:10.1103/PhysRevE.100.061102

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Lee CP, Wang TG. Acoustic Radiation Force on a Bubble. J Acoust Soc America (1993) 93:1637–40. doi:10.1121/1.406823

CrossRef Full Text | Google Scholar