Individual Roles of Network and Sheet Solids in Architectured Porous Materials

To understand the different roles played by sheet solids and network solids in complex porous biomaterials/native tissues, we designed a new kind of nature-inspired structure comprising these two solids by using triply periodic minimal surfaces and Voronoi diagrams using the CAD method and compared them with the previously reported Poisson-Voronoi (PV) solids that only comprise network solids. Here, we show that the sheet solids contribute greater stiffness and solid/void interface than the network solids, and our TPMS-Voronoi solids can improve/tune both the elastic moduli and specific surfaces even at fixed solid volume fraction and can be stiffer than the Poisson-Voronoi solids. This can directly guide the porous materials design for use in tissue engineering and aerospace.

Introduction

Porous materials have many applications. In engineering, porous metamaterials can realize sound absorption and insulation [1–3]. In medicine, porous structures can be used as implants and promote the growth of tissues and cells [4–7]. Natural porous structures, such as trabecular bones [4–7], consist of two kinds of solids: the network solid and the sheet solid. What are the different roles of these two solids? What are the benefits with this arrangement? Previous reports showed that at the same solid volume fraction (SVF), pure sheet solids tended to be stiffer than pure network solids [8, 9], but their roles in a hybrid complex structure still remain unclear. With nature materials, we cannot flexibly control the fraction of each solid. Thus, we designed a new kind of nature-inspired structure comprising both sheet and network solids by using triply periodic minimal surfaces (TPMS) and Voronoi diagrams [10–15]. Here we show that our TPMS-Voronoi (TV) solids allow us to flexibly vary the fraction of the sheet/network solids to obtain various elastic moduli and specific surfaces.

TPMS architectures are attractive candidates for designing innovative scaffold structures because they overcome the limitations of existing design and fabrication strategies, which require complex changes between different substructures during design and path planning for fabrication [16]. Even earlier, such triply periodic materials were discussed in soft materials, including biomorphic synthetic materials and biological structures (e.g., butterflies) [17, 18]. TPMS allows for scaffold structures to be simply represented using a single mathematical inequality and to be readily fabricated using additive manufacturing (AM) techniques [19–22]. Yoo proposed an effective method for arranging porosities for a porous scaffold using a thin-plate radial basis function based on distance field (DF)- and TPMS-based functions [23]. Melchels et al. [24] analyzed the porous structures and mechanical properties of conventional gyroid and diamond architectures. They also added a linear term in a conventional TPMS-based function to obtain gradient porosities [10, 25]. Kapfer et al. [8] proposed TPMS-based sheet solids that could provide a relatively high stiffness with a high porosity. This structure could also combine a high specific surface area with a high flux and the desired pore accessibility [26]. Pasko et al. [27] proposed lattice porous structures based on trigonometric functions and arranged their pore distribution using a DF method. Fryazinov et al. [28] proposed a cellular structure based on periodic functions and obtained metamorphosis inside a cellular structure, which resulted in gradient pores. However, the capabilities of these current strategies are too limited to construct complicated random structures. Here, we broaden the capability for TPMS architectures to flexibly generate complex porous structures and investigate the elastic moduli and specific surfaces of the resulting structures.

Materials and Methods

Construction of TV Solids

First, N Voronoi cells were obtained based on N random seed points in a region of interest with dimensions of w × w× w. N_s sheet solids and N_n network solids (where N = N_s + N_n) were randomly rotated, and each solid was then placed in a randomly chosen Voronoi cell as shown in Figure 1A. But the substructures may connect poorly on the Voronoi boundaries. Using the boundary strengthening and substructures’ smooth combination techniques for strong connections, all the substructures were integrated to form a hybrid structure as shown in Figure 1B. The sheet solids and network solids with SVF (ϕ) were combined to yield a hybrid solid with the same SVF value. The sheet solid fraction (α) is defined by α = N_s/N.

FIGURE 1

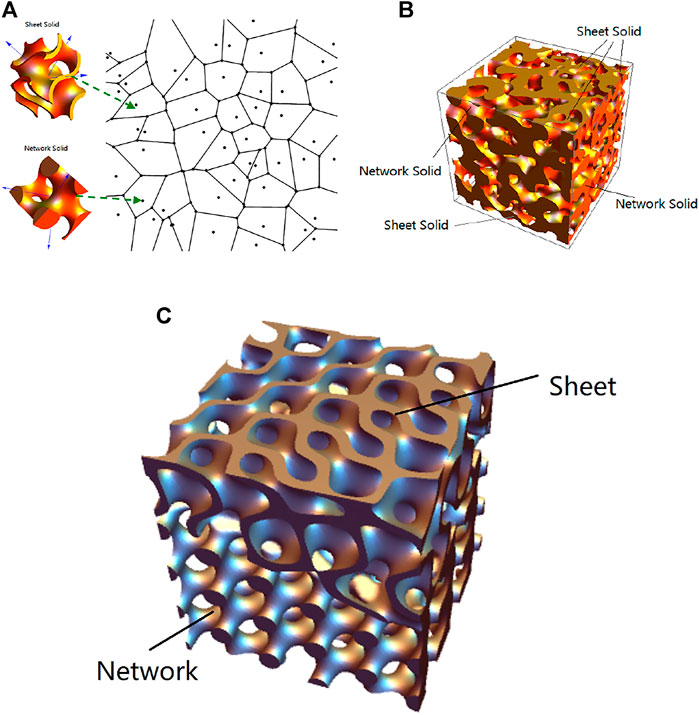
FIGURE 1. Construction of TV structure. (A) Randomly rotated sheet solids and network solids are assigned as substructures into the randomly chosen Voronoi cells. (B) The resulting TV structure comprising both sheet solids and network solids. (C) Amplified transition region between sheet and network solid.

We choose Gyroid TPMS for each network solid because this yields the stiffest network solid among the known minimal surfaces. An unrotated network solid (the solid phase) is defined by the 3D region $str{u}_{network}(x,y,z)\ge 0$ [11], according to the following:

$str{u}_{network}\left(x,y,z\right)=\cos \left(cx\right)\sin \left(cy\right)+\cos \left(cy\right)\sin \left(cz\right)+\cos \left(cz\right)\sin \left(cx\right)+d(1)$

Similarly, an unrotated sheet solid is defined by $str{u}_{sheet}(x,y,z)\ge 0$ , according to the following:

$str{u}_{sheet}\left(x,y,z\right)=d-\left|\cos \left(cx\right)\sin \left(cy\right)+\cos \left(cy\right)\sin \left(cz\right)+\cos \left(cz\right)\sin \left(cx\right)\right|(2)$

where c = 2pπ/q and implies that p pores are arranged within a distance q in one direction, thus controlling the pore density/size, d controls the SVF for each solid (Table 1), and x, y, and z are the three-dimensional coordinates. Since the elastic and shear modulus are not changed with the sizes, the structural models for modulus calculation are dimensionless. See Supplementary Material for the transition and connection between the sheet and network solids.

TABLE 1

TABLE 1. Relationship between d and SVF for the Gyroid TPMS sheet solid and network solid.

Elastic Moduli

Using the voxel-based finite element method [29], the elastic moduli of our TV solids were calculated as the minimized sum of the elastic energy stored in all the voxels with a given applied strain. The 3D region of interest containing the solid was discretized by 200³ voxels. The TV solids were constructed as collagen. The bulk modulus and shear modulus of collagen were set to K_s = 0.69 GPa and G_s = 0.18 Pa [29], where the subscript s denotes the non-porous solid.

Specific Surfaces

The specific surface was defined as the area of the solid/void interface divided by the solid volume in the region of interest, calculated using Rhinoceros software.

Results and Discussion

TV Solids

An example of TV solid is shown in Figure 1B, where the fraction of sheet solids is about 50%. The locations of sheet solids (plate elements) and network solids (rod elements) can be randomly assigned in a Voronoi diagram as shown in Figure 1A, and smooth transitions occur between these substructures. The numbers of sheet solids and network solids can be indicated by the designer to further study the properties of the resulting structures. Such a model can be exported as an STL file and then fabricated using the AM method for further geometrical measurement and mechanical test.

Linear-Elastic Moduli

Here, we analyze the effect of α on the elastic moduli of our TV solids and compare their moduli to that of the previously reported PV solid [29].

The elastic moduli of the TV solids are compared with those of the PV solids using the same calculation scheme and the same settings (where the PV solids were constructed based on Voronoi diagram alone, without TPMSs). The data for the moduli of our TV solids are shown by points in Figures 2A,B with the curved lines representing the PV solid moduli. Figure 2A shows that the TV solid bulk moduli are greater than those of the PV solids for all ϕ and increase with α at a given ϕ. Figure 2B shows that when α = 0, most of the TV solid shear moduli are lower than those of the PV solids for ϕ < 0.588, but exceed the PV solid values at the higher ϕ values. However, even for ϕ < 0.588, the TV solid shear moduli can exceed the PV solid values when sheet solids are fully introduced into the structure (α = 100%). While the bulk and shear moduli can be significantly adjusted at low SVF by changing α, the moduli vary only slightly with α at high ϕ values. Although the sheet solids tend to be stiffer than the network solids at low SVF, their moduli become similar at high SVF. This indicates that even at a specified SVF, the use of TV solids gives us flexibility in the design of biomaterials with different mechanical properties.

FIGURE 2

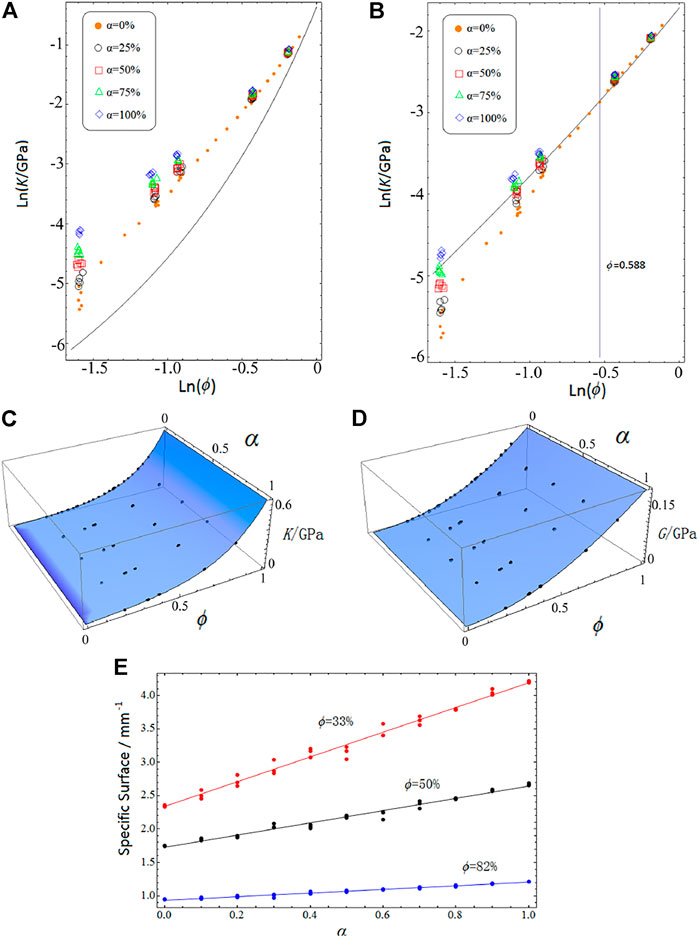
FIGURE 2. Comparisons of the logarithm of bulk moduli (A) and shear moduli (B) versus the logarithm of SVF (ϕ) for TV solids and PV solids, where the points represent the results for TV solids when α = 0 (orange dots), 25% (black circles), 50% (red squares), 75% (green triangles), and 100% (blue rhombi), and the solid lines represent the results for PV solids. The bulk moduli of TV solids are greater than those of the PV solids, but the shear moduli of TV solids without the sheet solids (α = 0) are lower than the PV solids for ϕ < 0.588 but exceed the PV solid values at higher ϕ. Moreover, for low SVF, the moduli of TV solids increase as the sheet solid fraction (α) increases at a given SVF; however, for high SVF, α has only a slight effect on the moduli. The blue surfaces (C) and (D) are the best fits of bulk modulus data and shear modulus data for TV solids (i.e., the data represented by dots, circles, squares, triangles, and rhombi in Panel 2A,B), respectively. Five structures were constructed for each α with each ϕ. (E) The relationship between the α and specific surface of TV solids for different ϕ, that is, ϕ = 33% (red), 50% (black), and 82% (blue). The specific surface increases with increased α for all ϕ, but the slope of each line decreases as ϕ increases. Three structures were built for each α with each ϕ.

Many porous structures exhibit a power–law relationship between the modulus and the SVF [29, 32]. Here, we use the following:

$K=\left(u_k\alpha +v_k\right){\mathrm{\phi }}^{n_k}{\left(\frac{K_s}{u_k\alpha +v_k}\right)}^{\mathrm{\phi }}(3)$

to fit the bulk modulus data with three free parameters (u_k, v_k, and n_k), and Eq. 3 can ensure that K→0 for ϕ→0, and K→K_s for ϕ→1. An analogous form is used for the shear modulus expression. The fitting results are n_k ≈ 0.5, u_k ≈ 0.0075 GPa, v_k ≈ 0.0132 GPa and n_g ≈ 2.29, u_g ≈ 0.083G Pa, v ≈ 0.22 GPa for the bulk and shear moduli, respectively (where the subscripts k and g denote the parameters for bulk and shear modulus, respectively). The best fit surfaces for the bulk and shear modulus data are shown in Figures 2C,D. Comparison to the PV solids (n_k ≈ 1.0 and n_g ≈ 1.69 [29]) shows that the values of shear and bulk moduli of our TV solids are more and less sensitive to the changes in SVF, respectively.

For the overlapped results, we can arrange the sheet and network solids with the same α and ϕ as shown in Figure 1A, but we can change their locations, thus slightly changing their moduli.

Specific Surface

We can tune the specific surface value of the TV solids by changing α at a given SVF. As shown in Figure 2E, the specific surface linearly increases with α for all ϕ (33, 50, or 82%); this is because a sheet solid has a bicontinuous surface that has two parallel interfaces with the void phases. Generally, the total area of the two interfaces is larger than that of the single interface in a network solid [8]. However, when ϕ is large, the specific surface can only be tuned slightly as indicated by the slopes of the best fit lines.

Discussion

Once the fabricated material, structural type, and SVF are fixed, it is not easy to tune the elastic moduli and specific surfaces for TPMS lattices. However, such properties can be adjusted by changing the numbers of sheet solids and network solids in a hybrid structure while keeping the fabricated material, structural type, and SVF constant. In other words, the structural property can be decoupled with the SVF, which is useful in the structural design process to independently achieve one property with fixing others.

Also, we can understand some mechanisms in the natural materials. Interestingly, similar geometries of the hybrid structures also occur elsewhere in biochemistry/biology. Such transition structures are commonly observed in the lipid analogues, for example, the coexistence between Diamond and Primitive morphologies in cubosomes [30], with similar dynamic transition structures described for lipid mesophase transitions [31]. But in these systems, there are much more rigorous requirements for how two domains of different types and orientation merge at their common interface, as the solid/void interface is determined by the optimization of surface curvature.

It shows that surface curvature (mean curvature H and Gaussian curvature K) is a key factor for guiding growth of cells and tissues [7]. For an individual cell, on a flat substrate (H=K=0), the cell nucleus tends to be flat with a small compressive force by the perinuclear actin. On a convex spherical surface (H > 0 and K > 0), the nucleus is flatter as that compressive force becomes larger. On a concave spherical surface (H > 0 and K < 0), the nucleus is lifted off and tends to be a spherical shape [6]. Compared to the hemispherical cap, a cell on the cylindrical surface is not likely to cause the osteogenic formation, as the fibers align to the longitudinal orientation and the force that compresses the nucleus is relatively small [33]. For collective cells, the tissue growth rate linearly increasing where the negative curvature occurs is used in the tissue deposition model and agrees well with the experimental results [34]. Inspired by this, the proposed method can integrate substructures with different surface curvatures for biomimetic design purpose and further study the curvature-guiding mechanism for cell and tissue growth.

By controlling the fraction of sheet solids based on our model, we can tune the elastic modulus with fixed SVF and understand how lower moduli of trabecular bone in postmenopausal women are associated with a reduced percentage of plate elements over all elements [4, 5].

Conclusion

Here, we show that morphology and structure are very important to determine elastic modulus and specific surface. To design porous biomaterials with desired moduli and specific surfaces, we can make them tunable by combining sheet solids with network solids with different fractions even at a specified porosity. On the other hand, we can understand the individual roles played by these two solids in natural porous materials based on the compound porous models. Not limited to the types of sheet and network solids chosen in this study, we can combine other mathematically defined structures using our method for porous scaffold design.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

NY: conceptualization, methodology, writing—original draft preparation, and supervision. SF, JZ, YZ, and ZQ: simulation.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank the National Natural Science Foundation of China (11872046), the Natural Science Foundation of Guangdong Province (2021A1515010318 and 2022A1515011024), the Natural Science Foundation in Shantou University (NTF19012), the Key Project of Guangdong Provincial Department of Education (2021ZDZX2007), and Cross-Disciplinary Research Funding (2020LKSFG01D).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.892525/full#supplementary-material

References

1. Gao N, Tang L., Deng J., Lu K., Hou H., Chen K. Design, Fabrication and Sound Absorption Test of Composite Porous Metamaterial with Embedding I-Plates into Porous Polyurethane Sponge. Appl Acoust (2021) 175:107845. doi:10.1016/j.apacoust.2020.107845

CrossRef Full Text | Google Scholar

2. Gao N., Wu J., Lu K., Zhong H. Hybrid Composite Meta-Porous Structure for Improving and Broadening Sound Absorption[J]. Mech Syst Signal Process (2021) 154. 107504. doi:10.1016/j.ymssp.2020.107504

CrossRef Full Text | Google Scholar

3. Gao N., Wang B., Lu K., Hou H. Teaching-learning-based Optimization of an Ultra-broadband Parallel Sound Absorber. Appl Acoust (2021) 178:107969. doi:10.1016/j.apacoust.2021.107969

CrossRef Full Text | Google Scholar

4. Liu X. S., Wang J., Zhou B., Stein E., Shi X., Adams M., et al. Fast Trabecular Bone Strength Predictions of HR-pQCT and Individual Trabeculae Segmentation-Based Plate and Rod Finite Element Model Discriminate Postmenopausal Vertebral Fractures. J Bone Miner Res (2013) 28:1666–1678. doi:10.1002/jbmr.1919

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Walker M. D., Liu X. S., Zhou B., Agarwal S., Liu G., McMahon D. J., et al. Premenopausal and Postmenopausal Differences in Bone Microstructure and Mechanical Competence in Chinese-American and White Women. J Bone Miner Res (2013) 28:1308–1318. doi:10.1002/jbmr.1860

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Callens S. J. P., Uyttendaele R. J. C., Fratila-Apachitei L. E., Zadpoor A. A. Substrate Curvature as a Cue to Guide Spatiotemporal Cell and Tissue Organization. Biomaterials (2020) 232:119739. doi:10.1016/j.biomaterials.2019.119739

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Callens S. J. P., Tourolle né Betts D. C., Müller R., Zadpoor A. A. The Local and Global Geometry of Trabecular Bone. Acta Biomater (2021) 130:343–361. doi:10.1016/j.actbio.2021.06.013

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Kapfer S. C., Hyde S. T., Mecke K., Arns C. H., Schröder-Turk G. E. Minimal Surface Scaffold Designs for Tissue Engineering. Biomaterials (2011) 32:6875–6882. doi:10.1016/j.biomaterials.2011.06.012

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Zhao M., Zhang D. Z., Liu F., Li Z., Ma Z., Ren Z. Mechanical and Energy Absorption Characteristics of Additively Manufactured Functionally Graded Sheet Lattice Structures with Minimal Surfaces. Int J Mech Sci (2020) 167:105262. doi:10.1016/j.ijmecsci.2019.105262

CrossRef Full Text | Google Scholar

10. Melchels F. P. W., Bertoldi K., Gabbrielli R., Velders A. H., Feijen J., Grijpma D. W. Mathematically Defined Tissue Engineering Scaffold Architectures Prepared by Stereolithography. Biomaterials (2010) 31:6909–6916. doi:10.1016/j.biomaterials.2010.05.068

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Yang N., Quan Z., Zhang D., Tian Y. Multi-morphology Transition Hybridization CAD Design of Minimal Surface Porous Structures for Use in Tissue Engineering. Computer-Aided Des (2014) 56:11–21. doi:10.1016/j.cad.2014.06.006

CrossRef Full Text | Google Scholar

12. Montazerian H., Mohamed M. G. A., Montazeri M. M., Kheiri S., Milani A. S., Kim K., et al. Permeability and Mechanical Properties of Gradient Porous PDMS Scaffolds Fabricated by 3D-Printed Sacrificial Templates Designed with Minimal Surfaces. Acta Biomater (2019) 96:149–160. doi:10.1016/j.actbio.2019.06.040

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Santos J., Pires T., Gouveia B. P., Castro A. P. G., Fernandes P. R. On the Permeability of TPMS Scaffolds. J Mech Behav Biomed Mater (2020) 110:103932. doi:10.1016/j.jmbbm.2020.103932

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Wang S., Shi Z. a., Liu L., Zhou X., Zhu L., Hao Y. The Design of Ti6Al4V Primitive Surface Structure with Symmetrical Gradient of Pore Size in Biomimetic Bone Scaffold. Mater Des (2020) 193:108830. doi:10.1016/j.matdes.2020.108830

CrossRef Full Text | Google Scholar

15. Abu Al-Rub R. K., Lee D.-W., Khan K. A., Palazotto A. N. Effective Anisotropic Elastic and Plastic Yield Properties of Periodic Foams Derived from Triply Periodic Schoen's I-WP Minimal Surface. J Eng Mech (2020) 146:04020030. doi:10.1061/(asce)em.1943-7889.0001759

CrossRef Full Text | Google Scholar

16. Giannitelli S. M., Accoto D., Trombetta M., Rainer A. Current Trends in the Design of Scaffolds for Computer-Aided Tissue Engineering. Acta Biomater (2014) 10:580–594. doi:10.1016/j.actbio.2013.10.024

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Stephen T.H., Gerd E.S.T. Geometry of Interfaces: Topological Complexity in Biology and Materials. Interf Focus (2012) 2:529–538.

Google Scholar

18. Stephen T. H., Michael O. K., Davide M. P. A Short History of an Elusive yet Ubiquitous Structure in Chemistry, Materials, and Mathematics. Angew Chem Int Ed (2008) 47:7996–8000.

Google Scholar

19. Tobias M., Martin L., Bill L., Zhang X., Qian M., Omar F., et al. SLM Lattice Structures: Properties, Performance, Applications and Challenges. Mater Des (2019) 183:108137.

Google Scholar

20. Nazir A., Abate K. M., Kumar A., Jeng J.-Y. A State-Of-The-Art Review on Types, Design, Optimization, and Additive Manufacturing of Cellular Structures. Int J Adv Manuf Technol (2019) 104:3489–3510. doi:10.1007/s00170-019-04085-3

CrossRef Full Text | Google Scholar

21. Yuan L., Ding S., Wen C. Additive Manufacturing Technology for Porous Metal Implant Applications and Triple Minimal Surface Structures: A Review. Bioactive Mater (2019) 4:56–70. doi:10.1016/j.bioactmat.2018.12.003

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Liu S., Shin Y. C. Additive Manufacturing of Ti6Al4V alloy: A Review. Mater Des (2019) 164:107552. doi:10.1016/j.matdes.2018.107552

CrossRef Full Text | Google Scholar

23. Yoo D. New Paradigms in Hierarchical Porous Scaffold Design for Tissue Engineering. Mater Sci Eng C (2013) 33:1759–1772. doi:10.1016/j.msec.2012.12.092

CrossRef Full Text | Google Scholar

24. Melchels F. P. W., Feijen J., Grijpma D.W. A Poly(d,l-Lactide) Resin for the Preparation of Tissue Engineering Scaffolds by Stereolithography. Biomaterials (2009) 30:3801–3809. doi:10.1016/j.biomaterials.2009.03.055

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Seck T. M., Melchels F. P. W., Feijen J., Grijpma D. W. Designed Biodegradable Hydrogel Structures Prepared by Stereolithography Using Poly(ethylene Glycol)/poly( D,l -Lactide)-Based Resins. J Controlled Release (2010) 148:34–41. doi:10.1016/j.jconrel.2010.07.111

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Sai H., Tan K. W., Hur K., Asenath-smith E., Hovden R., Jiang Y., et al. Hierarchical Porous Polymer Scaffolds from Block Copolymers. Science (2013) 341:530–534. doi:10.1126/science.1238159

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Pasko A., Fryazinov O., Vilbrandt T., Fayolle P.-A., Adzhiev V. Procedural Function-Based Modelling of Volumetric Microstructures. Graphical Models (2011) 73:165–181. doi:10.1016/j.gmod.2011.03.001

CrossRef Full Text | Google Scholar

28. Fryazinov O., Vilbrandt T., Pasko A. Multi-scale Space-Variant FRep Cellular Structures. Computer-Aided Des (2013) 45:26–34. doi:10.1016/j.cad.2011.09.007

CrossRef Full Text | Google Scholar

29. Nachtrab S., Kapfer S. C., Arns C. H., Madadi M., Mecke K., Schröder-Turk G. E. Morphology and Linear-Elastic Moduli of Random Network Solids. Adv Mater (2011) 23:2633–2637. doi:10.1002/adma.201004094

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Yaghmur A., Laggner P., Almgren M., Rappolt M. Self-assembly in Monoelaidin Aqueous Dispersions: Direct Vesicles to Cubosomes Transition. PLoS ONE (2008) 3:e3747. doi:10.1371/journal.pone.0003747

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Annela M.S., James H., Charlotte B., Tomás S.P., Adam M. Squires Experimental Confirmation of Transformation Pathways between Inverse Double diamond and Gyroid Cubic Phases. Langmuir (2014) 30:5705–5710.

PubMed Abstract | Google Scholar

32. Fan H., Hartshorn C., Buchheit T., Tallant D., Assink R., Simpson R., et al. Modulus-density Scaling Behaviour and Framework Architecture of Nanoporous Self-Assembled Silicas. Nat Mater (2007) 6:418–423. doi:10.1038/nmat1913

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Pieuchot L., Marteau J., Guignandon A., Dos Santos T., Brigaud I., Chauvy P.-F., et al. Curvotaxis Directs Cell Migration through Cell-Scale Curvature Landscapes. Nat Commun (2018) 9(1):3995. doi:10.1038/s41467-018-06494-6

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Rumpler M., Woesz A., Dunlop J. W. C., van Dongen J. T., Fratzl P. The Effect of Geometry on Three-Dimensional Tissue Growth. J R Soc Interf (2008) 5(27):1173–1180. doi:10.1098/rsif.2008.0064

CrossRef Full Text | Google Scholar