Numerical Computations of Non-Newtonian Fluid Flow in Hexagonal Cavity With a Square Obstacle: A Hybrid Mesh–Based Study

Thermal flow phenomena in a double lid–driven enclosure have many potential applications in numerous engineering domains. The present article theoretically investigates the heat transfer analysis of power-law fluid in a hexagonal cavity embedded with a square obstacle. The upper and lower lid walls of the cavity are considered heated along with the walls of the centered embedded square, while the rest of the cavity walls are thermally insulated. In addition, the horizontal lid walls of the cavity are uniformly moving in opposite horizontal directions. The mathematical modeling of the nonlinear fluid has been developed considering the continuity, momentum, and energy equations subjected to the appropriate boundary conditions. Due to the nonlinearity of the governing partial differential equations and of the viscosity models, we use the numerical scheme based on the finite element method The stable finite element pair (${\mathrm{\mathbb{P}}}_2/{\mathrm{\mathbb{P}}}_1$) has been selected for the discretization purpose. The discretized nonlinear system is solved with the Newton method in conjunction with a direct linear solver in the inner iterations. The thermal flow features are exposed via streamlines and temperature contours for a set of governing parameters such as Reynolds number (Re), Prandtl number $\left(\text{Pr}\right)$, and Grashof number (Gr) along with the power-law index (n). The values of local and average Nusselt numbers are calculated for the involved parameters. It is noted that the square obstacle has a strong impact for the formulation of streamlines and isotherms. Moreover, the power-law index has a strong impact on the values of the average Nusselt number and kinetic energy. The kinetic energy of the system increases with an increasing value of Gr and n, while Reynolds number has opposite effects on kinetic energy.

1 Introduction

The applications of heat transfer phenomena in heat carrier fluids include cooling systems in the transportation industry and cooling and heating systems in buildings, textile, electronic cooling devices, chemical, and other processing plants, making these fluids popular among researchers. Engineers and medical scientists paid special attention toward understanding the nature of fluids and more specifically to the fluids of engineering and biomedical engineering interest. The heat transfer flow in confined containers with different geometries such as cubic, rectangular, square, and hexagonal being the commonly used geometries where a simple driving force acts on the fluid is the tangential motion of the wall bounding. Practical examples of these problems include the nuclear reactor heat exchangers [1] and solar receivers [2]. Being the simplest geometries, cavity problems are the benchmark to test the efficiency of a numerical and computational method. The type of the confined geometry and the boundary conditions at the edges of the cavity play a fundamental part in the efficiency of the considered computational scheme and, consequently, the physical phenomena involved. These confined geometries possess ample potential to solve various problems of heat and mass transfer mechanisms in the industrial sector. Manju et al. [1] examined the flow of nonlinear fluids within the obstacle in a cavity with a power-law model to describe the fluid’s behavior. The multi-relaxation time (MRT) collision model of the Lattice–Boltzmann Method (LBM) was used for simulating nonlinear fluid flow with the obstacle in a cavity. They investigated the stability in the cell-Reynolds number of the MRT-LBM algorithm for nonlinear fluids, and the physical structural features and the analysis of streamlines and turbidity contours are conducted. For one single obstacle, the effects on flow characteristics and vortex formation of different parameters, such as Reynolds number (in terms of lid-dimension), obstacle dimension, the power-law index, and obstacle shape, were investigated. In addition, the impact of two embedded square obstacles in the cavity was analyzed side-by-side. In the end, the complex fluid flow was examined as a porous block for two obstruction ratios, over the multiple square obstacles inside the cavity. Li et al. [2] studied a three-dimensional incompressible resistive magnetic dynamic equation method of finite elements, in which there is a divergence between velocity, density, and magnetic induction. It is desirable for the discrete solutions, particularly for the momentum equations, to also meet divergence-free conditions. They designed a stable, mixed finite element method that can achieve the target, inspired by the restricted transportation method. The good standing of the discrete solutions was also demonstrated.

In a lid-driven cavity, Shafqat et al. [3] analyzed the characteristics of fins and the inclining magnetic field with nanofluid. They also studied the impact of the length and distance between these fins. The magnetic field and size of the fins were found to be effective parameters in the enhancement of the heat transfer mechanism. The use of the Galerkin finite element method discretized a two-dimensional system of partial differential equations. For the computation of the velocity and temperature fields, an FEM scheme involving the cubic polynomial (P3) has been implemented, while the pressure was calculated with a quadratic (P2). With the adaptive Newton method, the system of discrete equations was optimized. An experimental study was also conducted in order to validate the finite element code. The characteristics of thermal flow in a cavity in the presence of a hybrid mesh were discussed by Khalil et al. [4]. They assumed that the box has a porous medium root and non-Newtonian fluids. Through free convection, the fluid flow is reached. The Y-shaped uniform fin was installed on the lower cavity wall. The boundary conditions for their cavity were that the right and left walls were considered cold, while the upper walls were considered adiabatic. The extreme triangular ribs in the lower walls were considered cold, while the second and third ribs were taken as Y-shaped fins. In addition, the flux field was formulated and solved mathematically using the FEM technique with complex meshing. Xiong et al. [5] numerically discussed the thermal flow features in a cavity of a triangular lid-driven wall using the finite element method with various obstacle configurations.

In addition, Khan et al. [6] analyzed the characteristics of the nonlinear fluid and thermal flow in a cavity with an embedded fin. They assumed that the fluid was used for the first time on the square cavity of the bottom surface with a fin. The Y-shaped fin plays a vital role in understanding the underlying theory and enhancing the thermal flow rate through the fin. Studies show that the embedded fins can significantly increase the surface area and, hence, the heat transfer rate during the flow inside the cavities. The cavity and the appropriate boundary conditions used by Khan et al. show an enhancement in the convective heat transfer rate. They also considered the tips of fin to be hot, cold, and adiabatic. In the dynamic and energy equations, the effects of the magnetic field and radiation were analyzed during simulation.

A computational analysis was carried out with the FEM approach by Khan et al. [7] for the thermal flow of water-based ferrofluids in a cavity. They considered that the porous medium and the trapezoidal enclosure were filled with ferrofluid. To study ethylene glycol (EG)–based Fe₃O₄ nanofluid, Nguyen et al. [8] proposed a complete thermal conductive structure in the permeable curved domain. An electric force was introduced into the porous space in order to produce an electrohydrodynamic (EHD) effect. One of the striking features of the ferrofluid is the dependence of magnetization upon the temperature gradient, and this thermomagnetic coupling makes these fluids more demanding in various fields. Fe₃O₄ nanoparts of different shapes were introduced, namely: platelets, bricks, cylinders, and spherical are suspended in the considered base fluid. The CVFEM solves the systems of partial differential equations (PDEs).

The Boltzmann method (MRT-LBM) in-house multi-relaxation time lattice was designed for resolving and examining the Cu-water nano-fluid mixed convection (MHD) within a 3D geometry with the lid-driven walls by Ghasemi [9]. A mixed 3D convection is formed by considering different velocities of the walls in opposite directions (even natural due to differences in temperature and convection effects). Different aspect ratios and physical parameters are also the reason for the different results in flow analysis; the research by Haq et al. [10] considered the thermal flow behavior of a partially heated cavity that contains a heated cylinder inside it. To investigate flow analysis and heat transfer of nanoparticles in a triangular cavity with a bottom circular wall, the magnetic field was applied in order to control the flow field [11]. The condition is not only a benchmark for the numerical methods but also for the effectiveness and efficiency of these schemes. The thermal flow mixed convection that was studied by Alsabery et al. [12] took place in an enclosure, where the upper moving wall was considered.

Furthermore, Ching [13] conducted a computational feature of a magnet inclined on the mixed convection thermal transmission and entropy generation rates of Cu–water nanofluids in a cavity. The processes of heat energy transport in the cavity were illustrated with the contours of the energy flux vectors being traced. The computations demonstrated the effects on energy stream vectors for the various parameters such as the Hartmann’s number, Richardson number, Reynolds number, nanoparticle volume fraction, irreversibility distribution rate, and direction of the applied magnetic field. The transfer involved vertical rectangular cavities with convection heating and moving walls. Bondarenko et al. [14] numerically explored the thermal flow behaviors of hybrid nanoparticles filled in the cavity. The cavity with a triangular embedded obstacle and with constant heat flux was reported by Gangawane et al. [15] to explore the influence of the thermal flow. In the study published in [16] titled “The Mixed Convection Heat Transfer in Horizontal Rectangular Cavities with Single- and Double-Sided Moving Walls,” the authors Louaraychi et al. [16] considered a cavity with moving walls, among other factors, to investigate mixed convection heat transfer. In addition to these reports, please see [15, 17] for further reading on lid-driven flows. Many numerical approaches have been used to evaluate the thermal flow in enclosed domains. A great example of the FEM approach that was applied to a different context is the use of the.

In an attempt to understand how heat transfers in a cavity, with a bottom wall that is only partially heated, a study was conducted by Mahalakshmi et al. [18]. In addition, different positions of the inner heater were also reported to affect the characteristics of heat and flow transfer. One previous study investigated a square cavity that had openings on only two sides and found that the transfer of heat was aided by nanofluid as illustrated by Hassanpor et al. [19]. The cavity was exposed to a magnetic field, which had an effect on the interior. A cylinder inside the cavity held a constant amount of heat. A partially heated C-shaped cavity was demonstrated in the study by Haq et al. [20] for the flow and heat transition mechanism. Their results clearly enhanced the heat transfer rate with an increase in the heated length. The cylindrical cavity is an important and interesting cavity. To their credit, the authors of Guestal et al. [21] calculated the parameters of a cylindrical cavity that is partially heated at the bottom and neglected the wall sections that were considered to be cold. It was concluded that a cavity with wavy walls on the top and bottom would be useful in order to examine the characteristics of porous medium and corrugation on the heat transfer phenomenon. Heat transfer analysis for the rhombus cavity with an inner embedded square object in different thermal conditions was carried out by Haq et al. [22, 23]. A natural convection model to simulate an upside-down T-formed cavity filled with a heating element was analyzed in a previous study by Izadi et al. [24]. An inclined rectangular cavity with a big rectangular element was examined using the lid-driven heat transfer analysis in a [25] study. In a lid-driven trapezoidal cavity filled with alumina–water nanofluid, Fatih et al. [26] discussed the modeling and optimization and the effects of electric convection models using the FEM method of electric conductance modeling. In a 3D porous cavity, Sheikholeslami et al. [27] discussed with help of the Boltzmann methods the water-based nanofluid in the existence of the Lorenz force. Rizwan et al. [29] considered a numerical study on a lid-driven hexagonal cavity using Newtonian fluid. They noticed that the circular obstacle plays an important role in forming isotherms. They found that the Reynolds number and Richardson number are strongly related to heat transfer. Bourantas and Loukopoulos [30] introduced a meshless numerical scheme for accurate and efficient computational results of velocity and pressure profiles by using the backward-facing step. Recently, Toudja et al. [31] used an irregular hexagonal cavity to study mixed convection using the hybrid nano power-law fluid; they found an enhancement in heat and mass transfer when the Richardson number decreases. In contrast, the n has the opposite effect on heat and mass transfer. In this direction, some recent additions addressing significant physical features and computational schemes have been mentioned in [32–39].

As suggested by the aforementioned literature review, the heat transfer analysis within the lid-driven cavity has not been conducted in a lid-driven hexagon cavity using the power-law fluid. In this study, the power-law fluid has been used to conduct heat exchange analysis in a hexagonal cavity with several thermal condition square obstacles positioned at the center of the cavity. The upper and lower lids are supposedly heated and move with velocities u = 1 and u = -1, respectively. The weak form of a system of PDEs is obtained with the help of the finite element method. The article is constructed as follows: in Sections 2, 3, flow configuration and physical quantities of the problem along with mathematical modeling are developed. In Sections 4, 5, validation of the solution is discussed and the Result and Discussion sections contain the discussion based on the outcome of the solution. In the last section, Section 6, the main findings based on the outcome are discussed.

2 Problem Formulation

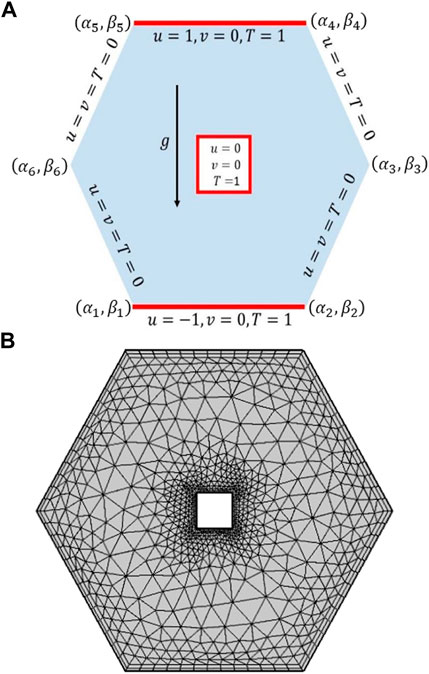
For the description of the mathematical formulations, we have considered several constraints that must be met in order to evaluate the theoretical assumptions inside the hexagonal cavity. In this section, equations with each constraint and boundary condition and the geometry of the problem are discussed (see Figure 1A). The vertices of the cavity are defined as

FIGURE 1

FIGURE 1. (A). Schematic diagram of the problem. Panel (B) computational grid at the coarse level.

Let $V=\left(u^{\ast },v^{\ast },0\right)$ is defined as the velocity field for two-dimensional flow. The initially defined pressure $p$ exerted by the fluid particles in the horizontal, x-direction and vertical, y-direction and afterward the Navier–Stokes equation is simplified as [40].

$\frac{\partial u^{\ast }}{\partial x^{\ast }}+\frac{\partial v^{\ast }}{\partial y^{\ast }}=0.(1)$

$\rho \left(u^{\ast }\frac{\partial u^{\ast }}{\partial x^{\ast }}+v^{\ast }\frac{\partial v^{\ast }}{\partial y^{\ast }}\right)=-\frac{\partial p^{\ast }}{\partial x^{\ast }}+\left(\frac{\partial {\tau }_{x^{\ast }{x}^{\ast }}}{\partial x^{\ast }}+\frac{\partial {\tau }_{x^{\ast }{y}^{\ast }}}{\partial y^{\ast }}\right).(2)$

$\rho \left(u^{\ast }\frac{\partial \underset{¯}{v}}{\partial x^{\ast }}+v^{\ast }\frac{\partial v^{\ast }}{\partial y^{\ast }}\right)=- \frac{\partial p^{\ast }}{\partial y^{\ast }}+\left(\frac{\partial {\tau }_{y^{\ast }{x}^{\ast }}}{\partial x^{\ast }}+\frac{\partial {\tau }_{y^{\ast }{y}^{\ast }}}{\partial y^{\ast }}\right)+g\beta \rho \left(T^{\ast }-T_c^{\ast }\right).(3)$

$\rho c_p\left(u^{\ast }\frac{\partial T^{\ast }}{\partial x^{\ast }}+v^{\ast }\frac{\partial T^{\ast }}{\partial y^{\ast }}\right)=k\left(\frac{{\partial }^2{T}^{\ast }}{\partial x^{\ast 2}}+\frac{{\partial }^2{T}^{\ast }}{\partial y^{\ast 2}}\right).(4)$

Here, $u^{\ast }$ and $v^{\ast }$ are the velocities of the fluid along $x^{\ast }$ and $y^{\ast }$ direction, respectively, and $T^{\ast }-T_c^{\ast }$ is the temperature difference of fluid molecules. For the power-law fluid, $\tau =K{\dot{\gamma }}^n$, and other constants are defined as.

The boundary conditions for the problem under consideration are defined as follows:

For the upper and lower walls of the hexagonal cavity

$u^{\ast }=v^{\ast }=0, T^{\ast }=T_h^{\ast }.(5)$

For all the other walls of the cavity

$u^{\ast }=v^{\ast }=0, T^{\ast }=T_c^{\ast }.(6)$

Introducing the nondimensional variables

$x=\frac{x^{\ast }}{L}, y=\frac{y^{\ast }}{L}, u=\frac{u^{\ast }}{U}, v=\frac{v^{\ast }}{U}, p=\frac{p^{\ast }}{\rho U^2}, \theta =\frac{T^{\ast }-T_c^{\ast }}{T_h^{\ast }-T_c^{\ast }}.(7)$

Combining Equation 8 into Equations 2–7, we have

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0.(8)$

$\left(u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right)=-\frac{\partial p}{\partial x}+\frac{1}{Re}\left(\frac{\partial {\tau }_{xx}}{\partial x}+\frac{\partial {\tau }_{xy}}{\partial y}\right).(9)$

$\left(u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}\right)=-\frac{\partial p}{\partial y}+\frac{1}{Re}\left(\frac{\partial {\tau }_{yx}}{\partial x}+\frac{\partial {\tau }_{yy}}{\partial y}\right)+\frac{Gr}{R{e}^2}\theta .(10)$

$\left(u \frac{\partial \theta }{\partial x}+v\frac{\partial \theta }{\partial y}\right)=\frac{1}{RePr}\left(\frac{{\partial }^2\theta }{\partial x^2}+\frac{{\partial }^2\theta }{\partial y^2}\right).(11)$

3 Physical Quantities

The important physical quantities such as local and average Nusselt number are defined as

$\begin{array}{c}N{u}_{local}=\left(\frac{\partial \theta }{\partial y}\right)\\ N{u}_{average}={\displaystyle \int {\left(N{u}_{local}\right)}_{wall}}\end{array}\}.(12)$

Here, Reynolds number. $Re=\frac{U_{\infty }D}{\upsilon }$Grashof number. $Gr=\frac{g\beta \left(T_h-T_0\right)D^3}{{\upsilon }^2}$ Prandtl number. $Pr=\frac{\upsilon }{\alpha }$

4 Solution Methodology

The system of governing Equations 8–11 does not contain analytical solution. It is, therefore, solved with the help of the FEM explained below.

1) Weak formulation

The weak form of Equations 8–11 is given as

${\displaystyle \underset{\mathrm{\Omega }}{\int }\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)}qd\mathrm{\Omega }=0,(13)$

$Re{\displaystyle \underset{\mathrm{\Omega }}{\int }\left(u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right)}wd\mathrm{\Omega }+Re{\displaystyle \underset{\mathrm{\Omega }}{\int }\frac{\partial p}{\partial x}}wd\Omega -{\displaystyle \underset{\mathrm{\Omega }}{\int }\left(\frac{\partial {\tau }_{xx}}{\partial x}+\frac{\partial {\tau }_{xy}}{\partial y}\right)}wd\mathrm{\Omega }=0,(14)$

$R{e}^2{\displaystyle \underset{\mathrm{\Omega }}{\int }\left(u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}\right)}wd\mathrm{\Omega }+R{e}^2{\displaystyle \underset{\mathrm{\Omega }}{\int }\frac{\partial p}{\partial y}}wd\mathrm{\Omega }-Re{\displaystyle \underset{\mathrm{\Omega }}{\int }\left(\frac{\partial {\tau }_{yx}}{\partial x}+\frac{\partial {\tau }_{yy}}{\partial y}\right)}wd\mathrm{\Omega }-Gr{\displaystyle \underset{\mathrm{\Omega }}{\int }\theta w}d\mathrm{\Omega }=0,(15)$

$PrRe{\displaystyle \underset{\mathrm{\Omega }}{\int }\left(u\frac{\partial \theta }{\partial x}+v\frac{\partial \theta }{\partial y}\right)}wd\mathrm{\Omega }-{\displaystyle \underset{\mathrm{\Omega }}{\int }\left(\frac{{\partial }^2\theta }{\partial x^2}+\frac{{\partial }^2\theta }{\partial y^2}\right)}wd\mathrm{\Omega }=0,(16)$

For numerical approximation, we compute the continuous solutions with the discrete ones in the finite-dimensional sub-spaces

$\begin{array}{l}u\approx u_{\hslash }\in W_{\hslash },\\ v\approx v_{\hslash }\in W_{\hslash },\\ \theta \approx {\theta }_{\hslash }\in W_{\hslash },\\ p\approx p_{\hslash }\in Q_{\hslash },\end{array}(17)$

where the basis functions are defined as

$\begin{array}{l}{u}_{\hslash }\approx {\displaystyle \sum _{k=1}^{\text{ndof}}{u}_k{\phi }_k(x,y)},\\ v_{\hslash }\approx {\displaystyle \sum _{k=1}^{\text{ndof}}{v}_k{\phi }_k(x,y)},\\ p_{\hslash }\approx {\displaystyle \sum _{k=1}^{\text{ndof}}{p}_k{\psi }_k(x,y)},\\ {\theta }_{\hslash }\approx {\displaystyle \sum _{k=1}^{\text{ndof}}{\theta }_k{\phi }_k(x,y)}.\end{array}(18)$

Here,$W$ = ${\left[H^1\left(\text{Ω}\right)\right]}^3$ test subspaces for $u, v,$ $\theta$$Q$ = $L^2\left(\text{Ω}\right)$ test subspace for pressure.$\text{Ω}$ = entire flow domain.Using (17) in (14–16), the following discrete version is obtained

$Re{\displaystyle \underset{\mathrm{\Omega }}{\int }\left(u_{\hslash }\frac{\partial u_{\hslash }}{\partial x}+v_{\hslash }\frac{\partial u_{\hslash }}{\partial y}\right)}{w}_{\hslash }d\mathrm{\Omega }+Re{\displaystyle \underset{\mathrm{\Omega }}{\int }\frac{\partial p_{\hslash }}{\partial x}}{w}_{\hslash }d\mathrm{\Omega }-{\displaystyle \underset{\mathrm{\Omega }}{\int }\left(\frac{\partial {\left({\tau }_{xx}\right)}_{\hslash }}{\partial x}+\frac{\partial {\left({\tau }_{xy}\right)}_{\hslash }}{\partial y}\right)}{w}_{\hslash }d\mathrm{\Omega }=0,(19)$

$R{e}^2{\displaystyle \underset{\mathrm{\Omega }}{\int }\left(u_{\hslash }\frac{\partial v_{\hslash }}{\partial x}+v_{\hslash }\frac{\partial v_{\hslash }}{\partial y}\right)}{w}_{\hslash }d\mathrm{\Omega }+R{e}^2{\displaystyle \underset{\mathrm{\Omega }}{\int }\frac{\partial p_{\hslash }}{\partial y}}{w}_{\hslash }d\mathrm{\Omega }-{\displaystyle \underset{\mathrm{\Omega }}{\int }\left(\frac{\partial {\left({\tau }_{yx}\right)}_{\hslash }}{\partial x}+\frac{\partial {\left({\tau }_{yy}\right)}_{\hslash }}{\partial y}\right)}{w}_{\hslash }d\mathrm{\Omega }-Gr{\displaystyle \underset{\mathrm{\Omega }}{\int }{\theta }_{\hslash }{w}_{\hslash }}d\mathrm{\Omega }=0,(20)$

${\displaystyle \underset{\mathrm{\Omega }}{\int }\left(\frac{\partial u_{\hslash }}{\partial x}+\frac{\partial v_{\hslash }}{\partial y}\right)}{q}_{\hslash }d\mathrm{\Omega }=0,(21)$

$RePr{\displaystyle \underset{\mathrm{\Omega }}{\int }\left(u_{\hslash }\frac{\partial {\theta }_{\hslash }}{\partial x}+v_{\hslash }\frac{\partial {\theta }_{\hslash }}{\partial y}\right)}{w}_{\hslash }d\mathrm{\Omega }-{\displaystyle \underset{\mathrm{\Omega }}{\int }\left(\frac{{\partial }^2{\theta }_{\hslash }}{\partial x^2}+\frac{{\partial }^2{\theta }_{\hslash }}{\partial y^2}\right)}{w}_{\hslash }d\mathrm{\Omega }=0,(22)$

In the matrix form

$\left[\begin{array}{cccc}Re.L_{\hslash }+N\left(u_{\hslash },v_{\hslash },{\theta }_{\hslash }\right)& 0& Re.B_1& 0\\ 0& R{e}^2.L_{\hslash }+N_{\hslash }\left(u_{\hslash },v_{\hslash },{\theta }_{\hslash }\right)& R{e}^2.B_2& -Gr.M_{\hslash }\\ B_1^T& B_2^T& 0& 0\\ 0& 0& 0& Pr.Re.L_{\hslash }+N_{\hslash }\left(u_{\hslash },v_{\hslash },{\theta }_{\hslash }\right)\end{array}\right]\left[\begin{array}{c}\underset{¯}{U}\\ \underset{¯}{V}\\ \underset{¯}{P}\\ \underset{¯}{\theta }\end{array}\right]=\left[\begin{array}{c}{\text{F}}_1\\ {\text{F}}_2\\ {\text{F}}_3\\ {\text{F}}_4\end{array}\right],(23)$

which can be written as follows: $\mathrm{A\xi =F}$

Here,

$L_h$ = discrete Laplace matrix.

$N_h$ = convection matrix (Non-linear)

$M_h$ = mass matrix.

$\xi$ = solution vector.

$F$ = RHS after implementation of boundary condition.

This nonlinear system is iterated until a given convergence condition is fulfilled in order to compute the solution. The nonlinear iterations are terminated after the residual has been reduced by ${10}^{-6}$ points. The steps carried out during the implementation of the scheme are disclosed in Figure 2C.

2) Validation of the numerical method

FIGURE 2

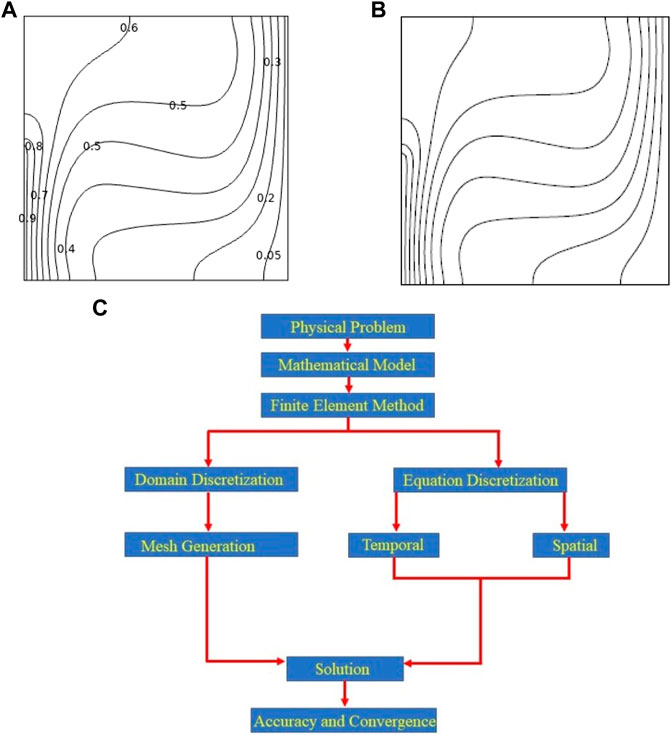
FIGURE 2. Isotherm comparison: (A) present work, (B) H.F. Oztop, E. Abu-Nada [28]. Panel (C): Flow chart of working rule.

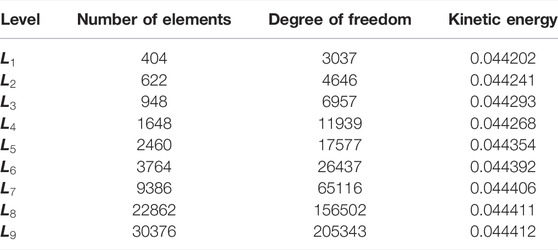
Before the simulation is performed, the verification of the code is carried out by reproducing the existing results. In this regard, the research work of H.F Oztop and E. Abu-Nada [28] is considered. In Figure 2A, the comparison of the results shows the code compatibility. The computational grid on a coarse level is shown in Figure 1B, where a hybrid meshing is carried out to capture the flow dynamics accurately near the boundaries. The second-order elements from the space $P_2$ are considered for velocity and temperature approximations, while the pressure uses linear approximations using the space $P_1$.

The discrete nonlinear system of equations has been addressed by the Newton method and the linearized inner system with a direct solver, PARDISO. There are many benefits of using the PARDISO solver (see [41–47] for further information). The PARDISO solver uses LU factorization and reduces the number of cycles required for the desired level of convergence. The kinetic energy is calculated for different grid levels (see Table 1). The percentage of errors decreases as the refinement level increases. During the study, the ninth refinement level is used as the error between levels 8 and 9 is minimum.

TABLE 1

TABLE 1. Grid convergence test at the extreme fine level.

5 Result and Discussion

The non-Newtonian power-law fluid along with the heat is studied in a hexagonal cavity having a square obstacle inside. The upper and lower wall and the obstacle are considered heated. The remaining walls of the obstacles are assumed cold. The suitable scales are used to non-dimensionalize the equations. A mathematical model containing Navier–Stokes and heat energy equations is obtained and handled with the help of a finite element system. Quadratic and triangular elements are used in the development of the FEM. On the nonlinear algebraic equations that have been obtained from the FEM formulation, Newton’s Raphson iteration scheme is applied. The range of the parameters involved in the study is defined as $\left(100\le Re\le 400\right)$, $\left(1\le Pr\le 10\right)$, $\left({10}^3\le Gr\le {10}^6\right)$, and $\left(0.5\le n\le 1.5\right)$.

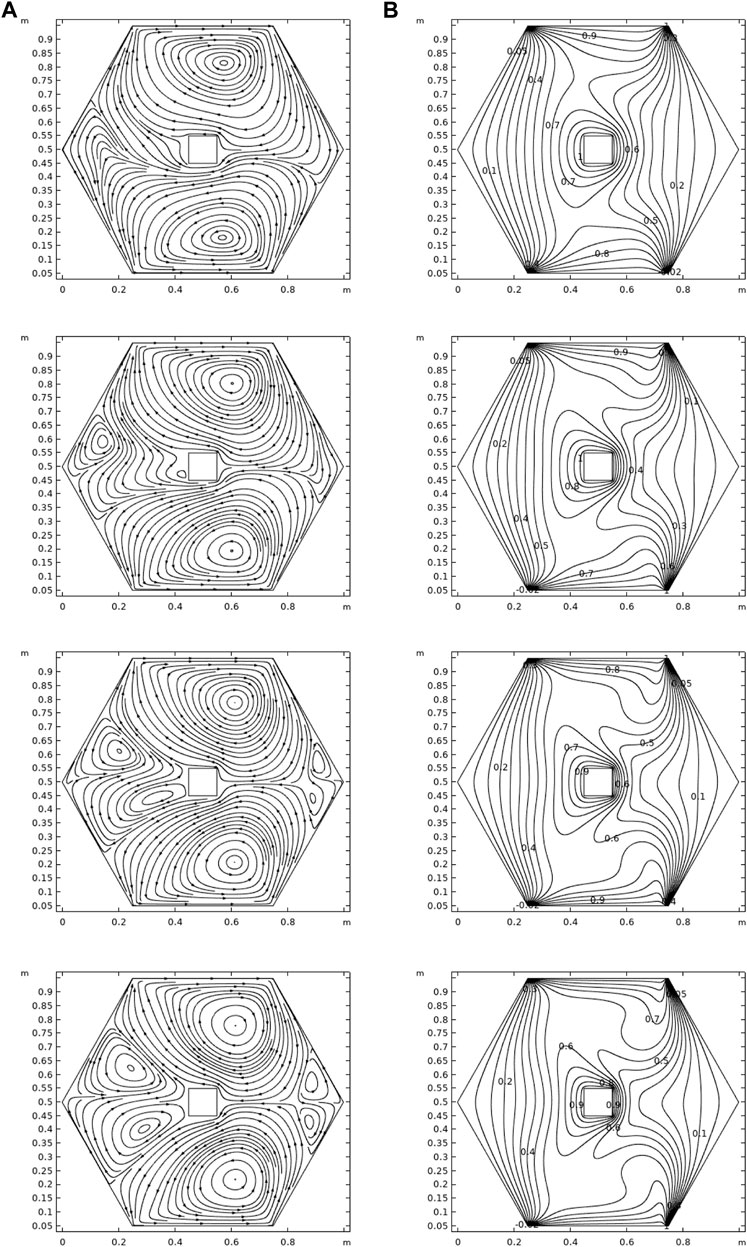
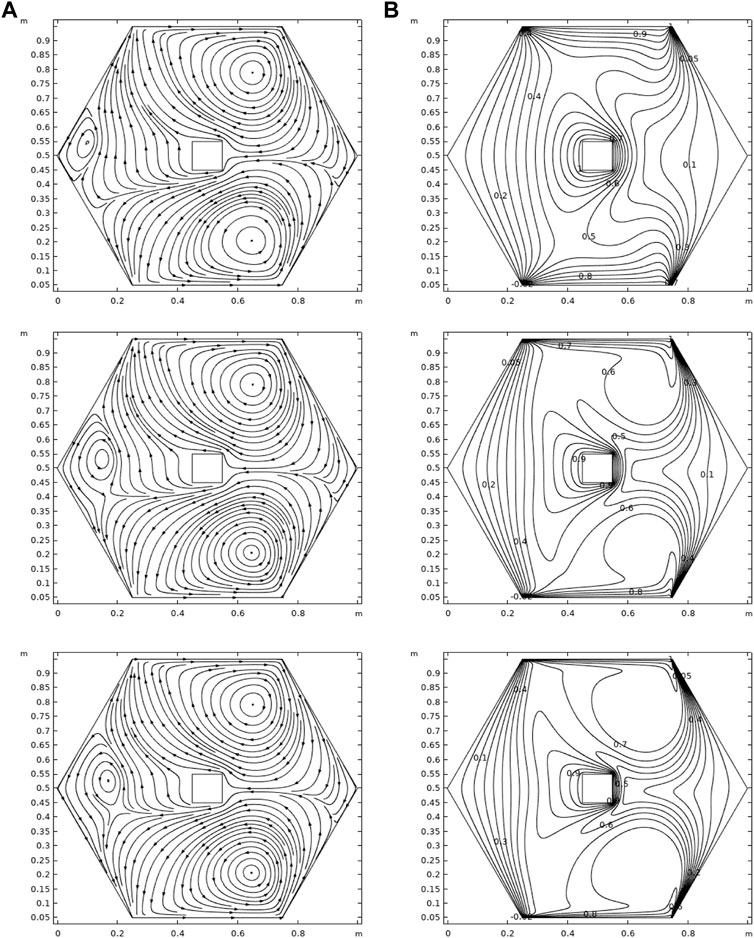
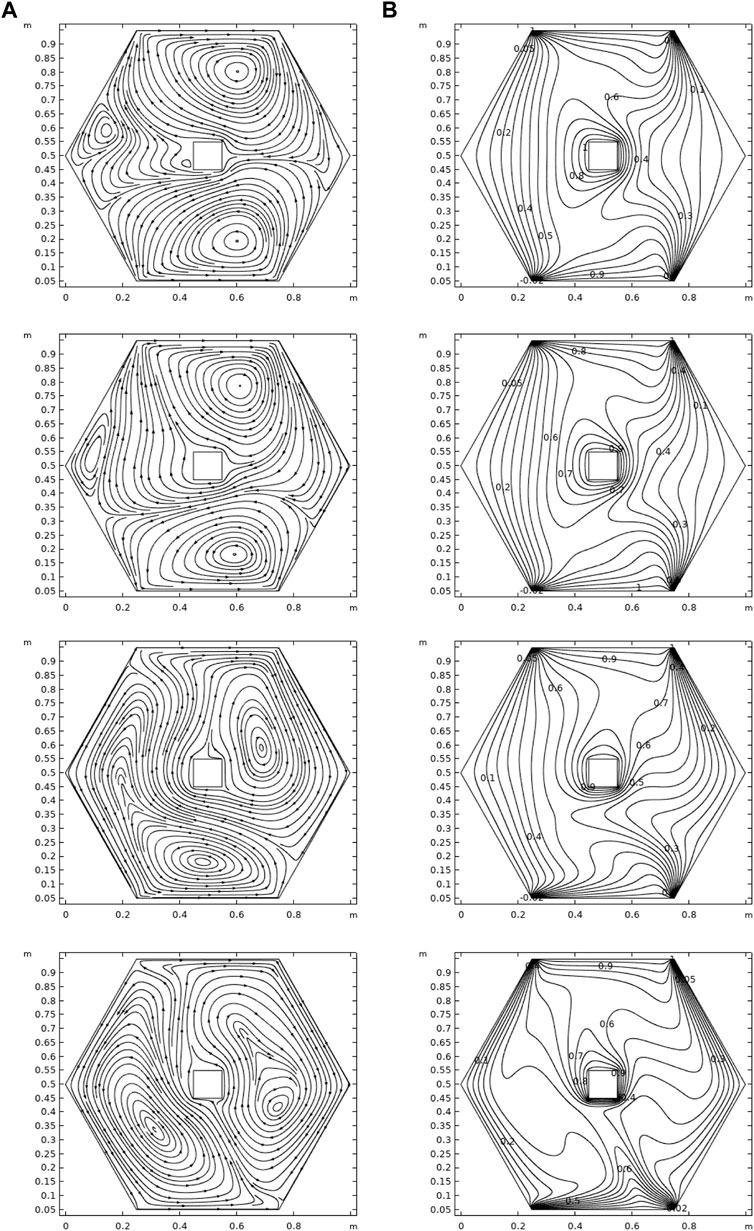
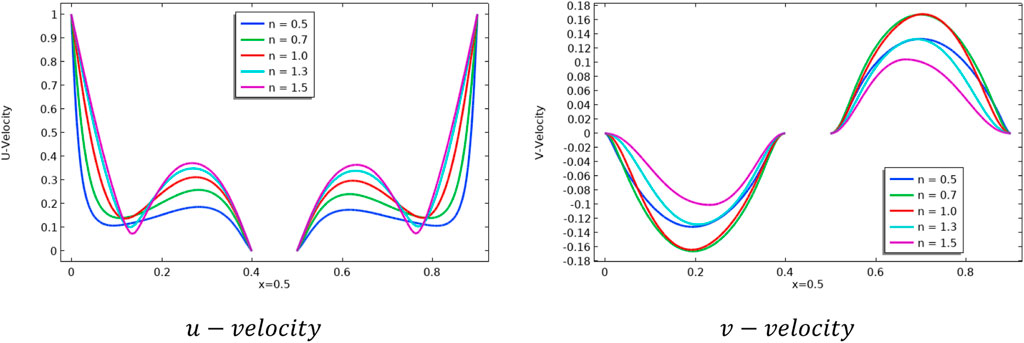
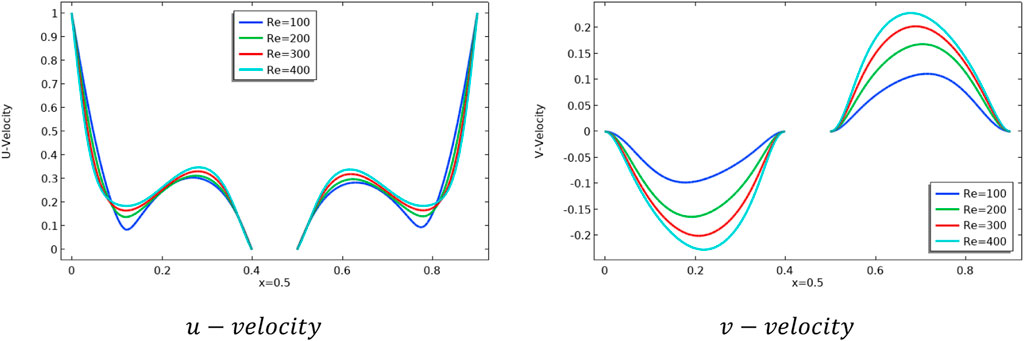
In Figures 3–5, the streamlines (left) and isotherms (right) are plotted for the variation of $Re, Pr$, and $Gr$. The streamlines and isotherms plots for increasing Reynolds number by fixing $n=0.5$ and $Pr=1$ are shown in Figure 3. The strength of the flow field increases with increasing values of $Re$. Due to the dominancy of conduction heat transfer, the isotherms at high $Re$ are parallel and smooth. The effects of $Pr$ on streamlines and isotherms are depicted through Figure 4. The streamlines are almost the same for the variation of $Pr$, while $Pr$ has significant effects on isotherms and can be seen in Figure 4A. Figure 5 is plotted to see the impact of Grashof number on streamline and isotherms, keeping $n=0.5,Re =200$, and $Pr=1$. There is significant change in streamline patterns as the Grashof number increases. For large values of $Gr$, it starts becoming symmetrical across the obstacle.

FIGURE 3

FIGURE 3. Influence on streamline (A) and isotherm (B) with different $Re$ with $n=0.5, Gr=1000$, and$Pr=1.$

FIGURE 4

FIGURE 4. Influence on streamline (A) and isotherm (B) with different $Pr$ with $n=0.5, Gr=1000$, and$Re=200.$

FIGURE 5

FIGURE 5. Influence on streamline (A) and isotherm (B) with different $Gr$ with $n=0.5, Pr=1$, and$Re=200.$

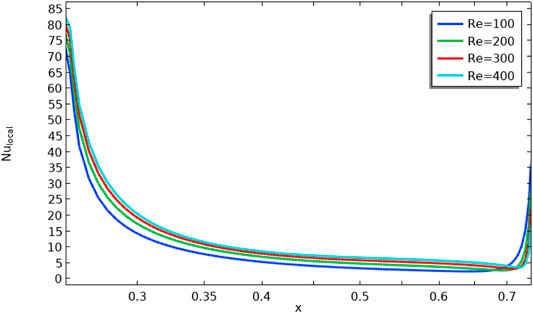
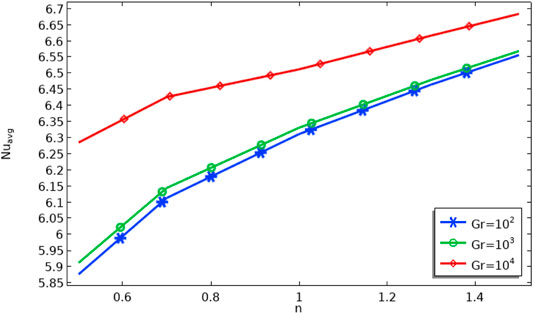
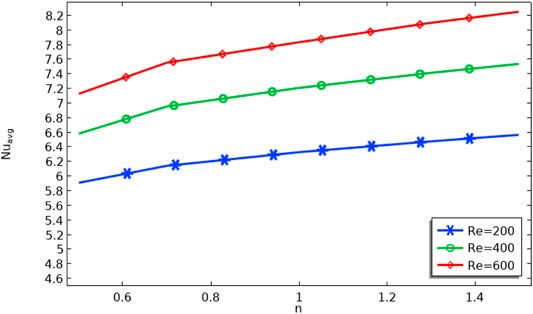
When it comes to heat transfer, the Nusselt number is a key parameter that can influence the rate of heat exchange. The line graphs for local and average Nusselt number have been displayed in Figures 6–11. Figure 6 displays the impact of n on $N{u}_{\text{local}}$ at the upper wall. The $N{u}_{\text{local}}$ increases as the value of n increases. The same trend can be seen for the values of Re as shown in Figure 7. Figures 8, 9 display the average Nusselt number plotted against n for the variation of Gr and Re number, respectively. The $N{u}_{avg}$ increases as the value of $Gr$ and Re increases. In Figure 10, the impact of n on u and v components of velocities is plotted. It can be seen from the figure that velocity increases as the n moved from shear thinning to shear thickening. Reynolds number has opposite effects on the velocity profile for x from 0 to 0.5 (see Figure 11).

FIGURE 6

FIGURE 6. Impact of different values of $n$ on local Nusselt number for the upper wall.

FIGURE 7

FIGURE 7. Impact of $Re$ on $N{u}_{\text{local}}$ for the upper wall.

FIGURE 8

FIGURE 8. Impact of $n$ on $N{u}_{avg}$ for different values of $Gr$.

FIGURE 9

FIGURE 9. Impact of $n$ on $N{u}_{avg}$ for different values of $Re$.

FIGURE 10

FIGURE 10. Velocity line profile against $n$ at position $x=0.5$.

FIGURE 11

FIGURE 11. Velocity line profile against $Re$ at position $x=0.5$.

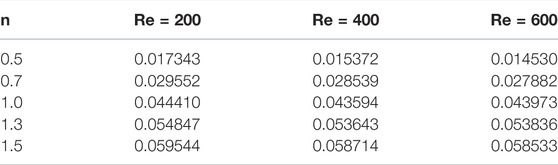
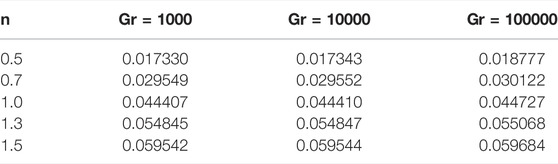
Table 2 displays the impact of n on kinetic energy for different Re. When n increases, the kinetic energy inside the cavity increases. The kinetic energy has opposite effects for increasing values of Reynolds numbers. In Table 3, the effects of the Grashof number on the kinetic energy are calculated. It is evident from the table that an increase in Gr increases the kinetic energy.

TABLE 2

TABLE 2. Impact of $n$ on the kinetic energy for different values of $Re$.

TABLE 3

TABLE 3. Impact of $n$ on the kinetic energy for different values of $Gr$.

6 Conclusion

A lid-driven hexagonal cavity with heated upper and lower walls with square obstacles has been discussed for the power-law fluid model. It is supposed that upper and lower walls have sliding velocities u = 1 and u = -1, respectively. The governing equations are converted into dimensionless form with the help of suitable scales. Then, the weak form of the equations is generated and solved with the Newton iterative scheme. The results have been depicted through the graphs to illustrate the physical consequences. By sketching streamlines and isothermal patterns against involved parameters, deviations in velocity and temperature fields are discussed. Effects of the involved parameter on velocity, temperature, and kinetic energy have been discussed. Local and average Nusselt numbers have been determined at various wall places to observe the heat transmission phenomenon. The major findings that are achieved through the abovementioned work are listed below.

• For streamlines, Prandtl number has almost the same effects as the Reynolds number, but for isotherms, $Pr$ effects are enhanced. There are strong isotherms near the heated object.

• The thermal flow rate increases with an increase in the Grashof number.

• The local Nusselt number increases as $Pr$ and $Re$ increase.

• The value of $N{u}_{avg}$ increases for increasing values of the $Gr$ and $Re$.

• The kinetic energy of the system increases with an increasing value of $Gr$ and $n$, while Reynolds number has the opposite effects on kinetic energy.

• The reverse appearance on the velocity profile is due to an increase in Reynolds number Re.

• The $N{u}_{avg}$ progressively increased with the enhancement in the values of n and Re.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

YK: funding; AM computed the results; HS and NF wrote the original draft; FA has supervised; KI wrote the review draft; MA: modeling; Conceptualization, YK and Validation, YK, AM and FA.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research, University of Hafr Al Batin for funding this work through the research group project no. (0033-1443-S).

References

1. Bisht M, Kumar P, Patil DV. Non-Newtonian Power-Law Fluid Flow over Obstacles Embedded inside a Cavity. Phys Fluids (2021) 33:043111. doi:10.1063/5.0046655

CrossRef Full Text | Google Scholar

2. Li L, Zhang D, Zheng W. A Constrained Transport Divergence-free Finite Element Method for Incompressible MHD Equations. J Comput Phys (2021) 428:109980. doi:10.1016/j.jcp.2020.109980

CrossRef Full Text | Google Scholar

3. Hussain S, Jamal M, Geridonmez BP. Impact of Fins and Inclined Magnetic Field in Double Lid-Driven Cavity with Cu-Water Nanofluid. Int J Therm Sci (2021) 161:106707. doi:10.1016/j.ijthermalsci.2020.106707

CrossRef Full Text | Google Scholar

4. Rehman KU, Algehyne EA, Shahzad F, Sherif E-SM, Chu Y-M. On Thermally Corrugated Porous Enclosure (TCPE) Equipped with Casson Liquid Suspension: Finite Element thermal Analysis. Case Stud Therm Eng (2021) 25:100873. doi:10.1016/j.csite.2021.100873

CrossRef Full Text | Google Scholar

5. Xiong P-Y, Hamid A, Iqbal K, Irfan M, Khan M. Numerical Simulation of Mixed Convection Flow and Heat Transfer in the Lid-Driven Triangular Cavity with Different Obstacle Configurations. Int Commun Heat Mass Transfer (2021) 123:105202. doi:10.1016/j.icheatmasstransfer.2021.105202

CrossRef Full Text | Google Scholar

6. Khan ZH, Khan WA, Hamid M. Non-Newtonian Fluid Flow Around a Y-Shaped Fin Embedded in a Square Cavity. J Therm Anal Calorim (2021) 143:573–85. doi:10.1007/s10973-019-09201-9

CrossRef Full Text | Google Scholar

7. Khan ZH, Makinde OD, Hamid M, Haq RU, Khan WA. Hydromagnetic Flow of Ferrofluid in an Enclosed Partially Heated Trapezoidal Cavity Filled with a Porous Medium. J Magnetism Magn Mater (2020) 499:166241. doi:10.1016/j.jmmm.2019.166241

CrossRef Full Text | Google Scholar

8. Nguyen TK, Soomro FA, Ali JA, Haq RU, Sheikholeslami M. Heat Transfer of Ethylene Glycol-Fe3O4 Nanofluid Enclosed by Curved Porous Cavity Including Electric Field. Physica(2020) xx:123945. doi:10.1016/j.physa.2019123945

CrossRef Full Text | Google Scholar

9. Ghasemi K, Siavashi M. Three-dimensional Analysis of Magnetohydrodynamic Transverse Mixed Convection of Nanofluid inside a Lid-Driven Enclosure Using MRT-LBM. Int J Mech Sci (2020) 165:105199. doi:10.1016/j.ijmecsci.2019.105199

CrossRef Full Text | Google Scholar

10. Ul Haq R, Soomro FA, Öztop HF, Mekkaoui T. Thermal Management of Water-Based Carbon Nanotubes Enclosed in a Partially Heated Triangular Cavity with Heated Cylindrical Obstacle. Int J Heat Mass Transfer (2019) 131:724–36. doi:10.1016/j.ijheatmasstransfer.2018.11.090

CrossRef Full Text | Google Scholar

11. Dogonchi AS, Ismael MA, Chamkha AJ, Ganji DD. Numerical Analysis of Natural Convection of Cu-Water Nanofluid Filling Triangular Cavity with Semicircular Bottom wall. J Therm Anal Calorim (2019) 135:3485–97. doi:10.1007/s10973-018-7520-4

CrossRef Full Text | Google Scholar

12. Alsabery AI, Ismael MA, Chamkha AJ, Hashim I. Effects of Two-phase Nanofluid Model on MHD Mixed Convection in a Lid-Driven Cavity in the Presence of Conductive Inner Block and Corner Heater. J Therm Anal Calorim (2019) 135:729–50. doi:10.1007/s10973-018-7377-6

CrossRef Full Text | Google Scholar

13. Cho C-C. Mixed Convection Heat Transfer and Entropy Generation of Cu-Water Nanofluid in Wavy-wall Lid-Driven Cavity in Presence of Inclined Magnetic Field. Int J Mech Sci (2019) 151:703–14. doi:10.1016/j.ijmecsci.2018.12.017

CrossRef Full Text | Google Scholar

14. Bondarenko DS, Sheremet MA, Oztop HF, Ali ME. Impacts of Moving wall and Heat-Generating Element on Heat Transfer and Entropy Generation of Al2O3/H2O Nanofluid. J Therm Anal Calorim (2019) 136:673–86. doi:10.1007/s10973-018-7715-8

CrossRef Full Text | Google Scholar

15. Gangawane KM, Oztop HF, Ali ME. Mixed Convection in a Lid-Driven Cavity Containing Triangular Block with Constant Heat Flux: Effect of Location of Block. Int J Mech Sci (2019) 152:492–511. doi:10.1016/j.ijmecsci.2019.01.020

CrossRef Full Text | Google Scholar

16. Louaraychi A, Lamsaadi M, Naïmi M, El Harfi H, Kaddiri M, Raji A, et al. Mixed Convection Heat Transfer Correlations in Shallow Rectangular Cavities with Single and Double-Lid Driven Boundaries. Int J Heat Mass Transfer (2019) 132:394–406. doi:10.1016/j.ijheatmasstransfer.2018.11.164

CrossRef Full Text | Google Scholar

17. Selimefendigil F, Öztop HF. MHD Mixed Convection of Nanofluid in a Flexible Walled Inclined Lid-Driven L-Shaped Cavity under the Effect of Internal Heat Generation. Physica A: Stat Mech its Appl (2019) 534:122144. doi:10.1016/j.physa.2019.122144

CrossRef Full Text | Google Scholar

18. Mahalakshami T, Nithyadevi N, Oztop HF, Abu-Hamdeh N. Natural Convective Heat Transfer of Ag-Water Nanofluid Flow inside Enclosure with center Heater and Bottom Heat Source. Chin J Phys (2018) 56:1497. doi:10.1016/j.cjph.2018.06.006

CrossRef Full Text | Google Scholar

19. Hassanpour A, Ranjbar AA, Sheikholeslami M. Numerical Study for Forced MHD Convection Heat Transfer of a Nanofluid in a Square Cavity with a cylinder of Constant Heat Flux. Eur Phys J Plus (2018) 133:66. doi:10.1140/epjp/i2018-11893-3

CrossRef Full Text | Google Scholar

20. Ul Haq R, Soomro FA, Hammouch Z, Ur Rehman S. Heat Exchange within the Partially Heated C-Shape Cavity Filled with the Water Based SWCNTs. Int J Heat Mass Transfer (2018) 127:506–14. doi:10.1016/j.ijheatmasstransfer.2018.07.101

CrossRef Full Text | Google Scholar

21. Guestal M, Kadja M, Ton Hoang M. Study of Heat Transfer by Natural Convection of Nanofluids in a Partially Heated Cylindrical Enclosure. Case Stud Therm Eng (2018) 11:135–44. doi:10.1016/j.csite.2018.01.008

CrossRef Full Text | Google Scholar

22. Haq RU, Soomro FA, Mekkaoui T, Al-Mdallal QM. MHD Natural Convection Flow Enclosure in a Corrugated Cavity Filled with a Porous Medium. Int J Heat Mass Transfer (2018) 121:1168–78. doi:10.1016/j.ijheatmasstransfer.2018.01.063

CrossRef Full Text | Google Scholar

23. Rizwan-ul-Haq RU, Soomro FA, Hammouch Z. Heat Transfer Analysis of CuO-Water Enclosed in a Partially Heated Rhombus with Heated Square Obstacle. Int J Heat Mass Transfer (2018) 118:773–84. doi:10.1016/j.ijheatmasstransfer.2017.11.043

CrossRef Full Text | Google Scholar

24. Izadi M, Mohebbi R, Karimi D, Sheremet MA. Numerical Simulation of Natural Convection Heat Transfer inside a ┴ Shaped Cavity Filled by a MWCNT-Fe3O4/water Hybrid Nanofluids Using LBM. Chem Eng Process - Process Intensification (2018) 125:56–66. doi:10.1016/j.cep.2018.01.004

CrossRef Full Text | Google Scholar

25. Goodarzi M, D’Orazio A, Keshavarzi A, Mousavi S, Karimipour A. Develop the Nano Scale Method of Lattice Boltzmann to Predict the Fluid Flow and Heat Transfer of Air in the Inclined Lid Driven Cavity with a Large Heat Source inside, Two Case Studies: Pure Natural Convection & Mixed Convection. Physica A: Stat Mech its Appl (2018) 509:210–33. doi:10.1016/j.physa.2018.06.013

CrossRef Full Text | Google Scholar

26. Selimefendigil F, Öztop HF. Modeling and Optimization of MHD Mixed Convection in a Lid-Driven Trapezoidal Cavity Filled with Alumina-Water Nanofluid: Effects of Electrical Conductivity Models. Int J Mech Sci (2018) 136:264–78. doi:10.1016/j.ijmecsci.2017.12.035

CrossRef Full Text | Google Scholar

27. Sheikholeslami M, Shehzad SA, Li Z. Water Based Nanofluid Free Convection Heat Transfer in a Three Dimensional Porous Cavity with Hot Sphere Obstacle in Existence of Lorenz Forces. Int J Heat Mass Transfer (2018) 125:375–86. doi:10.1016/j.ijheatmasstransfer.2018.04.076

CrossRef Full Text | Google Scholar

28. Oztop HF, Abu-Nada E. Numerical Study of Natural Convection in Partially Heated Rectangular Enclosures Filled with Nanofluids. Int J Heat Fluid Flow (2008) 29:1326–36. doi:10.1016/j.ijheatfluidflow.2008.04.009

CrossRef Full Text | Google Scholar

29. Haq RU, Soomro FA, Wang X, Tlili I. Partially Heated Lid-Driven Flow in a Hexagonal Cavity with Inner Circular Obstacle via FEM. Int J Heat Mass Trans (2020) 117;104732. doi:10.1016/j.icheatmasstransfer.2020.104732

CrossRef Full Text | Google Scholar

30. Bourantas GC, Loukopoulos VC. A Meshless Scheme for Incompressible Fluid Flow Using a Velocity-Pressure Correction Method. Comput Fluids (2013) 88:189–99. doi:10.1016/j.compfluid.2013.09.010

CrossRef Full Text | Google Scholar

31. Toudja N, Labsi N, Benkahla YK, Ouyahia SE, Benzema M. Thermosolutal Mixed Convection in a Lid-Driven Irregular Hexagon Cavity Filled with MWCNT–MgO (15–85%)/CMC Non-newtonian Hybrid Nanofluid. J Therm Anal Calorim (2020). doi:10.1007/s10973-020-10288-8

CrossRef Full Text | Google Scholar

32. Alkanhal TA, Sheikholeslami M, Usman M, Haq R-U, Shafee A, Al-Ahmadi AS, et al. Thermal Management of MHD Nanofluid within the Porous Medium Enclosed in a Wavy Shaped Cavity with Square Obstacle in the Presence of Radiation Heat Source. Int J Heat Mass Transfer (2019) 139:87–94. doi:10.1016/j.ijheatmasstransfer.2019.05.006

CrossRef Full Text | Google Scholar

33. Leontiev AI, Popov IA, Gortyshov YF, Olimpiev VV, Schelchkov AV, Kaskov SI. Hydrodynamics and Heat Transfer in Heat Exchanger Channels with Spherical Holes. Proc Int Mech Eng Congress Exposition (2006);1. doi:10.1115/IMECE2006-13552

CrossRef Full Text | Google Scholar

34. Nazir U, Sohail M, Hafeez MB, Krawczuk M, Askar S, Wasif S. An Inclination in thermal Energy Using Nanoparticles with Casson Liquid Past an Expanding Porous Surface. Energies (2021) 14:7328. doi:10.3390/en14217328

CrossRef Full Text | Google Scholar

35. Bhatti MM, Jun S. Lie Group Analysis and Robust Computational Approach to Examine Mass Transport Process Using Jeffrey Fluid Model. Appl Maths Comput (2022) 41:126936. doi:10.1016/j.amc.2022.126936

CrossRef Full Text | Google Scholar

36. Ushachew EG, Sharma MK, Makinde OD. Numerical Study of MHD Heat Convection of Nanofluid in an Open Enclosure with Internal Heated Objects and Sinusoidal Heated Bottom. Comput Therm Sci Int J (2021) 13(5):1–16. doi:10.1615/computthermalscien.2021035826

CrossRef Full Text | Google Scholar

37. Laidoudi H, Makinde OD. Computational Study of thermal Buoyancy from Two Confined Cylinders within a Square Enclosure Width Single Inlet and Outlet Ports. Heat Transfer-asian Res (2021) 50(2):1335–50. doi:10.1002/htj.21932

CrossRef Full Text | Google Scholar

38. Ushachew EG, Sharma MK, Makinde OD. Heat Convection in Micropolar Nanofluid through Porous Medium-Filled Rectangular Open Enclosure: Effect of an Embedded Heated Object with Different Geometries. Therm Anal Calorim (2021) 146:1865–81. doi:10.1007/s10973-020-10118-x

CrossRef Full Text | Google Scholar

39. Pushpa BV, Sankar M, Makinde OD. Optimization of Thermosolutal Convection in Vertical Porous Annulus with a Circular Baffle. Therm Sci Eng Prog (1007) 20(16pages):2020. doi:10.1016/j.tsep.2020.100735

CrossRef Full Text | Google Scholar

40. Li Q, Hong N, Shi B, Chai Z. Simulation of Power-Law Fluid Flows in Two-Dimensional Square Cavity Using Multi-Relaxation-Time Lattice Boltzmann Method. Commun Comput Phys (2014) 15(1):265–84. doi:10.4208/cicp.160212.210513a

CrossRef Full Text | Google Scholar

41. Majeed AH, Mahmood R, Abbasi WS, Usman K. Numerical Computation of MHD Thermal Flow of Cross Model over an Elliptic Cylinder: Reduction of Forces via Thickness Ratio. Math Probl Eng (2021) 1–13. doi:10.1155/2021/2550440

CrossRef Full Text | Google Scholar

42. Bilal S, Mahmood R, Majeed AH, Khan I, Nisar KS. Finite Element Method Visualization about Heat Transfer Analysis of Newtonian Material in Triangular Cavity with Square cylinder. J Mater Res Technol (2020) 9(3):4904–18. doi:10.1016/j.jmrt.2020.03.010

CrossRef Full Text | Google Scholar

43. Mahmood R, Bilal S, Majeed AH, Khan I, Sherif ESM. A Comparative Analysis of Flow Features of Newtonian and Power Law Material: A New Configuration. J Mater Res Technol 9(2):19782020–1987. doi:10.1016/j.jmrt.2019.12.030

CrossRef Full Text | Google Scholar

44. Mahmood R, Bilal S, Majeed AH, Khan I, Nisar KS. Assessment of Pseudo-plastic and Dilatant Materials Flow in Channel Driven Cavity: Application of Metallurgical Processes. J Mater Res Technol (2020) 9(3):3829–37. doi:10.1016/j.jmrt.2020.02.009

CrossRef Full Text | Google Scholar

45. Majeed AH, Jarad F, Mahmood R, Saddique I. Topological Characteristics of Obstacles and Nonlinear Rheological Fluid Flow in Presence of Insulated Fins: A Fluid Force Reduction Study. Math Probl Eng 2021:2021. doi:10.1155/2021/9199512

CrossRef Full Text | Google Scholar

46. Ahmad H, Mahmood R, Hafeez MB, Hussain Majeed A, Askar S, Shahzad H. Thermal Visualization of Ostwald-De Waele Liquid in Wavy Trapezoidal Cavity: Effect of Undulation and Amplitude. Case Stud Therm Eng (2021) 2021. doi:10.1016/j.csite.2021.101698

CrossRef Full Text | Google Scholar

47. Mahmood R, Majeed AH, Ain QU, Awrejcewicz J, Khan I, Shahzad H. Computational Analysis of Fluid Forces on an Obstacle in a Channel Driven Cavity: Viscoplastic Material Based Characteristics. Materials (2022) 15:529. doi:10.3390/ma15020529

PubMed Abstract | CrossRef Full Text | Google Scholar

Nomenclature

$V=\left(u^{\ast },v^{\ast },0\right)$ Velocity field

$u^{\ast }$ & $v^{\ast }$ fluid velocities along $x^{\ast }$ and $y^{\ast }$

$T^{\ast }$ Temperature

$Re=\frac{U_{\infty }D}{\upsilon }$ Reynolds number

$Gr=\frac{g\beta \left(T_h-T_0\right)D^3}{{\upsilon }^2}$ Grashof number

$Pr=\frac{\upsilon }{\alpha }$ Prandtl number

$\text{Ω}$ Entire flow domain

$W$ = ${\left[H^1\left(\text{Ω}\right)\right]}^3$ test subspaces for $u, v,$ $\theta$

$Q=L^2\left(\text{Ω}\right)$ Test subspace for pressure

$N{u}_{local}$ Local Nusselt number

$N{u}_{average}$ Average Nusselt number

$\tau$ Shear stress tensor

$\rho$ (kg/m³) Density

$g$ (m/s²) Gravity

$\beta$ (1/K) thermal expansion coefficient

$k$ (W/mK) thermal conductivity

$c_p$ (J/kgK) specific heat capacity

$L_h$ Discrete Laplace matrix

$N_h$ Convection matrix (nonlinear)

$M_h$ Mass matrix

$\xi$ Solution vector

$F$ RHS after implementation of boundary condition

FEM Finite element method