On the Role of Molecular Polarizability in Positron Coupling to Vibrations in Homonuclear Diatomics

In a previous work [Poveda, Varella, and Mohallem (Poveda et al., Atoms, 2021, 9: 64) it was shown that the bell-like shape of the 0 → 1 vibrational excitation cross section of H₂ as a function of the incoming positron energy, with its characteristic sharp onset at threshold, can be accounted for by a simple model which couples the positron to the vibrational mode of the molecule, throught the behavior of the target polarizabitity with the internuclear bond distance. The study, carried out via time-dependent wave-packet dynamics propagation, relies on a two-dimensional potential energy surface involving just the scattering (positron-target) and vibrational (target) coordinates. Here the model is extended to the full three-dimensional configuration space of the positron-diatomic complex, with the cross sections computed within a time-independent close-coupling approach. The present results confirm the previous findings, shedding light on the mechanisms through which a low-energy positron couples to the molecular vibrations.

1 Introduction

Understanding the physics involved in the interaction of a low energy positron with atoms and molecules is a long standing goal with both fundamental and technological implications [1,2]. The study in great detail of the phenomena of positron-matter interaction has been driven by the development of increasingly efficient positron energy moderators, which allow to obtain positron beams with appreciable fluxes and low energy spread [2]. Modern buffer-gas trap techniques allows the generation a high flow positron pulse, in the range of few eV and with energy spread of tens meV [3,4]. With such efficient mono-energetic positron beams, several state-resolved cross sections have been obtained, regarding to total, electronic excitation, ionization, and positronium formation in atomic and molecular targets [5], as well as vibrational excitation [6,7] and annihilation in molecules [4,8].

In particular the vibrational excitation of molecules by positron impact has attracted the attention of the scientific community, due to the striking manner in which a low energy positron couples to the nuclear degrees of freedom of polyatomic molecules. The physical richness of this phenomenon may involve vibrational resonances and even bound states, in which the positron is temporary trapped, before its final fate: annihilation. The theoretical models devoted to describe experimental data of vibrational excitation cross sections [9,10] and resonant annihilation spectra [11], coincide in attributing a leading role to molecular properties such as polarizability, dipole moment, ionization potential and number of π electrons [12–14].

In this work a generalization to the full three-dimensional positron-diatom configuration space, of a previously proposed two-dimensional model [15] (hereafter referred as paper I), is presented. In paper I the 0 → 1 vibrational excitation cross section of a hydrogen-like diatomic oscillator, was computed using time-dependent wave-packet propagation techniques over a two-dimensional model potential. The results suggested that the molecular polarizability of the target, as a function of the iternuclear separation, is a key property in describing the excitation of the fundamental mode of the oscillator. Here, the model potential is extended to cover the three coordinates of the positron-diatom complex and the scattering problem solved within the close-coupling formalism. The procedure is applied to the positron-H₂ system, as in paper I, but the positron-N₂ case is also studied. The present results corroborate the previous ones and suggest that the coupling of the positron to the fundamental vibrational mode of a homo-nuclear diatom can be described by a correlation-polarization potential, which involves, as the key property, the (an)isotropic molecular polarizability. The elastic cross sections for positron scattering from H₂ and N₂ are also well described below the positronium formation threshold.

In next section the model potential is described in detail. The close-coupling method is briefly summarized in Section 3. Results and discussion is presented in Section 4 and some conclusions given in Section 5.

2 The Potential Energy Surface

Following paper I the potential energy surface (PES) is written as the sum of oscillator (OSC) and positron (POS) components:

$V\left(R,r,\theta \right)=V_{osc}\left(R\right)+V_{pos}\left(R,r,\theta \right),(1)$

where R is the inter-nuclear distance and (r, θ) are the polar-Jacobi coordinates of the positron with respect to the center of mass of the target (see Figure 1 in [16]). The OSC part is represented as a harmonic oscillator potential

$V_{osc}\left(R\right)=\frac{1}{2}\mu {\omega }^2{R}^2,(2)$

with mass μ and frequency ω. The pair {μ, ω} is chosen to be, in atomic units (a.u.), {918.075, 0.020} and {12,861.925, 0.011} for H₂ and N₂, respectively.

FIGURE 1

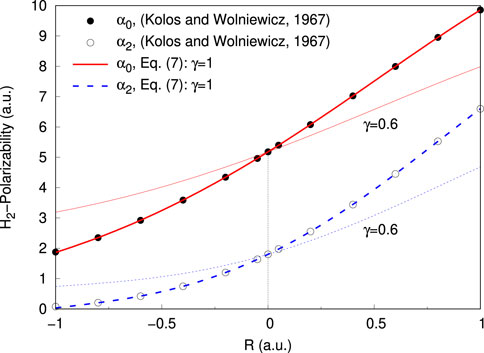
FIGURE 1. (Color online) Isotropic (α₀) and anisotropic (α₂) dipole polarizabilities for the hydrogen molecule, as a function of the internuclear separation. The thick solid and dashed lines represents the fits of Eq. 7 with γ =1, to the ab initio data. The same curves for γ =0.6 are shown in thin lines (see text for details).

In Eq. 1 the POS term refers to the positron-target interaction and includes the static (V_st) and correlation-polarization (V_cp) potentials. The former is taken to be the Hartree-Fock r-dependent spherically symmetric electrostatic potential of the diatom, clamped at the equilibrium bond distance. This term, for H₂ and N₂, is represented in the form

$V_{st}\left(r\right)=\kappa \sum _{i=1}^3{s}_i\exp \left[-t_i\left(r-r_i\right)\right],(3)$

where s_i, t_i and r_i are adjustable parameters and κ is a free parameter chosen ad hoc, in order to better reproduce reported total cross sections below the positronium formation threshold. It will be called the static parameter, which determines the amount of contribution of the V_st component to the potential.

The V_cp energy term, in turn, is represented using the analytical form proposed by Mitroy and Ivanov [17],

$V_{cp}\left(R,r,\theta \right)=-\frac{\alpha \left(R,\theta \right)}{2r^4}{f}_{\rho }\left(r\right),(4)$

where

$f_{\rho }\left(r\right)=1-\exp \left(-\frac{r^6}{{\rho }^6}\right),(5)$

is a cut-off function which damps the −1/r⁴ term at short distances and ρ is a free parameter chosen ad hoc, in order to better reproduce reported total cross sections below the positronium formation threshold. It will be called the correlation-polarization parameter, which determines the amount of contribution of the V_cp component to the potential.

In Eq. 4, α(R, θ) represents the molecular polarizability as a function of the inter-nuclear separation (R) and the positron-diatom relative orientation angle (θ). A simple form for this quantity will be

$\alpha \left(R,\theta \right)={\alpha }_0\left(R\right)+{\alpha }_2\left(R\right)P_2\left(\cos \theta \right),(6)$

where α₀(R) and α₂(R) are the isotropic and anisotropic polarizabilities, respectively, and P₂(cos θ) is the second-degree Legendre polynomial.

The dependence of α_⋆(R) (where ⋆ ≡ 0 or 2) on the R coordinate was represented in the form:

${\alpha }_{\star }\left(R\right)={\alpha }_{\star }\left(0\right)+\gamma \sum _{i=1}^4{a}_i{R}^i,(7)$

which fits, with high accuracy, the ab initio data reported by Kołos and Wolniewitz for H₂ [18] and the set of ab initio points previously reported for N₂ [19]. In Eq. 7 α_⋆(0) is the (an)isotropic polarizability at the equilibrium bond distance of the diatomic, a_i are adjustable parameters and γ is a free parameter chosen ad hoc, in order to reproduce reported vibrational excitation cross sections. It will be called the vibrational parameter, which determines the coupling strength between the positron and the target vibrational mode.

All the parameters involved in the present model potentials, for H₂ and N₂, are collected in tables 1 and 2. Figures 1, 2, show the isotropic and anisotropic molecular polarizabilities as functions of R, along with the curves from Eq. 7 for γ = 1 (thick lines) and for those values of γ (thin lines) for which the computed 0 → 1 vibrational excitation cross sections show good agreement with previous reports (see Section 4.2). Contour plots of the PESs for the positron around the diatoms, clamped at the equilibrium bond distances, are shown in Figures 3, 4. The salient feature of the PES for H₂ correspond to a minimum for geometries perpendicular to the molecular axis, suggesting that the positron tends to surrounds the hydrogen target favouring axial configurations. A different situations is observed for the positron-N₂ complex, with the minimum potential energy located on both side of the nitrogen atoms.

TABLE 1

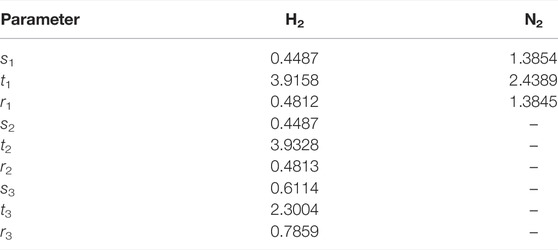
TABLE 1. Parameters of the static potential, Eq. 3 (in a.u.).

TABLE 2

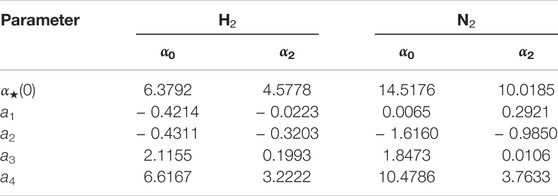
TABLE 2. Parameters of the polarizabilities, Eq. 7 (in a.u.).

FIGURE 2

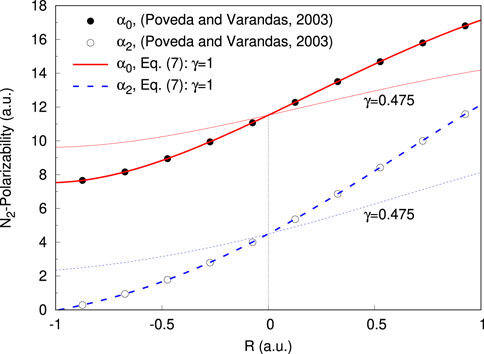
FIGURE 2. (Color online) Isotropic (α₀) and anisotropic (α₂) dipole polarizabilities for the nitrogen molecule, as a function of the internuclear separation. The thick solid and dashed lines represents the fits of Eq. 7 with γ =1, to the ab initio data. The same curves for γ =0.475 are shown in thin lines (see text for details).

FIGURE 3

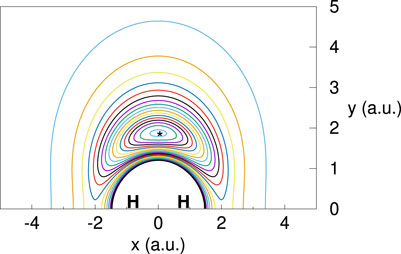
FIGURE 3. (Color online) Isoenergy Contour plot for a positron around the hydrogen molecule fixed at the equilibrium bond distance. Contours start at −8.4 eV (⋆) with a level incremental of 0.5 eV. The plot correspond to a model potential with κ =1, ρ =1.85 and γ =1

FIGURE 4

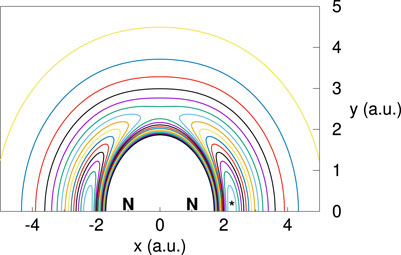
FIGURE 4. (Color online) Isoenergy Contour plot for a positron around the nitrogen molecule fixed at the equilibrium bond distance. Contours start at −4.5 eV (⋆) with a level incremental of 0.3 eV. The plot correspond to a model potential with κ =0.5, ρ =2.05 and γ =1.

3 The Close-Coupling Method

The close-coupling formalism for non-reactive collisions has been extensively revisited in the literature [20–22]. Here we present the main ideas behind the method, for the particular case of a structureless particle (the positron) scattering from a vibrating diatomic target.

Assuming a complete, discrete, orthonormal basis of the internal states of the system, the total wave function, in the space fixed reference frame, can be written in the form

${\mathrm{\Psi }}^{JMjlv}=\sum _{j^{\prime }{l}^{\prime }{\nu }^{\prime }}\frac{{\psi }_{j^{\prime }{l}^{\prime }{\nu }^{\prime }}^{Jjl\nu }\left(r\right)}{r}{Y}_{j^{\prime }{l}^{\prime }}^{JM}\left(\widehat{r},\widehat{R}\right){\chi }_{{\nu }^{\prime }}\left(R\right),(8)$

where χ_ν′(R) represents vibrational wavefunctions of the target and $Y_{j^{\prime }{l}^{\prime }}^{JM}$ is a basis for the total angular momentum (J) and projection (M), obtained by coupling the target (j) and the projectile (l) angular momentum, via the Clebsch-Gordan coefficients. Note that j does not include the angular momentum due to the movement of the electrons of the target. After substitution of Eq. 8 in the time-independent Schrödinger equation, the following set of coupled equations, for a given J and M, is obtained

$\left[\frac{d^2}{d{r}^2}+k_{j^{\prime }{\nu }^{\prime }}^2-\frac{l^{\prime }\left(l^{\prime }+1\right)}{r^2}\right]{\psi }_{j^{\prime }{l}^{\prime }{\nu }^{\prime }}^{Jjl\nu }=\frac{2m}{{\hslash }^2}\sum _{j^{″}{l}^{″}{\nu }^{″}}⟨j^{\prime }{l}^{\prime }{\nu }^{\prime }J|V|j^{″}{l}^{″}{\nu }^{″}J⟩{\psi }_{j^{″}{l}^{″}{\nu }^{″}}^{Jjl\nu },(9)$

where m is the reduced mass of the positron-diatom system, V is the projectile-target interaction potential and $k_{j^{\prime }{\nu }^{\prime }}^2$ is the wavenumber of the j′ν′-th channel.

Eq. 9 gives an exact solution for the quantum scattering problem, within the space expanded by Eq. 8, with the boundary condition ψ(r = 0) = 0.

As usually done, the interaction potential is represented in a basis of Legendre polynomials

$V\left(R,r,\theta \right)=\sum _{\lambda }{c}_{\lambda }\left(R,r\right)P_{\lambda }\left(\cos \theta \right),(10)$

leading in Eq. 9 to the matrix elements of the potential

$⟨j^{\prime }{l}^{\prime }{\nu }^{\prime }J|V|j^{″}{l}^{″}{\nu }^{″}J⟩=\sum _{\lambda }{c}_{\lambda {\nu }^{\prime }{\nu }^{″}}\left(r\right)f_{\lambda }\left(j^{\prime }{l}^{\prime }{j}^{″}{l}^{″}J\right),(11)$

where

$c_{\lambda {\nu }^{\prime }{\nu }^{″}}\left(r\right)=⟨{\chi }_{{\nu }^{\prime }}\left(R\right)|c_{\lambda }\left(r,R\right)|{\chi }_{{\nu }^{″}}\left(R\right)⟩,(12)$

and f_λ(j′l′j^″l^″J) are the Percival-Seaton coefficients [21,22].

The set of Eq. 9 is integrated using the Manolopoulos diabatic modified log-derivative method [23], as implemented in the MOLSCAT code [24], with r ranging from 0.01 to 100 a.u, with a fixed step of 0.01 a.u. The diatom was treated as a harmonic oscillator. The expansion (10) runs through the Legendre polynomials of even degree up to λ_max = 12, the vibrational quantum number includes ν = 0, 1, 2, 3 and the total angular momentum ranges from 0 to J_max = 12. Note that convergence is reached for these maximum values of λ, ν and J.

4 Results and Discussion

4.1 Elastic Cross Sections

First we check the capability of the model to describe the elastic cross section for energies below the positronium formation threshold. A comparison for H₂ is shown in Figure 5. The present result, in red solid line, corresponds to the elastic cross section, using the model potential calibrated to the free parameters κ = 1 and ρ = 1.85. Note that the present elastic cross section is nearly independent of the value of γ, in this case fixed in γ = 1 (see next section). These values were chosen so as to reproduce as much as possible the theoretical predictions from [25,26], for energies below 1 eV, assuming that these are the most accurate theoretical reports thus far, in this energy range. Also shown in Figure 5 are previous cross sections from close-coupling calculations [27] and experimental measurements [28–30].

FIGURE 5

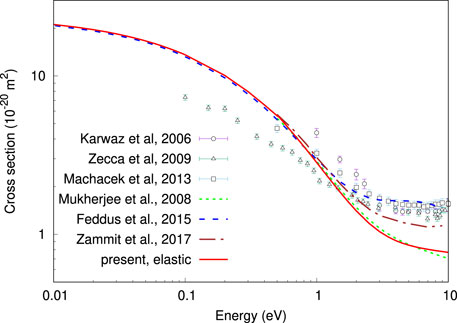
FIGURE 5. (Color online) Elastic (present result) and total cross sections for positron scattering from H₂. The present result correspond to a model potential with κ =1, ρ =1.85 and γ =1.

The appreciable discrepancies among the experimental data of total cross sections for H₂, mainly at very-low energies, were carefully analyzed [25] regarding the differences on the experimental setups, and a statistical correction was proposed taking as reference the value of the scattering length from [31], e.g. − 2.63a₀. Moreover, for energies above 3 eV the experiments show a nearly constant behavior, a feature hard to describe by the theoretical models (see Figure 1 in [25]). The disagreement between theory and experiment in the last part of the energy interval, has been attributed to the difficulty in describing virtual positronium effects, which become increasingly important when approaching the positronnium formation threshold ($\sim 8$ eV for H₂) [25]. However, note that above 3 eV the present elastic cross section show a tendency to flatten, although underestimating the experimental data. As pointed out in a previous work, using a simple rigid sphere plus polarization potential, the lack of virtual positronium and long-range higher multipole effects can be compensate by a deep enough dipole polarization potential [32]. In order to investigate the role of dipole polarizability on the vibrational excitation of the target, the present model was kept as simple as possible. The role of higher multipole contributions on the cross sections will be addressed in a future work. Finally, our calculations predicted a scattering length of −2.52a₀ for the H₂ target, in good agreement with the recommended value [25,31].

A comparison of the present elastic cross section with previous theories [16,32,33] and experiments [28,34], for positron-N₂ scattering is shown in Figure 6. Again the parameters κ and ρ were varied until our calculations reproduce, as best as possible, previous theories and experiments, taking as references the values reported in [16,32]. Although the present model potential involves two free parameters, it is not flexible enough to obtain a good agreement with all the reported values up to the positronium formation threshold. As observed for the H₂ target, our model allows for a good description of the cross section for energies below 2 eV, underestimating the cross section for higher energies. The present elastic cross section, in red solid line in Figure 6, corresponds to κ = 0.5 and ρ = 2.05 in the model potential. With these values of the parameters the scattering length for N₂ was predicted to be −5.17a₀, in good agreement with the value −5.21a₀ reported in [32]. Note that for κ = 1, which corresponds to include one hundred percent of the static term, the computed cross section becomes so small that not plausible value of ρ can yield a cross section in good agreement with the previous reports.

FIGURE 6

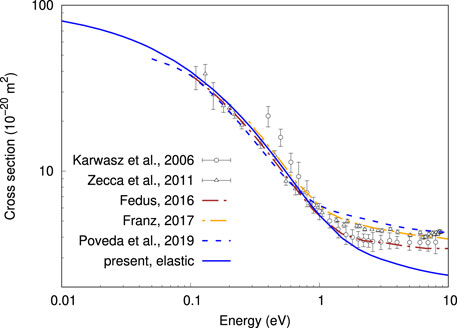
FIGURE 6. (Color online) Elastic (present result and [16]) and total cross sections for positron scattering from N₂. The present result correspond to a model potential with κ =0.5, ρ =2.05 and γ =1.

We have to emphasize that the values for the parameters κ and ρ were chosen such that the resulting elastic cross sections, for the targets here considered, show a good agreement with the reported data around the energy threshold for the fundamental vibrational mode. Note that the main goal of the present work is to shed light on the role of the target polarizability in the vibrational excitation cross section. A more realistic model for positron-N₂ have been already published by our group [16], and the same methodology [35] is being applied to compute elastic, vibrational and rotational cross sections for positron scattering from H₂ [36].

4.2 Vibrational Excitation Cross Sections

The 0 → 1 vibrational excitation cross sections, for H₂ and N₂, are shown in Figure 7. Note that each curve were obtained with the same model potential used to compute the corresponding elastic cross sections. In both cases the typical behavior with a sharp onset at threshold is observed, followed by a maximum and then a decrease with increasing energy. However, although the curves show what seems to be the correct behavior, their values appear well above the previous results. For example, the experimental measurements for H₂ [6] predicted a maximum of $\sim 0.12\times 10^{-20}{\mathrm{m}}^2$ around 0.7 eV, whereas the corresponding curve in Figure 7 presents an upper value 3 times higher, at the same energy. Similarly, for the vibrational excitation of N₂ the previous close-coupling calculation from [16] predicted a maximum of $\sim 0.02\times 10^{-20}{\mathrm{m}}^2$, located at $\sim 0.35$ eV, while the corresponding curve of Figure 7 reach its maximum five times above, around the same energy value. Apparently, the present more realistic 3D model reveals that the observed good quantitative agreement between the computed 0 → 1 vibrational cross section for H₂ and previous reports (see Figure 2 in [15]) is a coincidence, presumably due to the reduced dimensionality of the model.

FIGURE 7

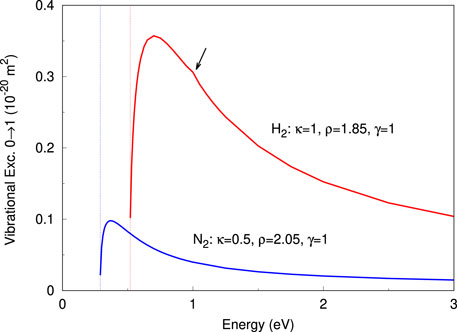
FIGURE 7. (Color online) 0→1 vibrational excitation cross sections for H₂ and N₂, obtained with model potentials calibrated to the values of the free parameters. The vertical lines indicate the threshold energies for the 0→1 vibrational mode and the arrow draws attention to the small peak caused by the opening of the 0→2 vibrational channel.

As shown in paper I, the height of 0 → 1 vibrational excitation cross section for H₂ depends on the rate of change of the target isotropic polarizability with R (see Figure 2 in [15]). The greater the slope of the polarizability as a function of R the higher the cross section and vice versa. In turn, the shape of the cross section remains almost unchanged with this variation of height. In the present model the slope of the isotropic and anisotropic polarizabilities is controlled by the parameter γ in Eq. 7, such that for γ < 1 the polarizability curve becomes less tilted (see Figures 1, 2), leading to a lower vibrational excitation cross section. Thus, for γ = 0.6, the resulting cross section for H₂ show a good agreement with the reported experiment [6] and theories [15,26,37], as can be seen in Figure 8. For the N₂ target we found that γ = 0.475 (see Figure 2) is the appropriated value which leads to a cross section close to the obtained in a previous close-coupling calculation [16]. Note that the present result almost match the previous one [16], showing a peak around the threshold energy, a feature absent in previous works [10,38,39]. The reader is referred to the text around Figure 9 and 10 of [16], for a detailed discussion about the plausibility of a threshold peak in the 0 → 1 vibrational excitation cross section for N₂. Moreover, this peaked behavior of the vibrational cross section for N₂ appears to be a key feature to explain measurements of positron cooling in a buffer gas of molecular nitrogen [16].

FIGURE 8

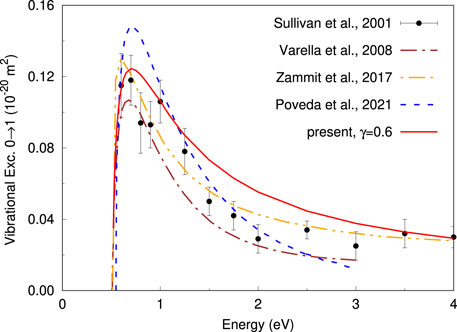
FIGURE 8. (Color online) Comparison of the 0→1 vibrational excitation cross sections for H₂. The present result correspond to a model potential with κ =1, ρ =1.85 and γ =0.6.

FIGURE 9

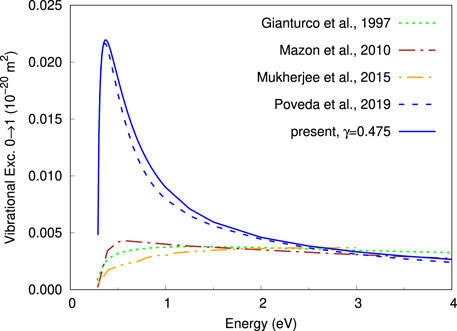
FIGURE 9. (Color online) Comparison of the 0→1 vibrational excitation cross sections for N₂. The present result correspond to a model potential with κ =0.5, ρ =2.05 and γ =0.475.

As discussed in paper I, the present results suggests a mechanism to understand how the positron couples to the vibrational modes of a homonuclear diatomic. In the model here presented the target potential energy V_osc is not affected by the proximity of the positron, which in turn is attracted by a correlation polarization potential, that alternates between greater and lesser attraction, as the diatom vibrates. The more stretched the diatom, the greater the molecular polarizability, making the potential more attractive, vide Eqs 4, 7. The observed good description of the vibrational excitation cross section, using this simple model, suggests that as the diatom vibrates the positron respond instantly to the nuclear motion, so coupling efficiently to the vibrational mode. This adiabatic picture can also be justified by considering the positron/nuclei small mass ratio and the low energies involved in the scattering event.

Taking this picture a little further, in a large molecule, for example an Alkane, the polarizability of the target would be a complicated function of the nuclear degrees of freedom. Hence, the attractive potential felt by the incoming positron will vary in a complicated way with the molecular vibrational modes. Then, if the positron is driven by the potential to “vibrates” in sync with the target oscillation, this would imply a coupling of the positron with all the vibrational modes of the molecule [40]. It is worth noting that the key property in the present model is the coordinate dependent molecular polarizability, just the same property that shows the strongest correlation with the positron-molecule binding energy, in Alkanes [12].

5 Conclusion

In this work a model potential is proposed, which describes the elastic and vibrational excitation cross sections of H₂ and N₂ by impact of a low energy positron. The potential energy surface depends on the three coordinates involved in a particle-diatom interaction, generalizing to the full configuration space a previous two-dimensional model. The coupling of the positron to the vibrational modes of the target is included in an attractive correlation polarization energy term, properly damped at short range, which involves the target (an)isotropic polarizability as a function of the vibrational coordinate. The dependence on the relative positron-target orientation is accounted for by the anisotropic component of the polarizability. A static spherically symmetric energy term describes the repulsive short range region. In addition to a set of adjustable parameters used to obtain an analytical representation of accurate ab initio points, the potential involves three free parameters, which serve to calibrate the static, correlation-polarization and vibrational parts of the potential, so as to reproduce reported cross sections.

The elastic and 0 → 1 vibrational excitation cross sections, computed using the close-coupling method, show good agreement with previous experimental and theoretical reports. This is achieved for specific values of the free parameters of the model potential. The good description of the here reported 0 → 1 vibrational excitation cross sections for H₂ and N₂, suggests a mechanism for the coupling of the positron to the vibration of the diatoms. In this picture the positron responds instantly to a correlation-polarization potential whose attractiveness oscillates following the vibrational mode of the target. This dependence of the potential on the vibrational coordinate is included through the variation of the molecular polarizability with the internuclear separation. This simple model can be arguably extended to a multimode situation where resonant positron annihilation is mediated by positron binding to a non-polar poliatomic molecule.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

LP, and JM contributed to conception and design of the study. LP organized the database, performed the statistical analysis and wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This research was funded by Conselho Nacional de Desenvolvimento Científico e Tecnológico, grant number 307125/2019-0.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Luis Poveda acknowledges support from the Centro Federal de Educação Tecnológica de Minas Gerais.

References

1. Charlton M, Humberston JW. Positron Physics. Cambridge: Cambridge University Press (2001).

Google Scholar

2. Gribakin GF, Young JA, Surko CM. Positron-molecule Interactions: Resonant Attachment, Annihilation, and Bound States. Rev. Mod. Phys. (2010) 82:2557–607. doi:10.1103/RevModPhys.82.2557

CrossRef Full Text | Google Scholar

3. Surko CM, Passner A, Leventhal M, Wysocki FJ. Bound States of Positrons and Large Molecules. Phys. Rev. Lett. (1988) 61:1831–4. doi:10.1103/PhysRevLett.61.1831

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Young JA, Surko CM. Feshbach-resonance-mediated Annihilation in Positron Interactions with Large Molecules. Phys. Rev. A (2008) 77:052704. doi:10.1103/PhysRevA.77.052704

CrossRef Full Text | Google Scholar

5. Brunger MJ, Buckman SJ, Ratnavelu K. Positron Scattering from Molecules: An Experimental Cross Section Compilation for Positron Transport Studies and Benchmarking Theory. J Phys. Chem. Reference Data (2017) 46:023102–1. doi:10.1063/1.4982827

CrossRef Full Text | Google Scholar

6. Sullivan JP, Gilbert SJ, Surko CM. Excitation of Molecular Vibrations by Positron Impact. Phys. Rev. Lett. (2001) 86:1494–7. doi:10.1103/PhysRevLett.86.1494

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Marler JP, Surko CM. Systematic Comparison of Positron- and Electron-Impact Excitation of Theν3vibrational Mode ofCF4. Phys. Rev. A (2005) 72:062702. doi:10.1103/PhysRevA.72.062702

CrossRef Full Text | Google Scholar

8. Gilbert SJ, Barnes LD, Sullivan JP, Surko CM. Vibrational-resonance Enhancement of Positron Annihilation in Molecules. Phys. Rev. Lett. (2002) 88:043201–1. doi:10.1103/PhysRevLett.88.043201

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Mukherjee T, Ghosh AS, Jain A. Low-energy Positron Collisions withH2andN2molecules by Using a Parameter-free Positron-Correlation-Polarization Potential. Phys. Rev. A (1991) 43:2538–41. doi:10.1103/PhysRevA.43.2538

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Gianturco FA, Mukherjee T. Dynamical Coupling Effects in the Vibrational Excitation ofH2sandN2scolliding with Positrons. Phys. Rev. A (2013) 55:1044–55. doi:10.1103/PhysRevA.55.1044

CrossRef Full Text | Google Scholar

11. Gribakin GF, Lee CMR. Positron Annihilation in Molecules by Capture into Vibrational Feshbach Resonances of Infrared-Active Modes. Phys. Rev. Lett. (2006) 97:193201. doi:10.1103/PhysRevLett.97.193201

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Danielson JR, Young JA, Surko CM. Analysis of Experimental Positron-Molecule Binding Energies. J. Phys Conf. Ser. (2010) 199:012012. doi:10.1088/1742-6596/199/1/012012

CrossRef Full Text | Google Scholar

13. Amaral PHR, Mohallem JR. Positron Binding to Atoms and Apolar Molecules: A Convergence of Theory and Experiment. Phys. Rev. A (2012) 86:042708. doi:10.1103/PhysRevA.86.042708

CrossRef Full Text | Google Scholar

14. Amaral PHR, Mohallem JR. Machine-learning Predictions of Positron Binding to Molecules. Phys. Rev. A (2020) 102:052808. doi:10.1103/PhysRevA.102.052808

CrossRef Full Text | Google Scholar

15. Poveda LA, Varella MT, Mohallem JR. Vibrational Excitation Cross-Section by Positron Impact: A Wave-Packet Dynamics Study. Atoms (2021) 9:64. doi:10.3390/atoms9030064

CrossRef Full Text | Google Scholar

16. Poveda LA, Assafrão D, Pinheiro JG, Mohallem JR. Close-coupling Scattering Cross Sections and a Model for Positron Cooling in a Buffer Gas of Molecular Nitrogen. Phys. Rev. A (2019) 100:062706. doi:10.1103/PhysRevA.100.062706

CrossRef Full Text | Google Scholar

17. Mitroy J, Ivanov IA. Semiempirical Model of Positron Scattering and Annihilation. Phys. Rev. A (2002) 65:042705. doi:10.1103/PhysRevA.65.042705

CrossRef Full Text | Google Scholar

18. Kol/os W, Wolniewicz L. Polarizability of the Hydrogen Molecule. J. Chem. Phys. (1967) 46:1426–32. doi:10.1063/1.1840870

CrossRef Full Text | Google Scholar

19. Poveda LA, Varandas AJC. Accurate Single-Valued Double Many-Body Expansion Potential Energy Surface for Ground-State HN2. J. Phys. Chem. A (2003) 107:7923–30. doi:10.1021/jp030571o

CrossRef Full Text | Google Scholar

20. Curtiss CF, Adler FT. The Scattering of Atoms from Diatomic Molecules. J. Chem. Phys. (1952) 20:249–56. doi:10.1063/1.1700387

CrossRef Full Text | Google Scholar

21. Arthurs AM, Dalgarno A. The Theory of Scattering by a Rigid Rotator. Proc. R. Soc. Lond. A (1960) 256:540–51. doi:10.1098/rspa.1960.0125

CrossRef Full Text | Google Scholar

22. Pack RT. Space‐fixed vs Body‐fixed Axes in Atom‐diatomic Molecule Scattering. Sudden Approximations. J. Chem. Phys. (1974) 60:633–9. doi:10.1063/1.1681085

CrossRef Full Text | Google Scholar

23. Alexander MH, Manolopoulos DE. A Stable Linear Reference Potential Algorithm for Solution of the Quantum Close‐coupled Equations in Molecular Scattering Theory. J. Chem. Phys. (1987) 86:2044–50. doi:10.1063/1.452154

CrossRef Full Text | Google Scholar

24. Hutson JM, Le Sueur CR. Molscat: A Program for Non-reactive Quantum Scattering Calculations on Atomic and Molecular Collisions. Comput. Phys. Commun. (2019) 241:9–18. doi:10.1016/j.cpc.2019.02.014

CrossRef Full Text | Google Scholar

25. Fedus K, Franz J, Karwasz GP. Positron Scattering on Molecular Hydrogen: Analysis of Experimental and Theoretical Uncertainties. Phys. Rev. A (2015) 91:062701. doi:10.1103/PhysRevA.91.062701

CrossRef Full Text | Google Scholar

26. Zammit MC, Fursa DV, Savage JS, Bray I, Chiari L, Zecca A, et al. Adiabatic-nuclei Calculations of Positron Scattering from Molecular Hydrogen. Phys. Rev. A (2017) 95:022707. doi:10.1103/PhysRevA.95.022707

CrossRef Full Text | Google Scholar

27. Mukherjee T, Sarkar NK. Ro-vibrational Close Coupling Study of Positron-Hydrogen Molecule Scattering Using the Parameter-free Model Correlation Polarization Potential. J. Phys. B At. Mol. Opt. Phys. (2008) 41:125201. doi:10.1088/0953-4075/41/12/125201

CrossRef Full Text | Google Scholar

28. Karwasz GP, Pliszka D, Brusa RS. Total Cross Sections for Positron Scattering in Argon, Nitrogen and Hydrogen below 20eV. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact Mater. Atoms (2006) 247:68–74. doi:10.1016/j.nimb.2006.01.065

CrossRef Full Text | Google Scholar

29. Zecca A, Chiari L, Sarkar A, Nixon KL, Brunger MJ. Total Cross Sections for Positron Scattering fromH2at Low Energies. Phys. Rev. A (2009) 80:032702. doi:10.1103/PhysRevA.80.032702

CrossRef Full Text | Google Scholar

30. Machacek JR, Anderson EK, Makochekanwa C, Buckman SJ, Sullivan JP. Positron Scattering from Molecular Hydrogen. Phys. Rev. A (2009) 88:042715. doi:10.1103/PhysRevA.88.042715

CrossRef Full Text | Google Scholar

31. Zhang J-Y, Mitroy J, Varga K. Positron Scattering and Annihilation from the Hydrogen Molecule at Zero Energy. Phys. Rev. Lett. (2009) 103:223202. doi:10.1103/PhysRevLett.103.223202

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Fedus K. A Rigid Sphere Approach to Positron Elastic Scattering by Noble Gases, Molecular Hydrogen, Nitrogen and Methane. Eur. Phys. J. D (2016) 70:261. doi:10.1140/epjd/e2016-70452-6

CrossRef Full Text | Google Scholar

33. Franz J. Positron-electron Correlation-Polarization Potentials for the Calculation of Positron Collisions with Atoms and Molecules*. Eur. Phys. J. D (2017) 71:44. doi:10.1140/epjd/e2017-70591-2

CrossRef Full Text | Google Scholar

34. Zecca A, Chiari L, Sarkar A, Brunger MJ. Positron Scattering from the Isoelectronic Molecules N2, CO and C2H2. New J. Phys. (2011) 13:115001. doi:10.1088/1367-2630/13/11/115001

CrossRef Full Text | Google Scholar

35. Mohallem JR, Rolim F, Gonçalves CP. A Molecular Model for Positron Complexes: Long-Range Effects on 2 Pair-Annihilation Rates. J. Phys. B At. Mol. Opt. Phys. (2004) 37:1045–53. doi:10.1088/0953-4075/37/5/007

CrossRef Full Text | Google Scholar

36. Pinheiro JG, Assafrão D, Poveda LA, Mohallem JR. Close-coupling Elastic and Inelastic Cross Sections for Positron Scattering from H₂ and O₂ (2022). (Work in progress).

Google Scholar

37. Varella MT, Lima MAP, Lima MAP. Near Threshold Vibrational Excitation of Molecules by Positron Impact: A Projection Operator Approach. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms (2008) 266:435–40. doi:10.1016/j.nimb.2007.12.020

CrossRef Full Text | Google Scholar

38. Mazon KT, Tenfen W, Michelin SE, Arretche F, Lee M-T, Fujimoto MM. Vibrational Cross Sections for Positron Scattering by Nitrogen Molecules. Phys. Rev. A (2010) 82:032704. doi:10.1103/PhysRevA.82.032704

CrossRef Full Text | Google Scholar

39. Mukherjee T, Mukherjee M. Low-energy Positron-Nitrogen-Molecule Scattering: A Rovibrational Close-Coupling Study. Phys. Rev. A (2015) 91:062706. doi:10.1103/PhysRevA.91.062706

CrossRef Full Text | Google Scholar

40. Jones ACL, Danielson JR, Natisin MR, Surko CM, Gribakin GF. Ubiquitous Nature of Multimode Vibrational Resonances in Positron-Molecule Annihilation. Phys. Rev. Lett. (2012) 108:093201. doi:10.1103/PhysRevLett.108.093201

PubMed Abstract | CrossRef Full Text | Google Scholar