Numerical Simulation of Water-Sediment Two-Phase Seepage Characteristics and Inrush Mechanism in Rough Rock Fractures

The water-sediment two-phase flow in the rough fracture is one of the main causes of water-sediment inrush. In this study, numerical simulation models of the water-sediment two-phase flow in the smooth and rough fractures were established by ANSYS Fluent software based on the seepage theory; the mechanical properties of the water-sediment two-phase flow under different conditions were systematically investigated, and the influence laws of the surface morphology of the fracture on sediment volume concentration, sediment particle size, and sediment particle mass density were analyzed. In addition, the influence laws of the sediment volume concentration, sediment particle size, and sediment particle mass density on the absolute value of the pressure gradient, mean velocity of the fluid, and fluid turbulent kinetic energy were also illustrated from the perspective of sediment particle distribution. Research shows that during the water-sediment flow in the smooth fracture, the absolute value of pressure gradient Gp, the sediment volume concentration Ф, the sediment particle size D_p, and the sediment mass density ρ_p are approximately linear, and the linearity of G_p and D_p is the lowest; during the water-sediment flow in the smooth fracture, the mean velocity v of the continuous-phase fluid rarely changes with Ф, D_p, and ρ_p. However, during the water-sediment flow in the rough fracture, v is greatly affected by Ф, D_p, and ρ_p. During the water-sediment flow in the smooth fracture, the fluid turbulent kinetic energy kt decreases with the increase of ρ_p and Ф and decreases with the decrease of ρ_p. During the water-sediment flow in the rough fracture, k_t is significantly affected by Ф, Dp, and ρ_p, which was manifested in the changes of curve shapes and deviation of the extreme points.

1 Introduction

Although coal resources are abundant in Northwest China, coal mining in this area is relatively difficult because of the fragile ecological environment and the thick sediment layer on the coal seam [1–4]. During the exploitation process of shallow coal seams, most faults are directly connected with overburden aquifers; in some extreme cases, subsidence areas may be directly connected with aquifers. At this point, the surface sediment layers and aquifers will be mixed; when the mixture flows underground, water-sediment inrush accidents will be induced [5–9]. Therefore, water-sediment flow characteristics in fractures should be comprehensively investigated so as to understand the disaster-causing mechanism of water-sediment inrush accidents and prevent the occurrence of water-sediment inrush accidents.

The physical and mechanical characteristics of the water-sediment mixture and the fracture surface characteristics are two key factors affecting the water-sediment two-phase flow [10, 12]. The characteristics of the water-sediment mixture, such as sediment volume concentration, sediment particle size, and sediment particle density, have been studied through laboratory experiments and theoretical analysis [13–17]. Jiang et al. investigated the flowing properties of crushed red sandstone with different particle sizes. It was concluded that the broken rocks with finer particles were likely to become unstable [13]. Through a self-developed seepage test system, Zhang et al. conducted the indoor tests and determined the optimal sand-filtration rate [18]. Pu et al. analyzed the influence of particle size grading on water-sediment seepage and found that the flow and height of the water-sediment mixture can be effectively reduced by decreasing the height of the aquifer by drilling [19].

The water-sediment mixtures show significant differences in fractures with different surface characteristics. In the initial stage of the research, parallel smooth fractures were prefabricated in these experiments. With the gradual progress of technology, the water-sediment two-phase flow in rough fractures has been studied, and some results have been achieved [20–24]. Researchers also have studied the influence of fracture aperture, directions, and amounts of fractures on the water-sediment two-phase flow [25–28]. In real working conditions, the factors affecting the water-sediment two-phase seepage are much more complex than those in the indoor seepage tests. For example, vortexes around the concave fracture surface greatly affect the pressure, sediment concentration distribution, and energy consumption during the water-sediment flow in fractures [29–36]. Although pressure gradient and flow rate can be used to analyze and invert the whole flow process in the laboratory tests, the evolution of water-sediment two-phase seepage in fractures cannot be illustrated. Therefore, it is necessary to adopt the numerical simulation method to study the water-sediment two-phase seepage in fractured rock masses.

In this study, considering the principle of water-sediment two-phase seepage, the mechanical models of water-sediment two-phase flow in smooth and rough fractures were established, and the numerical simulation experiment was performed by ANSYS Fluent. In addition, the influence of sediment volume concentration, sediment particle size, sediment mass density on pressure gradient, mean velocity distribution, and turbulent kinetic energy distribution was analyzed comprehensively. This study aims to reveal the disaster-causing mechanism of the water-sediment inrush and provide a reference for the precursor research of water-sediment inrush.

2 Experimental Principle and Model Overview

2.1 Principles of Water-Sediment Two-Phase Flow

2.1.1 Euler–Lagrange Method

The material description (or Lagrangian description) and spatial description method (or Eulerian description) are the main methods describing the motion of a continuous medium. In this study, the volume fraction of the sediment phase was less than 10%; thus, water was treated as the continuous phase and sediment particles were treated as the discrete phase. Specifically, the water phase was described by the conservation equation and transport equation of the turbulence in the Euler coordinate system, and the sediment movement was simulated by the discrete phase model (DPM) in the Lagrange coordinate system [37, 38]. It should be noted that the temperature change of the flow field [38] was ignored and water was treated as an incompressible fluid in this study.

2.1.2 Continuous Phase Governing Equations

As mentioned previously, water is treated as the continuous phase, and its flow is governed by the law of conservation. The governing equations included the mass conservation equation and momentum conservation equation. The former can be expressed by Eq. 1.

$\frac{\partial \rho }{\partial t}+\frac{\partial }{\partial \overrightarrow{X}}\left(\rho \overrightarrow{v}\right)=S_m.(1)$

The latter can be expressed by Eq. 2.

$\frac{\partial \left(\rho \overrightarrow{v}\right)}{\partial t}+\overrightarrow{\nabla }\cdot \left(\rho \overrightarrow{v}\overrightarrow{v}\right)=\overrightarrow{\nabla }\cdot \overleftrightarrow{\mathrm{\Sigma }}+\rho \overrightarrow{\text{g}}+{\overrightarrow{S}}_{DPM},(2)$

where $\overleftrightarrow{\mathrm{\Sigma }}$ is the stress tensor, $\overleftrightarrow{\mathrm{\Sigma }}={\sigma }_{ij}{\overrightarrow{e}}_i{\overrightarrow{e}}_j$; $\overrightarrow{g}$ is the acceleration of gravity; and ${\overrightarrow{S}}_{DPM}$ is the momentum source term reflecting the interaction between the sediment particle and water.

2.1.3 Discrete Phase Governing Equations

Both the rotation and moving of sediment particles should be considered to study the water-sediment flow in fractures. Based on the momentum theorem and the moment of momentum theorem, the governing equations of the discrete phase particles can be expressed by Eqs 3–5 in the Lagrange coordinate system:

$\frac{d{X}_{pi}}{dt}=v_{pi},(3)$

$m_p\frac{d{v}_{p_i}}{dt}=F_{Di}+m_p\frac{g_i\left({\rho }_p-\rho \right)}{{\rho }_p}+{\stackrel{⌢}{F}}_{\text{i}},(4)$

$I_{ij}\frac{d{\omega }_{pj}}{dt}+{\epsilon }_{ijk}{I}_{kl}{\omega }_j{\omega }_l=M_i,(5)$

where ${\Omega }_i$ is the angular velocity component of the water relative to the particle; $F_{Di}$ is the drag force component; $R{e}_p$ is the Reynolds number of the particle; $C_D$ is the dragging force coefficient; and $M_i$ is the torque applied to the particle and is proportional to the angular velocity of the particle.

2.2 Models of the Water-Sediment Two-Phase Flow in Fractures

In the numerical simulation of water-sediment flow in fractures, three basic assumptions are proposed as follows: (1) water is incompressible, and its density is a constant; (2) the sediment particle is assumed to be a rigid sphere of fixed radius, without obvious damage; and (3) the flow rate is uniformly distributed around the cross section of the fracture inlet, and the fluid velocity of the discrete phase sediment particle is the same as that of the continuous phase particle.

Figure 1 shows the computational domains of the smooth and rough fractures. In Figure 1A, the water-sediment flow in the area is defined by two parallel smooth fracture surfaces. The distance between the two surfaces is h, and the length of the fracture is L. The projection of the upper and lower surfaces on the OX₁X₂ section is a straight line. The boundary of the flow domain Ω comprises the inlet section $\overline{O{D}_1}$, the upper surface $\overline{D_1{D}_2}$, the outlet surface $\overline{D_2{D}_3}$, and the lower surface $\overline{D_{3}O}$. In Figure 1B, the water-sediment flow in the area is defined by two coincident surfaces. The projections of the upper and lower surfaces on the OX₁X section are broken lines, dividing the fracture surface into 50 equal broken line segments $F{L}_i^u$ and $F{L}_i^d$, where $i=1,\mathrm{...50}$. The boundary of the flow domain Ω consists of the inlet section $\overline{O{C}_1}$, upper surface ${\displaystyle \underset{i=1}{\overset{50}{\cup }}F{L}_i^u}$, outlet section $\overline{C_2{C}_3}$, and lower surface ${\displaystyle \underset{i=1}{\overset{50}{\cup }}F{L}_i^d}$.

FIGURE 1

FIGURE 1. Flow domains of fractures. (A) Smooth fracture; (B) rough fracture.

ANSYS Fluent 17.0 numerical simulation software was used to establish models of the water-sediment two-phase flow in smooth and rough fractures. Since the boundary of the smooth fracture model was relatively regular, structured grids were used for division in the ANSYS ICEM CFD. The evenly distributed grid nodes were arranged at the inlet to make the sediment particles uniformly distributed along the X₂ direction. In addition, the Stress-Omega RSM turbulence model was used in this study. It was required that y⁺ (the dimensionless distance to the wall) at the first layer of grid nodes near the wall was approximately 1; thus, fine grids were arranged. After calculation, y⁺ was checked. To ensure the accuracy and efficiency of the calculation results, after the grid independence test, the boundary layer grid size was set as 0.005 mm, and the global grid size was 0.08 mm. Figure 2 shows the final division result.

FIGURE 2

FIGURE 2. Grids of the smooth fracture.

Considering the severe bending of the wall boundary of the rough fracture model, hybrid grids were chosen for division in the meshing module on ANSYS Workbench, as shown in Figure 3. Multilayer structured grids were arranged in the boundary layer, and unstructured quadrilateral-dominant grids were used in other domains. After the division, y⁺ was checked and a grid-independent test was conducted. The total number of the grids was 145,000, as shown in Figure 3A. Figure 3B shows the grids in the boundary layer.

FIGURE 3

FIGURE 3. Grids of the rough fracture. (A) Grids of the rough fracture; (B) boundary grids of the rough fracture.

The parameters were adjusted according to the results of the laboratory test, and the material properties were determined, as shown in Table 1. Similarly, the interaction parameters between the sediment particle and the wall were determined. The friction coefficient, normal restitution coefficient, and tangential restitution coefficient were 0.45, 0.2, and 0.9, respectively. The interaction parameters among sediment particles were fixed. The static friction coefficient, sliding friction coefficient, and restitution coefficient were 0.3, 0.2, and 0.05, respectively.

TABLE 1

TABLE 1. Material properties.

2.3 Numerical Simulation Schemes and Methods

In this study, the sediment volume concentration, sediment particle size, and sediment mass density were taken as variables to investigate the evolution characteristics of the pressure gradient, mean velocity distribution, and turbulent kinetic energy distribution of the water-sediment two-phase flow under two fracture surface conditions. When a variable was used, the other two variables were fixed. Table 2 shows the specific values.

TABLE 2

TABLE 2. Parameters in the numerical simulation.

In particular, the inlet segment (X₁ = 5 mm), the middle segment (X₁ = 50 mm) of the smooth fracture surface, the bending segment (X₁ = 5 mm), and the parallel segment (X₁ = 50.5 mm) of the rough fracture surface were selected as the typical segments to comprehensively study the change laws of mean velocity distributions. Similarly, the inlet velocity was fixed as 0.869 m/s, the observation time node t was 0.3 s, and the number of variables was reduced.

3 Analysis of the Numerical Simulation Results

3.1 Change Law of the Absolute Value of the Pressure Gradient

Pressure gradient is one of the main parameters describing the seepage, which can reflect the pressure change along the flow direction. Figure 4 shows the absolute value of pressure gradient–sediment volume concentration (G_p–Ф) curves. In Figure 4A, when the water-sediment flowed in the smooth fracture, with a gradual increase of Ф, G_p decreased linearly from 6.51 kPa m⁻¹ to 6.39 kPa m⁻¹, decreasing by 1.72%. In Figure 4B, during the flow of water-sediment in the rough fracture, with a gradual increase of Ф, G_p first increased and then decreased. When Ф increased from 0 to 1.02%, G_p sharply decreased from 191.68 kPa m⁻¹ to 181.57 kPa m⁻¹, decreasing by 5.27%. When Ф increased from 1.02 to 4.06%, G_p gradually increased from 181.57 kPa m⁻¹ to 185.08 kPa m⁻¹, increasing by 1.93%. Through comparisons, it can be found that under the same conditions, the absolute value of the pressure gradient of the water-sediment flow in the rough fracture was about 40 times that in the smooth fracture. In addition, the change characteristics of the absolute value of the pressure gradient with the volume concentration of sediment particles were different under different fracture conditions. It indicates that the fracture surface morphology affects the influence of the volume concentration of sediment particles on the pressure gradient.

FIGURE 4

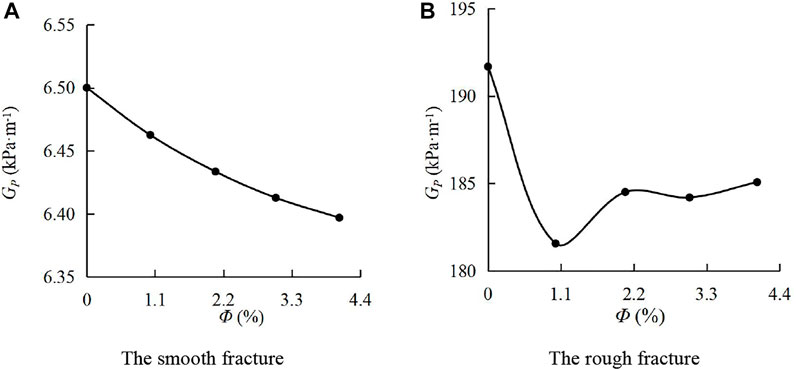
FIGURE 4. Absolute value of the pressure gradient–volume concentration of sediment particle curves. (A) Smooth fracture; (B) rough fracture.

Figure 5 shows the absolute value of the pressure gradient–sediment particle size (G_p-D_p) curves. In Figure 5A, during the water-sediment flow in the smooth fracture, G_p gradually decreased in a nonlinear form with the increase of D_p. As D_p increased from 0 to 0.12 mm, G_p quickly decreased from 6.51kPa m⁻¹ to 6.34 kPa m⁻¹, decreasing by 2.61%. In Figure 5B, during the water-sediment flow in the rough fracture, G_p first decreased, then increased, and decreased again. As D_p increased from 0 to 0.12 mm, G_p rapidly decreased from 191.68 kPa m⁻¹ to 171.76 kPa m⁻¹, decreasing by 10.39%. It can be found that during the water-sediment flow in the rough fracture, when the sediment particle size is small, the pressure loss increases with the increase of the particle size; when the sediment particle size is relatively large, the pressure loss decreases with the increase of the particle size. Through the comparisons, it can be found that the absolute value of the pressure gradient varies with the change of the sediment volume concentration under two types of fractures. It proves that the surface morphology of fractures affects the influence of sediment particle size on the pressure gradient.

FIGURE 5

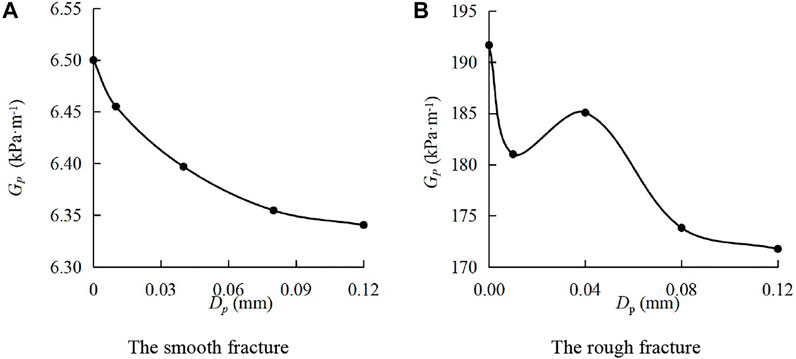
FIGURE 5. Absolute value of the pressure gradient–sediment particle size curves. (A) Smooth fracture; (B) rough fracture.

Figure 6 shows the absolute value of the pressure gradient–sediment particle mass density (G_P-ρ_p) curves. In Figure 6A, when the water sediment flowed in the smooth fracture, with the increase of ρ_p, G_P decreased in an approximately linear form. As ρ_p increased from 0 kg/m³ to 4,500 kg/m³, G_P rapidly decreased from 6.51kPa m⁻¹ to 6.33 kPa m⁻¹, decreasing by 2.84%. In Figure 6B, during the water-sediment flow in the rough fracture, G_P was smaller than that in the single-phase flow, and it first increased and then decreased with the increase of ρ_p. When ρ_p was 4,500 kg/m³, the minimum G_P was obtained. Through the comparison, it is found that the absolute value of the pressure gradient during the water-sediment flow in the rough fracture is about 30 times that in the smooth fracture under the same conditions. In addition, the absolute value of the pressure gradient varies with the sediment particle mass density. It indicates that the surface morphology of the fracture affects the impact of sediment particle mass density on the pressure gradient.

FIGURE 6

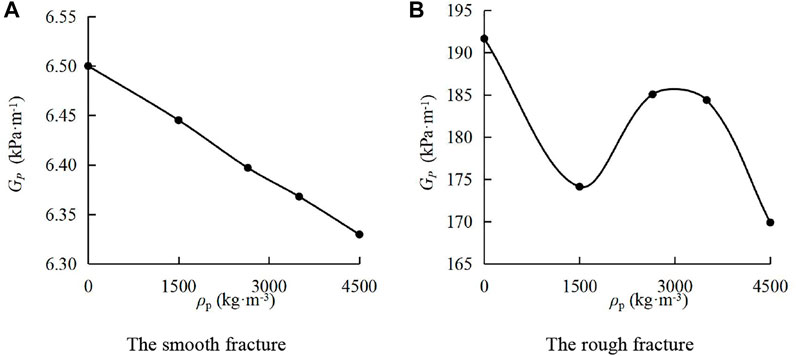
FIGURE 6. Absolute value of the pressure gradient–sediment particle mass density curves. (A) Smooth fracture; (B) rough fracture.

In summary, under the conditions of two types of surface fractures, the absolute value of the pressure gradient with different sediment particle volume concentrations, sediment particle sizes, and sediment particle mass density in the two-phase flow was smaller than that in the single-phase flow. Under the smooth fracture surface, the absolute value of the pressure gradient changed linearly with the change of sediment particle volume concentrations, sediment particle sizes, and sediment particle mass density, while this value has different changing trends under the rough fracture.

3.2 Variation Law of the Mean Fluid Velocity Distribution

The mean velocity distribution is one of the important technical indicators for the study of seepage problems. Figure 7 and Figure 8 show the mean velocity distributions of the continuous-phase fluid on typical cross sections of smooth and rough fractures under various sediment volume concentrations. In Figure 7A, at a cross section of X₁ = 5 mm, the water-sediment fluid was not fully developed on the smooth fracture surface. In Figure 7B, the flow became fully developed. Through the comparison, it can be found that the mean velocity distributions on the two sections rarely change with the sediment volume concentration Ф, and they were symmetrically distributed along the center line of X₂ = 0.9 mm.

FIGURE 7

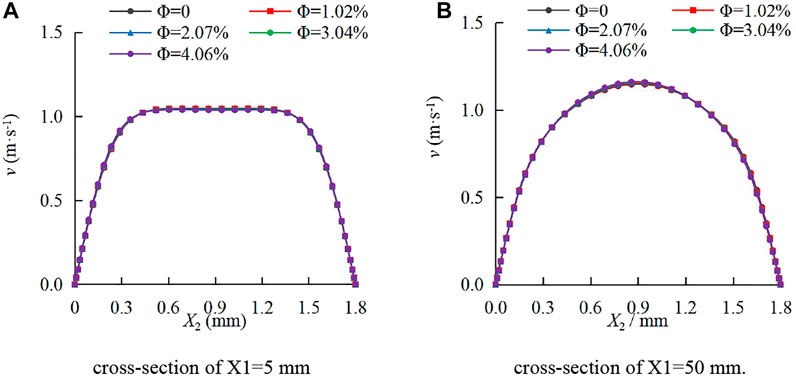
FIGURE 7. Mean velocity distributions of the continuous-phase fluid on smooth fracture sections under different sediment volume concentrations. (A) Cross section of X1=5 mm; (B) cross section of X1=50 mm.

FIGURE 8

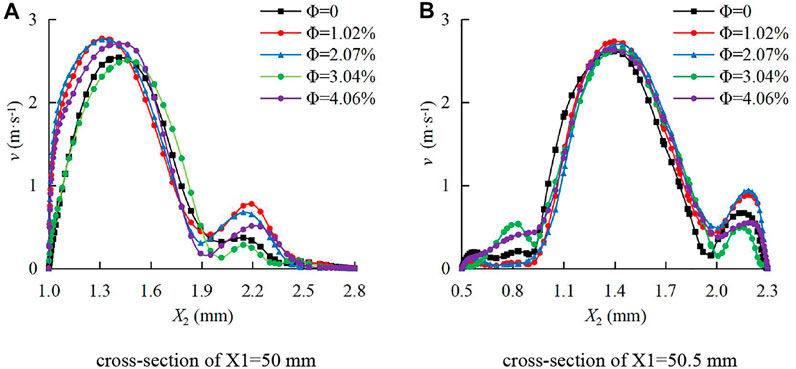
FIGURE 8. Mean velocity distribution of the continuous-phase fluid on cross sections of the rough fracture with different sediment volume concentrations. (A) Cross section of X1=50 mm; (B) cross section of X1=50.5 mm.

In Figure 8, when the water sediment flowed in the rough fractures, the mean velocity distributions of the continuous-phase fluid presented remarkable differences. In Figure 8A, v showed the asymmetric M-shaped distribution at the cross-section of X₁ = 50 mm, with two extreme points, and the peak values were within 1.2 mm ≤ X₂ ≤ 1.5 mm. In Figure 8B, there were multiple extreme points at the cross section of X₁ = 50.5 mm, and the peak values were near the center line X₂ = 1.4 mm. Compared with other positions, v has the greatest change with Ф near the wall.

As shown in Figure 7 and Figure 8, v of the continuous-phase fluid was dramatically different under two types of fracture conditions. The maximum v in the rough fracture was about three times that in the smooth fracture. In addition, the distribution curves are different. During the continuous-phase fluid flow in the smooth fracture, v-X₂ curves are rectangular or semi-sine shaped, while they are M-shaped during the continuous-phase fluid flow in the rough fracture.

Figure 9 and Figure 10 show the mean velocity distribution of the continuous-phase fluid on the typical cross sections of the smooth and rough fractures under different sediment particle sizes. In Figure 9A, when the water sediment flowed in the smooth fracture, the fluid was not fully developed at the cross section of X₁ = 5 mm. In Figure 9B, the fluid became fully developed at the cross section of X₁ = 50 mm. It can be observed that v rarely changed with D_p under two types of cross sections and the distribution of v was symmetrical along the center line of X₂ = 0.9 mm.

FIGURE 9

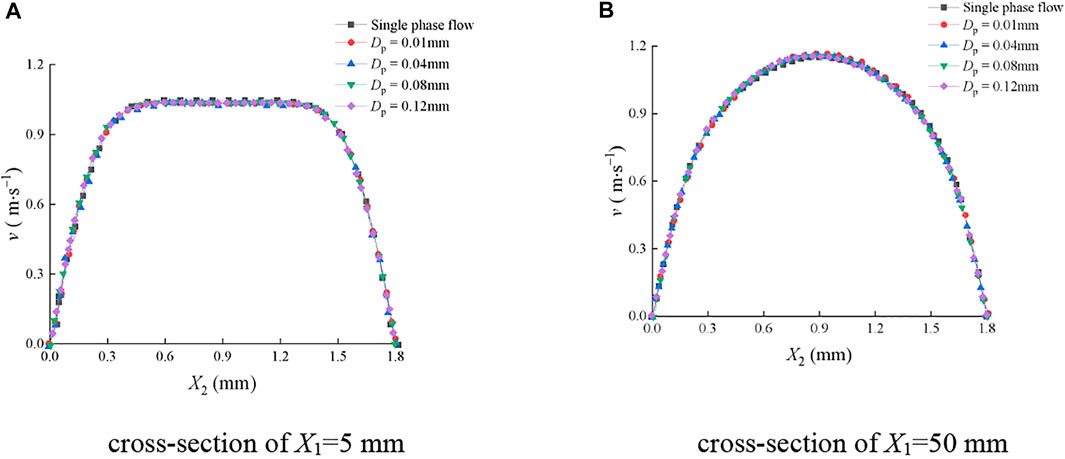
FIGURE 9. Mean velocity distribution of the continuous-phase fluid on cross sections of the smooth fracture with different sediment particle sizes. (A) Cross section of X1=5 mm; (B) cross section of X1=50 mm.

FIGURE 10

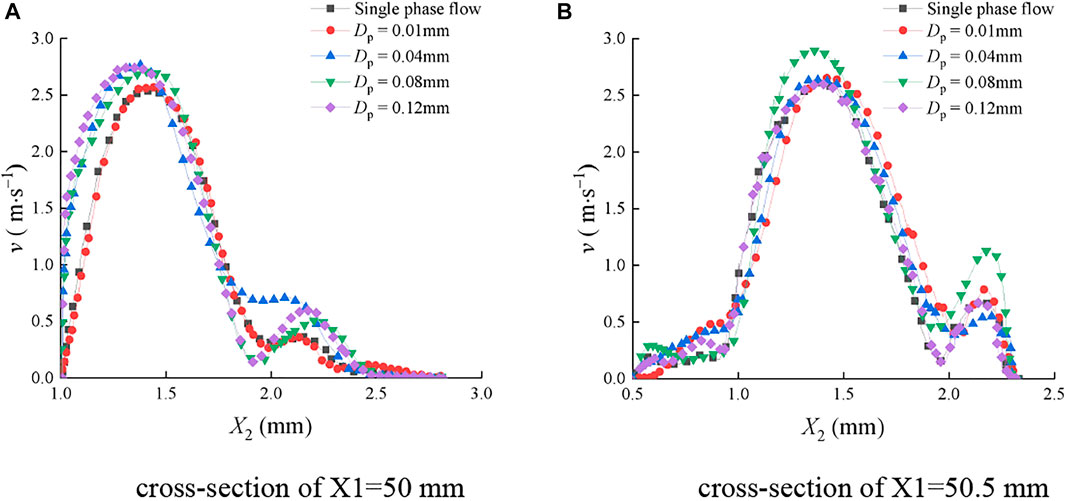
FIGURE 10. Mean velocity distribution of the continuous-phase fluid on cross sections of the rough fracture with different sediment particle sizes. (A) Cross section of X1=50 mm; (B) cross section of X1=50.5 mm.

Figure 10 shows that when the water sediment flowed in the rough fracture, v of the continuous-phase fluid was greatly influenced by D_p. Different v-X₂ curves varied significantly. In Figure 10A, on the cross section of X₁ = 50 mm, v first increased and then decreased with the increase of X₂, and the maximum value was between 1.2 and 1.5 mm. In Figure 10B, at the cross section of X₁=50.5mm, v also first increased and then decreased with the increase of X₂. In addition, there was an upward fluctuation at X₂ = 2.1 mm, and the peak value was within 1.2 mm ≤ X₂ ≤ 1.5 mm.

Figure 11 and Figure 12 show the mean velocity distribution of the continuous-phase fluid on the typical cross sections of the smooth and rough fractures under different sediment particle mass densities, respectively. In Figure 11, at the cross sections of X₁ = 5 mm and X₁ = 50 mm, v rarely changed with the sediment particle size, and v was symmetrically distributed along the center line of X₂ = 0.9 mm.

FIGURE 11

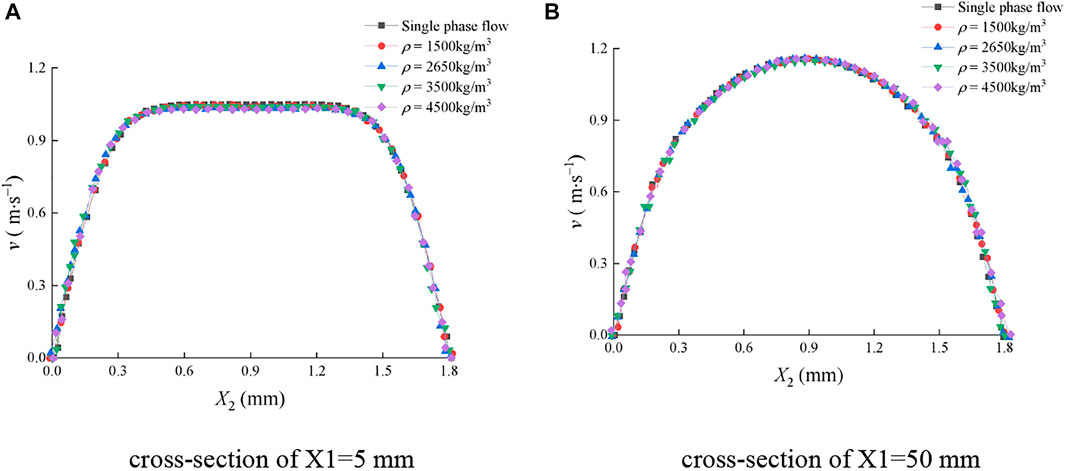
FIGURE 11. Mean velocity distribution of the continuous-phase fluid on the cross sections of the smooth fracture under different sediment particle mass densities. (A) Cross section of X1=5 mm; (B) cross section of X1=50 mm.

FIGURE 12

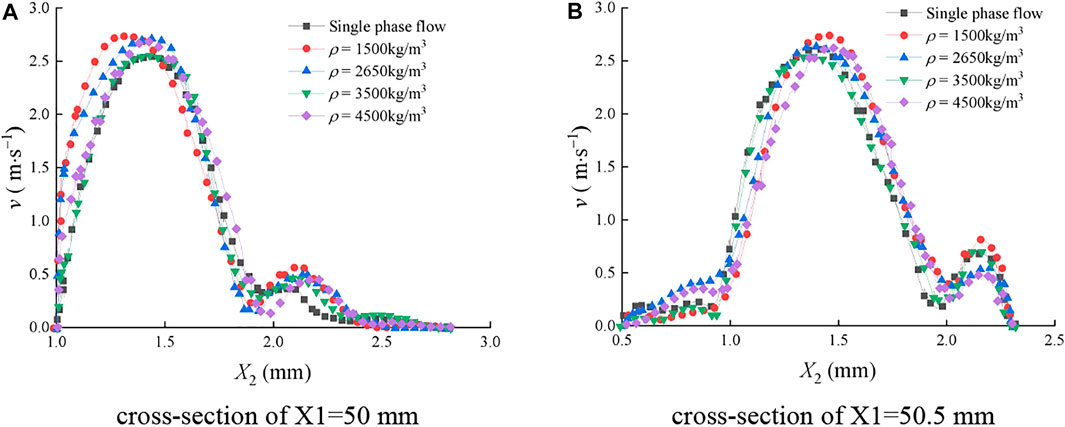
FIGURE 12. Mean velocity distribution of the continuous-phase fluid on cross sections of the rough fracture under different sediment particle mass density. (A) Cross section of X1=50 mm; (B) cross section of X1=50.5 mm.

In Figure 12, v was greatly affected by the sediment particle size during the flow in the rough fracture, and multiple extreme points can be observed. On the section of X₂ = 50 mm, v of the fluid particle at each position was significantly affected by the sediment volume concentration, and the maximum v was in the range of 1.2 mm ≤ X₂ ≤ 1.5 mm. On the section of X₂ = 50.5 mm, the peak value was near the center line of X₂ = 1.4 mm.

In summary, in the smooth fracture, the changes of the sediment particle volume concentration, sediment particle mass density, and sediment particle size rarely affect the mean velocity distribution of the continuous-phase fluid, while these influencing factors significantly affect the mean velocity distribution of the continuous-phase fluid in the rough fracture.

3.3 Variation Law of the Turbulent Kinetic Energy

The turbulent kinetic energy is an indicator to measure the development and decline of turbulence. Figure 13 and Figure 14 show the distribution of turbulent kinetic energy of the continuous-phase fluid on typical cross sections of smooth and rough fractures at various sediment particle volume concentrations. As shown in Figure 13A, on the section of X₁ = 5 mm in the smooth fracture, k_t first increased and then decreased with X₂, and k_t reached the maximum at X₂ = 0.9 mm. The distribution curves of k_t are symmetrical along with X₂ = 0.9 mm under various Ф. In particular, within X₂ = 0.15–0.45 mm and X₂ = 1.35–1.65 mm, there was a significant negative correlation between Ф and k_t. It indicates that the movement of sediment particles can inhibit the turbulent kinetic energy of the continuous-phase fluid. However, on the section of X₁ = 50 mm, the k_t–X₂ curves are M-shaped, as shown in Figure 13B. Differing from the situation on the section of X₁ = 5 mm, k_t reached a minimum value at X₂ = 0.9 mm. At this point, Ф affected k_t in the entire X₂ interval, namely, the greater the Ф, the smaller the k_t. It can be observed that the distribution of k_t–X₂ curves was approximately symmetrical along X₂ = 0.9 mm.

FIGURE 13

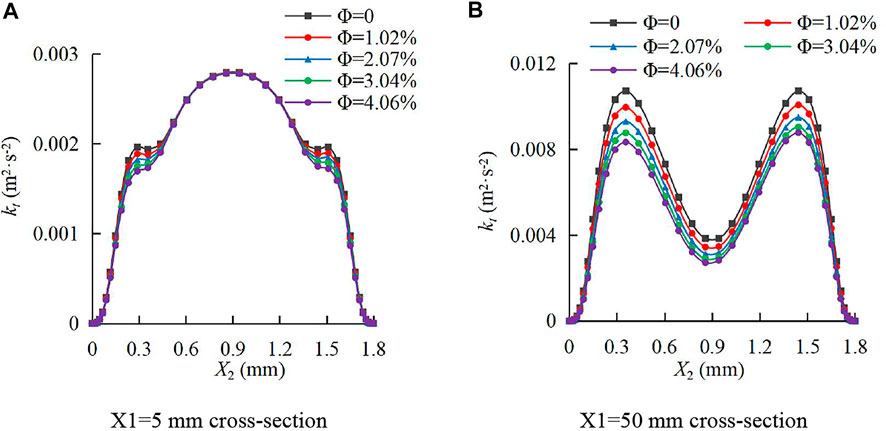
FIGURE 13. Distribution of turbulent kinetic energy of the continuous-phase fluid on cross sections of the smooth fracture. (A) X1=5 mm cross section; (B) X1=50 mm cross section.

FIGURE 14

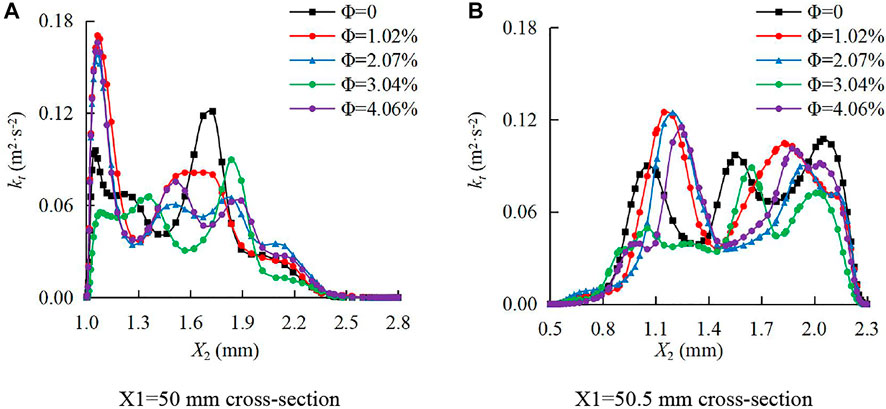
FIGURE 14. Distribution of turbulent kinetic energy of the continuous-phase fluid on cross sections of the rough fracture. (A) X1=50 mm cross section; (B) X1=50.5 mm cross section.

As presented in Figure 14, the distribution of k_t on the cross section of the rough fracture can be greatly affected by the sediment particle volume concentration Ф, which was manifested as the deviation of the extreme point position. In Figure 14A, on the section of X₁ = 50 mm, k_t fluctuated in the interval of 0 mm ≤ X₂ ≤ 2 mm and gradually decreased within 2 mm ≤ X₂ ≤ 2.8 mm. In Figure 14B, on the section of X₁ = 50.5 mm, k_t gradually increased in the interval of 0.5 mm ≤ X₂ ≤ 0.8 mm and fluctuated in the interval of 0.8 mm ≤ X₂ ≤ 2.3 mm. It can be observed that the maximum k_t was in the interval of 1.0 mm ≤ X₂ ≤ 1.3 m on both sections. In addition, the fluctuations of k_t can be found on both sections, indicating that the turbulence intensity was higher in the rough fracture.

As shown in Figure 13 and Figure 14, the turbulent kinetic energy of the fluid in the rough fracture was an order of magnitude higher than that in the smooth fracture under the same conditions. The distribution of fluid turbulent kinetic energy in the X₁ direction was numerically different, and the distribution curves were completely different during the water-sediment flow in the smooth and rough fractures. The impacts of the sediment volume concentration in the smooth fracture on the continuous-phase fluid turbulent kinetic energy had significant laws, while no obvious laws were observed in the rough fracture.

Figure 15 and Figure 17 show the distribution of turbulent kinetic energy of the continuous-phase fluid on typical cross sections of smooth and rough fractures under various sediment particle sizes. In Figure 15A, on the section of X₁ = 5 mm of the smooth fracture, k_t first increased and then decreased with X₂, and the maximum k_t was obtained at X₂ = 0.9 mm. The sediment particles significantly reduced k_t in the intervals of 0.15 mm ≤ X₂ ≤ 0.45 and 1.35 mm ≤ X₂ ≤ 1.65 mm, but the influence laws were different. In the interval of 0.15 mm ≤ X₂ ≤ 0.45, the distribution curves of k_t were basically consistent, and D_p had no obvious influence on k_t, while in the interval of 1.35 mm ≤ X₂ ≤ 1.65 mm, k_t gradually decreased with the decrease of D_p. When D_p was 0.01 mm, the distribution curve of k_t was symmetrically distributed along X₂ = 0.9 mm. When the values of D_p were 0.04, 0.08, and 0.12 mm, the distribution curves of k_t were asymmetrical along X₂ = 0.9 mm. On the section of X₁ = 5 mm, k_t was slightly affected by D_p in intervals other than X₂ = 0.15–0.45 mm and X₂ = 1.35–1.65 mm, and the curves were relatively consistent.

FIGURE 15

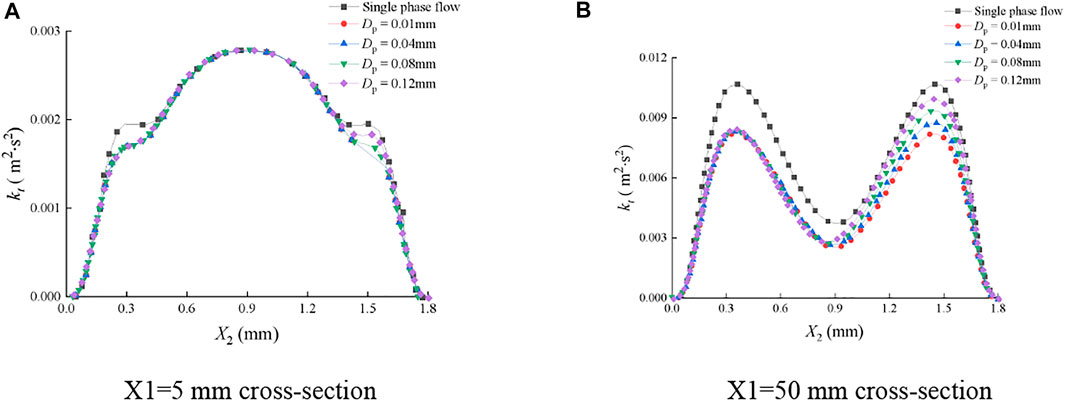
FIGURE 15. Distribution of turbulent kinetic energy of the continuous-phase fluid on cross sections of the smooth fracture. (A) X1=5 mm cross section; (B) X1=50 mm cross section.

In Figure 15B, on the section of X₁ = 50 mm, k_t changed with X₂ in an M shape and reached the minimum at X₂ = 0.9 mm. At this point, D_p had effects on k_t in the entire X₂ interval, and k_t gradually decreased with the decrease of D_p. The influence laws of D_p on k_t were different in the intervals of X₂ ≤ 0.9 mm and X₂ ≥ 0.9 mm. In the interval of X₂ ≤ 0.9 mm, the distribution curves of k_t were nearly consistent with various D_p, indicating that D_p had no obvious effect on k_t. However, in the interval of X₂ ≥ 0.9 mm, k_t gradually reduced with the decrease of D_p. When D_p was 0.01 mm, the distribution curve of k_t was symmetrical along with X₂ = 0.9 mm, and the curves are asymmetrical with a D_p of 0.04, 0.08, and 0.12 mm.

To illustrate the cause of the asymmetry in Figure 15, the distributions of sediment particles in fractures were given, as shown in Figure 16. The size of the sediment particle was doubled, and the concentration was diluted by one-tenth in order to clearly show the distribution of particles in the fracture. It can be observed that the sediment particles of 0.01 mm had no contact with the upper and lower walls of the fracture and were distributed symmetrically along X₂ = 0.9 mm. The sediment particles of 0.04, 0.08, and 0.12 mm were gradually shifted downward under the action of gravity, and some of them settled on the bottom wall. This is because the sediment particles with smaller sizes have better flowability and are not easy to settle under the action of gravity, while the sediment particles with larger sizes have larger Stokes numbers and are easily affected by gravity. According to the aforementioned analysis, the sediment particles of 0.01 mm were symmetrically distributed along with X₂ = 0.9 mm, and the turbulent kinetic energy of the fluid subjected to them was also symmetrically distributed along X₂ = 0.9 mm. The sediment particles of 0.04, 0.08, and 0.12 mm were asymmetrical along with X₂ = 0.9 mm and so was the turbulent kinetic energy.

FIGURE 16

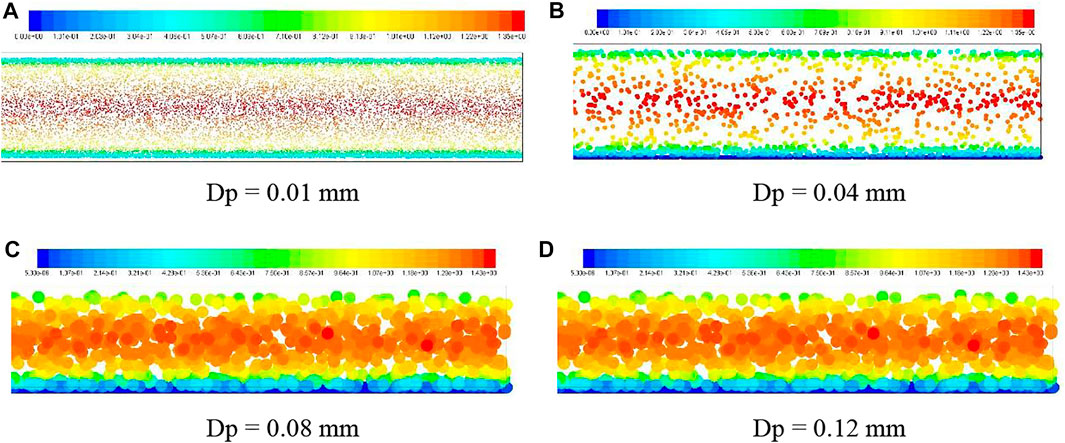
FIGURE 16. Distributions of sediment particles at the outlet of the fracture. (A) Dp = 0.01 mm, (B) Dp = 0.04 mm, (C) Dp = 0.08 mm, (D) Dp = 0.12 mm.

In Figure 17, the turbulent kinetic energy distribution of the continuous-phase fluid on the cross section of the fracture was greatly affected by sediment particle size, which was manifested as the deviation of the extreme points. On the section of X₁ = 50 mm, k_t was relatively large in the interval of X₂ ≤ 2 mm, while it was smaller in the interval of X₂ ≥ 2 mm. On the section of X₁ = 50.5 mm, k_t was relatively small when X₂ ≤ 0.8 mm, and it was larger when X₂ ≥ 0.8. The distribution of the fluid turbulent kinetic energy was disordered on the aforementioned two cross sections, indicating that the fluid pulsation was severe in the rough fracture and the turbulence intensity was high. Through the comparison of Figure 15 and Figure 17, it is found that the impacts of the sediment particle size on the fluid turbulent kinetic energy are completely different in smooth and rough fractures, and the difference is nearly an order of magnitude.

FIGURE 17

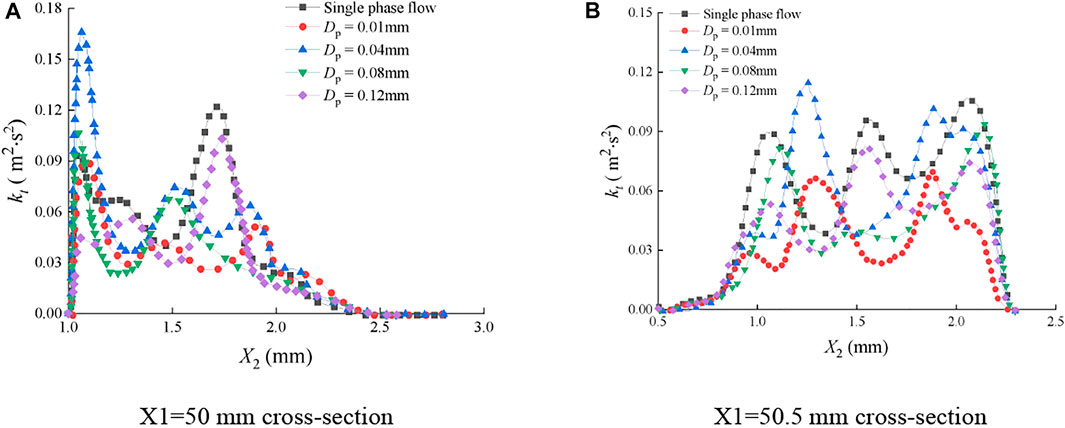
FIGURE 17. Distribution of turbulent kinetic energy of the continuous-phase fluid on cross sections of the rough fracture. (A) X1=50 mm cross section; (B) X1=50.5 mm cross section.

Figure 18 and Figure 19 show the distribution of turbulent kinetic energy of the continuous-phase fluid on typical cross sections of the smooth fracture and rough fracture under various sediment mass densities.

FIGURE 18

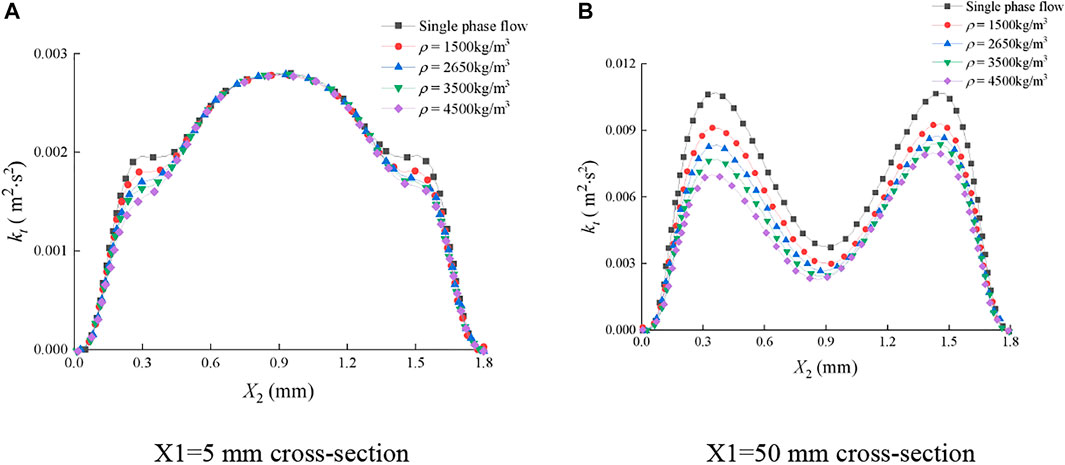
FIGURE 18. Distribution of turbulent kinetic energy of the continuous-phase fluid on cross sections of the smooth fracture. (A) X1=5 mm cross section, (B) X1=50 mm cross section.

FIGURE 19

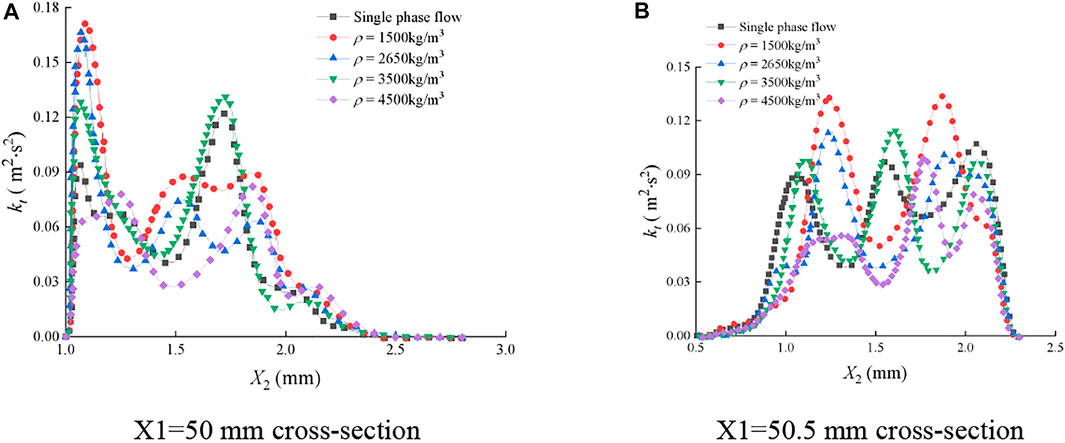
FIGURE 19. Distribution of turbulent kinetic energy of the continuous-phase fluid on cross sections of the rough fracture. (A) X1=50 mm cross section; (B) X1=50.5 mm cross section.

In Figure 18A, on the section of X₁ = 5 mm of the smooth fracture, k_t first increased and then decreased and reached the maximum when X₂ = 0.9 mm. Obviously, the effects of the sediment volume concentration on k_t were very significant in the intervals of 0.15 mm ≤ X₂ ≤ 0.45 and 1.35 mm ≤ X₂ ≤ 1.65 mm, where k_t decreased with the increase of ρ_p. It was indicated that the movement of sediment particles can inhibit the turbulent kinetic energy with the increase of ρ_p. During the single-phase flow, when ρ_p was 1,500 kg/m³, k_t was distributed symmetrically along X₂ = 0.9 mm. When the values of ρ_p were 2650 kg/m³, 3500 kg/m³, and 4,500 kg/m³, k_t in the interval of 0.15 mm ≤ X₂ ≤ 0.45 mm was smaller than that in the interval of 1.35 mm ≤ X₂ ≤ 1.65 mm, indicating that the sediment particle in the interval of 0.15 mm ≤ X₂ ≤ 0.45 mm had a greater impact on the turbulent kinetic energy. This is because the sediment particles are more affected by gravity as the mass density increases, and they are easily deposited on the lower wall. In the intervals except for 0.15 mm ≤ X₂ ≤ 0.45 and 1.35 mm ≤ X₂ ≤ 1.65 mm, the distribution curves of k_t were basically consistent and were symmetrical along X₂ = 0.9 mm. It indicated that k_t was slightly affected by the sediment particle mass density in these intervals. In Figure 18B, on the section of X₁ = 50 mm, k_t- X₂ curves were M-shaped, and ρ_p affected k_t in the whole X₂ interval. The larger the ρ_p, the smaller the k_t. In the single-phase flow, when ρ_p was 1,500 kg/m³, k_t was symmetrically distributed along X₂ = 0.9 mm. When the values of ρ_p were 2650 kg/m³, 3500 kg/m³, and 4,500 kg/m³, k_t under X₂ ≤ 0.9 mm was smaller than that under X₂ ≥ 0.9 mm. It indicates that the sediment particles with the aforementioned mass densities have a greater influence on the turbulent kinetic energy in the interval of X₂ ≤ 0.9 mm. This is because the sediment particles are more affected by gravity and easily deposited on the lower wall, as the mass density of sediment particles increases.

In Figure 19, the distribution of k_t was greatly affected by ρ_p during the water-sediment flow in the rough fracture. The extreme points were shifted. On the section of X₁ = 50 mm, k_t was larger in the interval of X₂ ≤ 2 mm than that in the interval of X₂ ≥ 2 mm. On the section of X₁ = 50.5 mm, k_t was smaller when X₂ ≤ 0.8 mm. It can be observed that the distribution of k_t was disordered on both the cross sections, suggesting that the fluid pulsation was violent in the rough fracture and the turbulence intensity was high.

In summary, under the conditions of the same sediment mass density, same sediment size, same sediment volume concentration, and same inlet velocity, the influence of sediment mass density on fluid turbulent kinetic energy exhibits completely different laws in smooth and rough fractures, with the difference of nearly an order of magnitude.

4 Conclusion

In this study, ANSYS Fluent software was used to perform numerical simulations on the water-sediment two-phase flow in smooth and rough fractures. Then, the influences of the sediment volume concentration, sediment particle size, and sediment mass density on pressure gradient, mean velocity distribution, and turbulent kinetic energy distribution were analyzed. The following conclusions were obtained:

(1) During the water-sediment flow in the smooth fracture, the absolute values of pressure gradient G_p, the sediment volume concentration Ф, the sediment particle size D_p, and the sediment mass density ρ_p are approximately linear, and the linearity of G_p and D_p is the lowest. In other words, G_p decreases with the increase of Ф, D_p, and ρ_p. During the water-sediment flow in the rough fracture, the pressure loss of sediment particles is reduced. When Ф is 1.02%, G_p is the smallest. When Ф ≥ 2.07%, G_p changes slightly. When D_p is small, the pressure loss increases with the increase of D_p. When D_p is relatively large, the pressure loss decreases with the increase of D_p, and G_p first increased and then decreased with the increase of ρ_p.

(2) During the water-sediment flow in the smooth fracture, the mean velocity v of the continuous-phase fluid rarely changes with Ф, D_p, and ρ_p. However, during the water-sediment flow in the rough fracture, v is greatly affected by Ф, D_p, and ρ_p, which can be observed through the changes of curve shapes and deviations of extreme points.

(3) During the water-sediment flow in the smooth fracture, the fluid turbulent kinetic energy k_t decreases with the increase of ρ_p and Ф and decreases with the decrease of ρ_p. During the water-sediment flow in the rough fracture, k_t is significantly affected by Ф, D_p, and ρ_p, which was manifested in the changes of curve shapes and the deviation of the extreme points. This is obtained based on the distribution of sediment particle sizes and Stokes number.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.

Author Contributions

XS: conceptualization, methodology, funding acquisition, writing—original draft, and writing—review and editing; ML: methodology; YH: writing—original draft, and writing–review and editing; QC: writing—review and editing; ZC: writing—original draft and writing—review and editing; YC: writing—original draft and writing—review and editing; DM: conceptualization, supervision, funding acquisition, writing—original draft, and review and editing.

Funding

This research was funded by the National Natural Science Foundation of China for Young (52104153), the National Natural Science Foundation of China (41977238), and the National Science Fund for Excellent Young Scholars of China (52122404).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to acknowledge the editor and reviewers for their valuable comments for the improvement of this article.

References

1. Zhang D, Fan G, Wang X. Characteristics and Stability of Slope Movement Response to Underground Mining of Shallow Coal Seams Away from Gullies. Int J Mining Sci Technol (2012) 22:47–50. doi:10.1016/j.ijmst.2011.06.005

CrossRef Full Text | Google Scholar

2. Fan G, Zhang D, Zhang S, Zhang C. Assessment and Prevention of Water and Sand Inrush Associated with Coal Mining under a Water-Filled Buried Gully: A Case Study. Mine Water Environ (2018) 37:565–76. doi:10.1007/s10230-017-0487-8

CrossRef Full Text | Google Scholar

3. Ma D, Zhang J, Duan H, Huang Y, Li M, Sun Q, et al. Reutilization of Gangue Wastes in Underground Backfilling Mining: Overburden Aquifer protection. Chemosphere (2021) 264:128400. doi:10.1016/j.chemosphere.2020.128400

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Xue Y, Liu J, Liang X, Wang S, Ma Z. Ecological Risk Assessment of Soil and Water Loss by thermal Enhanced Methane Recovery: Numerical Study Using Two-phase Flow Simulation. J Clean Prod (2022) 334:130183. doi:10.1016/j.jclepro.2021.130183

CrossRef Full Text | Google Scholar

5. Wu Q, Zhou W. Prediction of Groundwater Inrush into Coal Mines from Aquifers Underlying the Coal Seams in China: Vulnerability index Method and its Construction. Environ Geol (2008) 56:245–54. doi:10.1007/s00254-007-1160-5

CrossRef Full Text | Google Scholar

6. Elbaz K, Shen JS, Arulrajah A, Horpibulsuk S. Geohazards Induced by Anthropic Activities of Geoconstruction: a Review of Recent Failure Cases. Arab J Geosci (2016) 9:708. doi:10.1007/s12517-016-2740-z

CrossRef Full Text | Google Scholar

7. Peng K, Zhou J, Zou Q, Zhang J, Wu F. Effects of Stress Lower Limit during Cyclic Loading and Unloading on Deformation Characteristics of Sandstones. Construction Building Mater (2019) 217:202–15. doi:10.1016/j.conbuildmat.2019.04.183

CrossRef Full Text | Google Scholar

8. Wang XF, Zhang DS, Zhang CG, Fan GW. Mechanism of Mining-Induced Slope Movement for Gullies Overlaying Shallow Coal Seams. J Mt Sci (2013) 10:388–97. doi:10.1007/s11629-013-2455-5

CrossRef Full Text | Google Scholar

9. Ma D, Duan H, Zhang J, Liu X, Li Z. Numerical Simulation of Water-Silt Inrush Hazard of Fault Rock: A Three-Phase Flow Model. Rock Mech Rock Eng (2022), in press.

Google Scholar

10. Qiao S, Zhong W, Wang S, Sun L, Tan S. Numerical Simulation of Single and Two-phase Flow across 90° Vertical Elbows. Chem Eng Sci (2021) 230:116185. doi:10.1016/j.ces.2020.116185

CrossRef Full Text | Google Scholar

11. Han L, Wang Y, Liu K, Ban Z, Liu H. Theoretical Modeling for Leakage Characteristics of Two-phase Flow in the Cryogenic Labyrinth Seal. Int J Heat Mass Transfer (2020) 159:120151. doi:10.1016/j.ijheatmasstransfer.2020.120151

CrossRef Full Text | Google Scholar

12. Ma D, Duan H, Zhang J. Solid Grain Migration on Hydraulic Properties of Fault Rocks in Underground Mining Tunnel: Radial Seepage Experiments and Verification of Permeability Prediction. Tunn Undergr Sp Tech (2022), in press.

CrossRef Full Text | Google Scholar

13. Liu Y, Li S. Influence of Particle Size on Non-darcy Seepage of Water and Sediment in Fractured Rock. Springerplus (2016) 5:2099. doi:10.1186/s40064-016-3778-9

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Ma D, Wang J, Cai X, Ma X, Zhang J, Zhou Z, et al. Effects of Height/diameter Ratio on Failure and Damage Properties of Granite under Coupled Bending and Splitting Deformation. Eng Fracture Mech (2019) 220:106640. doi:10.1016/j.engfracmech.2019.106640

CrossRef Full Text | Google Scholar

15. Xiao T, Huang M, Gao M. Triaxial Permeability Experimental Study on Deformation and Failure Processes of Single-Fractured Rock Specimens. Shock and Vibration (2020) 2020:1–12. doi:10.1155/2020/7329825

CrossRef Full Text | Google Scholar

16. Ye F, Duan JC, Fu WX, Yuan XY. Permeability Properties of Jointed Rock with Periodic Partially Filled Fractures. Geofluids (2019) 2019:1–14. doi:10.1155/2019/4039024

CrossRef Full Text | Google Scholar

17. Guo B, Wang C, Wang L, Chen Y, Cheng T. A Modified Cubic Law for Rough-Walled Marble Fracture by Embedding Peak Density. Adv Civil Eng (2020) 2020:1–10. doi:10.1155/2020/9198356

CrossRef Full Text | Google Scholar

18. Zhang B, He Q, Lin Z, Li Z. Experimental Study on the Flow Behaviour of Water-Sand Mixtures in Fractured Rock Specimens. Int J Mining Sci Technol (2021) 31:377–85. doi:10.1016/j.ijmst.2020.09.001

CrossRef Full Text | Google Scholar

19. Xu J, Pu H, Chen J, Sha Z. Experimental Study on Sand Inrush Hazard of Water-Sand Two-phase Flow in Broken Rock Mass. Geofluids (2021) 2021:1–9. doi:10.1155/2021/5542440

CrossRef Full Text | Google Scholar

20. Zhou Z, Zhang J, Cai X, Wang S, Du X, Zang H. Permeability Experiment of Fractured Rock with Rough Surfaces under Different Stress Conditions. Geofluids (2020) 2020:1–15. doi:10.1155/2020/9030484

CrossRef Full Text | Google Scholar

21. Liu Q, Liu B. Experiment Study of the Failure Mechanism and Evolution Characteristics of Water-Sand Inrush Geo-Hazards. Appl Sci (2020) 10:3374. doi:10.3390/app10103374

CrossRef Full Text | Google Scholar

22. Yin Q, Ma G, Jing H, Wang H, Su H, Wang Y, et al. Hydraulic Properties of 3D Rough-Walled Fractures during Shearing: An Experimental Study. J Hydrol (2017) 555:169–84. doi:10.1016/j.jhydrol.2017.10.019

CrossRef Full Text | Google Scholar

23. Wang J, Ma D, Li Z, Huang Y, Du F. Experimental Investigation of Damage Evolution and Failure Criterion on Hollow Cylindrical Rock Samples with Different Bore Diameters. Eng Fracture Mech (2022) 260:108182. doi:10.1016/j.engfracmech.2021.108182

CrossRef Full Text | Google Scholar

24. Zhong Z, Wang L, Song L, Gao C, Hu Y, Gao H, et al. Size Effect on the Hydraulic Behavior of Fluid Flow through a Single Rough-Walled Fracture. Soil Dyn Earthquake Eng (2021) 143:106615. doi:10.1016/j.soildyn.2021.106615

CrossRef Full Text | Google Scholar

25. Ma D, Duan H, Li X, Li Z, Zhou Z, Li T. Effects of Seepage-Induced Erosion on Nonlinear Hydraulic Properties of Broken Red Sandstones. Tunnelling Underground Space Technol (2019) 91:102993. doi:10.1016/j.tust.2019.102993

CrossRef Full Text | Google Scholar

26. Ma D, Duan H, Liu W, Ma X, Tao M. Water-Sediment Two-phase Flow Inrush Hazard in Rock Fractures of Overburden Strata during Coal Mining. Mine Water Environ (2020) 39:308–19. doi:10.1007/s10230-020-00687-6

CrossRef Full Text | Google Scholar

27. Liu J, Xue Y, Zhang Q, Wang H, Wang S. Coupled Thermo-Hydro-Mechanical Modelling for Geothermal Doublet System with 3D Fractal Fracture. Appl Therm Eng (2022) 200:117716. doi:10.1016/j.applthermaleng.2021.117716

CrossRef Full Text | Google Scholar

28. Yang Z, Li D, Xue S, Hu R, Chen Y-F. Effect of Aperture Field Anisotropy on Two-phase Flow in Rough Fractures. Adv Water Resour (2019) 132:103390. doi:10.1016/j.advwatres.2019.103390

CrossRef Full Text | Google Scholar

29. Yang X, Liu YJ, Xue M, Yang TH, Yang B. Experimental Investigation of Water-Sand Mixed Fluid Initiation and Migration in Porous Skeleton during Water and Sand Inrush. Geofluids (2020) 2020:1–18. doi:10.1155/2020/8679861

CrossRef Full Text | Google Scholar

30. Yang W, Jin L, Zhang X. Simulation Test on Mixed Water and Sand Inrush Disaster Induced by Mining under the Thin Bedrock. J Loss Prev Process Industries (2019) 57:1–6. doi:10.1016/j.jlp.2018.11.007

CrossRef Full Text | Google Scholar

31. Yu Y, Xin Q, Cheng W, Rui J, Zhang X. Numerical Simulation Study on the Seepage Characteristics of Coal Seam Infusion Effected by Mining-Induced Stress. Bull Eng Geol Environ (2021) 80:9015–28. doi:10.1007/s10064-021-02483-0

CrossRef Full Text | Google Scholar

32. Ma D, Kong S, Li Z, Zhang Q, Wang Z, Zhou Z. Effect of Wetting-Drying Cycle on Hydraulic and Mechanical Properties of Cemented Paste Backfill of the Recycled Solid Wastes. Chemosphere (2021) 282:131163. doi:10.1016/j.chemosphere.2021.131163

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Khan MIH, Wellard RM, Nagy SA, Joardder MUH, Karim MA. Experimental Investigation of Bound and Free Water Transport Process during Drying of Hygroscopic Food Material. Int J Therm Sci (2017) 117:266–73. doi:10.1016/j.ijthermalsci.2017.04.006

CrossRef Full Text | Google Scholar

34. Si G, Belle B. Performance Analysis of Vertical Goaf Gas Drainage Holes Using Gas Indicators in Australian Coal Mines. Int J Coal Geology (2019) 216:103301. doi:10.1016/j.coal.2019.103301

CrossRef Full Text | Google Scholar

35. Chen J, Zhu C, Du J, Pu Y, Pan P, Bai J, et al. A Quantitative Pre-warning for Coal Burst hazard in a Deep Coal Mine Based on the Spatio-Temporal Forecast of Microseismic Events. Process Saf Environ Prot (2022) 159:1105. doi:10.1016/j.psep.2022.01.082

CrossRef Full Text | Google Scholar

36. Si G, Cai W, Wang S, Li X. Prediction of Relatively High-Energy Seismic Events Using Spatial-Temporal Parametrisation of Mining-Induced Seismicity. Rock Mech Rock Eng (2020) 53:5111–32. doi:10.1007/s00603-020-02210-3

CrossRef Full Text | Google Scholar

37. Cao W, Shi J-Q, Durucan S, Si G, Korre A. Gas-driven Rapid Fracture Propagation under Unloading Conditions in Coal and Gas Outbursts. Int J Rock Mech Mining Sci (2020) 130:104325. doi:10.1016/j.ijrmms.2020.104325

CrossRef Full Text | Google Scholar

38. Si G, Durucan S, Shi JQ, Korre A, Cao W. Parametric Analysis of Slotting Operation Induced Failure Zones to Stimulate Low Permeability Coal Seams. Rock Mech Rock Eng (2019) 52(1):163–82. doi:10.1007/s00603-018-1579-x

CrossRef Full Text | Google Scholar

39. Li Q, Ma D, Zhang Y, Liu Y, Ma Y. Insights into Controlling Factors of Pore Structure and Hydraulic Properties of Broken Rock Mass in a Geothermal Reservoir. Lithosphere (2022) 2021(5):3887832. doi:10.2113/2022/3887832

CrossRef Full Text | Google Scholar