God (≡ Elohim), The First Small World Network

In this article, the approach of network mapping of words in literary texts is extended to “textual factors”: the network nodes are defined as “concepts”; the links are “community connexions.” Thereafter, the text network properties are investigated along modern statistical physics approaches of networks, thereby relating network topology and algebraic properties to literary text contents. As a practical illustration, the first chapter of Genesis in the Bible is mapped into a 10-node network, as in the Kabbalah approach, mentioning God (≡ Elohim). The characteristics of the network are studied starting from its adjacency matrix and the corresponding Laplacian matrix. Triplets of nodes are particularly examined in order to emphasize the “textual (community) connexions” of each agent “emanation,” through the so-called clustering coefficients and the overlap index, hence measuring the “semantic flow” between the different nodes. It is concluded that this graph is a small world network and weakly dis-assortative, because its average local clustering coefficient is significantly higher than a random graph constructed on the same vertex set.

1 Introduction

“Good lord, it is a small world, isn't it?” [1]

An answer is intended here below:

“Yes, it is: the Good Lord is a small world network.”

… It is even the first one [2].

In modern statistical physics [3], networks [4], underlying opinion formation of agents located at nodes [5], with links defined from data pertaining to social aspects [6], have gathered much interest. Many cases can be found in the literature [7]. Among particularly interesting topics, one encounters the case of finite-size networks in which agents have small connectivity values; such cases are known to be “sociologically more realistic” [1, 8].

On the other hand, texts carry messages; they have been statistically studied since Shannon’s introduction of the information entropy definition [9]. More recently, it has been discussed that texts can be transformed into trees [10, 11] or better into networks in order to study their structure besides finding word and idea correlations [12].

Thereafter, one may point to interesting quantitative considerations about network-related analyses of the characteristics of literary texts; for example, see other studies [13] about the morphological complexity of a language, [14] about word length frequencies, or about sequences in Ukrainian texts [15–17], and still more recently, enjoyable text analyses of fables in Slovenia [18, 19]. There are many other articles reporting studies of word and sequence frequencies, or different language connections as on networks. However, to quote all such articles would lead to a useless digression, but a recent review [18] and other articles [20–28]should be noted. In brief, the present study pertains to applications of statistical physics measures and models like those studied in language evolution and linguistics [20–28].

In all cases, relevant scientific questions pertain to the dynamics of collective properties, not only of agents on the network but also by the network structure itself [29]. An interesting structure is the “small world network” (SWN), introduced by Watts and Strogatz [30]. In an SWN, the neighbors of any given node are both likely to be neighbors of each other and also reachable from every other node by a small number of linking “steps” [31, 32]. In this paper, we discuss a 10-node network, as obtained from the first chapter of Genesis [33], the so-called “Tree of Life,” through the kabbalistic (yosher) tradition [34].

Notice that due to its size, this Genesis network might be also expected to become as useful as the karate club data (which has 44 nodes) [35] or the acquaintance network of Mormons (which has 43 nodes) [36], both previously known in the literature for paradigmatic studies of SWNs. ¹

One might wonder why as “serious scientists,” interested in social networks for describing communications between agents, we should care about the structure of such an a priori “mystic network.” Such a network is based on the information flow between concepts—not between words—as it should be emphasized. The matter seems not to have been studied from a statistical physics point of view. Nevertheless, other studies have adopted [37] a thermodynamic approach. Thus, we hope to connect the network analysis methodology with that followed in kabbalistic studies—which is very much tied to numerology. Moreover, the present work aims to contribute to introducing a quantitative approach to the analysis of the interaction between “agents”—herein being called sephiroth [38–40] in small networks.

Thus, in this article, the previous approaches on text structure studies through word correlations are extended to “textual factors.” Indeed, the network nodes are defined as “concepts” and the links are “community connexions.” The characteristics of the network are studied starting from its adjacency matrix—its eigenvalues, hence providing a measure of the “semantic flows” between the different nodes. The network Laplacian matrix is also studied along the same lines. Together with Kirchhoff’s theorem and Cheeger’s inequality, the “spectrum gap” (between the two smallest eigenvalues) can be used to calculate the number of spanning trees for a given graph [41]. Indeed, the sparsest cut of a graph can be approximated through the second smallest eigenvalue of its Laplacian matrix by Cheeger’s inequality. Furthermore, the spectral decomposition of the Laplacian matrix allows constructing low dimensional embeddings that appear in many machine learning applications and determines a spectral layout in graph drawing, as claimed in https://en.wikipedia.org/wiki/Laplacian_matrix (accessed on March 26, 2022).

In doing so, one adds a quantitative set of values for an answer to a question raised in a previous study [42] on the classes of SWN examined in the literature [43].

Besides, the present numerical approach might be in line with modern studies in Kabbalah research about numbering [44, 45] and quantitative studies on religious adhesion or religiosity aspects [46–53], as recently used in sociophysics for examining growth processes, opinion formation, and other related topics. This article is in line with such a frontier in physics approaches.

After introducing the dataset and its origin in Section 2, it seems rather appropriate to provide the whole adjacency matrix (10 × 10). Its construction follows other studies on large-scale networks, like co-authorship networks [43, 54]. The present network’s structural aspects are first outlined, before searching for subsequent numerical and statistical aspects, through a few usual network characteristics in Section 3. A similar study is performed for the network Laplacian matrix.

Nevertheless, let it be pointed out here that triplets of nodes are particularly examined in order to emphasize the agent (“emanation”) community connexions through the so-called clustering coefficient [30] and the overlap index [55], in Section 4 and Section 5, respectively. The results prove the SWN nature of 10 sephiroth networks. For completeness, some other network characteristics, like the assortativity coefficient [56], are calculated and reported. A kabbalistic “generalized point of view” is provided.

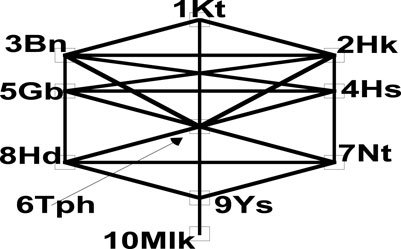
2 The Dataset

Let us consider, as the demonstration of the approach, a text in which concepts are somewhat hidden—in the present case, within some mystical concept but without any loss of generality from a theoretical point of view. The data, downloaded from a previous study [34], emerges from the kabbalistic interpretation of the occurrence of “spiritual principles” at the Universe’s creation. In brief, the Kabbalah ² [38–40] seems to infer, from the first chapter of Genesis, that “The Infinite” (God) has “emanations” which form a network of 10 nodes, like in Figure 1; the “node names” are given for further reference in Table 1. The network so symmetrically displayed is made of three “columns” (alternative configurations are given by different schools in the historical development of Kabbalah, with each articulating different spiritual aspects; to distinguish the variants is not very relevant for the present investigation. ³ The enumeration of the 10 nodes, as in Figure 1, is stated in the Sefer Yetzirah [38–40].) Notice that the Tree of Life nodes are arranged onto seven planes; seven being a mystic (or sacred) number.

FIGURE 1

FIGURE 1. The network of 10 sephiroths; notations of node labels are found in the main text.

TABLE 1

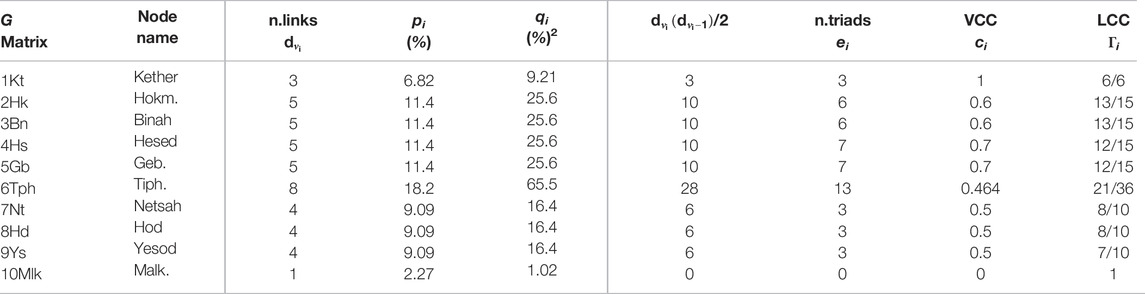
TABLE 1. Characteristics of the network matrix G, with hereby defined node (i) notations (Hokm. = Hokmah; Geb. = Gebourah; Tiph. = Tiphereth; and Malk. = Malkouth) in the first and second columns, and their corresponding number of links $(d_{{\nu }_i})$. The values of usual structural information for networks are given: the probability p_i that a vertex ν_i has a degree $d_{{\nu }_i}$; q_i is fully defined in Eq. 8 in terms of p_i and the i vertex degree $d_{{\nu }_i}$; the possible maximum number of different wedges, $(d_{{\nu }_i}(d_{{\nu }_i}-1)/2)$; the number of triads (e_i) associated to a given node (i) in G; VCC, the corresponding clustering coefficient (c_i) of a vertex i, from which one deduces the global clustering coefficient (GCC) of the network, and Γ_i, the local clustering coefficient (LCC) of a vertex i, from which one deduces the average local clustering coefficient for the network, see Section 4.2.

Between the 10 sephiroths, run 22 channels or paths [59]. These links are interpreted as the specific connections of (“spiritual”) information flow. In the present case, the flow of information goes according to the node number hierarchy; such a type of directed flow consideration has been recently studied [60] in a different context.

In doing so, an adjacency matrix G = (g_ij) ∈ R^N×N can be built, with g_ij = 1 for an existing link between two connected nodes, ν_i and ν_j, selected among the N = 10 nodes here, and g_ij = 0 otherwise, i.e.,

$g_{ij}=\left\{\begin{array}{c}1\text{\hspace{0.17em}\hspace{0.17em}if}{\nu }_i\mathrm{a}\mathrm{n}\mathrm{d}{\nu }_j\text{\hspace{0.17em}are\hspace{0.17em}connected\hspace{0.17em}nodes\hspace{0.17em}}\hfill \\ 0\text{\hspace{0.17em}\hspace{0.17em}otherwise.\hspace{0.17em}\hspace{0.17em}}\hfill \end{array}\right.(1)$

Thus, all diagonal terms are 0; the matrix is symmetrical; it has 44 finite elements, i.e., 2 L, the number of links. In this study, the links are neither directional nor weighted; the nodes also have no “strength.”

For further reference, let us introduce here an alternative to the adjacency matrix, i.e., the so-called Laplacian matrix of the network: Λ = (λ_ij) ∈ R^10×10, with

${\lambda }_{ij}=\left\{\begin{array}{c}-1\text{\hspace{0.17em}\hspace{0.17em}if}{\nu }_i\mathrm{a}\mathrm{n}\mathrm{d}{\nu }_j\text{\hspace{0.17em}are\hspace{0.17em}connected\hspace{0.17em}nodes\hspace{0.17em}}\hfill \\ d_{{\nu }_i}\text{\hspace{0.17em}\hspace{0.17em}if}{\nu }_i\equiv {\nu }_j\hfill \\ 0\text{\hspace{0.17em}\hspace{0.17em}otherwise,\hspace{0.17em}\hspace{0.17em}}\hfill \end{array}\right.(2)$

where $d_{{\nu }_i}$ is the degree of the node ν_i, i.e., the number of links at the node. In brief, the Laplacian matrix Λ is the difference between a diagonal matrix Δ reporting the degree of the node and the adjacency matrix of the graph. For completeness, let us mention the finite elements of Δ = (d_ij) ∈ R^N×N through the degree list defined as $D=(d_{{\nu }_1},d_{{\nu }_2},\dots ,d_{{\nu }_N})$, which reads here as D = (3, 5, 5, 5, 5, 8, 4, 4, 4, 1).

Thus, the adjacency matrix reads

$G=\left(\begin{array}{cccccccccc}\hfill -\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill -\hfill & \hfill -\hfill & \hfill 1\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill \\ \hfill 1\hfill & \hfill -\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill -\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill \\ \hfill -\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill -\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill \\ \hfill -\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill -\hfill & \hfill 1\hfill & \hfill -\hfill & \hfill 1\hfill & \hfill -\hfill & \hfill -\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill -\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill -\hfill \\ \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill 1\hfill & \hfill -\hfill & \hfill 1\hfill & \hfill -\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill -\hfill \\ \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill -\hfill & \hfill 1\hfill & \hfill -\hfill \\ \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill -\hfill & \hfill 1\hfill \\ \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill 1\hfill & \hfill -\hfill \end{array}\right)(3)$

in which each 0 is replaced by a “-” for better readability. The Λ matrix is written and analyzed below.

Most people know that when there is a matrix, one looks for eigenvalues and eigenvectors: the (necessarily real) eigenvalues are found to be equal to:

5.02314, 2.21045, 0.61803, 0.13191, 0.00000, −1.00000, −1.36550, −1.61803, −2.00000, and −2.00000.

They are distributed in (quasi logarithmically) decreasing order: y = 4.503–6.865 log(x), with R² = 0.977.

Thereafter, one can look for the 10 eigenvectors; however, they are not shown to save space—their writing being irrelevant within the present aim. Nevertheless, the aforementioned data suggest that principal component analysis can be a complementary valuable investigation for “community detection.”

The network Laplacian matrix reads

$\mathrm{\Lambda }=\left(\begin{array}{cccccccccc}\hfill 3\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -1\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill \\ \hfill -1\hfill & \hfill 5\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill \\ \hfill -1\hfill & \hfill -1\hfill & \hfill 5\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill \\ \hfill -\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill 5\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill \\ \hfill -\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill 5\hfill & \hfill -1\hfill & \hfill -\hfill & \hfill -1\hfill & \hfill -\hfill & \hfill -\hfill \\ \hfill -1\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill 8\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill -\hfill \\ \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -1\hfill & \hfill -\hfill & \hfill -1\hfill & \hfill 4\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill -\hfill \\ \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill 4\hfill & \hfill -1\hfill & \hfill -\hfill \\ \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill 4\hfill & \hfill -1\hfill \\ \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -\hfill & \hfill -1\hfill & \hfill 1\hfill \end{array}\right)(7)$

Its eigenvalues are: 9.01939, 6.61803, 6.48072, 6.00000, 5.13659, 4.38197, 3.48940, 2.13004,0.74387, 0.00000.

They are distributed according to: y≃9.478–0.923 x; with R²= 0.971

Together with Kirchhoff's theorem, the Laplacian matrix eigenvalue spectrum can be used to calculate the number of spanning trees for a given graph, η. The sparsest cut of a graph can be approximated through the second smallest eigenvalue of its Laplacian, i.e. λ₂ = 0.74387, here, by Cheeger’s inequality. Since the Laplacian matrix spectral gap is also obviously equal to 0.74387, one finds

$\frac{{\lambda }_2}{2}\le \eta \sqrt{{\lambda }_2\left(2d_{{\nu }_j}^{\left(M\right)}-{\lambda }_2\right)}(8)$

where $d_{{\nu }_j}^{(M)}(=8)$ is the largest node degree. Thus, 0.372 ≤ η ≤ 3.369.

3 Data Statistical Analysis

Next, one proceeds with performing some classical structural analysis as usual on such networks, i.e., an analysis of indicative coefficients: one obtains the network node in- and out-degree distributions, the network assortativity, the (global and local) clustering coefficients, and the average overlap index.

In the present case, the matrix, or network, is symmetrical, hence the number of links exiting from node ν_j, i.e., the out-degree, is equal to the in-degree number. The largest degree (=8) is for node 6; the smallest (=1) is for node 10; the average degree, counting both out-degrees and in-degrees is easily found to be 4.4.

In Table 1, one also gives for each node, the degree, i.e., the number of links $(d_{{\nu }_i})$ exiting from or entering into each node (i). Table 1 also reports the possible maximum number of different wedges, $(d_{{\nu }_i}(d_{{\nu }_i}-1)/2)$, and triads, (e_i), associated to a given node (i) in G.

In addition, we report the number (N_i,j) of different paths going through the nearest neighbor k of two nearest neighbors i and j in Table 2. This number is equivalent to the number of triangles sharing the link (i, j).

TABLE 2

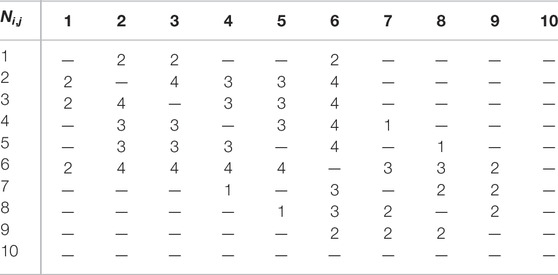
TABLE 2. The (N_i,j) number of different (undirected information flow) paths between two nearest neighbors i and j, through a nearest neighbor k.

4 Clustering

The tendency of the network nodes to form local interconnected groups is a convincing argument for describing social networks according to statistical physics modern formalism. Such a behavior is usually quantified by a measure referred to as the clustering coefficient [30]. The amount of studies on this characteristic of networks has led to the particularization of the term in order to focus on different complex features of networks. Here, one considers the global clustering coefficient and the local clustering coefficient, together with the overlapping index, and the assortativity for a text mapped into a network.

Indeed, the most relevant elements of a heterogeneous agent interaction network can be identified by analyzing global and local connectivity properties. In the present case, this can be attempted by analyzing the number of triangles with agent (or “emanation”) nodes belonging to the same “community” or not, depending on the type of connexions. The former number gives some hierarchy information, and the latter some reciprocity measure, i.e., recognition of leadership or proof of some challenging conflict among the emanations.

4.1 Global Clustering Coefficient

The global clustering coefficient (GCC) of the network is defined as $<c_i>$, the average of c_i over all the vertices in the network, $<c_i>=\sum c_i/N$, where N is the number of nodes of the network, and where the clustering coefficient c_i of vertex i is given by the ratio between the number e_i of triangles sharing that specific vertex i, and the maximum number of triangles that the vertex could have. If node i has $d_{{\nu }_i}$ neighbors, then the so-called clique, i.e., a complete graph, in fact, would have $d_{{\nu }_i}(d_{{\nu }_i}-1)/2$ triangles at the most, thus one has,

$c_i=\frac{2}{d_{{\nu }_i}\left(d_{{\nu }_i}-1\right)}{e}_i(4)$

The value of GCC is found to be $<c_i>=0.5564$, from the raw data in Table 1.

4.2 Local Clustering Coefficient

In the literature [43], the term “clustering coefficient” refers to various quantities, relevant to understanding the way in which nodes form communities, under some criterion. By definition, the “local clustering coefficient” (LCC) Γ_i for node i is the number of links between the vertices within the nearest neighborhood of i divided by the maximum number of links that could possibly exist between them. It is relevant to note that the aforementioned GCC is not trivially related to the LCC, e.g., the GCC is not the mean of the LCC. In the former case, the triangles with common edges are emphasized, while in the latter case, only the number of links is relevant. This number of links common to the triangles sharing node i can vary with the number of connected nearest neighbor nodes. Basically, the GCC value quantifies how close the neighbors of i are to being part of a complete graph. By contrast, LCC rather serves to determine whether a network is an SWN [30] or not.

The LCC (Γ_i) values are given in Table 1, under a ratio form in order to emphasize that the numerator of the fraction is the sum of $d_{{\nu }_i}$ plus the number of links making triangles in the nearest neighborhood of i, while the denominator is obviously $d_{{\nu }_i}(d_{{\nu }_i}+1)/2$. It is easily deduced that $<{\mathrm{\Gamma }}_i>=0.8217$.

There is no drastic conclusion to draw from this specific value, since not many corresponding values are reported in the literature allowing a comparison with other networks [61]. Yet, let it be recalled that the lower the Γ_i values, the less “fully connected” the network appears to be. This is not the present case.

However, let it be emphasized that a graph is considered to be small world, if its average local clustering coefficient is significantly higher than a random graph constructed on the same vertex set, i.e., here with N = 10. Thus, one confirms that the present network looks like an SWN rather than either a random network (RN) or a complete graph (CG).

5 Average Overlap Index

Finally, for characterizing members of communities, in another hierarchical way, let us also calculate the average overlap index (AOI) O_ij; its mathematical formulation and its properties are found in a previous study [55] in the case of an unweighted network made of N nodes linked by (ij) edges,

$O_{ij}=\frac{N_{ij}\left(d_{{\nu }_i}+d_{{\nu }_j}\right)}{4\left(N-1\right)\left(N-2\right)},i\ne j(5)$

where N_ij is the measure of the common number of (connected) neighbors to the i and j nodes. In the present case: 4(N − 1)(N − 2) = 288. N.B. in a fully connected network, N_ij = N − 2. Of course, O_ii = 0 by definition.

The average overlap index for node i is defined as:

$⟨O_i⟩=\frac{1}{N-1}\sum _{j=1}^N{O}_{ij}.(6)$

The values are given in Table 3.

TABLE 3

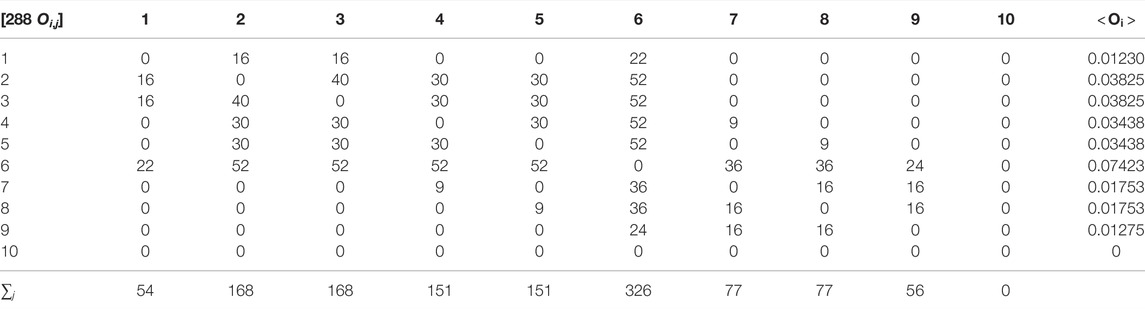
TABLE 3. [288 O_i,j]: the numerator of the overlap index, Eq. 5, of the neighboring ν_i and ν_j nodes; and $<O_i>$, the average overlap index, Eq. 6. N.B. 288 = 4(N − 1)(N − 2), while ∑_i ∑_jO_i,j = 1228.

This measure, $⟨O_i⟩$, can be interpreted indeed as another form of a clustering attachment measure: the higher the number of nearest neighbors, the higher the $⟨O_i⟩$, more so if the i node has a high degree $d_{{\nu }_i}$. Since the summation is made over all possible j sites connected to i (over all sites in a fully connected graph), $⟨O_i⟩$ expresses a measure of the local (node) density near the i site.

Recall also that in magnetic networks, the links are like exchange integrals between spins located at i and j. An average over the exchange integrals provides an estimate of the critical (Curie) temperature at which a spin system undergoes an order–disorder transition, and conversely. Therefore $⟨O_i⟩$ can also be interpreted, in a physics sense, as a measure of the stability of the node versus perturbations due to an external (for example, thermal) cause. In other words, in the present context, a high $⟨O_i⟩$ value reflects the i node’s strong attachment to its community; the main “textual factor” is thereby emphasized. Here, for our illustrative example, the highest value (≃ 0.074) corresponds to the 6th node (“emanation”), Tiphereth, as should have also been visually expected from Figure 1.

The average overlap index of each node, obtained according to Eq. 6, is given in Table 3. The order of magnitude of the $⟨O_i⟩$ values are $\sim 0.05$, much smaller than in other investigated cases [55] [62]. This is due to the low value of N_ij in the present case.

For completeness, observe that ∑_i ∑_iO_i,j = 1228, hence 1288/288 = 4.264, which when divided by N leads to ∼ 0.4264, as another characteristic of the average overlap number of triangles throughout the network.

In order to indicate some aspect of the attachment process in a network, one can calculate its so called ”assortativity” [56]. The term refers to a preference for a network node to be attached to others, depending on one out of many node properties [56]. Assortativity is most often measured after a (Pearson) node degree correlation coefficient r

$r=\frac{{\sum }_{i,j=1}^N{q}_i{q}_j{g}_{ij}-{\left[{\sum }_{i,j=1}^N\left(q_i+q_j\right)g_{ij}\right]}^2/L}{{\sum }_{i,j=1}^N\left(\left(q_i^2+q_j^2\right)g_{ij}\right)-{\left[{\sum }_{i,j=1}^N\left(q_i+q_j\right)g_{ij}\right]}^2/L}(7)$

where

$q_i=\frac{k_i{p}_i}{{\sum }_i{k}_i{p}_i},(8)$

where k_i is the i vertex (total) degree $d_{{\nu }_i}$, in which p_i is the probability that a vertex i has a degree $d_{{\nu }_i}$ (this can be here obtained/read from Fig. 1 or Table 1); L = is the number of connecting channels (=22, here); r = 1 indicates perfect assortativity, r = −1 indicates perfect ”disassortativity”, i.e. a perfectly negative correlation.

For the (text based) network of interest here, we have found, r= -0.229, a quite negative value for the assortativity notion, in most networks. The present finding is somewhat surprising, since according to Newman [56], almost all “non-social networks” [56] seem to be quite dis-assortative, even though the “social networks” usually present significantly assortative mixing. However, the technological and biological network usually are all dis-assortative: the hubs are (primarily) connected to less connected nodes, dixit Newman [56]. The present case is a weakly dis-assortative network.

In order to show a positive value of r, a network must have some specific additional structure that favors assortative mixing, i.e. a division into communities or groups; a contrario, to see significant disassortativity, the highest degree vertices in the network need to have degree on the order of √N, where N is the total number of vertices, so that there is a substantial probability of some vertex pairs sharing two or more edges. Here √22 ≃ 4.69 the highest degree which is for Tiphereth = 8 is (at once visually found from Fig. 1) the “knowledge transfer hub”, ‐ the most important emanation.

One may consider the practical aspects resulting from the node characteristics, next those from links. In relation to a “generalized kabbalistic point of view”, one may make the following comments.

Let us observe two integer numbers appearing through the study: 288⁴ and 1228 Notice that • 228: this number contains profound significance; in Kabbalah, it refers to the number of “sparks” that God had to remove in order to create the world; see https://www.biblegematria.com/288-holy-sparks.html (Accessed March 01, 2022)•1228: the Hebrew name of Simon Peter, Symehon Hacephi, in Hebrew name numeration; ([69], p. 54).

Comments and suggestions on such a “society structure” within formal texts can be thought to arise from similar numerical perspectives.

6 Conclusion

In frontiers science, prior to scientific excitations and paper avalanches, there were modest interconnections between authors and between fields.

This is one of the underlying ideas for the present problem, not at the level of the authors but at the semantic level—justifying the study. Two apparently unrelated research fields are interconnected. One can study texts through network mappings—nothing new. We can recall that the Ukrainian language network used in studied selected fables [15] is a strongly correlated, scale-free, small world network. In the present case, one goes a little bit further: instead of another word correlation study, one examines textual concept distributions. Moreover, picking up a basic text with some mystic ingredient, one covers a wide gap between various disciplines, with physics support.

One has proposed to examine a theoretical question on applied linguistics, with a specific illustration, but in so doing also asks: do the sephiroth, thus nodes and links of a mystic network, mean something from a statistical physics point of view, knowing their “esteem” or “sense” in kabbalistic work? Thus, in fact, the study has some similarity to other “social network” considerations: mutatis mutandis; in the present problem, the agents are the sephiroth, while the links carrying the information flow between emanations.

Practically, the yosher kabbalistic mapping of a selection of concepts from Genesis in the Bible produces a network [34]. In order to characterize the necessarily small network, based on its adjacency matrix, one has calculated a few specialization coefficients. Surely, in future work, one could consider many other quantities of interest for networks [63]; the matter is left to the imagination of concerned researchers.

In particular, assortativity characteristics of the network have been examined in doing so, searching for proof of any preference of a sephiroth attachment to some subnetworks. Examining the whole network, through their communities and the intercommunity links, it is found that the sephiroths are neither perfectly assortative nor perfectly dis-assortative. From the values of the Pearson node degree correlation coefficient r, it is asserted that the network is rather dis-assortative—but weakly correlated in contrast to the previously studied fables [15]. This is in contrast to fictional social networks [64, 65], which are found to be small world, highly clustered, and hierarchical and which typically differ from real ones in connectivity and the levels of assortativity [18].

In order to characterize in greater detail the intercommunity structure complexity—its “information flow,” one can also consider elementary entities made of a few sephiroths. The smallest (geometric) cluster to be examined is the triangle. In this respect, the study of the local clustering coefficients indicates a low value for these intercommunity subnetworks. The average overlap index (AOI) [55] allows for extracting from the clusters those nodes which inside their community and with respect to the others are the centers of more attention. One may claim that one gives some scientific (statistical physics) emphasis to one kabbalistic emanation.

From a fundamental statistical physics point of view, one may emphasize the “added value” of the present investigation. Returning to Amaral et al. [42], who have proposed three classes of SWN: 1) scale-free networks, characterized by a vertex connectivity distribution that decays as a power law; 2) broad-scale networks, characterized by a connectivity distribution that has a power law regime followed by a sharp cutoff; and 3) single-scale networks, characterized by a connectivity distribution with a fast decaying tail. The analyses presented in the main text suggest that the network belongs to the third category. It should be of course of interest to find out if this conclusion holds for other “textual factors” in other literary texts.

Finally, let it be recalled that some time ago, “God is a mathematician,” was concluded by Newman [66] and questioned by Livio [67]. Elsewhere, one may find the question: “Is God a geometer?” [68].

Apparently, according to the present text analysis of Genesis, God (≡ Elohim) is also the (chronologically) first small world network—for monotheistic religions.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This work was partially supported by the Romanian National Authority for Scientific Research and Innovation, under UEFISCDI PN-III-P4-ID-PCCF-2016-0084 research grant.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Thanks to Prof. Emmanuel E. Haven and Prof. Claudiu Herteliu, for numerous and encouraging comments. Thanks also to Prof. Roy Cerqueti and Prof. Krzysztof Kulakowski for comments on a previous version. Moreover, special thanks go to Rabbi Mark L. Solomon for his very kind highlighting comments.

Footnotes

¹Other small networks, recently studied, are the Intelligent design–Darwin evolution controversy, or financial and geopolitical networks.

²This article is not intended to justify infirm studies of the Bible through Kabbalah methods [57, 58]. However, it can be pointed out that the interaction of Kabbalah with modern physics has generated its own literature, up to including renaming the elementary particles with kabbalistic (Hebrew) names or developing kabbalistic approaches to debates on evolution.

³For example, instead of a “tree” with three “columns,” the iggulim representation depicts the sefiroth as a succession of concentric circles [34].

⁴It is thought that the earth’s average surface temperature = 288 K, but that might neither be relevant, nor suggests further investigation.

References

1. Milgram S. The Small World Problem. Psychol Today (1967) 2(1):60–7. doi:10.1037/e400002009-005

CrossRef Full Text | Google Scholar

2.Milgram Could also have Written: “Oh my god, What a Small World”. He did not. Could he? But we all can understand that “Good Lord, “≡”My god!.

3. Stauffer D. Introduction to Statistical Physics outside Physics. Physica A: Stat Mech its Appl (2004) 336:1–5. doi:10.1016/j.physa.2004.01.004

CrossRef Full Text | Google Scholar

4. Pastor-Satorras R, Vespignani A. Evolution and Structure of the Internet: A Statistical Physics Approach. Cambridge, UK: Cambridge University Press (2007).

Google Scholar

5. Lambiotte R, Ausloos M. Coexistence of Opposite Opinions in a Network with Communities. J Stat Mech (2007) 2007(08):P08026. doi:10.1088/1742-5468/2007/08/p08026

CrossRef Full Text | Google Scholar

6. Chakrabarti B, Chakraborti A, Chatterjee A. Econophysics and Sociophysics: Trends and Perspectives. Hoboken, NJ, USA: John Wiley & Sons (2006).

Google Scholar

7. Costa LdF, Oliveira ON, Travieso G, Rodrigues FA, Villas Boas PR, Antiqueira L, et al. Analyzing and Modeling Real-World Phenomena with Complex Networks: a Survey of Applications. Adv Phys (2011) 60(3):329–412. doi:10.1080/00018732.2011.572452

CrossRef Full Text | Google Scholar

8. Killworth PD, Johnsen EC, Bernard HR, Shelley GA, McCarty C. Estimating the Size of Personal Networks. Social Networks (1990) 12(4):289–312. doi:10.1016/0378-8733(90)90012-x

CrossRef Full Text | Google Scholar

9. Shannon CE. A Mathematical Theory of Communication. Bell Syst Tech J (1948) 27(3):379–423. doi:10.1002/j.1538-7305.1948.tb01338.x

CrossRef Full Text | Google Scholar

10. Benedetto D, Caglioti E, Loreto V. Language Trees and Zipping. Phys Rev Lett (2002) 88(4):048702. doi:10.1103/PhysRevLett.88.048702

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Khmelev DV, Teahan WJ. Comment on “Language Trees and Zipping”. Phys Rev Lett (2003) 90(8):089803–4. doi:10.1103/PhysRevLett.90.089803

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Masucci AP, Rodgers GJ. Network Properties of Written Human Language. Phys Rev E Stat Nonlin Soft Matter Phys (2006) 74(2):026102. doi:10.1103/PhysRevE.74.026102

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Liu H, Xu C. Can Syntactic Networks Indicate Morphological Complexity of a Language? Epl (2011) 93:28005. doi:10.1209/0295-5075/93/28005

CrossRef Full Text | Google Scholar

14. Smith R. Distinct Word Length Frequencies: Distributions and Symbol Entropies. Glottometrics (2012) 23:7–22.

Google Scholar

15. Holovatch Y, Palchykov V. Complex Networks of Words in Fables. In: Kenna R, MacCarron M, and MacCarron P, (editors). Maths Meets Myths: Quantitative Approaches to Ancient Narratives. Understanding Complex Systems. Cham: Springer (2017). p. 159–75. doi:10.1007/978-3-319-39445-9_9

CrossRef Full Text | Google Scholar

16. Buk S, Krynytskyi Y, Rovenchak A. Properties of Autosemantic Word Networks in Ukrainian Texts. Advs Complex Syst (2019) 22(06):1950016. doi:10.1142/s0219525919500164

CrossRef Full Text | Google Scholar

17. Rovenchak A, Buk S. Part-of-Speech Sequences in Literary Text: Evidence from Ukrainian. J Quantitative Linguistics (2018) 25(1):1–21. doi:10.1080/09296174.2017.1324601

CrossRef Full Text | Google Scholar

18. Markovič R, Gosak M, Perc M, Marhl M, Grubelnik V. Applying Network Theory to Fables: Complexity in Slovene Belles-Lettres for Different Age Groups. J Compl Netw (2019) 7(1):114–27.

Google Scholar

19. Perc M. Beauty in Artistic Expressions Through the Eyes of Networks and Physics. J R Soc Interf (2020) 17(164):20190686. doi:10.1098/rsif.2019.0686

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Costa LdF, Sporns O, Antiqueira L, das Graças Volpe Nunes M, Oliveira ON. Correlations Between Structure and Random Walk Dynamics in Directed Complex Networks. Appl Phys Lett (2007) 91(5):054107. doi:10.1063/1.2766683

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Antiqueira L, Nunes MGV, Oliveira Jr. ON, Costa LdF. Strong Correlations between Text Quality and Complex Networks Features. Physica A: Stat Mech its Appl (2007) 373:811–20. doi:10.1016/j.physa.2006.06.002

CrossRef Full Text | Google Scholar

22. Sheng L, Li C. English and Chinese Languages as Weighted Complex Networks. Physica A: Stat Mech its Appl (2009) 388(12):2561–70. doi:10.1016/j.physa.2009.02.043

CrossRef Full Text | Google Scholar

23. Mehri A, Darooneh AH. Keyword Extraction by Nonextensivity Measure. Phys Rev E Stat Nonlin Soft Matter Phys (2011) 83(5):056106. doi:10.1103/PhysRevE.83.056106

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Ausloos M. Generalized Hurst Exponent and Multifractal Function of Original and Translated Texts Mapped into Frequency and Length Time Series. Phys Rev E Stat Nonlin Soft Matter Phys (2012) 86(3):031108. doi:10.1103/PhysRevE.86.031108

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Ausloos M. Measuring Complexity with Multifractals in Texts. Translation Effects. Chaos, Solitons & Fractals (2012) 45(11):1349–57. doi:10.1016/j.chaos.2012.06.016

CrossRef Full Text | Google Scholar

26. Amancio DR. Probing the Topological Properties of Complex Networks Modeling Short Written Texts. PLoS One (2015) 10(2):e0118394. doi:10.1371/journal.pone.0118394

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Kalimeri M, Constantoudis V, Papadimitriou C, Karamanos K, Diakonos FK, Papageorgiou H. Word-Length Entropies and Correlations of Natural Language Written Texts. J Quantitative Linguistics (2015) 22(2):101–18. doi:10.1080/09296174.2014.1001636

CrossRef Full Text | Google Scholar

28. Stanisz T, Kwapień J, Drożdż S. Linguistic Data Mining with Complex Networks: A Stylometric-Oriented Approach. Inf Sci (2019) 482:301–20. doi:10.1016/j.ins.2019.01.040

CrossRef Full Text | Google Scholar

29. Lambiotte R, Panzarasa P. Communities, Knowledge Creation, and Information Diffusion. J Informetrics (2009) 3(3):180–90. doi:10.1016/j.joi.2009.03.007

CrossRef Full Text | Google Scholar

30. Watts DJ, Strogatz SH. Collective Dynamics of ‘Small-World' Networks. Nature (1998) 393(6684):440–2. doi:10.1038/30918

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Watts DJ. Small Worlds: The Dynamics of Networks between Order and Randomness. Princeton: Princeton University Press (2000).

Google Scholar

32. Newman ME. Models of the Small World. J Stat Phys (2000) 101(3):819–41. doi:10.1023/a:1026485807148

CrossRef Full Text | Google Scholar

33.Holy Bible. New International Version®, NIV® Copyright, 1978 (1973). p. 1984. 2011 by Biblica, Inc.® Used by Permission. All Rights Reserved Worldwide.

Google Scholar

34.Sefirot (2021). Available at: https://en.wikipedia.org/wiki/Sefirot (Accessed Dec. 30, 2020).

35. Zachary WW. An Information Flow Model for Conflict and Fission in Small Groups. J Anthropological Res (1977) 33(4):452–73. doi:10.1086/jar.33.4.3629752

CrossRef Full Text | Google Scholar

36. Bernard HR, Killworth PD, Evans MJ, McCarty C, Shelley GA. Studying Social Relations Cross-Culturally. Ethnology (1988) 27(2):155–79. doi:10.2307/3773626

CrossRef Full Text | Google Scholar

37. Rovenchak A, Buk S. Defining Thermodynamic Parameters for Texts from Word Rank-Frequency Distributions. J Phys Stud (2011) 15:1005. doi:10.30970/jps.15.1005

CrossRef Full Text | Google Scholar

38. Idel M. The Early Kabbalah. Mahwah, NJ, USA: Paulist Press (1986).

Google Scholar

39. Idel M. Absorbing Perfectionss: Kabbalah and Interpretation. New Haven, CT, USA: Yale University Press (2008).

Google Scholar

40.Kabbalah A Very Short Introduction. Oxford: Oxford University Press (2007).

Google Scholar

41. Watanabe T, Masuda N. Enhancing the Spectral Gap of Networks by Node Removal. Phys Rev E Stat Nonlin Soft Matter Phys (2010) 82(4):046102. doi:10.1103/PhysRevE.82.046102

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Amaral LAN, Scala A, Barthélémy M, Stanley HE. Classes of Small-World Networks. Proc Natl Acad Sci U.S.A (2000) 97(21):11149–52. doi:10.1073/pnas.200327197

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Newman MEJ. The Structure of Scientific Collaboration Networks. Proc Natl Acad Sci U.S.A (2001) 98(2):404–9. doi:10.1073/pnas.98.2.404

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Huss B. The New Age of Kabbalah. J Mod Jewish Stud (2007) 6(2):107–25. doi:10.1080/14725880701423014

CrossRef Full Text | Google Scholar

45. Garb J. The Modernization of Kabbalah: A Case Study. Mod Judaism (2010) 30(1):1–22. doi:10.1093/mj/kjp022

CrossRef Full Text | Google Scholar

46. Ausloos M, Petroni F. Statistical Dynamics of Religions and Adherents. Europhys Lett (2007) 77:38002. doi:10.1209/0295-5075/77/38002

CrossRef Full Text | Google Scholar

47. Ausloos M, Petroni F. Statistical Dynamics of Religion Evolutions. Physica A: Stat Mech its Appl (2009) 388:4438–44. doi:10.1016/j.physa.2009.06.051

CrossRef Full Text | Google Scholar

48. Ausloos M, Herteliu C. Statistical Analysis of the Membership Management Indicators of the Church of England UK Dioceses during the Recent (XXth Century) “Decade of Evangelism”. Stats (2021) 4(4):1069–79. doi:10.3390/stats4040061

CrossRef Full Text | Google Scholar

49. Hayward J. Mathematical Modeling of Church Growth. J Math Sociol (1999) 23:255–92. doi:10.1080/0022250x.1999.9990223

CrossRef Full Text | Google Scholar

50. Hayward J. A General Model of Church Growth and Decline. J Math Sociol (2005) 29:177–207. doi:10.1080/00222500590889721

CrossRef Full Text | Google Scholar

51. Picoli S, Mendes RS. Universal Features in the Growth Dynamics of Religious Activities. Phys Rev E Stat Nonlin Soft Matter Phys (2008) 77:036105. doi:10.1103/PhysRevE.77.036105

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Rotundo G, Ausloos M. Organization of Networks with Tagged Nodes and Biased Links: A Priori Distinct Communities. Physica A: Stat Mech its Appl (2010) 389:5479–94. doi:10.1016/j.physa.2010.07.029

CrossRef Full Text | Google Scholar

53. Herteliu C, Ileanu BV, Ausloos M, Rotundo G. Effect of Religious Rules on Time of conception in Romania from 1905 to 2001. Hum Reprod (2015) 30(9):2202–14. doi:10.1093/humrep/dev129

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Hellsten I, Lambiotte R, Scharnhorst A, Ausloos M. Self-Citations, Co-Authorships and Keywords: A New Approach to Scientists' Field Mobility? Scientometrics (2007) 72(3):469–86. doi:10.1007/s11192-007-1680-5

CrossRef Full Text | Google Scholar

55. Gligor M, Ausloos M. Clusters in Weighted Macroeconomic Networks: the EU Case. Introducing the Overlapping index of GDP/Capita Fluctuation Correlations. Eur Phys J B (2008) 63(4):533–9. doi:10.1140/epjb/e2008-00176-y

CrossRef Full Text | Google Scholar

56. Newman MEJ. Assortative Mixing in Networks. Phys Rev Lett (2002) 89(20):208701. doi:10.1103/physrevlett.89.208701

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Ginzberg L, Kohler K. Cabala Jewish Encyclopedia. Philadelphia, PA: Kopelman Foundation (1906).

Google Scholar

58. Dennis GW. “What is Kabbalah?”. New York City: ReformJudaism.org. Union for Reform Judaism (2014).

Google Scholar

59.Such a Number of Links can be Associated with the 22 Letters of the Hebrew Alphabet.

Google Scholar

60. Suchecki K, Hołyst JA. Hierarchy Depth in Directed Networks. Entropy (2022) 24(2):252. doi:10.3390/e24020252

PubMed Abstract | CrossRef Full Text | Google Scholar

61.The Clustering Coefficient of a Random Graph is Equal to < k > / N, i.e., ≈ 0.44 in the Present Text Case.

Google Scholar

62. Redelico FO, Proto AN, Ausloos M. Hierarchical Structures in the Gross Domestic Product Per Capita Fluctuation in Latin American Countries. Physica A: Stat Mech its Appl (2009) 388(17):3527–35. doi:10.1016/j.physa.2009.05.033

CrossRef Full Text | Google Scholar

63. Bernard HR, Johnsen EC, Killworth PD, McCarty C, Shelley GA, Robinson S. Comparing Four Different Methods for Measuring Personal Social Networks. Soc Networks (1990) 12(3):179–215. doi:10.1016/0378-8733(90)90005-t

CrossRef Full Text | Google Scholar

64. Newman ME, Park J. Why Social Networks Are Different from Other Types of Networks. Phys Rev E Stat Nonlin Soft Matter Phys (2003) 68(3):036122. doi:10.1103/PhysRevE.68.036122

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Choi Y-M, Kim H-J. A Directed Network of Greek and Roman Mythology. Physica A: Stat Mech its Appl (2007) 382(2):665–71. doi:10.1016/j.physa.2007.04.035

CrossRef Full Text | Google Scholar

66. Newman K. God is a Mathematician (2009). Available at: http//www.biblebelievers.org.au/panin2.htm (Accessed Aug. 27, 2015).

Google Scholar

67. Livio M. Is God a Mathematician? New York, NY, USA: Simon & Schuster (2010).

Google Scholar

68. Stewart I, Golubitsky M. Fearful Symmetry: Is God a Geometer? Chelmsford, MA, USA: Courier Corporation (2010).

Google Scholar

69. Skinner S. The Complete Magician’s Tables. Singapore: Golden Hoard Press (2006).

Google Scholar